Metoda Janssena (1895) do obliczania
Metoda Janssena (1895) do obliczania
naporu w silosach
naporu w silosach
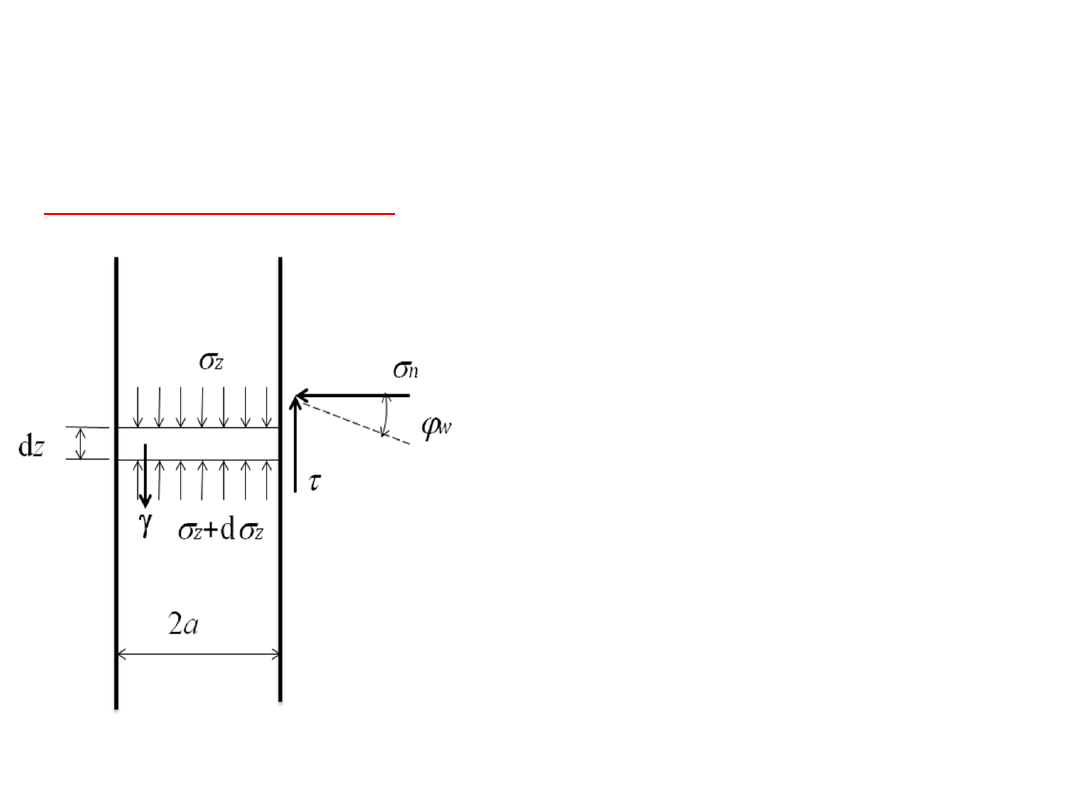
Kanał równoległy
Rysunek pokazuje naprężenia działające na
warstwę materiału sypkiego o grubości dz.
x
–
średnie
pionowe
naprężenie normalne,
n
- poziome naprężenie
normalne na ścianie,
- naprężenie styczne na
ścianie,
w
– kąt tarcia na ścianie,
- ciężar objętościowy,
dz – wysokość,
2a – szerokość kanału
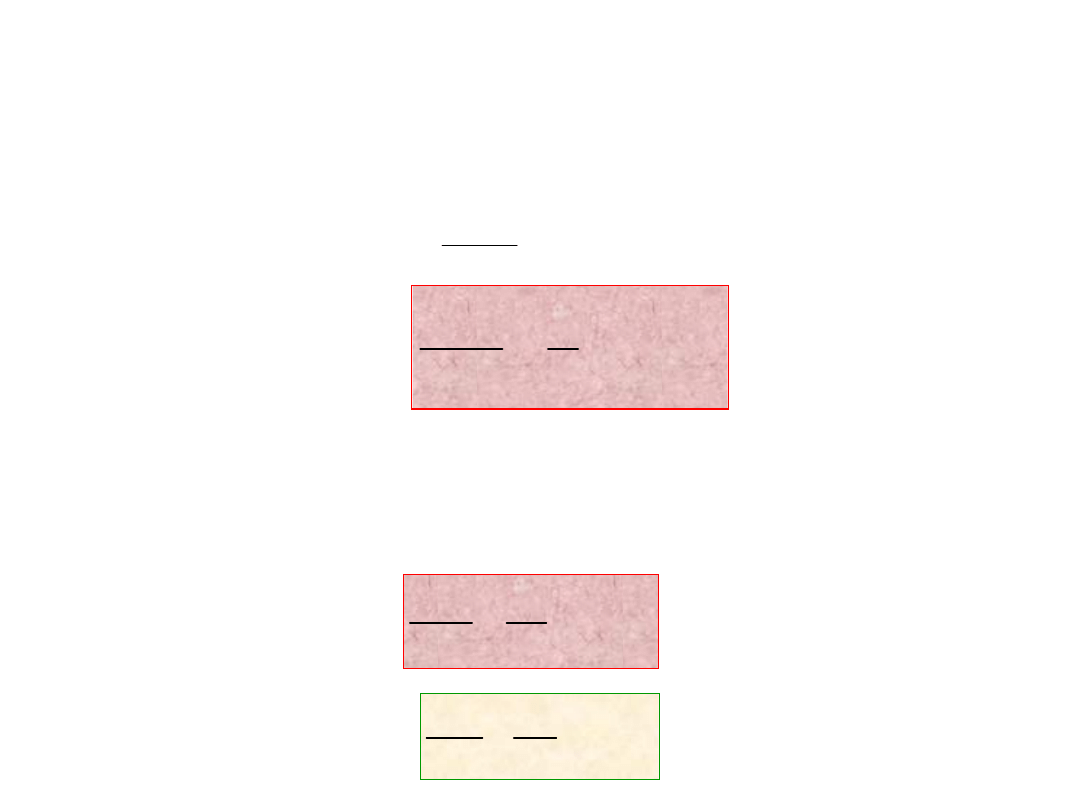
2 1.0 (
) 2 1.0 2
1.0
2
1.0 0
z
z
z
a
d
a
dz
a dz
s
s
s
t
g
� � -
+
� � -
� � + � � � =
0
z
dz
d
dz
a
t
s
g
�
-
-
+ � =
0
z
d
dz
a
s
t
g
+ - =
Warunek równowagi dla kanału szczelinowego
(bez sił bezwładności) jest następujący (depth
b>> width a)
Warunek równowagi dla kanału walcowego (bez sił bezwładności)
2
2
2
(
)
2
0
z
z
z
a
d
a
a dz
a dz
s
p
s
s
p
t p
g p
� � -
+
� � - � � � + � � � =
2
0
z
d
dz
a
s
t
g
+
- =
0
z
d
m
dz
a
s
t
g
+
- =
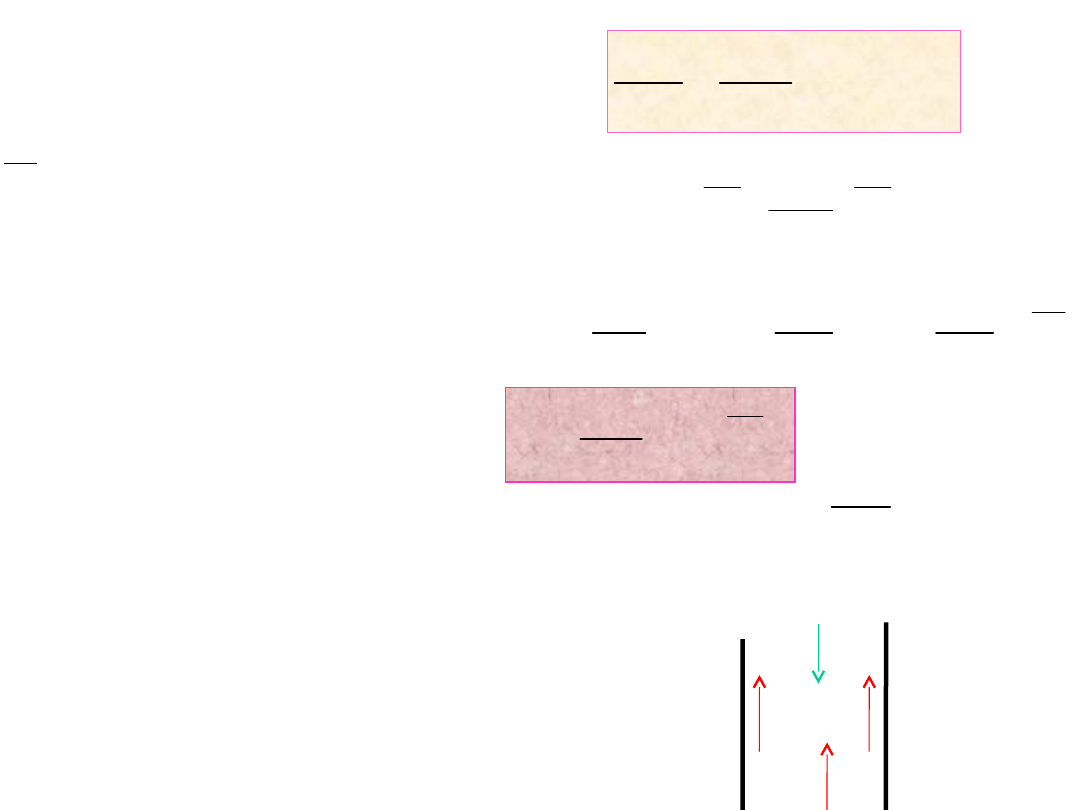
Rów. przybiera następującą postać
0
z
z
d
mM
dz
a
s
s
g
+
- =
/
tan
n
w
t s
j
=
n
z
K
s
s
=
tan
w
M K
j
= �
(
)
mM
mM
z
z
a
a
z
a
e
e
C
mM
g
s
-
=
+
0,
z =
0
z
z
s
s
=
0
z
a
C
mM
g
s
=
-
dla
0
(
)
mM
z
a
z
z
a
a
e
mM
mM
g
g
s
s
-
=
+
-
0,
z=
0
z
s =
(1
)
mM
z
a
z
a
e
mM
g
s
-
=
-
Dla nieskończenie wysokiego kanału (z=)
(
)
z x
a
mM
g
s
=�
=
Dla kanału idealnie gładkiego (
w
=0
o
)
z
z
s
g
=
n
z
K
s
s
= �
z
M
t
s
= �
dla
G T R
= +
G
T
R
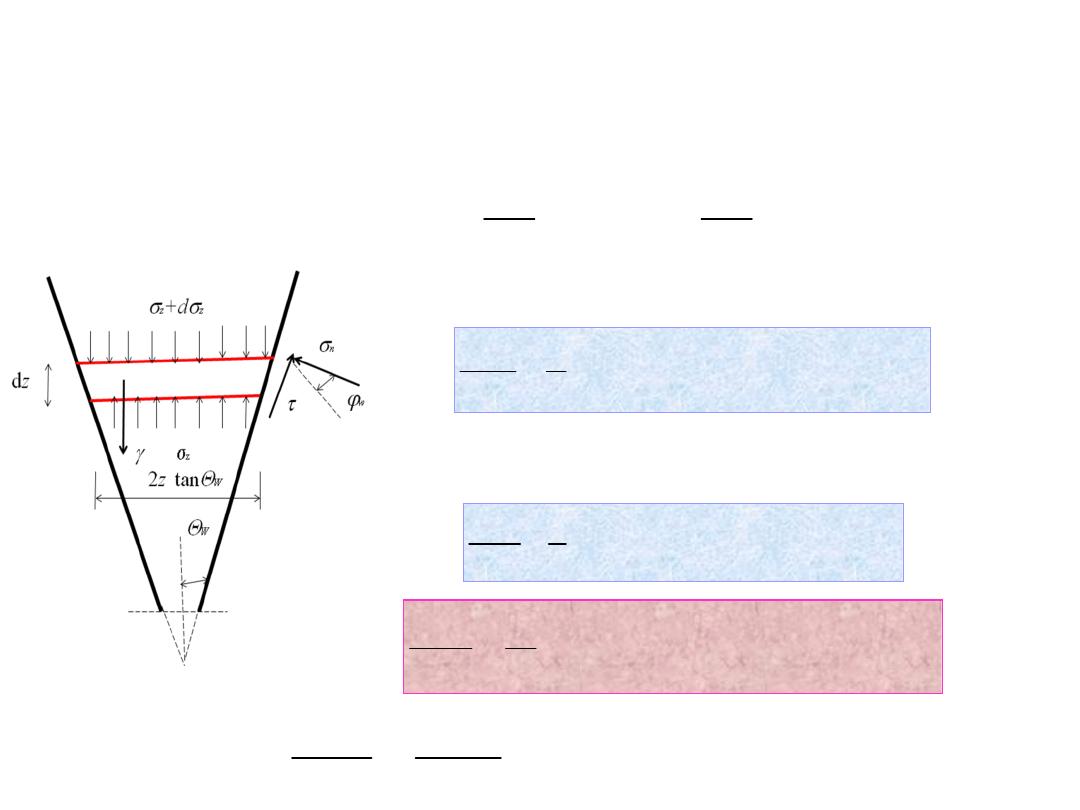
Kanał zbieżny
2
2
cos
cos
2
(
) (
)
(
)
(
cos
sin
)2
(
)
0
w
w
z
z
w
z
w
w
dz
dz
w
b
w
w
w
d
z tg
z tg
dz tg
z tg
dz
z tg
q
q
s
s p
q
s p
q
q
t
q
s
q
p
q
g
p
q
-
+
�
+
�
-
�
+
�
+ �
� �
-
� � � �
=
2
(
)
0
z
z
n
w
d
ctg
dz
z
s
s
s
t
q
g
+
-
- �
+ =
Dla przypadku warstwy płaskiej z warunku
równowagi sił (pomija się wyrazy wyższego rzędu)
otrzymujemy
Dla kanału stożkowego
1
(
)
0
z
z
n
w
d
ctg
dz
z
s
s
s
t
q
g
+
-
- �
+ =
(
)
0
z
z
n
w
d
m
ctg
dz
z
s
s
s
t
q
g
+
-
- �
+ =
[(1
(
)]
0
z
z
w
w
d
m
M ctg
ctg
dz
z
s
s
j
q
g
+
-
+
+ =
Dla kanału klinowego
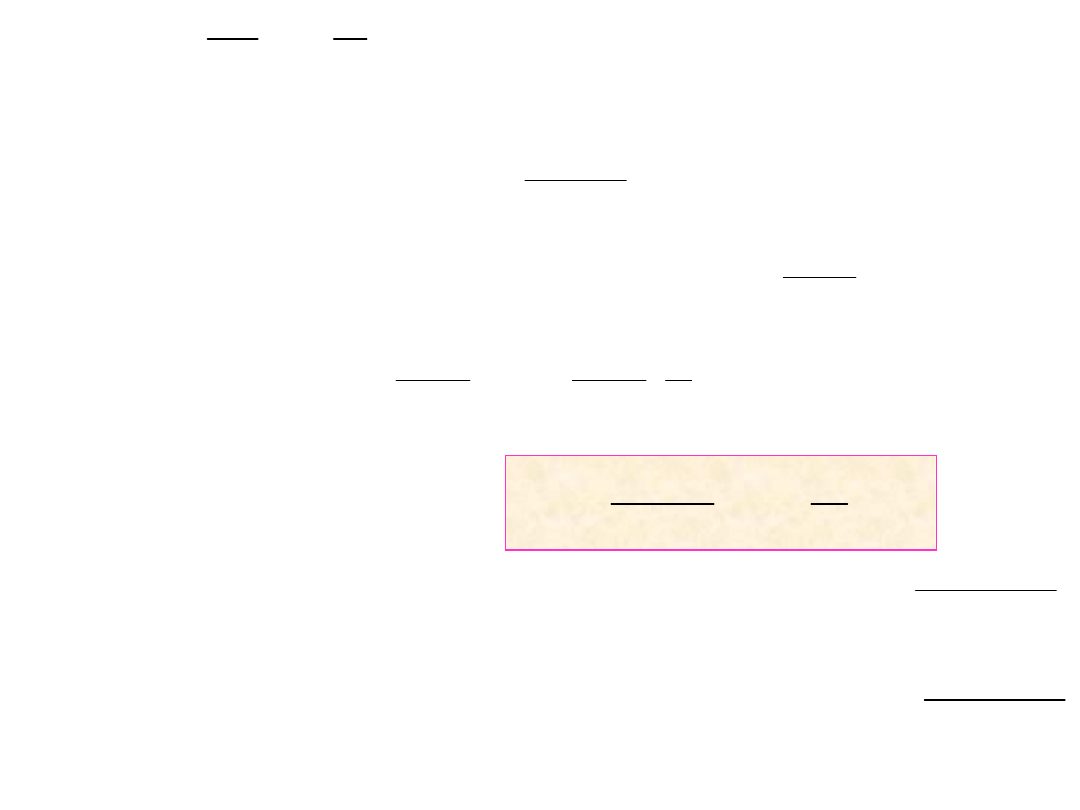
0
z
z
d
mN
dz
z
s
s
g
+
+ =
[1
(
)]
w
w
N
M ctg
ctg
j
q
= -
+
1
mN �-
A) Jeśli
1
mN
z
z Cz
mN
g
s
-
=-
+
+
z H
=
dla
0
z
z
s
s
=
0
(
)
1
mN
z
H
C H
mN
g
s
=
+
+
0
(
)( )
1
1
mN
z
z
H
H
z
mN
mN
z
g
g
s
s
=-
+
+
+
+
z H
=
0
z
s =
dla
1
[ 1 ( )
]
1
mN
z
H
mN
z
g
s
+
=-
- +
+
W wierzchołku kanału (z=0)
z
s =�
1
w
w
M
ctg
ctg
j
q
<
+
gdy mN>0
0
z
s =
1
w
w
M
ctg
ctg
j
q
>
+
gdy mN<0
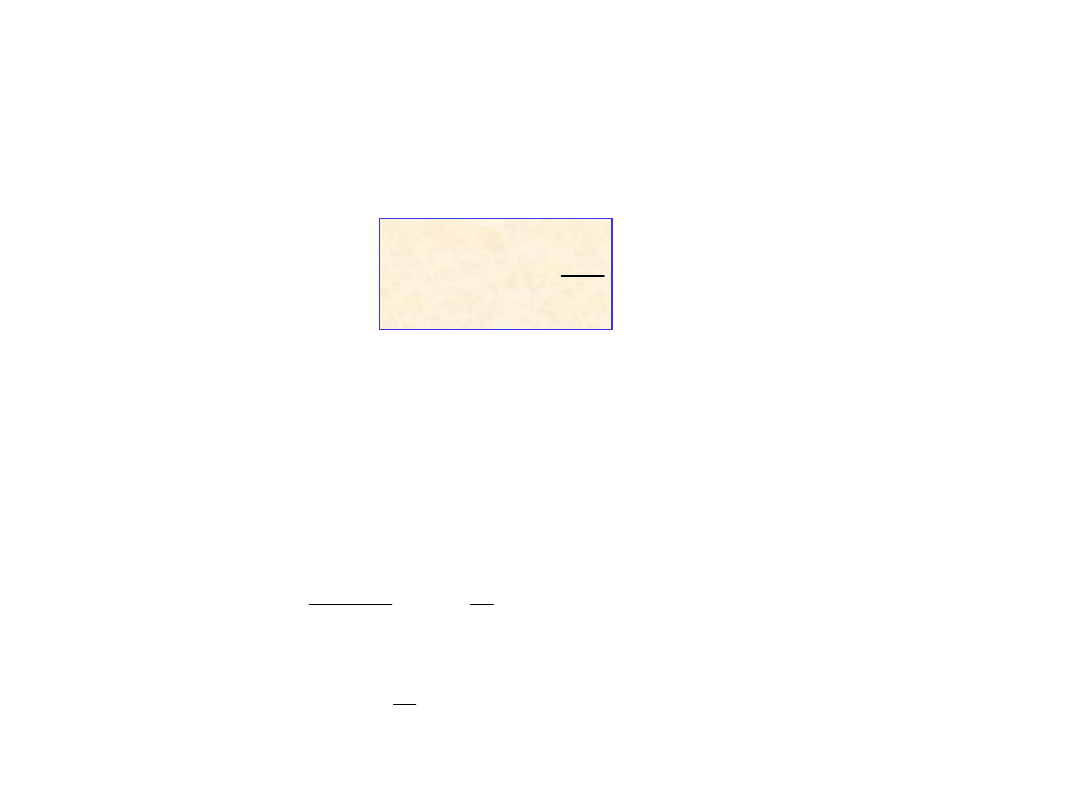
B) Jeśli mN=-1 rozwiązaniem jest
(
ln )
z
C
z z
s
g
=-
-
ln
z
H
z
z
s
g
=
Dla elementu o kształcie warstwy walcowej lub kulistej
Dla elementu o kształcie warstwy walcowej lub kulistej
Rozwiązanie jest następujące dla brzegu nieobciążonego (r=r
z
)
1
[ 1 ( )
]
1
mN
z
z
r
K
mN
r
g
s
+
=
- +
+
ln
z
z
r
Kr
r
s
g
=
1
mN �-
1
mN =-
Określenie stałej M (kanał równoległy)
Stałą M można określić na podstawie 3 różnych założeń:
- uplastycznienie materiału przy ścianie silosu,
- uplastycznienie materiału w środku silosu,
- uplastycznienie materiału w środku i przy ścianie.
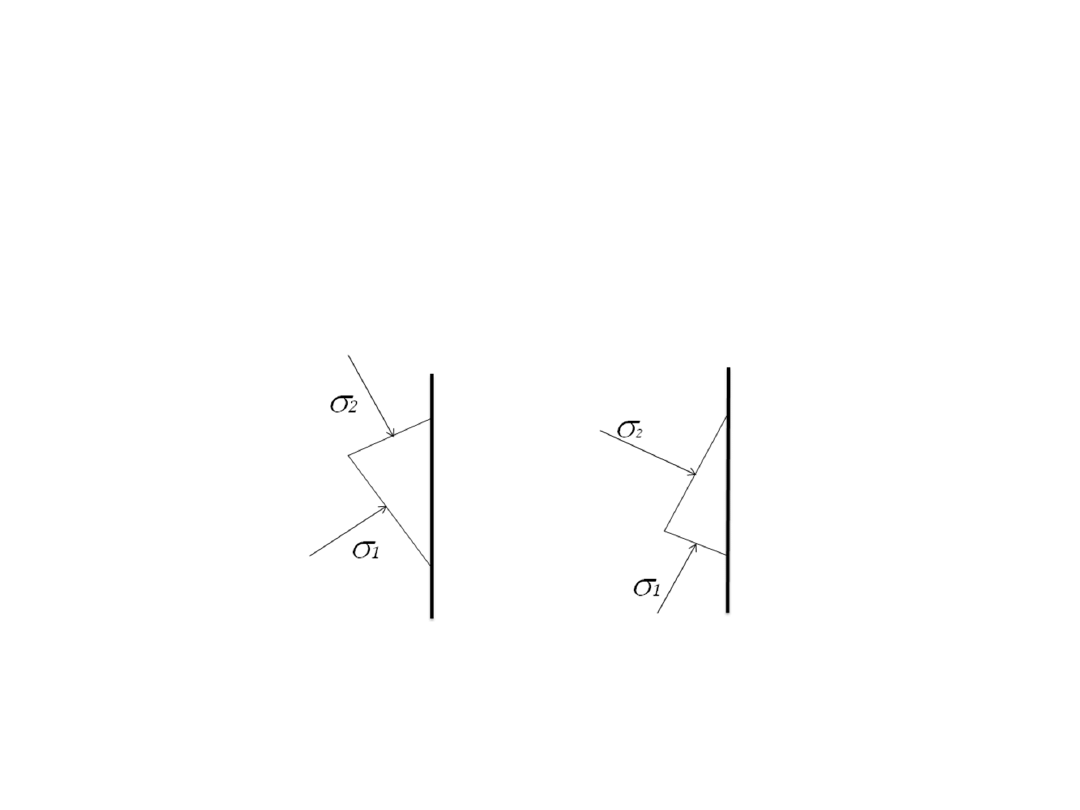
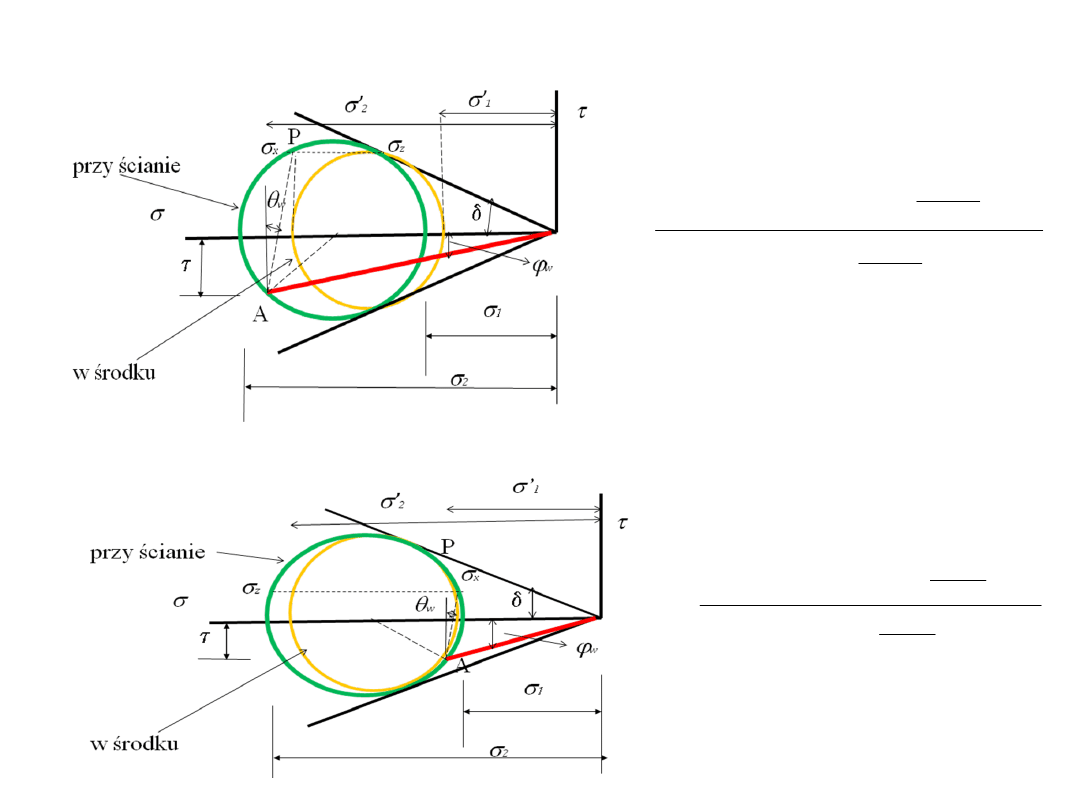
Naprężenia główne w stanie czynnym (a) i
biernym (b)
a
b
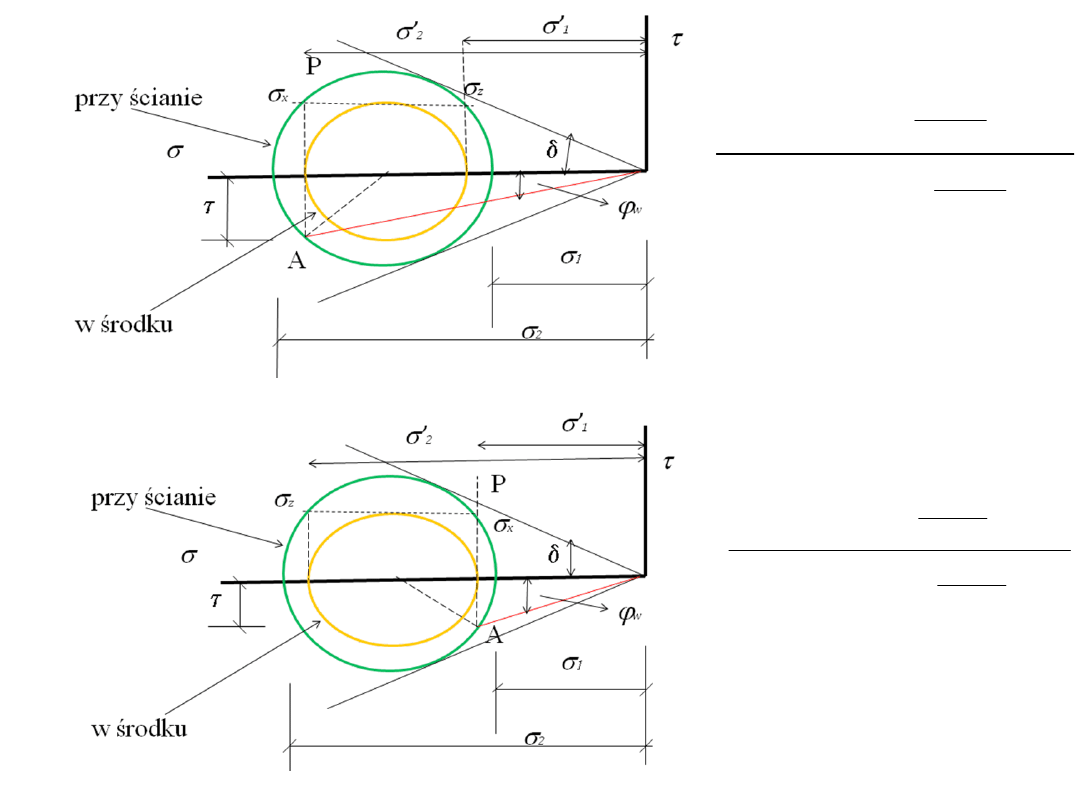
napełnianie
opróżnianie
opróżnianie
sin
sin sin[arcsin
]
sin
sin
1 sin cos[arcsin
]
sin
w
w
w
w
M
j
d
j
d
j
d
j
d
+
=
-
+
sin
sin sin[arcsin
]
sin
sin
1 sin cos[arcsin
]
sin
w
w
w
w
M
j
d
j
d
j
d
j
d
-
=
+
-

Określenie stałej M (kanał zbieżny)
Stałą M można określić na podstawie 3 różnych założeń:
- uplastycznienie materiału przy ścianie silosu,
- uplastycznienie materiału w środku silosu,
- uplastycznienie materiału w środku i przy ścianie.
opróżnianie
napełnianie
2
sin
(1 sin )sin sin[arcsin
]
sin
sin
1 sin cos[arcsin
2 ]
sin
w
w
w
w
w
M
j
d
d
j
d
j
d
j
q
d
+
+
=
-
+ +
2
sin
(1 sin )sin sin[arcsin
]
sin
sin
1 sin
cos[arcsin
2 ]
sin
w
w
w
w
w
M
j
d
d
j
d
j
d
j
q
d
-
-
=
-
-
-
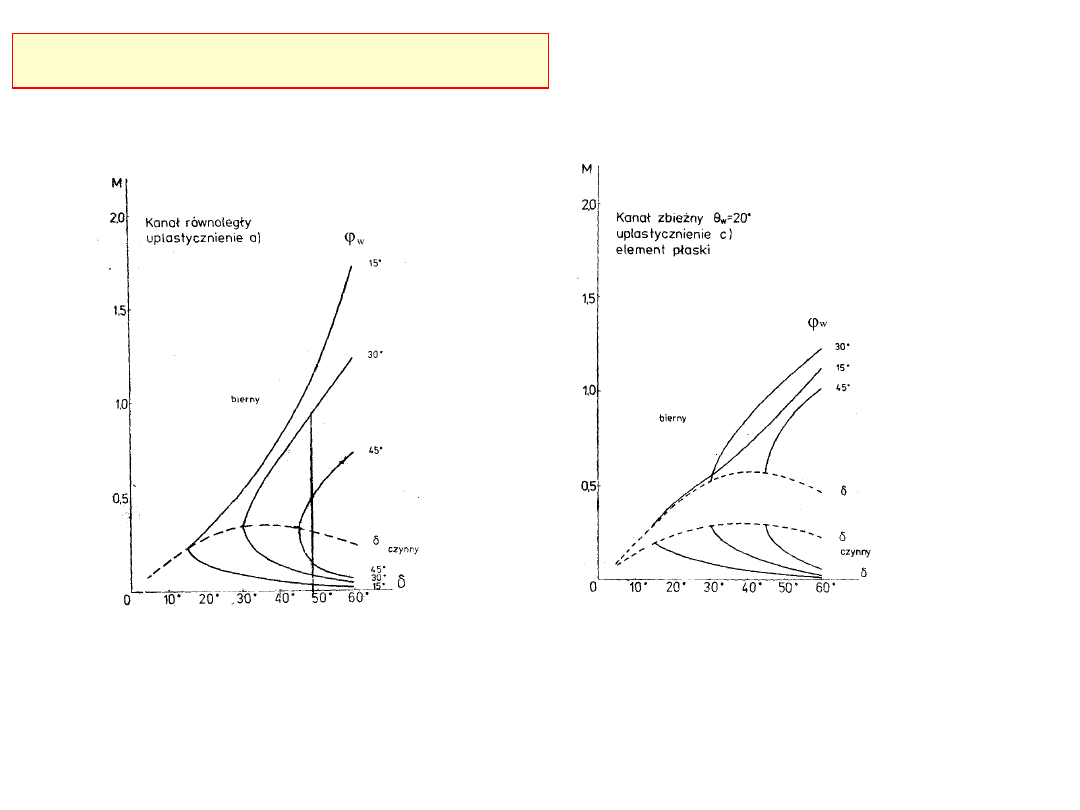
Porównanie parametru
Porównanie parametru
M
M
Zależność stałej
Zależność stałej
M
M
od efektywnego kąta tarcia
od efektywnego kąta tarcia
wewnętrznego
wewnętrznego
i kąta tarcia na ścianie (a) kanał równoległy, b)
i kąta tarcia na ścianie (a) kanał równoległy, b)
kanał zbieżny)
kanał zbieżny)
a
b
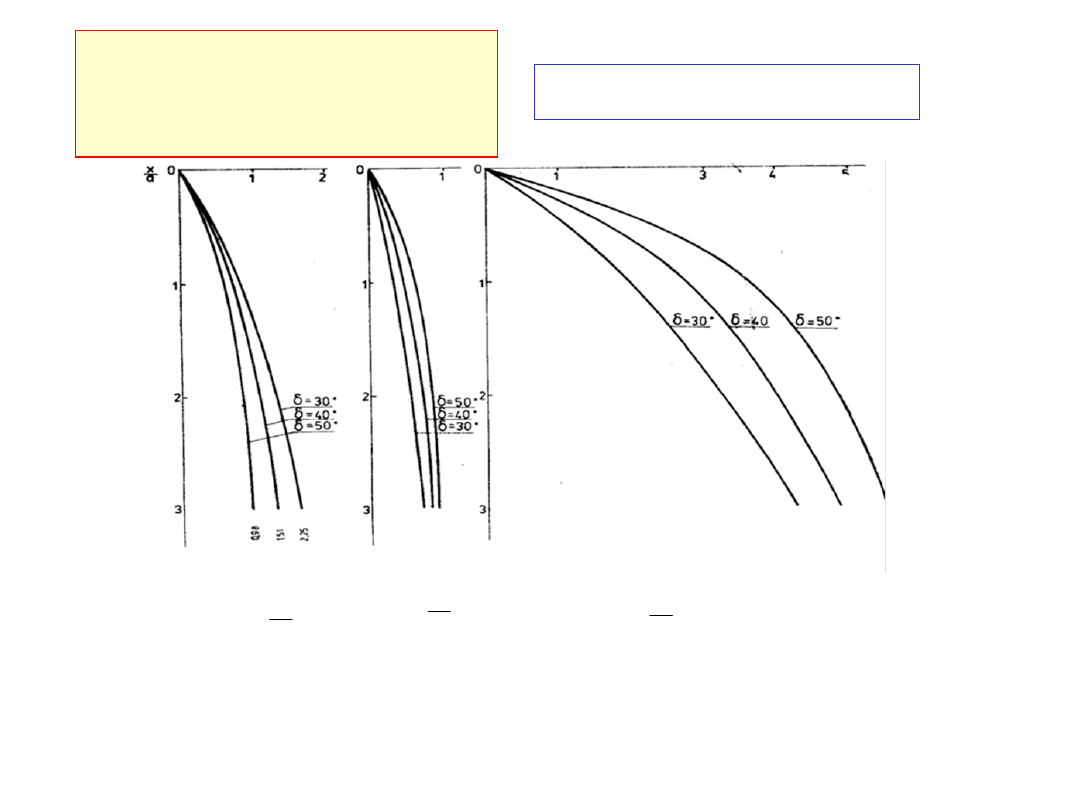
Analiza
Analiza
naprężeń
naprężeń
Rozkłady bezwymiarowych naprężeń wzdłuż ściany
nieobciążonego u góry kanału płaskiego (opróżnianie
uplastycznienie przy ścianie,
w
=10
o
)
z
z
a
s
s
g
-
=
a
t
t
g
-
=
n
n
a
s
s
g
-
=
Kanał równoległy
Kanał równoległy
Kanał zbieżny
Kanał zbieżny
napełnianie
napełnianie i opróżnianie
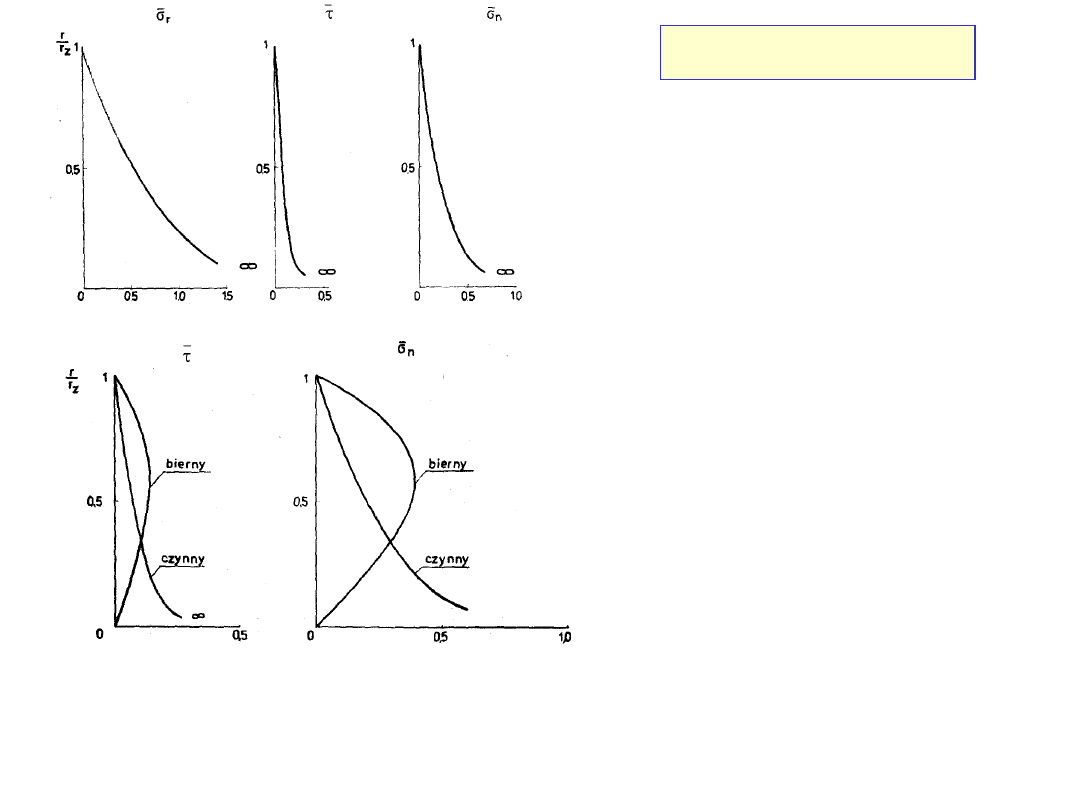
Rozkłady bezwymiarowych naprężeń wzdłuż ściany
nieobciążonego u góry kanału zbieżnego (stan czynny i
czynny, element walcowy, uplastycznienie przy ścianie i w
środku,
=30
o
,
w
=10
o
,
w
=20
o
)
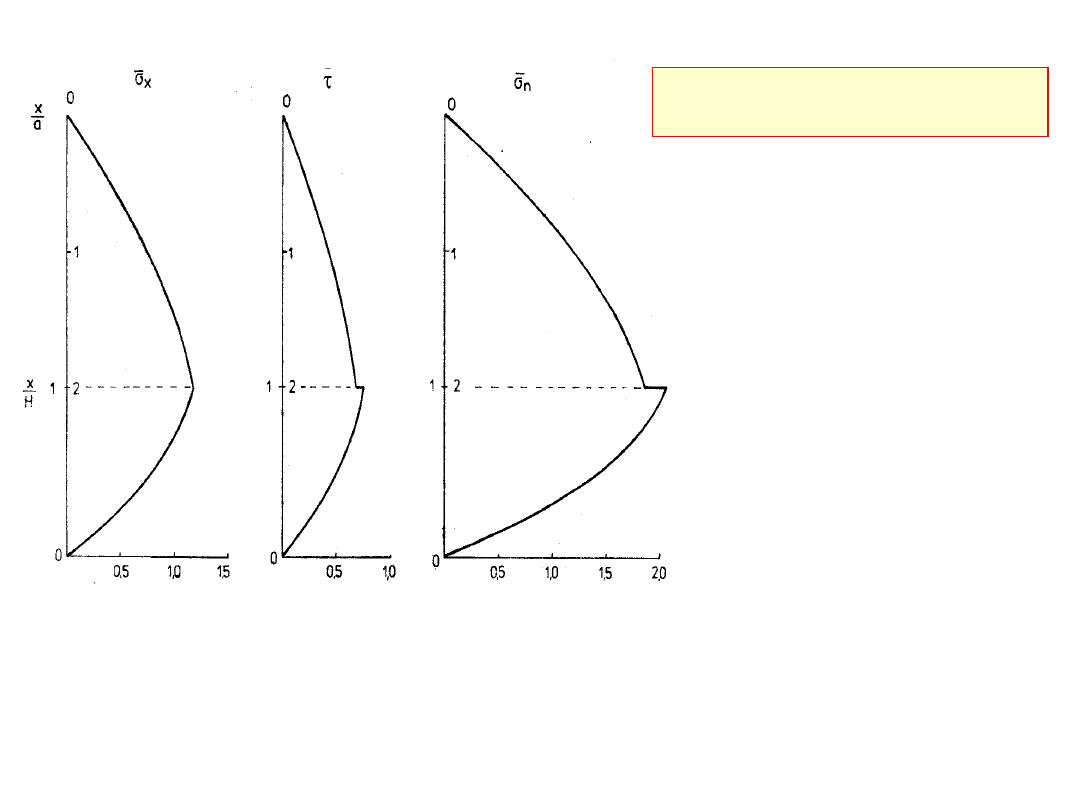
Rozkłady bezwymiarowych naprężeń wzdłuż
ściany
nieobciążonego
u
góry
kanału
złożonego
opróżnianie (
=30
o
,
w
=10
o
,
w
=20
o
)
Kanał złożony
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
Wyszukiwarka
Podobne podstrony:
Silosy section 3 6
Silosy section 12
Silosy section 12
Silosy section zadanie
Silosy section kolokwium
Silosy section 7
Silosy section 3 6
06 BS Module 1 Section 6
ISO128 50 areas of sections
2 Advanced X Sectional Results Using Paths to Post Process
opis zalesie fi 14 1, Praca, mkbud, Domaszowice hale silosy, dokumentacja, zalesie projekt wykonawcz
03 BS Module 1 Section 3
01 LISTENING SECTION, Listening Section
Posadzki section 2 1 studenci
więcej podobnych podstron