TECHNIKA CYFROWA I MIKROKOMPUTERY

WYKŁAD 8

17.04.2003

TECHNIKA CYFROWA I MIKROKOMPUTERY

PYTANIE 1

Jedną z cech n-bitowego kodu Gray'a jest to, że:

A sąsiednie cyfry tworzące kod różnią się na jednej pozycji
B sąsiednie cyfry tworzące liczbę w tym kodzie są przeciwne

względem siebie

C nie jest on kodem cyklicznym
D jest on kodem refleksyjnym

TECHNIKA CYFROWA I MIKROKOMPUTERY

PYTANIE 2

Wskaż zdania prawdziwe:

A zamiana sygnału cyfrowego na analogowy to kodowanie
B zamiana liczby dziesiętnej na binarną to kodowanie
C przypisywanie różnym informacjom pewnych symboli to

kodowanie

D minimalizacja w logice zbiorów to kodowanie

TECHNIKA CYFROWA I MIKROKOMPUTERY

PYTANIE 3

Liczba (333)

10

po zamianie na NKB ma postać:

A 100110010
B 010010011
C 101001101
D 011000011

TECHNIKA CYFROWA I MIKROKOMPUTERY

PYTANIE 4

Twierdzeniem w Algebrze Boole'a jest równość:

A a+0=0
B (a+b)’=a’*b’
C a+(a*b)=a
D (a*b)’=(a+b)’

TECHNIKA CYFROWA I MIKROKOMPUTERY

PYTANIE 5

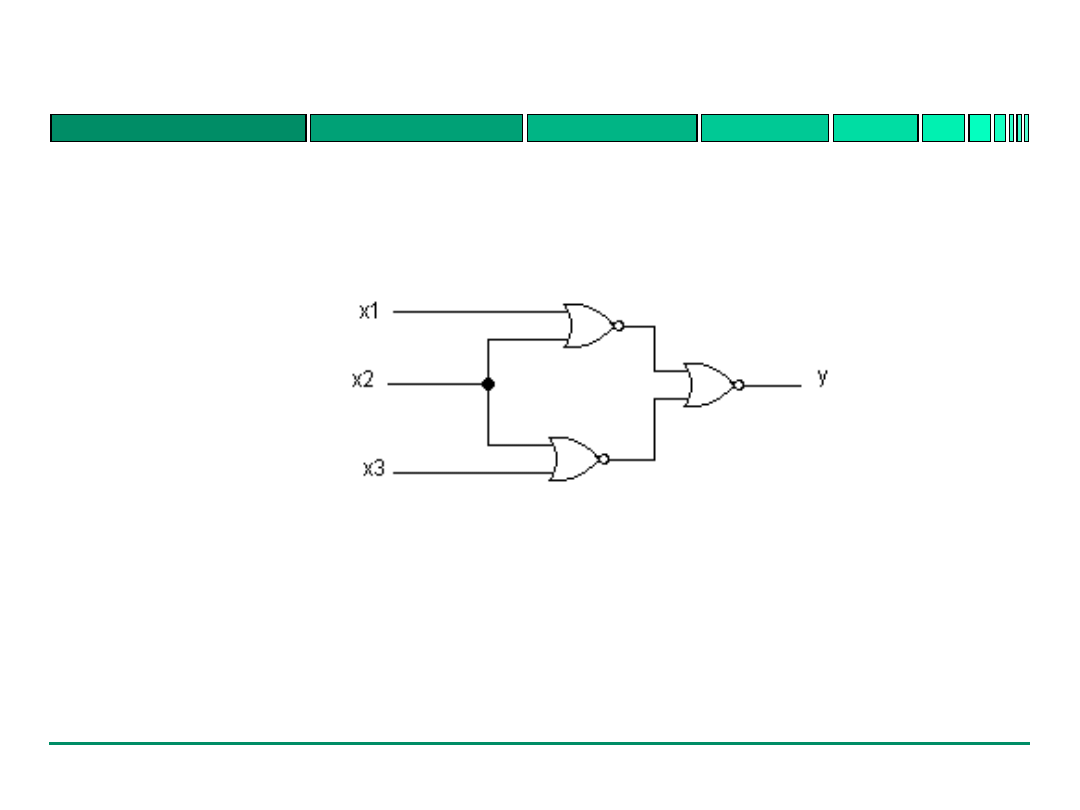
Poniższy układ realizuje funkcję boolowską:

A (x

1

+x

2

)(x

2

+x

3

)

B x

1

+x

2

(x

1

+x

3

)

C x

1

x

2

+x

3

x

2

D (x

1

+x

2

)x

3

TECHNIKA CYFROWA I MIKROKOMPUTERY

PYTANIE 6

Funkcja boolowska może być zadana za pomocą:

A wykresu czasowego
B opisu słownego
C tabeli prawdy
D skróconego zapisu dziesiętnego

TECHNIKA CYFROWA I MIKROKOMPUTERY

PYTANIE 7

System Funkcjonalnie Pełny reprezentuje na przykład:

A różnica symetryczna
B strzałka Sheffer'a
C negacja iloczynu
D suma modulo 2

TECHNIKA CYFROWA I MIKROKOMPUTERY

PYTANIE 8

Funkcja y=(0, 1, 2, 3, 8, 9, 10, 11)

x1,x2,x3,x4

po

minimalizacji metodą Quine’a McCluskey’a przyjmuje
postać:

A

y=x

1

x

2

’+x

4

B

y=x

2

+x

1

’x

4

C

y=x

1

+x

2

D

y=x

2

’

TECHNIKA CYFROWA I MIKROKOMPUTERY

PYTANIE 9

Równoważna postać zapisu (ab)c to:
A y=ab’
B y=a+b’
C y=(a+b)c
D y=(a+b)c’

TECHNIKA CYFROWA I MIKROKOMPUTERY

PYTANIE 10

Wskaż zdanie opisujące hazard dynamiczny:

A Ujawnia się on przy przejściu jednej zmiennej z 0 do 1 (lub

odwrotnie)

B Jest bardzo trudny do wykrycia i wyeliminowania
C Polega on na powstaniu na wyjściu układu np. sekwencji

1010 (choć powinno być 10)

D Odznacza się on dynamiczną zmianą stanów na wyjściu przy

podawaniu stałej kombinacji "zero-jedynkowej" na wejście
układu

TECHNIKA CYFROWA I MIKROKOMPUTERY

PYTANIE 11

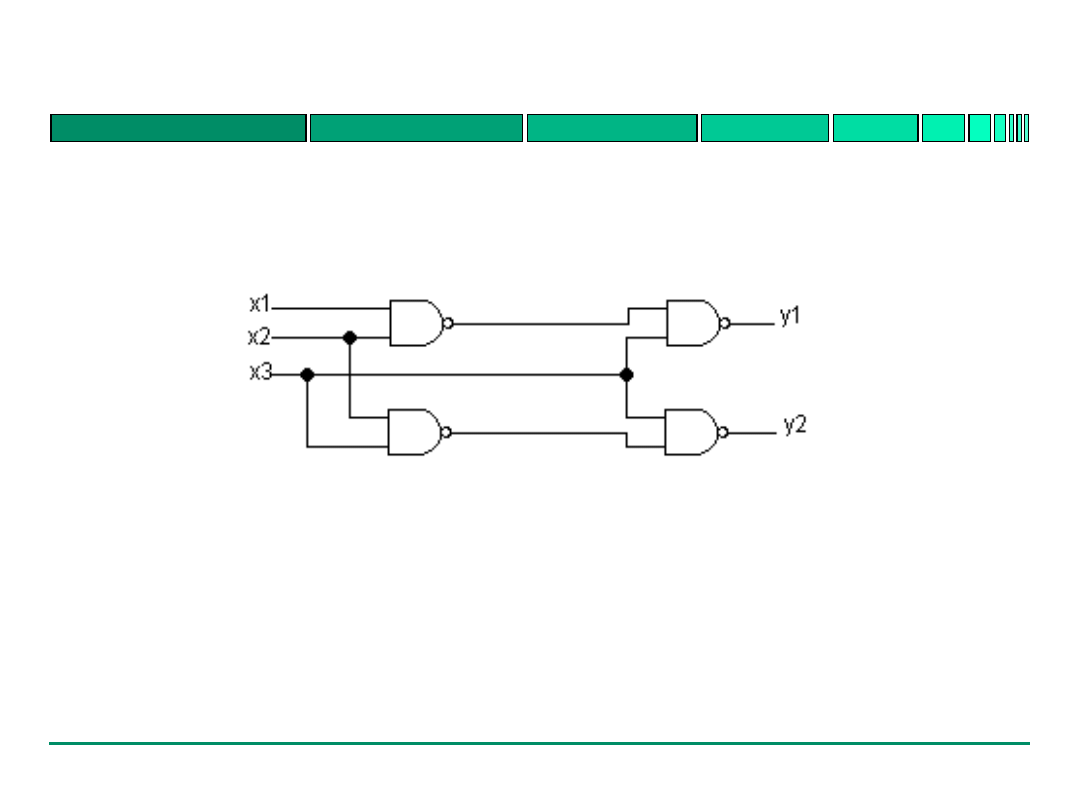
Gdy na wejście poniższego układu podamy kombinację
000 to na wyjściach y1 i y2 otrzymamy odpowiednio:

A

0 i 0

B

0 i 1

C

1 i 0

D

1 i 1

TECHNIKA CYFROWA I MIKROKOMPUTERY

PYTANIE 12

Technologia MOS jest bardziej opłacalna od technologii

TTL gdyż:

A nie wymaga dużego poboru mocy
B jest szybka w działaniu
C jest tańsza
D zapewnia dobrą gęstość upakowania

TECHNIKA CYFROWA I MIKROKOMPUTERY

PYTANIE 13

Z poniższych zapisów wskaż “prawo sklejania”:
A a(a+b)=a
B (a*b)’=a’+b’
C ab’+ab=a
D a+ab=a

TECHNIKA CYFROWA I MIKROKOMPUTERY

PYTANIE 14

Jeśli w dowolnym UK wymienimy wszystkie bramki NOR
(innych w układzie nie ma!) na bramki NAND nie
zmieniając struktury połączeń, to utworzony układ:
A realizuje funkcje identyczne jak układ początkowy (tj. z
bramkami

NOR)

B realizuje negację funkcji z układu początkowego
C realizuje różnicę symetryczną funkcji z układu
początkowego
D realizuje funkcję zupełnie inną niż podane wyżej

TECHNIKA CYFROWA I MIKROKOMPUTERY

PYTANIE 15

Wskaż zdania prawdziwe:
A Postać sumy iloczynów można otrzymać na podstawie tabeli

prawdy, wybierając te wiersze, dla których wartość funkcji wynosi
0 i przypisując '1' niezanegowanym zmiennym a '0' zanegowanym

B Postać sumy iloczynów można otrzymać na podstawie tabeli

prawdy, wybierając te wiersze, dla których wartość funkcji wynosi
1 i przypisując '0' niezanegowanym zmiennym a '1' zanegowanym

C Postać iloczynu sum można otrzymać na podstawie tabeli prawdy,

wybierając te wiersze, dla których wartość funkcji wynosi 0 i
przypisując '0' niezanegowanym zmiennym a '1' zanegowanym

D Postać iloczynu sum można otrzymać na podstawie tabeli prawdy,

wybierając te wiersze, dla których wartość funkcji wynosi 1 i
przypisując '0' niezanegowanym zmiennym a '1' zanegowanym

TECHNIKA CYFROWA I MIKROKOMPUTERY

ZADANIE 1
Znaleźć minimalną postać normalną funkcji:
y=f(x

1

, x

2

, x

3

, x

4

)=[1,3,5,10,11,12,13,14,15,(0,4)]

Narysować schemat realizacji otrzymanej funkcji minimalnej za
pomocą dowolnych bramek i za pomocą bramek NOR

ZADANIE 2
Zrealizować funkcję logiczną:
y=f(x

1

, x

2

, x

3

, x

4

)={00xx1,1xx10,011xx,010x1)

za pomocą multipleksera o dwóch wejściach adresujących