Materiały pochodzą z Platformy

Edukacyjnej Portalu

www.szkolnictwo.pl

Wszelkie treści i zasoby edukacyjne publikowane na łamach Portalu www.szkolnictwo.pl mogą być wykorzystywane przez jego
Użytkowników

wyłącznie

w zakresie własnego użytku osobistego oraz do użytku w szkołach podczas zajęć dydaktycznych. Kopiowanie, wprowadzanie zmian,
przesyłanie,

publiczne

odtwarzanie

i wszelkie wykorzystywanie tych treści do celów komercyjnych jest niedozwolone. Plik można dowolnie modernizować na potrzeby
własne

oraz

do

wykorzystania

w szkołach podczas zajęć dydaktycznych.

NIERÓWNOŚCI

KWADRATOWE

NIERÓWNOŚCI

KWADRATOW

E

Aby rozwiązać nierówność z niewiadomą x należy
wyznaczyć zbiór tych wartości x, dla których
nierówność jest spełniona.

Kolejne kroki rozwiązywania nierówności kwadratowej:

• musimy wyznaczyć współczynniki a, b, c dla funkcji
kwadratowej,

• obliczyć deltę (wyróżnik funkcji kwadratowej),

• w zależności od delty wyznaczyć miejsca zerowe,

• narysować wykres funkcji kwadratowej – nie musi być

dokładny, wystarczą miejsca zerowe i informacja o
tym, czy
ramiona skierowane są do góry czy na dół,

• zaznaczyć na osi liczbowej kółeczka zamalowane lub
nie
w zależności od nierówności,

• z wykresu odczytać zbiór wartości x, dla których
nierówność jest spełniona.

Wykonując powyższe kroki rozwiążemy nierówności

kwadratowe.

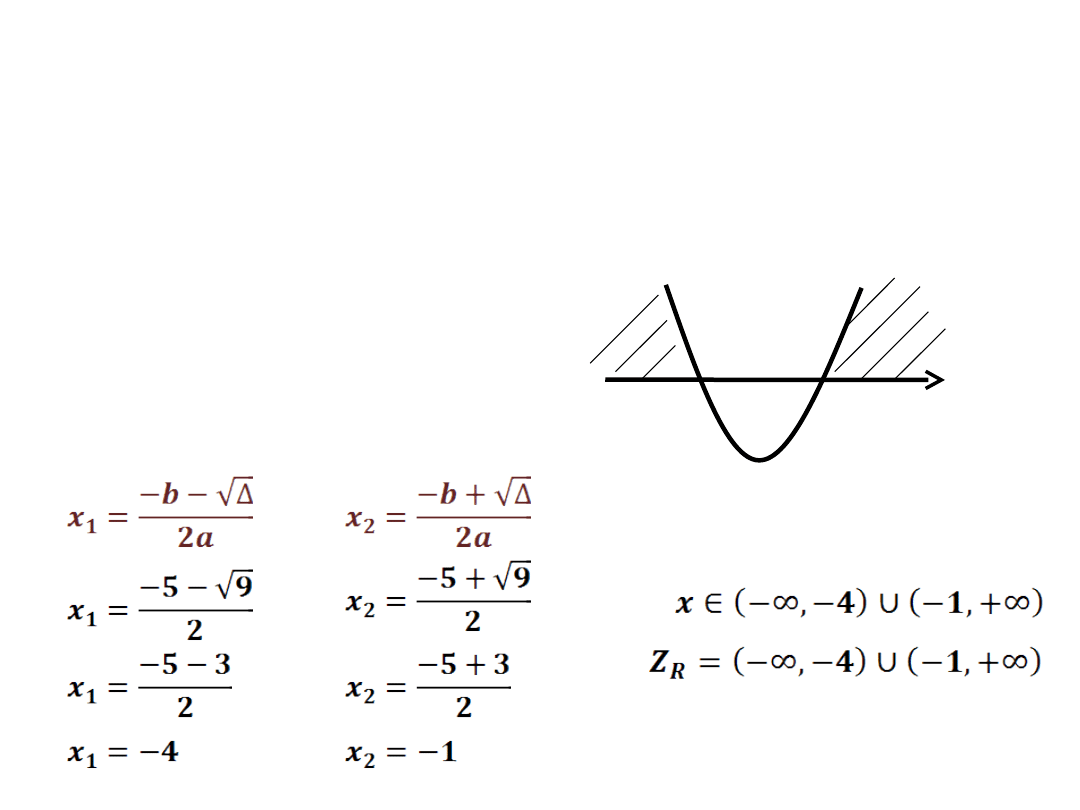
o

-4

x

o

-1

+

-

+

x

2

+5x+4 > 0

a=1 b=5 c=4
Δ = b

2

- 4ac

Δ = 5

2

- 4·1·4

Δ = 25 -16
Δ = 9
Δ

>

0

- wyznaczamy dwa

miejsca zerowe

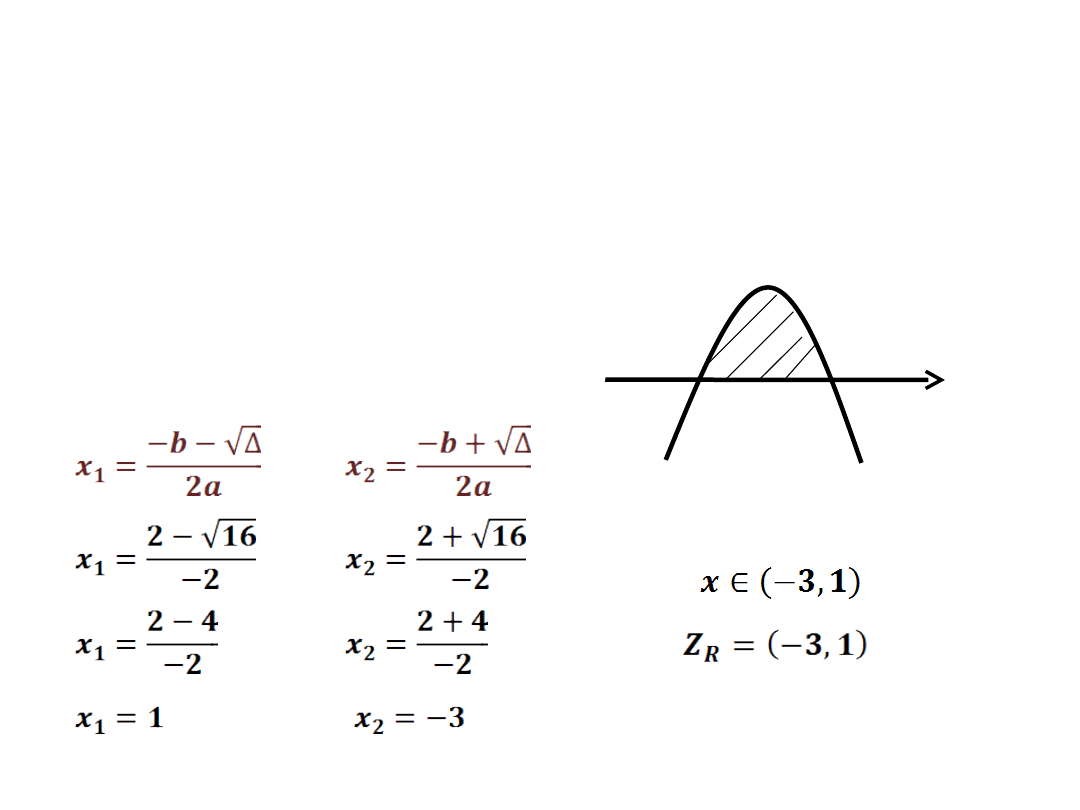
-x

2

-2x+3 > 0

a=-1 b=-2 c=3
Δ = b

2

- 4ac

Δ = (-2)

2

- 4·(-1)·3

Δ = 4+12
Δ = 16
Δ

>

0

- wyznaczamy dwa

miejsca zerowe

o

-3

x

o

1

+

-

-

·

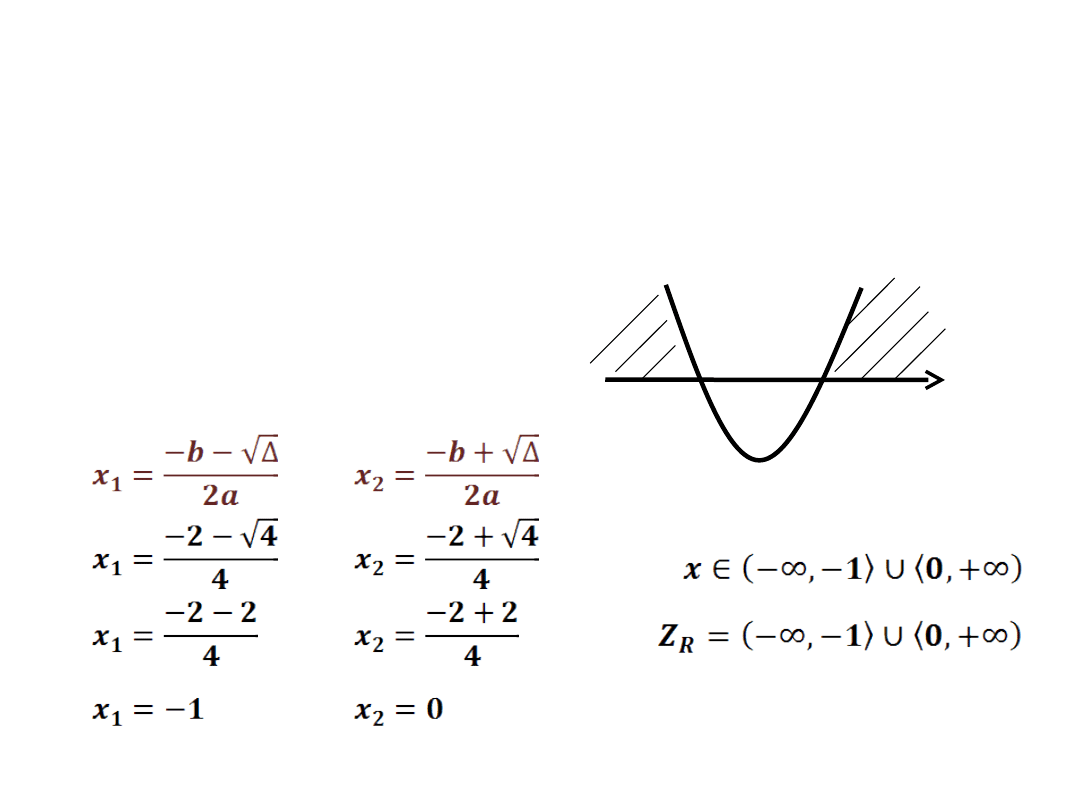
x

-1

+

-

+

2x

2

+2x ≥ 0

a=2 b=2 c=0
Δ = b

2

- 4ac

Δ = 2

2

- 4·2·0

Δ = 4 -0
Δ = 4
Δ

>

0

- wyznaczamy dwa

miejsca zerowe

·

0

·

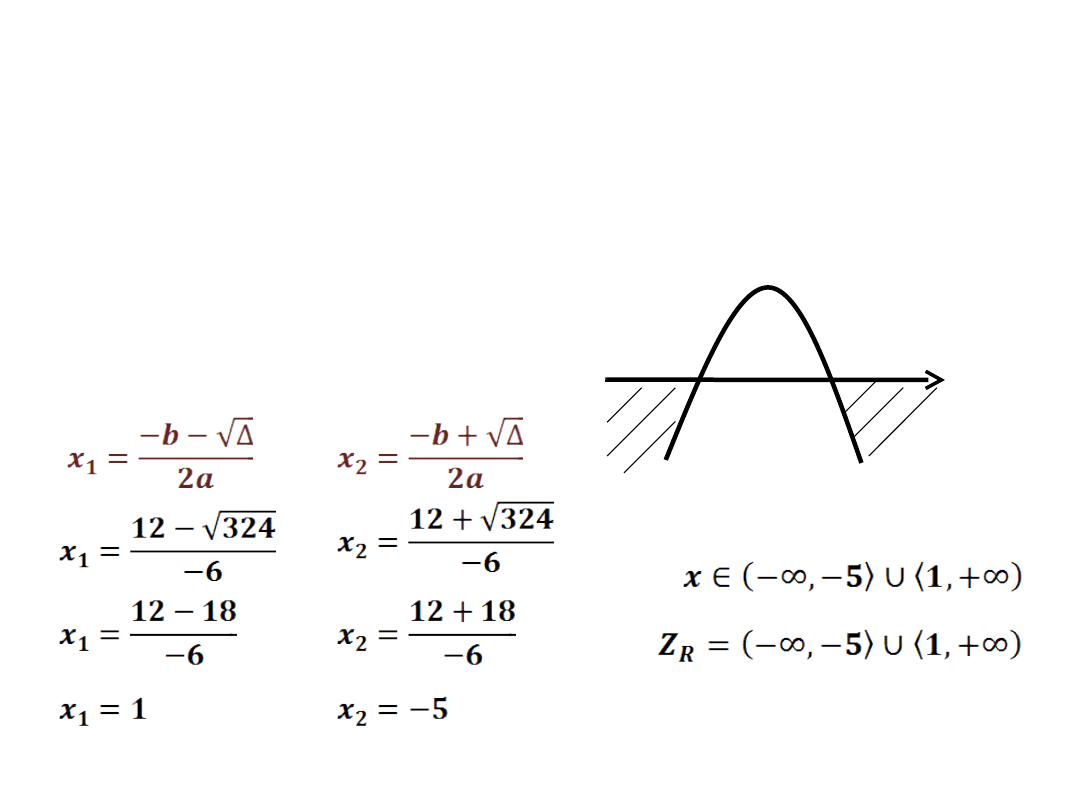
x

-5

-

-

+

-3x

2

-12x+15 ≤ 0

a=-3 b=-12 c=15
Δ = b

2

- 4ac

Δ = (-12)

2

- 4·(-3)·15

Δ = 144 + 180
Δ = 324
Δ

>

0

- wyznaczamy dwa

miejsca zerowe

·

1

x

o

-2

+

+

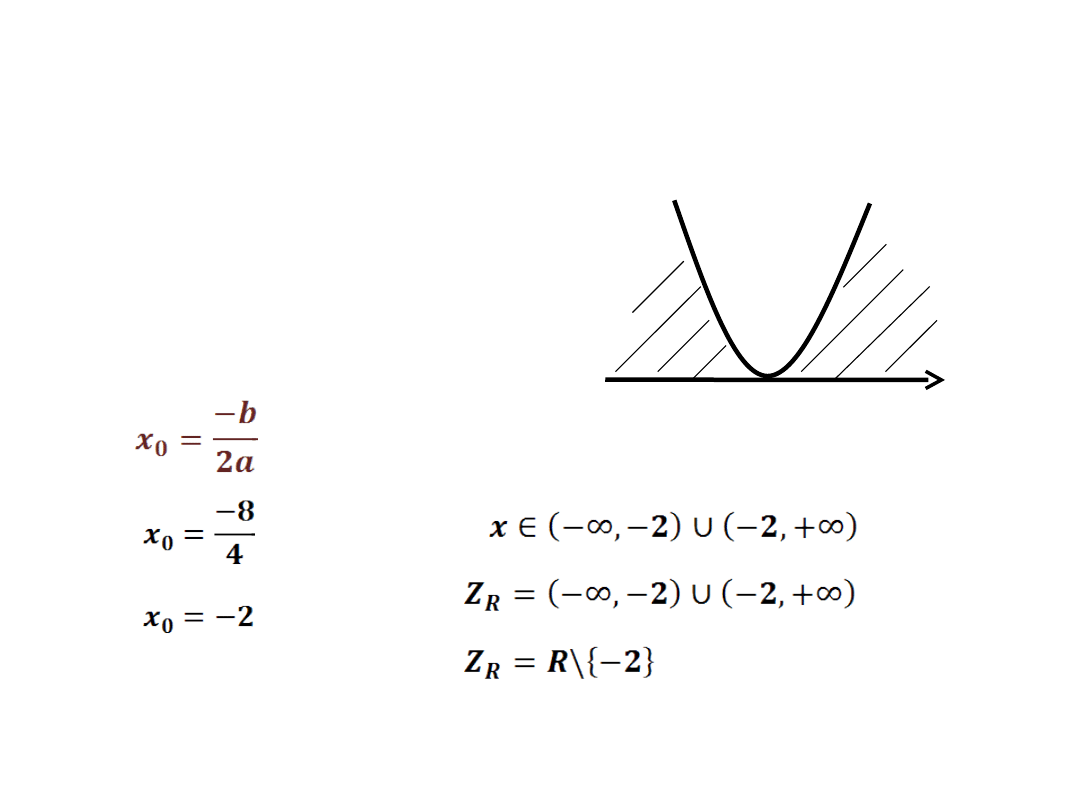
2x

2

+8x+8 > 0

a=2 b=8 c=8
Δ = b

2

- 4ac

Δ = 8

2

- 4·2·8

Δ = 64 -64
Δ = 0

- wyznaczamy jedno

miejsce zerowe

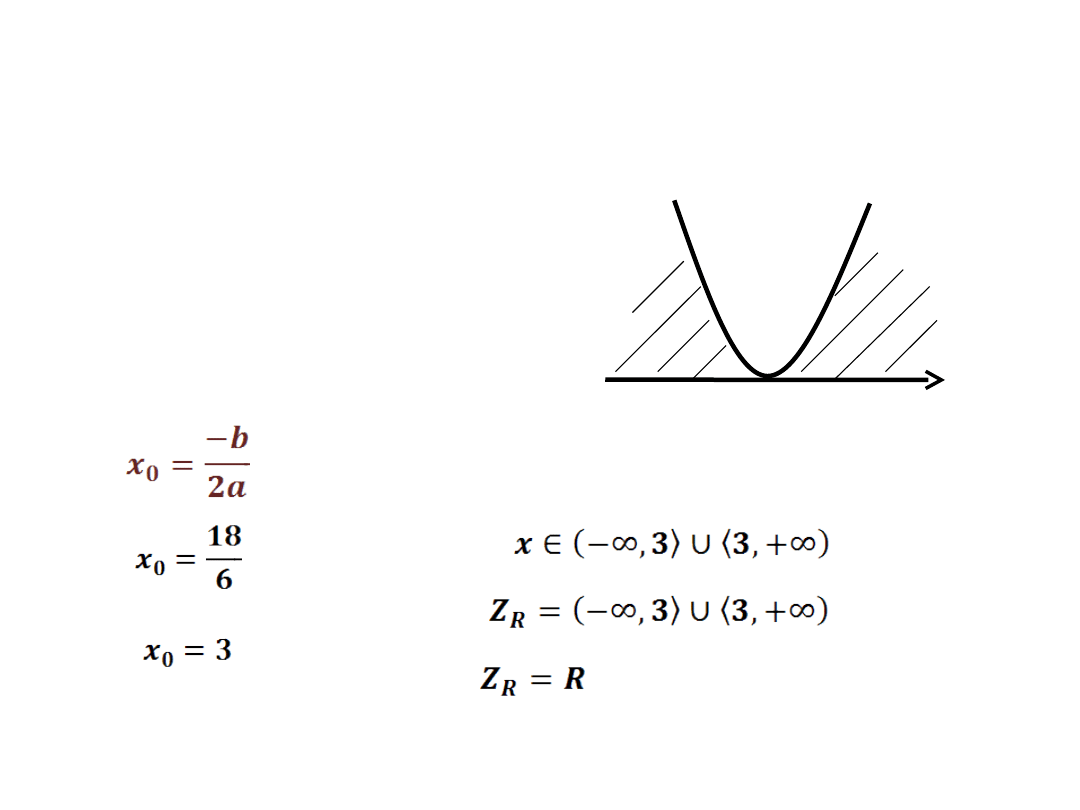
x

3

+

+

3x

2

-18x+27 ≥ 0

a=3 b=-18 c=27
Δ = b

2

- 4ac

Δ = (-18)

2

- 4·3·27

Δ = 324 - 324
Δ = 0

- wyznaczamy jedno

miejsce zerowe

·

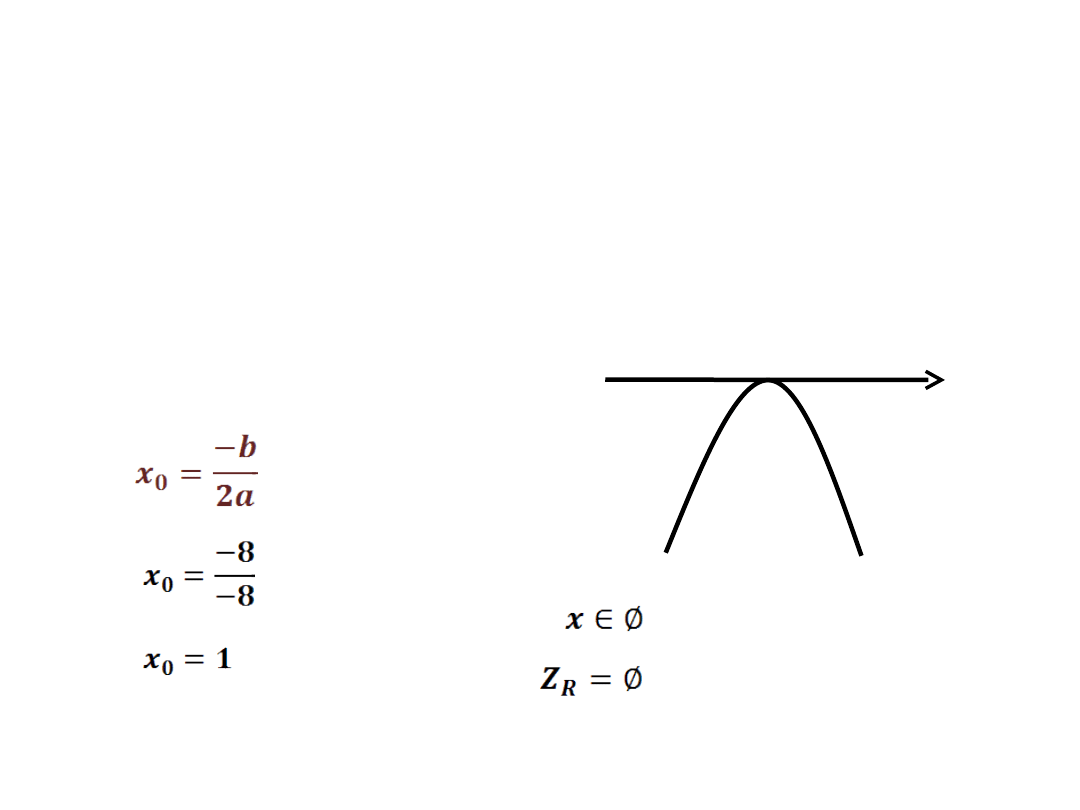
x

o

1

-

-

-4x

2

+8x-4 > 0

a=-4 b=8 c=-4
Δ = b

2

- 4ac

Δ = 8

2

- 4·(-4)·(-4)

Δ = 64 -64
Δ = 0

- wyznaczamy jedno

miejsce zerowe

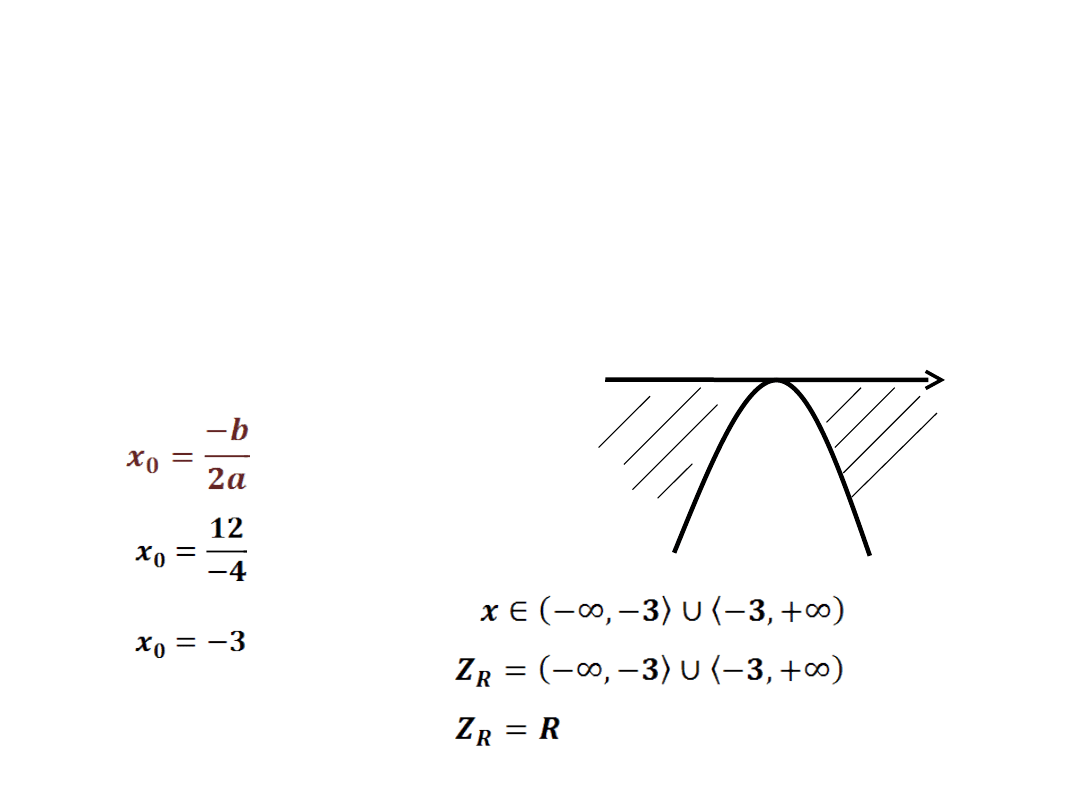
x

-3

-

-

-2x

2

-12x-18 ≤ 0

a=-2 b=-12 c=-18
Δ = b

2

- 4ac

Δ = (-12)

2

- 4·(-2)·(-18)

Δ = 144 - 144
Δ = 0

- wyznaczamy jedno

miejsce zerowe

·

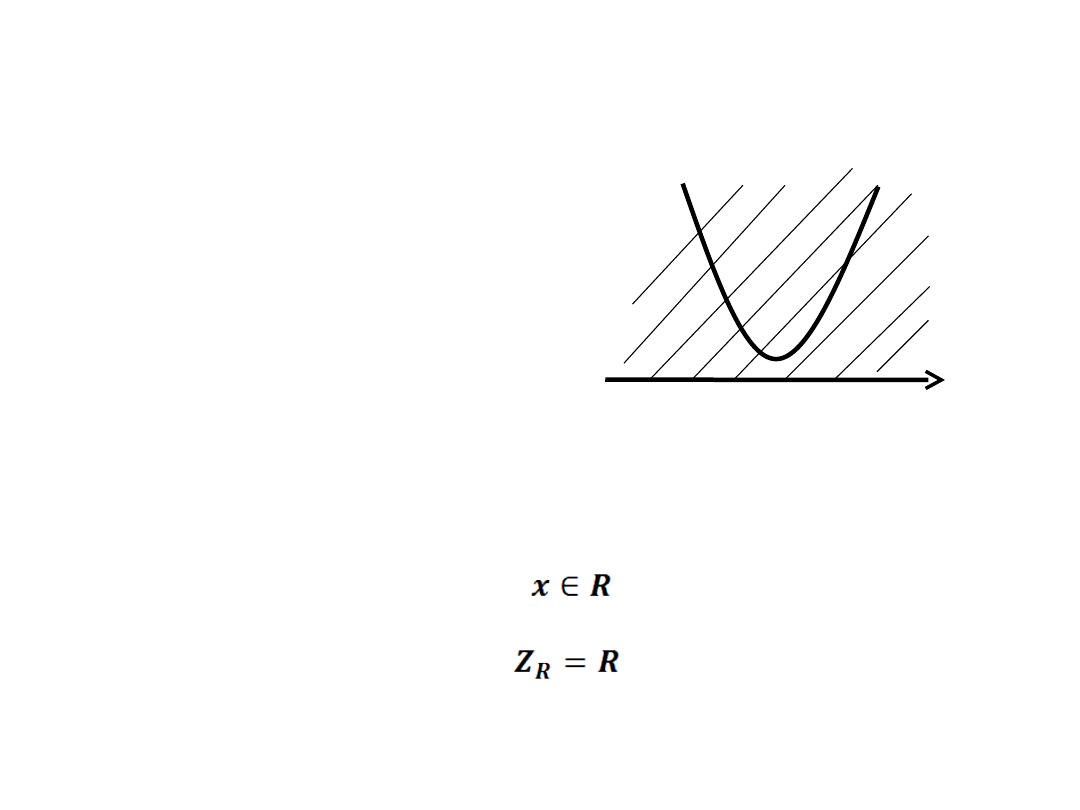
x

+

+

2x

2

+x+3 > 0

a=2 b=1 c=3

Δ = b

2

- 4ac

Δ = 1

2

- 4·2·3

Δ = 1 - 24

Δ = -23

– funkcja kwadratowa

nie ma miejsca zerowego

+

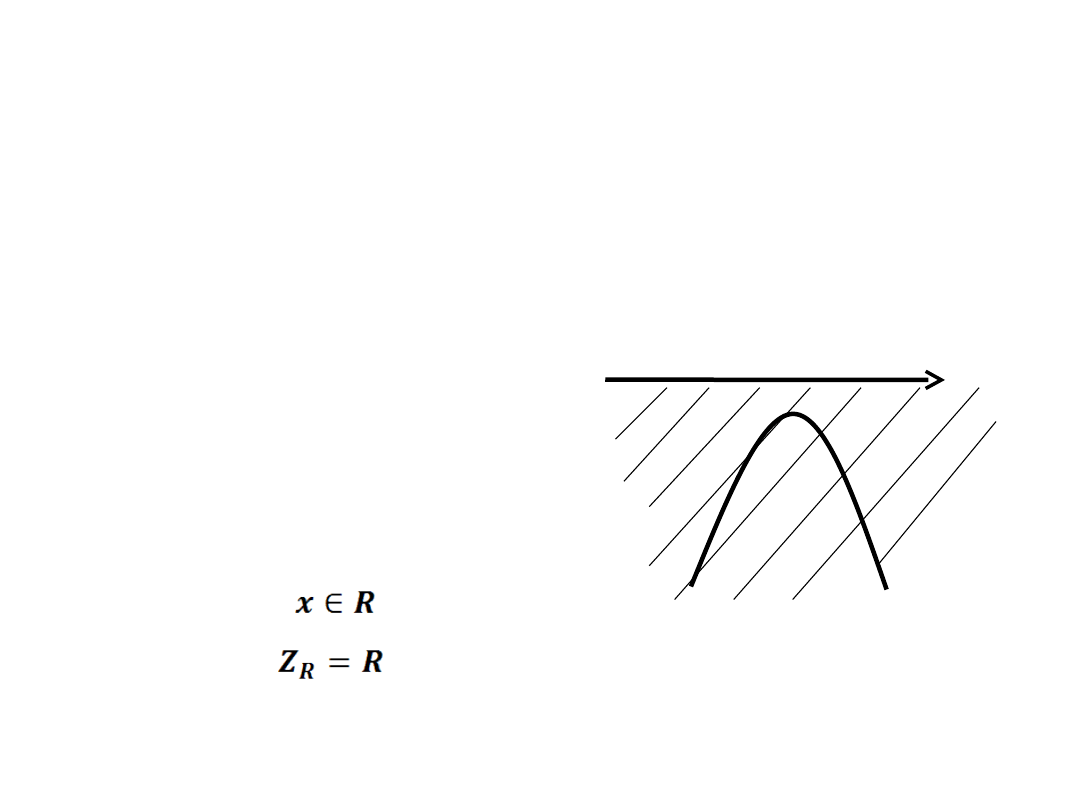
x

-

-x

2

+2x-6 ≤ 0

a=-1 b=2 c=-6

Δ = b

2

- 4ac

Δ = 2

2

- 4·(-1)·(-6)

Δ = 4 - 24

Δ = -20

– funkcja kwadratowa

nie ma miejsca zerowego

-

-

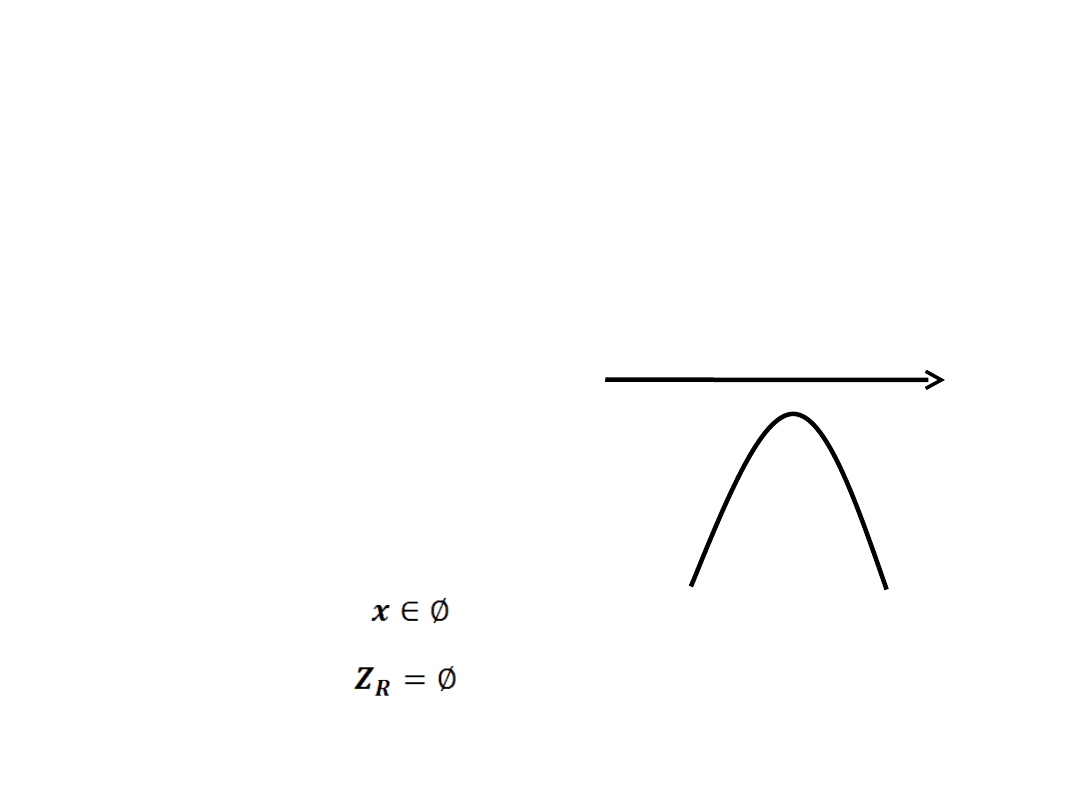
x

-

-3x

2

-x-6 ≥ 0

a=-3 b=-1 c=-6

Δ = b

2

- 4ac

Δ = (-1)

2

- 4·(-3)·(-6)

Δ = 1 - 72

Δ = -71

– funkcja kwadratowa

nie ma miejsca zerowego

-

-

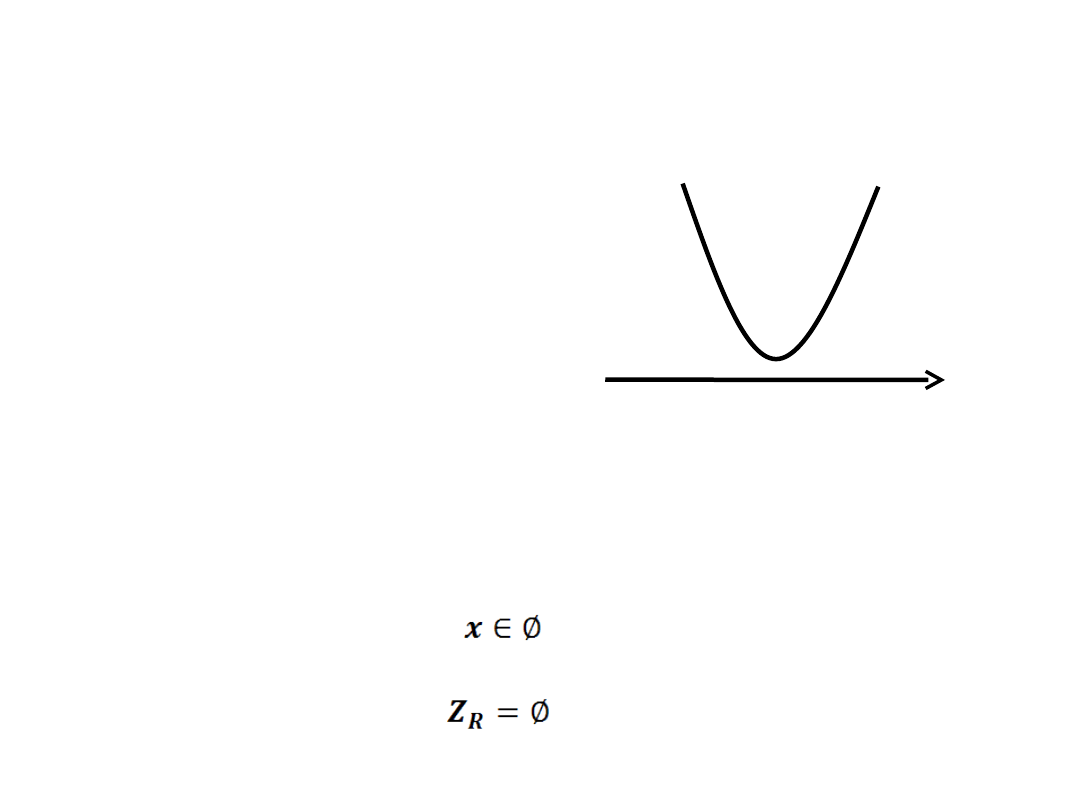
x

+

+

2x

2

+8 < 0

a=2 b=0 c=8

Δ = b

2

- 4ac

Δ = 0

2

- 4·2·8

Δ = 0 - 64

Δ = -64

– funkcja kwadratowa

nie ma miejsca zerowego

+

-(x+1)

2

+2(x-3)

2

< 17

-(x

2

+2x+1)+2(x

2

-6x+9) < 17

-x

2

-2x-1+2x

2

-12x+18 < 17

x

2

-14x+17 < 17

x

2

-14x < 0

a=1 b=-14 c=0
Δ = b

2

- 4ac

Δ = (-14)

2

– 4·1·0

Δ = 196-0
Δ = 196

– wyznaczamy dwa miejsca zerowe

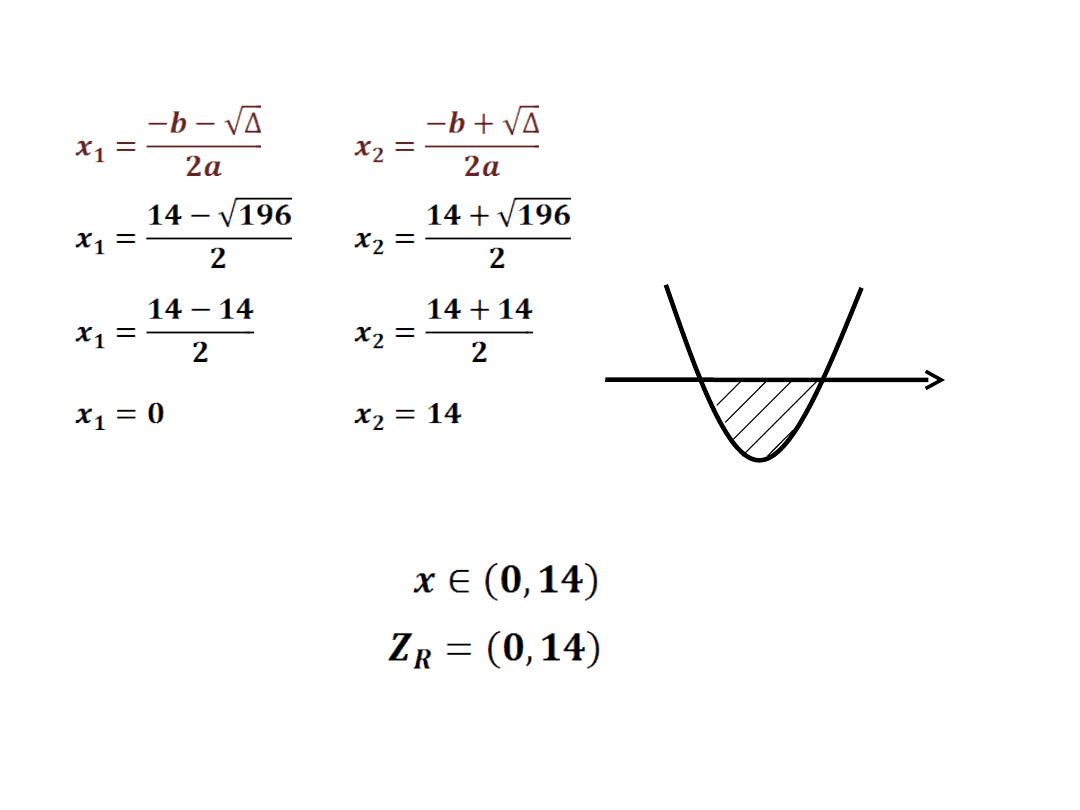
o

0

x

o

14

+

-

+

x

-

-

+

o

-8

o

0

(x+2)

2

-2(x+3)

2

< -14

x

2

+4x+4-2(x

2

+6x+9) < -14

x

2

+4x+4-2x

2

-12x-18 < -14

-x

2

-8x-14 < -14

-x

2

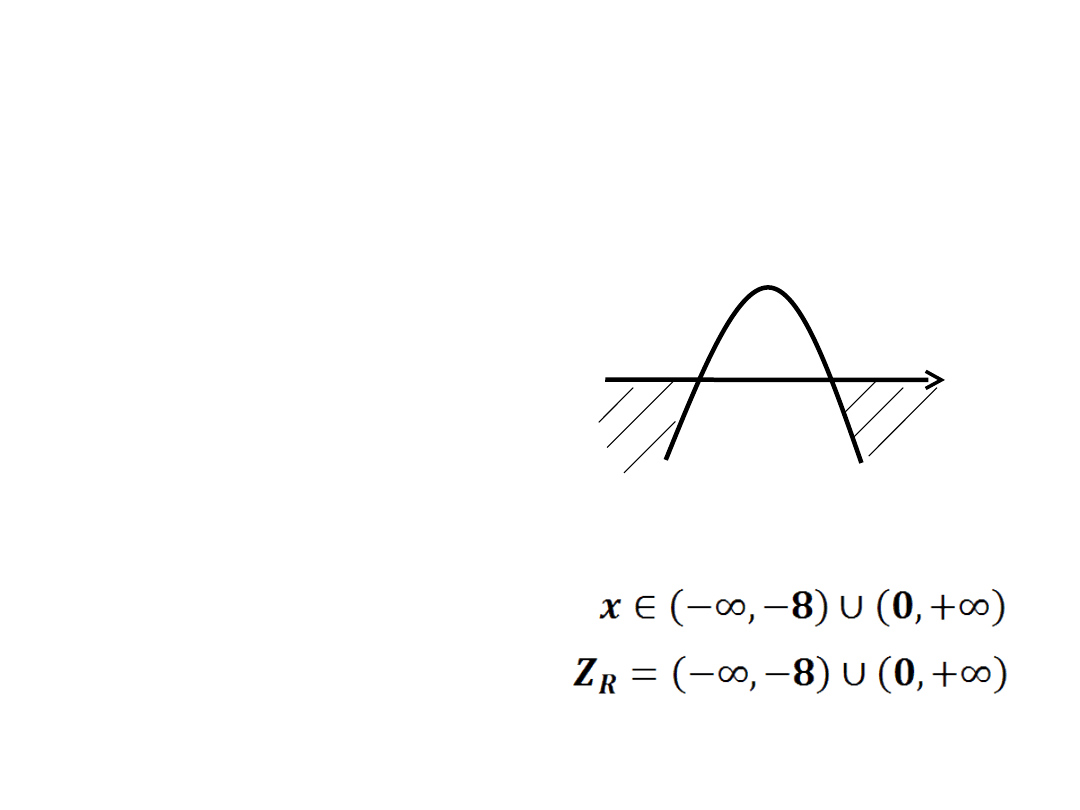
-8x < 0

-x(x+8) < 0

-x=0

∨

x+8=0

x

1

=0

∨

x

2

=-8

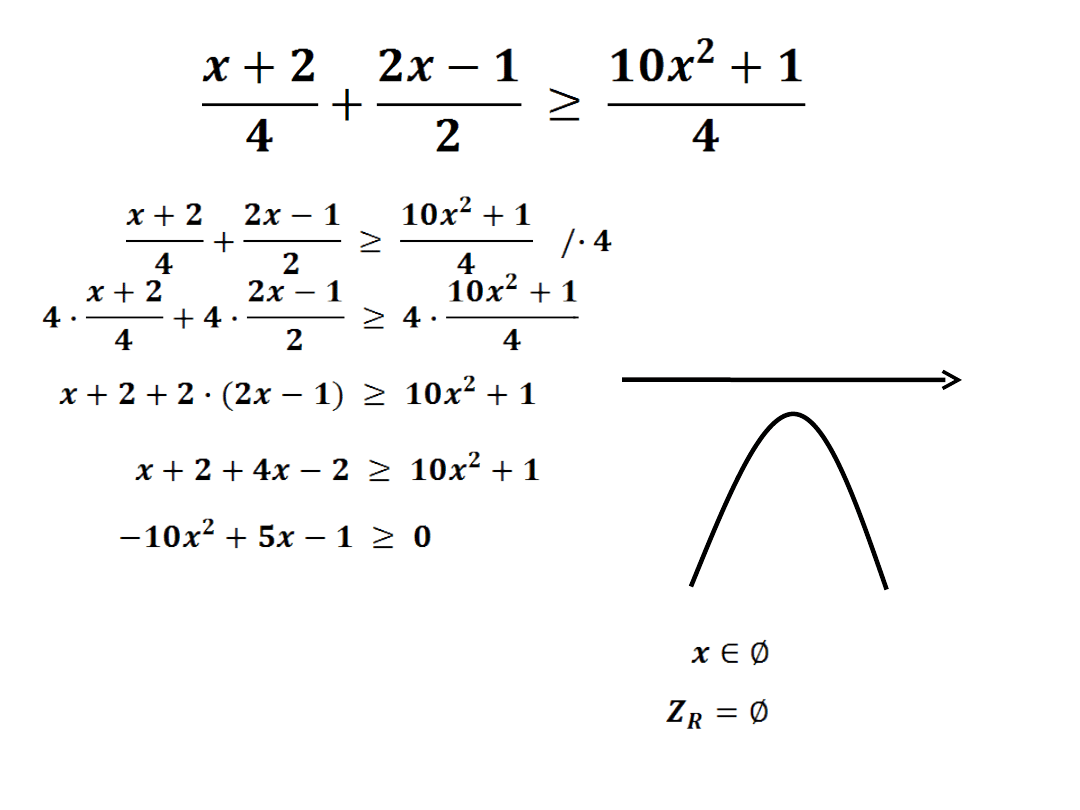
a=-10 b=5 c=-1
Δ = b

2

- 4ac

Δ = 5

2

– 4·(-10)·(-1)

Δ = 25-40
Δ = -15

x

-

-

-

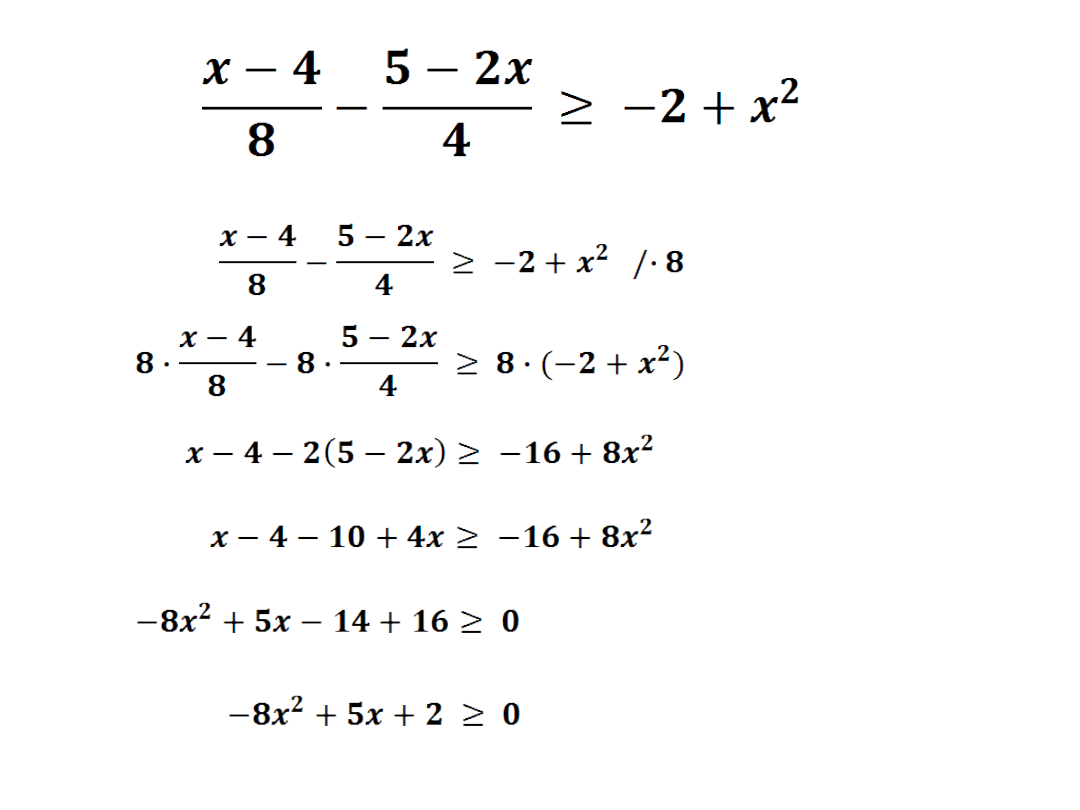
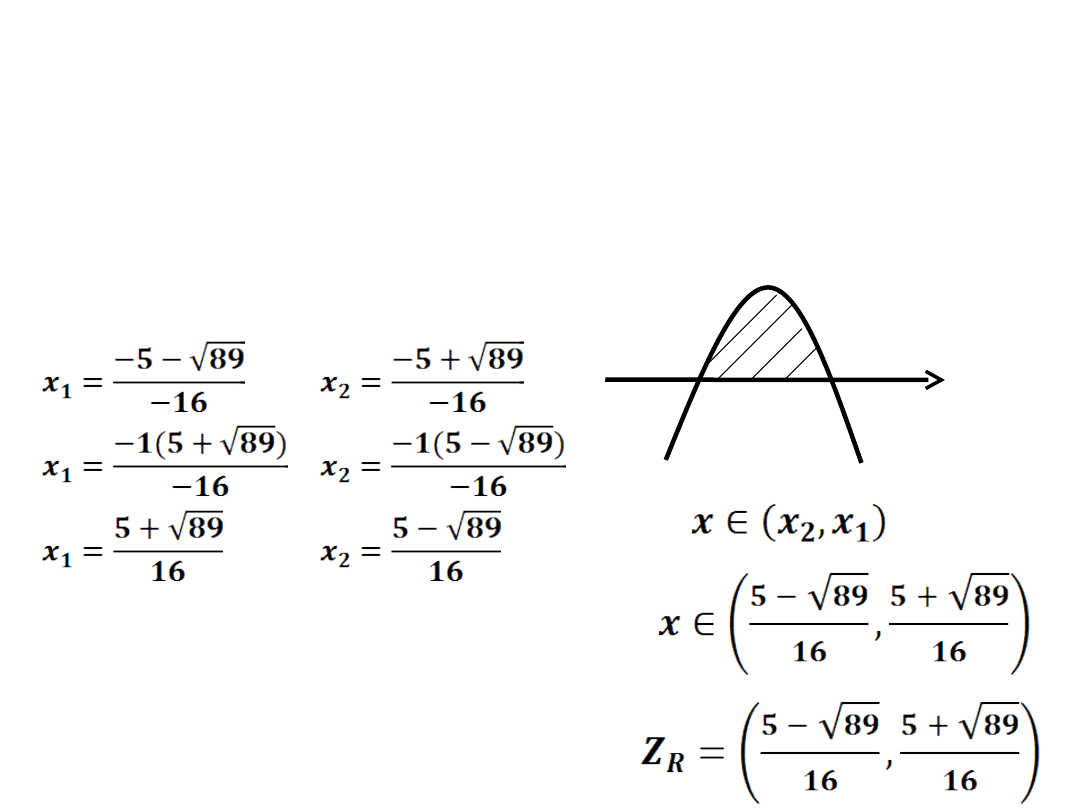
a=-8 b=5 c=2
Δ = b

2

- 4ac

Δ = 5

2

– 4·(-8)·2

Δ = 25+64
Δ = 89 –

wyznaczamy dwa miejsca

zerowe

x

x

2

-

-

+

x

1

·

·