Literatura

Bendat J.S., Piersol A.G. – Metody analizy i pomiaru sygnałów
losowych,
Biblioteka Naukowa Inżyniera, PWN, Warszawa 1976

Bielińska Ewa i inni. – Identyfikacja Procesów, Wyd. Politechniki
Śląskiej,
Gliwice 1997

Kamen E., – Introduction to Signals and Systems, Macmillan
Publishing
Company, New York, 1987.

Larminat P., Thomas Y. – Automatyka – układy liniowe, Sygnały i
układy,
Wydawnictwo Naukowo-Techniczne, Warszawa 1983

Larminat P., Thomas Y. – Automatyka – układy liniowe,
Identyfikacja,
Wydawnictwo Naukowo-Techniczne, Warszawa 1983

Mańczak K., Nahorski Z., – Komputerowa Identyfikacja Obiektów
Dynamicznych, Biblioteka Naukowa Inżyniera, PWN, Warszawa
1983

Niderliński A., – Systemy i Sterowanie, Wstęp do Automatyki i
Cybernetyki
Technicznej PWN, Warszawa 1983

Soderstrom T., Stoica P., Identyfikacja systemów, PWN, Warszawa
1997

Szabatin J., – Podstawy teorii sygnałów, Wydawnictwa
Komunikacji i
Łączności, Warszawa 1982

Zieliński T.P. - Od teorii do cyfrowego przetwarzania sygnałów,
Wydział EAIiE,
Kraków 2002

Podział sygnałów

Podział sygnałów

1. Zdeterminowane, stochastyczne
2. Ciągłe, dyskretne
3. Rzeczywiste, zespolone

Sygnały zdeterminowane
1. Okresowe, Nieokresowe, Prawieokresowe
2. Harmoniczne, Poliharmoniczne
3. Przejściowe, Ustalone

Sygnały stochastyczne
1. Stacjonarne, niestacjonarne
2. Ergodyczne, nieergodyczne

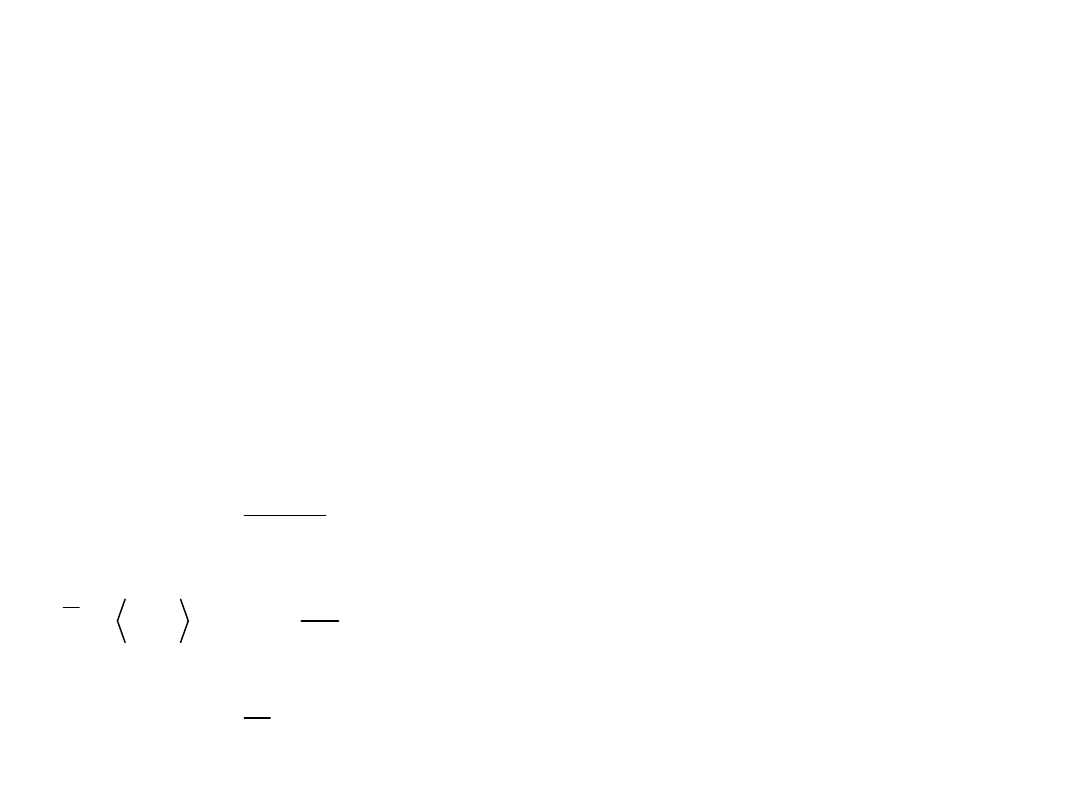
Sygnały zdeterminowane – całka sygnału,

wartość średnia

 

 

 

 























dt

t

x

dt

t

x

t

x

t

t

2

1

Całka sygnału

Wartość średnia sygnału

 

 

 

 















































T

t

t

dt

t

x

T

dt

t

x

lim

dt

t

x

t

t

t

x

x

0

1

2

1

2

1

1

2

1

Sygnał określony w przedziale
ograniczonym

Sygnał określony w przedziale
nieograniczonym

Sygnał okresowy

Sygnał określony w przedziale
ograniczonym

Sygnał określony w przedziale
nieograniczonym

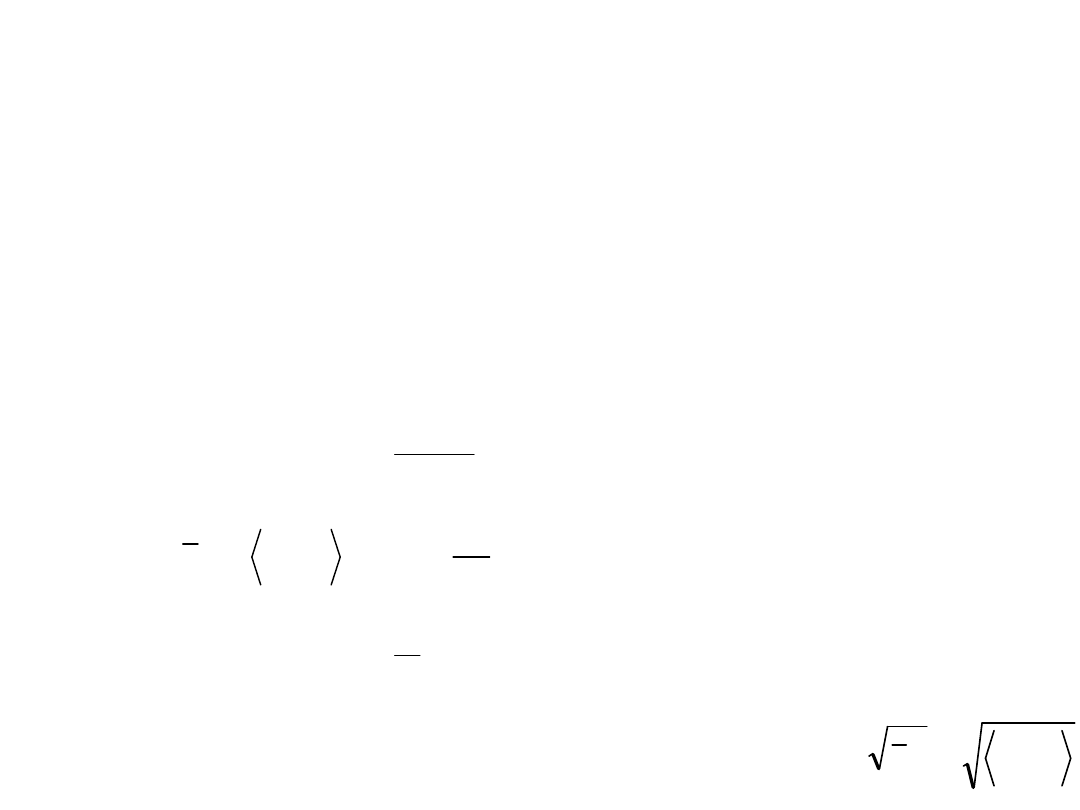
Sygnały zdeterminowane – energia sygnału, moc

sygnału

 

 

 

 

























dt

t

x

dt

t

x

t

x

E

t

t

x

2

2

2

2

1

Energia sygnału (sygnały o ograniczonej energii)

Moc sygnału (sygnały o ograniczonej mocy)

 

 

 

 

















































T

t

t

x

dt

t

x

T

dt

t

x

dt

t

x

t

t

t

x

x

P

lim

0

2

2

2

1

2

2

2

1

2

1

1

2

1

Sygnał określony w przedziale
ograniczonym

Sygnał określony w przedziale
nieograniczonym

Sygnał okresowy

Sygnał określony w przedziale
ograniczonym

Sygnał określony w przedziale
nieograniczonym

Wartość skuteczna sygnału, RMS (root mean square)

 

t

x

x

x

x

RMS

sk

2

2







Sygnały zdeterminowane – przykłady

Sygnały o ograniczonym czasie trwania i ograniczonej energii

 

 

1

1

5

0

1

5

0

5

0

5

0

0























x

E

x

.

t

dla

.

t

dla

.

.

t

dla

t

x

Impuls prostokątny

Sygnały o nieograniczonym czasie trwania i ograniczonej energii

Sygnał wykładniczy
malejący

 

 































2

0

0

0

0

2

A

E

A

x

t

dla

t

dla

Ae

t

x

x

t

Sygnał sinusoidalny
tłumiony

 

 

2

2

2

2

2

2

4

0

0

0











































A

E

A

x

t

dla

t

dla

t

sin

Ae

t

x

x

t

Sygnały zdeterminowane – przykłady

Sygnały o nieograniczonym czasie trwania i ograniczonej energii

Sygnał gaussowski

 

 

2

1

1

2











x

t

E

x

e

t

x

Sygnały o nieograniczonym czasie trwania i ograniczonej mocy

   

2

1

2

1

0

0

0

5

0

0

1

1

























x

P

x

t

dla

t

dla

.

t

dla

t

t

x

Skok jednostkowy

Sygnał wykładniczy
narastający

 





 

2

1

2

1

0

1

1



















x

t

P

x

t

e

t

x

Sygnały zdeterminowane – przykłady

Sygnały okresowe i o ograniczonej mocy

Sygnał sinusoidalny

 

 

2

0

2

A

P

x

t

sin

A

t

x

x









Fala prostokątna o amplitudzie A
i okresie T

2

0

A

P

x

x





Sygnał dystrybucyjny (delta Diraca)

 

 

 

 

 

 

   

 











































































0

1

1

1

2

2

2

2

x

dt

t

t

x

dt

t

dt

t

s

t

n

n

t

t

lim

t

n

n

n

n

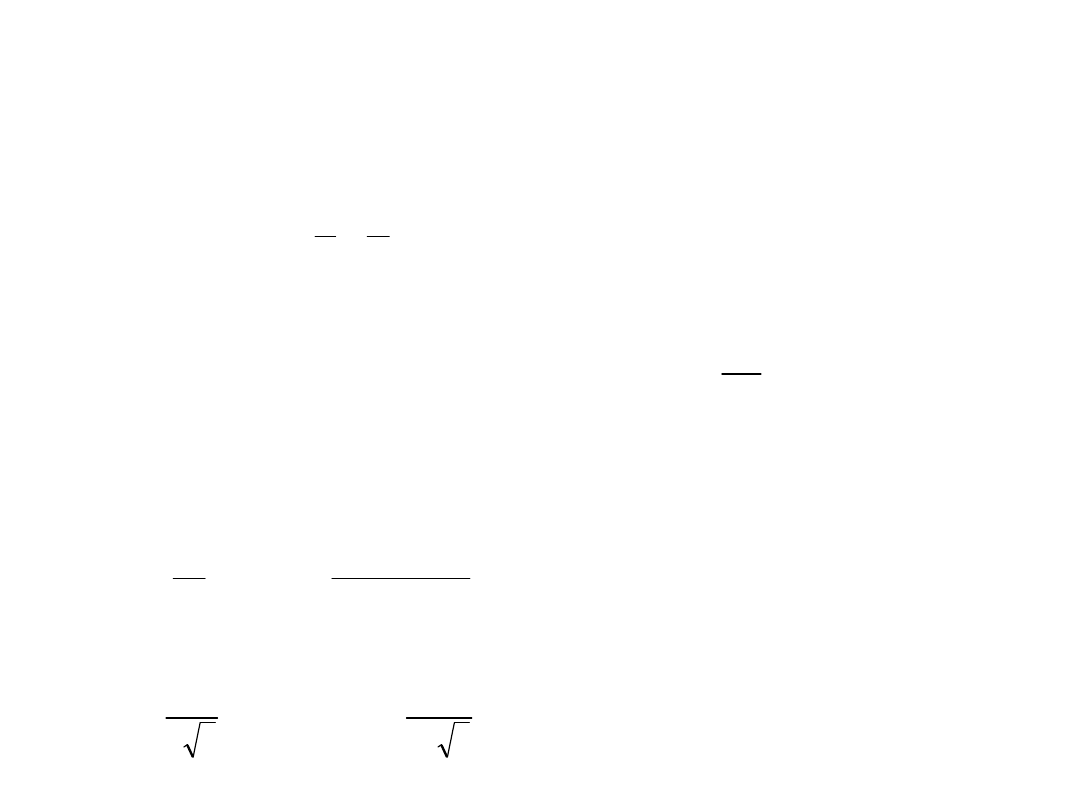
Sygnał dystrybucyjny – całka i pochodna delty

Diraca

 

 

t

lim

t

n

n











Całka delty Diraca

Pochodna delty Diraca

 

 

 

nt

arctg

d

t

t

n

n





















1

2

1

1

 

 

t

lim

t

n

n

1

1







 

 





1

2

2

2

3















t

n

t

n

t

dt

d

t

n

n

 

3

8

9

3

1

2











n

n

t

extr

n

extr



   

t

t

dt

d





1

delta Diraca jest pochodną
dystrybucyjną skoku jednostkowego

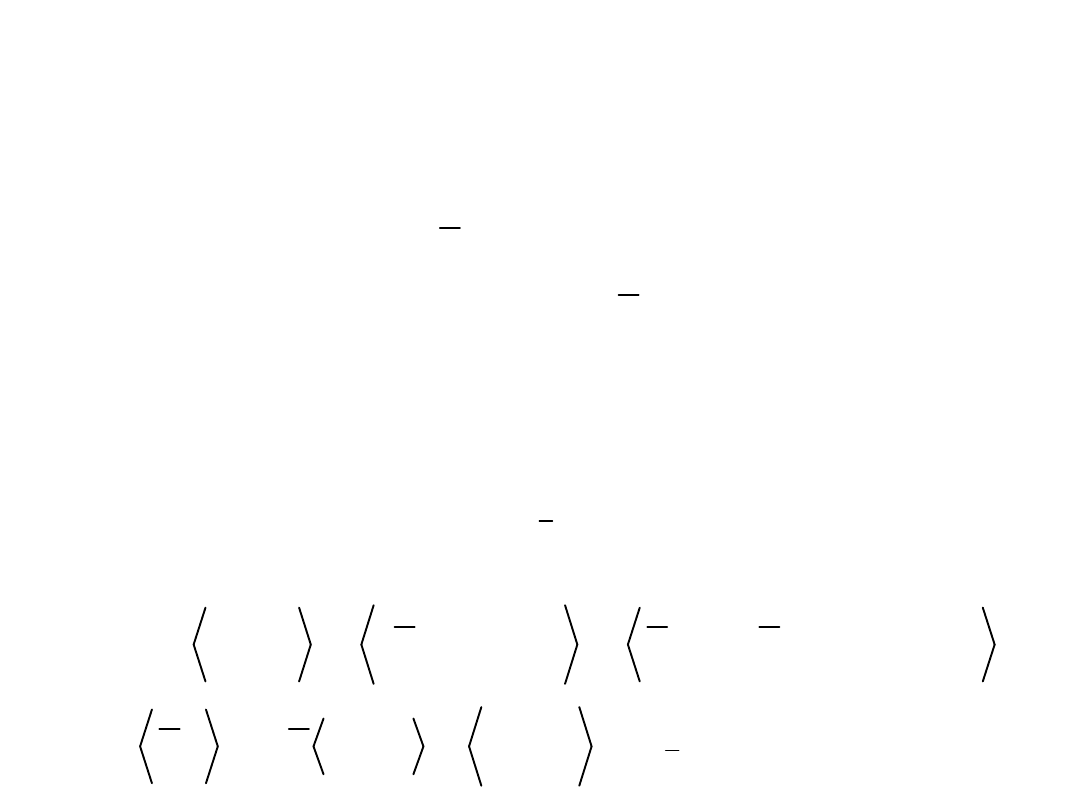
Sygnały zdeterminowane – składowa stała i

zmienna

x

Składowa stała i składowa zmienna sygnału

Moc sygnału jest sumą mocy składowej stałej i składowej zmiennej

x

~

x

x

P

P

P





Składowa stała

Składowa zmienna

 

x

t

x

x~





 

 





 

 

 

x

~

x

x

P

P

t

x~

)

t

(

x

~

x

x

t

x~

t

x

~

x

x

t

x

~

x

t

x

P

























2

2

2

2

2

2

2

2

składowa stała jest równa wartości średniej

Sygnały zdeterminowane – momenty

sygnałów

 

 

 

 









2

1

2

2

1

2

t

t

r

r

x

t

t

r

r

x

dt

t

x

t

m

dt

t

x

t

m

Momenty sygnału

Unormowane momenty sygnału

 

 

 







2

1

2

1

2

2

2

t

t

t

t

r

r

x

dt

t

x

dt

t

x

t

t

Punkt skupienia sygnału

 

 







2

1

2

1

2

2

2

t

t

t

t

x

dt

t

x

dt

t

x

t

t

Sygnały zdeterminowane – momenty

sygnałów

Unormowany moment centralny sygnału

Rozrzut sygnału wokół punktu skupienia - średniokwadratowe odchylenie

 





 

 

 











2

1

2

1

2

2

2

)

(

2

t

t

t

t

r

x

__

__________

dt

t

x

dt

t

x

t

t

r

x

t

t

 





 

 













2

1

2

1

2

2

2

2

2

2

2

2

)

(

t

t

t

t

x

__

__________

x

dt

t

x

dt

t

x

t

t

T

x

t

t

Sygnały zdeterminowane – funkcja korelacji

Funkcja korelacji sygnałów (dla sygnałów o ograniczonej energii)

 

  



















dt

t

y

t

x

K

xy

Funkcja autokorelacji sygnału (dla sygnału o ograniczonej energii)

 

  



















dt

t

x

t

x

K

xx

Funkcja autokorelacji sygnału (dla sygnału o ograniczonej mocy)

 

  



















T

.

T

.

T

xx

dt

t

x

t

x

T

lim

K

5

0

5

0

1