Drgania

Drgania



1. Ruch harmoniczny



2. Prosty oscylator harmoniczny



3. Ruch harmoniczny prosty



4. Przykład 1



5. Przykład 2



6. Energia w ruchu harmonicznym



7. Drgania tłumione



8. Drgania wymuszone i rezonans

1. Ruch harmoniczny

1. Ruch harmoniczny



ruch okresowy (periodyczny)



równania ruchu - funkcje harmoniczne



ruch po tej samej drodze



charakterystyki: okres -

częstotliwość -
amplituda -

const

const





a

v





,

T

T

f 1



A

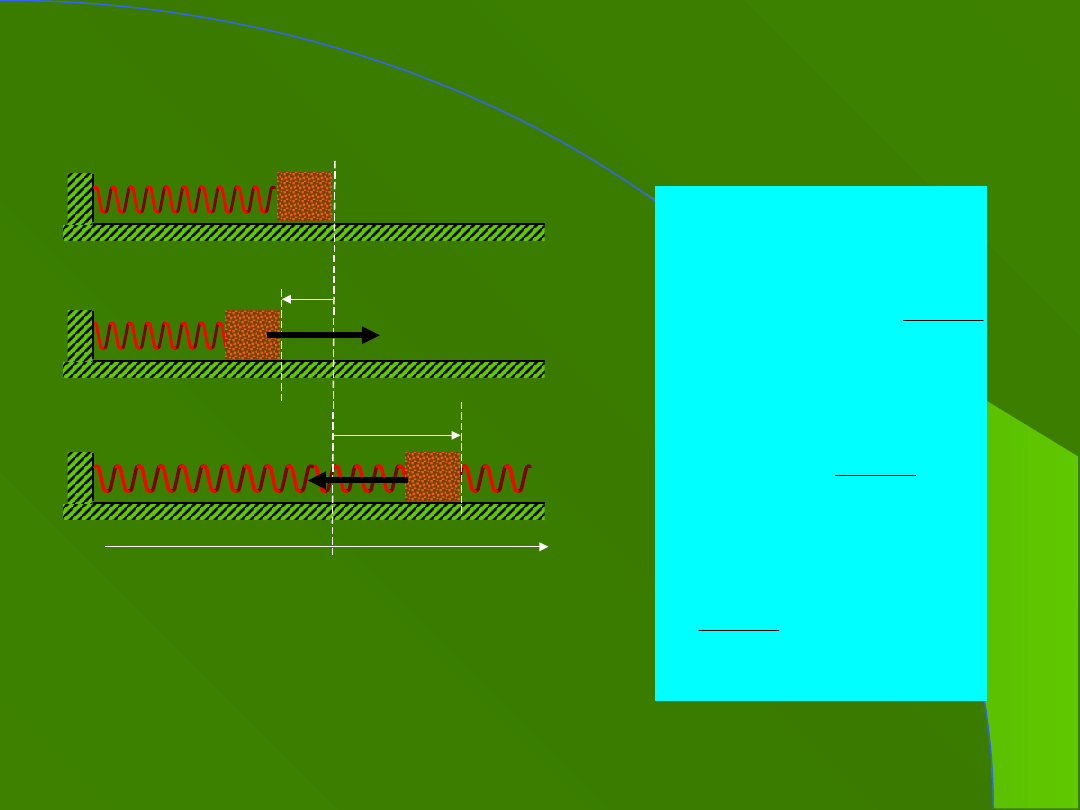
2. Prosty oscylator

2. Prosty oscylator

harmoniczny

harmoniczny



równanie ruchu

harmonicznego prostego

m

m

m

x

0

x<0

x>0

F=-kx

F

kx

F ma m

d x

dt

kx m

d x

dt

m

d x

dt

kx















2

2

2

2

2

2

0

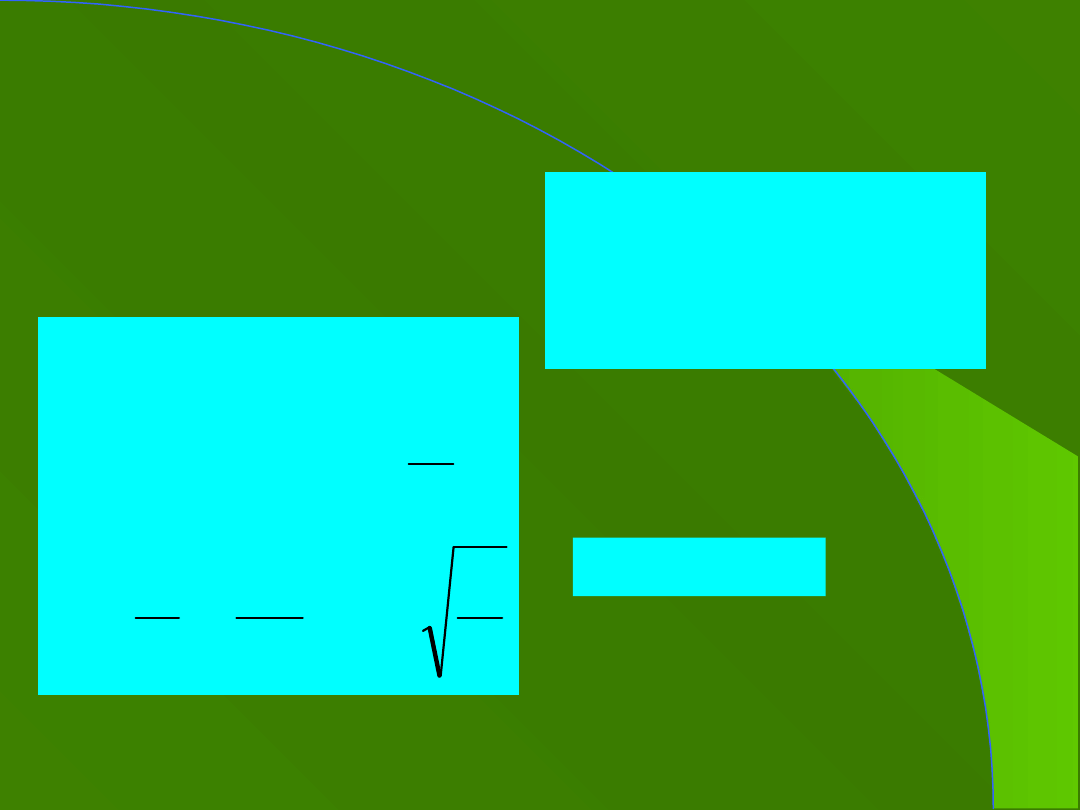
3. Ruch harmoniczny

3. Ruch harmoniczny

prosty

prosty



rozwiązanie ogólne:













































t

A

x

t

A

x

t

A

x

cos

sin

cos

2





k

m

f

T

m

k

k

m

kx

x

m











2

2

1

;

0

2

2

















 - przesunięcie fazowe

t+ - faza ruchu - kąt





 x

x

2



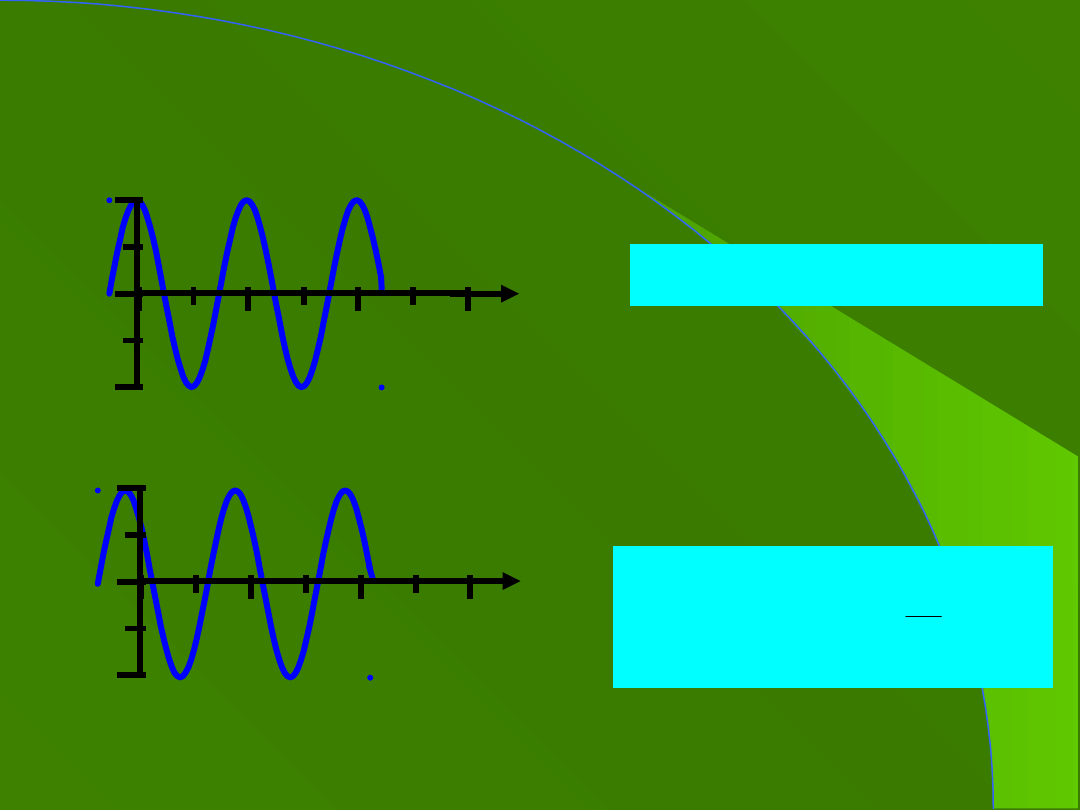
3a. Ruch harmoniczny prosty,

3a. Ruch harmoniczny prosty,

c.d.

c.d.

0.

4

6

2

-1

1



x

0.

2T

3T

T

-1

1

t

x



















t

A

x

cos





















T

t

A

x

2

cos

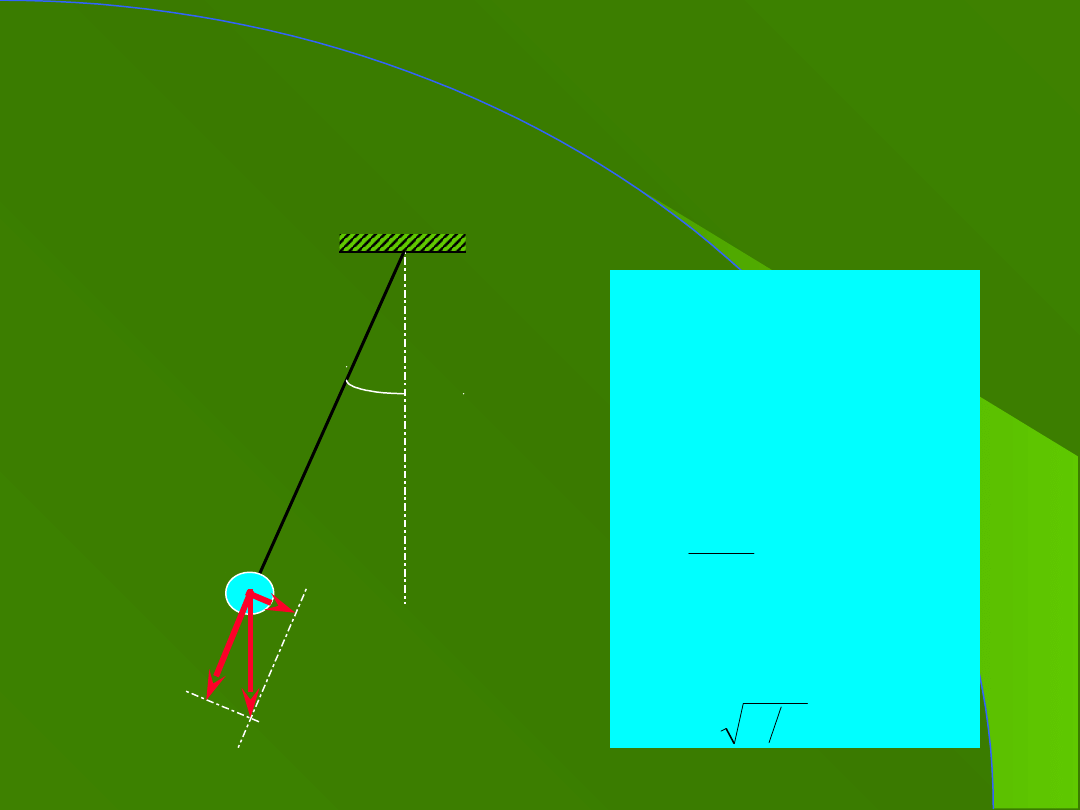
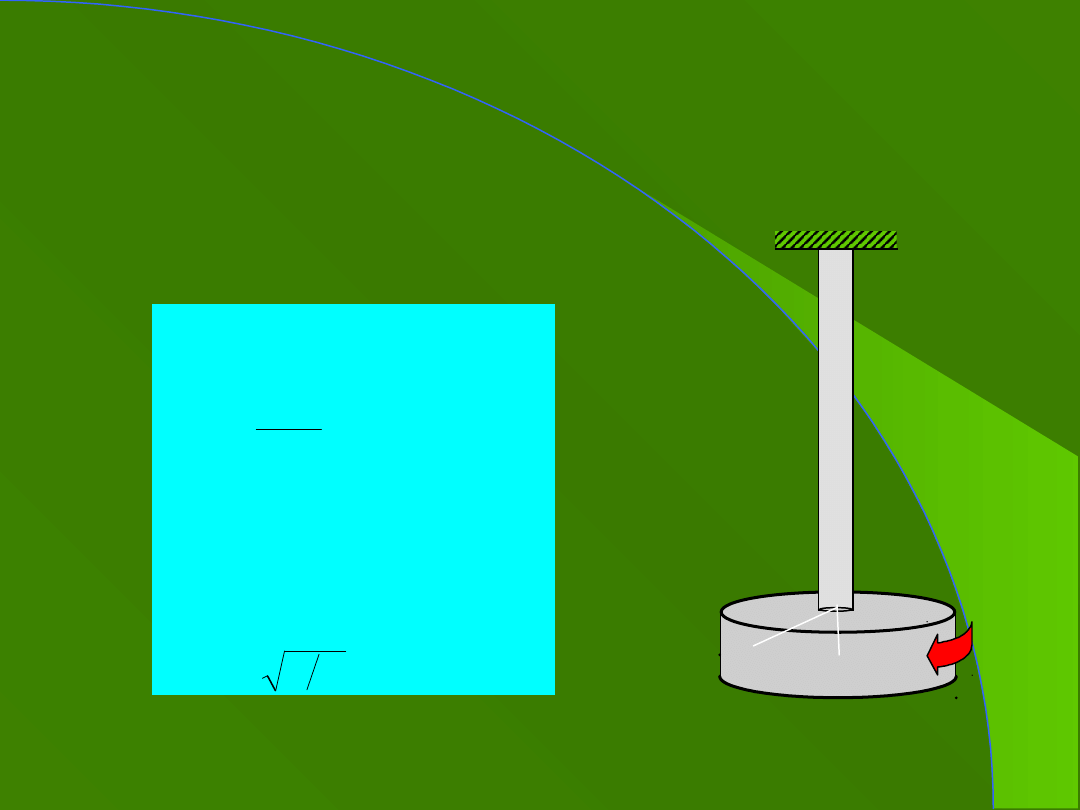
4. Przykład 1

4. Przykład 1



wahadło matematyczne

g

m



sin

g

m



cos

g

m



L

g

L

T

g

L

g

L

dt

d

L

g

L

a

mg

ma

F

o

t

t

























2

0

sin

90

sin

sin

2

2































dla

5. Przykład 2

5. Przykład 2



wahadło torsyjne (skrętne)



























I

T

t

I

dt

d

I

I

I

M

m

2

)

cos(

0

)

(

2

2

























Hooka

pr.



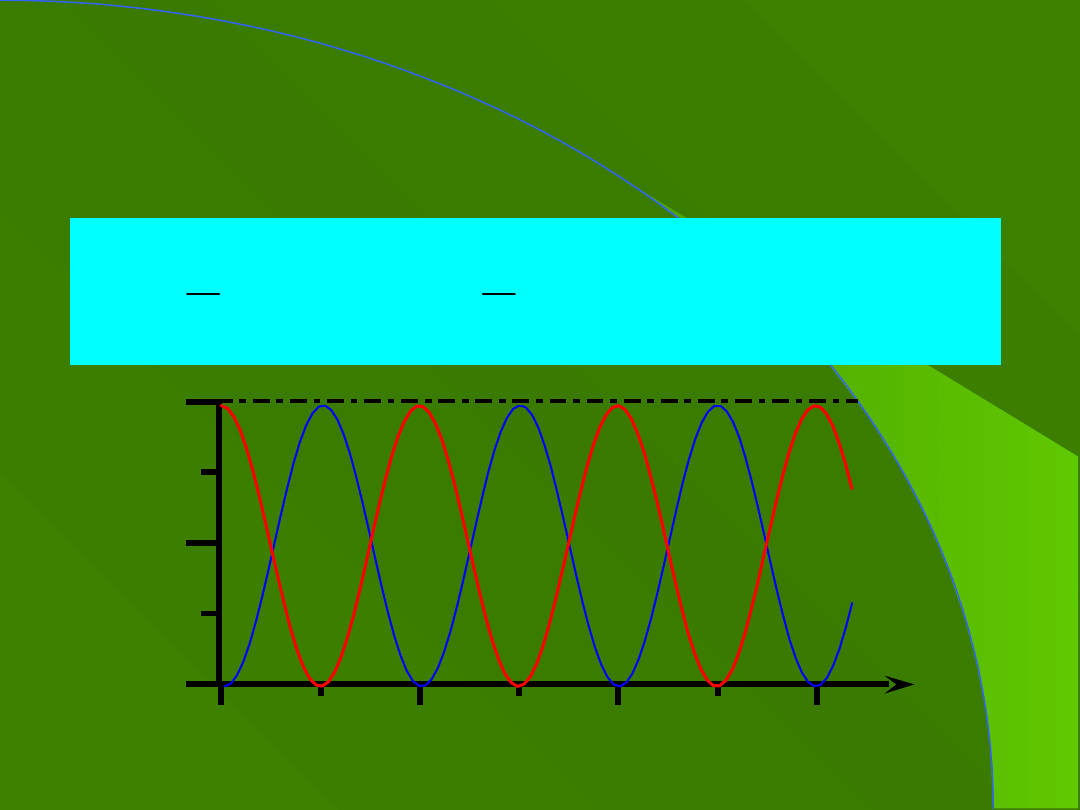
6a. Energia w ruchu

6a. Energia w ruchu

harmonicznym, c.d.

harmonicznym, c.d.

0

2


3




kA

2

/2



t+



E

E

k

E

p

E

-

E

E

p

c

E

kx

kA

E

k

p

c







2

2

2

1

2

1

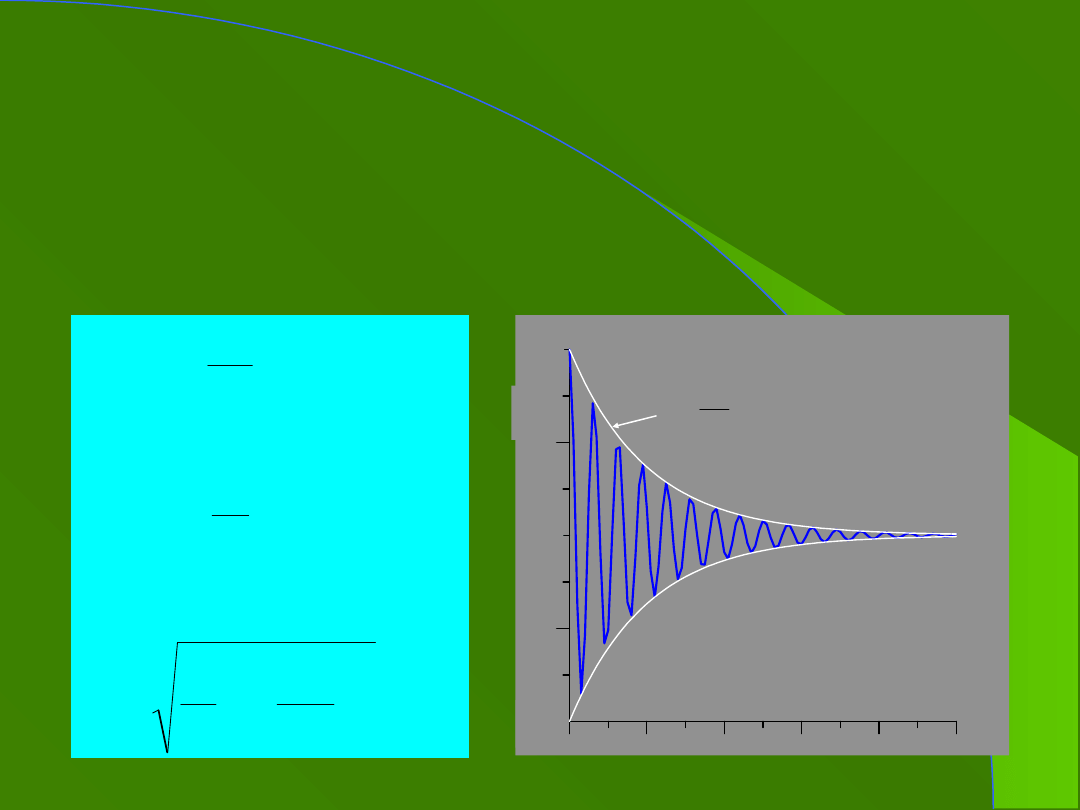
7. Drgania tłumione

7. Drgania tłumione



siła tłumiąca proporcjonalna do prędkości





2

2

2

'

'

cos

0





































m

b

m

k

t

Ae

x

kx

x

b

x

m

x

b

dt

dx

b

F

m

bt

t













x

0

A

-A











t

'

m

bt

e

2



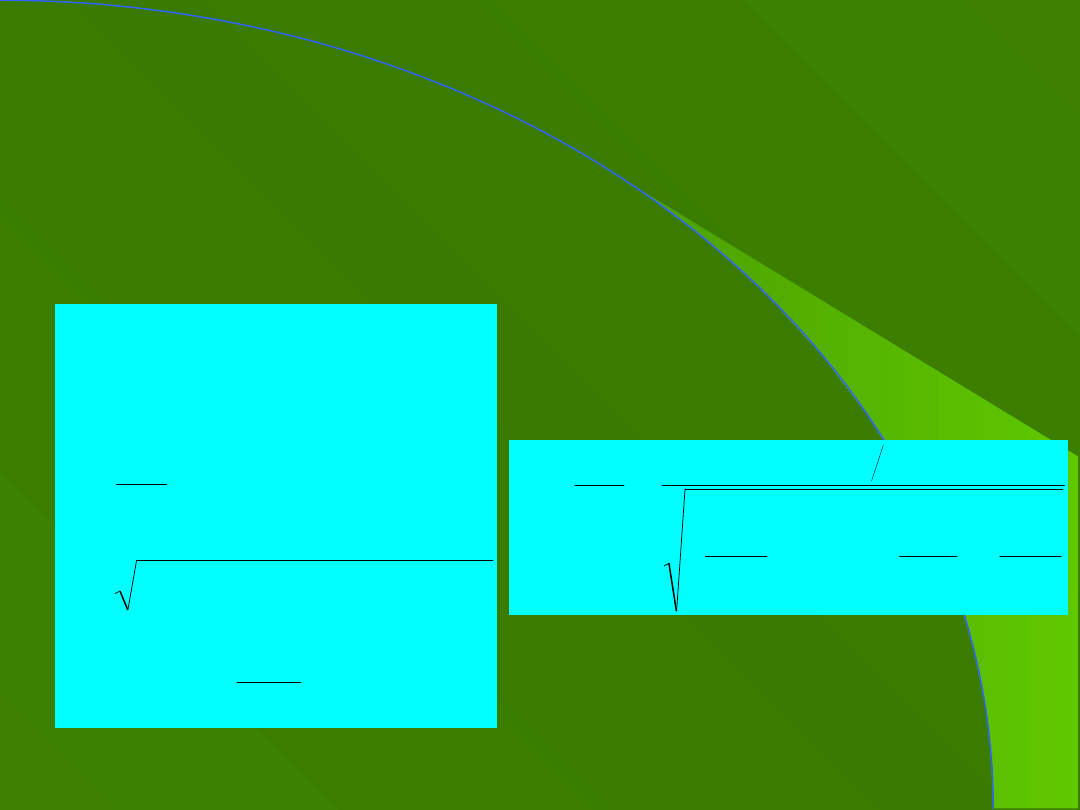
8. Drgania wymuszone i

8. Drgania wymuszone i

rezonans

rezonans



siła wymuszająca o częstości



’’





























''

cos

''

)

''

(

''

sin

)

''

cos(

)

''

cos(

2

2

2

2

2

2

b

b

m

t

F

x

t

F

kx

x

b

x

m

t

F

F

m

m

m

t

arc

























2

2

2

2

2

2

''

1

''















































m

b

k

F

F

A

m

m

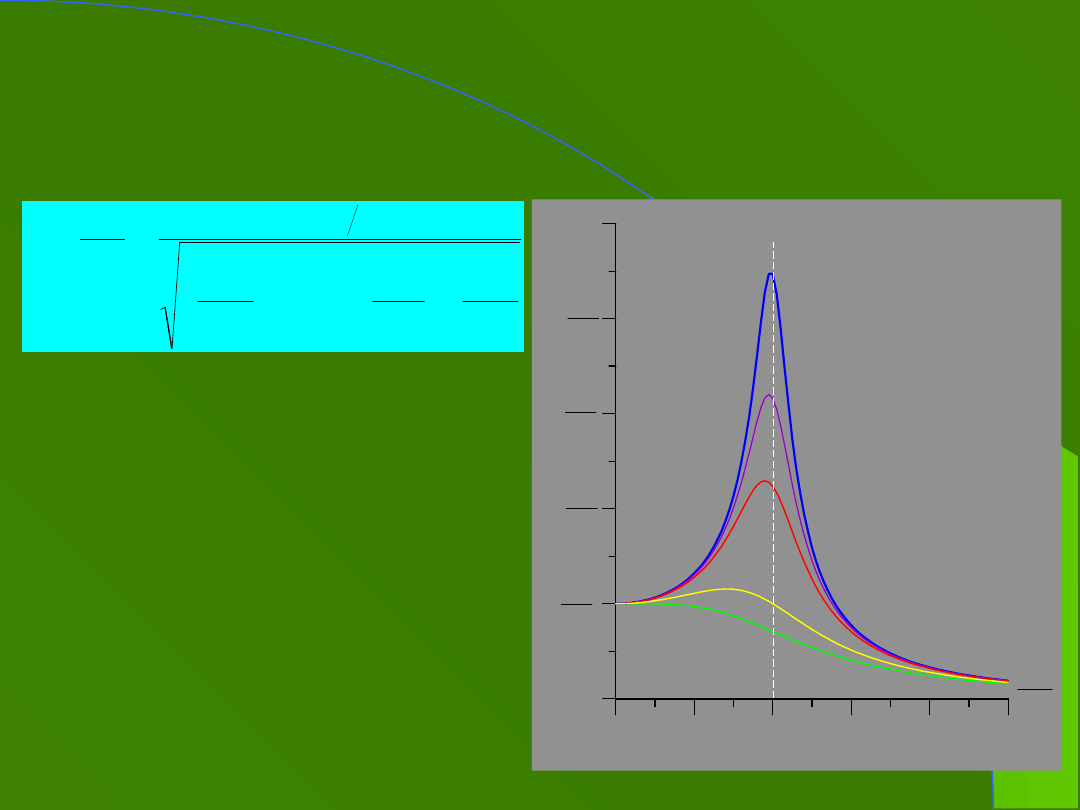
8a. Drgania wymuszone i

8a. Drgania wymuszone i

rezonans, c.d.

rezonans, c.d.





- częstotliwość

drgań

własnych układu

bez

tłumienia





’’







-

częstotliwość

rezonansowa

2

2

2

2

2

2

''

1

''















































m

b

k

F

F

A

m

m

0

A





''

 . 

 . 5

1 . 

1 . 5

2 . 

2 . 5

k

F

m

k

F

m

2

k

F

m

3

k

F

m

4

b=0,2m


b=m

