„Matematyka to gra

rozgrywana według pewnych

prostych reguł z nic nie

znaczącymi znakami na

papierze.”

David Hilbert

WZÓR FUNKCJI A WYKRES.

Funkcję można przedstawiać na wiele
sposobów jednak wszystkie te sposoby są ze
sobą ściśle powiązane. Kiedy weźmiemy do
ręki przepis na ciasto, nie widzimy co nam z
niego wyjdzie, ale jeśli będziemy postępowali
zgodnie z podaną procedurą, upieczemy
smakowity deser. Wzór funkcji możemy
traktować jako przepis na jej wykres, jeśli
będziemy się go trzymać zobaczymy jak
wygląda nasza funkcja.

JAK KORZYSTAĆ ZE

WZORU?

Przyjrzyjmy się funkcji określonej wzorem:

y = 2x - 2

Zauważmy, że nie podano dziedziny tej funkcji,
przyjmujemy więc, że do jej dziedziny należą
wszystkie liczby, dla których da się obliczyć wartość
tej funkcji – czyli w tym przypadku są to wszystkie
liczby rzeczywiste.
Korzystając ze wzoru funkcji możemy obliczać jej
wartość dla różnych argumentów (wyliczać y dla
różnych x). Argumenty wybieramy my, wstawiamy
do wzoru i obliczamy wartość funkcji, np.:
dla argumentu x = 0 funkcja przyjmuje wartość: y =
2· 0 – 2 = -2
dla argumentu x = 1 funkcja przyjmuje wartość: y =
2· 1 – 2 = 0
dla argumentu x = -1 funkcja przyjmuje wartość:
y = 2· (-1) – 2 = -4
itd.

JAK KORZYSTAĆ ZE

WZORU?

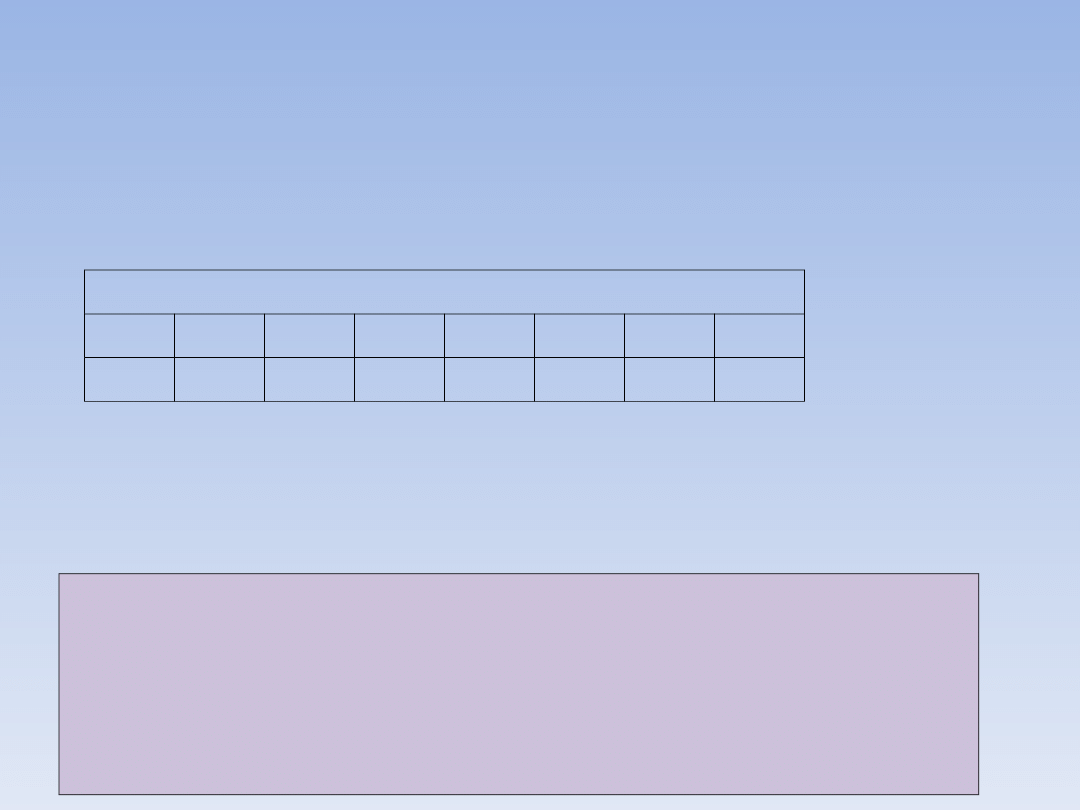
Po obliczeniu kilku, jeśli trzeba nawet kilkunastu
wartości dla wybranych przez nas argumentów,
możemy

sporządzić

tabelkę,

która

ułatwi

zaznaczanie punktów na wykresie:

Współrzędne odczytujemy parami góra – dół, w tej
tabelce mamy punkty o współrzędnych: (-2, -6); (-1,
-4); (0, -2); (1, 0);
(2, 2); (3, 4); (4, 6)

y = 2x - 2

x

-2

-1

0

1

2

3

4

y

-6

-4

-2

0

2

4

6

UWAGA

Argumenty należy dobierać tak, aby

punkty zmieściły się na wykresie i aby

łatwo było je zaznaczyć.

JAK KORZYSTAĆ ZE

WZORU?

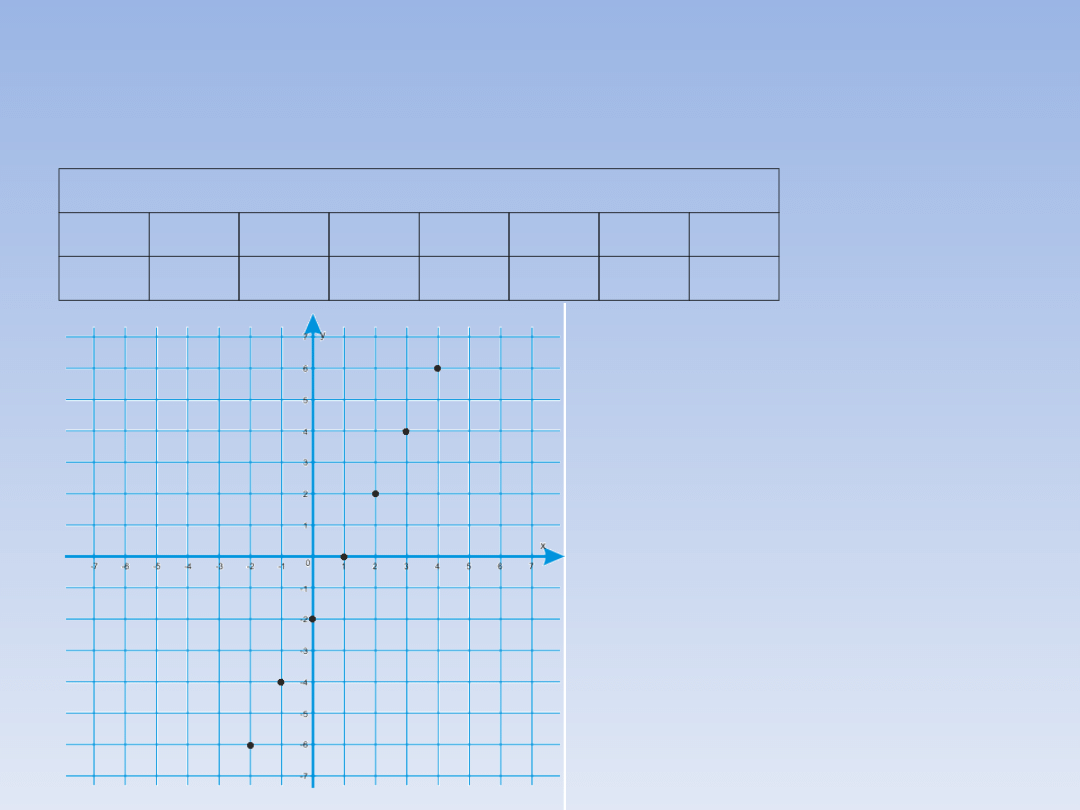
Punkty z tabeli zaznaczamy w układzie
współrzędnych

Zauważmy,

że

zaznaczone

punkty

układają się w linie
prostą. Dziedziną tej
funkcji jest zbiór liczb
rzeczywistych, możemy
więc połączyć nasze
punkty.

y = 2x - 2

x

-2

-1

0

1

2

3

4

y

-6

-4

-2

0

2

4

6

JAK KORZYSTAĆ ZE

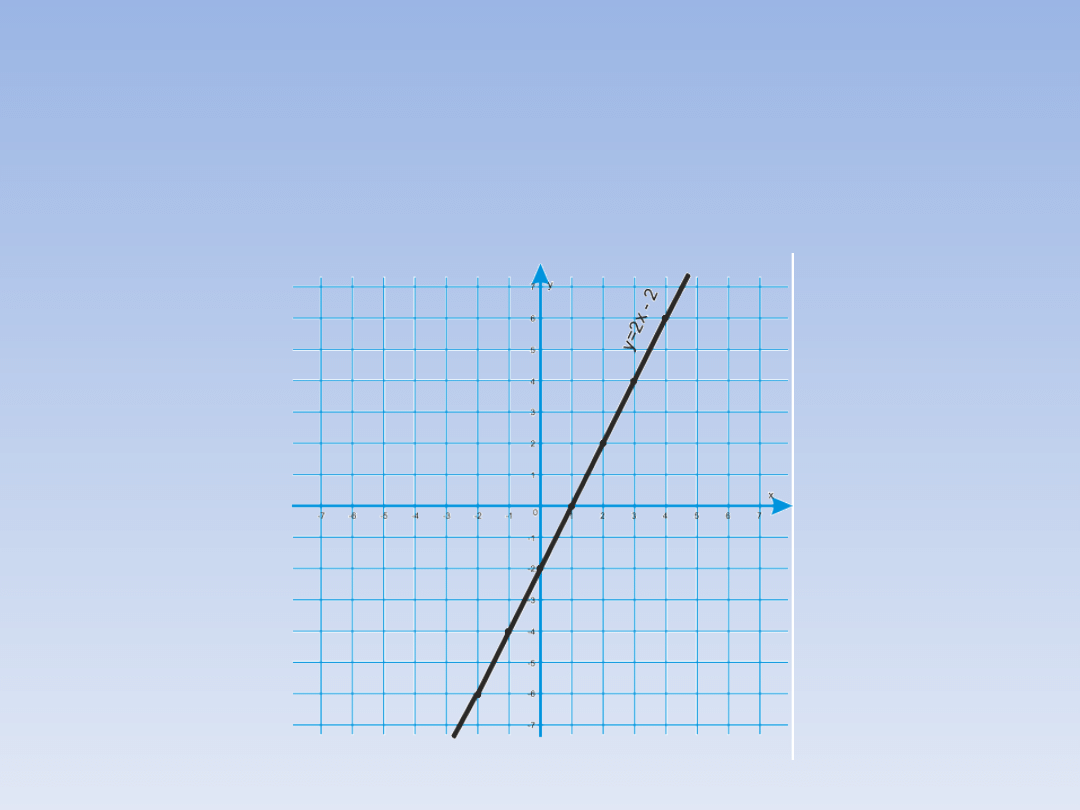
WZORU?

A oto wykres naszej funkcji:

y = 2x - 2

FUNKCJE LINIOWE.

Funkcje których wykresem jest linia prosta
nazywamy funkcjami liniowymi, do ich
narysowania wystarczą nam dwa punkty.
Funkcję liniową można rozpoznać po wzorze,
ma on zawszę postać:

y = ax + b

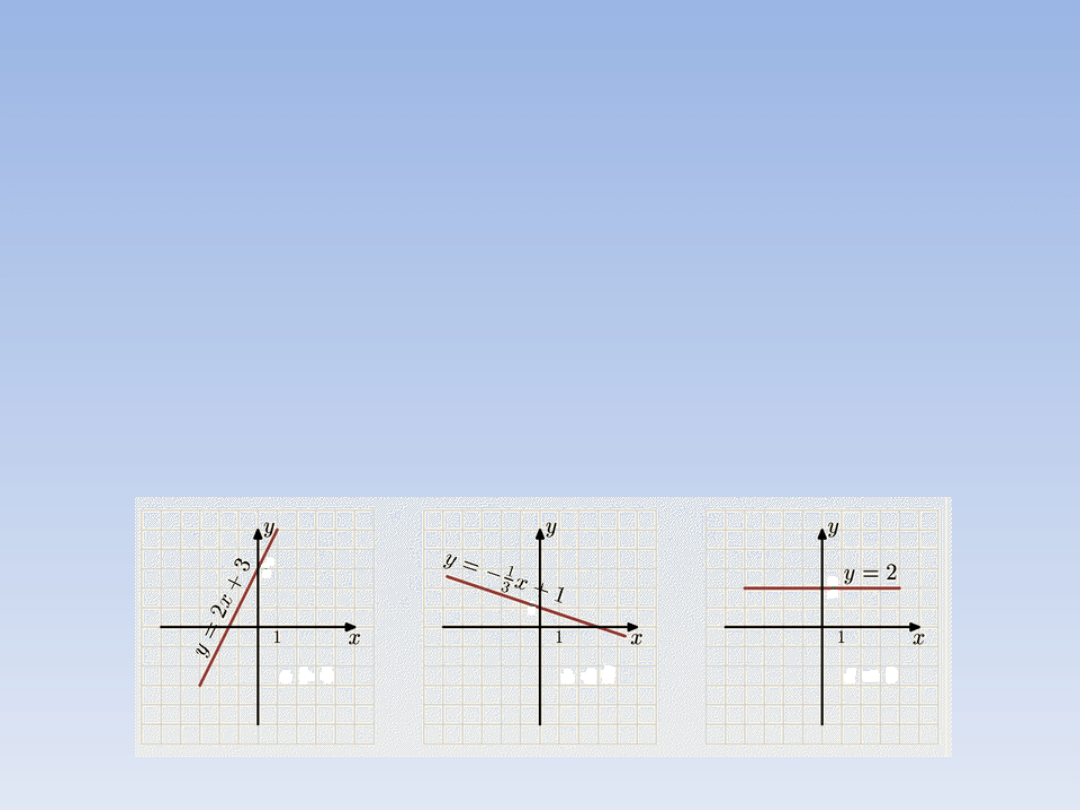
gdzie a i b to liczby rzeczywiste. Oto
przykłady innych funkcji liniowych i ich
wykresów:

FUNKCJE KWADRATOWE.

Nie, wykresem takich funkcji nie jest kwadrat,
ale jeśli spotasz wzór funkcji w którym
najwyższa potęga argumentu to dwa (czyli
kwadrat) np. y = 2x

2

+ 2, to możesz się

spodziewać, że wykresem tej funkcji będzie
parabola.
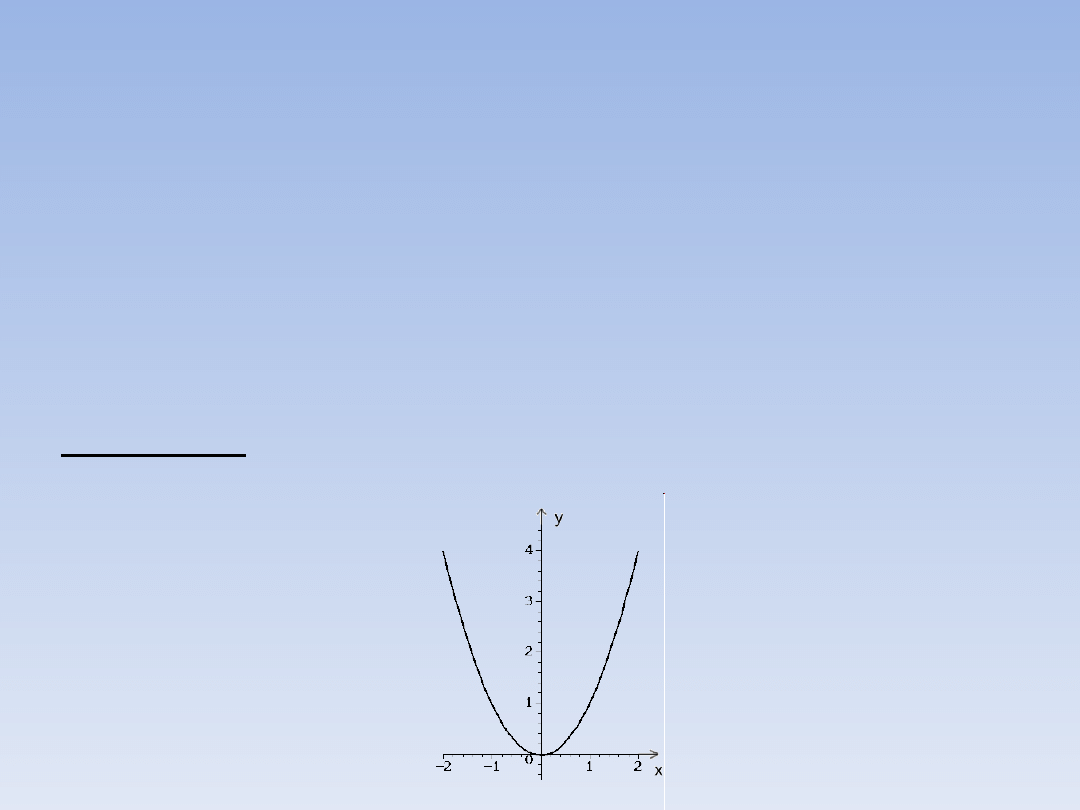
Najprostsza parabola to wykres funkcji y = x

2

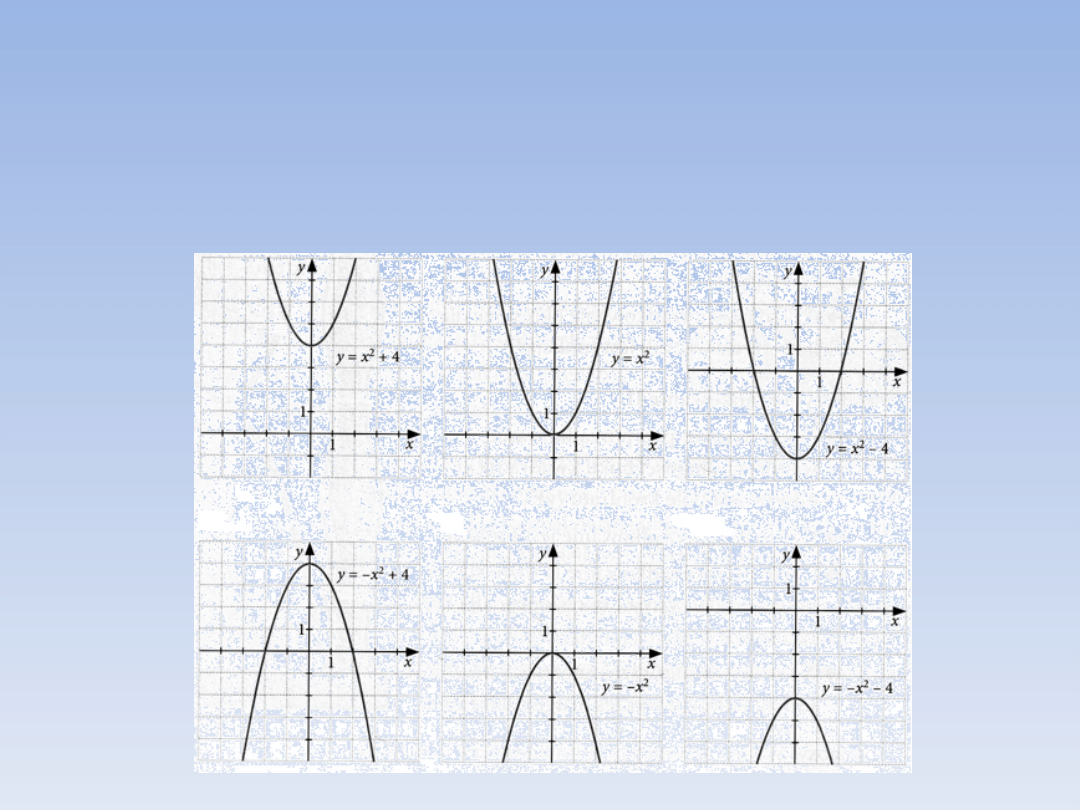
FUNKCJE KWADRATOWE.

Oto przykłady funkcji kwadratowych i ich
wykresów:

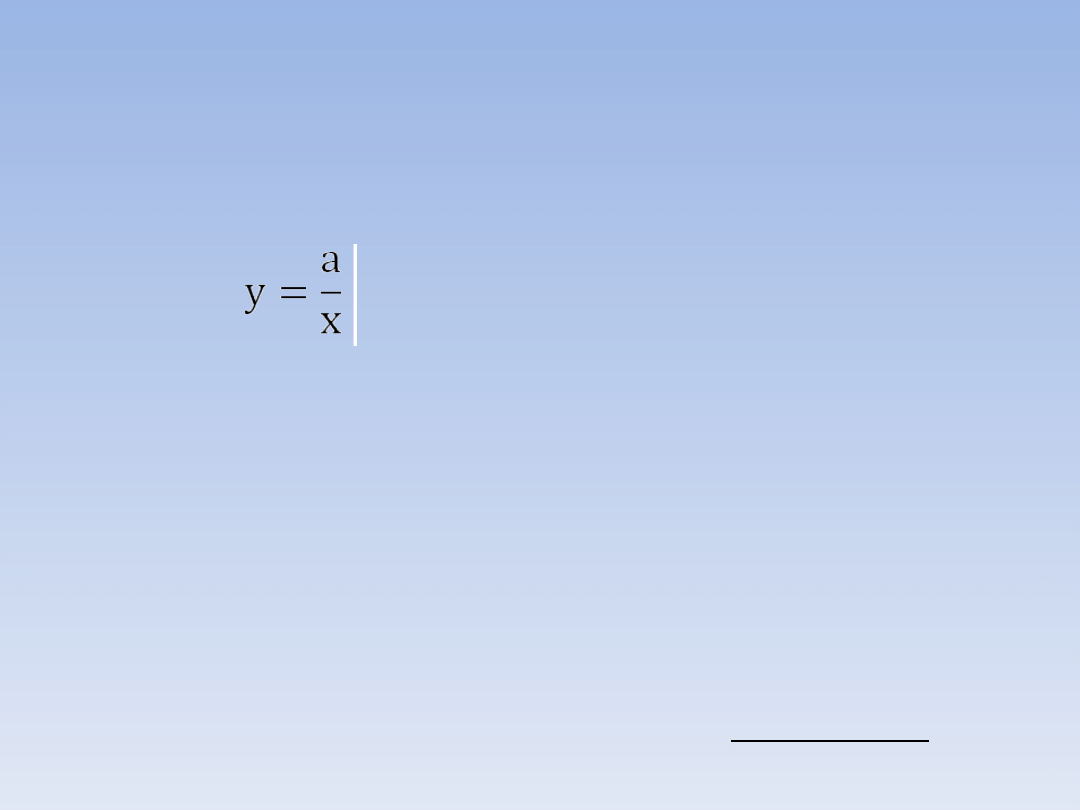
PROPORCJONALNOŚĆ

ODWROTNA

Proporcjonalność

odwrotna

to

każda

funkcja opisana

równaniem , gdzie a jest ustaloną
liczbą różną od 0

i oczywiście x ≠ 0 – pamiętajmy, nie można
dzielić przez 0. Jeśli nie ma podanej dziedziny
tej funkcji to przyjmujemy, że jest ona
określona dla wszystkich liczb rzeczywistych z
wyjątkiem

zera,

wtedy

wykresem

proporcjonalności odwrotnej jest hiperbola.

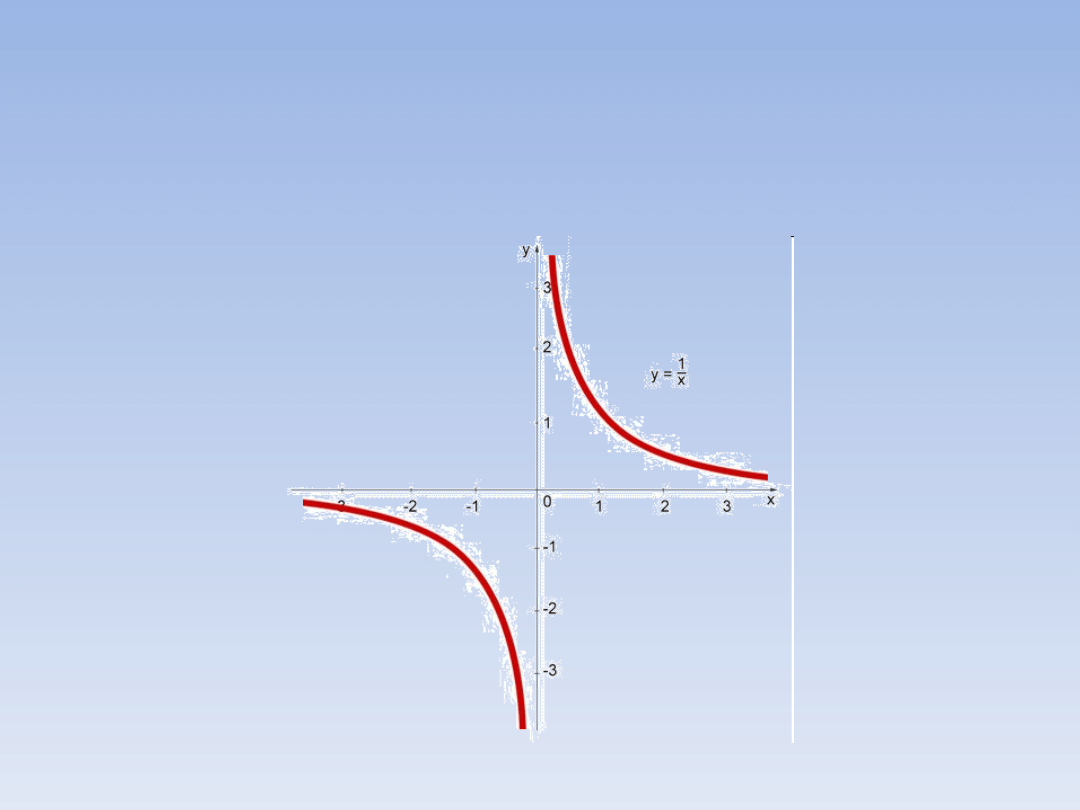
HIPERBOLA.

Oto przykład wykresu proporcjonalności
odwrotnej dla
a = 1:

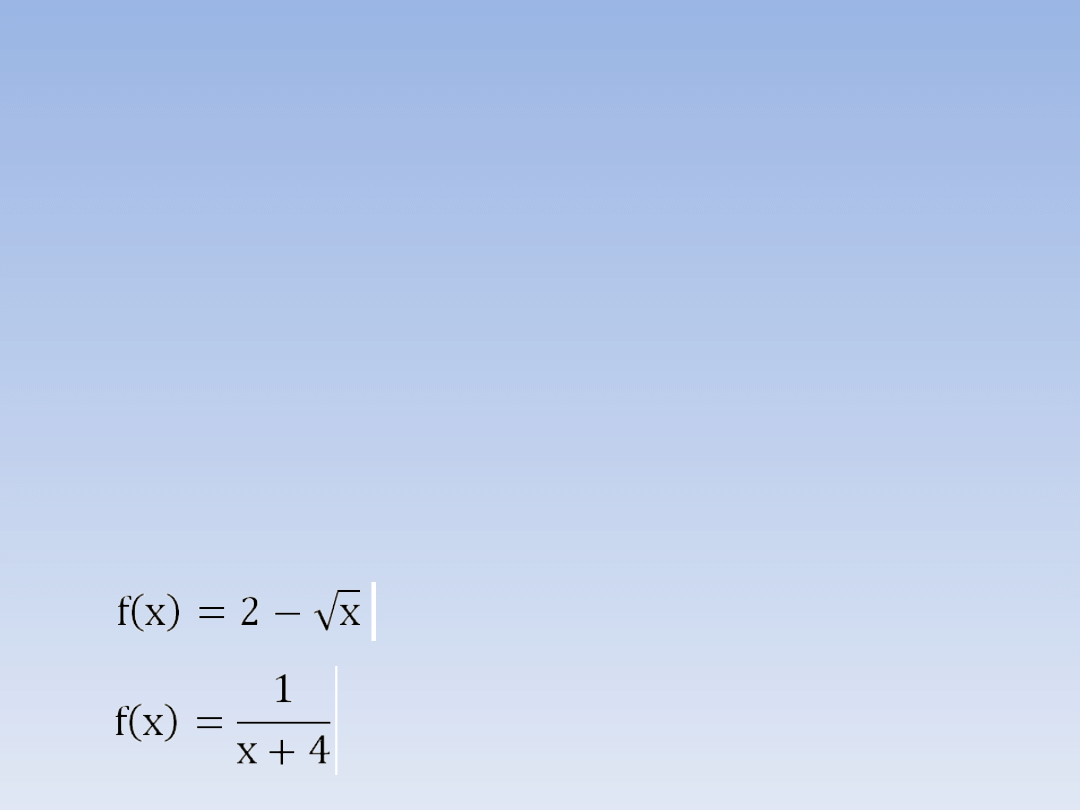
PRZYKŁADOWE

ZADANIA.

ZADANIE 1.
Jaką wartość przyjmuje dana funkcja dla
argumentu
x = 0, oraz dla argumentu x = 1.
Zamiast zapisywać ciągle „dla argumentu x
= … fukcja przyjmuje wartość y = …” łatwiej
jest używać zapisu f(x), który oznacza
„wartość funkcji f dla argumentu x”.

a)f(x) = x

3

b)

c)

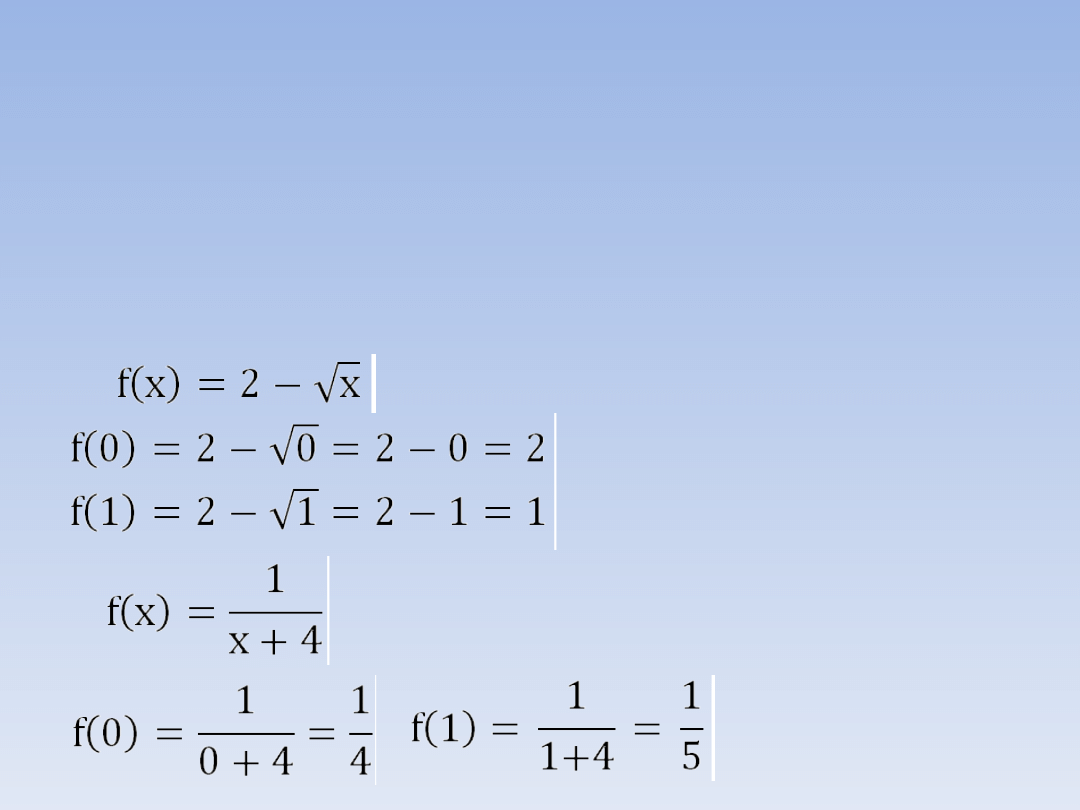
PRZYKŁADOWE

ZADANIA.

ZADANIE 1 – ciąg dalszy.
a) f(x) = x

3

f(0) = 0

3

= 0

f(1) = 1

3

= 1

b)

c)

,

PRZYKŁADOWE

ZADANIA.

ZADANIE 2.
Punkty A, B i C należą do wykresu podanej
funkcji. Jakie są drugie współrzędne tych
punktów?
f(x) = 4x(x – 2) A = (-2, _), B = (0, _), C = (-1,
_)
Pierwsza współrzędna każdego punktu to x
czyli nasz argument, aby znaleźć drugą
współrzędną wystarczy obliczyć wartość
funkcji dla podanych argumentów.
f(-2) = 4 · (-2) · (-2 – 2) = -8 · (-4) = 32
f(0) = 4 · 0 · (0 – 2) = 0
f(-1) = 4 · (-1) · (-1 – 2) = -4 · (-3) = 12
Nasze punkty to: A = (-2, 32), B = (0, 0), C =
(-1, 12)

PRZYKŁADOWE ZADANIA.

ZADANIE 3.
Sprawdź, które z podanych w nawiasie są
miejscem

zerowym

funkcji

określonej

wzorem f(x) = 1 – x

3

(1, -1, 0).

Wystarczy sprawdzić dla której z tych liczb
funkcja przyjmuje wartość 0:
f(1) = 1 – 1

3

= 1 – 1 = 0

f(-1) = 1 – (-1)

3

= 1 – (-1) = 2

f(0) = 1 – 0

3

= 1 – 0 = 1

Miejscem zerowym tej funkcji jest 1.

PRZYKŁADOWE ZADANIA.

ZADANIE 4.
Uzupełnij tabelkę:

W pierwszych dwóch kolumnach wystarczy
podstawić podane argumenty do wzoru
funkcji:

f(2) = 8 – 2 · 2 = 8 – 4 = 4
f(3) = 8 – 2 · 3 = 8 – 6 = 2

y = 8 – 2x

x

2

3

y

5

0

PRZYKŁADOWE ZADANIA.

ZADANIE 4 – ciąg dalszy.
W dwóch ostatnich kolumnach mamy
podaną wartość funkcji, musimy więc wpisać
ją do wzoru zamiast y i rozwiązać równanie:

Nasza tabelka po uzupełnieniu powinna
wyglądać tak:

5 = 8 – 2x

5 – 8 = - 2x

-3 = -2x /: (-2)
1,5 = x

0 = 8 – 2x

-8 = -2x / : (-2)

4 = x

y = 8 – 2x

x

2

3

1,5

4

y

4

2

5

0

PRZYKŁADOWE ZADANIA.

Zadanie 5.
Dla jakiego argumentu funkcja o podanym
wzorze przyjmuje wartość 5?
y = 0,2x – 1

Wystarczy wpisać 5 zamiast y we wzorze i
rozwiązać równanie:
5 = 0,2x – 1
5 + 1 = 0,2x
6 = 0,2x / : 0,2
30 = x

PRZYKŁADOWE ZADANIA.

Zadanie 6.
Znajdź miejsce zerowe funkcji y = 0,5x + 5.

Zamiast y we wzorze wstawiamy 0 i
rozwiązujemy równanie:
0 = 0,5x + 5
-5 = 0,5x / : 0,5
-10 = x

Miejscem zerowym funkcji y = 0,5x + 5 jest
x = -10