GEODEZJA

Rachunek

współrzędnych

Metody obliczeń geodezyjnych stosowane do

obliczenia współrzędnych punktów

:

-osnów

geodezyjnych,

- szczegółów terenowych przy

aktualizacji map

gospodarczych,

- obiektów przy wyznaczaniu kształtu lub zmian
ich kształtu (

przemieszczeń i odkształceń

budowli),

- projektowanych budowli

przy opracowaniu

geodezyjnym projektów zagospodarowania
terenu,

- obiektów przy

inwentaryzacji powykonawczej

i

pomiarach kontrolnych.

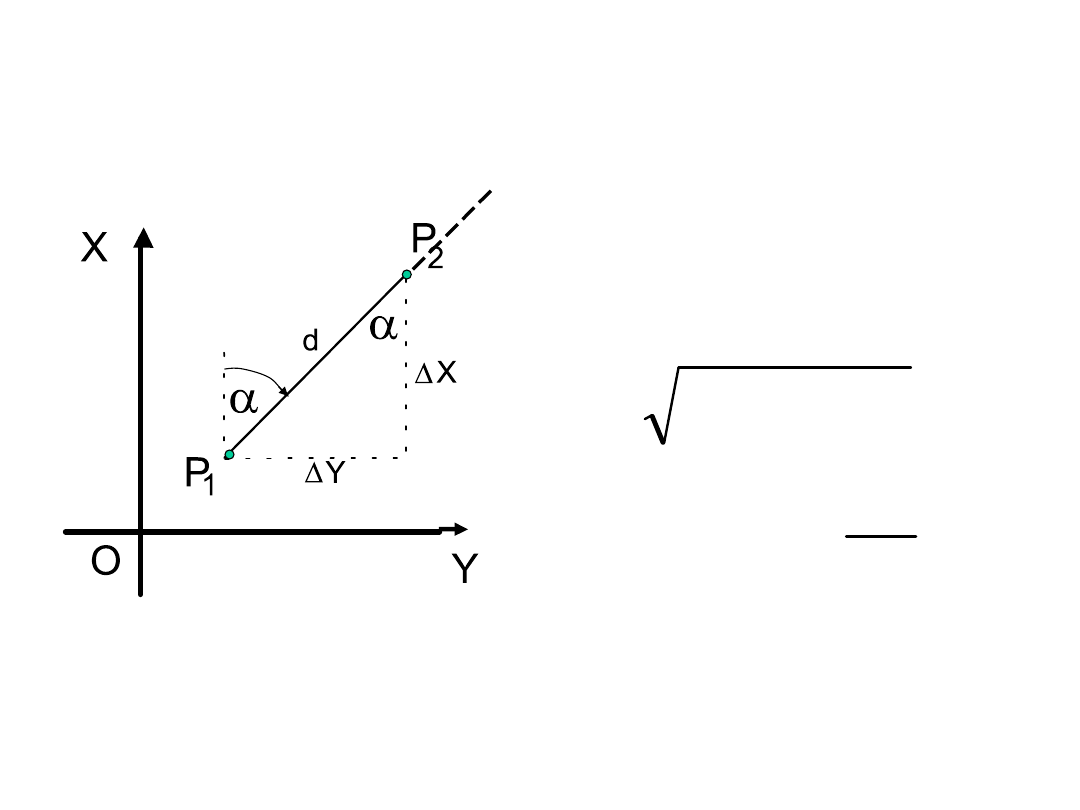
Punkt P

2

na prostej (koniec odcinka)

2

1

1

2

2

1

1

2

sin

cos

















d

y

y

d

x

x

r

x

y

arctg

y

x

d



















)

(

2

1

2

2



Δx

1,2

= x

2

– x

1

, Δy

1,2

= y

2

– y

1

.

Oznaczenia:

d – długość odcinka P

1

P

2

,



1-2

– azymut odcinka P

1

P

2

,

x, y – przyrosty (różnice) współrzędnych:
x

1-2

= x

2

– x

1

, y

1-2

= y

2

– y

1

,

r – składnik redukcyjny zależny od orientacji odcinka,

(ćwiartki układu współrzędnych):

I.

x



0 i y>0 r = 0,

II.

x



0 i y>0 r =



III.

x



0 i y<0 r =



,

IV.

x



0 i y<0 r = 2



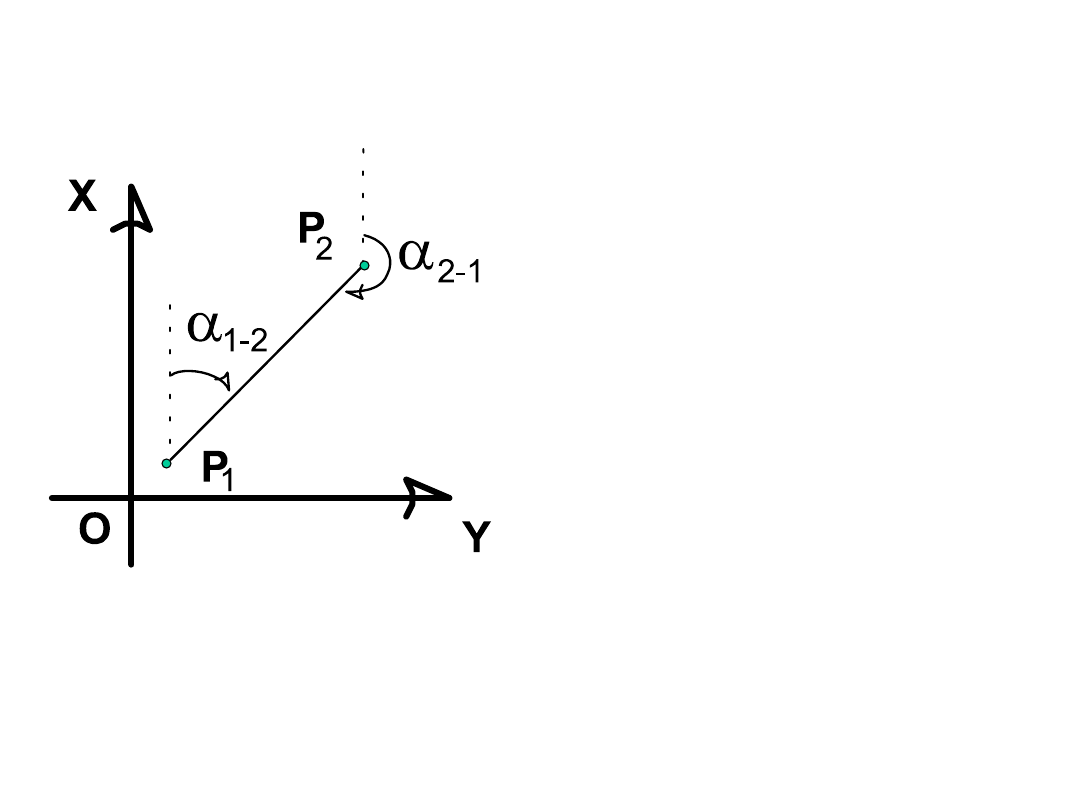
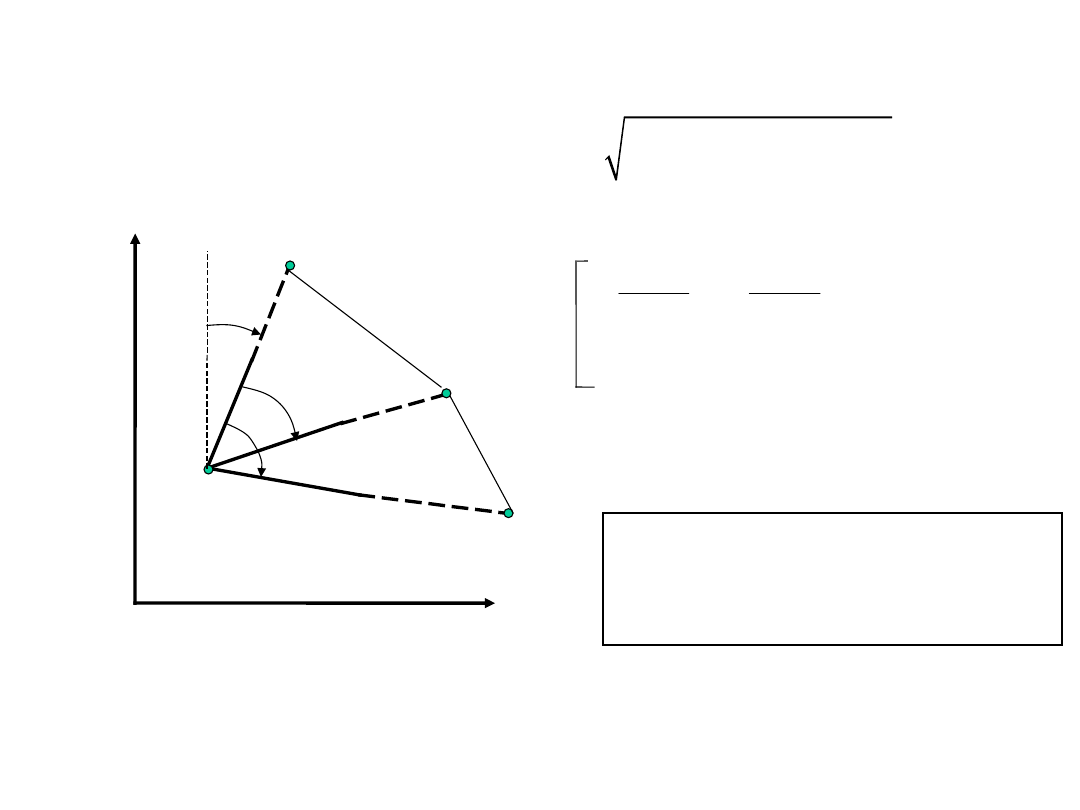
Azymut odcinka i azymut odwrotny:



2-1

= 

1-2

±





1-2

= 

2-1

±



W jednostkach miary stopniowej



= 180

o

, gradowej



= 200

g

,

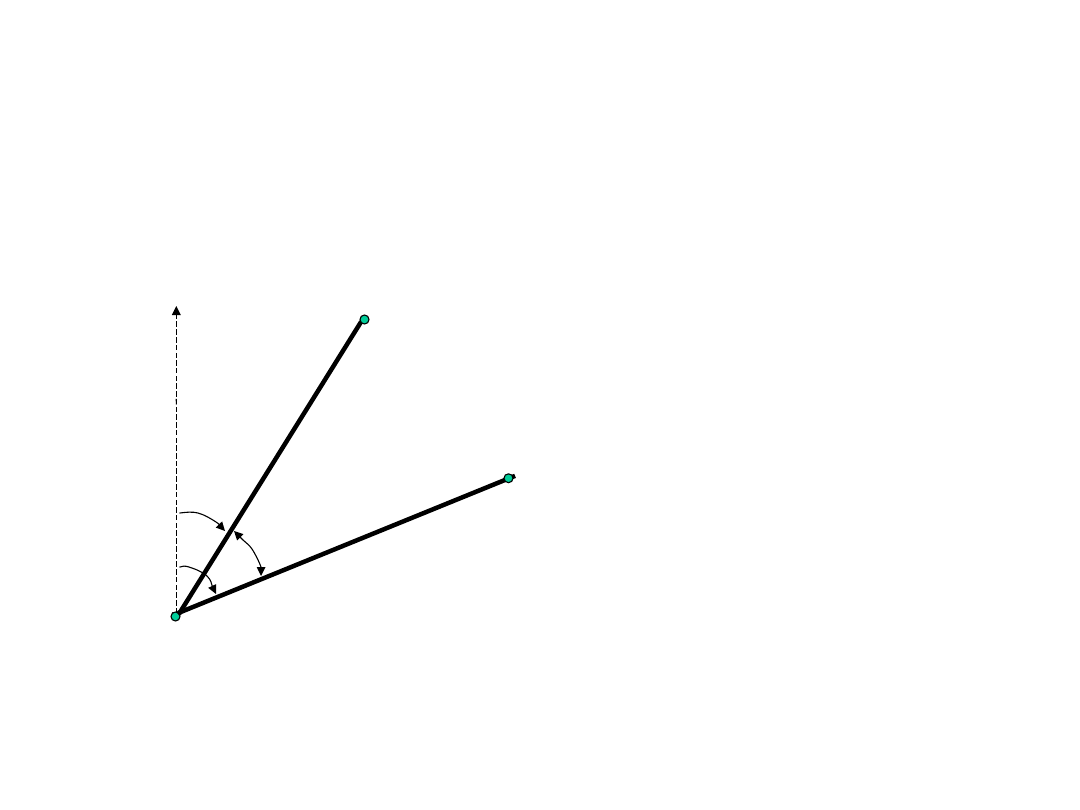
Obliczenie kąta:



1-

2





1-3

P

1

P

2

P

3

 = 

1-3

- 

1-

2

Kąt poziomy  jako różnica azymutów odcinków.

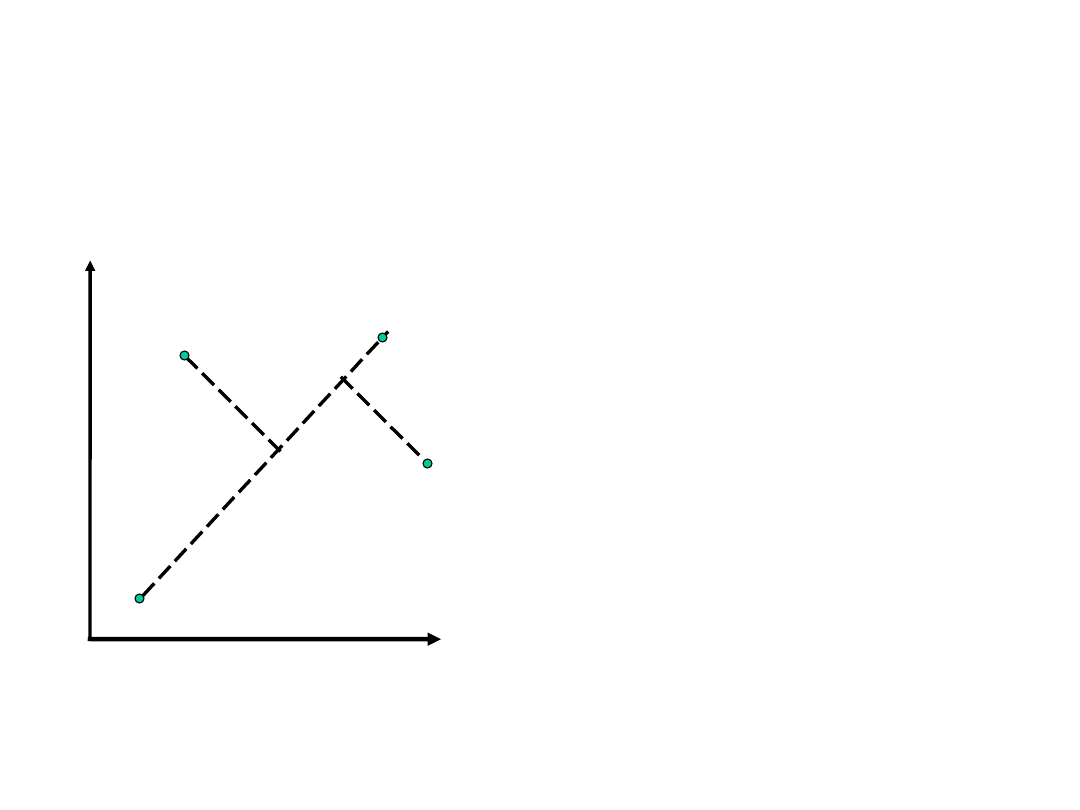
Punkty na prostopadłej:

X

Y

P

1

P

2

P

L

P

P

d

L

d

P

b

L

b

P

P

L

:

x

L

= x

1

+ b

L

cos



1-2

+ d

L

sin



1-2

y

L

= y

1

+ b

L

sin



1-2

- d

L

cos



1-2

P

P

:

x

P

= x

1

+ b

P

cos



1-2

- d

P

sin



1-2

y

P

= y

1

+ b

P

sin



1-2

+ d

P

cos



1-2

b

P

, d

P

– miara bieżąca i domiar prostokątny

punktu P

P

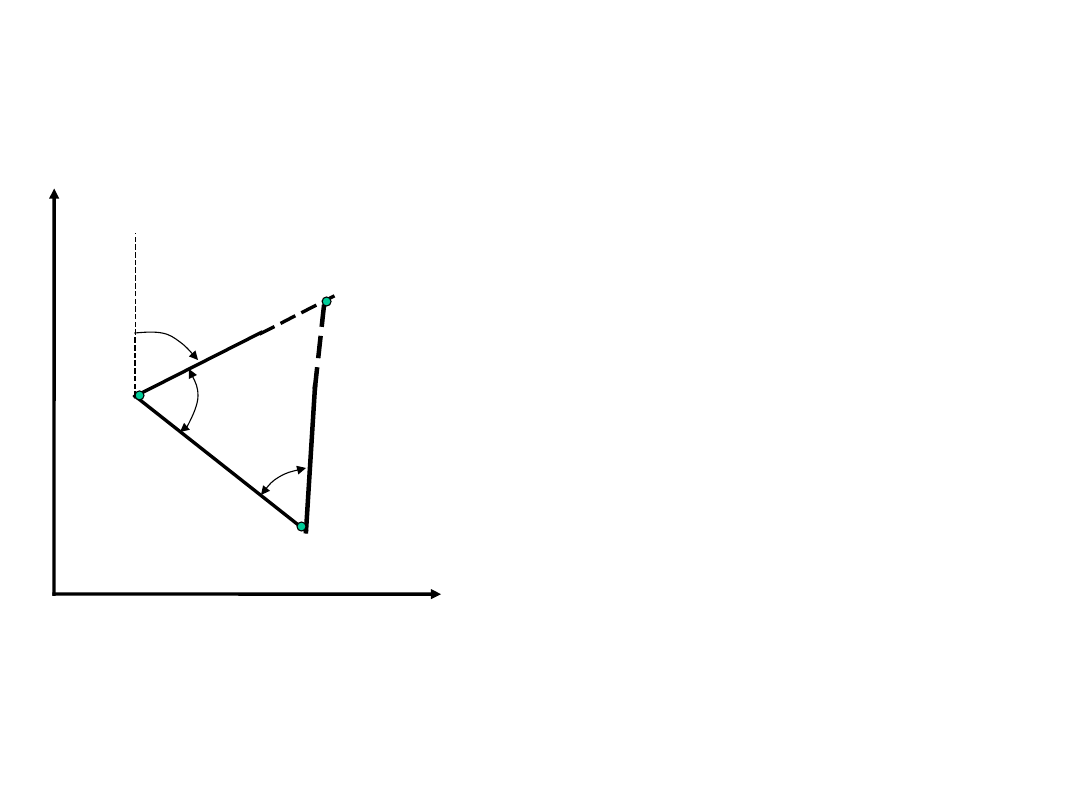
Zasady obliczania wcięcia kątowego w
przód

X

Y

A

B

P



A-P



A



B



A-P

– azymut kierunku wcinającego

AB – baza wcięcia



A-P

= 

A-B

– 

A

d

A-B

= [(x

B

– x

A

)

2

+ (y

B

– y

A

)

2

]

1/2

d

A-P

= (d

AB

sin 

B

)/sin(

A

+

B

)

x

P

= x

A

+d

AP

cos



A-P

y

P

= y

A

+ d

AP

sin



A-P

d

A-B

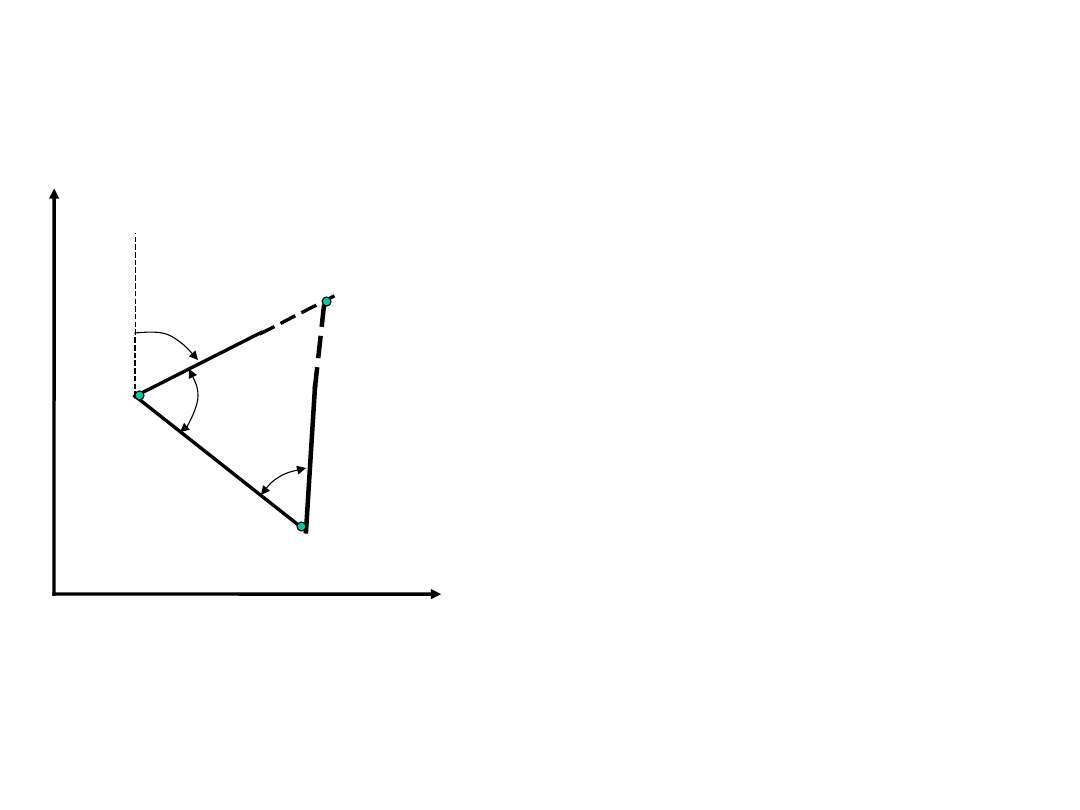
Zasady obliczania wcięcia liniowego w przód



A-P

= 

A-B

– 

A

d

A-B

= [(x

B

– x

A

)

2

+ (y

B

– y

A

)

2

]

1/2

cos(

A

)

= (d

2

A-B

+ d

2

A-P

- d

2

B-P

)/(2d

A-B

d

A-B

)

x

P

= x

A

+d

A-P

cos



A-P

y

P

= y

A

+ d

A-P

sin



A-P

X

Y

A

B

P



A-P



A



B

d

A-B

d

A-P

d

B-P

d

A-P

, d

B-P

– długości odcinków (z pomiaru)



A

, 

B

- wartości kątów poziomych (obliczone)

Obliczenie wcięcia wstecz:

P

1

P

2

P

3



S-P1

S



1



2



1

,

2

– kąty poziome z pomiaru, pomocnicze obliczone:

, ,,,
S – punkt wyznaczany z wcięcia

(

) (

)

2

2

1 2

2

1

2

1

d

x x

y y

-

=

-

+ -

(

)

45

2

2

o

tg

tg

tg

j y

j y

m

-

+

=

-









+ = 360

º

– ( +  +



2

)

 = 180

º

– (

1

+)

 = 180

º

– (

2

- 

1

+)

X

Y

d

1-2

d

2-

3

ctg  = (d

2-3

sin 

1

)/(d

1-2

sin(

2

-



1

))

d

S-P1

= (d

1-2

sin )/ sin 

1



S-P1

= 180

º

+ (

1-2

+)

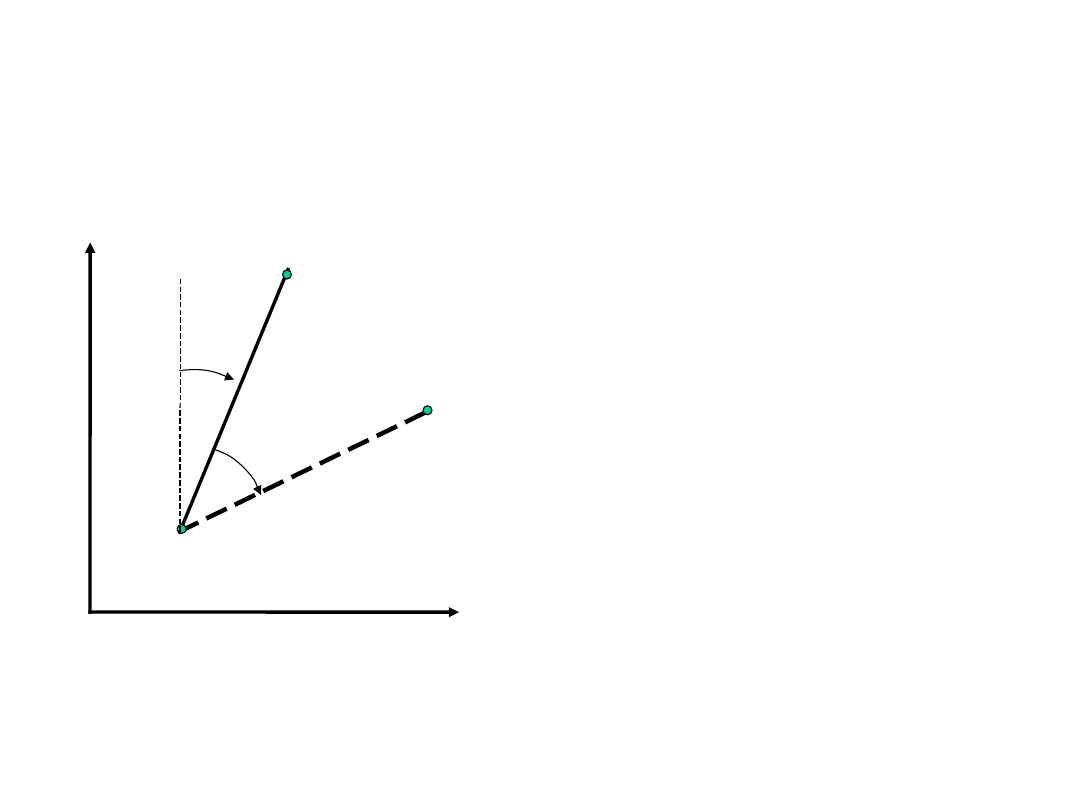
X

Y

B

C

P

i

Przeliczenie współrzędnych z układu

biegunowego



i

- kąt biegunowy punktu

P

i

d

i

- odległość biegunowa



i

d

i



B-Pi

= 

B-C

+ 

i

x

Pi

= x

B

+d

i

cos



B-Pi

y

Pi

= y

B

+ d

i

sin



B-Pi



B-C

B – biegun układu - (stanowisko pomiarowe)

BC – oś biegunowa

Dane:

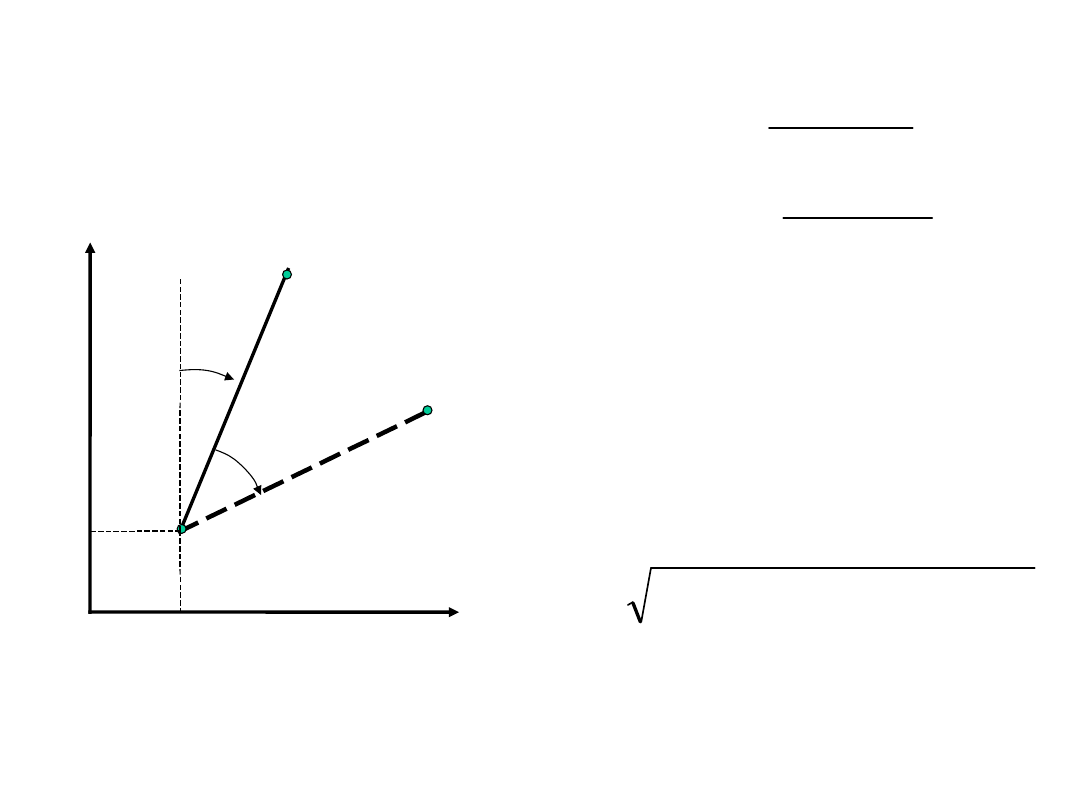
Przeliczenie współrzędnych z układu
prostokątnego

X

Y

B

C

P

i



i

- kąt biegunowy punktu

P

i

d

i

- odległość biegunowa



i

d

i



i

=



B-Pi

- 

B-C



A-P

Do
obliczenia:

Y

B

X

B

Dane:

X

B

, Y

B

współrzędne bieguna układu

X

C

, Y

C

współrzędne punktu na osi biegunowej

2

B

Pi

2

B

Pi

i

)

Y

-

(Y

)

X

(X

d







)

Y

X

Y

Y

(

arctg

B

C

B

C

C

B-









)

Y

X

Y

Y

(

arctg

B

Pi

B

Pi

Pi

B-









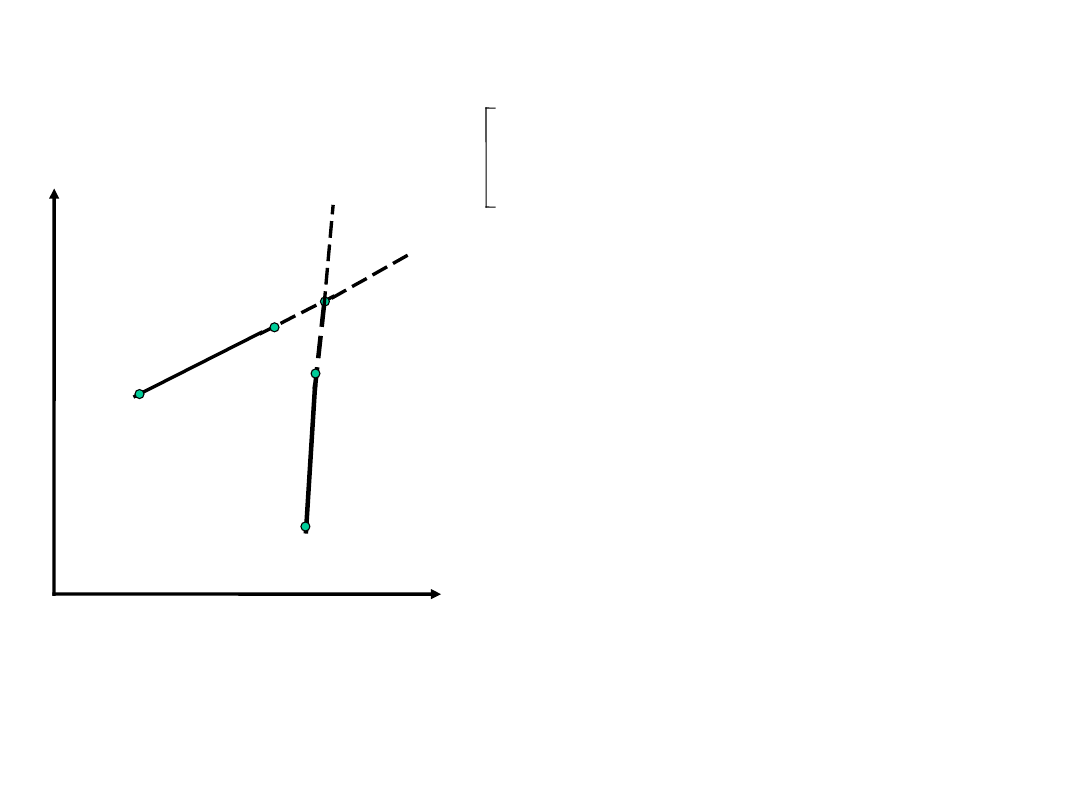
Punkt przecięcia dwóch prostych (odcinków)

X

P

1

P

o

P

4

P

3

P

2

A

1

x + B

1

y + C

1

= 0

A

2

x + B

2

y + C

2

= 0

X

O

= (C

1

A

2

- C

2

A

1

)/(A

1

B

2

- A

2

B

1

)

Y

O

= (C

2

B

1

– C

1

B

2

)/(A

1

B

2

- A

2

B

1

)

Y

x

1-2

= x

P2

– x

P1

, y

1-2

= y

P2

– y

P1

x

3-4

= x

P4

– x

P3

, y

3-4

= y

P4

– y

P3

współczynniki

A = - y, B = x,
C = y x

Pk

- x y

Pk

(k=1 lub

3)

Układ
równań:

OBLICZENIE POLA POWIERZCHNI FIGUR

Pole figury na podstawie miar:

• Z bezpośredniego pomiaru
• Z mapy

Metody:

- graficzna (podział figury na trójkąty, trapezy,
prostokąty)

- analityczna (z pomierzonych wymiarów, współrzędnych)
- mechaniczna (planimetry)

Metoda

graficzna

wyznaczania

pól

bazuje

na

miarach

pomierzonych na mapie Stawia metodę graficzną w grupie metod

niższej dokładności

. Pomiary na mapie elementów potrzebnych do

obliczenia wyznaczanego pola zawierają błędy.

Błąd względny

wyznaczania pola metodą graficzną

w = 1/200.

Działkę wybraną do

pomiaru dzieli się na figury proste (trójkąty, prostokąty i trapezy), w
których potrzebne długości odcinków wyznaczamy za pomocą cyrkla i
podziałki.

Metoda analityczna

- elementy potrzebne do obliczenia są

mierzone w terenie, a pole powierzchni określone jest na podstawie
tych

pomiarów

lub

ich

funkcji

(współrzędnych).

Błąd względny pola:

w = 1/1000

(gdy błąd pomiaru kątów będzie

±1” , a błąd względny pomiaru długości boków nie większy od
1/2000).

Metoda mechaniczna

polega na pomiarze powierzchni na mapach

przy użyciu planimetrów. Urządzenia te w wyniku przeprowadzonego
pomiaru dają wartość odczytu kółka całkującego. Do obliczenia pola
wykorzystuje się wzór: P = C

1

*n. C

1

– stała planimetru zależna od

skali rysunku i długości ramienia wodzącego przyrządu. Dokładność
jest równoważna metodzie graficznej.

Często stosowana w praktyce jest kombinacja metody analitycznej i
graficznej. Ma szczególne zastosowanie przy pomiarach wąskich i
długich działek. Z wstępnej analizy dokładności na podstawie wzoru:
P = a*b, wnioskujemy, że decydujący wpływ na błąd pola, ma błąd
boku krótkiego.

Błąd względny pola:

w = 1/2000 - 1/500 zależnie od

skali mapy.

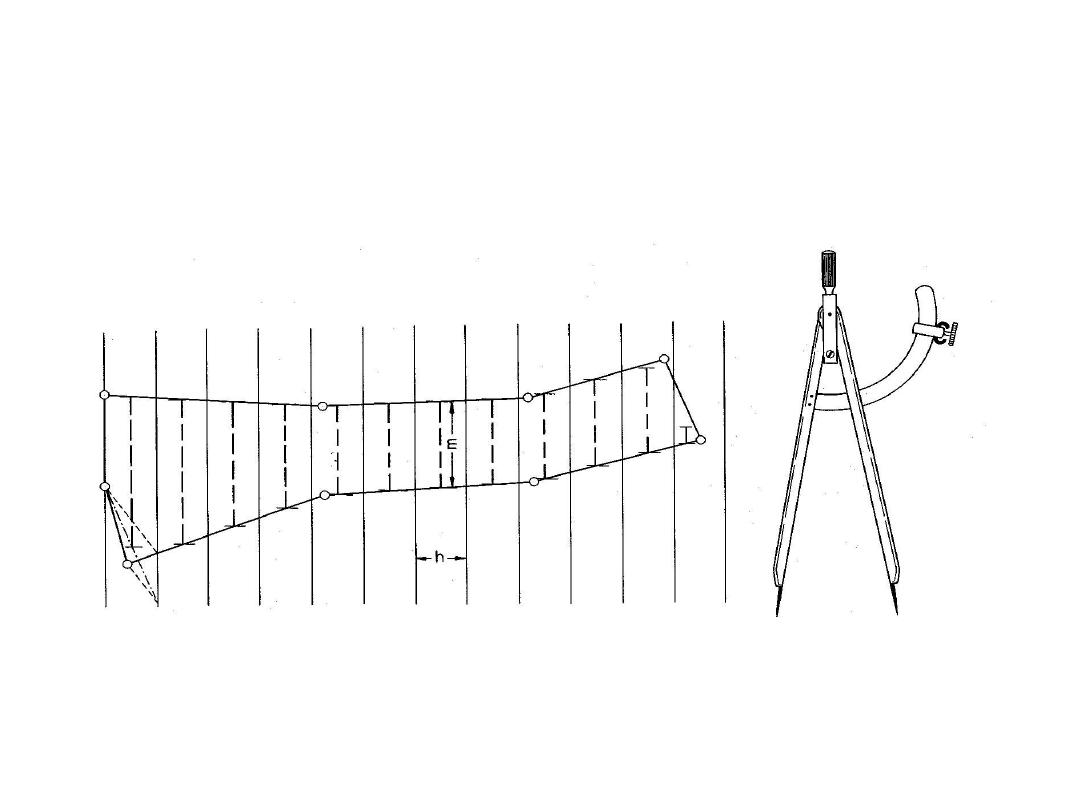
1. Metoda graficzna podział figury na trapezy

Szablon linii równoległych w równych odstępach = h, na kalce
(przeźroczystej folii), dzieli figurę na n trapezów. Cyrkiel pomaga w
pomiarach średniej z obu podstaw każdego trapezu.

b

i

cyrkie
l

P = h

 b

i

Automatyzacja obliczania powierzchni na mapach

Znaczne przyspieszenie obliczania pola figur na

mapach

analogowych i

zwiększenie dokładności umożliwiają

digimetry.

Digimetr, to przetwornik graficzno-cyfrowy lub

koordynatometr (digitizer), jest urządzeniem, które
przetwarza informacje graficzne (rysunek, mapa) na

postać cyfrową

.

Wyznaczenie pól figur na

mapach numerycznych

:

przebiega automatycznie pod kontrolą programów
systemu graficznego obsługującego mapę numeryczną.
Sprowadza się to do wskazania kursorem ikony z paska
narzędziowego,

a

następnie

kolejnych

punktów

(wierzchołków) figury na obrazie mapy wyświetlonej w
oknie monitora.

Systemy informatyczne

posiadają specjalne

moduły

,

które ułatwiają proces obliczania pola w typowych
zadaniach. W tym przypadku figury na mapach
(rysunkach projektów) są obiektami, a pole figury jest
jedną z cech, które uzyskuje się przez wskazanie
dowolnego punktu obiektu.

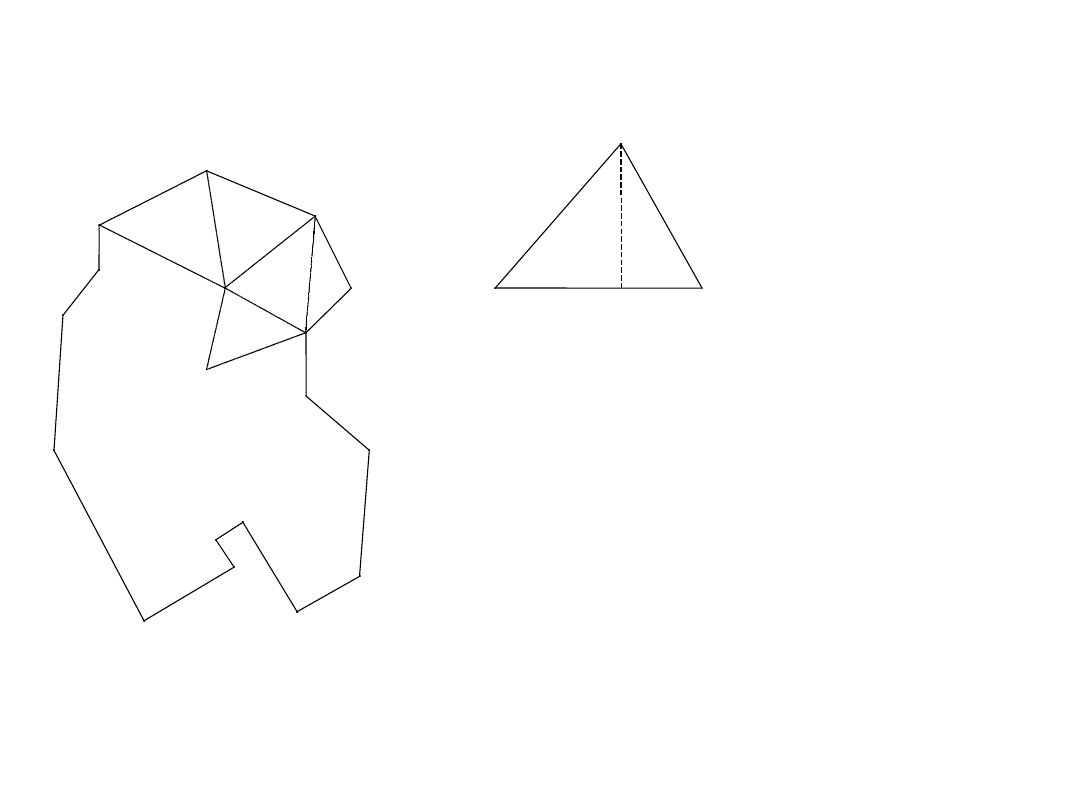
Metoda graficzna - podział na trójkąty:

1

2

3 4

a

h

P

i

= (a

i

h

i

)/2









n

i

1

i

i

P

P

b

c

lub wz. Herona:

q = (a+b+c)/2

P

i

={q(q-a)(q-b)(q-

c)}

½

Pole figury = Suma pól
trójkątów:

1

2

3

2

4

1
2

n-1

n

S





i

= 

i+1

-



i

Różnica kątów
biegunowych:

d

s.-i

d

s.-{i+1}















n

i

1

i

i

1

i

1

i

i

)

sin(

d

d

0.5

P





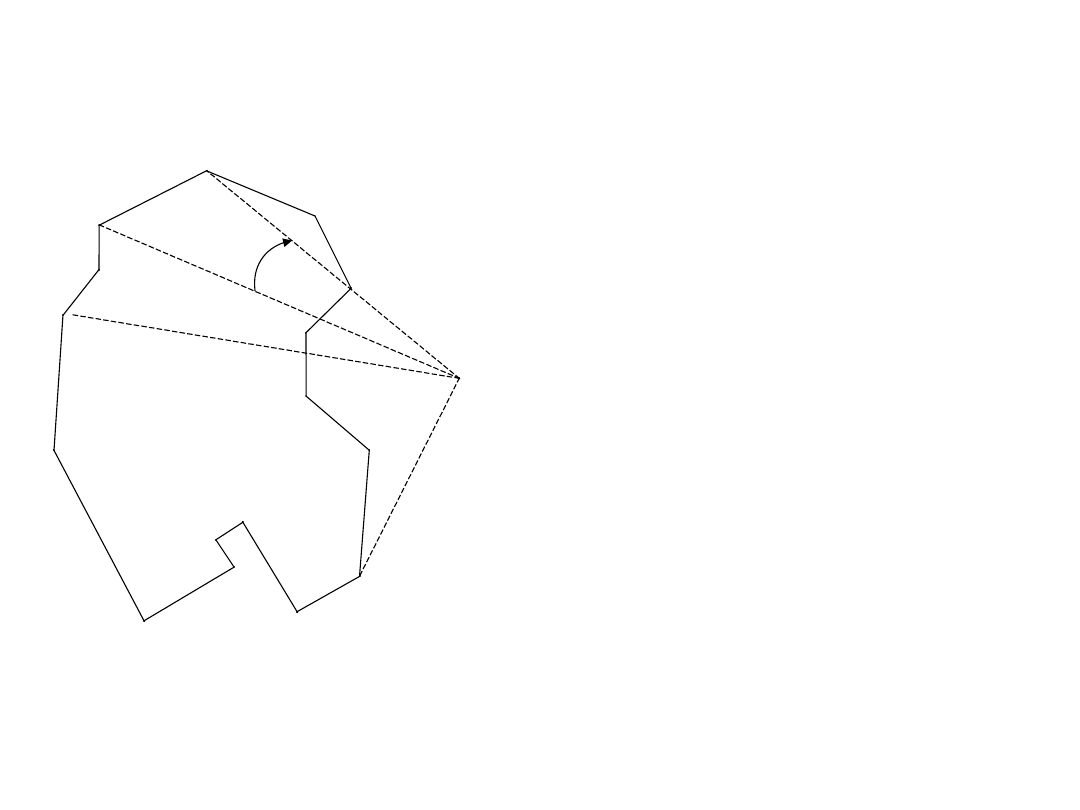
3. Metoda analityczna - obliczenie pola ze współrzędnych
biegunowych:

S – biegun (stanowisko pomiarowe)

współrzędne biegunowe:

Punkt nr 1

,



1

, d

s.-1

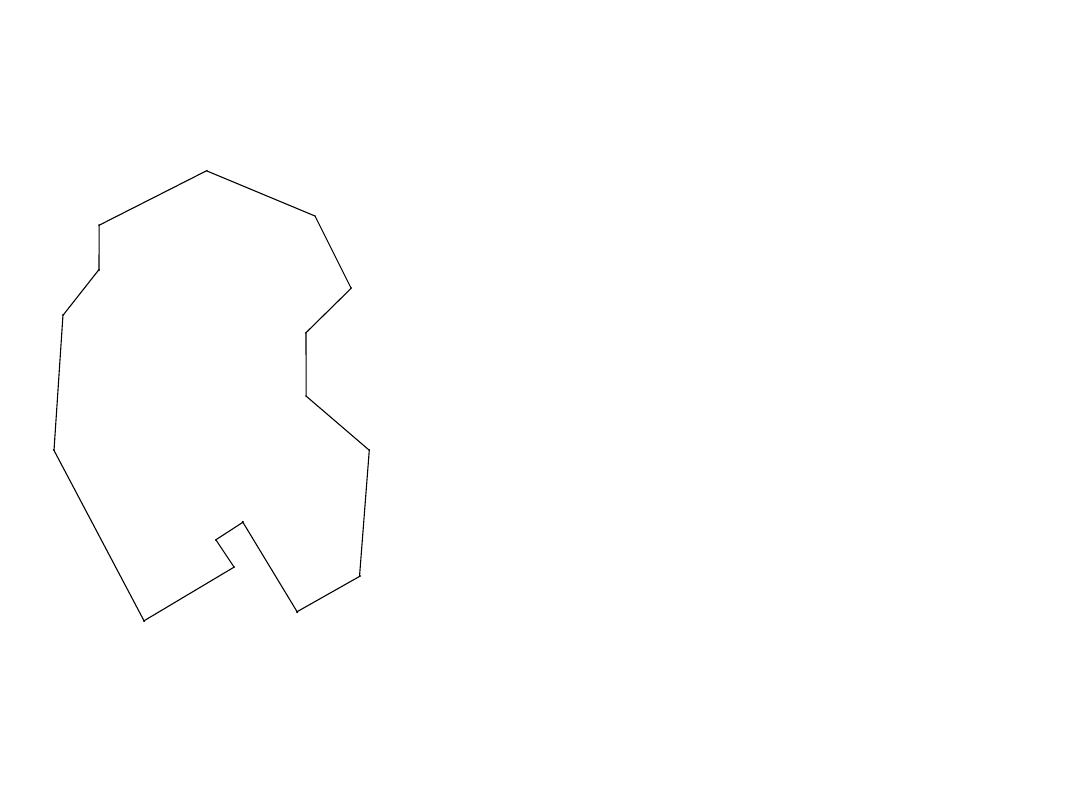
Metoda analityczna - obliczenie pola ze współrzędnych

prostokątnych:

1

11

3

2

4

1
2

n

Obliczamy współrzędne wierzchołków
figury lub odczytujemy z mapy.

Wzór Gaussa:











n

i

1

i

1

-

i

1

i

i

)

y

-

y

(

x

0.5

P

Planimetry

- biegunowe
- wózkowe

Planimetry biegunowe

mechaniczny

elektroniczny

1/300

1/1000

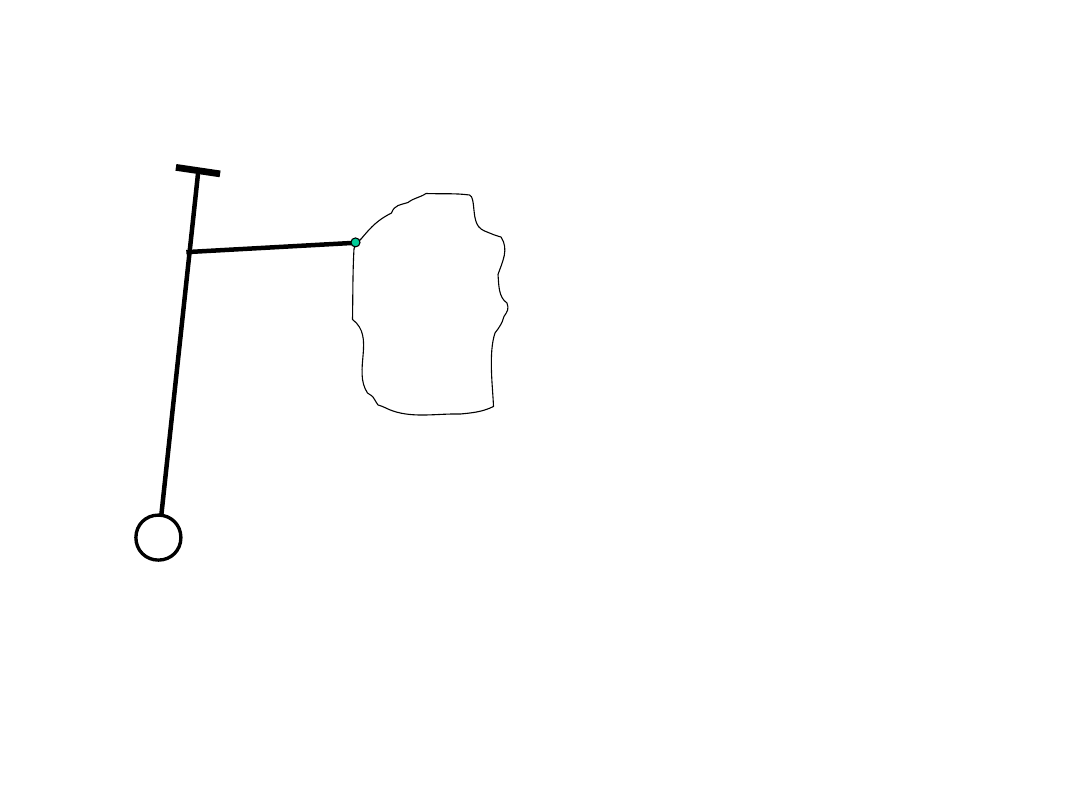
B

KC

W

O

Zasada planimetru biegunowego

B – biegun

OW - R

w

= długość ramienia

wodzącego

W – wodzik

BO - R

B

= długość ramienia

biegunowego

KC – kółko całkujące

r = promień kółka

całkującego

P = (2



r/1000)R

W

M

2

(O

k

-O

p

)

C

1

= (2



r/1000) R

W

M

2

P = C

1

(O

k

– O

p

)

C

1

= stała planimetru [m

2

]

O

k

– O

p

- różnica odczytów

kółka

P = C

1

(O

k

– O

p

) + C

0

– biegun

wewnątrz

C

0

= stała planimetru [m

2

]

Wyznaczenie stałej planimetru

C

1

: C

2

: C

3

: . . . = R

W1

: R

W2

: R

W3

: . . .

C

1

: C

2

: C

3

: . . . = M

1

2

: M

2

2

: M

3

2

: . . .

M

i

– mianowniki skal rysunków

C

1

= P

t

/ (O

k

– O

p

)

P

t

= pole

figury testowej [m

2

]

O

k

, O

p

= odczyty kółka całkującego

Aby uprościć obliczenia, można zmienić długość ramienia
biegunowego, z R

1

ustawionej na początku testu, na R

2

,

przy której stała C

2

będzie równa np. 10. Obliczamy

długość : R

2

= R

1

* C

2

/ C

1

,

Obliczanie objętości budowli ziemnych

Do określenia objętości bryły zawartej między powierzchnią terenu a
powierzchnią projektowaną najczęściej stosowany jest sposób
podziału tej bryły na

graniastosłupy

o podstawie

kwadratu,

prostokąta lub trójkąta

.

1. Metoda

siatki kwadratów, prostokątów lub

trójkątów

.

Wyznaczamy na powierzchni działki siatką figur (np. kwadratów) o
określonej długości boku, np. a, w terenie (lub na mapie). dla każdego
z wierzchołka figury określa się wysokość

H

k

z pomiaru

wysokościowego (

na mapie z interpolacji

między warstwicami).

Na podstawie danych możemy wyznaczyć różnice wysokości punktów
terenu i powierzchni projektowanej w wierzchołkach kwadratów o
średnią dla graniastosłupa numerze k,

h

k

= H

k

- H

k

Objętość k-tego

graniastosłupa: V

k

= h

k

P

k

. Dla całej bryły: V =  V

k

.

P

k

= pole podstawy graniastosłupa.

W skryptach spotykamy wzory dla typowych zadań:

 H

i

= H

i

- H

i

- różnice wysokości punktów (wierzchołków siatki

kwadratów i=1,2,3,4)





























4

3

2

1

2

4

3

2

4

H

H

H

H

a

V

P

1

P

2

P

3

H

1

H

2

H

3

H

1

H

2

H

3

Poziom porównawczy H

o

Powierzchnia dolna (spód
bryły)

powierzchnia górna
bryły

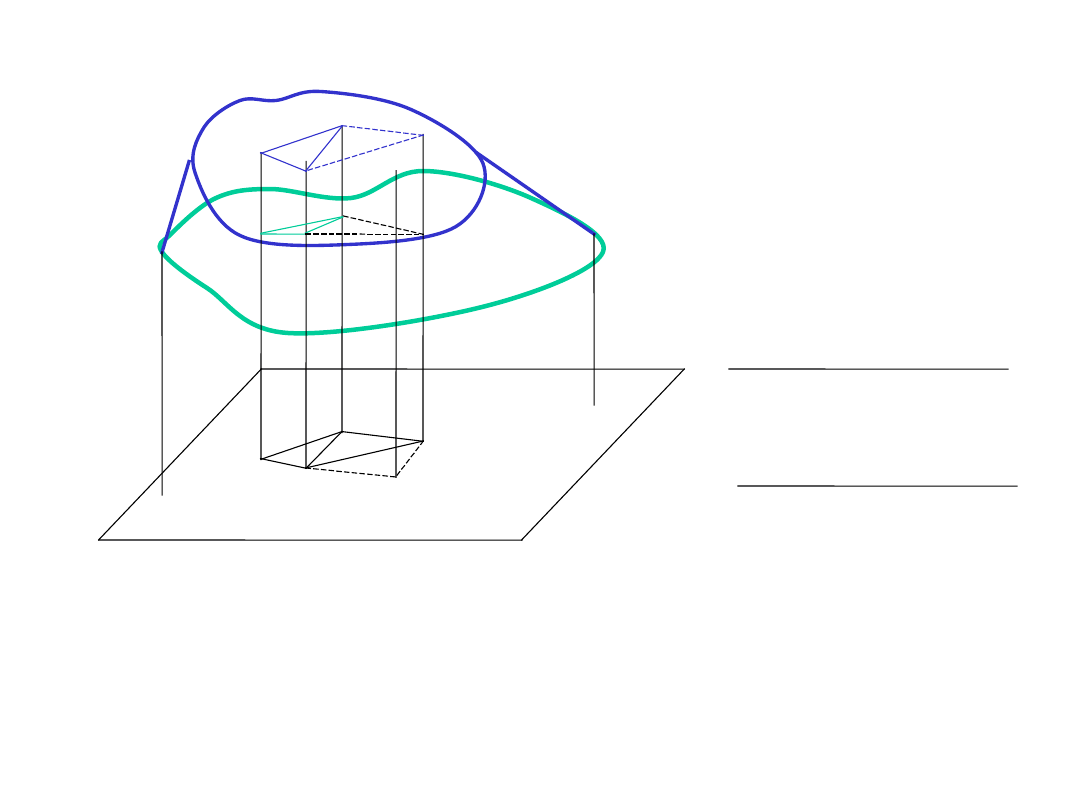
Interpretacja wyznaczenia objętości nasypu metodą siatki figur

V

i

=

P

i

[(

H

1

+ H

1

+ H

1

)/3

- H

o

]

V

i

=

P

i

[(

H

1

+ H

1

+ H

1

)/3

- H

o

]

V

’

=



V

i

V”

=



V

i

Objętość nadkładu: V = V

’ -

V”

P

i

– pole trójkąta (figury będącej podstawą graniastosłupa)

V

’ –

suma objętości graniastosłupów do poziomu wtórnego (kolor

niebieski)

V”

–

suma objętości graniastosłupów do poziomu pierwotnego (kolor

zielony)

Punkty powierzchni górnej mogą tworzyć inną siatkę niż punkty
powierzchni dolnej. Figury muszą jednak wypełniać obszar
ograniczony brzegiem obu powierzchni.

Obliczanie objętości nasypu

Obliczanie objętości pryzmy węgla

Podział na elementy podłoża pryzmy

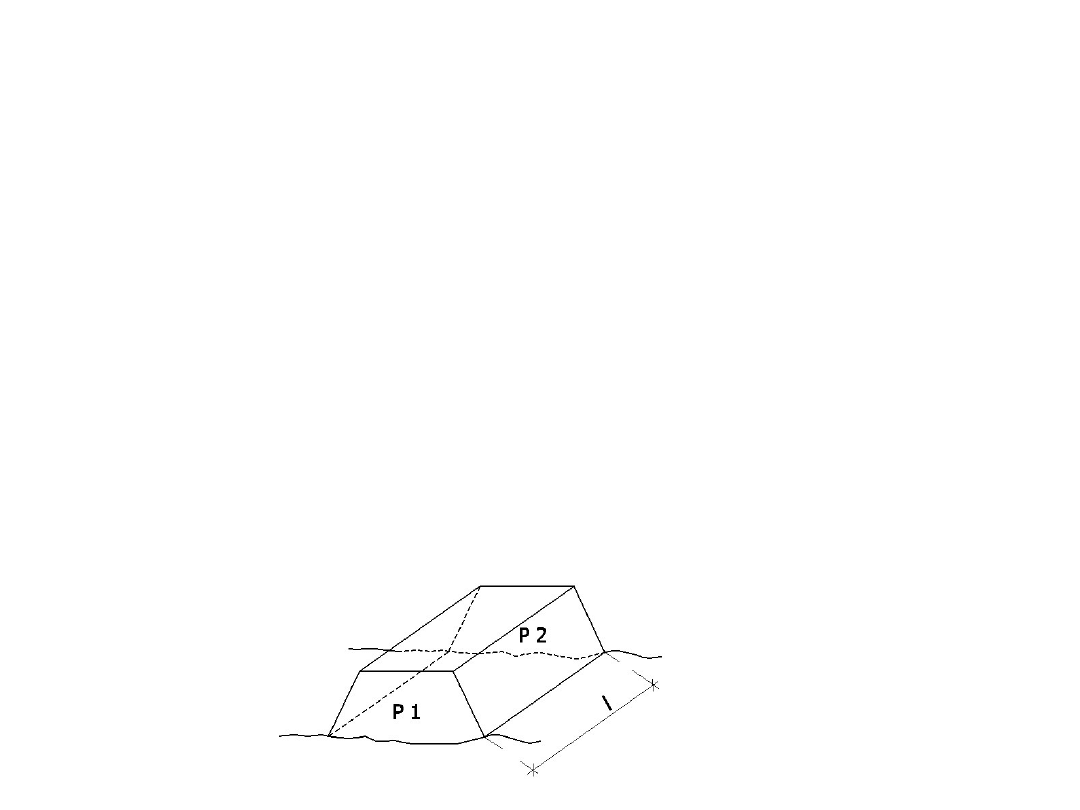
Obliczanie objętości robót ziemnych

cd

a — długość boku kwadratu.

  H

1

— suma dla punktów występujących pojedynczo

  H

2

— suma dla punktów wspólnych dla dwóch kwadratów,

  H

3

— suma dla punktów wspólnych dla trzech kwadratów,

  H

4

— suma dla punktów wspólnych dla czterech kwadratów,

Dodatkowo należy obliczyć objętości graniastosłupów dla kwadratów
z przebiegającą przez nie linią granicy obszaru.

2. Metoda przekrojów obiektu

:

V = 0.5(P1+P2)*d

,

Dokładność wyznaczenia objętości zależy o odległości pomiędzy
przekrojami. Powierzchnie przekrojów można wyznaczyć na
przekrojach graficznie lub za pomocą planimetru.

przekrój 1

przekrój 2

d

Metoda przekrojów poprzecznych

stosowana powszechnie przy

obliczaniu robót ziemnych w opracowaniach projektów tras
komunikacyjnych i obwałowań.

H— odstęp (różnica wysokości) sąsiednich warstwic,
h — odległość powierzchni terenu od najwyższej lub najniższej

płaszczyzny warstwowej o nr n,

P

i

— pole powierzchni ograniczonej i-tą warstwicą, które można

wyznaczyć przy pomocy planimetru lub obliczyć ze współrzędnych

2

d

d

m

m

1

i

śr

o

V









n

i

3. Metoda przekrojów poziomych - obliczenie objętości w oparciu o
dane z map warstwicowych

Przy wyznaczaniu pojemności zbiorników wodnych oraz mas
ziemnych na większych obszarach, dla których posiadamy mapę
warstwicową, objętość obliczymy jako sumę brył ograniczonych
płaszczyznami warstwic i powierzchnią terenu.

Obliczana objętość jest sumą objętości warstw gruntu zawartego
pomiędzy płaszczyznami warstwic w granicach budowli.

Błąd obliczenia
objętości
m

o

- błąd pomiaru lub wyznaczenia z mapy wysokości punktów

przekroju

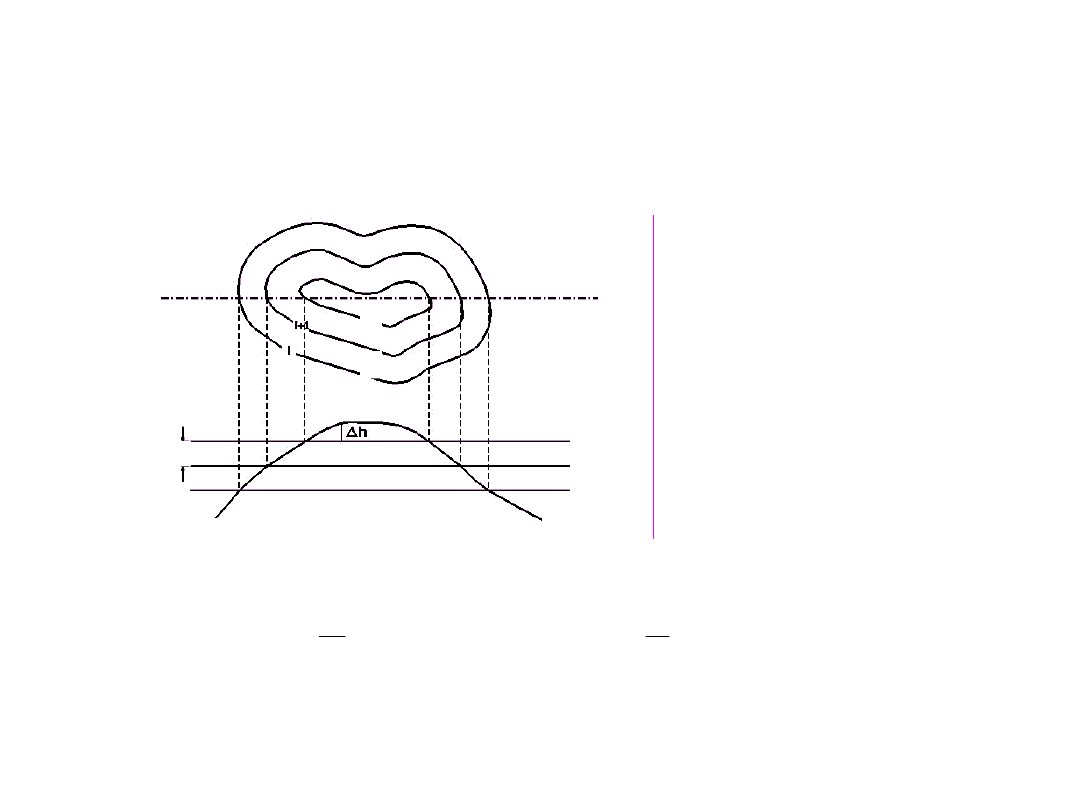
obiekt

mapa
warstwicowa

P

P

i+1

P

i



















n

i

i

P

h

P

P

H

V

3

1

2

1

1

H

Metoda przekrojów poziomych – interpretacja geometryczna

P

i

– Pola powierzchni figury ograniczonej warstwicą i brzegiem

obszaru opracowania,

Wyznaczona planimetrem z błędem m

S

= 0.005*S.

Wymagania dokładnościowe

Materiały i opracowania geodezyjne potrzebne do obliczania objętości

1. Mapy sytuacyjno wysokościowe (m

o

25 cm - 50 cm zależnie od

skali),

2. Pomiary geodezyjne

-

niwelacja metodą siatki kwadratów (boiska, place) m

o

2 cm,

-

niwelacja metodą punktów rozproszonych (dla powierzchni
falistych) m

o

5 cm,

-

niwelacja metodą przekrojów podłużnych i poprzecznych (trasy
komunikacyjne, brzegi rzek) m

o

5 cm,

-

tachimetria, dla zadań nie wymagających dużej dokładności
(wysypiska, hałdy wyrobiska) m

o

10 cm,

-

fotogrametria naziemna lub aerofotogrametria dla terenów bez
pokrycia obiektami m

o

20 cm.

Dokładność potrzebna do obliczenia objętości gruntu przy

projektowaniu budowli ziemnych (wg normy PN-68/B-06050,
dopuszczalna odchyłka wysokości punktu w siatce kwadratów
40X40 m wynosi



H

= 0.04m

)

Błąd dopuszczalny ukształtowania terenu m

= 40*40*0.04 = = 64m

3

Dla całego obiektu – figury o powierzchni S m

2

, wystąpi n = s/64

kwadratów,

Wymagania dokładnościowe

cd

S

1.6

n

64

m

V









Grunty podlegają zagęszczeniu

. Wskaźnik zagęszczenia D zależy od

rodzaju gruntu (wg normy D = <0,0.9 – 1.15>). Tolerancja dla

wskaźnika zagęszczenia

wynosi 2%

Dopuszczalna odchyłka objętości z tytułu zagęszczenia gruntu równa
się: 0.02D*V.

Możemy do analiz przyjmować m

z

= 0.02 V.

Rzeczywista dokładność obliczenia objętości gruntu zależy jeszcze
od wilgotności, a także od osiadania. Największy wpływ ma jednak
błąd metody numerycznej przyjętej do obliczeń.

Wpływ błędów danych wysokościowych (z pomiarów lub
odczytanych z mapy) na objętość gruntu zależy od liczby punktów
obranych na powierzchni terenu.

k

S

m

m

o

Vh





m

o

– błąd wyznaczenia wysokości punktu (0.02 –0.20 zależnie od

metody),

k - liczba punktów wierzchołków siatki.

Dziękuję za uwagę