4. Metoda parametryczna

Wyrównanie sieci niwelacyjnej

4.1. Model zagadnienia wyrównawczego

W metodzie parametrycznej zwanej również metodą pośredniczącą wielkości podlegające pomiarowi są funkcją wyznaczanych wielkości (parametrów), czyli

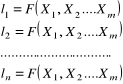
. (4.1)

Parametrami X_i są współrzędne X,Y,H, a wielkościami obserwowanymi „l” kąty, odległości i różnice wysokości. Wartości obserwowane l^ob różnią się o poprawkę v_i od wartości poprawnej, którą jest wartość wyrównana l^wyr (w rzeczywistości najbardziej prawdopodobna)

. (4.2)

Wartości obserwowane l_i^ob oraz l^wyr są zestawiane w układzie „n” równań poprawek

, (4.3)

w którym wartości wyrównane l^wyr są wyrażone w postaci funkcji parametrów X_i

.

(4.4)

Przy wyrównaniu sieci niwelacyjnych ze względów (rachunkowych) przyjmuje się

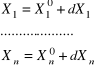
(4.5)

Stąd

. (4.6)

W zapisie macierzowym układ (4.6) zapisujemy jako

, (4.7)

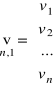
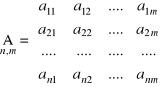
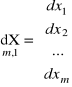
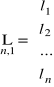
(4.8)

4.2. Metoda najmniejszych kwadratów. Układ równań normalnych

Dla rozwiązania układu równań (4.7) konieczne jest takie jego przekształcenie, by liczba równań równała się liczbie niewiadomych. Najbardziej powszechnym, a w geodezji praktycznie jedynym sposobem rozwiązania tego problemu, jest wprowadzenie założenia dotyczącego sumy kwadratów poprawek v:

F = Σv² = v­^T v = min (4.9)

Efekt przekształcenia łatwo zilustrować przykładem, w którym na podstawie zbioru danych {h_i, x_i} wyznaczane są parametry a, b równania prostej h = ax + b. Podstawiając wartości poprawek v = ax + b - h do równania (4.9) i przyrównując pochodne (względem szukanych niewiadomych a i b) otrzymanego wyrażenia do zera, wyznaczane są dwa równania normalne. Można je zapisać w ogólnej postaci

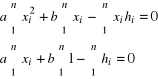
(4.10)

albo macierzowo:

A^TA X + A^TL = 0 (4.11)

W przypadku, gdy obserwacje wykonane są z różną dokładnością, w równaniach poprawek (4.7) oraz równaniach normalnych (4.10) uwzględnia się macierz wag w postaci

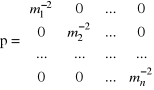
co przekształca układ równań (4.11) do postaci

A^T P A X + A^T P L = 0 (4.12)

Aby rozwiązać powstały układ należy pomnożyć obie strony równania odpowiednio przez (A^TA)^-1 lub (A^TPA) ^-1

(A^TA)^-1 A^TA X = - (A^TA)^-1 A^TL

Stąd

X = - (A^TA)^-1A^TL (4.13)

W przypadku obserwacji o różnych dokładnościach

X = - (A^T P A) ^-1A^T P L (4.14)

W zadaniu jak powyższe (tj. zapisanym równaniami liniowymi) wartości parametrów otrzymane przy rozwiązaniu układu równań normalnych są wynikami końcowymi. Można bowiem przyjąć, że wartości przybliżone są równe zero. Gdy układ równań jest nieliniowy, uzyskuje się tylko korekty dX do wcześniej przyjętych wartości przybliżonych bowiem zgodnie z (4.5)

X = X⁰ + dX

Procedurę obliczeń powtarza się w procesie iteracyjnym tak długo, aż wartości dX będą odpowiednio małe.

Uwaga na znak „±”! Jeśli układ równań normalnych (4.11) zapisano w postaci

A^TA X = A^TL

a w przypadku obserwacji różnodokładnych jako

A^T P A X = A^T P L,

to wektor niewiadomych X jest wyznaczany z zależności

X = (A^TA)^-1A^TL (4.15)

X = (A^T P A) ^-1A^T P L (4.16)

Ocena dokładności. Po rozwiązaniu układu równań
wyznaczany jest współczynnik wariancji m_o²

(4.17)

Gdy wagi wszystkich obserwacji są jednakowe, zachodzi

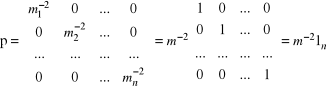
(4.18)

(4.19)

Macierz kowariancji

(4.20)

(4.21)

Błędy średnie parametrów X₁, X₂, ...X_i

,

..........

(4.22)

Błędy średnie wyrównanych wielkości obserwowanych. Błędy średnie obserwacji można wyznaczyć dwoma sposobami. W pierwszym wykorzystuje się prawo przenoszenia się błędów

(4.23)

gdzie:

Drugi sposób wyznaczenia błędów średnich wyrównanych obserwacji wymaga wyznaczenia ich macierzy kowariancji

(4.24)

4.3. Algorytm obliczeń

Obliczenia wykonywane są według algorytmu, który oparty jest na metodzie najmniejszych kwadratów. Algorytm jest realizowany w następujących etapach.

Zestawienie wyników obserwacji

Układ równań obserwacyjnych

Równania poprawek

Układ równań normalnych.

Rozwiązanie układu równań normalnych

Wektor poprawek

Wyrównane wartości wielkości obserwowanych

Kontrole obliczeń

Współczynnik wariancji m_o²

Macierz kowariancji i błędy średnie wyznaczanych parametrów

Błędy średnie wyrównanych wielkości obserwowanych

Przedziały ufności

Kontrola 1 polega na porównaniu wartości s = s' obliczonych ze wzorów

s = v^T v lub s = v^TP v

s' = L^{T თ}PთAთX + L^{T თ}PთL

Kontrola 2. Wartości wyrównane obserwacji h_i^wyr mogą być wyznaczone dwoma sposobami, a mianowicie wzorem (4.2)

l^wyr = l_i^obs + v_i

oraz z funkcji parametrów X za pomocą formuły

l^wyr = A⋅X

W przypadku sieci niwelacyjnej będą to wzory

h^wyr = h^obs + v

h^wyr = A⋅H = A⋅dH + L⁰

Wyniki powinny być identyczne.

4.4. Przykład wyrównania sieci niwelacyjnej

Dla sieci jak na rys. 4.1 wyniki pomiarów różnic wysokości h_i zestawiono w tablicy 4.1. Obliczyć:

• rzędne reperów H_1­, H₂,

• błędy średnie wyrównanych wysokości H_1­, H₂,

• błędy średnie wyrównanych przewyższeń m_h1, m_h2, m_h3, m_h4, m_h5.

Rys.4.1

Tablica 4.1

	hi^ob	mi
h1^ob	3,241	0,02
h2^ob	- 0,901	0,01
h3^ob	- 0,540	0,02
h4^ob	2,865	0,01
h5^ob	0,355	0,02

Macierz wag P

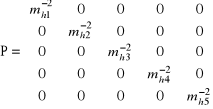
W algorytmie wprowadzono wartości przybliżone niewiadomych H₁⁰_­, H₂⁰.

H₁⁰ = H_Rp.1+ h₁^ob = 112,455 + 3,241 = 115,696

H₂⁰ = H_Rp.1+ h₄^ob = 112,455 + 2,865 = 115,320

Równania poprawek v_i = h_i + h_i^ob

v = A ⋅dH + L

v₁ = dH₁ + H₁⁰ - H_R1 - h₁^ob

v₂ = - dH₁ - H₁⁰ + H_R2 - h₂^ob

v₃ = - dH₂ - H₂⁰ + H_R2 - h₃^ob

v₄ = dH₂ + H₂⁰ - H_R1 - h₄^ob

v₅ = dH₁ - dH₂ + H₁⁰ - H₂⁰ - h₅^ob

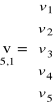
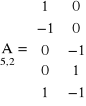
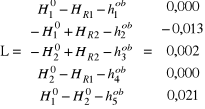
Układ równań normalnych A^TA ⋅dH + A^TL = 0

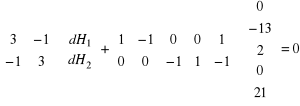
Rozwiązanie układu równań normalnych dH = - (A^T P A)^-1A^T PL

Wektor poprawek

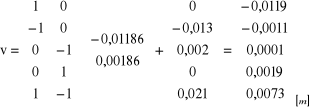
Wyrównane wartości wielkości obserwowanych h^wyr = h^obs + v

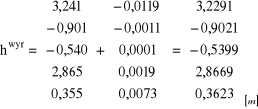
Kontrola obliczeń 1. s = v^T P v

s' = L^{T თ}P·AთdH + L^TთP·L

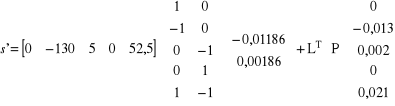
s' = -2,270714286+ 2,8025 = 0,531786

Kontrola 2. h_i^wyr = F(H₁, H₂)

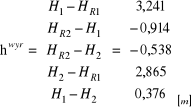
Wartości h_i^wyr są identyczne jak w pozycji „wyrównane wartości wielkości obserwowanych” gdzie zastosowano wzór h_i^wyr = h_i^obs + v_i

Współczynnik wariancji m_o²

m₀ = 0,52 (wartość m₀ - niemianowana)

Macierz kowariancji

Błędy średnie wyznaczanych parametrów

Błędy średnie wyrównanych obserwacji

27

h₅

h₄

h₃

h₂

h₁

1

2

Rp. 2

Rp. 1

Rzędne reperów nawiązania

H_Rp.1 = 112,455

H_Rp.2 = 114,782

a₁

a_n

---