3. Wyrównanie obserwacji bezpośrednich

Propagacja błędów

3.1. Wyrównanie obserwacji bezpośrednich

Wyrównanie obserwacji zbioru
obejmuje wyznaczenie wartości przeciętnych oraz błędów standardowych.

Przykład 3.1. Różnicę wysokości Δh_AB pomierzono 4 razy z jednakową dokładnością. Wyznaczyć wartość średnią, błąd średni pojedynczej obserwacji i błąd średni wartości przeciętnej.

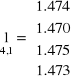
l_śr = 1.473 v_i = l_śr - l_i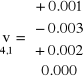

Błąd średni pojedynczej obserwacji wynosi

m =

Błąd średni wartości przeciętnej

m_śr = 0.003 mm

Interpretacja błędów

l₁ = 1.474 ± 0.006 ს1.468, 1.480ჱ

l₂ = 1.470 ± 0.006 ს1.464, 1.476ჱ

l₃ = 1.475 ± 0.006 ს1.469, 1.481ჱ

l₄ = 1.473 ± 0.006 ს1.467, 1.469ჱ

L = 1.473 ± 0.003 ს1.470, 1.476ჱ

Błąd standardowy średniej arytmetycznej

Na podstawie prawa przenoszenia błędów można przyjąć, że

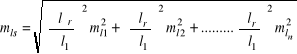
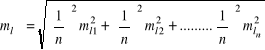
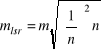
Wyrównanie obserwacji bezpośrednich niejednakowo dokładnych

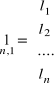
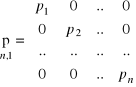
Przykład 3.2. Różnicę wysokości Δh_AB pomierzono 4 razy. Każdy pomiar wykonano innym instrumentem z różną dokładnością (m). Wyznaczyć wartość najprawdopodobniejszą, błąd średni wartości przeciętnej m_śr i błędy średnie poszczególnych obserwacji m_ii.

=

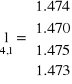
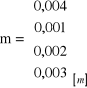
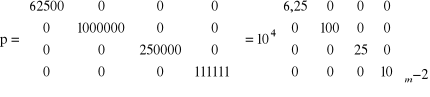
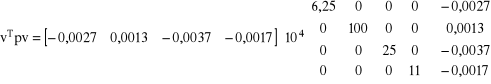
v^Tpv = 5,8389

- wartość niemianowana

Błąd średni wartości przeciętnej m_śr

Błędy średnie obserwacji m_i.

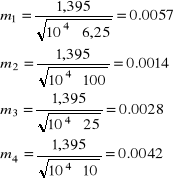
3.2. Propagacja błędów pomiaru

W większości zadań geodezyjnych poszukiwane wartości wyznaczane są pośrednio ze związku funkcyjnego u = f(x,y,z…), w którym bezpośrednio mierzone są wielkości x, y, z. Jeśli wielkości mierzone bezpośrednio są losowe i znane są parametry ich rozkładów normalnych (wartości przeciętne i błędy średnie), to błąd średni m_u można wyznaczyć za pomocą prawa przenoszenia się błędów.

(3.1)

Δx = x - x₀, Δy = y - y₀, Δz = z - z_0.

(3.2)

Bląd standardowy m_u wyznaczany jest ze wzoru

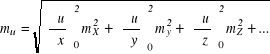
(3.3)

Wzór (3.4) jest poprawny pod warunkiem, że zmienne x,y,z,… są losowe i nieskorelowane, czyli wzajemnie niezależne. W przypadku, gdy ten ostatni warunek nie jest spełniony prawo przenoszenia się błędów wymaga uwzględnienia ich korelacji co jest uwzględniane za pomocą macierzy kowariancji.

Przykład 3.3. Współrzędne punktu 1 wyznaczono metodą biegunową ze stanowiska B w nawiązaniu do punktu osnowy A, jak na rys. 3.2. Obliczyć błędy standardowe m_X1, m_Y1 punktu 1 dla danych:

Azumut Az_BA = 165.88^g , m_BA= 0.02^g

β = 72.40^g , m_β = 0.01^g

l = 87.10 m, m_l = 0.02^g

m_XB = 0.06 m , m_Y1 = 0.04 m

Współrzędne punktu 1 wyznaczane są z zależności:

Na podstawie prawa propagacji błędów losowych błędy standardowe wyznaczane są z zależności:

Uwzględniając w powyższych zależnościach, że

oraz wyrażając błędy standardowe kąta β oraz wyznaczonych azymutów, tj. Az_B1, Az_BA, Az_B1 w jednostkach łukowych (w zadaniu podano je w jednostkach gradowych)

wzory na m_X1, m_Y1 przyjmują postać

Podstawiając do powyższych wzorów dane liczbowe otrzymujemy

Szukane wartości błędów standardowych współrzędnych punktu 1 wynoszą:

m_X1 = 0.07 [m]

m_Y1 = 0.05 [m]

3.3. Optymalizacja programu obserwacji

Prawo przenoszenia się błędów jest wykorzystywane pry projektowaniu pomiaru. Zadanie polega na dopasowaniu błędów składowych tak, by ich suma wyznaczona z prawa przenoszenia się błędów nie przekroczyła przyjętej wartości.

Przykład 3.4. Z jaką dokładnością należy wykonać pomiary zbiornika o wymiarach (przybliżonych) h  = 12 m i promieniu R = 8 m, aby jego kubaturę wyznaczyć z błędem standardowym m_V = 0,1%.

Ponieważ kubatura zbiornika w przybliżeniu wynosi V = π R² h = 2400 m³, stąd oczekiwany błąd standardowy wynosi m_V  ၀ 2,5 m³. Przyjmując, że promień walca zostanie wyznaczony na podstawie pomiaru obwodu zbiornika, tj. ze wzoru R = L/π, objętość obliczyć można ze wzoru

Stosując prawo przenoszenia się błędów

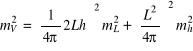
i podstawiając L = 2πR oraz m_L = m_h = m otrzymujemy

.

Stąd szukana dokładność pomiaru m wynosi

0,14 [m]

20

Rys. 3.2

A º

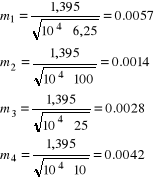
º 1

l

B º

β

---