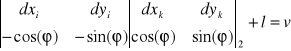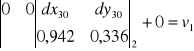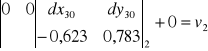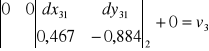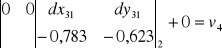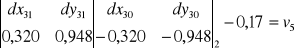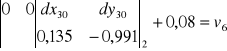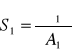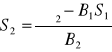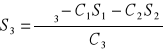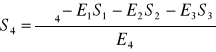Wyrównanie sieci liniowych

Siecią liniową nazywamy zespół punktów geodezyjnych, których wzajemne położenie scharakteryzowane jest przez pomiar długości odcinków między punktami sieci. W takiej sieci znane są współrzędne przynajmniej dwóch jej punktów. Położenie innego punktu, można wyznaczyć mierząc długości odcinków łączących ten punkt z punktami o znanych współrzędnych. Tak, więc w sieci o k punktach wyznaczanych trzeba zmierzyć więcej, aby zagadnienie miało charakter wyrównawczy, niż 2k odcinków określających położenie tych punktów. Wyrównanie sieci liniowej wymaga nadania obserwacjom liniowym L takich poprawek, w aby suma [pww], gdzie p wagi obserwacji, była minimalna.

Wyrównanie metodą spostrzeżeń pośrednich sprowadza się tu do:

• obliczenia przybliżonych wartości współrzędnych wszystkich wyznaczanych punktów sieci,

• wyznaczenia różnic między długościami obliczo­nymi z przybliżonych współrzędnych, a długościami zmierzonymi:
  ,

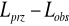
• zapisania dla każdej obserwacji równania obserwacyjnego (równania poprawek) postaci:

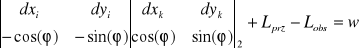
gdzie
,
,
,
są poszukiwanymi niewiadomymi (zaburzeniami), które trzeba dodać do przybliżonych wartości współrzędnych początku i końca odcinka,
kątem kierunkowym odcinka (patrz symbole pomocnicze), tzn.

;
,

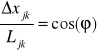
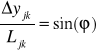
• wyznaczenia układu równań poprawek

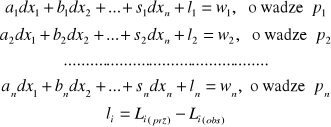
tj.

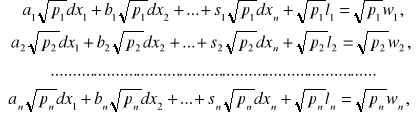
gdzie zastosowano operację równoważenia polegającą na obustronnym pomnożeniu kolejnych równań układu przez pierwiastki wag obserwacji W ten sposób zrównoważone wyrazy obserwacyjne
mają jednakową dokładność scharakteryzowaną błędem średnim równym jedności.

• zestawienia i rozwiązania układu równań normalnych Gaussa

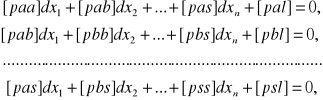
Rozwiązując ten układ otrzymamy wartości
,

a w konsekwencji wartości poprawek
,
, wartość błędu średniego

i błędów średnich poszukiwanych współrzędnych wyznaczanych punktów sieci.

W poniższym przykładzie wyrównano układ sześciu obserwacji liniowych. Obserwacje te wykonano w celu wyznaczenia położenia dwóch punktów. Za spostrzeżenie o wadze jedność przyjęto pomiar odcinka o długości 100 m, ponieważ błędy średnie pomiarów liniowych są proporcjonalne do pierwiastków z długości tj.

,

wagę p pomiaru odcinka o długości L wyznaczamy przyjmując
i
. Ponieważ

, to
.

Po napisaniu układu równań poprawek każde z tych równań zostało pomnożone przez
. Z przekształconego tak układu równań poprawek otrzymano układ równań normalnych, który został rozwiązany metodą pierwiastka krakowianowego z łącznym wyznaczeniem współczynników wagowych
. Po wyznaczeniu niewiadomych podstawiono ich wartości do układów równań poprawek, zarówno pierwotnego, jak i sprowadzonego do jednostkowej wagi. Obliczono w ten sposób zarówno poprawki obserwacji w jak i iloczyny
, których suma kwadratów pozwoliła wyznaczyć błąd średni

,

odnoszący się do pomiaru stumetrowego odcinka. Mnożąc ten błąd średni przez pierwiastki z współczynników wagowych wyznaczono błędy średnie niewiadomych. Ze względu na małą ilość spostrzeżeń nadliczbowych te wartości błędów średnich są zresztą mało miarodajne. Po poprawieniu współrzędnych obliczono z nich długości odcinków po wyrównaniu i stwierdzono, zgodność z wartościami obserwacji poprawionych
.

Wyrównanie sieci liniowej (kolorem czerwonym oznaczono wielkości otrzymane w wyniku wyrównania)

Oznaczenie boku	Przyrosty współrzędnych wzdłuż mierzonego boku , 1) ze współrzędnych przybliżonych 2) ze współrzędnych wyrównanych	Suma kwadratów przyrostów	Długość boku		l = Lprz- - Lobs	Kosinusy kierunkowe		Równanie obserwacyjne boku
										Obliczona z przybliżonych współrzędnych Lprz	obserwowana Lobs v -poprawka L długość wyrównana
I2-30	939,32 334,64 939,27 334.60	994306	997,15	997,1'5 -0,06 997, 09	0	0,942	0,336
15-30	-557,60 701,84 -557,85 701,80	603720	896,50	896,50 0,00 896,50	0	- 0,623	0,783
20-31	283,88 -541,86 283,89 -541,80	375340	612,65	612,65 -0,04 612,61	0	0,467	-0,884
18-31	-372,17 -296,11 -372,16 -296,05	226192	475,60	475,60 -0,05 475,55	0	-0,783	-0,623
31-30	-151,08 -447,65 -151,12 -447,75	223210	472,45	472,62 -0,06 4 72,56	-0,17	-0,320	-0,948
20-30	134,82 -983,31 134,77 -389,55	997306	998,65	998.57 0,11 998,68	0,08	0,135	-0,991

Układ równań poprawek

Bok
I2-30	0,904	0,336	0	0	0	997,1'5	0,317
15-30	-0,623	0,783	0	0	0	896,50	0,334
20-31	0	0	0,467	-0,884	0	612,65	0,404
18-31	0	0	-0,783	-0,623	0	475,60	0,459
31-30	-0,320	-0,948	0,320	0,948	-0,17	472,62	0,460
20-30	0,135	-0,991	0	0	0,08	998,57	0,317
	a	b	c	e	l

Zrównoważony układ równań poprawek

Bok
I2-30	0,299	0,107	0	0	0
15-30	-0,208	0,262	0	0	0
20-31	0	0	0,189	-0,357	0
18-31	0	0	-0,359	-0,286	0
31-30	-0,147	-0,436	0,147	0,436	-0,078
20-30	0,043	-0,314			0,025

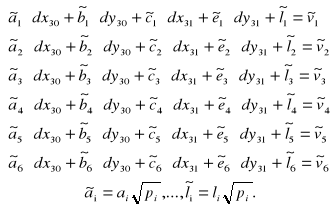
Układ równań normalnych ma postać:

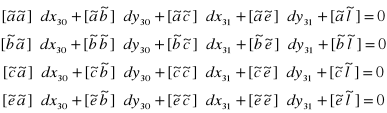
gdzie:

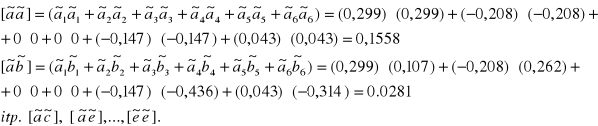
Po wyznaczeniu wartości współczynników
itp. otrzymujemy:

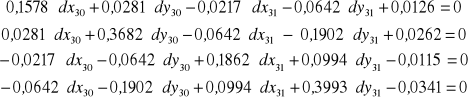
Układ ten rozwiązujemy metodą pierwiastka krakowianowego:

Rozwiązanie układu równań normalnych (metoda Banachiewicza)

Patrz następna strona.

[aa]	[ab]	[ac]	[ae]	[la]	1	0	0	0
	[bb]	[bc]	[be]	[lb]	0	1	0	0
		[cc]	[ce]	[lc]	0	0	1	0
			[ee]	[le]	0	0	0	1
A1	B1	C1	E1	L1	M1	0	0	0		S1w= A1+B1+C1+ E1+L1+M1
0	B2	C2	E2	L2	M2	N2	0	0		S2w= B2 +C2+E2+L2+M2+N2
0	0	C3	E3	L3	M3	N3	P3			S3w =C3+E3+L3+M3+N3+P3
0	0	0	E4	L4	M4	N4	P4	R4		S4w= E4+L4+M4+N4+P4+R4
									S

Wartości niewiadomych wyznacza się na podstawie zależności

,
,
,

Błąd średni pojedynczej obserwacji
otrzymujemy wyznaczając poprawki
tj. z równań obserwacyjnych podstawiając do nich wartości znalezionych niewiadomych
,
,
,
. Błąd
, gdzie n to ogólna ilość obserwacji,
ilość obserwacji nadliczbowych, k - ilość niewiadomych. Sumę
kwadratów poprawek można obliczyć także ze wzorów:
. (Czynimy to w celach kontrolnych).

Błędy średnie niewiadomych w powyższym przypadku wyrażone są wzorami:

,

0,1578	0,0281	-0,0217	-0,0642	0,0126	1	0	0	0
	0,3682	-0,0642	-0,1902	0,0262	0	1	0	0
		0,1862	0,0994	-0,0115	0	0	1	0
			0,3993	-0,0341	0	0	0	1
*	*	*	*		*	0	0	0	S1	*
0	*	*	*		*	*	0	0	S2	*
0	0	*	*		*	*	*		S3	*
0	0	0	*		*	*	*	*	S4	*

0,1578	0,0281	-0,0217	-0,0642	0,0126	1	0	0	0	1,1106
	0,3682	-0,0642	-0,1902	0,0262	0	1	0	0	1,1681
		0,1862	0,0994	-0,0115	0	0	1	0	1,1882
			0,3993	-0,0341	0	0	0	1	1,2102
0,3947	0,0712	-0,0549	-0,1626	0,0309	2,5337	0	0	0	2,8140	2,8140
0	0,6026	-0,1000	-0,2963	0,0396	-0,2995	1,6595	0	0	1,6058	1,6058
0	0	0,4161	0,1461	-0,0139	0,2622	0,3988	2,4032	0	3,6126	3,6126
0	0	0	0,5135	-0,0295	0,6848	0,8441	-0,6838	1,9473	3,1466	3,2765
= -0,0451	= -0,0354	= 0,0133	= 0,0574						S

0,1578	0,0281	-0,0217	-0,0642	0,0126	1	0	0	0	1,1106
	0,3682	-0,0642	-0,1902	0,0262	0	1	0	0	1,1681
		0,1862	0,0994	-0,0115	0	0	1	0	1,1882
			0,3993	-0,0341	0	0	0	1	1,2102
*	*	*	*		*	0	0	0	S1	*
0	*	*	*		*	*	0	0	S2	*
0	0	*	*		*	*	*		S3	*
0	0	0	*		*	*	*	*	S4	*
									S

;
;
;
;
.

1

Obliczenie przybliżonych współrzędnych punktu 30

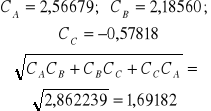
997,15

896,50

1541,49

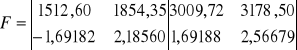
Obliczenie przybliżonych współrzędnych punktu 31

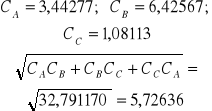
475,60

612,65

702,44

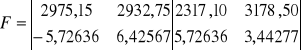
Kontrola
;

475,60

896,50

997,15

998,57

612,65

472,62

X = 2451,92

Y = 2188,99

X = 2317,10

Y = 3178,50

X = 3009,72

Y = 1487,15

30

24

12

15

X₀ = 2602,69

Y₀ = 2636,64

31

20

18

20

X = 2975,15

Y = 2932,75

X = 1512,60

Y = 1854,35

A

B

C

B

A

C

15

30

18

18

20

31

Kontrola
;

---