Wyrównanie spostrzeżeń bezpośrednich jednakowo dokładnych

Źródła błędów:

1) niedoskonałość zmysłów obserwatora,

2) narzędzia pracy (taśma, teodolit, niwelator, łata itp.),

3) warunki pracy: czyli środowisko (temperatura, wiatr, teren pagórkowaty lub zadrzewiony).

Podział błędów:

1) absolutne (
)to błędy przypadające na całą mierzoną wielkość

2) błędy względne (
)wyrażają stosunek błędu absolutnego do wielkości mierzonej, a więc są to błędy przypadające na jednostkę wielkości mierzonej; błędy względne służą do oceny dokładności pomierzonych wielkości; w tym celu przedstawiamy je zazwyczaj w postaci ułamka lub w procentach.

1) błędy grube (omyłki) - zostają wykryte i wyeliminowane przez podwójne pomiary tych samych wielkości}

2) błędy systematyczne (stałe) - mają stały znak (+ lub -) a czasem stałą wartość i najczęściej dają się usunąć z dokonanych obserwacji przez wprowadzenie do wyniku odpowiedniej poprawki (np. wpływ temperatury na pomiar długości taśmą stalową), lub przez zastosowanie odpowiedniej metody pomiaru (np. usunięcie błędu ekscentryczności alidady przez wzięcie średniej arytmetycznej z odczytów dwóch, noniuszy).

3) błędy przypadkowe - niewielkie i z różnymi znakami są nieuchwytne i dlatego niemożliwe do usunięcia. Rachunek wyrównawczy zajmuje się tylko błędami przypadkowymi. Błędy przypadkowe dzielimy na;

1) błędy prawdziwe (rzeczywiste),

2) błędy pozorne.

Najczęściej w praktyce mamy do czynienia z błędami pozornymi.

Błąd prawdziwy ε jest to różnica między wartością prawdziwą X a obserwowaną l:

czyli

Błąd pozorny v jest to różnica między wartością najprawdopodobniejszą
(średnią arytmetyczną) a wartością obserwowaną (pomierzoną) l:

czyli

Dla charakterystyki dokładności pomiarów przyjmuje się najczęściej następujące wielkości:

1) błąd średni m,

2) błąd graniczny

Błąd średni spostrzeżeń jednakowo dokładnych

Błąd średni - wskaźnik dokładności w geodezji - pozwala na ocenę dokładności wykonanej pracy. Rozróżniamy błędy średnie: pojedynczego spostrzeżenia i średniej arytmetycznej.

Błąd średni m pojedynczego spostrzeżenia wyrażony przez błędy prawdziwe określony jest wzorem:

gdzie liczba pomiarów
.

W praktyce stosujemy zazwyczaj błąd średni pojedynczego spostrzeżenia wyrażony przez błędy pozorne:

Błąd średni m pozwala ocenić dokładność wykonania poszczególnego pojedynczego pomiaru, czyli przy kilku pomiarach tej samej wielkości charakteryzuje nam dokładność każdego z nich.

Jeśli mamy n obserwacji (spostrzeżeń) tej samej wielkości X, np.
to najprawdopodobniejszą wartością tej mierzonej wielkości będzie średnia arytmetyczna

Oczywiście wyznaczona z tego wzoru średnia arytmetyczna jest również obarczona pewnym błędem. Ten średni błąd średniej arytmetycznej (tzw. wartości wyrównanej)

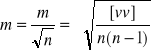
Zatem błąd średni średniej arytmetycznej jest
razy mniejszy od błędu średniego pojedynczego spostrzeżenia. Błąd ten pozwala ocenić dokładność przyjętej przez nas najprawdopodobniejszej wartości wyrównanej.

Błąd graniczny

Błędem granicznym nazywamy największą liczbową wartość błędu dopuszczalną dla danego szeregu spostrzeżeń. Z teorii błędów wynika, że na 1000 spostrzeżeń (dotyczących tej samej wielkości) należy się spodziewać zaledwie trzech spostrzeżeń z błędami większymi od trzykrotnego błędu średniego. Stąd przyjęto uważać trzykrotny błąd średni za błąd graniczny, czyli dopuszczalny;

Często też za błąd graniczny przyjmuje się podwójny błąd średni. Błędy większe od błędu granicznego uważa się już za błędy grube.

Własności średniej arytmetycznej i błędów pozornych

1) Przy wzrastaniu liczby spostrzeżeń (
) średnia arytmetyczna (
) spostrzeżeń tej samej wielkości dąży do rzeczywistej wartości tej wielkości (X):

2) Suma błędów pozornych równa się zeru

Zależność powyższą stosujemy do kontroli rachunku.

3) Suma kwadratów błędów pozornych powinna być minimum:

Na tej zasadzie opiera się rachunek wyrównawczy i od niej nosi nazwę „metody najmniejszych kwadratów".

Zadania

Zadanie 1. Zmierzono długości trzech różnych odcinków:

140 m - z błędem absolutnym 7 cm,

204 m - z błędem absolutnym 8 cm,

247 m - z błędem absolutnym 13 cm.

który odcinek został zmierzony najdokładniej?

Rozwiązanie. Obliczamy błędy względne pomierzonych długości;

Odp. Najdokładniej został zmierzony odcinek długości 204 m, gdyż błąd względny pomiaru tej długości jest najmniejszy.

Zadanie 2. Pewną długość pomierzono taśmą dziewięciokrotnie i otrzymano wyniki:

1 = 182,06 m, l. = 182,15 m, l = 182,07 m,

l = 182,13 m, l = 132,05 m, l = 182,12 m,

l = 182,10 m, l = 182,08 m, l = 182,14 m.

Obliczyć najprawdopodobniejszą długość, błąd średni pojedynczego spostrzeżenia oraz błąd średni wartości wyrównanej (średniej arytmetycznej).

Rozwiązanie. W celu uproszczenia obliczeń wprowadzamy wartość przybliżoną
szukanej wielkości. Jest to zwykle najmniejsza wartość
- tutaj przyjęto
. Wówczas w celu wyznaczenia średniej
obliczamy średnią arytmetyczną różnic
między rezultatami pomiarów a przyjętą przybliżoną wartością
. Dla przejrzystości obliczenia wykonano w poniższej tabeli.

Lp.	Wyniki pomiarów	t w cm	v	vv	tt	Obliczenia błędów średnich
1	182.06	6	+4	16	36	Średnia arytmetyczna; , gdzie Błąd średni pojedynczego spostrzeżenia: Błąd średni średniej arytmetycznej Kontrola:
2	182,13	13	-3	9	169
3	182,10	10	0	0	100
4	182,15	15	-5	25	225
5	182,05	5	+5	25	25
6	182,08	8	+2	4	64
7	182,07	7	+3	9	49
8	182,12	12	-2	4	144
9	182,14	14	-4	16	196
x0	182,00	90	0	108	1008

Dla kontroli obliczonej sumy kwadratów błędów pozornych wykorzystano wzór

.

Zadanie 3. Na pewnym punkcie zmierzono kąt 5 razy z tą samą dokładnością i otrzymano wyniki podane poniżaj w tabelce w drugiej kolumnie. Obliczyć najprawdopodobniejszą wartość kąta, błąd" średni pojedynczego pomiaru oraz błąd średni wartości wyrównanej (średniej arytmetycznej).

Rozwiązanie podano w tabeli.

Lp.	Wyniki pomiarów	t	v	vv	tt	Obliczenia błędów średnich
1	82°41'15"	15"	+12"	144	225	Kontrola:
2	82°41 '30"	30	- 3	9	900
3	82°42 '00"	60	-33	1089	3600
4	82°41"00"	0	+27	729	0
5	82°41'30"	30	- 3	9	900
x0	82°41'00"	135	0	1980	5625

Zadanie 4. Błąd średni pojedynczego pomiaru kąta
. Ile razy trzeba zmierzyć kąt, aby otrzymać wynik, z błędem średnim
?

Rozwiązanie

,
,

,
.

Kąt należy pomierzyć 9 razy, bo wtedy błąd średni średniej arytmetycznej wyniesie
.

Błędy średnie funkcji pomiarów bezpośrednich

1. Zamierzono wielkość x z błędem średnim
. Błąd śre­dni
iloczynu
gdzie a jest wielkością stałą, wynosi:
.

2. Zmierzono dwie niezależne od siebie wielkości
i
ze średnimi błędami
i
. Błąd średni sumy lub różnicy tych wielkości mierzonych, czyli błąd
funkcji
, wynosi:

Jeśli
i
to
.

Dla n obserwacji przy

.

Wiemy, że błędy systematyczne rosną proporcjonalnie do wartości wielkości mierzonej (lub liczby spostrzeżeń na przykład odłożeń taśmy przy pomiarze długości). Natomiast ze wzoru
wynika, że błędy przypadkowe rosną proporcjonalnie do pierwiastka kwadratowego z wartości wielkości mierzonej (lub z liczby spostrzeżeń).

Błąd średni funkcji liniowej

gdzie
- stałe współczynniki,
- wielkości zmierzone z błędami średnimi

wynosi

.

Błąd średni dowolnej funkcji

- wielkości mierzone z błędami średnimi

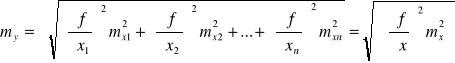
(bf)

Wzór ten jest wzorem ogólnym, na podstawie, którego możemy obliczyć błędy średnie wszystkich wymienionych powyżej funkcji.

Zadanie 5. Obliczyć błędy średnie następujących funkcji

a)
; b)
; c)
; d)

Rozwiązania

a)
. Na podstawie tego wzoru, określamy odległość pomierzoną dalmierzem. We wzorze tym wielkość stała
, a l to odczyt na łacie zawarty między kreskami skrajnymi dalmierza. Błąd średni odległości
. Zatem błąd
odległości pomierzonej dalmierzem jest stukrotnie większy od błędu odczytu na łacie
.

W przykładach b), c), d) korzystamy z zależności (bf)

b)
, ponieważ:
,

c)
,

d)
, ponieważ

Zadanie 6. W trójkącie zmierzono dwa kąty
i
z błędami średnimi
i
. Obliczyć trzeci kąt trójkąta
i jego błąd średni
.

Rozwiązanie

Zadanie 7. Przy jednym odłożeniu taśmy 20-metrowej błąd systematyczny
, a błąd przypadkowy
. Jakie będą błędy systematyczne i przypadkowe dla mierzonego tą taśmą boku długości 500 m (25 odłożeń taśmy)?

Rozwiązanie, Oznaczając
Otrzymujemy:

,

Zadanie 8. Siatkę kwadratów można wykreślić za pomocą zwykłego cyrkla pełniącego rolę odmierzacza i podziałki dwoma sposobami:

a) odmierzamy jeden raz na podziałce odcinek 10 cm (bok kwadratu) i odkładamy go wielokrotnie wzdłuż brzegu arkusza pierworysu

b) przed każdym odłożeniem odcinka 10 cm odmierzamy go na podziałce.

Który sposób jest dokładniejszy, jeśli uwzględnimy tylko błędy odmierzenia odcinka?

Rozwiązanie. W pierwszym wypadku popełniamy błąd stały
przy naniesieniu każdego odcinka. Błąd naniesienia końcowego punktu siatki kwadratów przy n bokach wyniesie:

Dla
,
;
.

W drugim wypadku za każdym odłożeniem boku kwadratu popełniamy błąd średni m, który będzie błędem przypadkowym, a więc z, różnymi znakami. Błąd naniesienia końcowego punktu siatki kwadratów wyniesie;

Dla
,
;
.

A więc drugi sposób jest niewątpliwie dokładniejszy.

Zadanie 9. Wyprowadzić wzór na odchyłkę kątową w ciągu poligonowym.

Rozwiązanie. Kąt
obliczamy z różnicy dwóch pomierzonych kierunków K₁ i K₂, czyli
. Błędy pomiaru kierunku
są to błędy przypadkowe, zatem błąd pomiaru kata

.

Kąty mierzymy w dwóch położeniach lunety, zatem błąd średni pomiaru kąta
(średniej arytmetyczne z dwóch położeń lunety)

.

Jeśli ciąg poligonowy składa się z n kątów, to błąd kątowy ciągu jest równy

Zadanie 10. Błąd pomiaru kierunku odczytanego na jednym noniuszu teodolitu wynosi
. Zmierzono kąt w dwóch położeniach lunety i w trzech seriach. Obliczyć błąd średni pomierzonego kąta (średniej arytmetycznej z trzech serii).

Rozwiązanie. Wprowadzamy oznaczenia pomocnicze; kierunek K odczytany na jednym noniuszu, średnia z odczytów dwóch noniuszy
,

kąt pomierzony w jednym położeniu lunety
,

kąt pomierzony w dwóch położeniach lunety

kąt pomierzony w trzech seriach
.

Błąd odczytu kierunku na jednym noniuszu

.

Błąd odczytu kierunku z dwóch noniuszy (błąd średni średniej arytmetycznej z dwóch odczytów);

Błąd pomiaru kąta
(
):

Błąd pomiaru kąta
(średniej arytmetycznej z dwóch położeń lunety)

Błąd średni pomiaru kąta
(średniej arytmetycznej z trzech serii):

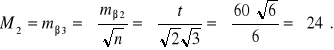
Odpowiedź. Błąd średni kąta pomierzonego w trzech seriach wynosi

Uwaga. Należy rozróżniać, kiedy błąd średni mnożymy, a kiedy dzielimy przez pierwiastek z ilości spostrzeżeń (
):

1) Mając do czynienia z funkcją spostrzeżeń obliczamy jej błąd mnożąc błąd średni pojedynczego spostrzeżenia przez
.

2) Gdy obliczamy błąd średni średniej arytmetycznej, oczywistym jest, że błąd ten będzie mniejszy od błędu średniego pojedynczego pomiaru, a zatem należy ten ostatni podzielić przez
.

Zadanie 11. Błąd średni pojedynczego pomiaru kąta teodolitem wynosi
W trójkącie zmierzono tym teodolitem kąt
cztery razy, a kąt
dziewięć razy. Jaki jest błąd średni trzeciego kąta w trójkącie?

Rozwiązanie. Z warunków zadania

Błąd średni średniej arytmetycznej z 4-krotnego pomiaru kąta
wynosi

Błąd średni średniej arytmetycznej z 9-krotnego pomiaru kąta
wynosi;

Trzeci kąt w trójkącie;

Błąd średni kąta
wynosi:

Zadanie 12, Błąd średni pojedynczego pomiaru kąta teodolitem wynosi
Ile razy należy zmierzyć tym teodolitem kąty
i
w trójkącie, jeśli chcemy, aby błąd średni trzeciego obliczanego kąta
(o niedostępnym wierzchołku) nie przekraczał ±15”?

Rozwiązanie. Po oznaczeniu
, otrzymamy:

.

Błąd średni średniej arytmetycznej z nieznanej liczby n pomiarów kątów
i

Ale

,

Stąd

.

Odpowiedź. Gdy w trójkącie pomierzymy kąty
i
po 8 razy, to błąd średni trzeciego kąta
o niedostępnym wierzchołku będzie wynosił ±15”.

Sprawdzenie

,

Zadanie 13. Błąd azymutu wyjściowego
i błąd każdego pomierzonego kąta
Wyznaczyć błąd średni azymutu dziesiątej linii w tym ciągu.

Rozwiązanie. W ciągu poligonowym azymut dowolnej linii przy pomierzonych kątach prawych definiuje następująca zależność:

Przy bezbłędnym azymucie wyjściowym błąd średni azymutu dziesiątej linii wynosiłby

Po uwzględnieniu błędu azymutu wyjściowego błąd średni azymutu dziesiątej linii wyniesie

.

Odpowiedź. Błąd średni azymutu dziesiątej linii wynosi

Zadanie 14. Z jaką dokładnością należy mierzyć kąt pochylenia
, aby błąd średni poprawki obliczanej z wzoru
był równy błędowi średniemu pomiaru 100 metrowego boku

Przyjąć
i

,

(
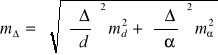
może być zaniedbana jako wielkość mała w porównaniu z drugim składnikiem).

Ponieważ

Więc

,

dla

,

dla

,

dla

,

dla

.

Ogólnie można stwierdzić, że kąty pochylenia zawarte w przedziale
wystarczy mierzyć z dokładnością 0,1° (6'), a kąty mniejsze z jeszcze mniejszą dokładnością.

Zadanie 15. Pomierzono długość prostej d = 220,41 m ze średnim błędem
i azymut prostej
ze średnim błędem
Wyznaczyć błędy średnie przyrostów
,
.

Rozwiązanie. Korzystając z wzoru, na błąd średni dowolnej funkcji
otrzymamy

,

,

,

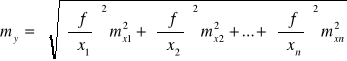
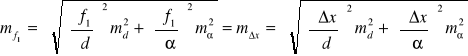
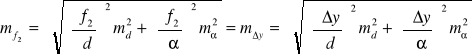
Odpowiedź. Błędy średnie przyrostów wynoszą:

Zadanie 16. W trójkącie pomierzono podstawę a = 241,60 m z błędem średnim
i wysokość h =136,20 m z błędem średnim
. Obliczyć pole trójkąta i jego błąd średni.

Rozwiązanie.

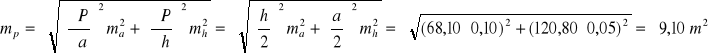
Odpowiedź. Pole trójkąta P = 1 ha 6453 m²

Opracowano na podstawie Ćwiczeń z geodezji. J. Ząbek, Z. Adamczewski, S. Kwiatkowski

1

---