MECHANIKA RUCHU

KRZYWOLINIOWEGO

Andrzej Reński

Politechnika Warszawska

Instytut Pojazdów

Warszawa 2007

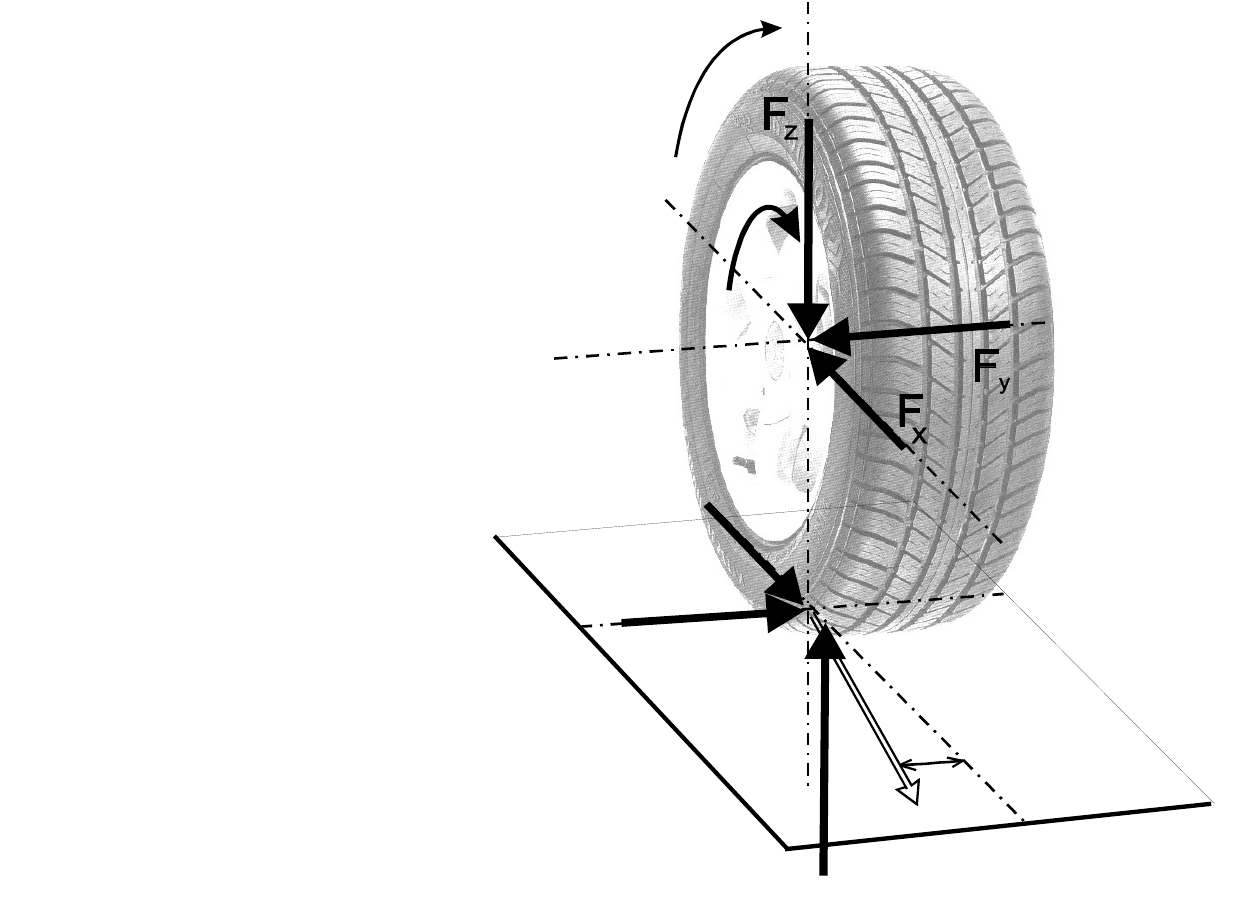
Współpraca

Współpraca

opony z

opony z

nawierzchnią

nawierzchnią

Z

Y

v



M

X



Siły działające na
koło

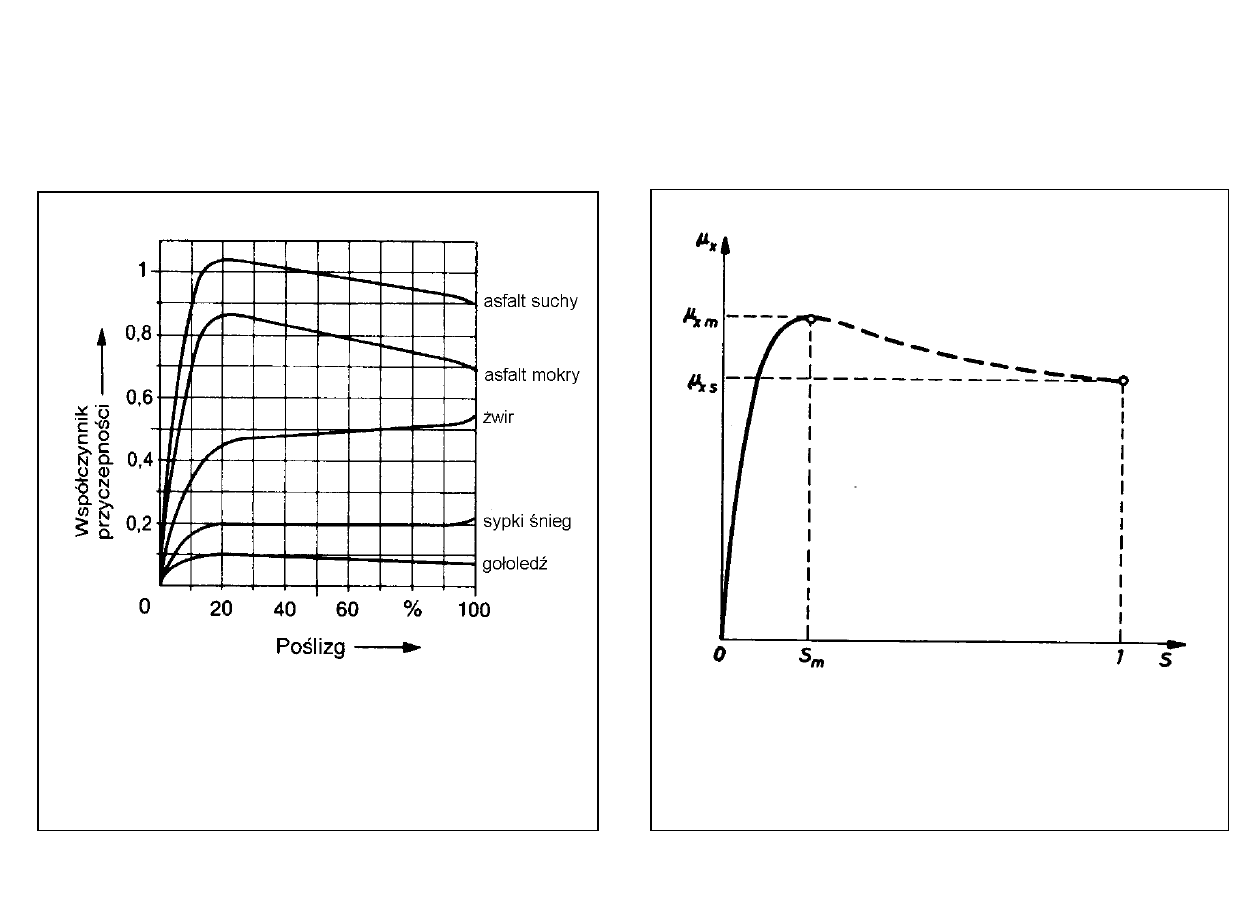
Współpraca opony z nawierzchnią

Współczynnik

przyczepności w

funkcji poślizgu

Współczynnik przyczepności
przylgowej i poślizgowej

Przyczepność wzdłużna

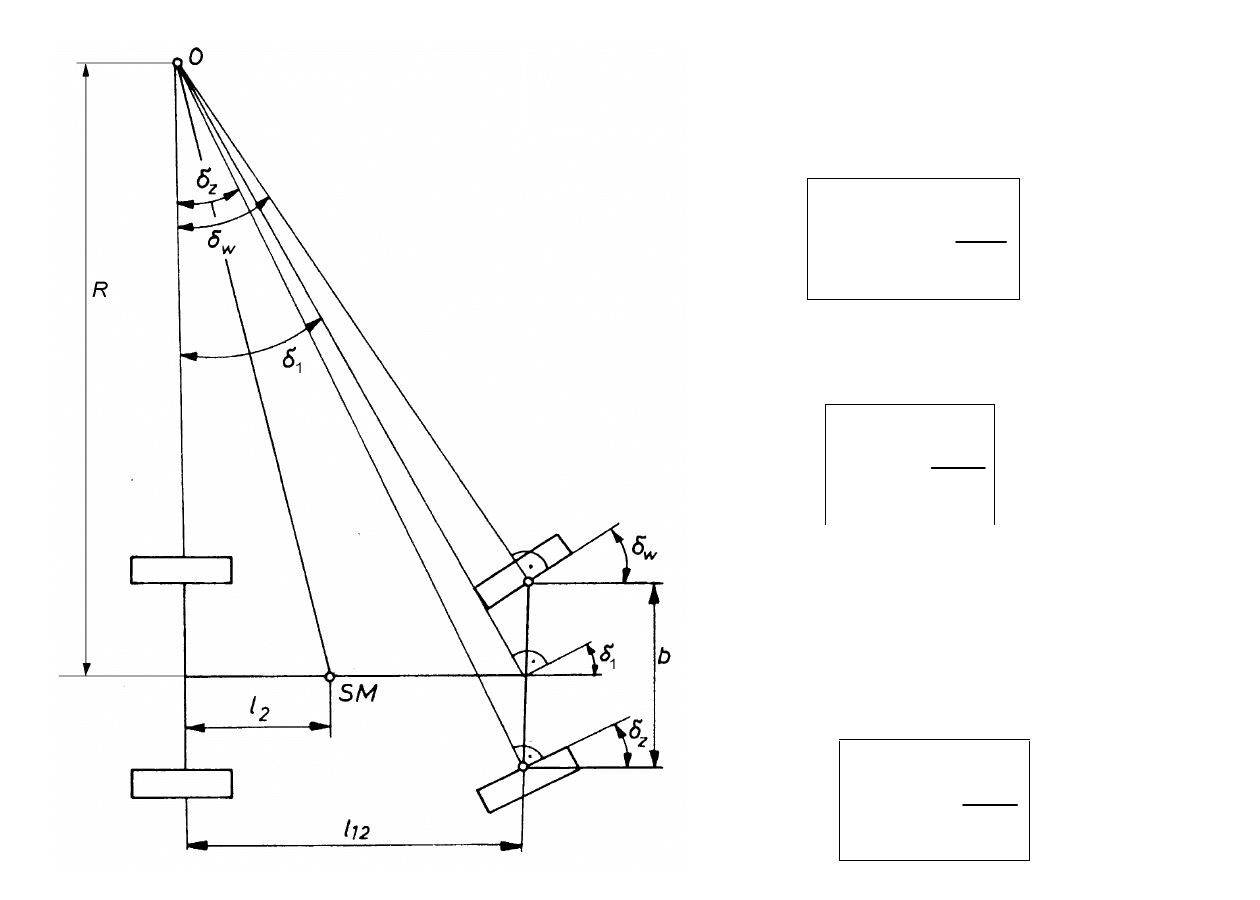
ZALEŻNOŚCI

GEOMETRYCZNE

R

l

tg

12

1





Dla małych kątów 

1

:

R

l

12

1





Teoretyczny kąt
skrętu kół
kierowanych - kąt
Ackermana δ

A

:

R

l

12

A





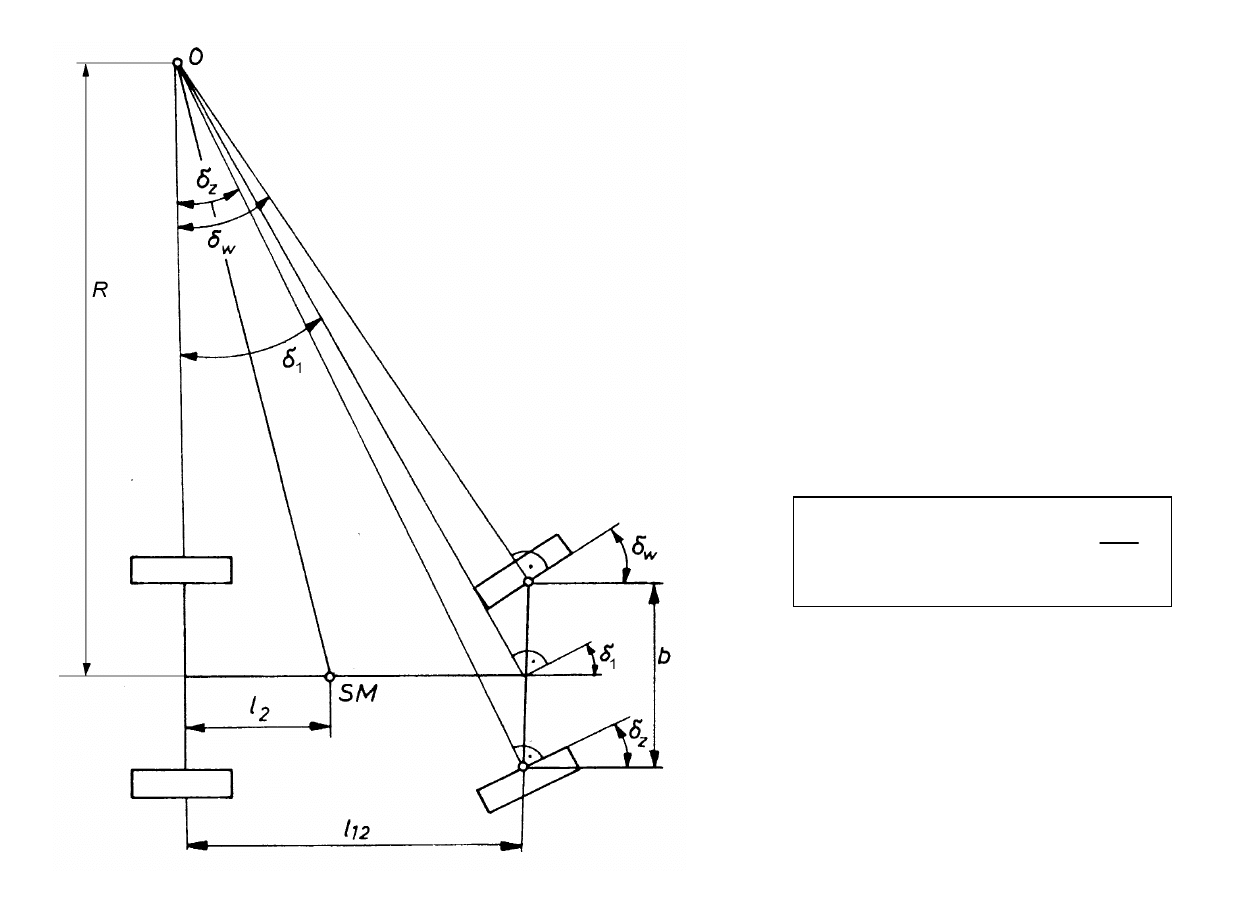
ZALEŻNOŚCI

GEOMETRYCZNE

Zależnośc pomiędzy
kątem skrętu koła
wewnętrznego 

w

i

zewnętrznego 

z

:

12

w

z

l

b

ctg

ctg









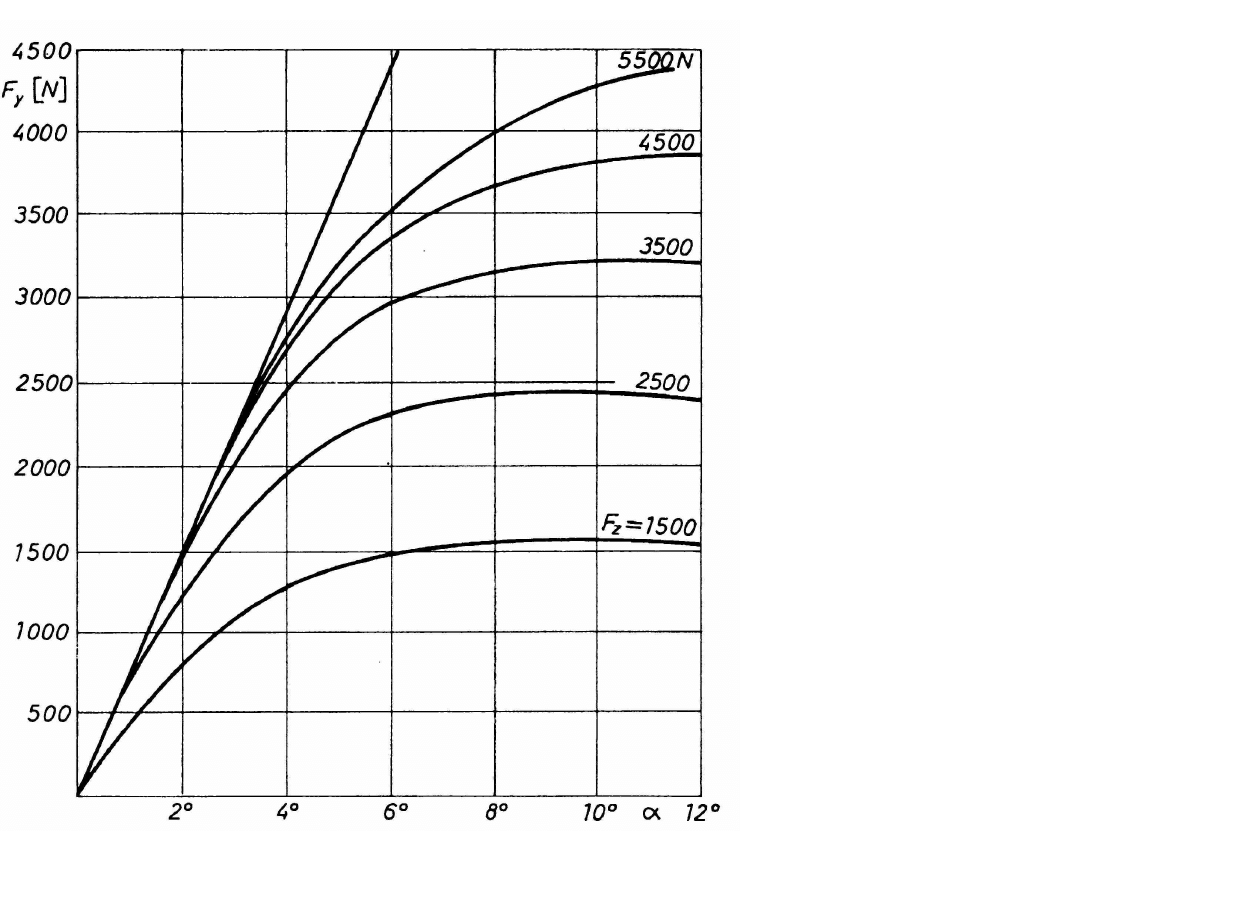
CHARAKTERYSTYKI
OPON

(

opona

175HR14

)

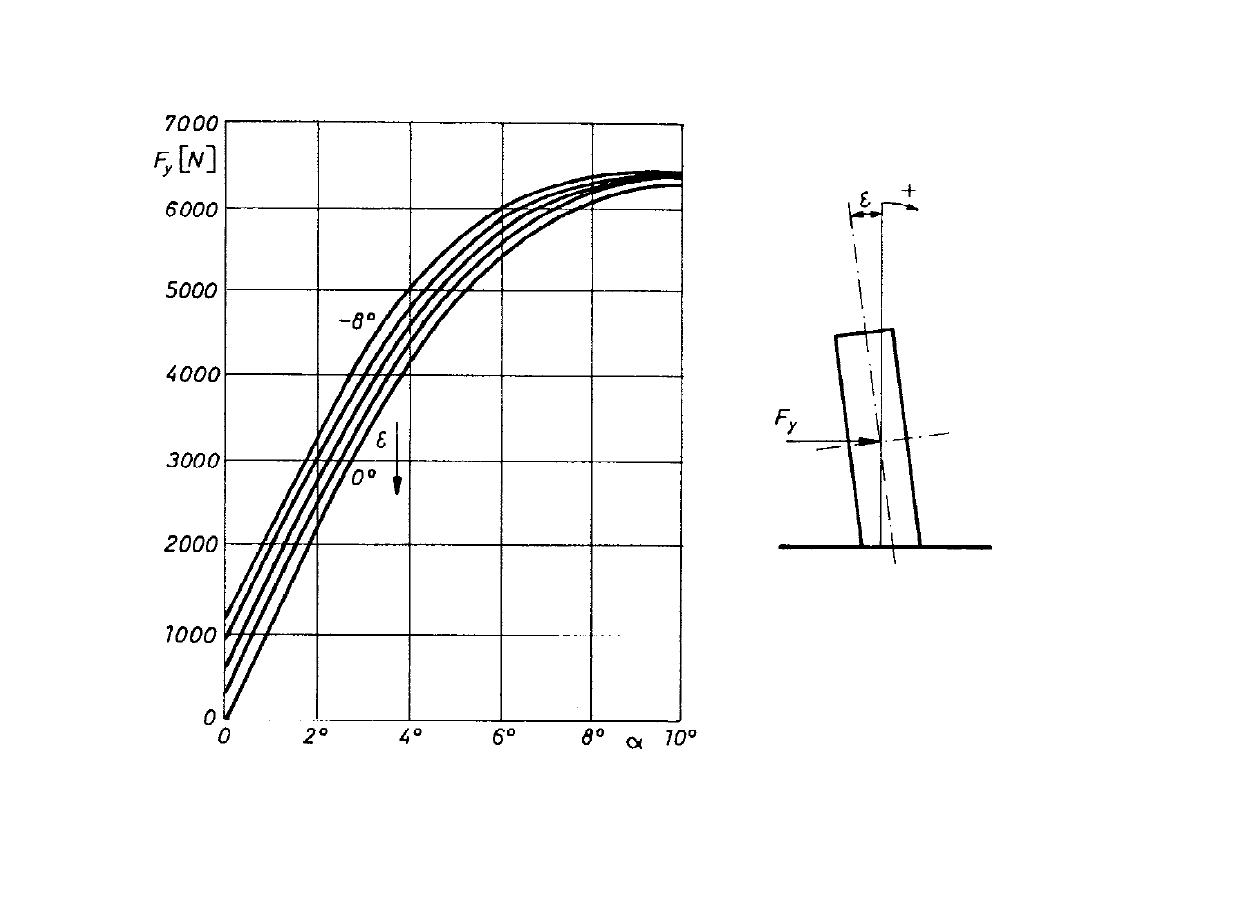
CHARAKTERYSTYKI OPON

Wpływ kąta pochylenia koła

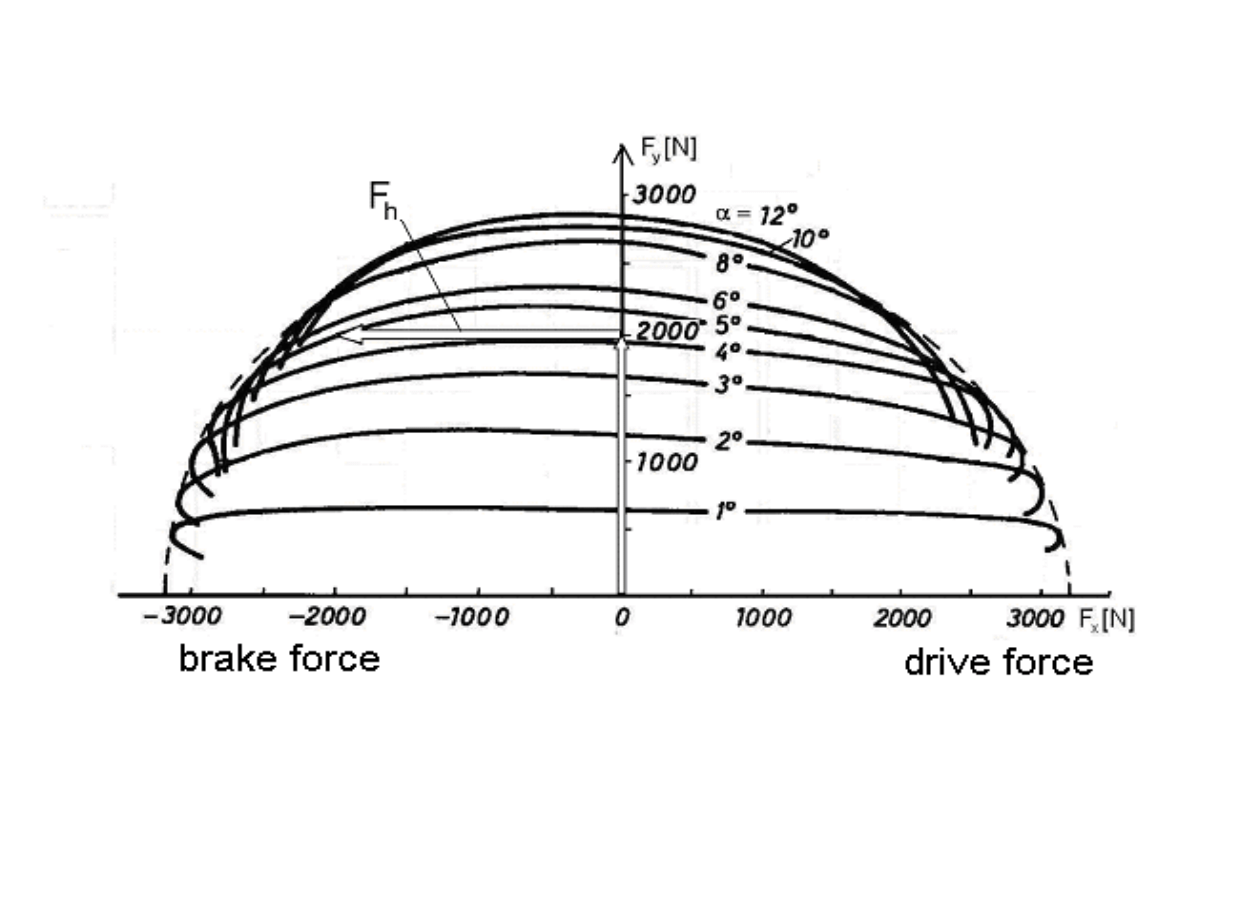
CHARAKTERYSTYKI OPON

Wpływ siły wzdłużnej F

x

na zależność kąta znoszenia α od

siły poprzecznej F

y

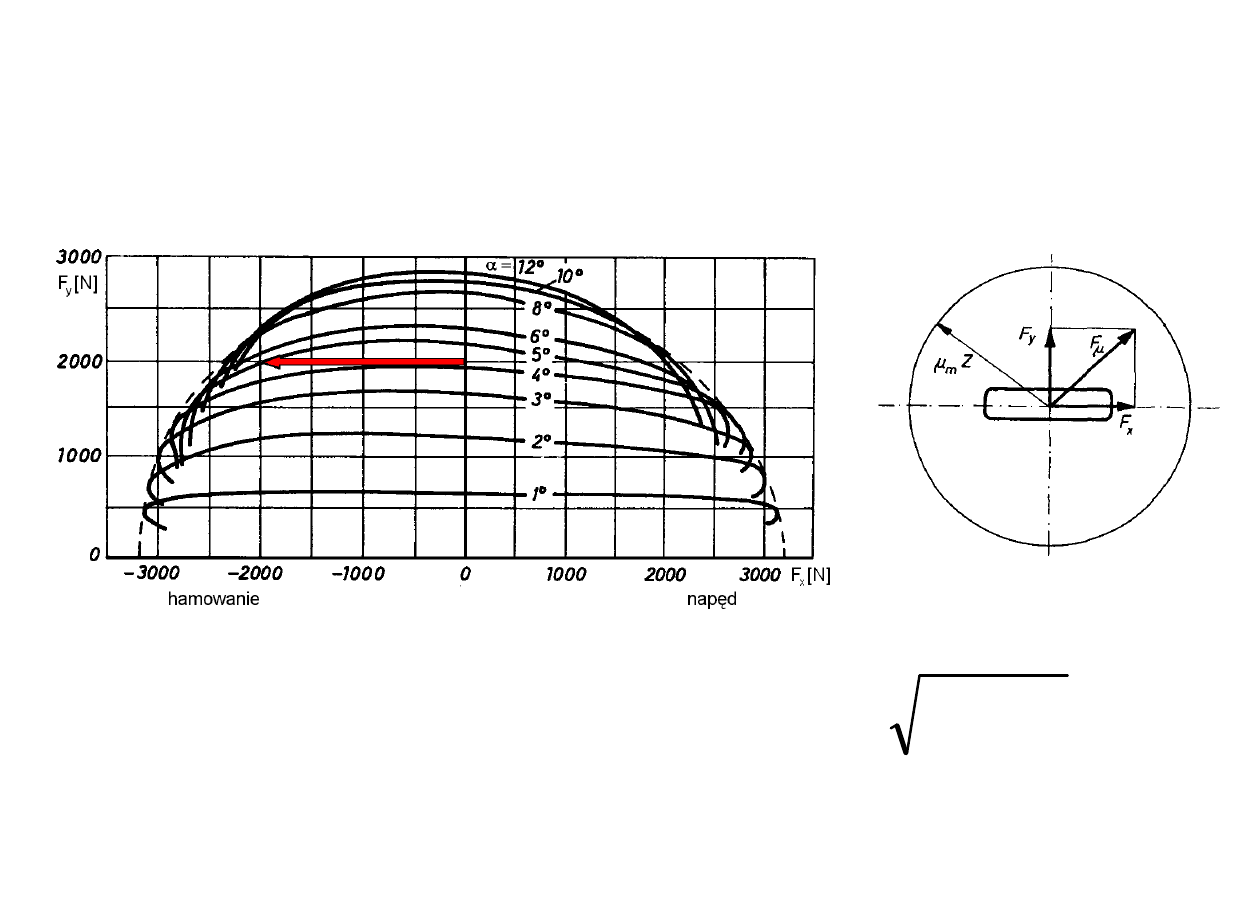
Współpraca opony z

nawierzchnią

Boczne znoszenie opony, przyczepność poprzeczna

Zależność pomiędzy siłą wzdłużną F

x

i poprzeczną F

y

dla różnych wartości kąta znoszenia  i poślizgu wzdłużnego S

Granica przyczepności

F

F

Z

x

y

m

2

2







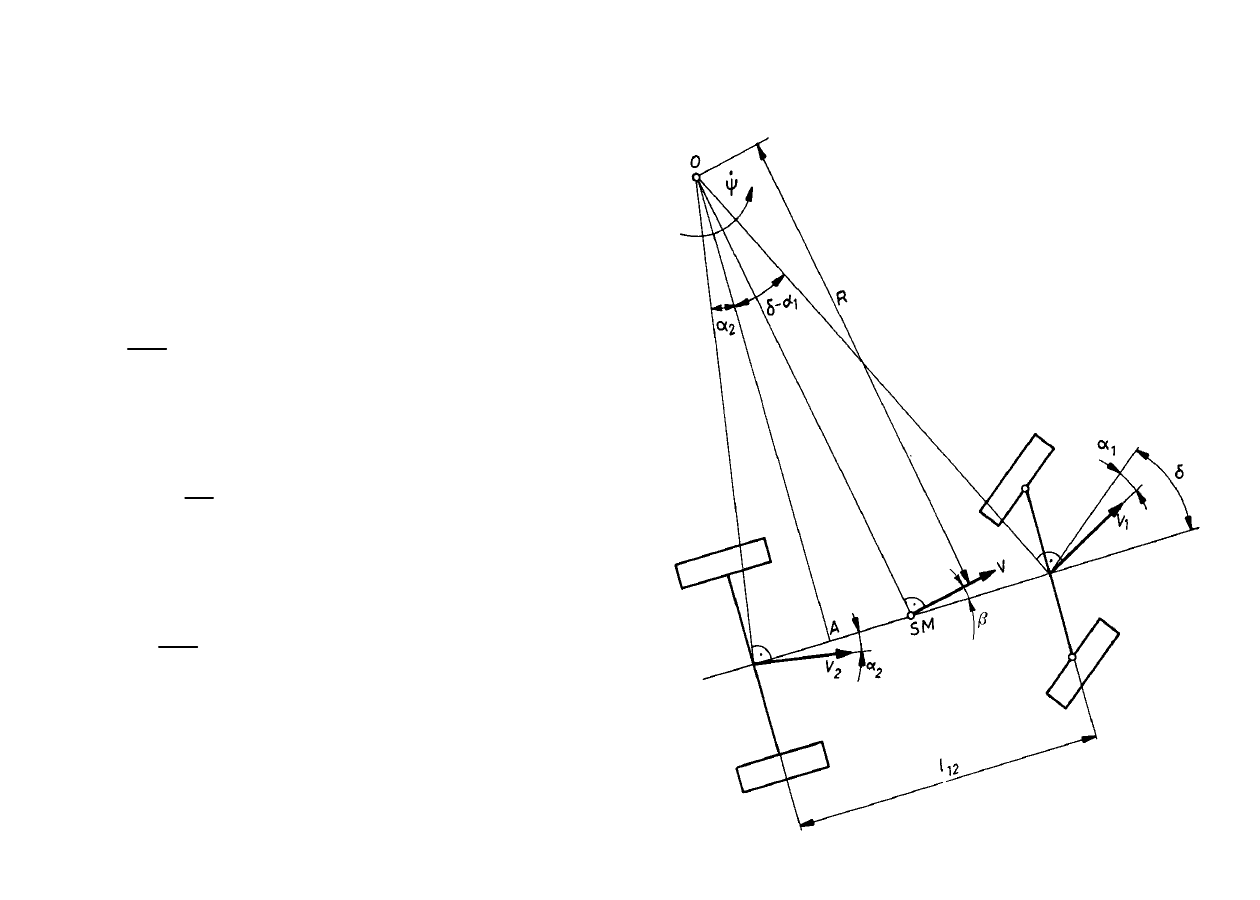
Mechanika ruchu krzywoliniowego

Zależności kinematyczne w ruchu po okręgu





2

1

12

1

2

12

v

l

R

v

R

l



































Mechanika ruchu po krzywoliniowego

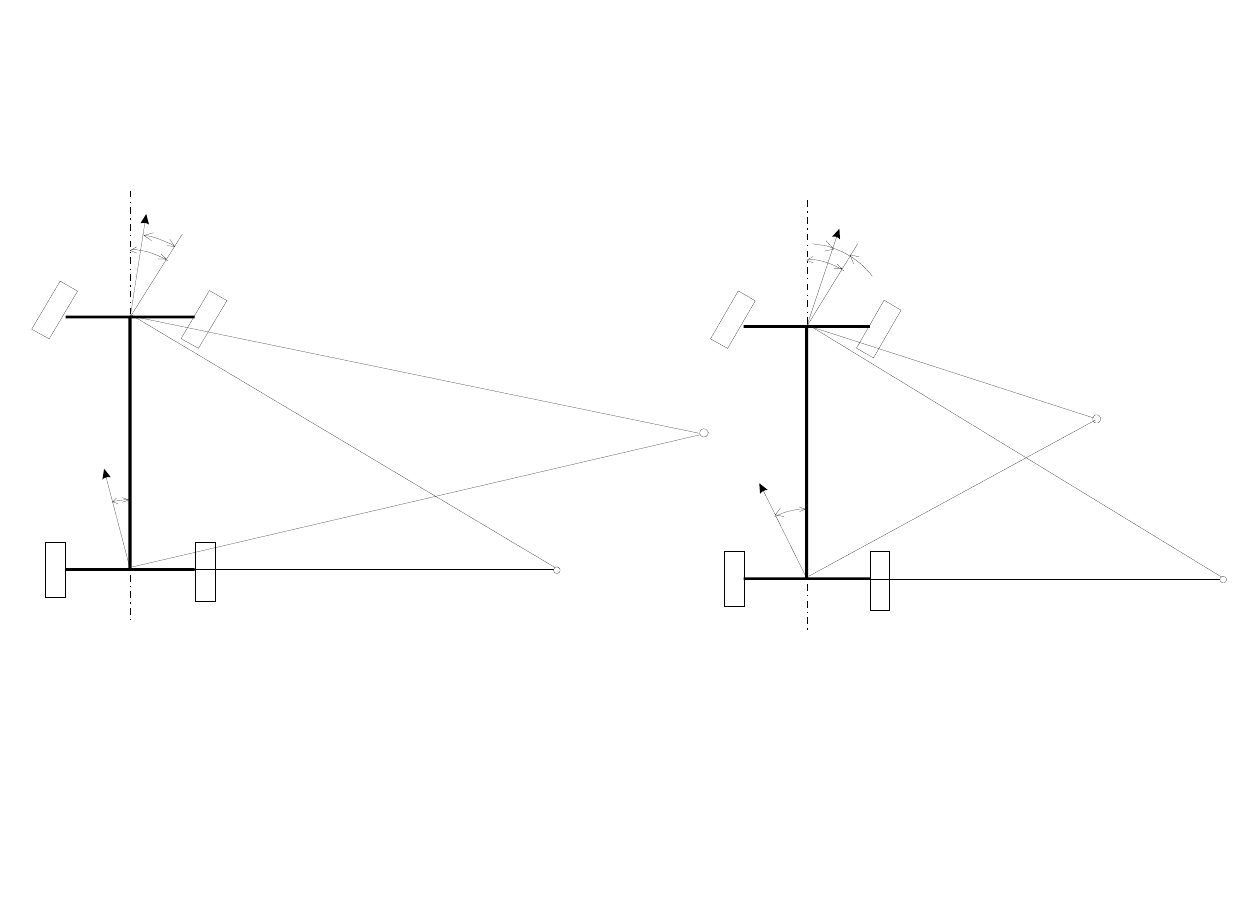
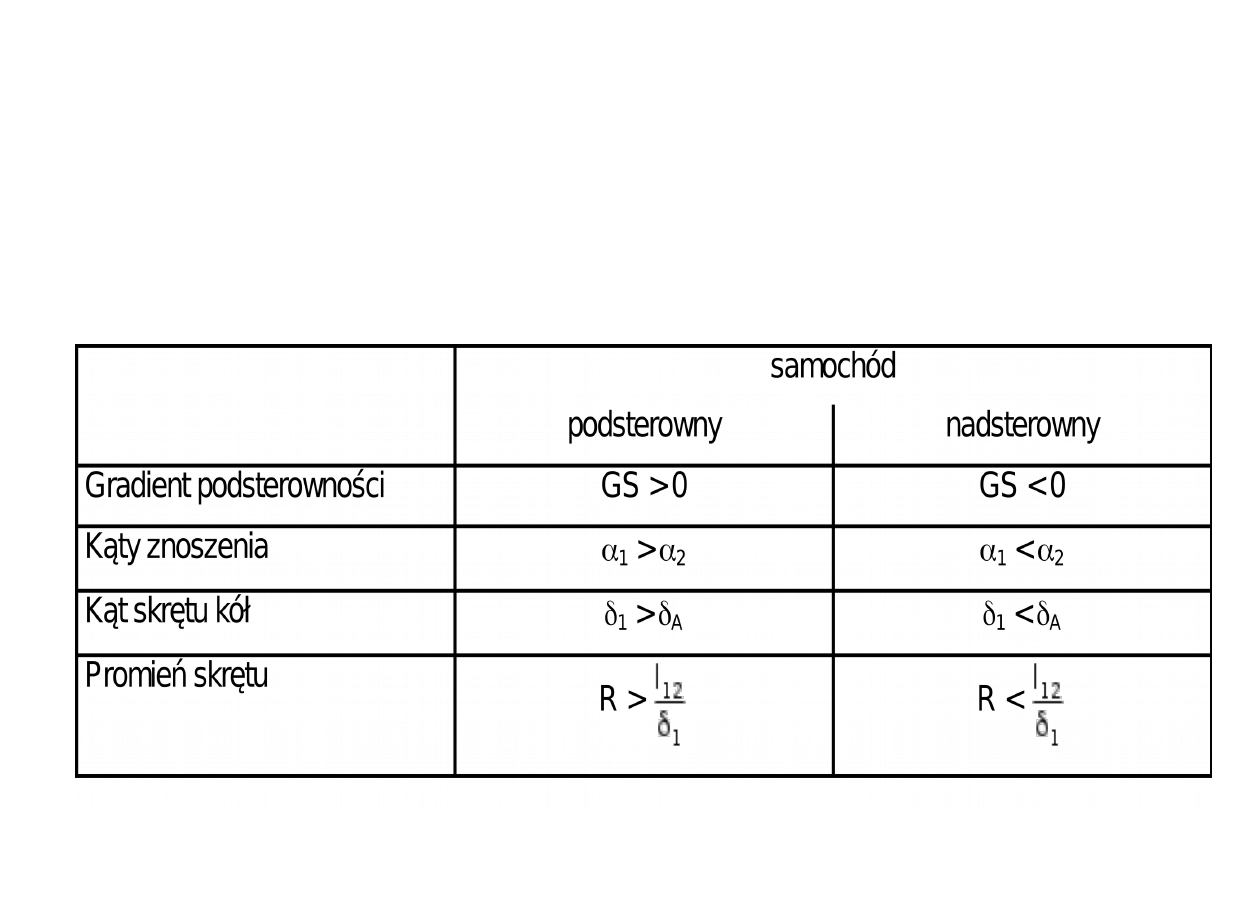
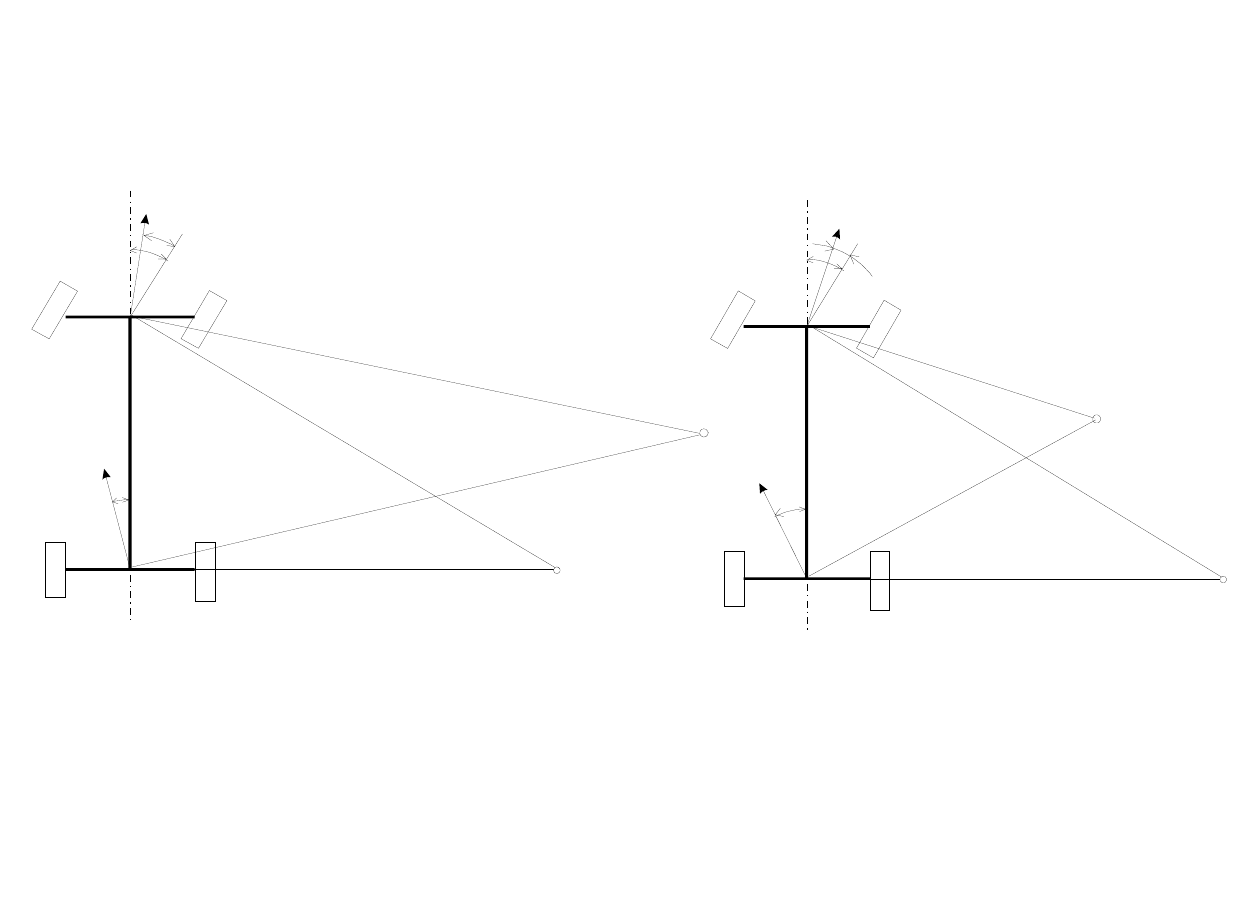
Pod- i nadsterowność

δ

δ

α

1

α

1

α

2

α

2

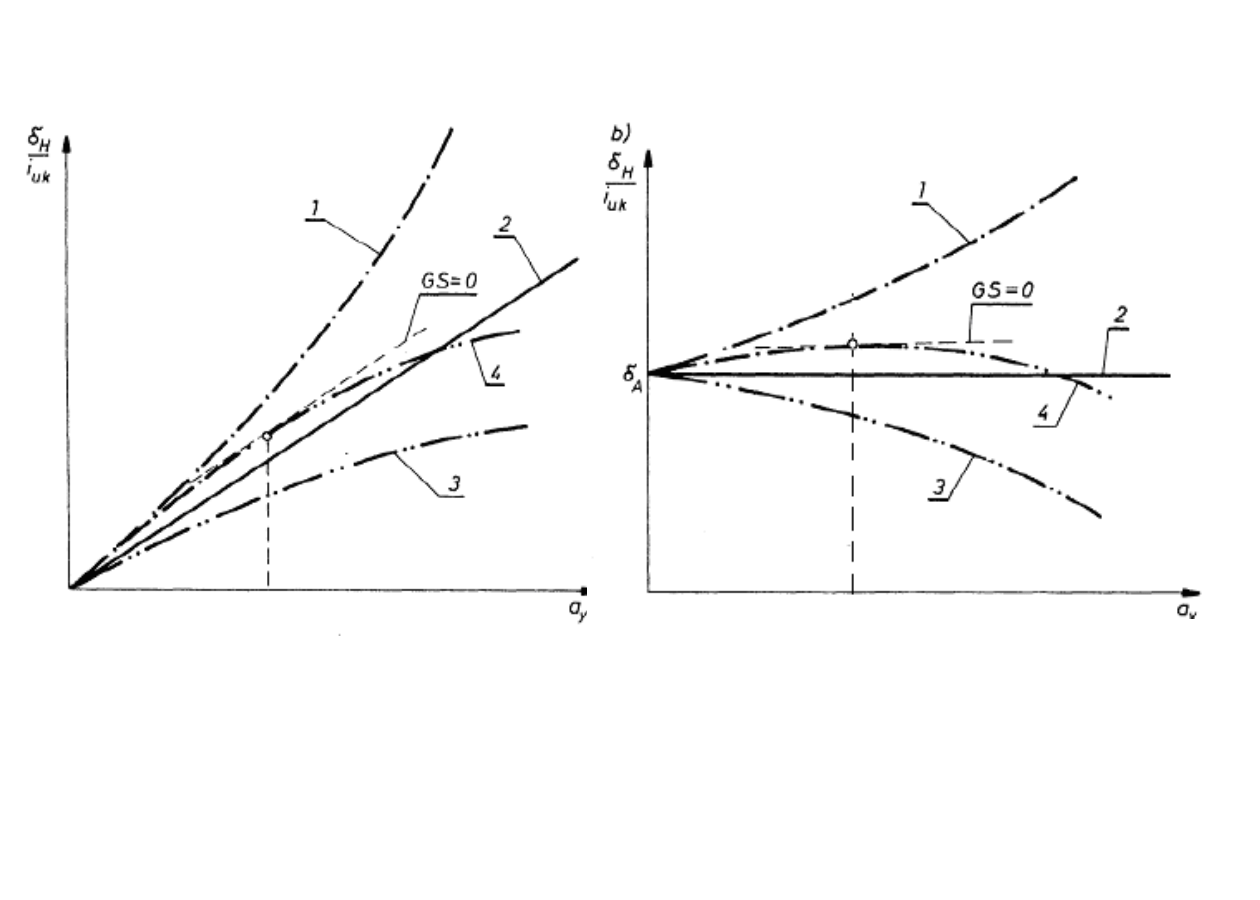
Samochód podsterowny

α

1

> α

2

Samochód nadsterowny

α

1

< α

2

Mechanika ruchu krzywoliniowego

Zależności

dynamiczne

2

2

1

1

y

2

2

2

1

1

2

1

K

K

F

v

v

m

l

K

l

K

y

v

K

K

y

m





























2

2

2

1

1

1

z

2

2

1

1

2
2

2

2

1

1

l

K

l

K

M

y

v

l

K

l

K

v

l

K

l

K

J





























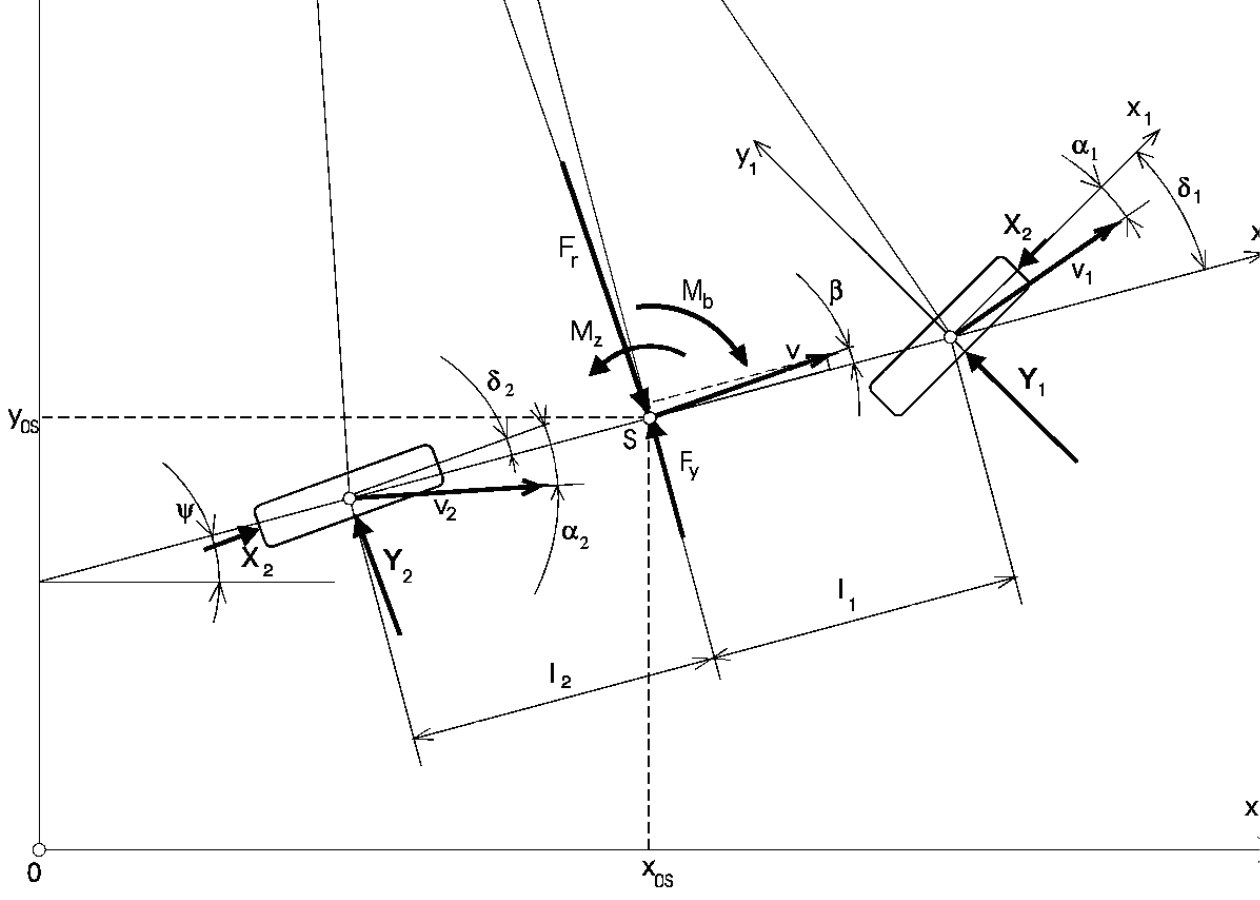
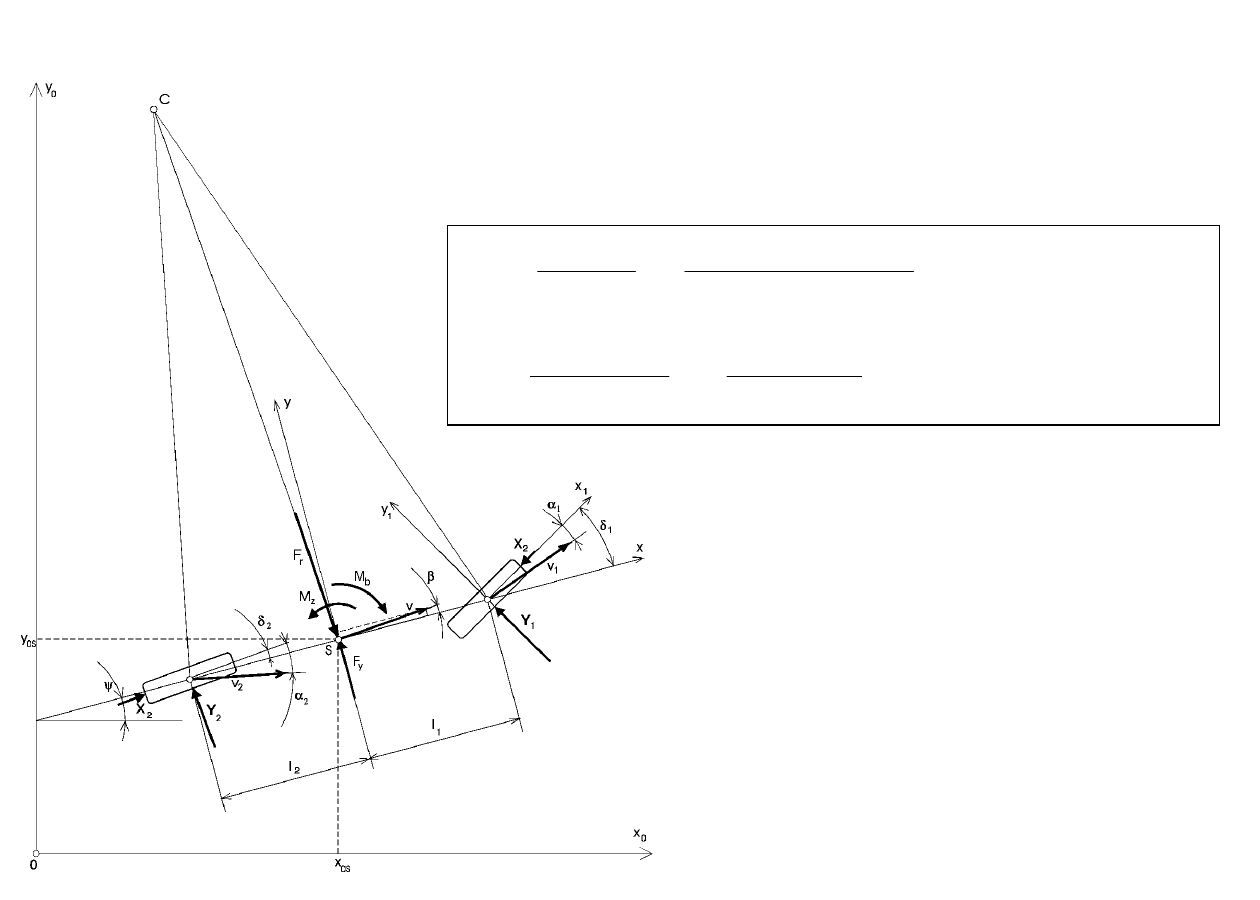
Mechanika ruchu krzywoliniowego

Mechanika ruchu krzywoliniowego

Mechanika ruchu krzywoliniowego

Równanie sił w kierunku osi y

-F

by

+ Y

1

cos

1

+ Y

2

cos

2

+ F

y

= 0

Równanie momentów

-M

b

+ Y

1

cos

1

l

1

- Y

2

cos

2

l

2

+ M

z

= 0

Siła bezwładności F

by

jest sumą rzutów na oś y siły

odśrodkowej F

r

 = m v  i siły bezwładności wynikającej ze

zmiany prędkości v



F

by

= m v cos + m sin = m + m



v

x

y





Równania ruchu

-m ( ) + Y

1

+ Y

2

+ F

y

= 0

-J + Y

1

l

1

- Y

2

l

2

+ M

z

= 0



y

x











Mechanika ruchu krzywoliniowego

Y

1

= K

1

α

1

x

l

1

1

1

















x

y









Mechanika ruchu krzywoliniowego

Y

2

= K

2

α

2

x

l

2

2

2

















x

y









Mechanika ruchu krzywoliniowego

-m ( ) + Y

1

+ Y

2

+ F

y

= 0

-J + Y

1

l

1

- Y

2

l

2

+ M

z

= 0

y

x

















0

F

x

l

x

y

K

x

l

x

y

K

y

x

m

y

2

2

2

1

1

1













































































0

M

x

l

x

y

l

K

x

l

x

y

l

K

J

z

2

2

2

2

1

1

1

1







































































Mechanika ruchu krzywoliniowego





0

F

x

l

x

y

K

x

l

x

y

K

y

x

m

y

2

2

2

1

1

1













































































0

M

x

l

x

y

l

K

x

l

x

y

l

K

J

z

2

2

2

2

1

1

1

1







































































2

2

1

1

y

2

2

2

1

1

2

1

K

K

F

v

v

m

l

K

l

K

y

v

K

K

y

m





























2

2

2

1

1

1

z

2

2

1

1

2
2

2

2

1

1

l

K

l

K

M

y

v

l

K

l

K

v

l

K

l

K

J





























const

v

x







Mechanika ruchu krzywoliniowego

2

2

1

1

y

2

2

2

1

1

2

1

K

K

F

v

v

m

l

K

l

K

y

v

K

K

y

m





























2

2

2

1

1

1

z

2

2

1

1

2
2

2

2

1

1

l

K

l

K

M

y

v

l

K

l

K

v

l

K

l

K

J





























Dla ustalonego stanu ruchu: δ

2

= 0, δ

1

= const, = const,

= const,

y



0

,

0

y











1

1

y

2

2

2

1

1

2

1

K

F

v

v

m

l

K

l

K

y

v

K

K





















1

1

1

z

2
2

2

2

1

1

2

2

1

1

l

K

M

v

l

K

l

K

y

v

l

K

l

K



















Mechanika ruchu krzywoliniowego

1

1

y

2

2

2

1

1

2

1

K

F

v

v

m

l

K

l

K

y

v

K

K





















1

1

1

z

2
2

2

2

1

1

2

2

1

1

l

K

M

v

l

K

l

K

y

v

l

K

l

K



















Dla F

y

= 0, M

z

= 0





1

2

2

1

1

2

2

12

2

1

12

2

1

l

K

l

K

v

m

l

K

K

v

l

K

K











1

1

2

2

1

12

2

12

K

l

K

l

l

m

v

l

v























lub

Mechanika ruchu krzywoliniowego

Inaczej
zapisując

























1

2

2

1

12

12

1

K

l

K

l

l

m

v

v

l





Podstawiając

R

1

v





oraz

y

a

v 























1

2

2

1

12

y

12

1

K

l

K

l

l

m

a

R

l

Kąt obrotu kierownicy: δ

H

= δ

1

i

uk

; i

uk

– przełożenie układu

kierowniczego

Kąt Ackermana:

R

l

12

A



























2

1

1

2

12

y

A

H

uk

K

l

K

l

l

m

a

i

1

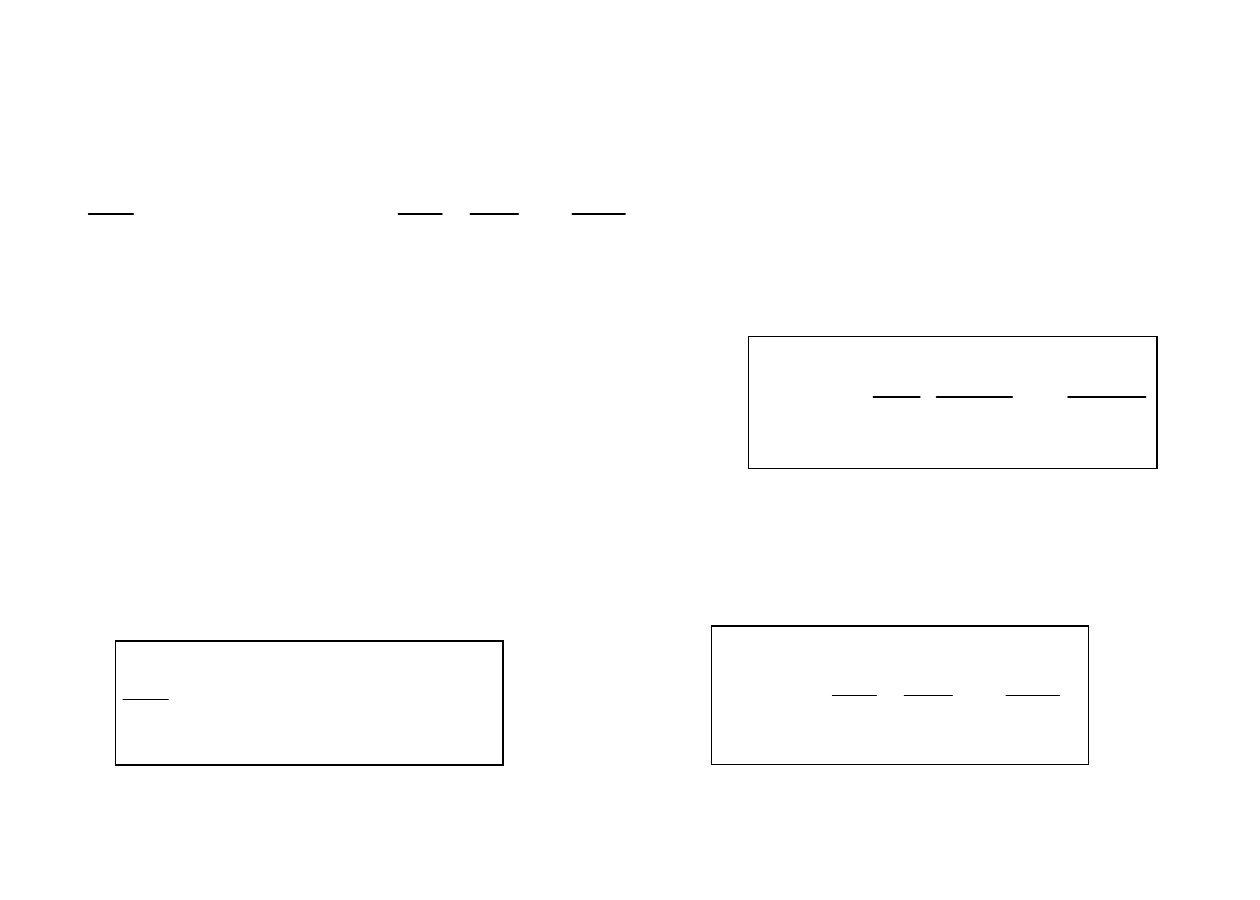
Mechanika ruchu krzywoliniowego























2

1

1

2

12

y

A

H

uk

K

l

K

l

l

m

a

i

1

Gradient podsterowności wg ISO 4138:

y

A

y

H

uk

da

d

da

d

i

1

GS









Dla ustalonego stanu ruchu: δ

H

= const, δ

A

= const, a

y

=

const

GS

a

i

1

y

A

H

uk

























2

1

1

2

12

K

l

K

l

l

m

GS

Mechanika ruchu krzywoliniowego

Ruch samochodu ze stałą
prędkością po okręgach o
różnych promieniach R

Ruch samochodu po okręgu o
stałym promieniu z różnymi
stałymi prędkościami v

1 – samochód podsterowny, 2 – neutralny, 3 – nadsterowny,
4 – samochód o zmiennej charakterystyce sterowności

Mechanika ruchu krzywoliniowego

R >

R <

R >

R <

Porównanie zachowania się samochodu pod- i
nadsterownego w ustalonym stanie ruchu

Mechanika ruchu po krzywoliniowego

Pod- i nadsterowność

δ

δ

α

1

α

1

α

2

α

2

Samochód podsterowny

α

1

> α

2

Samochód nadsterowny

α

1

< α

2

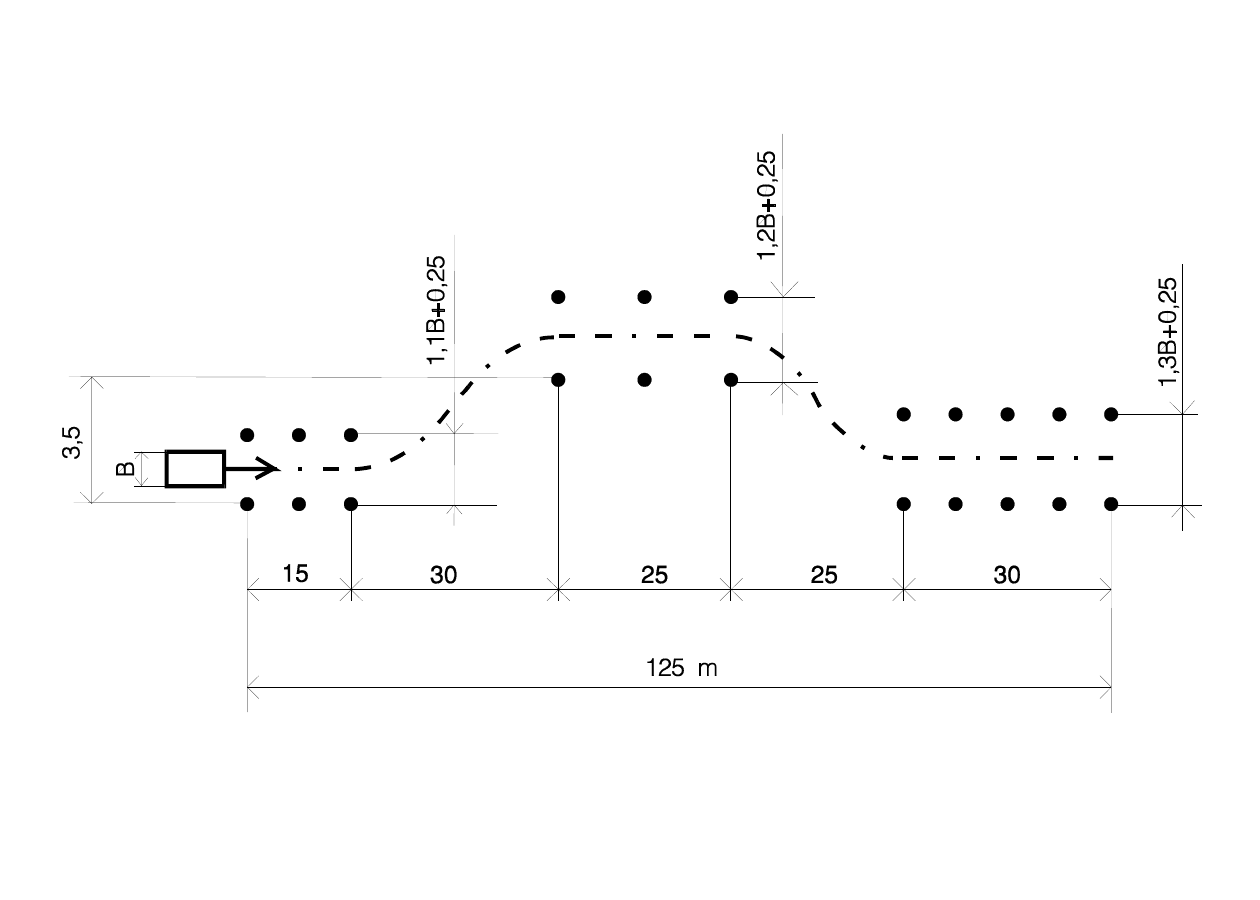
Mechanika ruchu krzywoliniowego

Tor jazdy stosowany w teście „podwójna zmiana pasa
ruchu” wg normy ISO 3888; B – szerokość samochodu

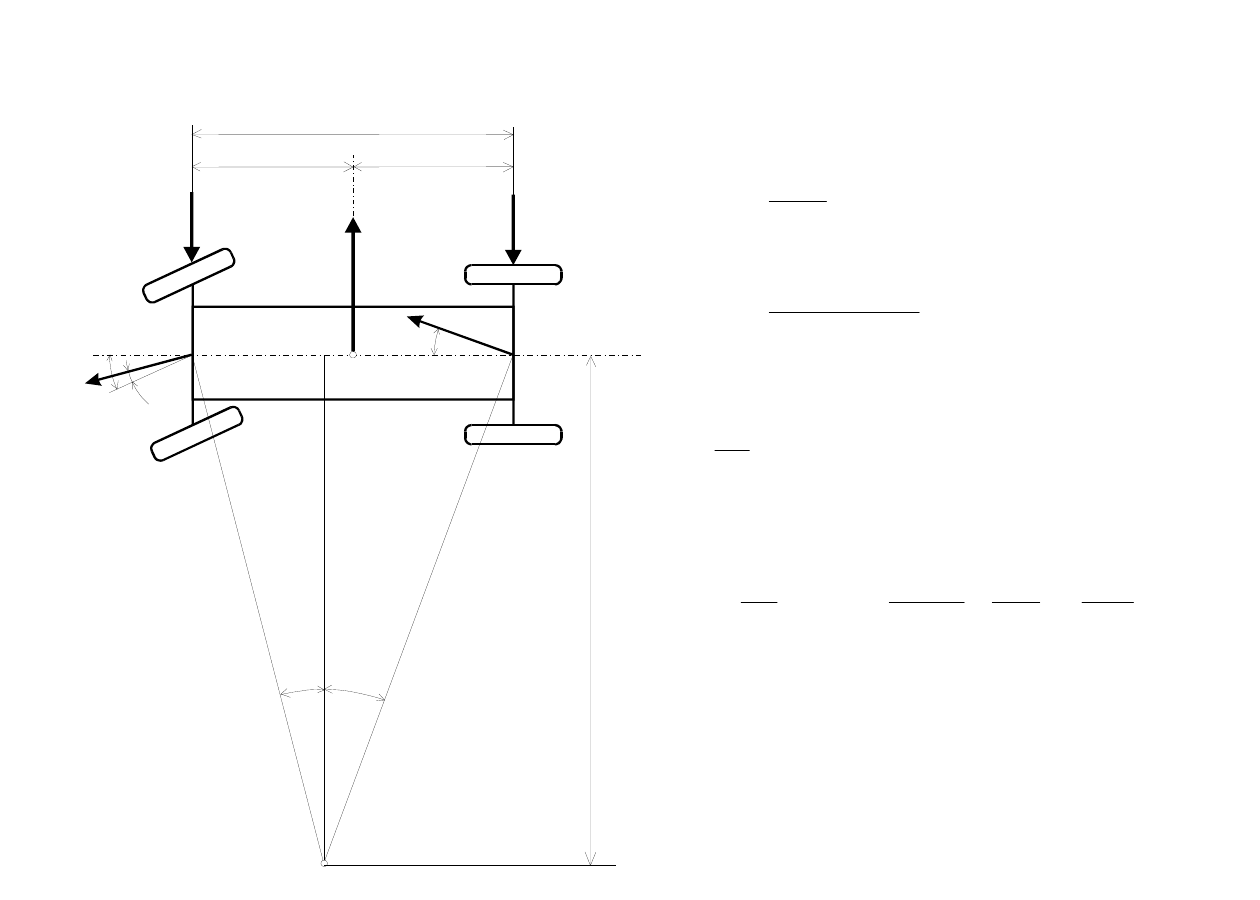
Mechanika ruchu krzywoliniowego

Zależności dynamiczne w
ruchu po okręgu



2



2



v

1

v

2

F

y

Y

1

Y

2

1

 

-



1

l

l

1

2

l

1 2

R

S M

O

y

2

y

a

m

v

m

R

v

m

F













2

1

12

l

R







































2

1

1

2

12

y

12

k

l

k

l

l

a

m

v

l





2

1

12

R

l











