WYTRZYMAŁOŚĆ MATERIAŁÓW

prowadzący

prof. dr hab. inż. Kazimierz WÓJS

Wykład 15

Opracował

Andrzej Sitka

HIPOTEZY WYTĘŻENIA

HIPOTEZY WYTĘŻENIA

HIPOTEZY WYTĘŻENIA

W celu przeprowadzenia analizy teoretycznej stopnia
zagrożenia

elementów

wprowadza

się

pojęcie

wytężenia materiału

, czyli stopnia zbliżenia stanu

fizycznego

materiału

do

stanu

granicznego

(niebezpiecznego).

Konieczność

stosowania

odpowiednich kryteriów oceny możliwości zniszczenia
elementów

konstrukcji

wymaga

postawienia

stosownych hipotez –

hipotez wytężenia

.

 

HIPOTEZY WYTĘŻENIA

Hipotezy wytężenia w zależności od przyjętej miary
wytężenia dzielimy na:

-         naprężeniowe,

-         odkształceniowe,

-         energetyczne,

-         mieszane.

Pojęcia podstawowe

Załóżmy że pewien stan naprężenia (wyrażony

przez naprężenia główne) charakteryzuje stosunek:

(1)

c

b

a

:

:

:

:

3

2

1









Jeżeli naprężenia zwiększają się proporcjonalnie,
wytężenie zwiększa się również osiągając wartość
odpowiadającą granicy plastyczności, a następnie
wytrzymałości na rozciąganie.

Pojęcia podstawowe

W układzie naprężeń głównych każdemu stanowi

naprężenia odpowiada punkt o współrzędnych: 

1







 



np. punkt A na rys. 1 a więc przy założeniu

ciągłości związków zachodzących między wytężeniem

a stanem naprężenia, taki punkt określa również

wytężenie materiału odpowiadające danemu stanowi

naprężenia.

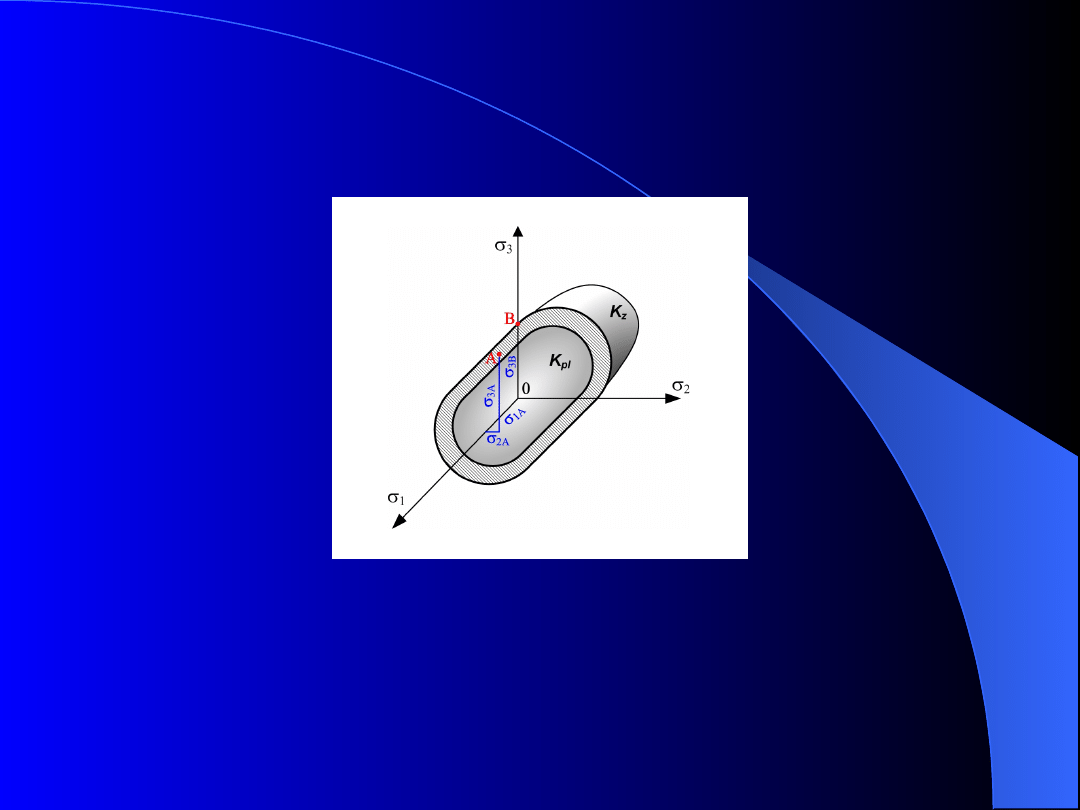
Pojęcia podstawowe

Rys. 1. Powierzchnie wytężenia odpowiadające wejściu

w stan plastyczny K

pl

i zniszczeniu K

z

Pojęcia podstawowe

Nieskończenie

wiele

takich

punktów,

to

powierzchnie wytężenia odpowiadające np. wejściu
materiału w stan plastyczny K

pl

lub zniszczeniu K

z

.

Taką powierzchnię w układzie naprężeń głównych
opisuje funkcja:





0

,

,

,

3

2

1



i

C

F







a w przypadku dowolnego stanu naprężenia:





0

,

,

,

,

,

,



i

zx

yz

xy

z

y

x

C

F













(2)

(3)

Parametry C

i

charakteryzują materiał.

Pojęcia podstawowe

Celem hipotez wytężenia

jest określenie

związku między wytężeniem W a składowymi stanu
naprężenia:

(4)

Krytyczne wartości wytężenia można wyznaczyć
przeprowadzając

doświadczenie

dla

jednego

określonego stanu naprężenia 

0

, najlepiej dla

jednoosiowego rozciągania (np. punkt B, rys.1 )

(5)





i

zx

yz

xy

z

y

x

C

F

W

,

,

,

,

,

,



















i

C

F

W

,

0

,

0

,

0

,

0

,

0

,

0





Pojęcia podstawowe

gdyż

krytyczne

wytężenie

dla

ogólnego

i

jednoosiowego stanu naprężenia jest równe:

(6)

Rozwiązując to równanie ze względu na



0

, otrzymamy:









i

i

zx

yz

xy

z

y

x

C

F

C

F

,

0

,

0

,

0

,

0

,

0

,

,

,

,

,

,

,

0





















zx

yz

xy

z

y

x

f















,

,

,

,

,

0



(7)

Prawą stronę tego równania określimy jako naprężenie
redukowane



red

, a więc:





zx

yz

xy

z

y

x

red

f















,

,

,

,

,



(8)

Pojęcia podstawowe

Znając naprężenie niebezpieczne dla jednoosiowego

stanu naprężenia i uwzględniając, że

, można

wyznaczyć składowe dowolnego niebezpiecznego

stanu naprężenia.

red







0

Hipoteza największego

naprężenia rozciągającego

Według tej hipotezy miarą wytężenia jest

największe naprężenie rozciągające. Jest to

hipoteza

naprężeniowa

. Stosowana jest do mechaniki pękania.

Hipoteza największego

wydłużenia

Miarą wytężenia według tej hipotezy jest największe
wydłużenie

względne.

Jest

to

hipoteza

odkształceniowa

, którą w układzie odkształceń

głównych wyrazimy wzorami:

(9)

Za

przyjęto wydłużenie odpowiadające

wytrzymałości na rozciąganie R

m

.

kryt







1

kryt







2

kryt







3

kryt



Zr



Hipoteza największego

wydłużenia

Po zastosowaniu do zależności (9) uogólnionego prawa
Hooke’a otrzymamy:

(10)





kryt

















3

2

1





kryt

















1

3

2





kryt

















2

1

3

Hipoteza największego

wydłużenia

Dla płaskiego stanu naprężeń

wzory

przyjmują postać:





0

,

0

,

0

3

2

1













kryt













2

1

kryt













1

2





kryt















2

1

(11)

Na rys.  za



kryt

przyjęto R

m

(przypadek rozciągania).

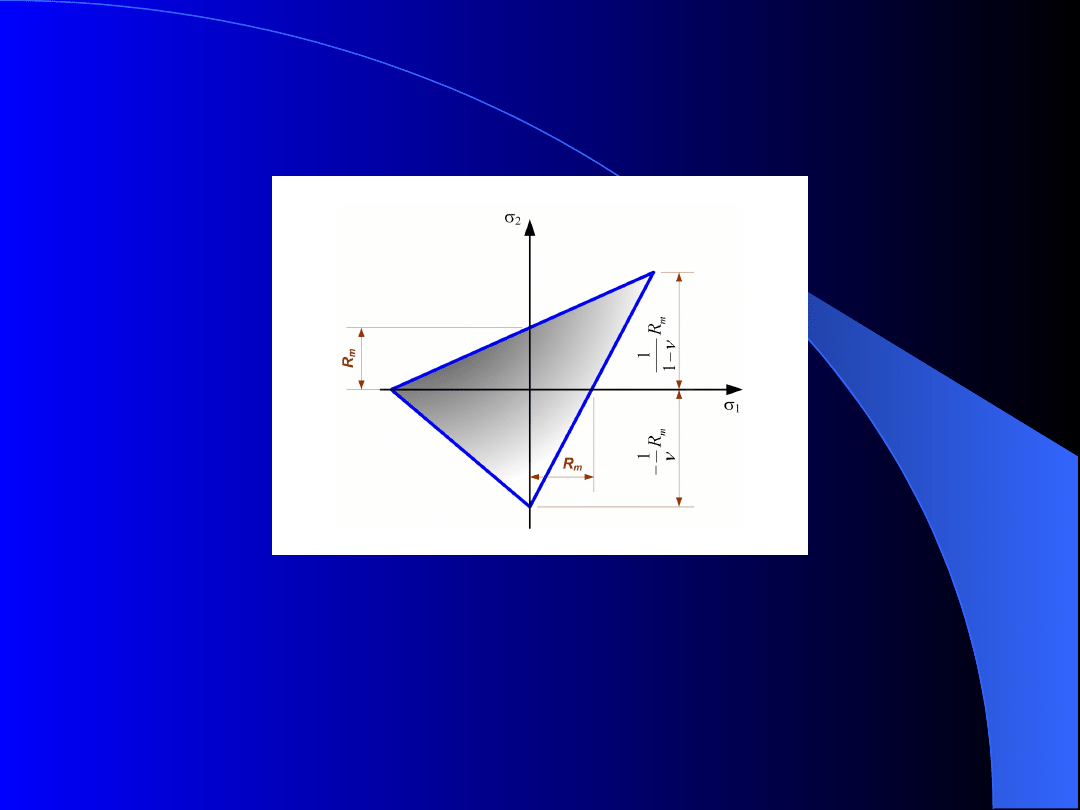
Hipoteza największego

wydłużenia

Rys. . Wykreślne odwzorowanie hipotezy największego

wydłużenia właściwego w układzie naprężeń głównych

Hipoteza największego

wydłużenia

W przypadku, gdy płaski stan naprężenia jest
wyrażony za pomocą naprężeń

to naprężenia

główne wyznacza się ze wzoru:

(1)

a naprężenia redukowane wyznaczymy z jednego z
trzech równań (11). Za naprężenia redukowane należy
przyjąć lewą stronę tego równania, która będzie
większa od lewej strony każdego z pozostałych dwóch
równań.

xy

y

x







,

,









2

2

2

,

1

4

2

1

2

1

xy

y

x

y

x























Hipoteza największego

wydłużenia

Jeśli

to wzór na naprężenie

redukowane przyjmie następującą postać:

















xy

y

x

,

0

,

2

2

4

2

1

2

1





























 



red

(1)

Przyjmując dla stali otrzymamy

(14)

3

,

0





2

2

4

65

,

0

35

,

0















red

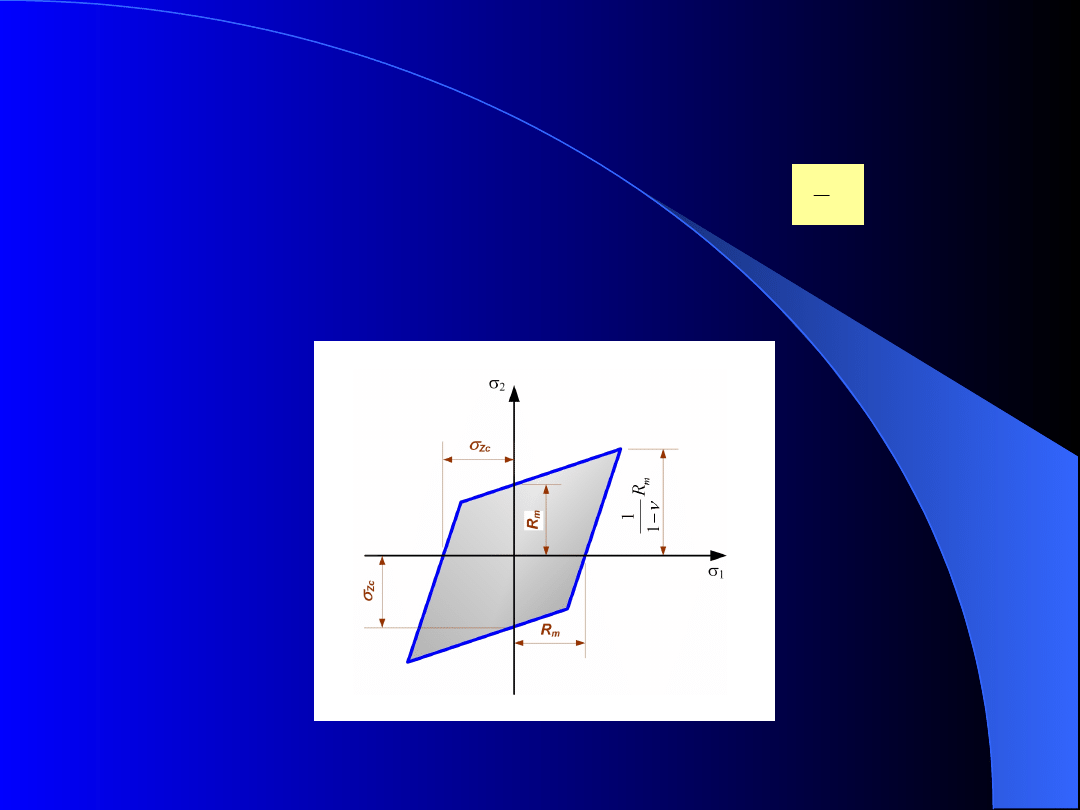
Hipoteza największego

wydłużenia

Stosunek wartości bezwzględnych wytrzymałości

przy rozciąganiu R

m

do wytrzymałości przy ściskaniu

jest równy



(rys. ). Ogranicza to

stosowanie tej hipotezy do materiałów spełniających
ten warunek.

Rys. . Wykreślne odwzorowanie zmodyfikowanej

hipotezy Grashofa

m

R



1



Hipoteza największego

wydłużenia

Modyfikacja tej hipotezy polega na przyjęciu
dodatkowego ograniczenia, aby żadne z głównych
odkształceń

liniowych

nie

było

mniejsze

od

odkształcenia

liniowego



Zc

,

odpowiadającego

wytrzymałości na ściskanie. Wykreślne odwzorowanie
tak zmodyfikowanej hipotezy dla płaskiego stanu
naprężenia, gdy |

Zc

|=|R

m

| pokazano na rys. .

Hipoteza największych

naprężeń stycznych

Miarą wytężenia tej hipotezy jest największe
naprężenie styczne. Jest to

hipoteza naprężeniowa

.

(15)

2

min

max

max











W przypadku prostego rozciągania , to równanie na
naprężenia redukowane ma postać:

(16)

kryt

red















min

max

bo:

(17)

0







red

W przypadku, gdy

i

, to równanie (16)

będzie miało następującą postać:

(18)

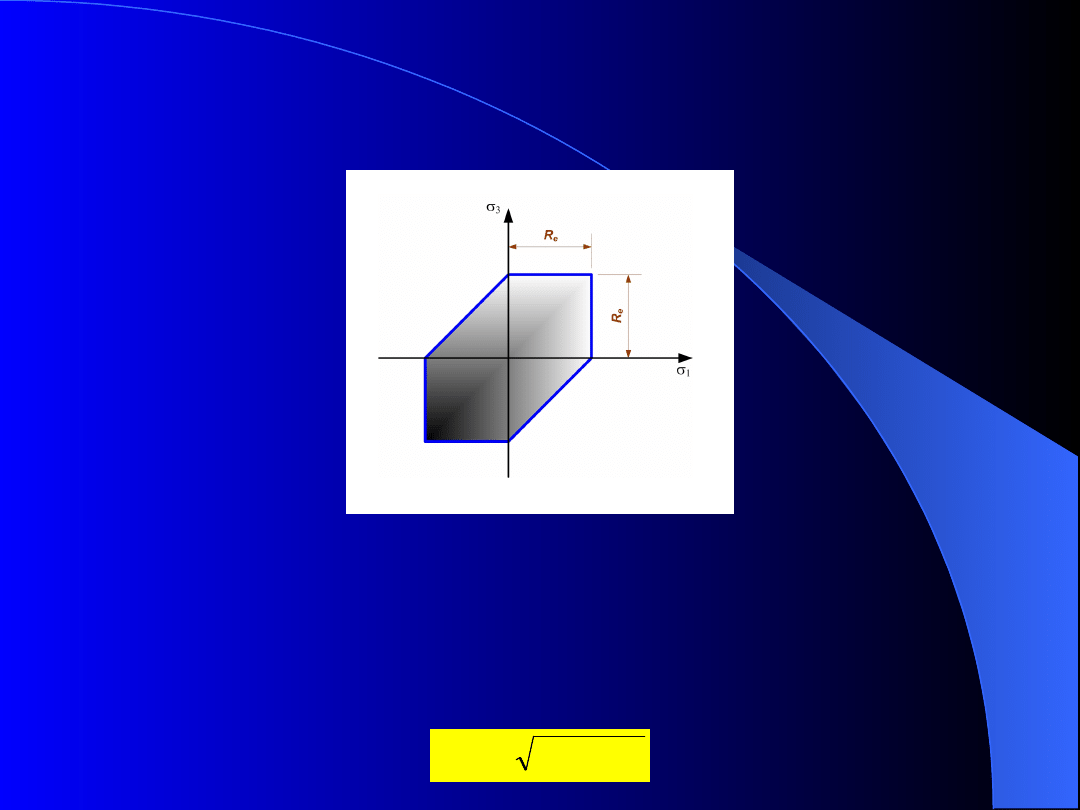
Hipoteza największych

naprężeń stycznych

1

max







3

min







kryt

red















3

1

Wykreślne odwzorowanie tej hipotezy dla materiałów o
jednakowej wartości granicy plastyczności podczas
rozciągania i ściskania w układzie naprężeń głównych


1

i 



pokazano na rysunku 4.

Za 

kryt

przyjęto R

e

.

W przypadku płaskiego stanu naprężenia, gdy: 

x

=



y

= 

0 

xy

= naprężenia redukowane można

wyznaczyć:

(19)

Hipoteza największych

naprężeń stycznych

Rys. 4. Wykreślne odwzorowanie hipotezy największych

naprężeń stycznych w układzie naprężeń głównych

2

2

4











red

Za miarę wytężenia wg tej hipotezy przyjmuje się

energię właściwą odkształcenia postaciowego, która w
dowolnym przestrzennym stanie naprężenia wynosi:

Hipoteza energii właściwej

odkształcenia postaciowego

(hipoteza Hubera)



 















2

2

2

2

2

2

6

6

1

zx

yz

xy

x

z

z

y

y

x

E











































(0)

W jednoosiowym stanie naprężenia energia właściwa
odkształcenia postaciowego będzie:

(1)

2

0

2

6

1







E





Porównując równania (0) i (1) wyznaczymy
naprężenie redukowane z zależności:

()

Naprężenie

redukowane

w

układzie

naprężeń

głównych można wyznaczyć z równania:

Hipoteza energii właściwej

odkształcenia postaciowego

(hipoteza Hubera)



 











2

2

2

2

2

2

6

2

1

zx

yz

xy

x

z

z

y

y

x

red









































 

 



2

1

3

2

3

2

2

2

1

2

1



























red

()

Wykreślnym odwzorowaniem tej hipotezy w

układzie naprężeń głównych jest walec kołowy
jednakowo nachylony do osi σ

1

, σ



, σ



, a śladem tego

walca w płaskim układzie naprężeń σ

1

, σ



jest elipsa

(rys.5).

W elipsę jest wpisane wykreślne odwzorowanie
hipotezy największych naprężeń stycznych.

Hipoteza energii właściwej

odkształcenia postaciowego

(hipoteza Hubera)

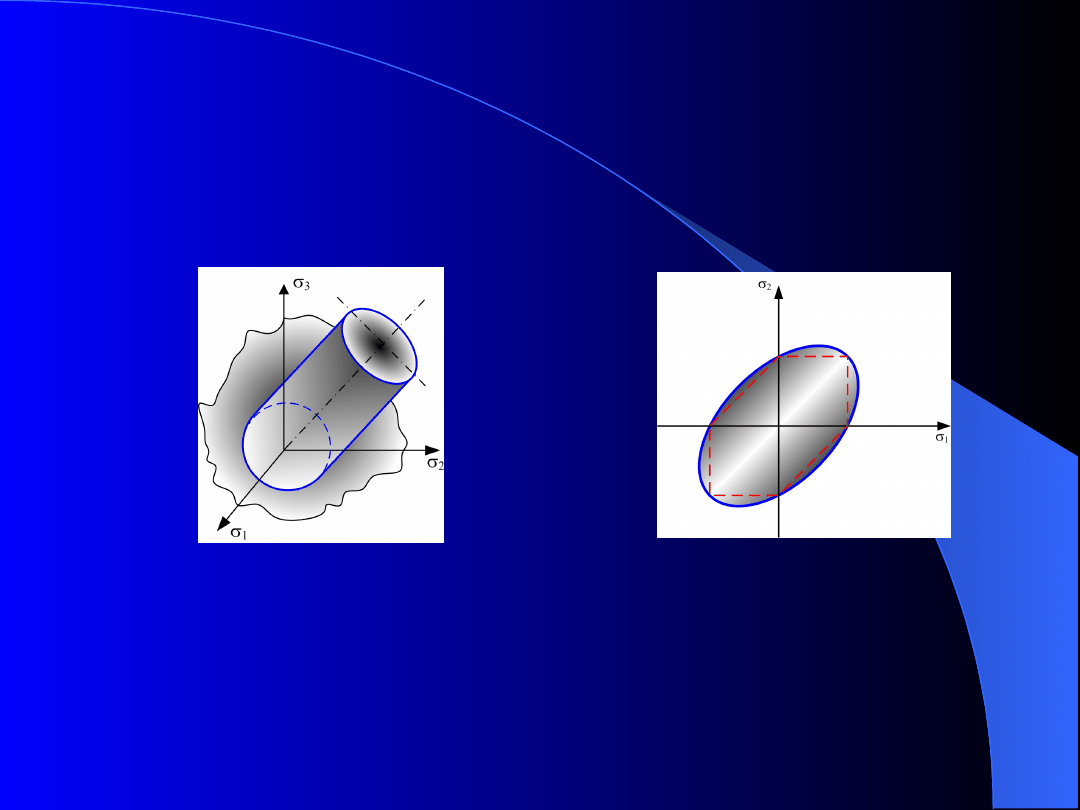
Rys. 5. Wykreślne odwzorowanie hipotezy Hubera; a) w

przestrzennym stanie naprężenia, b) w płaskim stanie

naprężenia

Hipoteza energii właściwej

odkształcenia postaciowego

(hipoteza Hubera)

a
)

b)

Dla płaskiego stanu naprężenia σ

x

, σ

y

, τ

xy

naprężenia

redukowane wyraża równanie:

(4)

Hipoteza energii właściwej

odkształcenia postaciowego

(hipoteza Hubera)





2

2

3















y

x

red

















xy

y

x

,

0

,

Jeśli

to wzór na naprężenie

redukowane przyjmie następującą postać:

(5)

2

2

3











red

Hipotezy

energii

właściwej

odkształcenia

postaciowego i największych naprężeń stosuje się do

określenia stanów granicznych przejścia materiału w

stan plastyczny (kryterium plastyczności). Hipotezy

odkształceń i największego naprężenia normalnego są

stosowane dla złomu rozdzielczego oraz kruchego.

Przykłady stosowania hipotez

wytężenia

Zastosowanie hipotez wytężenia można pokazać

na przykładach:

•

rozciąganie ze skręcaniem,

•

zginanie ze skręcaniem.

Dla prętów o przekroju kołowym w tych przypadkach
występują tylko naprężenia  i , a więc naprężenia
redukowane można wyznaczyć z hipotezy Hubera.

Przykłady stosowania hipotez

wytężenia

Naprężenia normalne pochodzące od rozciągania:

Rozciąganie ze skręcaniem

A

N





(6)

Naprężenia styczne pochodzące od skręcania:

(7)

0

max

W

M

s





Niebezpiecznym miejscem przekroju jest to, w którym
naprężenie styczne jest maksymalne (warstwa
wierzchnia).

Naprężenia redukowane wyznaczamy z hipotezy
Hubera :

Rozciąganie ze skręcaniem

(8)

2

2

3











red

2

0

2

3





























W

M

A

N

s

red



Naprężenie normalne pochodzące od zginania:

Zginanie ze skręcaniem

(9)

(0)

Niebezpiecznym miejscem przekroju są punkty
najbardziej odległe od środka, w których naprężenia są
ekstremalne.

Naprężenie redukowane wyznaczymy z hipotezy
Hubera :

W

M

g



max



2

2

3











red

2

0

2

3





























W

M

W

M

s

g

red



ale:

Zginanie ze skręcaniem

(1)

()

Równanie na naprężenia redukowane w przypadku
skręcania ze zginaniem można przedstawić również w
postaci:

32

2

2

16

3

3

0

d

W

d

W











więc:

W

M

M

W

M

W

M

s

g

s

g

red

2

2

2

0

2

75

,

0

3



































()

W

M

red

red





w którym:

2

2

4

3

s

g

red

M

M

M





(4)

ZŁOŻONE

ZŁOŻONE

ZAGADNIENIA

ZAGADNIENIA

ZGINANIA

ZGINANIA

Zbadajmy

przypadek

zginania

belki

siłą

poprzeczną i wyznaczmy rozkład naprężeń stycznych

w przekroju poprzecznym belki, a także przypadki, w

których działają jednocześnie składowe naprężeń

(normalne do przekroju poprzecznego) wywołane

działaniem sił i momentów.

NAPRĘŻENIA PRZY ZGINANIU

SIŁĄ POPRZECZNĄ

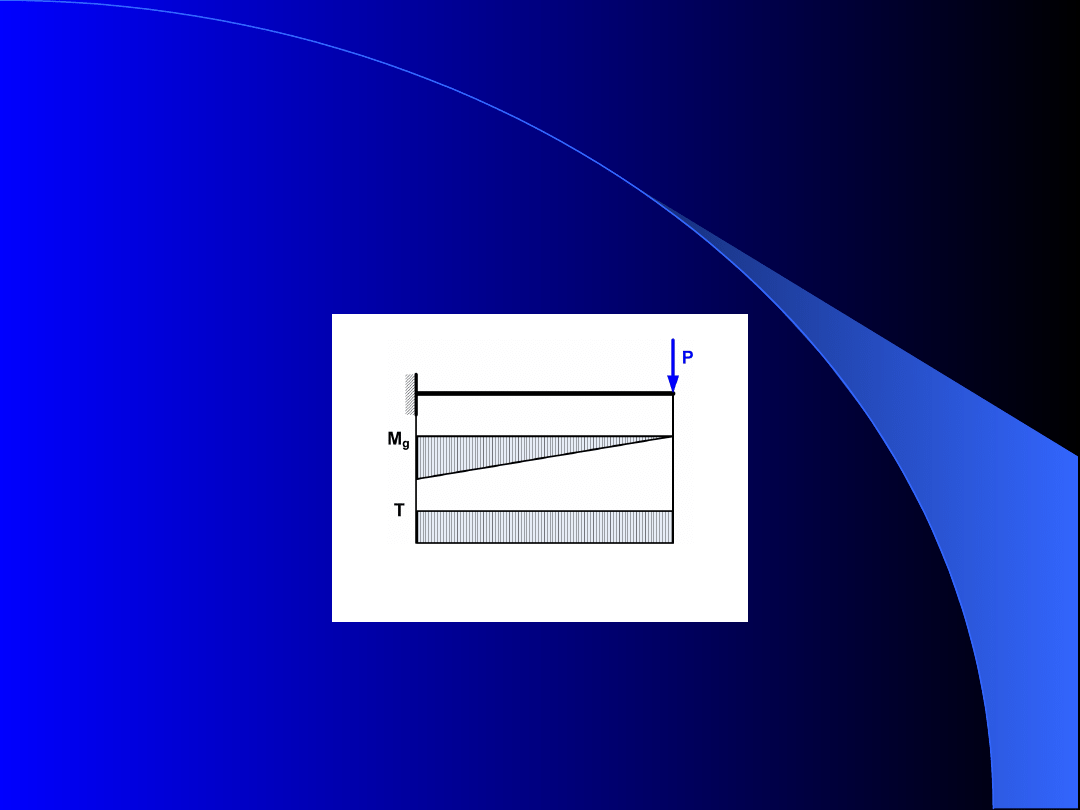
Taki przypadek pokazano na rys. 1. Belka jest
obciążona momentem gnącym M

g

i siłą tnącą T.

NAPRĘŻENIA PRZY ZGINANIU

SIŁĄ POPRZECZNĄ

Rys. 1. Zginanie belki siłą poprzeczną

Na powierzchni bocznej belki zginanej siłą poprzeczną
narysujemy linie równoległe oraz prostopadłe do osi
belki (rys. ).

NAPRĘŻENIA PRZY ZGINANIU

SIŁĄ POPRZECZNĄ

Rys. . Obraz linii pierwotnie równoległych i

prostopadłych do osi belki po odkształceniu

Działanie naprężeń stycznych  oraz zmiana wartości

naprężeń normalnych  wzdłuż osi belki, wywołane

zmianą wartości momentu gnącego, powodują
powstanie różnic w obrazie odkształceń belki w
stosunku do obrazu odkształceń w belce poddanej
zginaniu czystemu.

 

Różnice te są następujące:

•

Kąty między bokami odkształconej siatki nie są

na ogół proste. Największe zmiany występują w
warstwach bliższych osi belki, a w warstwach
skrajnych są tak małe, że można je pominąć.

•

Naprężenia

styczne

są

rozłożone

nierównomiernie w przekroju belki.

NAPRĘŻENIA PRZY ZGINANIU

SIŁĄ POPRZECZNĄ

Rozpatrzmy przypadek zginania siłą poprzeczną

nie przyjmując żadnego uproszczenia.

Wytnijmy z belki element o długości dx. Działanie
odrzuconych części belki wyrażają siły wewnętrzne
jak na rys. .

Kierunki naprężeń 

A

i 

B

w punktach A i B są styczne do

konturu. W naprężenia w innych punktach mają inne
kierunki (np. punkt C), a więc nie są równoległe do osi
z.

Analiza rozkładu naprężeń

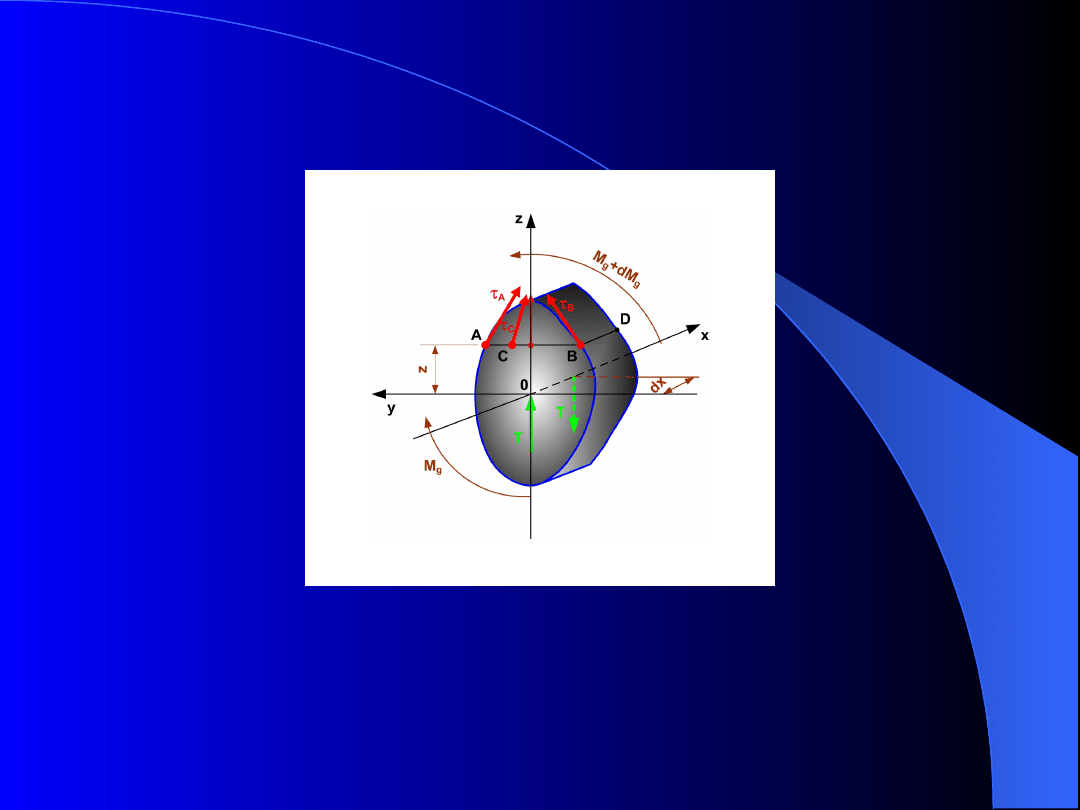
Analiza rozkładu naprężeń

Rys. . Element belki o długości dx w równowadze

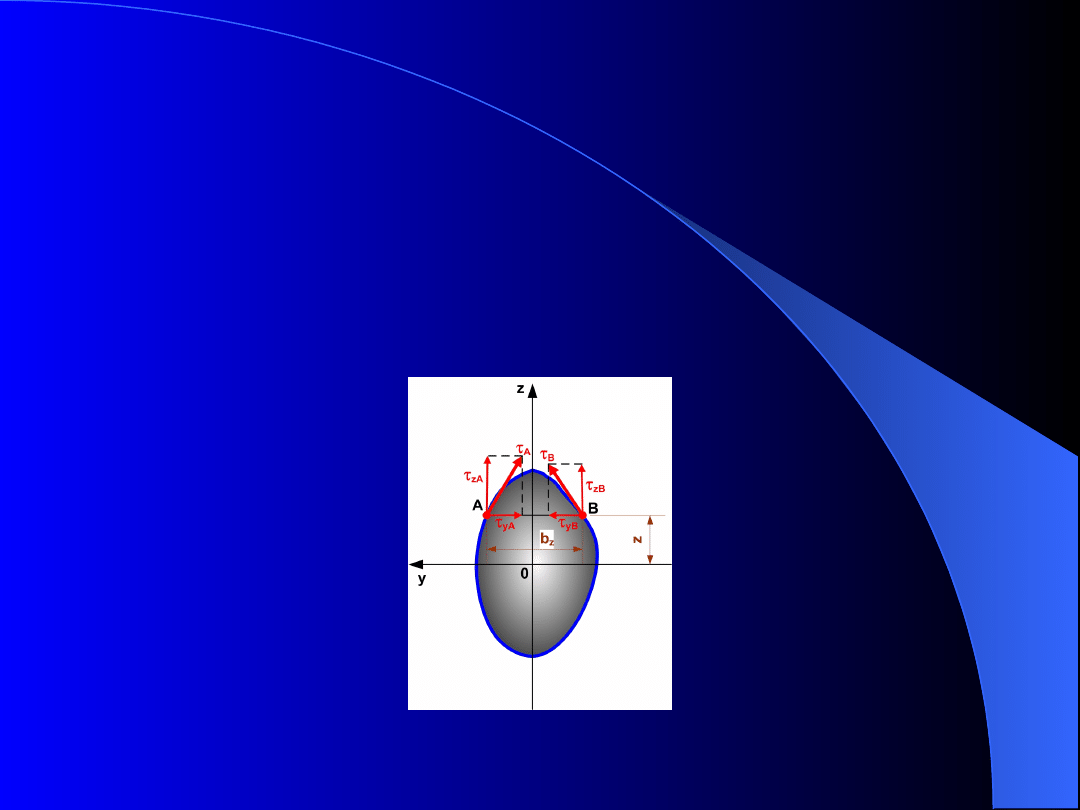
Rozłóżmy naprężenia na składowe równoległe do

osi y i do osi z (rys. 4). W kolejnym przybliżeniu
(pastowanym w tej analizie) składowe naprężeń w
płaszczyźnie yz na linii AB równoległe do osi z

zastąpimy naprężeniami średnimi 

zśr

.

Analiza rozkładu naprężeń

Rys. 4. Rozkład naprężeń 

A

i 

B

na składowe

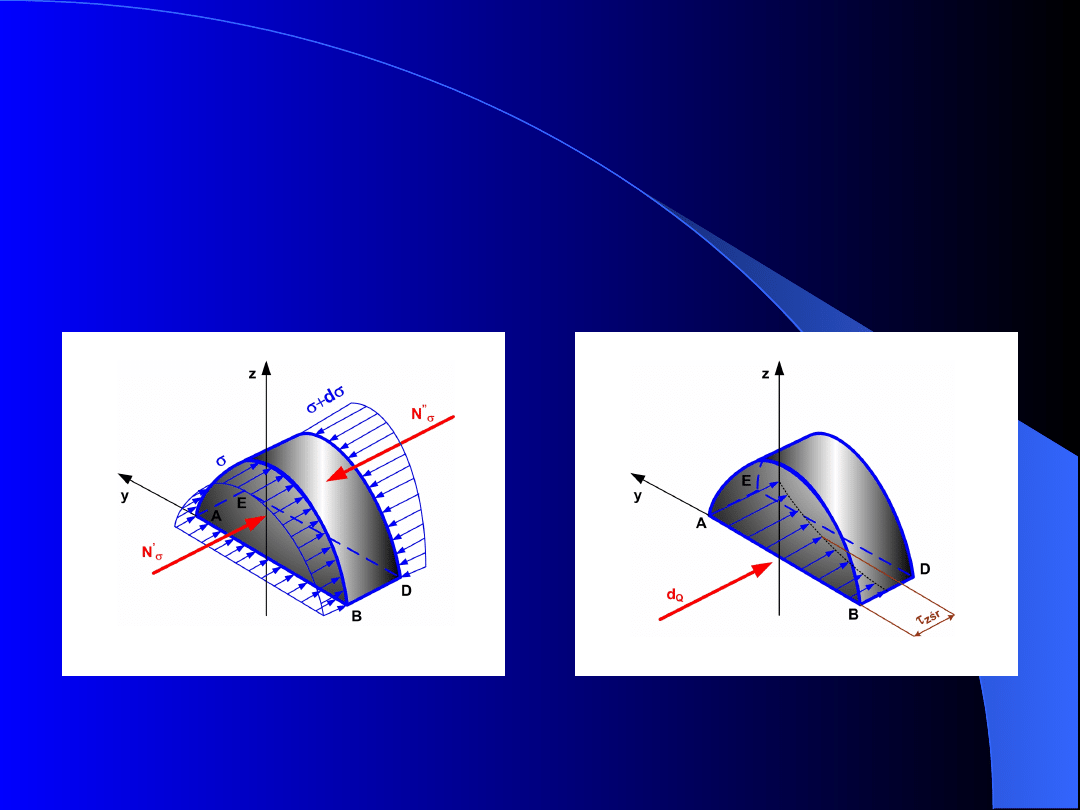
Odrzućmy

dolną

część

elementu

poniżej

płaszczyzny ABDE i rozpatrzmy równowagę górnej
części

elementu

z

uwzględnieniem

naprężeń

normalnych, wywołujących zginanie (rys. 5a) i
stycznych (rys. 5b)

Warunki równowagi

Rys. 5. Równowaga elementu belki; a) naprężenia

normalne, b) naprężenia styczne

Warunki równowagi

Na górną część elementu działają następujące siły
równoległe do osi x:

(1)





AB

dA

N





'











AB

dA

d

N







''

()

dx

b

dQ

z

śr

z





()

gdzie:

τ

zśr

– średnia wartość naprężeń stycznych w

płaszczyźnie ABDE

Po podstawieniu do wzoru (1) zależność na naprężenia
σ:

Warunki równowagi

(4)

(5)

*

z

I

M

y

g





gdzie:
z

*

- odległość wektora σdA od płaszczyzny obojętnej

otrzymamy:

y

z

y

g

AB

y

g

AB

y

g

AB

I

S

M

dA

z

I

M

dA

z

I

M

dA

N

)

(

*

*

'



















gdyż

Warunki równowagi

)

(

*

z

y

AB

S

dA

z





(6)

- moment statyczny (względem osi obojętnej)

części powierzchni przekroju poprzecznego ponad linią
AB (część zakreskowana na rys. 6).

)

(z

y

S

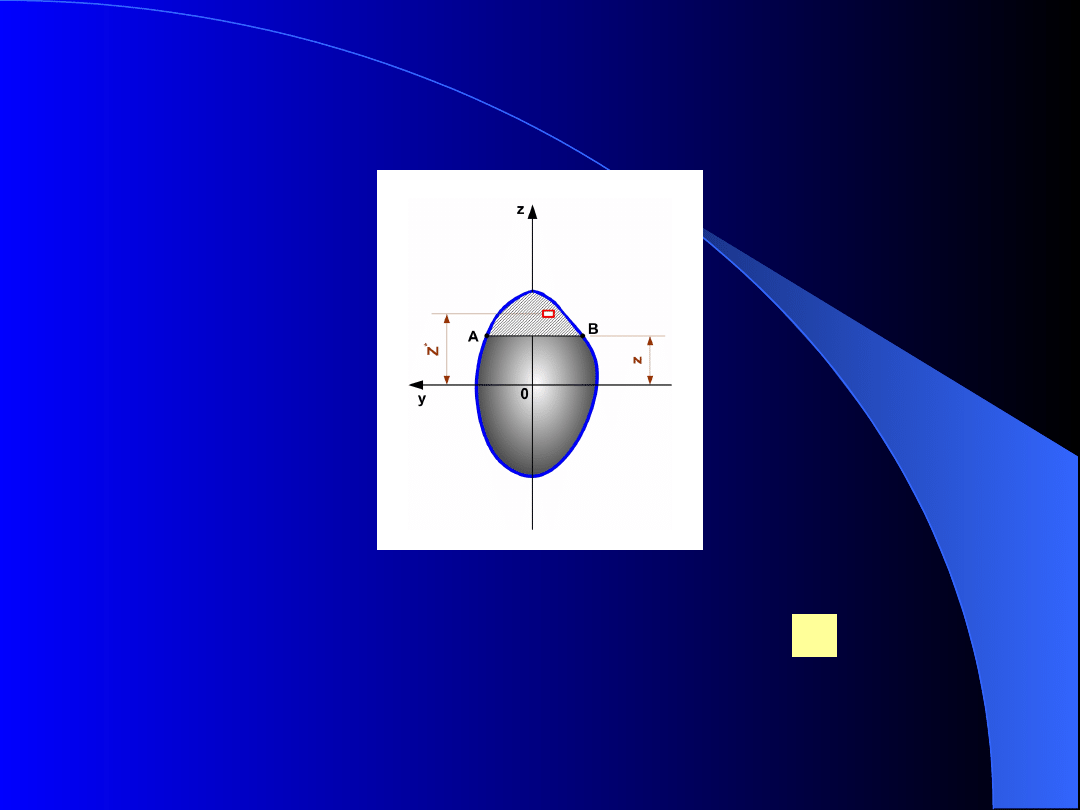
Warunki równowagi

Rys.6. Część powierzchni przekroju poprzecznego

elementu, dla którego wyznacza się moment statyczny

)

(z

y

S

Ze wzoru ()

otrzymamy:

Warunki równowagi

(7)

(9)











AB

dA

d

N







''





y

z

y

g

g

I

S

dM

M

N

)

(

''







Warunek równowagi sił w kierunku osi x można zapisać
w postaci:

(8)

0

''

'











dQ

N

N

X





Po podstawieniu zależności (), (5) i (7) do wzoru (8) i
po wykonaniu obliczeń otrzymamy wzór do obliczenia
naprężeń stycznych w belkach zginanych siłami
poprzecznymi:

y

z

y

g

z

śr

z

I

S

dx

dM

b

)

(





Uwzględniając twierdzenie Schwedlera:

Warunki równowagi

dx

dM

T

g



(10)

otrzymamy ostatecznie:

(11)

z

y

z

y

śr

z

b

I

S

T

)

(





Warunki równowagi

Z analizy powyższego wzoru wynika, że jeśli

położenie płaszczyzny ABDE przyjmiemy w górnym
skrajnym położeniu, to moment statyczny części
elementu ponad tą płaszczyzną będzie równy zeru:

(1)

0

)

(



z

y

S

a więc naprężenia w tej płaszczyźnie będą równe zeru
(

Z

=0). Największe naprężenia styczne wystąpią w

płaszczyźnie środkowej belki, czyli w płaszczyźnie
obojętnej, w której naprężenia od zginania są równe
zeru.

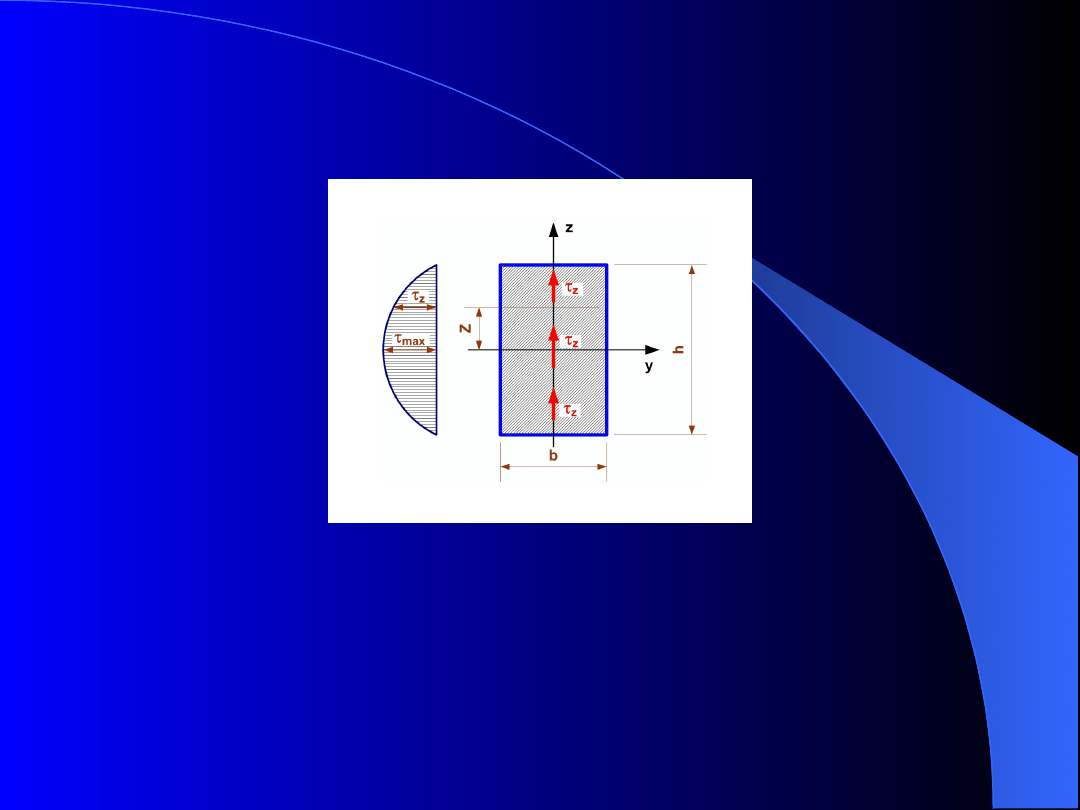
Warunki równowagi

Rys. 7. Rozkład naprężeń stycznych w belce o przekroju

poprzecznym prostokątnym zginanej siłą poprzeczną

WYBOCZENIE

Analiza zachowania pręta smukłego poddanego

działaniu sił ściskających

Smukłość

jest to stosunek długości pręta do

promienia bezwładności jego przekroju poprzecznego.

Każde ciało jest narażone na działanie różnych
czynników zewnętrznych, które mogą to ciało
wyprowadzić ze stanu równowagi. Takimi czynnikami
może być małe odstępstwo od osiowości obciążenia. W
przypadku ściskania prętów smukłych czynniki te w
sposób istotny mogą być przyczyną przejścia z
jednego położenia równowagi do innego położenia
równowagi.

WYBOCZENIE

Jeśli stan równowagi takiego pręta jest trwały, to

po ustaniu działania takich czynników pręt wraca do
pierwotnego położenia równowagi. W przypadku
równowagi chwiejnej, to nawet po ustaniu działania
bodźców chwilowych pręt nie powróci do stanu
pierwotnego, przejdzie natomiast do nowej postaci
równowagi. Nowa postać równowagi może być równa
zniszczeniu konstrukcji. Jest to zjawisko

wyboczenia

pręta

.

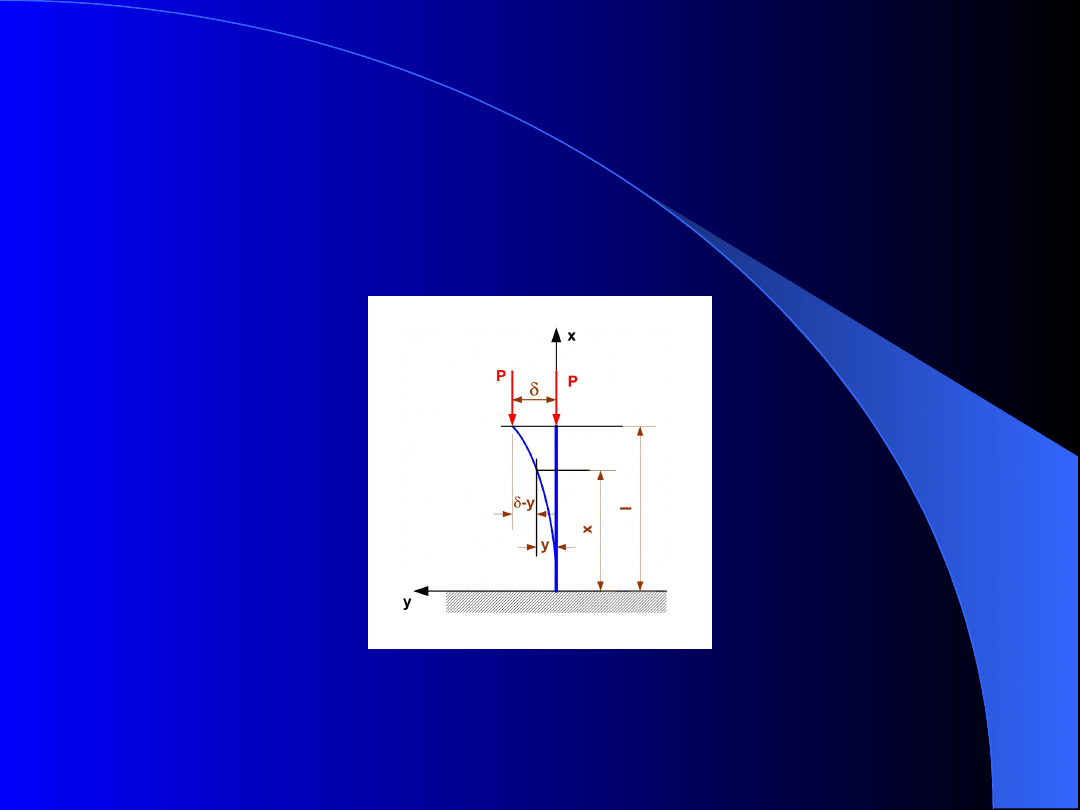
Sprężyste wyboczenie pręta

Rozpatrzmy smukły pręt utwierdzony w jednym

końcu i obciążony w drugim (swobodnym) końcu
siłą ściskającą (rys. 8).

Rys. 8. Pręt smukły obciążony siłą osiową

Sprężyste wyboczenie pręta

Należy wyznaczyć siłę krytyczną dla pręta

ściskanego, czyli określić warunki konieczne dla
zachowania równowagi tego pręta w postaci wygiętej
w zakresie sprężystości materiału.

Wyboczenie nastąpi w płaszczyźnie najmniejszej
sztywności zginania EI, w której promień bezwładności
przekroju poprzecznego jest najmniejszy.

Sprężyste wyboczenie pręta

W nowym stanie równowagi w postaci wygiętej w

pręcie pojawi się moment gnący oprócz siły podłużnej
(ściskającej). Moment ten w dowolnym przekroju
odległym o x od początku układu współrzędnych x,y
będzie:

(1)

Podstawiając ten wzór do zależności:





y

P

M

g







(14)

g

M

dx

y

d

EI



2

2

Sprężyste wyboczenie pręta

otrzymamy równanie różniczkowe linii ugięcia:

(15)





y

P

dx

y

d

EI







2

2

a po przekształceniu:

(16)

0

2

2









P

Py

dx

y

d

EI

Podstawiając za:

(17)

EI

P

k 

2

otrzymamy równanie:

(18)

0

2

2

2

2









k

y

k

dx

y

d

Sprężyste wyboczenie pręta

Rozwiązanie tego równania ma postać:

(19)

(0)

Stałe

całkowania

wyznaczymy

z

warunków

brzegowych,

dla x=0 mamy y=0 oraz dy/dx=0, a więc:

(1)

 

 









x

k

B

x

k

A

y

sin

cos







A

0



B

()

Równanie różniczkowe linii ugięcia ma więc postać
cosinusoidy:

 





x

k

y

cos

1





Sprężyste wyboczenie pręta

Warunek określający wielkość k w stanie nowej
krzywoliniowej równowagi pręta, a więc w stanie
krytycznym wyniknie z równania:

 





l

k

y

l

x

cos

1

)

(













()

Będzie to spełnione dla:

(4)

 

0

cos



l

k

Równanie (4) będzie spełnione gdy:

(5)





2

1

2





 n

l

k

Sprężyste wyboczenie pręta

oraz n = 1, 2, 3, 4.....

(6)

Po podstawieniu do równania (5) wyrażenia na k w
stanie krytycznym otrzymamy:





l

n

EI

P

k

kryt

2

1

2









(7)

a najmniejszą wartość siły krytycznej (dla n=0)
wyznaczymy z zależności:

2

2

4l

EI

P

kryt





Jest to

wzór Eulera

do obliczania siły krytycznej w

zakresie sprężystości materiału. Jest słuszny dla pręta
utwierdzonego jednym końcem i obciążonego siła
ściskającą w końcu swobodnym.

Sprężyste wyboczenie pręta

Uniezależniając obliczenia od sposobu zamocowania
pręta (od warunków brzegowych) należy wprowadzić
pojęcie długości redukowanej l

red

. Wielkość tę określa

wzór:

(8)

Współczynnik  zależy od warunków brzegowych
pręta, a jego wartość dla czterech najbardziej
typowych sposobów zamocowania pokazano na rys. 9.

l

l

red





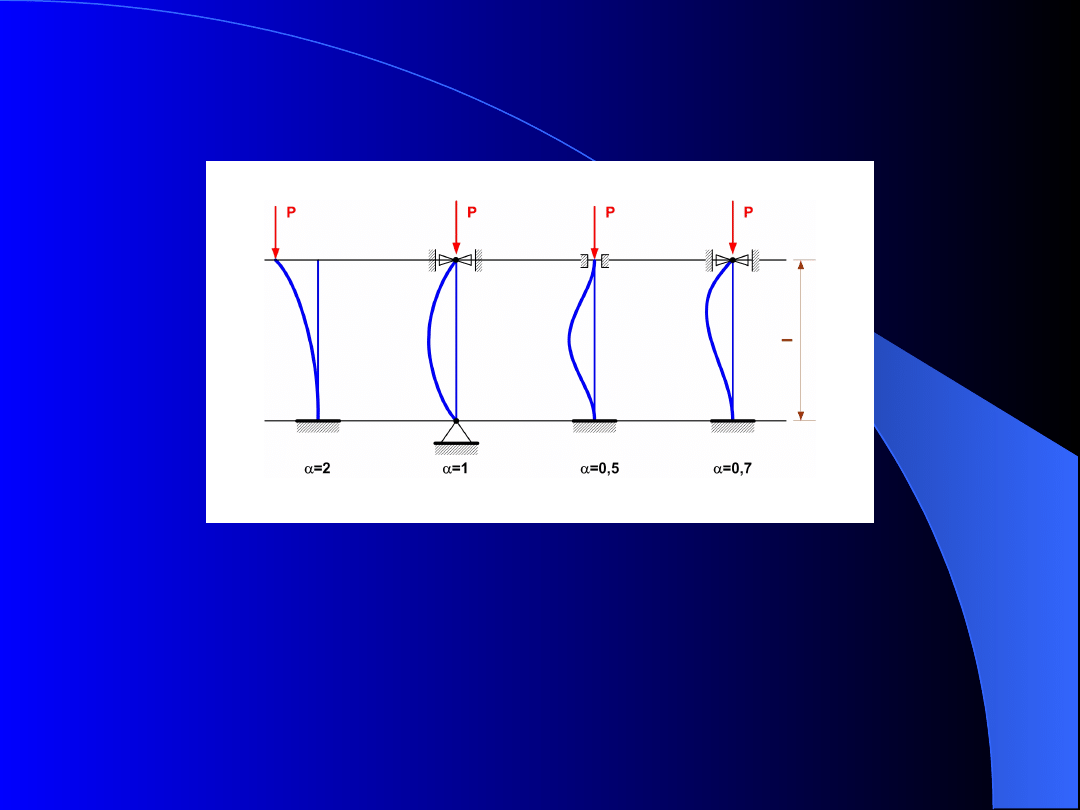
Sprężyste wyboczenie pręta

Rys. 9. Przypadki zamocowania pręta

Wzór Eulera z uwzględnieniem pojęcia długości

redukowanej ma postać:

(9)

Sprężyste wyboczenie pręta

2

2

red

kryt

l

EI

P





Dzieląc obustronnie równanie (9) przez przekrój

poprzeczny A

0

pręta otrzymamy równanie do

obliczenia naprężenia krytycznego:

(0)

2

0

2

red

kryt

l

A

EI







Za

- jest to kwadrat promienia bezwładności

przekroju poprzecznego. Po uwzględnieniu tej wielkości

i równania na smukłość pręta

(1)

Sprężyste wyboczenie pręta

otrzymamy równanie Eulera do obliczania naprężenia

krytycznego w postaci:

()

2

0

i

A

I



min

i

l

red





2

2







E

kryt



Jest to hiperboliczna zależność naprężenia krytycznego

od smukłości pręta ściskanego.

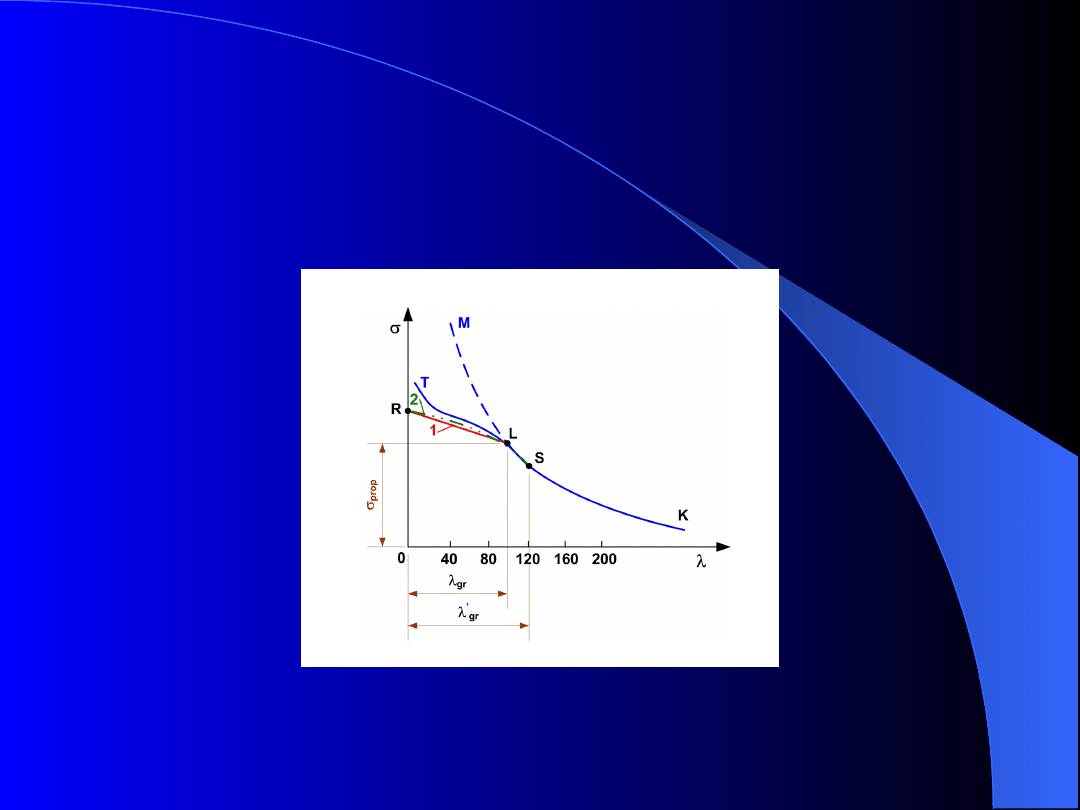
Hiperbolę Eulera w układzie współrzędnych 

kryt

, 

pokazano na rys.10.

Wyboczenie poza zakresem

sprężystości materiału

Rys. 10. Hiperbola Eulera KLM i zależności

doświadczalne: 1 – prosta Tetmajera – Jasińskiego,  –

parabola Johnsona – Ostenfelda

Porównanie hiperboli Eulera z wynikami doświadczeń

(linia KLT) wykazało, że równanie Eulera odpowiada

tym wynikom tylko wtedy, gdy smukłość przekracza

pewną wartość – zwaną smukłością graniczną 

gr

.

Wyznaczymy ją podstawiając do równania Eulera

wartość

granicy

proporcjonalności

w

miejsce

naprężenia krytycznego (np. Dla stali: 

prop

=00 MPa)

oraz modułu Younga E=10

5

MPa:

Wyboczenie poza zakresem

sprężystości materiału

100

200

10

2

10

5

2











prop

gr

E







()

W zakresie smukłości mniejszej niż smukłość

graniczna, a więc poza zakresem sprężystości

(proporcjonalności) stosuje się wzory doświadczalne:

Wyboczenie poza zakresem

sprężystości materiału

(4)

Tetmajera-Jasińskiego

(prosta LR):





b

a

kryt





(5)

Johnsona-Ostenfelda

(parabola SR)





B

A

kryt





w których a, b, A, B – stałe materiałowe.

Stałe materiałowe a, b wyznaczymy przyjmując, że dla

=0 (punkt R – rys. 10)



kryt

=R

e

. Podstawiając te

wartości do równania (4) otrzymamy:

Wyboczenie poza zakresem

sprężystości materiału

(6)

(8)

e

kryt

R

b

a









0



a stąd:

(7)

e

R

a 

Dla =

gr

(punkt L – rys. 10)



kryt

=



prop

. Podstawiając tę

wartość do równania (4) i wykorzystując równanie
() i (7) otrzymamy:

prop

prop

e

gr

prop

e

E

R

R

b











2









Wierzchołkiem paraboli (5) jest punkt R (rys. 10) o

współrzędnych =0 i 

kryt

=R

e

. Podstawiając tą wartość

do równania (5) otrzymamy:

Wyboczenie poza zakresem

sprężystości materiału

(9)

Parabola jest styczna do hiperboli Eulera, a w punkcie

styczności mamy

(40)

e

R

A

'

gr







to można napisać:

(41)

hiperb

kryt

parab

kryt

d

d

d

d



































Po podstawieniu do równania (41) zależności (5)

i ()

i po zróżniczkowaniu

otrzymamy:

Wyboczenie poza zakresem

sprężystości materiału

(4)

W punkcie S dla 

’

gr

naprężenie 

kryt

obliczone wg

równania (5) musi być takie samo jak obliczone ze

wzoru (), a więc:

(4)





B

A

kryt





2

2







E

kryt



 

4

'

2

gr

E

B







     

2

'

2

2

'

4

'

2

gr

gr

gr

e

E

E

R















Stąd otrzymamy:

Wyboczenie poza zakresem

sprężystości materiału

(44)

Równanie (4) można zapisać w postaci:

(45)

e

gr

R

E

2

'

2







   

2

'

2

2

'

gr

gr

e

E

B

R











i podstawiając do tego równania zależność (44)

otrzymamy:

(46)

E

R

B

e

2

2

4





WYTRZYMAŁOŚĆ

MATERIAŁÓW

prowadzący

prof. dr hab. inż. Kazimierz WÓJS

Wykład 15b

Opracował

Andrzej Sitka

ANALIZA STANU NAPRĘŻE

ANALIZA STANU NAPRĘŻE

Ń

Ń

Analiza stanu napręże

Analiza stanu napręże

ń

ń

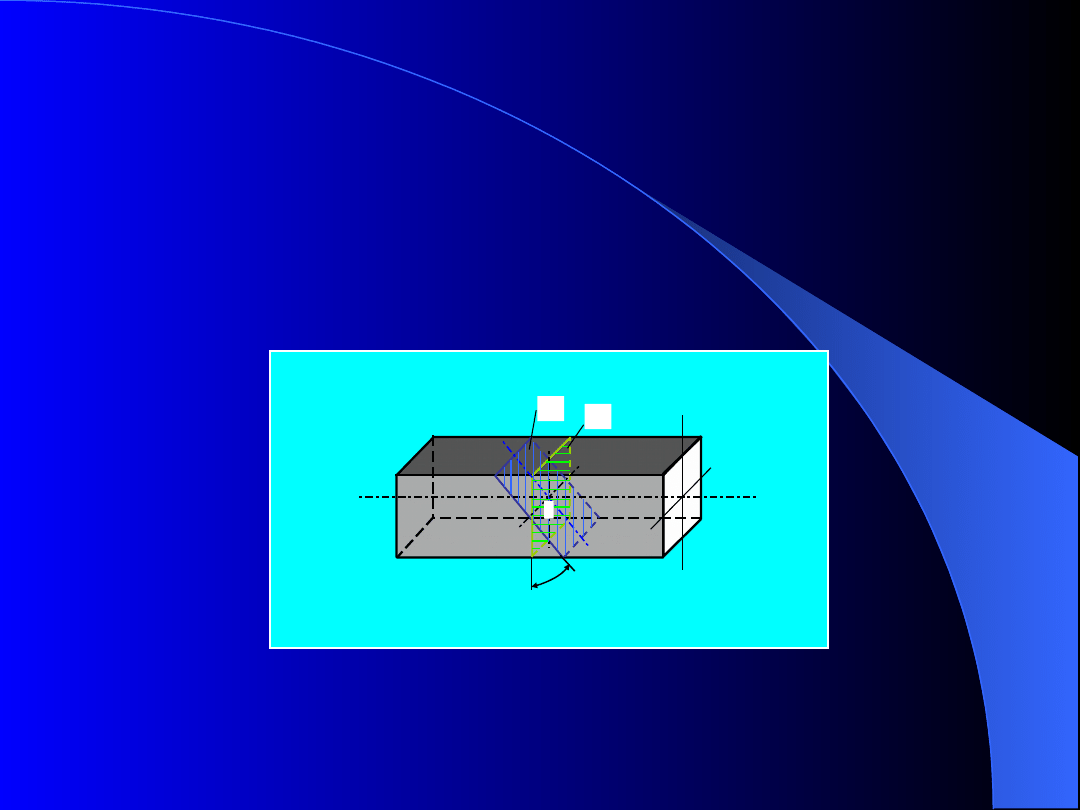
Przez dany punkt 0 można przeprowadzić

nieskończenie wiele przekrojów danego ciała, a zatem
istnieje nieskończenie wiele wektorów naprężenia,
które opisują stan naprężenia w tym punkcie.

0

A



A



Rys. 1. Przekrój poprzeczny belki i przekrój

nachylony do osi belki pod kątem 

Analiza naprężeń w

Analiza naprężeń w

jednokierunkowym stanie

jednokierunkowym stanie

napięcia

napięcia

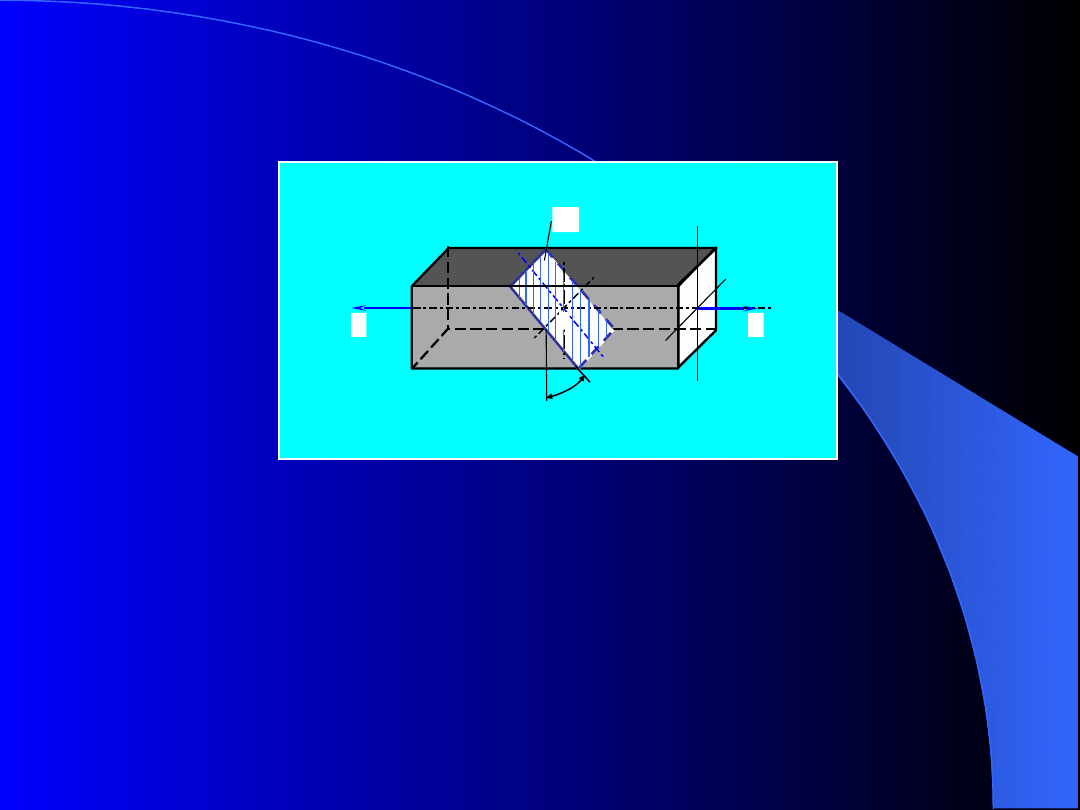
Rozpatrzmy

naprężenia

w

przekroju

A



nachylonym pod kątem  do przekroju poprzecznego
pręta poddanego rozciąganiu. Jedną część pręta
odrzucamy, a rozpatrujemy pozostałą część, np. lewą
(rys.2).

Rys. 2. Przekrój nachylony do osi belki pod

kątem 

P

0

A





P

Analiza naprężeń w

Analiza naprężeń w

jednokierunkowym stanie

jednokierunkowym stanie

napięcia

napięcia

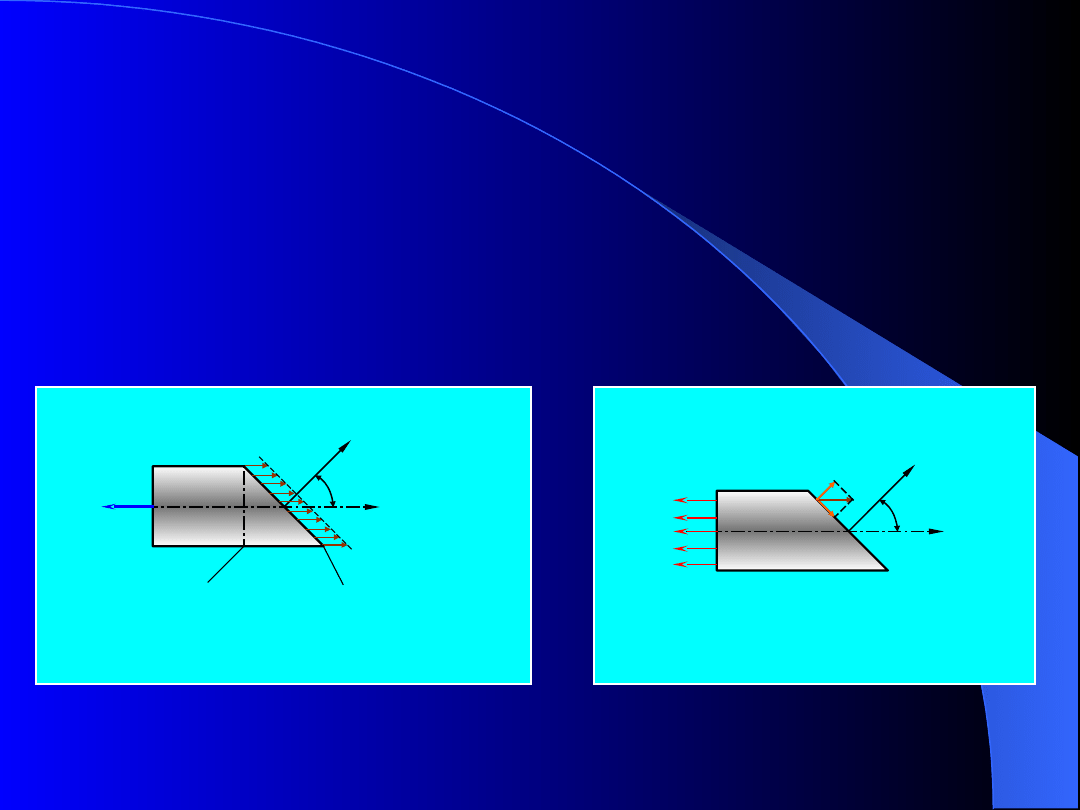
Rozpatrywana część pręta (rys.3a) znajduje się

w równowadze dzięki temu, że w przekroju przecięcia
odrzucona prawa część pręta działa na część
rozpatrywaną naprężeniami p.

Rys. 3. Jednokierunkowy stan naprężenia; a) część pręta w

równowadze, b) rozkład naprężenia p na składowe



p

n

x











b
)



p

n

x

kierunek
normalnej
zewnętrznej

P

a
)

A

przekrój poprzeczny

przekrój ukośny

Analiza naprężeń w

Analiza naprężeń w

jednokierunkowym stanie

jednokierunkowym stanie

napięcia

napięcia

Z warunku równowagi sił działających na

rozpatrywaną część pręta:

(1)

(2)

stąd:











0



pA

P

X



A

P

p 

Uwzględniając,
że:

(3)





cos

A

A 

Analiza naprężeń w

Analiza naprężeń w

jednokierunkowym stanie

jednokierunkowym stanie

napięcia

napięcia

otrzymamy:

(4)

(5)

gdyż

Po rozłożeniu naprężenia p na składowe – normalną





i

styczną





otrzymamy:

(6)







cos

cos





A

P

p

A

P















2

cos

cos 

 p

(7)













cos

sin

sin 

 p

Analiza naprężeń w

Analiza naprężeń w

jednokierunkowym stanie

jednokierunkowym stanie

napięcia

napięcia

i podstawiając tożsamość

sin2



= 2sin



cos



równanie (7) przyjmuje postać:

(8)

Występujący w powyższych wzorach kąt 

zawarty

jest między kierunkiem działania sił

rozciągających a kierunkiem normalnej zewnętrznej
danego przekroju.









2

sin

2

1



Analiza naprężeń w

Analiza naprężeń w

jednokierunkowym stanie

jednokierunkowym stanie

napięcia

napięcia

Dodatnią wartość naprężeń normalnych 

przypisywać będziemy naprężeniom rozciągającym, a
więc mającym zwrot zgodny z kierunkiem normalnej
zewnętrznej.

Dodatnią

wartość

naprężeń

tnących



przypisywać będziemy naprężeniom usiłującym obrócić
rozpatrywaną część w kierunku zgodnym z ruchem
wskazówek zegara.

Równania równowagi

Równania równowagi

wewnętrznej

wewnętrznej

W przypadku niejednorodnego stanu naprężenia

wartości składowych stanu naprężenia zmieniają się ze
zmianą położenia rozpatrywanego punktu ciała.

Rozpatrzmy

ciało

obciążone

będące

w

równowadze (siły masowe pominiemy). Wycięty z tego
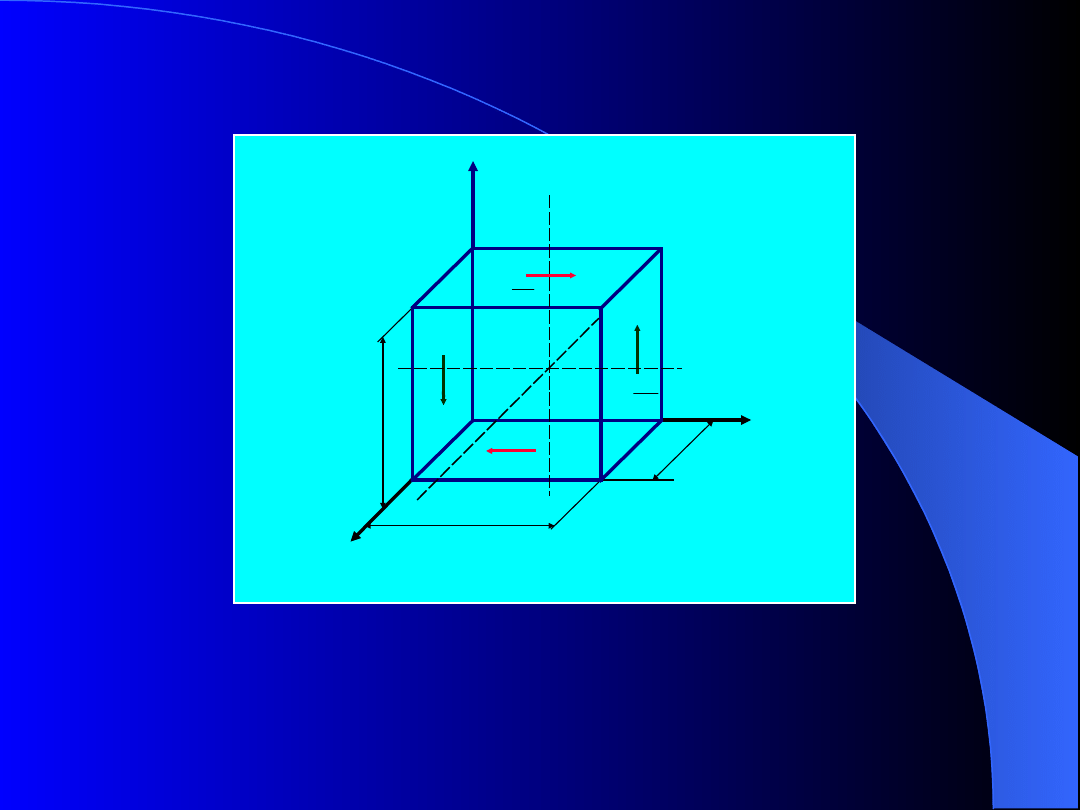
ciała prostopadłościan (rys. 4) o krawędziach dx, dy, dz
znajduje się w niejednorodnym stanie naprężenia.

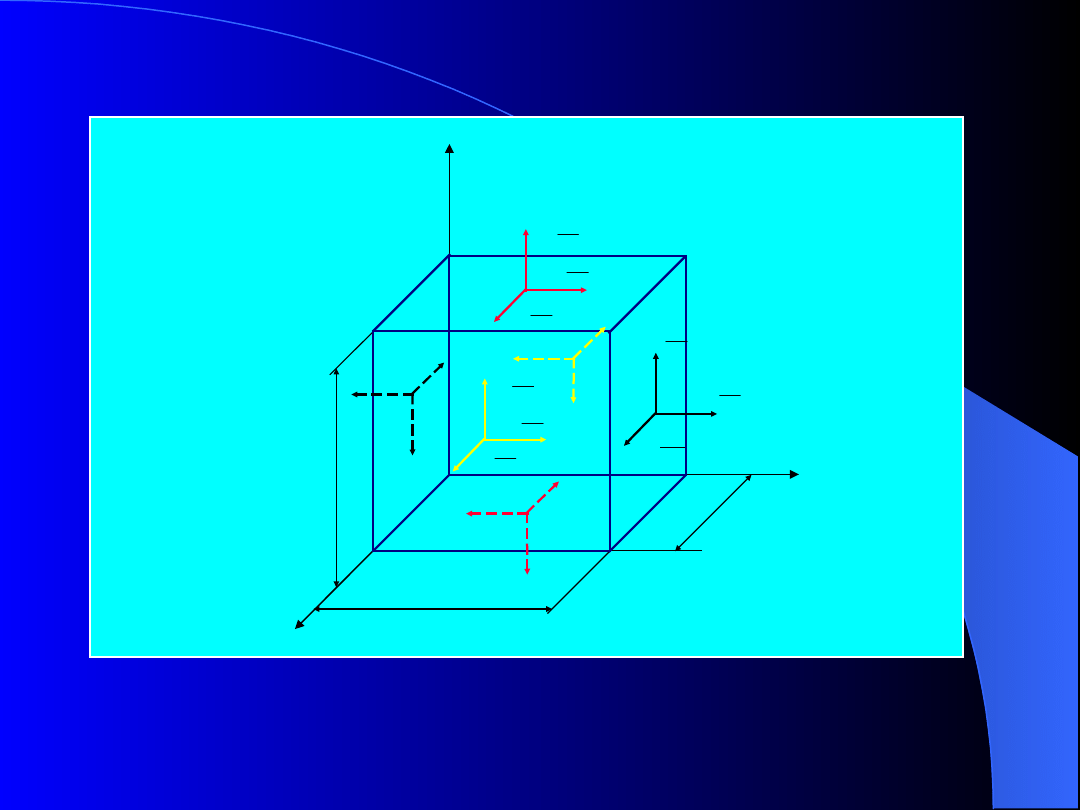
Równania równowagi

Równania równowagi

wewnętrznej

wewnętrznej

Rys. 4. Naprężenia na ścianach prostopadłościanu o krawędziach

dx, dy, dz

dy

d

z

dx

x

y

z

dy

y

yx

yx











dy

y

y

y











dy

y

yz

yz











z



zx



zy



dx

x

x

x











dx

x

xy

xy











dx

x

xz

xz











xz



xy



x



yz



yx



y



dz

z

z

z











dz

z

zy

zy











dz

z

zx

zx











(9)

Równania równowagi

Równania równowagi

wewnętrznej

wewnętrznej

Warunek równowagi sił działających w kierunku

osi x można zapisać w postaci równania:

0









































































dxdy

dz

z

dxdy

dxdz

dy

y

dxdz

dydz

dx

x

dydz

X

zx

zx

zx

yx

yx

yx

x

x

x



















(10)

Równania równowagi

Równania równowagi

wewnętrznej

wewnętrznej

Po uporządkowaniu i uproszczeniu otrzymamy:

0



















z

y

x

zx

yx

x







Z pozostałych warunków równowagi sił względem
pozostałych osi y, z otrzymamy:

(11)

(12)

0



















z

y

x

zy

y

xy







0



















z

y

x

z

yz

xz







(13)

Równania równowagi

Równania równowagi

wewnętrznej

wewnętrznej

Równania (13) nazywamy

równaniami równowagi

wewnętrznej

:

0



















z

y

x

zx

yx

x







0



















z

y

x

zy

y

xy







0



















z

y

x

z

yz

xz







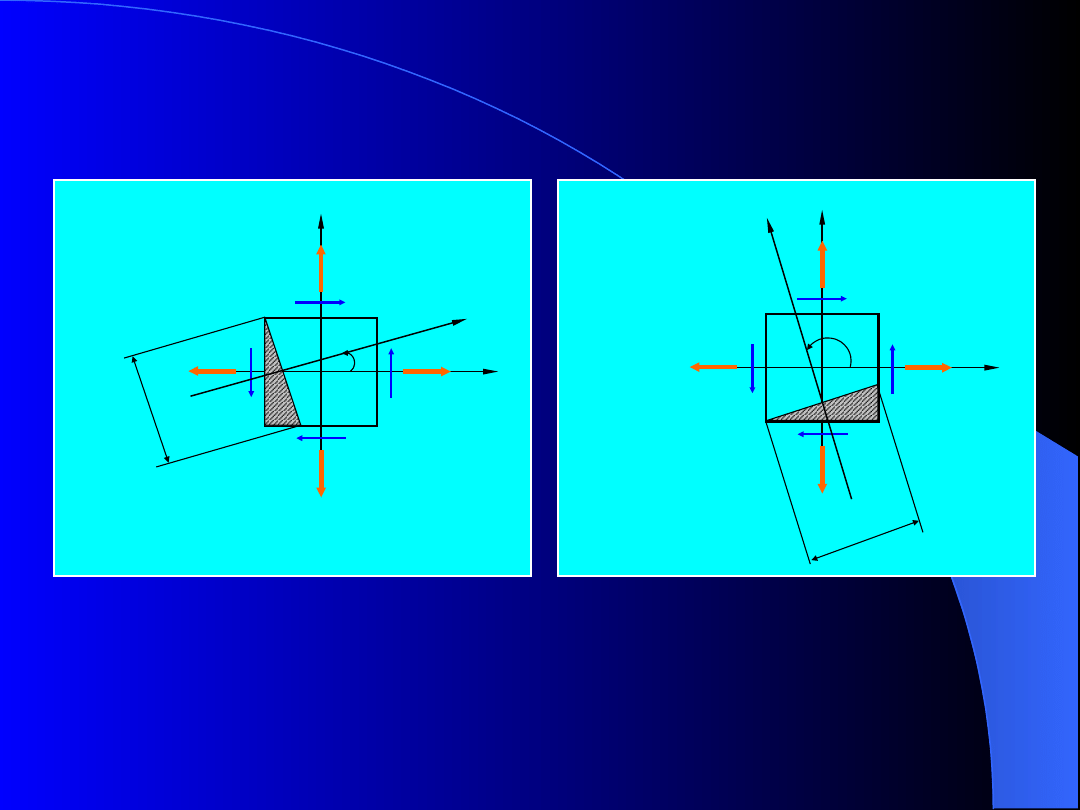
Aksjomat Boltzmanna

Aksjomat Boltzmanna

Rys. 5. Naprężenia na ścianach prostopadłościanu

wywołujące momenty względem osi x’

d
y

d

z

d
x

x

y

z

x’

z’

y’

dy

y

yz

yz











zy



yz



dz

z

zy

zy











Aksjomat Boltzmanna

Aksjomat Boltzmanna

Na przedstawionym rysunku początek układu

współrzędnych

został

przeniesiony

do

środka

prostopadłościanu. Przedstawiono tylko te naprężenia,
których momenty względem osi x

’

są różne od zera.

Wykorzystując

równanie

równowagi

momentów

względem osi x’ otrzymamy:

0

2

1

2

1

2

1

2

1

'

















































dz

dxdy

dz

dxdy

dz

z

dy

dzdx

dy

dzdx

dy

y

M

zy

zy

zy

yz

yz

yz

x













(14)

Aksjomat Boltzmanna

Aksjomat Boltzmanna

Po wykonaniu działań i pominięciu małych

wyrażeń wyższego rzędu otrzymamy:

Wykorzystując dwa pozostałe równania równowagi
momentów otrzymamy:

(16)

yz

zy







(15)

zx

xz







xy

yx







(17)

Równania (15), (16) i (17) nazywane są

aksjomatem

Boltzmanna

, który można wyrazić słowami:

składowe naprężeń stycznych  prostopadłe do
krawędzi

przecięcia

się

dwu

przekrojów

wzajemnie prostopadłych są sobie równe.

Płaski stan naprężenia

Płaski stan naprężenia

Płaski stan naprężenia występuje wtedy, gdy



x

0, 

y

0 oraz 

xy

0, a pozostałe naprężenia są równe

zeru.

W wielu praktycznych przypadkach w elementach

cienkościennych wartości naprężeń 

z

, 

yz

, 

zx

są na tyle

małe, że można je pominąć i w tych przypadkach
przyjąć

płaski

stan

naprężenia.

Rozpatrzmy

prostokątny arkusz cienkiej blachy o grubości t
obciążony w swej płaszczyźnie w taki sposób, że na
ściankach wystąpią naprężenia 

x

, 

y

oraz 

xy

(rys.6).

Płaski stan naprężenia

Płaski stan naprężenia

Rys. 6. Płaski stan naprężenia; a) przekrój prostopadły do osi

, b) przekrój prostopadły do osi 

x



x



x



y



y

y





1

a)

xy



xy



xy



xy



x



x



x



y



y

y



+/

2

1

b)

xy



xy



xy



xy



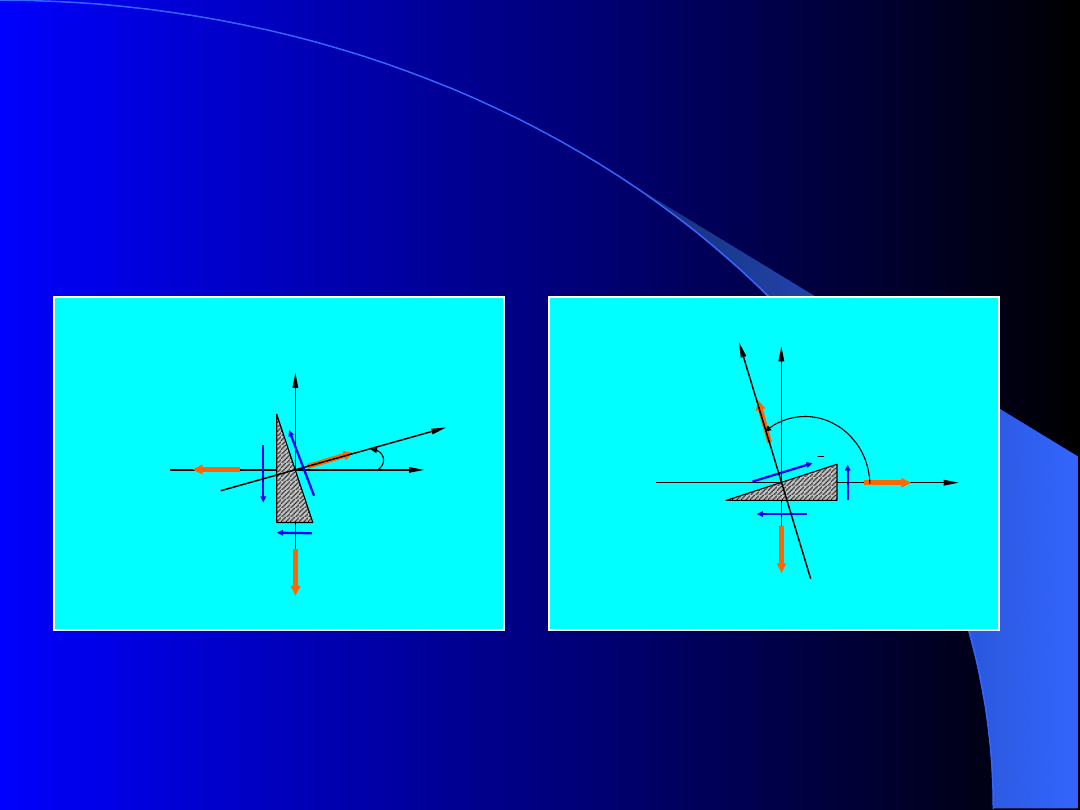
Płaski stan naprężenia

Płaski stan naprężenia

Rozpatrzymy lewą, odciętą tym przekrojem część
arkusza, a działanie lewej (odrzuconej) części
zastąpimy naprężeniami 



i 



(rys.7).

Rys. 7. Część arkusza w równowadze; a) przekrój

prostopadły do osi , b) przekrój prostopadły do osi 

x



x







y

y





a)





xy



xy



x





+



/2



x



y

y



+/

2

b)

2









xy



xy



Płaski stan naprężenia

Płaski stan naprężenia

Poszczególne przekroje tej części wyrażą się wzorami

(19)

(18)

(20)

t

A 1











cos

1

cos

t

A

A

x











sin

1

sin

t

A

A

y





Płaski stan naprężenia

Płaski stan naprężenia

Z warunków równowagi sił względem osi

normalnej i stycznej do przekroju A



otrzymamy

równania (po uwzględnieniu aksjomatu Boltzmanna):

(22)

(21)

0

sin

cos

cos

sin

sin

sin

cos

cos













































t

t

t

t

t

F

xy

xy

y

x

0

cos

cos

sin

sin

cos

sin

sin

cos













































t

t

t

t

t

F

xy

xy

y

x

Płaski stan naprężenia

Płaski stan naprężenia

Po

uporządkowaniu

równań

(21)

i

(22)

otrzymamy:

(23)



















cos

sin

2

sin

cos

2

2

xy

y

x

































2

2

sin

cos

cos

sin











xy

y

x

(24)

Dla przekroju A

+/2

= A



prostopadłego do osi 

(rys.5b) i rozpatrując równowagę części arkusza
(rys.6b) otrzymamy:





















cos

sin

2

cos

sin

2

2

2

xy

y

x









(25)

Naprężenie styczne



+/2

=





Płaski stan naprężenia

Płaski stan naprężenia

Wszystkie wzory transformacyjne dla płaskiego

stanu naprężenia można zapisać w postaci:

(26)

(27)

(28)

















2

sin

sin

cos

2

2

xy

y

x

























2

sin

cos

sin

2

2

2

xy

y

x









2

2

cos

2

sin

2

































xy

y

x

Płaski stan naprężenia

Płaski stan naprężenia

wiedząc , że:

(29)

(30)

(31)

2

2

cos

1

sin

2









i

2

2

cos

1

cos

2









równania (26–28) przyjmą postać:



















2

sin

2

cos

2

2

xy

y

x

y

x































2

sin

2

cos

2

2

2

xy

y

x

y

x













2

2

cos

2

sin

2

































xy

y

x

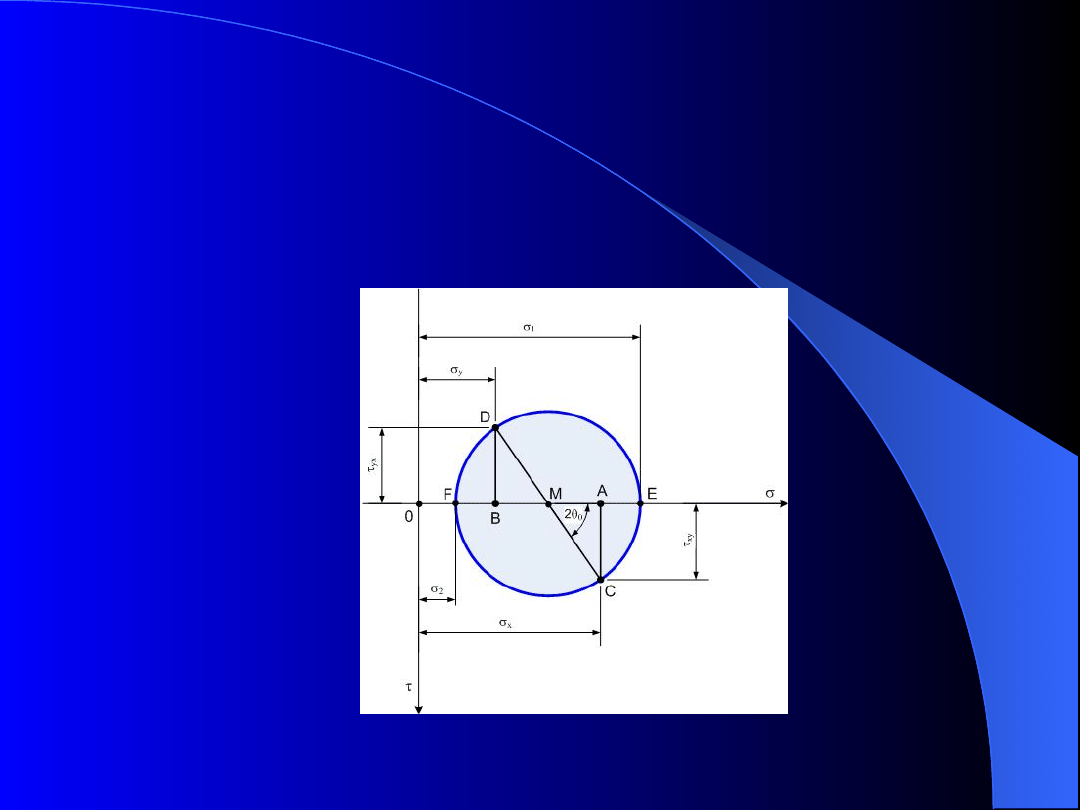
Koło Mohra

Koło Mohra

Wzory transformacyjne (29-31), określające

wartość naprężeń w przekroju określonym kątem 
układu znajdującego się w płaskim stanie naprężeń,
dają się łatwo przedstawić wykreślnie.

Rys. 8. Koło Mohra dla płaskiego stanu naprężeń

Koło Mohra

Koło Mohra

Uzyskane

wyniki

można

odwzorować

na

płaszczyźnie w układzie współrzędnych , przyjmując:

x

A





0

y

B





0

xy

AC





xy

yx

BD











Koło Mohra

Koło Mohra

Aby poprawnie wykreślić naprężenia styczne

należy przyjąć umowę trygonometryczną dotyczącą
znaków naprężeń. Na jej podstawie aksjomat
Boltzmanna przyjmuje postać:

xy

yx









Środek M koła Mohra:









y

x

B

M

M













2

1

0

0

2

1

0

(32)

(33)

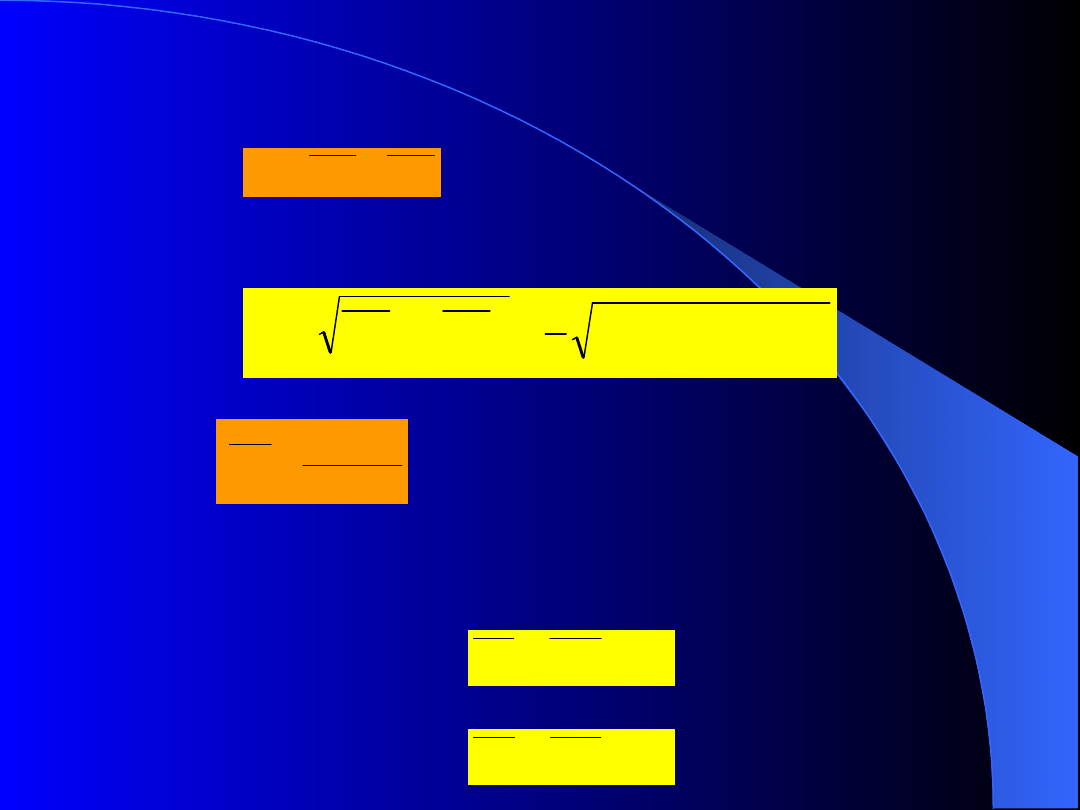
Koło Mohra

Koło Mohra

Na osi poziomej promień r

M

wyznaczają punkty E oraz

F:

ponieważ

(35)

(34)

Promienie
m

MD

MC

r

M





kreślimy

koło,

przy

czym

można
zauważyć:





2

2

2

2

4

2

1

xy

y

x

M

AC

MA

r

















2

y

x

MA









M

r

M

E



0

0

(36)

M

r

M

F



0

0

Koło Mohra

Koło Mohra

Odcinek

wyznacza największe, a odcinek

najmniejsze naprężenia normalne. W punktach E i F

koło Mohra przecina oś naprężeń normalnych .

Oznacza to, że naprężenie styczne  jest równe zeru.

E

0

F

0

Koło Mohra

Koło Mohra

(38)

(37)

Podstawiając do wzorów (35) i (36) zależność (34)
otrzymamy wzory określające

wartości ekstremalne

naprężeń normalnych

nazywane również

naprężeniami

głównymi

(

1

i 

2

):





2

2

1

4

2

1

2

0

xy

y

x

y

x

E





























2

2

2

4

2

1

2

0

xy

y

x

y

x

F

























Kierunki naprężeń głównych

Kierunki naprężeń głównych

Kierunki naprężeń głównych (ekstremalnych)

można wyznaczyć przyrównując do zera pochodną 



względem :

(40)

(39)





0

sin

cos

2

cos

sin

2

sin

cos

2

0

0

2

0

0

0

0





































xy

y

x

d

d

a więc:





0

2

cos

2

2

sin

0

0



















xy

y

x

Kierunki naprężeń głównych

Kierunki naprężeń głównych

Przekrój, w którym wystąpią naprężenia główne

wyznaczymy określając kąt 

0

, czyli kąt transformacji

głównej z zależności (40):

(42)

(41)

więc:





0

0

2

sin

2

cos

2











y

x

xy





y

x

xy

tg



















2

2

cos

2

sin

2

0

0

0

Kierunki naprężeń głównych

Kierunki naprężeń głównych

Przekształcając wzór (31)

otrzymamy:

(44)

(43)

Porównując wzory (40) oraz (43)

2

2

cos

2

sin

2

































xy

y

x























2

2

cos

2

2

sin

0

0











xy

y

x





0

2

cos

2

2

sin

0

0



















xy

y

x























2

2

cos

2

2

sin

0

0











xy

y

x

ora
z

można zauważyć że:

0

0







Kierunki naprężeń głównych

Kierunki naprężeń głównych

W przekroju, w którym występują normalne

naprężenia główne to naprężenia styczne są równe
zeru. Potwierdza to wnioski wyprowadzone z analizy
koła Mohra.

(45)

Kierunki

ekstremalnych

wartości

naprężeń

stycznych określone są z warunku:









0

2

sin

2

2

cos

0

0



























xy

y

x

d

d

(47)

Mnożąc równanie (42) przez (46) otrzymamy:

Kierunki naprężeń głównych

Kierunki naprężeń głównych

Kąt 

0

został wprowadzony dla odróżnienia od

kąta 

0

:

(46)

xy

y

x

tg









2

2

0







y

x

xy

tg



















2

2

cos

2

sin

2

0

0

0

xy

y

x

tg









2

2

0









1

2

2

0

0









tg

tg

(49)

Kierunki

ekstremalnych

wartości

naprężeń

stycznych zawierają kąty /4 z kierunkami głównymi
naprężeń normalnych. Wartość 

ekstr

otrzymamy z

zależności:

Kierunki naprężeń głównych

Kierunki naprężeń głównych

stąd otrzymamy:

(48)

4

0

0















2

2

4

2

1

xy

y

x

ekstr















Wartość ta równa jest co do modułu promieniowi koła
Mohra r

M

:





2

1

2

1











ekstr

(50)

Koło Mohra jest wykreślnym odwzorowaniem

wszystkich stanów naprężenia w otoczeniu danego
punktu. Z koła Mohra możemy odczytać bezpośrednio
widoczne właściwości płaskiego stanu naprężenia,
czyli:

•

Istnieją tylko dwa przekroje, w których występują

tylko naprężenia normalne 



= 

1

, 

+/2

= 

2

oraz 



= 0. Przekroje te prostopadłe względem siebie
nazywamy

przekrojami głównymi

, a naprężenia

normalne w tych przekrojach 

1

i 

2

naprężeniami

głównymi.

•

Naprężenia główne (

1

, 

2

) są ekstremalnymi

wartościami naprężenia 



i zawsze jest spełniona

nierówność 

2

 



 

1

, jeśli 

1

> 

2

.

•

Ekstremalne naprężenia styczne ekstr występują

w przekrojach obróconych względem przekrojów

głównych o kąt   /4. Ich bezwzględna wartość
jest ta sama i wynosi , a więc równa się połowie

różnicy naprężeń głównych

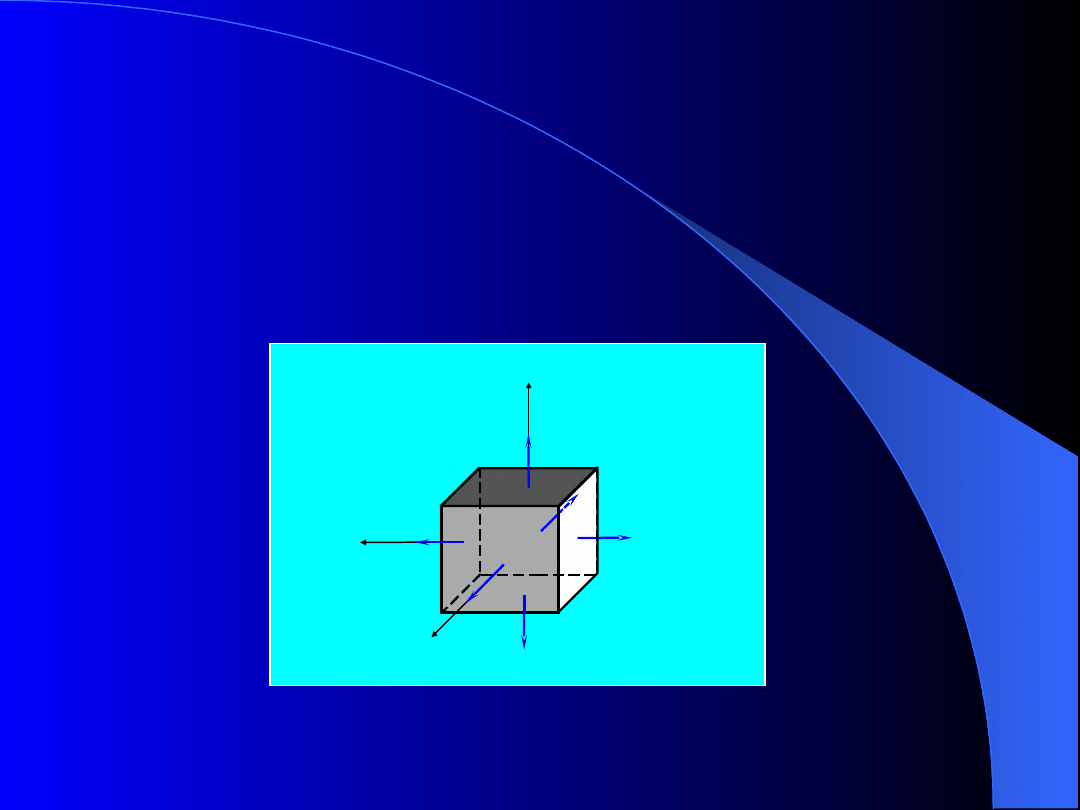
Uproszczona analiza naprężeń

Uproszczona analiza naprężeń

w przestrzennym stanie

w przestrzennym stanie

napięcia

napięcia

Przestrzenny stan napięcia możemy otrzymać,

jeżeli do układu płaskiego, rozciąganego naprężeniami
głównymi 

1

, 

2

dodamy naprężenia rozciągające 

3

.



2

3

2

1



1



1



2



3



3

Rys. 9. Naprężenia główne w trójwymiarowym stanie

naprężeń

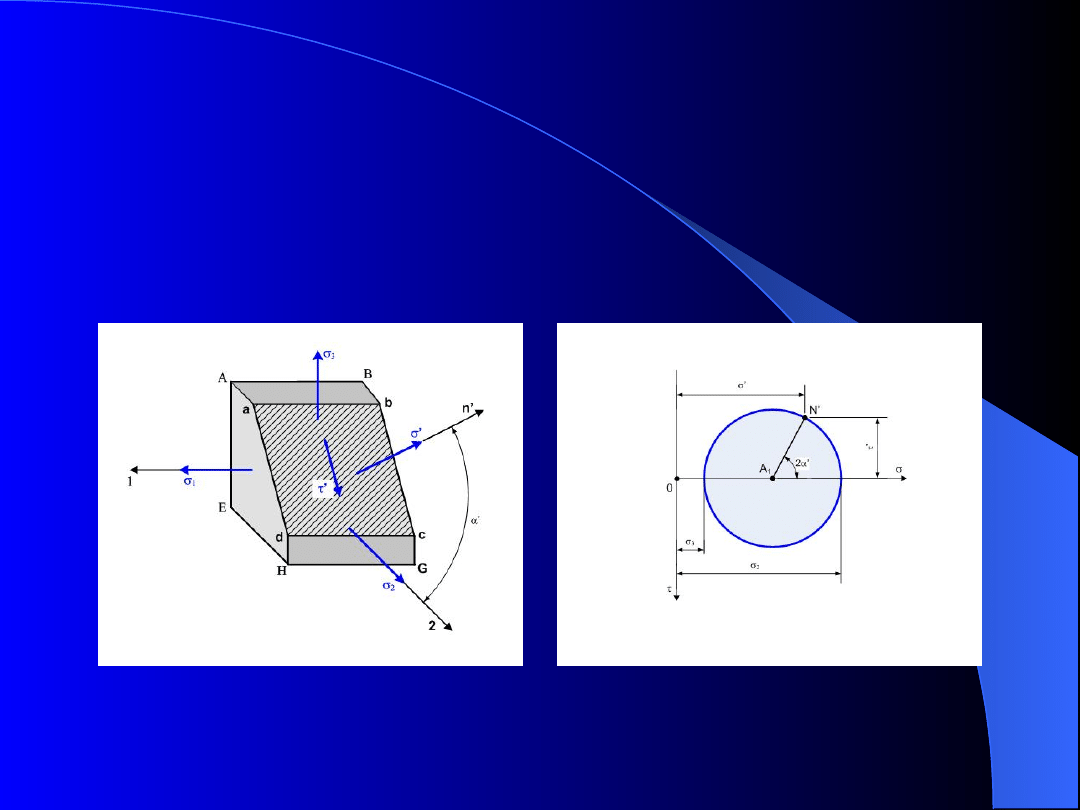
Uproszczona analiza naprężeń

Uproszczona analiza naprężeń

w przestrzennym stanie

w przestrzennym stanie

napięcia

napięcia

Wyznaczmy naprężenia w przekroju abcd równoległym
do osi 1 (rys.10)

Rys. 10. Naprężenia w przekroju równoległym do kierunku

naprężenia 

1

; a) naprężenia w przekroju abcd, b) koło

Mohra

a)

b)

Uproszczona analiza naprężeń

Uproszczona analiza naprężeń

w przestrzennym stanie

w przestrzennym stanie

napięcia

napięcia

Naprężenie 

1

nie wpływa na wartość naprężeń 

’

i 

’

, które określa punkt N

’

na kole Mohra

narysowanego dla naprężeń głównych 

2

i 

3

.

Naprężenie 

’

jest ujemne i dlatego na rys.10b jego

zwrot jest zgodny z ujemnym zwrotem osi .

Podobnie postępujemy dla przekrojów efgh oraz

ijkl równoległych odpowiednio do osi 2 i 3, otrzymując
punkty N

”

i N

”’

określające naprężenia 

”

, 

”

oraz 

”’

, 

”’

w tych przekrojach.

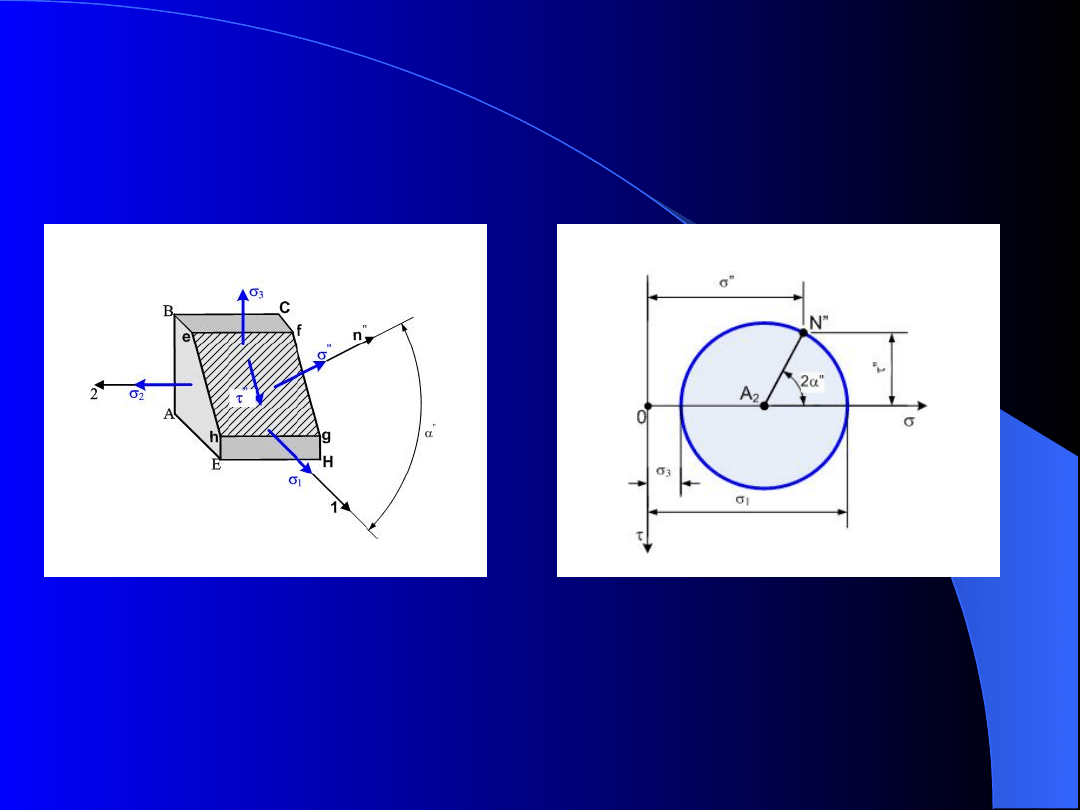
Uproszczona analiza naprężeń

Uproszczona analiza naprężeń

w przestrzennym stanie

w przestrzennym stanie

napięcia

napięcia

Rys. 11. Naprężenia w przekroju równoległym do kierunku

naprężenia 

2

; a) naprężenia w przekroju efgh, b) koło

Mohra

a
)

b
)

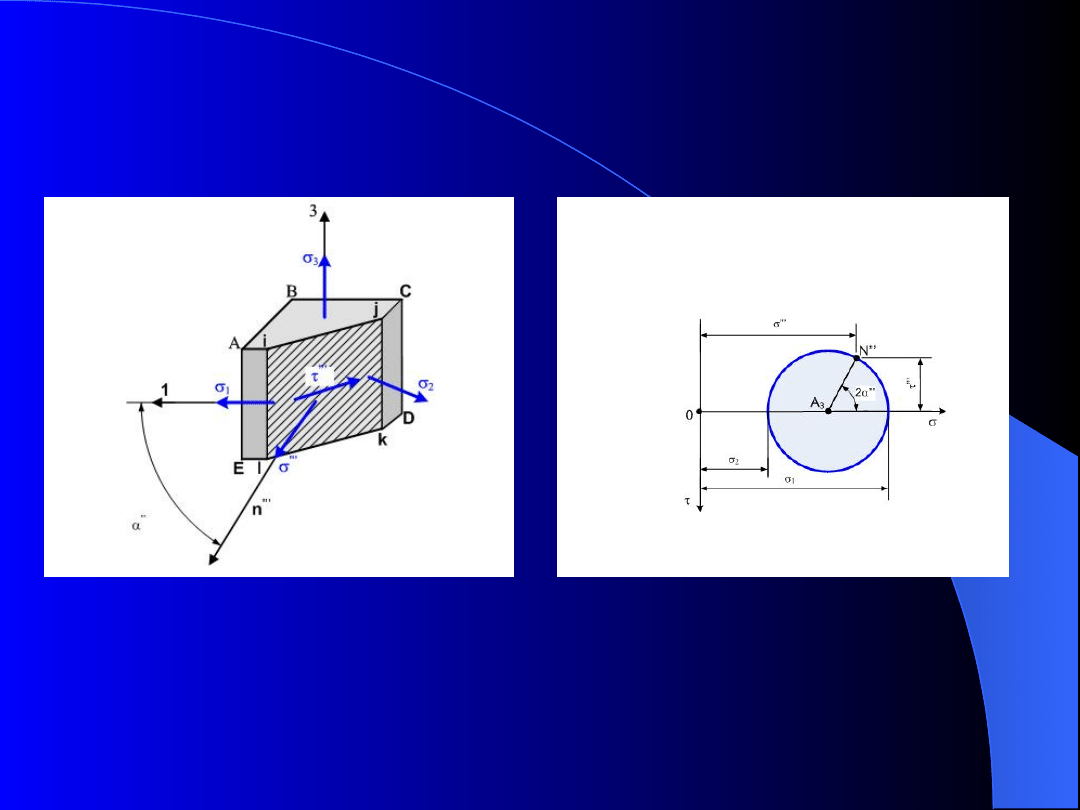
Uproszczona analiza naprężeń

Uproszczona analiza naprężeń

w przestrzennym stanie

w przestrzennym stanie

napięcia

napięcia

Rys. 12. Naprężenia w przekroju równoległym do kierunku

naprężenia 

3

; a) naprężenia w przekroju ijkl, b) koło Mohra

a
)

b
)

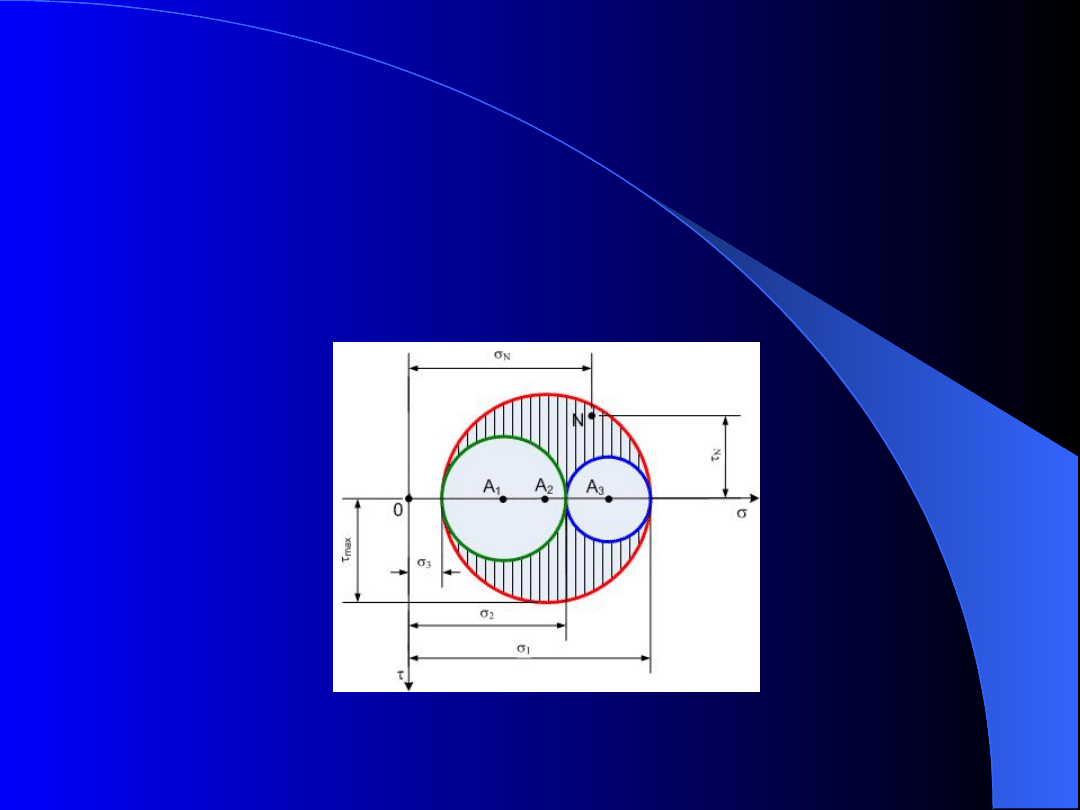
Uproszczona analiza naprężeń

Uproszczona analiza naprężeń

w przestrzennym stanie

w przestrzennym stanie

napięcia

napięcia

Rys. 13. Koło Mohra dla trójosiowego stanu naprężenia

Przenosząc te trzy koła Mohra na jeden wykres

mamy obraz, który w analizie trójwymiarowego stanu
naprężenia spełnia podobną rolę jak pojedyncze koło
Mohra dla stanu płaskiego.

Uproszczona analiza naprężeń

Uproszczona analiza naprężeń

w przestrzennym stanie

w przestrzennym stanie

napięcia

napięcia

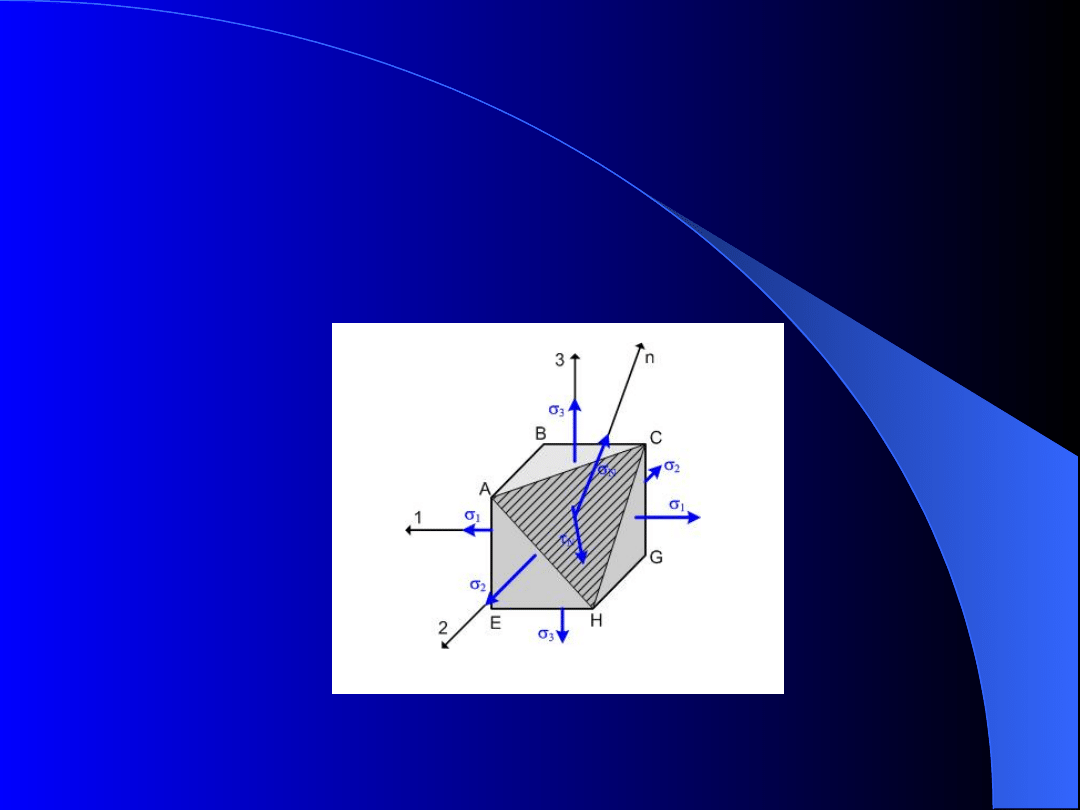
Rys. 14. Naprężenia w przekrojach ACH nachylonym do osi

1, 2, 3

Naprężenia 

N

i 

N

w przekroju ACH (rys.14)

nachylonym do wszystkich osi 1, 2, 3, reprezentuje
punkt N leżący w polu zakreskowanym (rys. 13).

Uproszczona analiza naprężeń

Uproszczona analiza naprężeń

w przestrzennym stanie

w przestrzennym stanie

napięcia

napięcia

Maksymalne naprężenie styczne ma wartość

równą promieniowi największego koła Mohra i dla
przypadku 

1

>

2

> 

3

jego moduł wynosi:

2

3

1

max











(51)

Przykład 1.

Dany jest płaski stan naprężenia: 

x

, 

y

, 

xy

, 

yx

(rys. 1.1). Wyznaczyć naprężenia: 



, 



, 



, 



, jeśli

układ osi ,  jest obrócony o kąt  względem układu
osi x,y.

x



x



x



y



y

y







xy



xy



yx



yx



Rys. 1.1. Element w płaskim stanie naprężenia

1.

Wyznaczenie naprężeń w układzie osi ,  za

pomocą koła Mohra.

Odwzorujemy zadany stan naprężenia na kole

Mohra (rys.1.2) przyjmując

,

, ,

(zgodnie z trygonometryczna umową o

znakach). Narysujmy prostą G, M, H obróconą o kąt 2
względem prostej C, M, D.

Rys. 1.1. Element w płaskim stanie naprężenia

x

A





0

y

B





0

xy

AC





xy

yx

BD











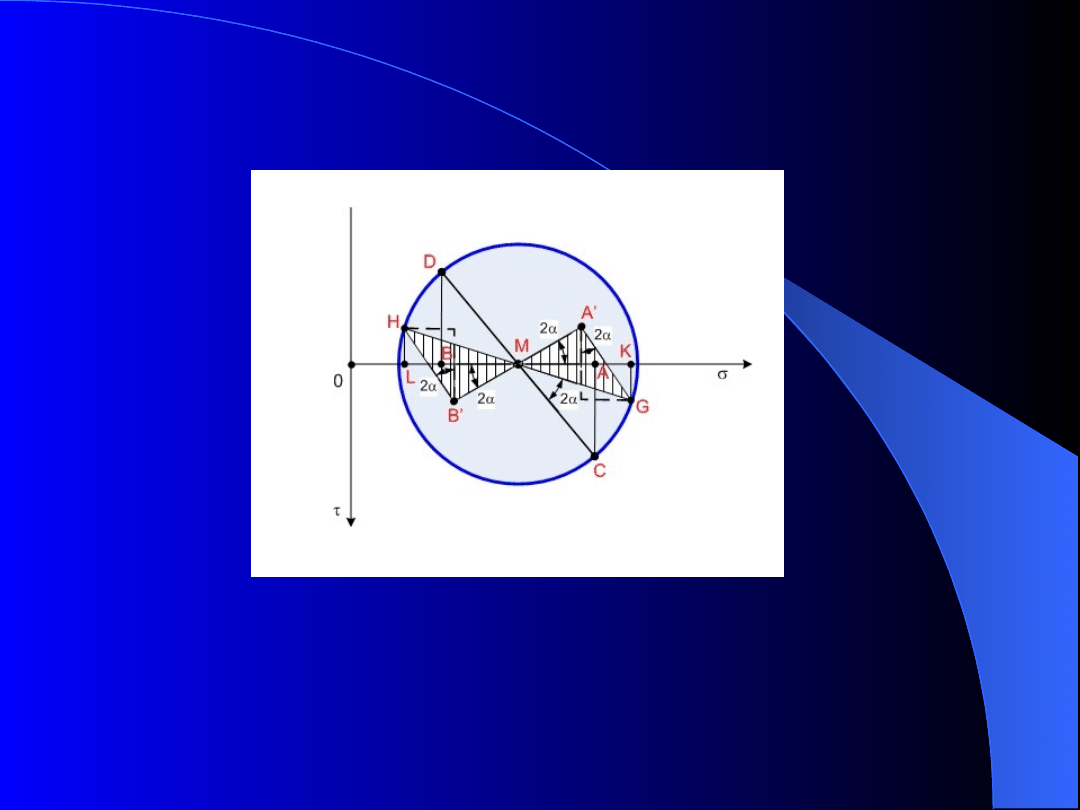
Rys. 1.2. Element w płaskim stanie naprężenia

Rzutując punkty G i H na osie  i  otrzymamy:







K

0







L

0









GK



















HL

Jeżeli obrócimy trójkąty CMA i DMB względem punktu
M o kąt 2, to otrzymamy trójkąty GMA’ i HMB’.

Z analizy koła Mohra wynika, że:









2

sin

'

2

cos

'

0

0

GA

MA

M

K

















2

sin

'

2

cos

'

0

0

HB

MB

M

L



















2

cos

'

2

sin

'

GA

MA

GK



















2

cos

'

2

sin

'

HB

MB

HL







Uwzględniając, że

oraz

2

'

'

y

x

MA

MB

MA

MA















xy

BD

HB

AC

GA











'

'

Z tego wynika, że:



















2

sin

2

cos

2

2

xy

y

x

y

x





























2

sin

2

cos

2

2

xy

y

x

y

x



























2

cos

2

sin

2

xy

y

x

























2

cos

2

sin

2

xy

y

x







2.

Wyznaczenie

naprężeń

za

pomocą

wzorów

transformacyjnych

jeśli

kąt

 = /2. Zgodnie z

matematyczną umową o znakach 

xy

= 

yx

, a więc:

y

y

x

y

x

y

x

y

x

y

x

y

x

























































sin

cos

2

2

2

sin

2

cos

2

2

x

y

x

y

x

y

x

y

x

y

x

y

x

























































sin

cos

2

2

2

sin

2

cos

2

2

























































y

x

y

x

y

x

y

x

y

x

cos

sin

2

2

cos

2

sin

2