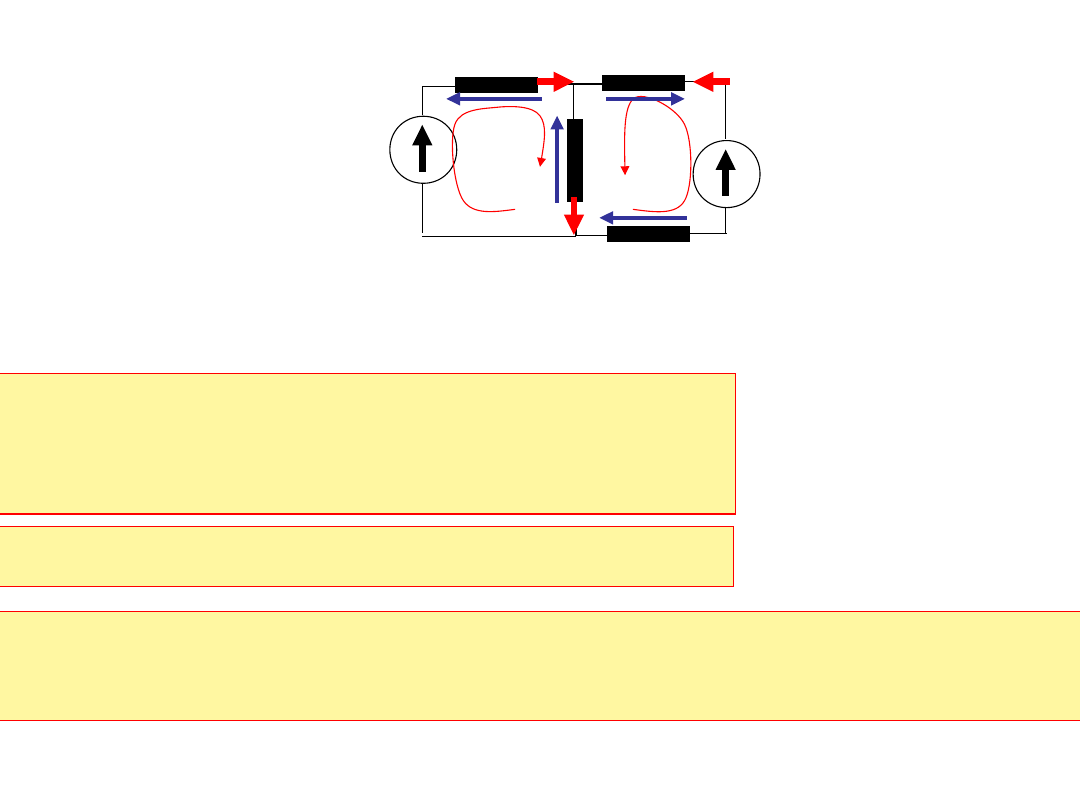
Zadanie 1.
Dany jest obwód:

E

1

R

3

R

4

E

2

R

1

R

2

Napisać równania Kirchhoffa dla wyznaczenia prądów.

I

1

I

2

I

3

Liczba niewiadomych prądów: 3
Liczba niezależnych węzłów: 1
Liczba niezależnych oczek: 3 – 1=2

Prądowe prawo Kirchhoffa: I

1

+I

2

=I

3

1

2

Napięciowe prawo Kirchhoffa, oczko 1: I

3

R

3

+I

1

R

1

=E

1

oczko 2: I

3

R

3

+I

2

R

2

+I

2

R

4

=E

2

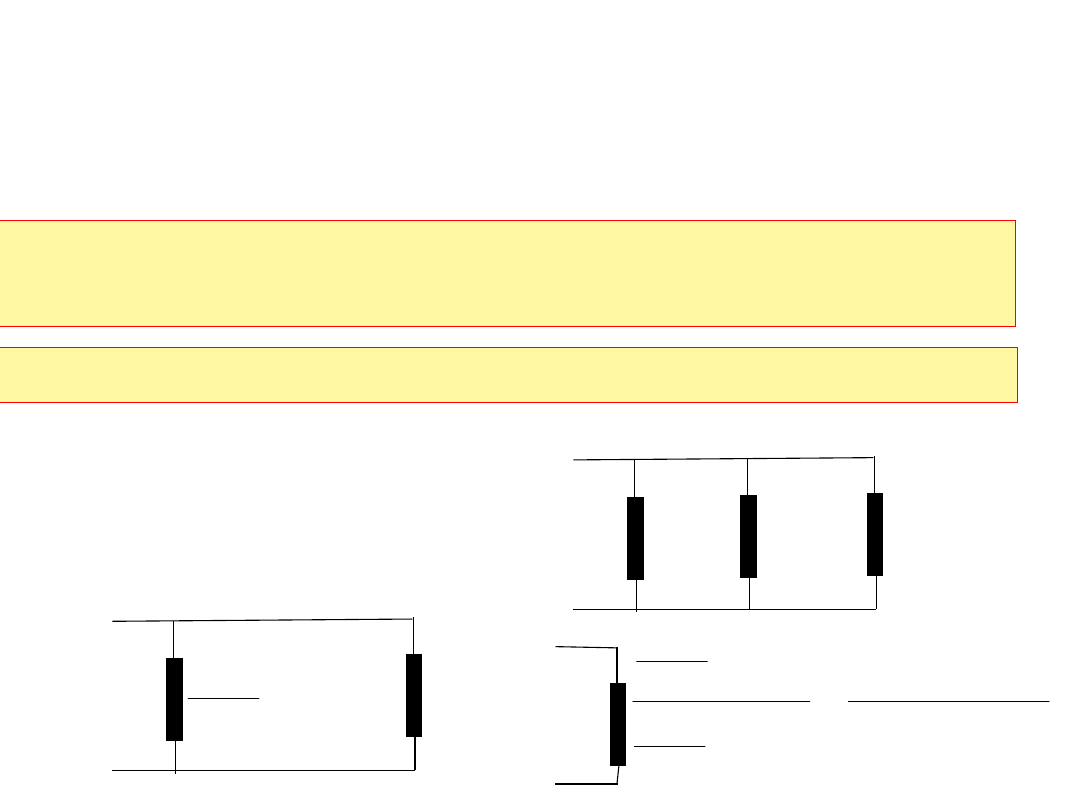
Zadanie 2.
Przez rezystor o rezystancji R=(a+b)[mΩ] płynie prąd równy 10A.
Ile wynosi spadek napięcia na tym rezystorze?

Spadek napięcia na rezystorze jest: U=IR
czyli: U=10·(a+b)·10

-3

Niech a=8, b=6, to U=0.14 V lub U=140 mV

Zadanie 3.
Dany jest układ rezystorów:

a

b

a+b

A

B

Obliczyć rezystancję R

AB

.

→

→

a+b=14

A

B

→

43

.

3

b

a

b

a







A

B













2

b

a

b

a

b

a

b

a

b

a

b

a

b

a

b

a

b

a

b

a





































43

.

3

b

a

b

a











2.754

14

43

.

3

14

43

.

3

R

AB

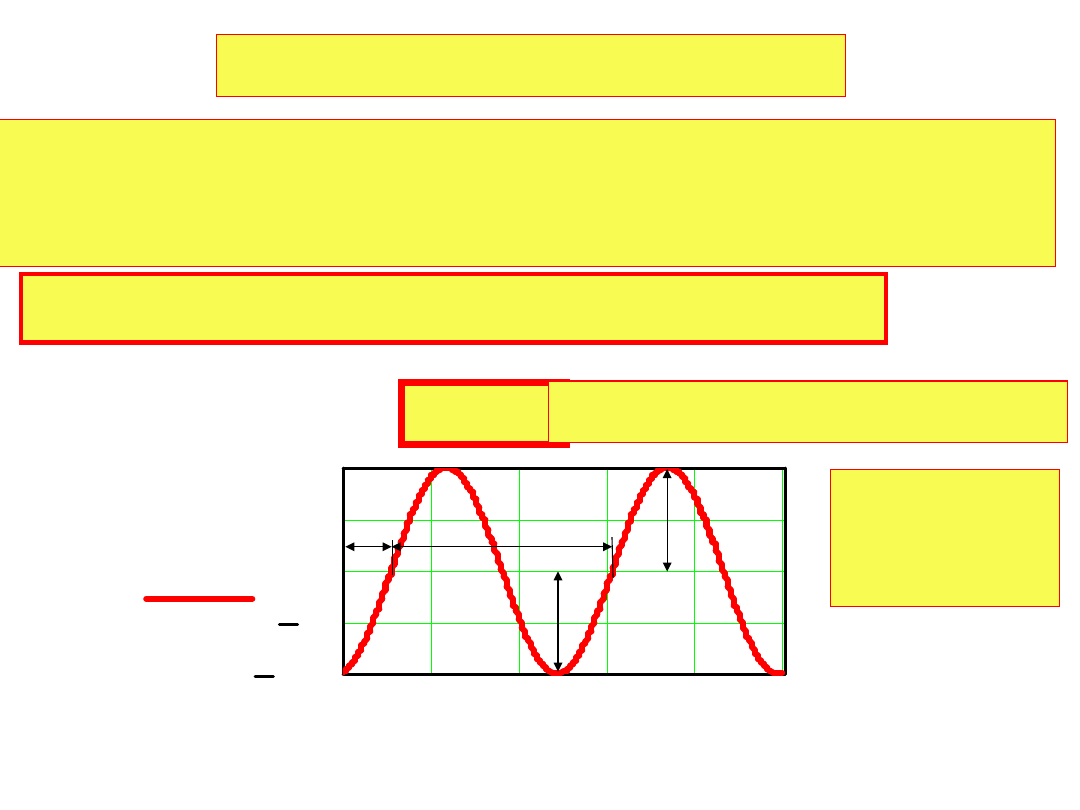
Obwody prądu zmiennego

Siła elektromotoryczna sinusoidalnie zmienna

e(t)=E

m

sin(t+)

E

m

– amplituda,  - pulsacja,  - faza

0 0.008

0.016

0.024

0.032

0.04

10

5

0

5

10

e t

( )

t



T

E

m

E

m

=2πff – częstotliwość [Hz]

f=1/T

T - okres

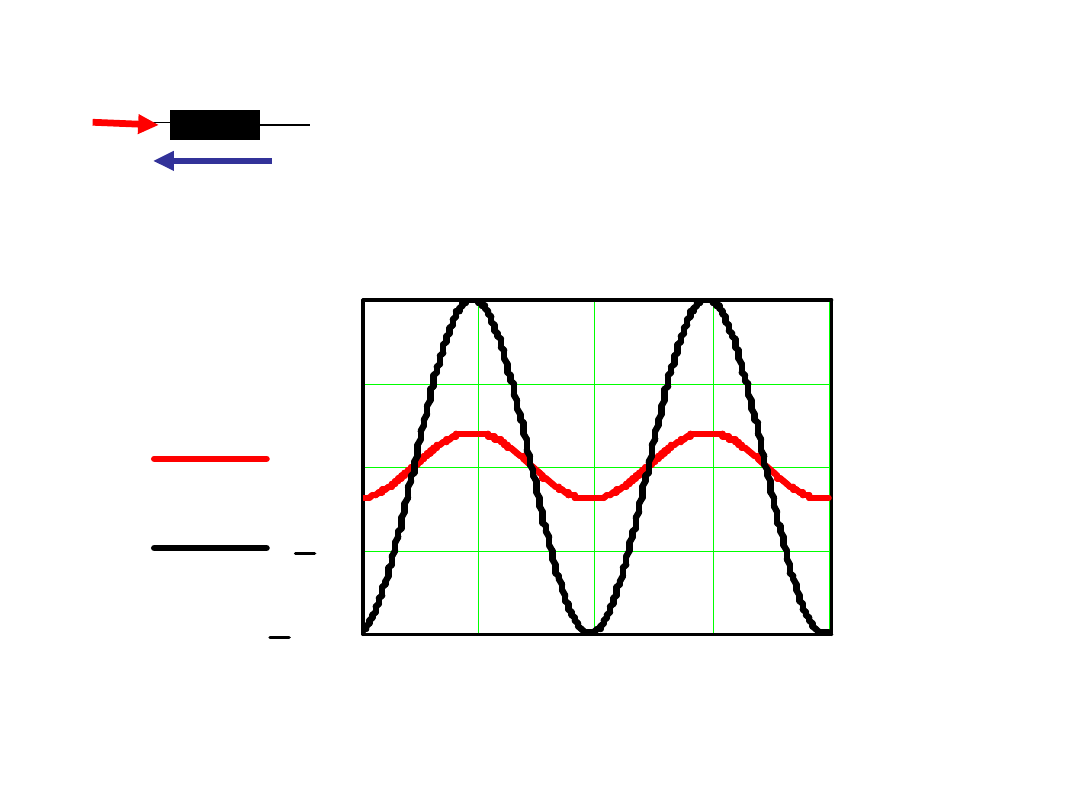
R

i(t)

u

R

(t)=Ri(t)

i(t)=I

m

sin(t+)

u

R

(t)=RI

m

sin(t+)

0 0.010.020.030.04

10

5

0

5

10

i t

( )

uRt

( )

t

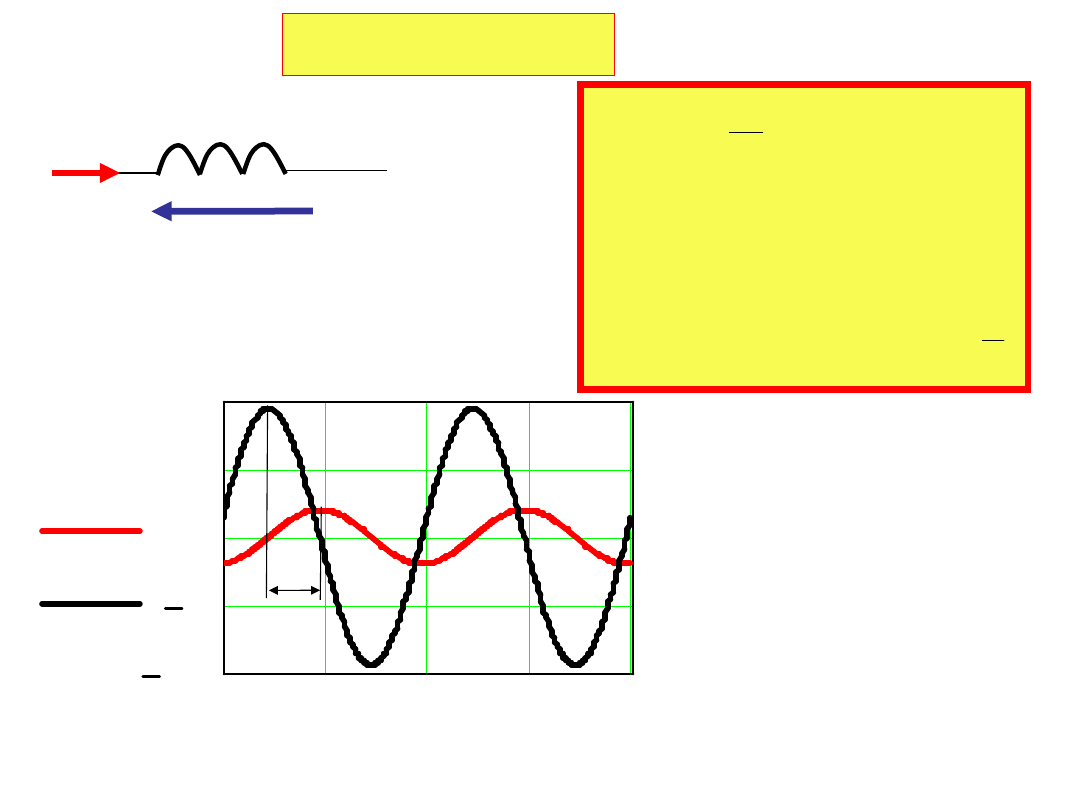
Indukcyjność

i(t)

L

u

L

(t)

 
 





 





 















































2

t

sin

LI

t

u

t

cos

LI

t

u

t

sin

I

t

i

dt

di

L

t

u

m

L

m

L

m

L

0

0.010.020.030.04

10

5

0

5

10

i t

( )

uLt

( )

t

/2

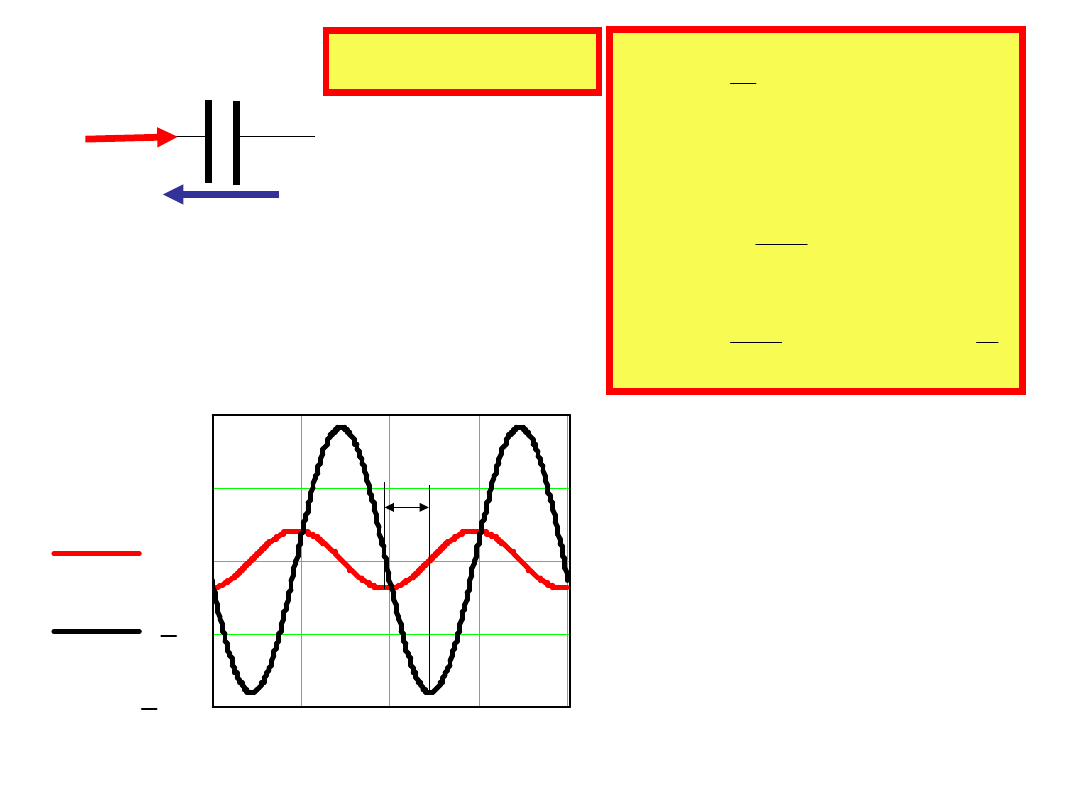
Pojemność

i(t)

u

C

(t)

 

 

 





 





 



























































2

t

sin

C

I

t

u

t

cos

C

I

t

u

t

sin

I

t

i

d

i

C

1

t

u

m

C

m

C

m

t

C

0 0.010.020.030.04

10

5

0

5

10

i t

( )

uCt

( )

t

/2

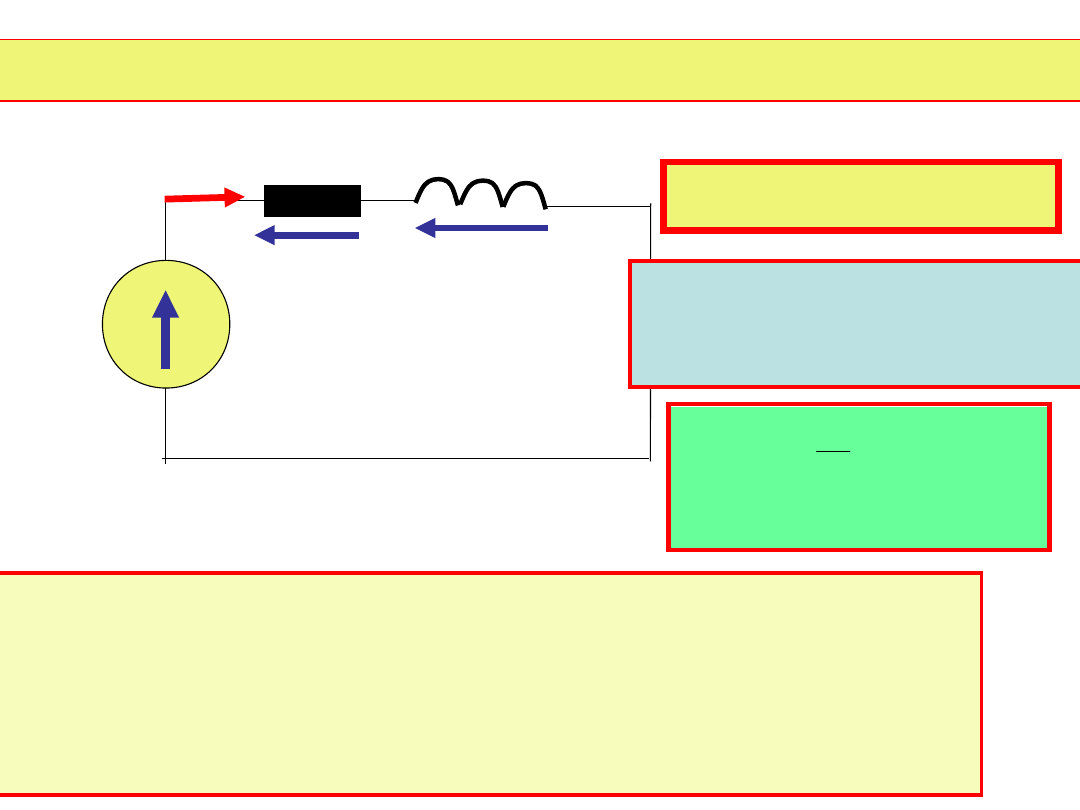
Szeregowe połączenie rezystancji i indukcyjności

R

L

e(t)=E

m

sin(t)

i(t)

u

R

(t)

u

L

(t)

i(t)=I

m

sin(t+)

u

R

(t)=Ri(t)

u

R

(t)=RI

m

sin(t+)

 
 

















t

cos

LI

t

u

dt

di

L

t

u

m

L

L

Z napięciowego prawa Kirchhoffa mamy:

u

R

(t)+u

L

(t)=e(t)

RI

m

sin(t+)+LI

m

cos(t+)=E

m

sin(t)

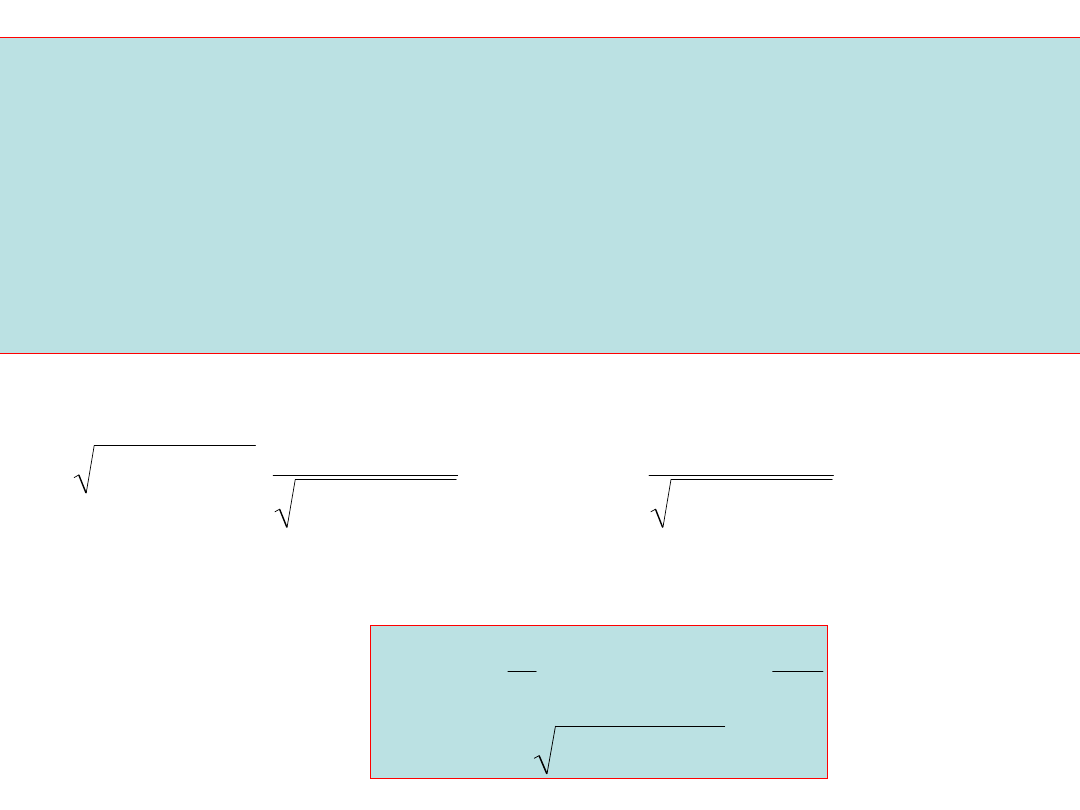
aby równanie: RI

m

sin(t+)+LI

m

cos(t+)=E

m

sin(t)

było spełnione dla dowolnej chwili czasowej musi mieć

postać: I

m

Zsin(t)= E

m

sin(t)

gdzie I

m

=E

m

/Z.













 

 

 





 





 

t

sin

E

t

cos

L

R

L

t

sin

L

R

R

L

R

I

t

sin

E

t

cos

L

t

sin

R

I

m

2

2

2

2

2

2

m

m

m







































































Podstawiamy:

 

 

 

2

2

L

R

Z

Z

L

sin

i

Z

R

cos



















Z – nazywamy impedancją

po podstawieniu mamy:













 

  



  







 





 

t

sin

E

t

sin

Z

I

t

sin

E

t

cos

sin

t

sin

cos

Z

I

t

sin

E

t

cos

L

t

sin

R

I

m

m

m

m

m

m

























































a więc aby powyższe równanie było spełnione dla

dowolnej chwili czasowej musi zachodzić równość:

=

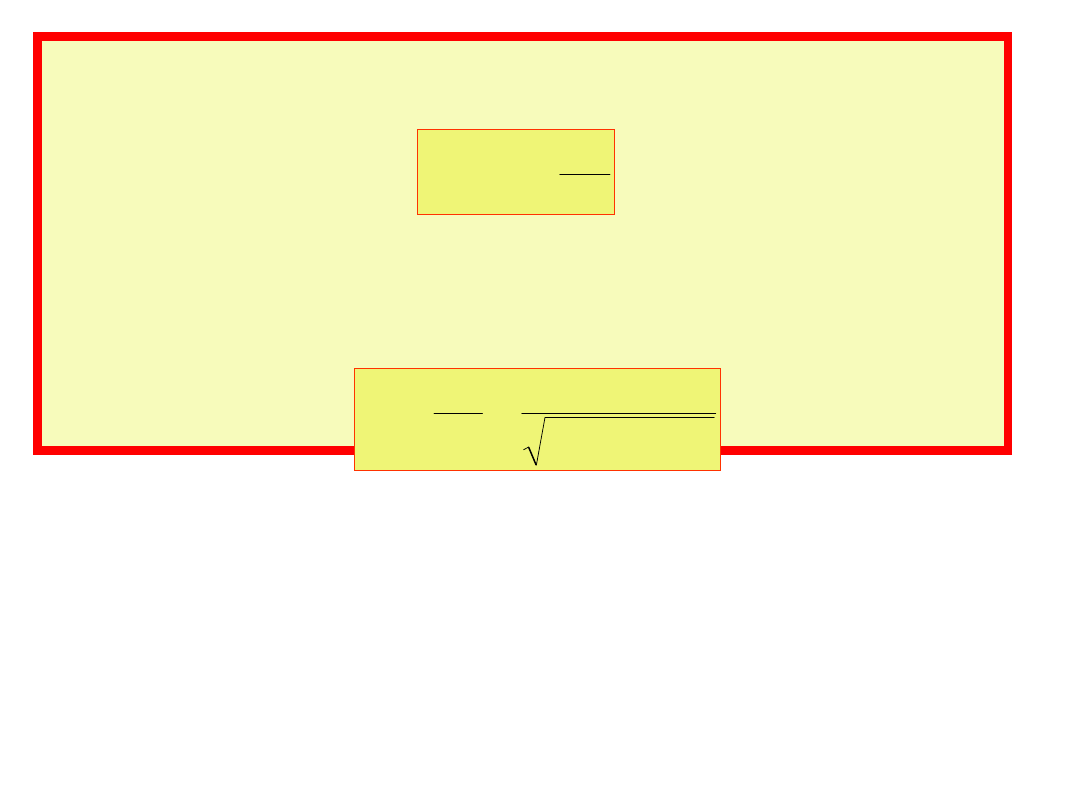
 - faza prądu jest określana z równania:

a amplituda prądu I

m

jest:

 

R

L

tg









 

2

2

m

m

m

L

R

E

Z

E

I









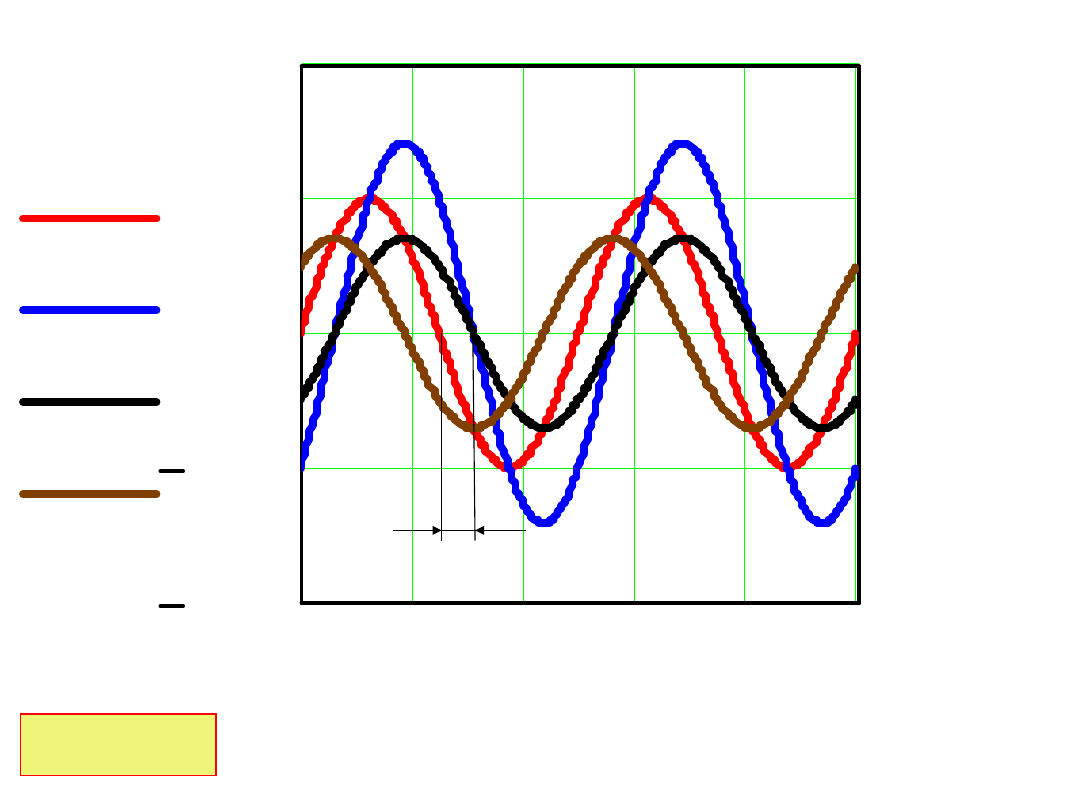
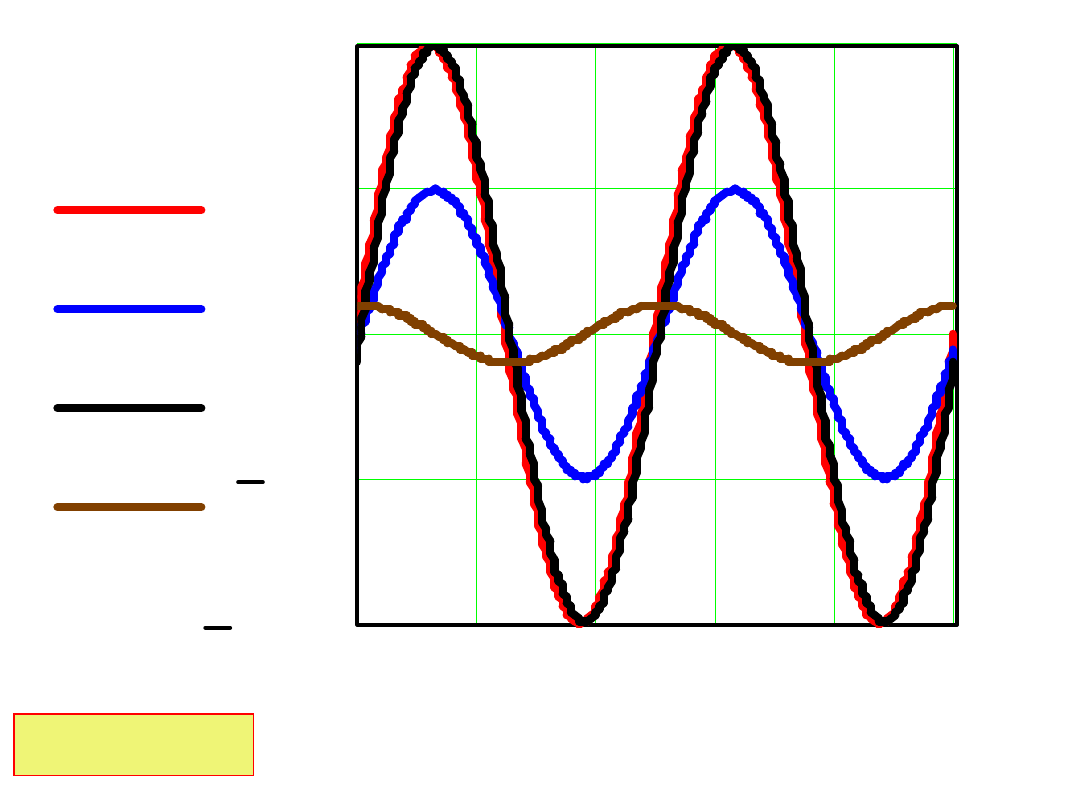
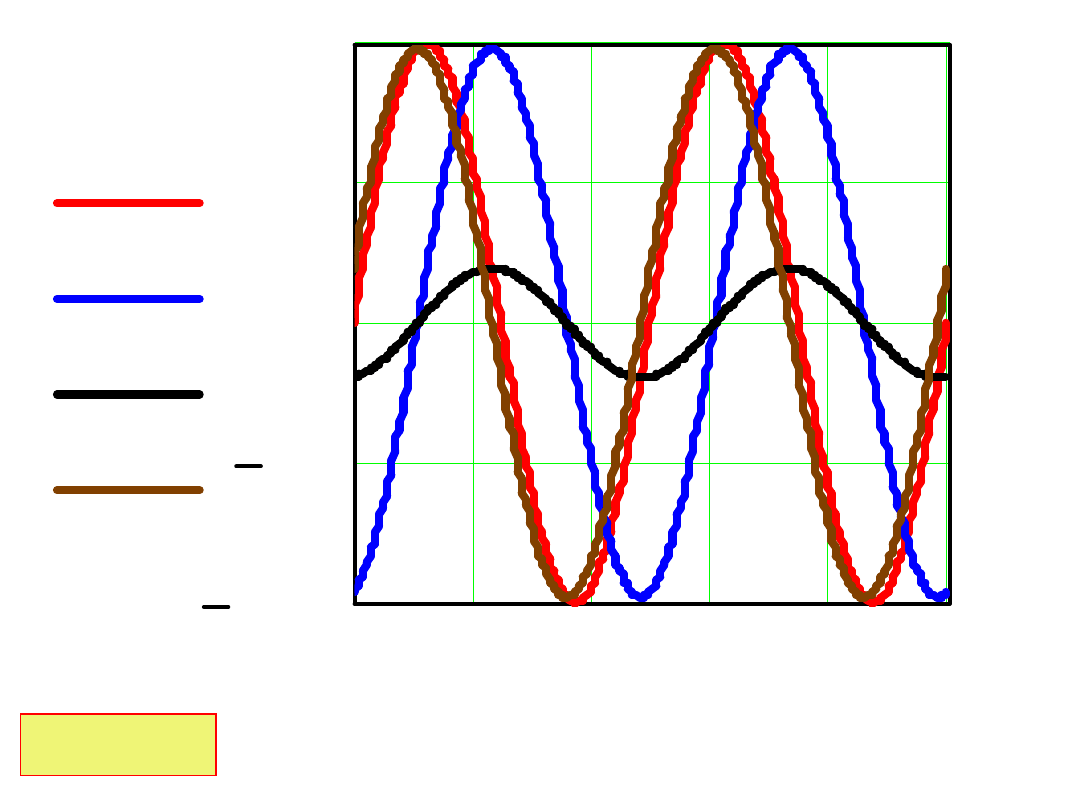
Przebieg prądu i(t) oraz spadki napięcia u

R

(t) i u

L

(t)

przedstawiono na wykresach:

0 0.008

0.016

0.024

0.032

0.04

200

100

0

100

200

e t

( )

i t

( )

uRt

( )

uLt

( )

t

L/R=1

/4

0 0.008

0.016

0.024

0.032

0.04

100

50

0

50

100

e t

( )

i t

( )

uRt

( )

uL t

( )

t

L/R=0.1

0 0.008

0.016

0.024

0.032

0.04

100

50

0

50

100

e t

( )

i t

( )

uRt

( )

uL t

( )

t

L/R=5

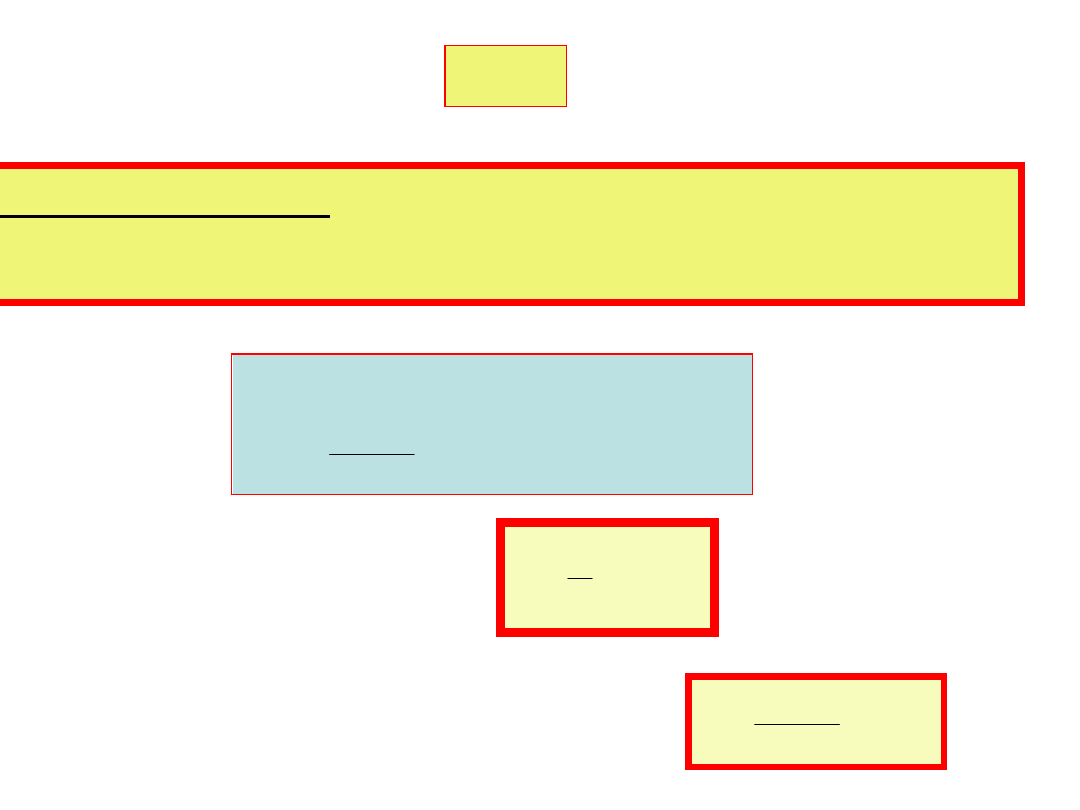
Moc

Moc chwilowa dostarczana do obwodu jest:

p(t)=e(t)i(t)

 

  



 

 































t

2

cos

cos

2

I

E

t

p

t

sin

t

sin

I

E

t

p

m

m

m

m

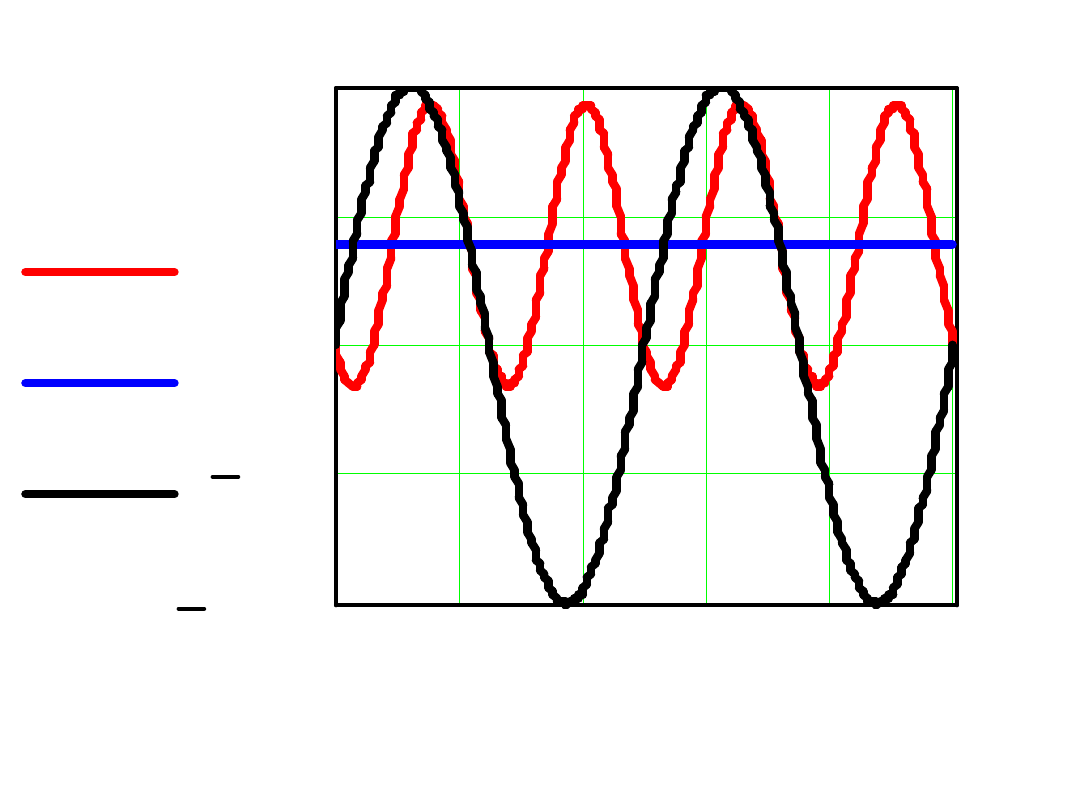
Średnia moc jest:

 





T

0

dt

t

p

T

1

P

po wykonaniu całkowania mamy:

 





cos

2

I

E

P

m

m

0 0.008

0.016

0.024

0.032

0.04

100

50

0

50

100

p t

( )

P

e t

( )

t

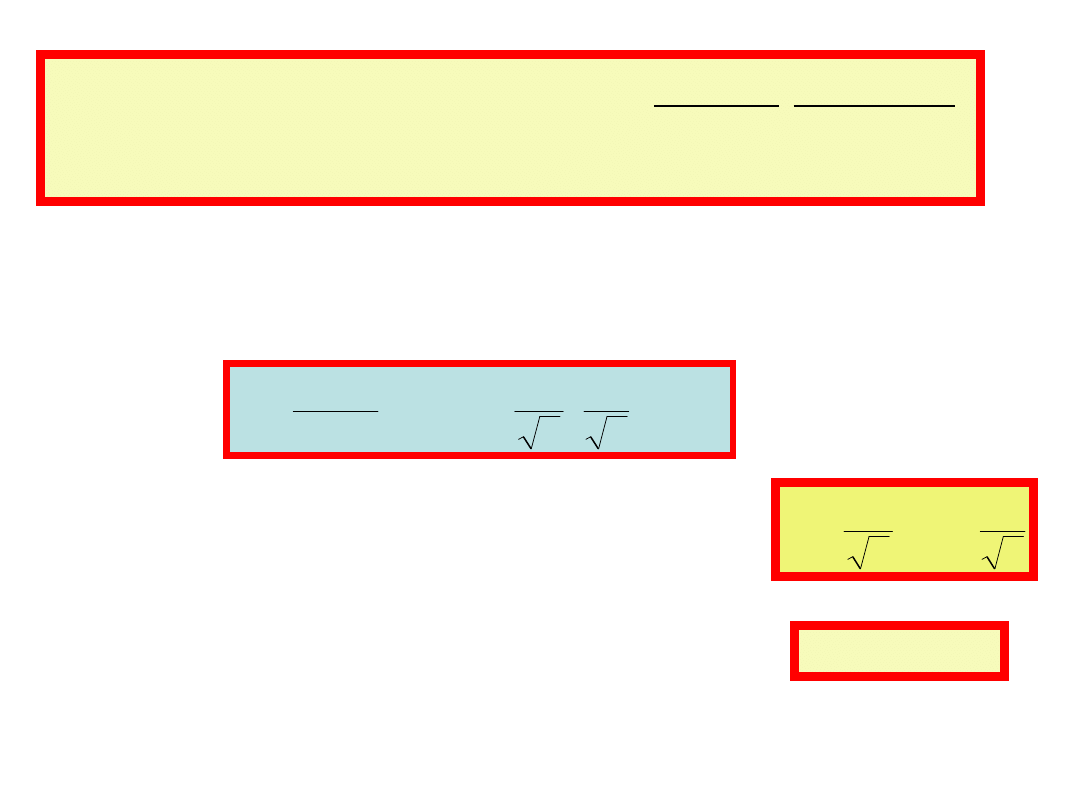
Moc średnią P nazywamy mocą czynną.

Jednostką mocy czynnej jest wat [W]

Wygodnie jest przekształcić zależność:

 

 











cos

2

I

2

E

cos

2

I

E

P

m

m

m

m

i wprowadzamy wartości skuteczne:

2

I

I

2

E

E

m

m





Wzór na moc czynną przyjmuje postać:

 



 cos

EI

P

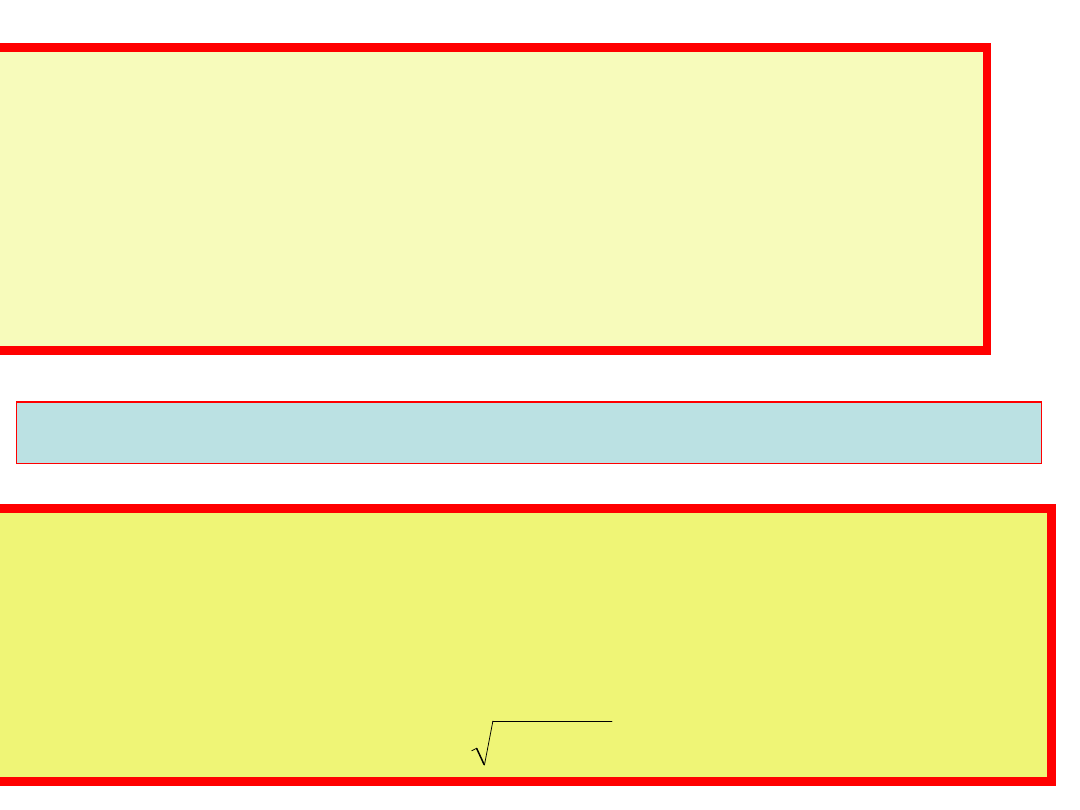
Wprowadzamy dodatkową charakterystykę

zwaną mocą bierną:

Q=EIsin()

Jednoską mocy biernej jest var [VAr].

Ponieważ P

2

+Q

2

=(EI)

2

(cos

2

+sin

2

)=(EI)

2

Wielkość: S=EI
nazywamy mocą pozorną.
Jednostką mocy pozornej jest voltamper [VA].

2

2

Q

P

S





Moc tracona w rezystancji: p

R

(t)=u

R

(t)i(t)

Ponieważ u

R

(t)=Ri(t) więc p

R

(t)=Ri

2

(t)

 











































2

t

2

cos

1

2

I

R

t

sin

RI

t

p

2

m

2

2

m

R

i średnia moc jest: P

R

=RI

2

Ze względu na fakt, że kąt fazowy między spadkiem

napięcia u

R

(t)=RI

m

sin(t+) i prądem i(t)=I

m

sin(t+)

jest równy 0, więc Q

R

=0

Chwilowa moc tracona w indukcyjności jest

p

L

(t)=u

L

(t)i(t)

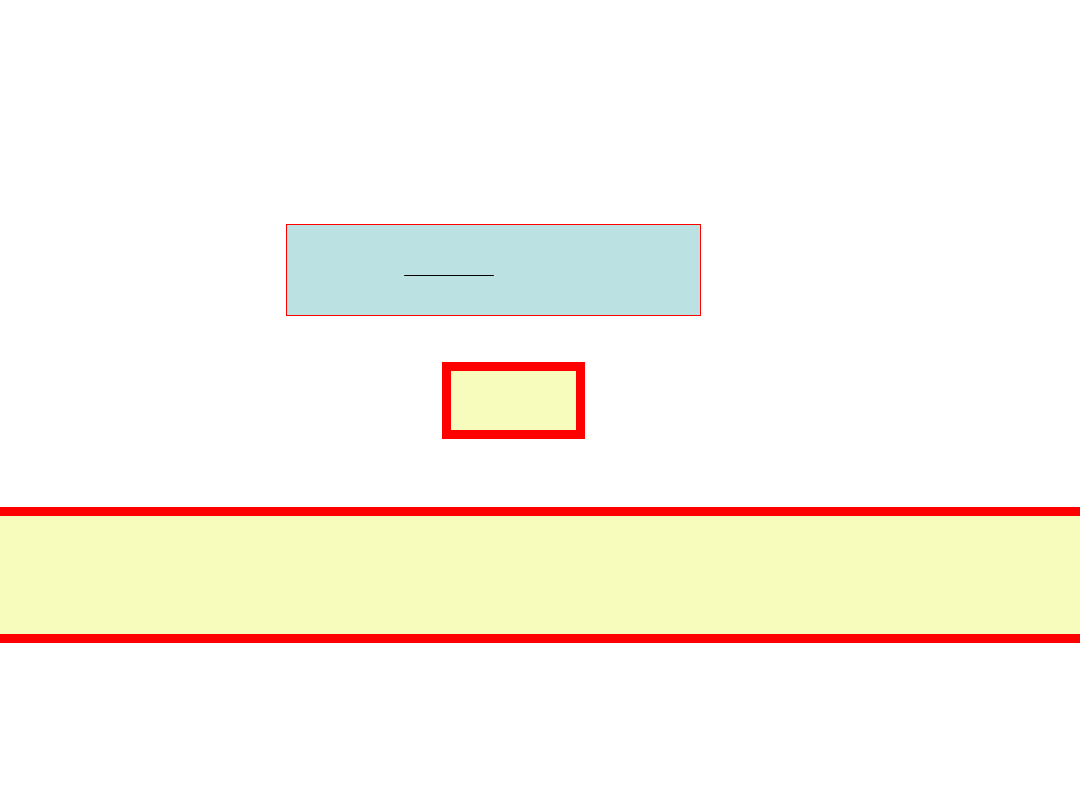
ponieważ u

L

(t)=LI

m

cos(t+) więc moc chwilowa jest

p

L

(t)=LI

m

cos(t+)I

m

sin (t+)

czyli

 















2

t

2

sin

2

LI

t

p

2

m

L

Moc średnia jest: P

L

=0

Moc czynna pobierana przez indukcyjność jest równa

zeru.

Ponieważ spadek napięcia na indukcyjności:

u

L

(t)=LI

m

cos(t+)=LI

m

sin(t++π/2),

a prąd i(t)=I

m

sin(t+), a więc kąt przesunięcia

między prądem a spadkiem napięcia na indukcyjności

wynosi /2, a więc moc bierna pobierana przez

indukcyjność jest Q

L

=LI

2

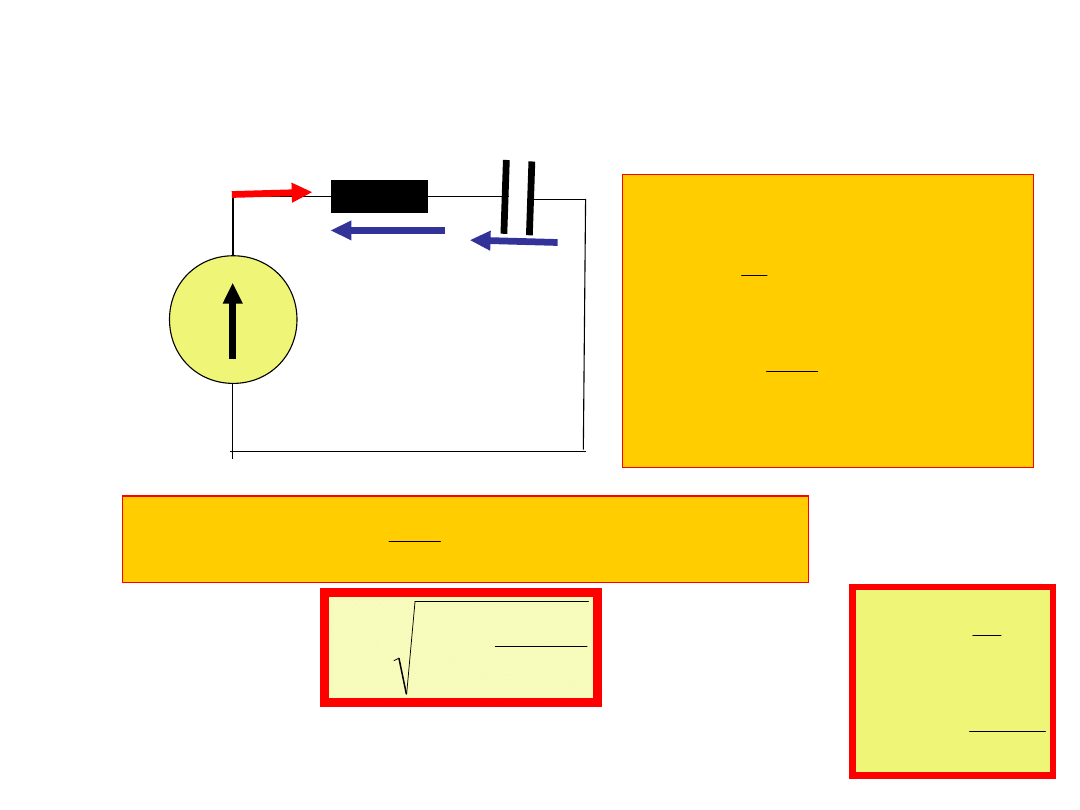
e(t)=E

m

sin(t)

u

R

(t)

R

C

u

C

(t)

i(t)=I

m

sin(t+)

Obwód RC

 





 





 





 

   

t

e

t

u

t

u

t

cos

I

C

1

t

u

dt

t

sin

I

C

1

t

u

t

sin

RI

t

u

C

R

m

C

m

C

m

R











































 

t

sin

E

t

cos

C

I

t

sin

RI

m

m

m





















Impedancja:





2

2

C

1

R

Z







Oznaczamy:

CZ

1

sin

Z

R

cos











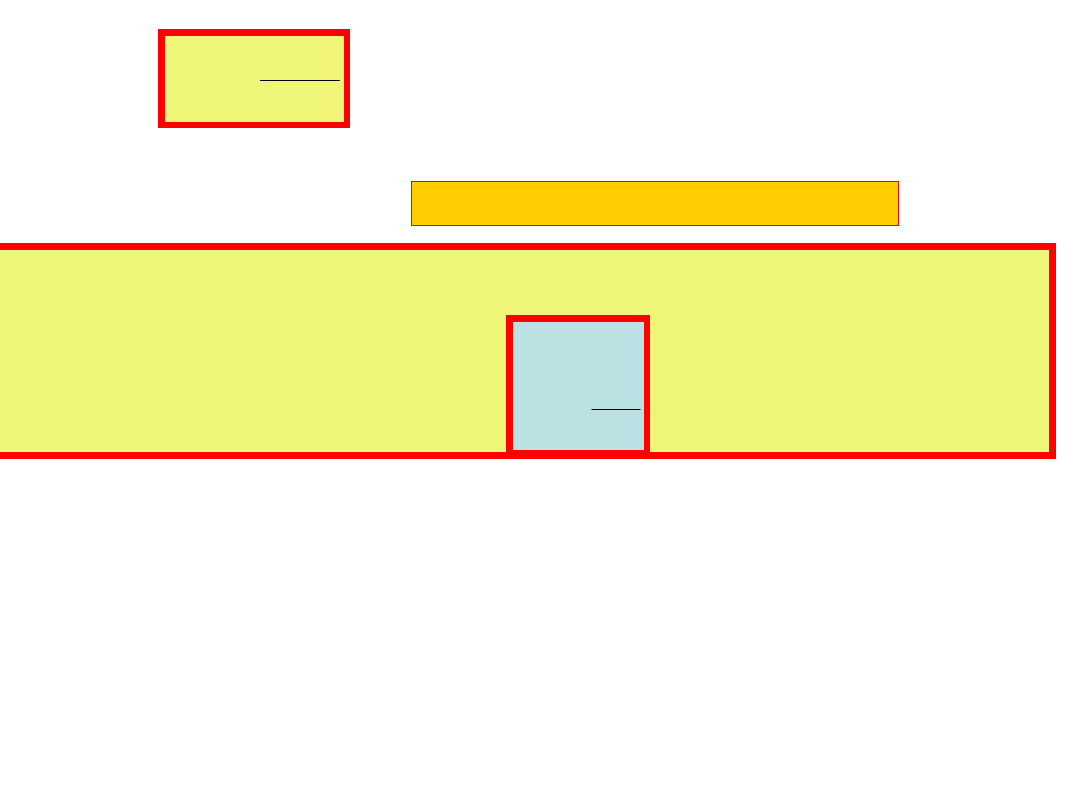
lub

CR

1

tg







i otrzymujemy:





 

t

sin

E

t

sin

ZI

m

m















Warunkiem spełnienia równania dla dowolnej
chwili czasowej jest:

Z

E

I

m

m









Przebieg prądu i spadków napięć przedstawiono
na wykresach:

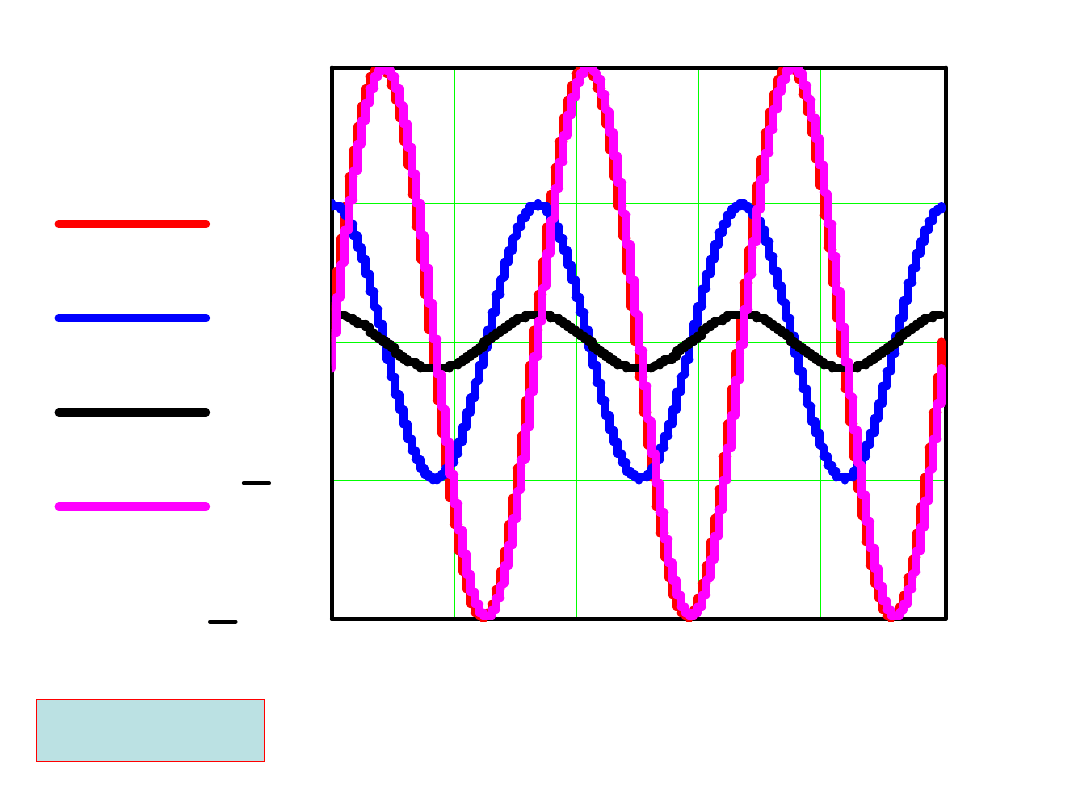
RC=0.1

0 0.012

0.024

0.036

0.048

0.06

10

5

0

5

10

e t

( )

i t

( )

uRt

( )

uC t

( )

t

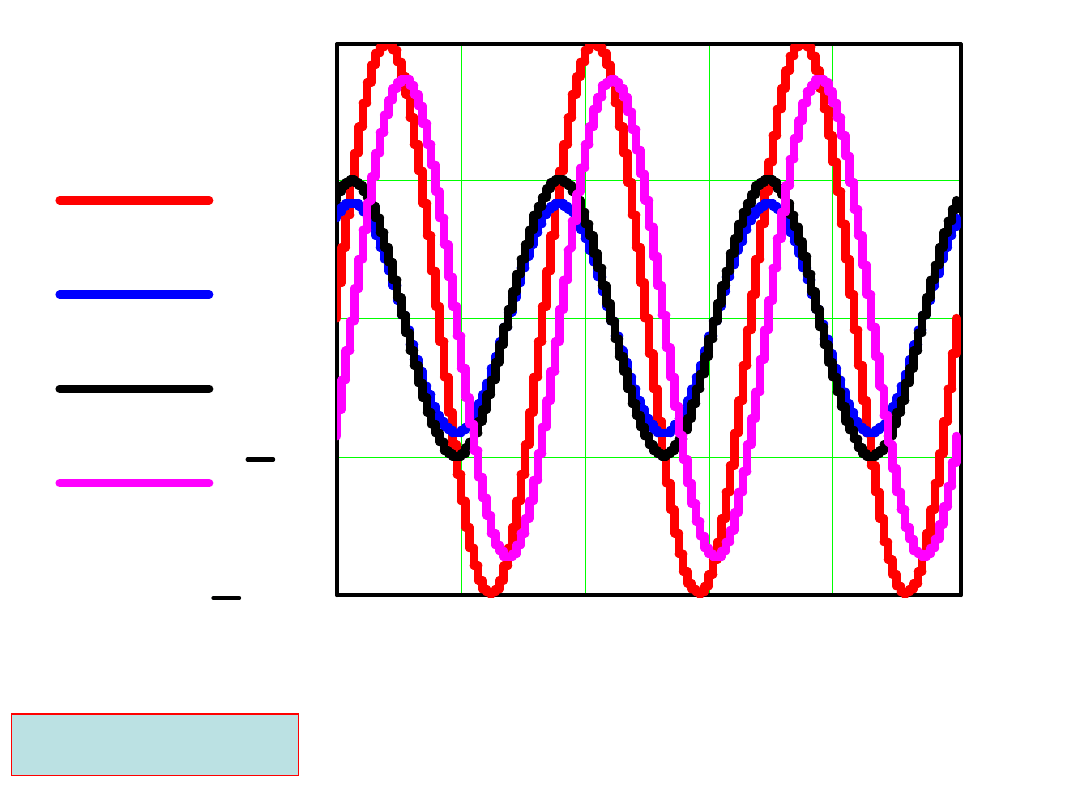
RC=0.577

0 0.012

0.024

0.036

0.048

0.06

10

5

0

5

10

e t

( )

i t

( )

uRt

( )

uC t

( )

t

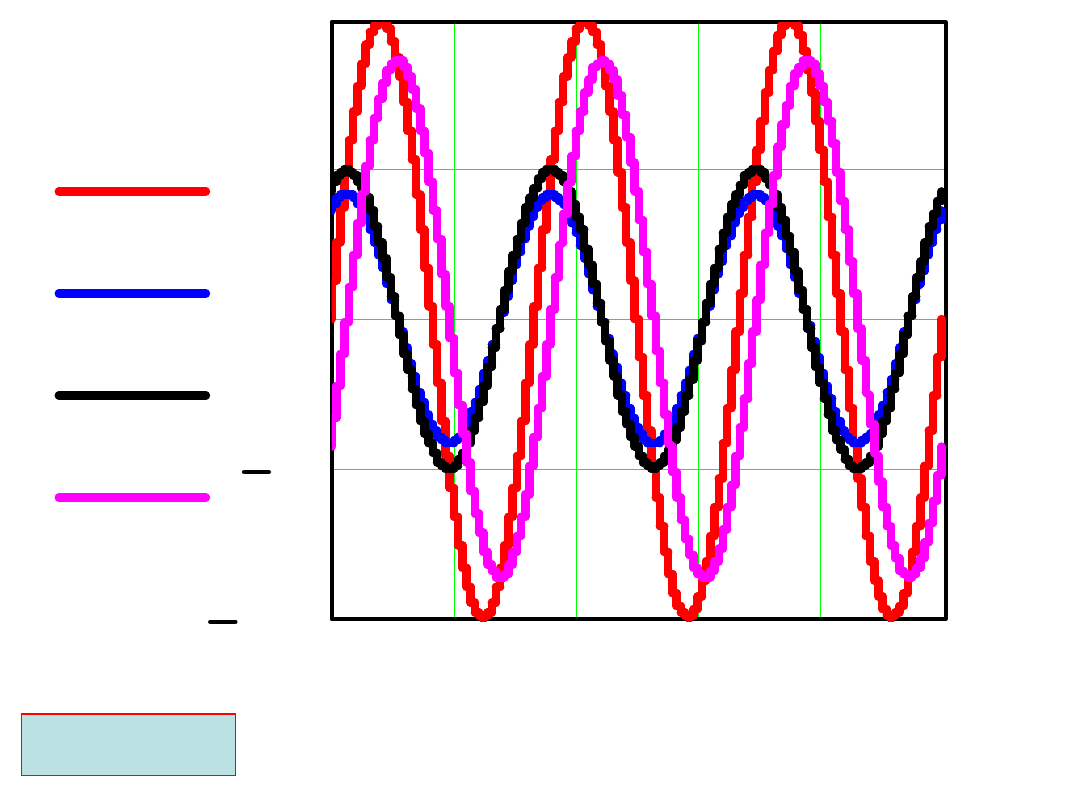
RC=10

0 0.012

0.024

0.036

0.048

0.06

10

5

0

5

10

e t

( )

i t

( )

uRt

( )

uC t

( )

t

Moce chwilowe:

     

 

   

 

   

t

i

t

u

t

p

t

i

t

u

t

p

t

i

t

e

t

p

C

C

R

R







Moc czynna = moc średnia

   

 









cos

I

E

2

1

dt

t

i

t

e

T

1

P

m

m

T

0

Moc czynna tracona w rezystancji:

   

2

m

R

T

0

R

R

RI

2

1

P

dt

t

i

t

u

T

1

P







Moc czynna tracona w pojemności:

   

0

P

dt

t

i

t

u

T

1

P

C

T

0

C

C







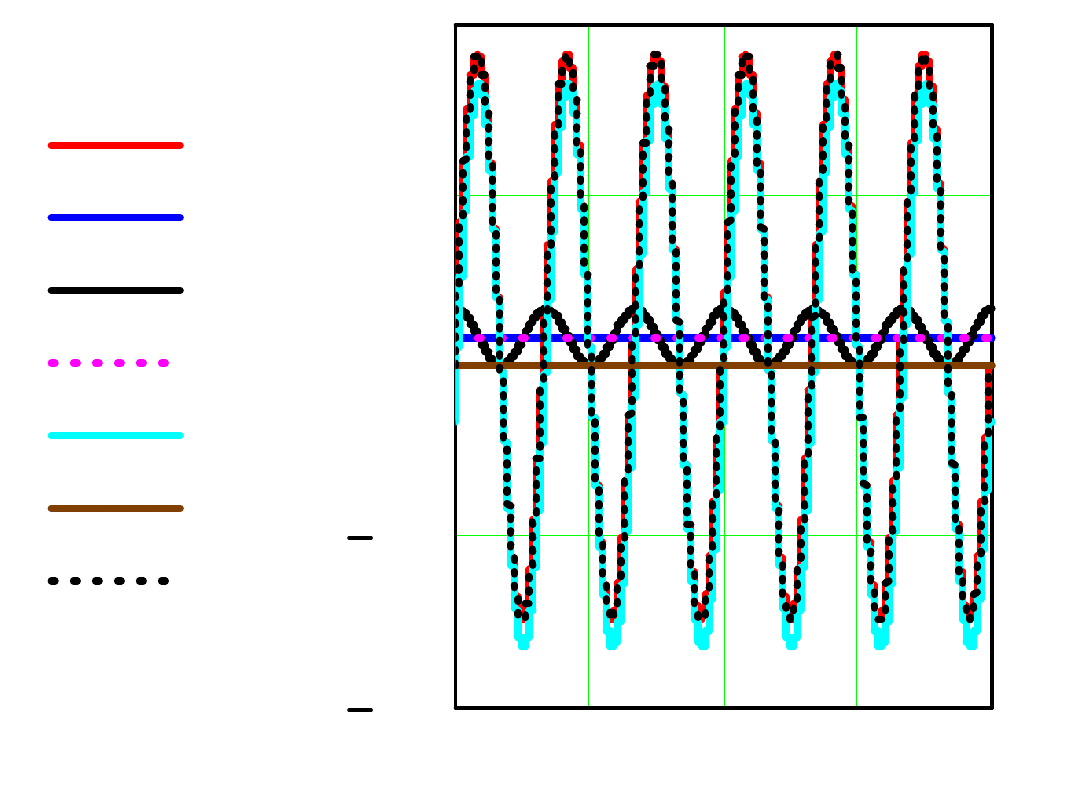
0

0.0150.030.0450.06

30

15

0

15

30

p t

( )

P

pR t

( )

PR

pC t

( )

PC

pR t

( ) pC t

( )



t

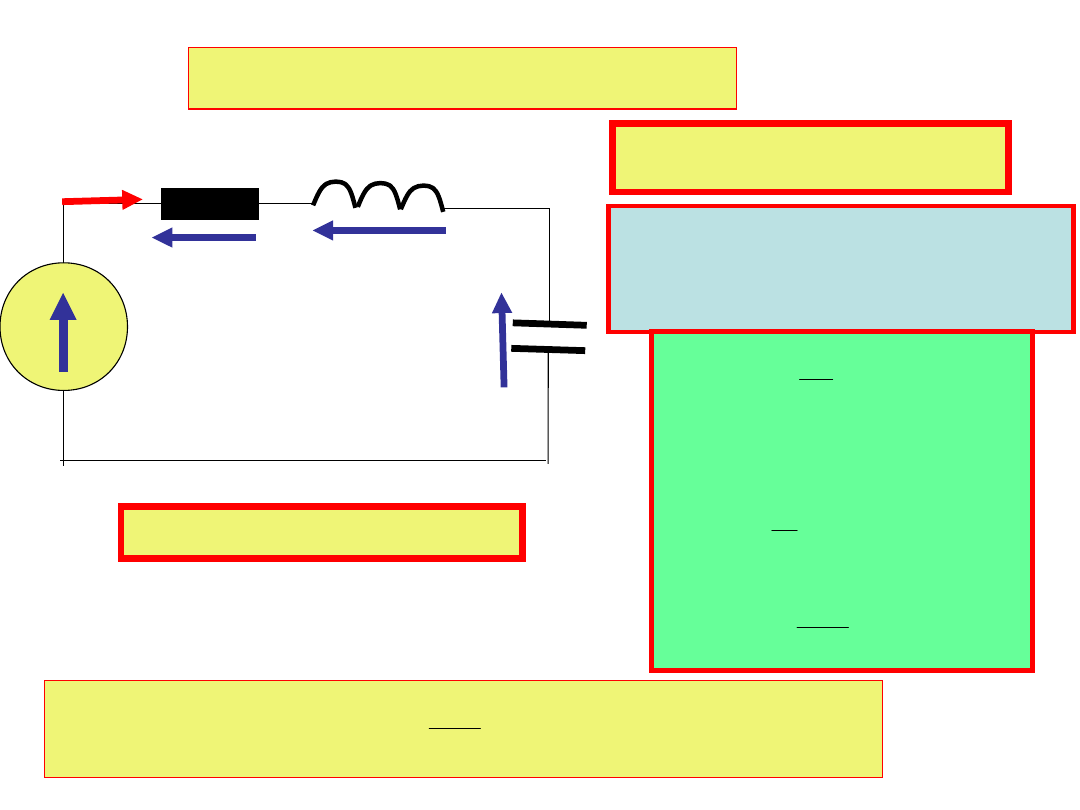
Obwód szeregowy RLC

R

L

e(t)=E

m

sin(t)

i(t)

u

R

(t)

u

L

(t)

C

u

c

(t)

i(t)=I

m

sin(t+)

u

R

(t)=Ri(t)

u

R

(t)=RI

m

sin(t+)

 
 





 

 

 

































t

cos

C

I

t

u

dt

t

i

C

1

t

u

t

cos

LI

t

u

dt

di

L

t

u

m

C

C

m

L

L

 

 

   

t

e

t

u

t

u

t

u

C

L

R







Podstawiając mamy:









 

t

sin

E

t

cos

C

1

L

t

sin

R

I

m

m













































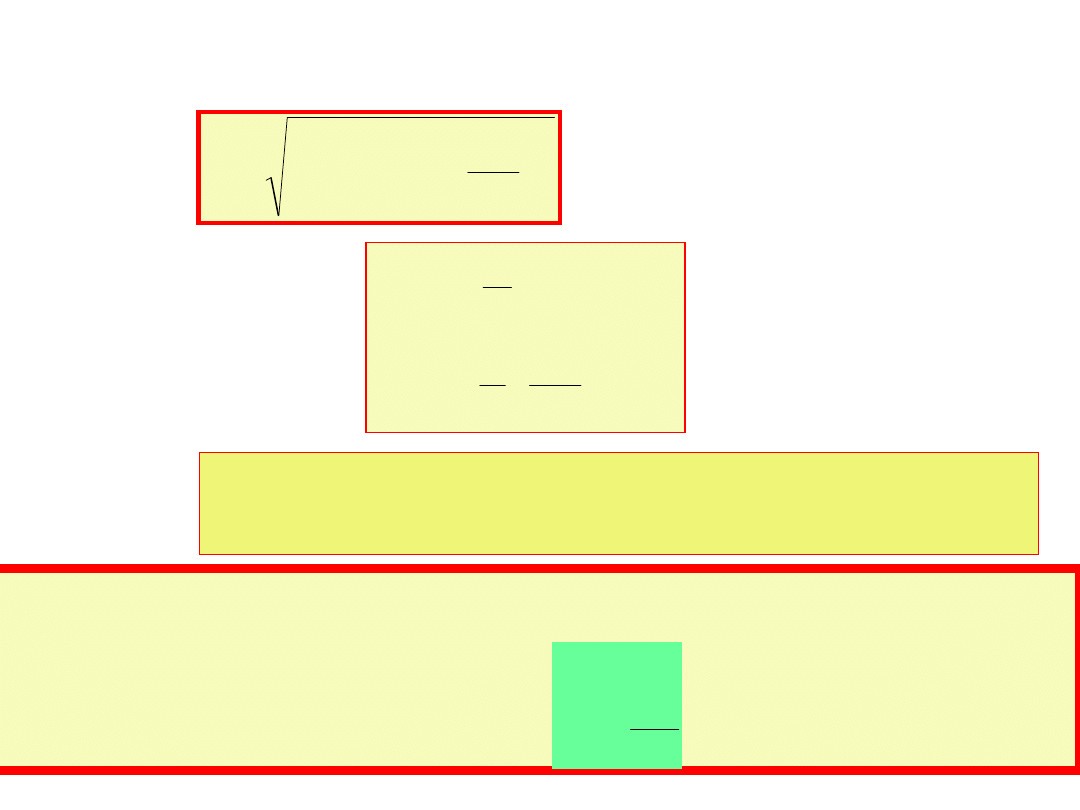
Oznaczając:

2

2

C

1

L

R

Z























impedancja obwodu.



























L

C

1

Z

1

sin

Z

R

cos

mamy:

  



  







 





 

t

sin

E

t

sin

Z

I

t

sin

E

t

cos

sin

t

sin

cos

Z

I

m

m

m

m





































ostatnie równanie będzie spełnione dla dowolnej
chwili czasowej t, jeżeli:

Z

E

I

m

m









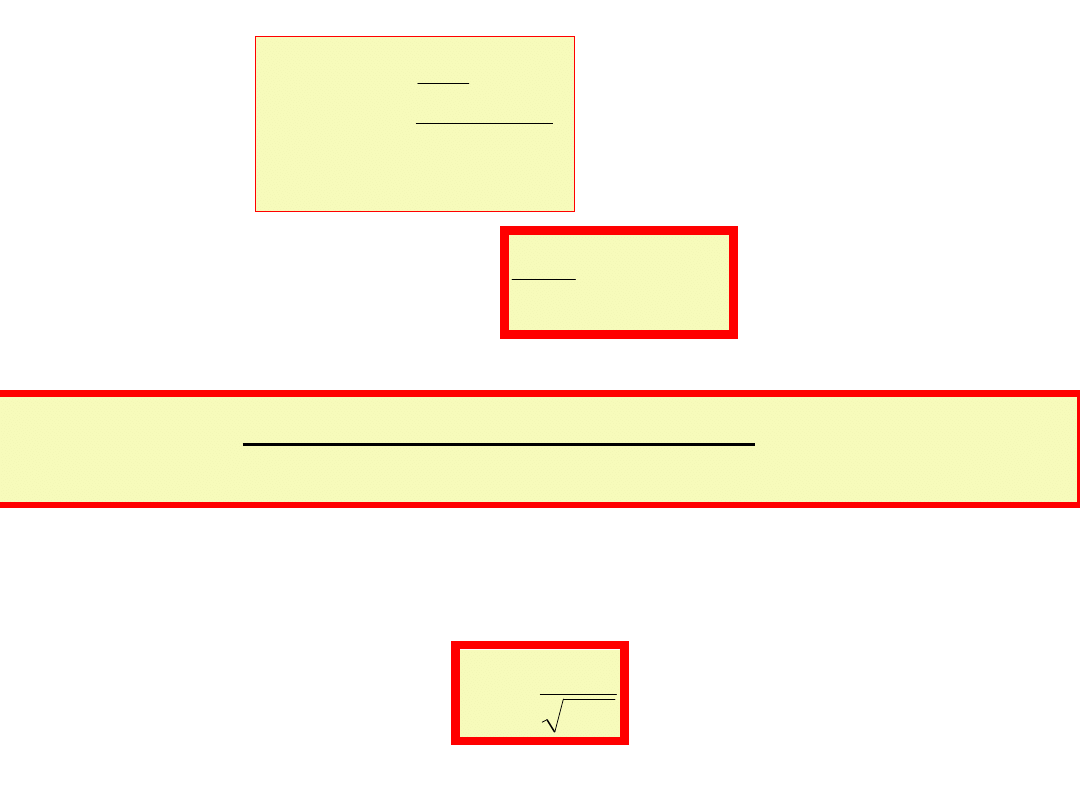
czyli































R

L

C

1

arctg

Pulsację 

0

, dla której

0

L

C

1

0

0









nazywamy pulsacją rezonansową szeregowego

obwodu RLC

Pulsację rezonansową określa zależność:

LC

1

0





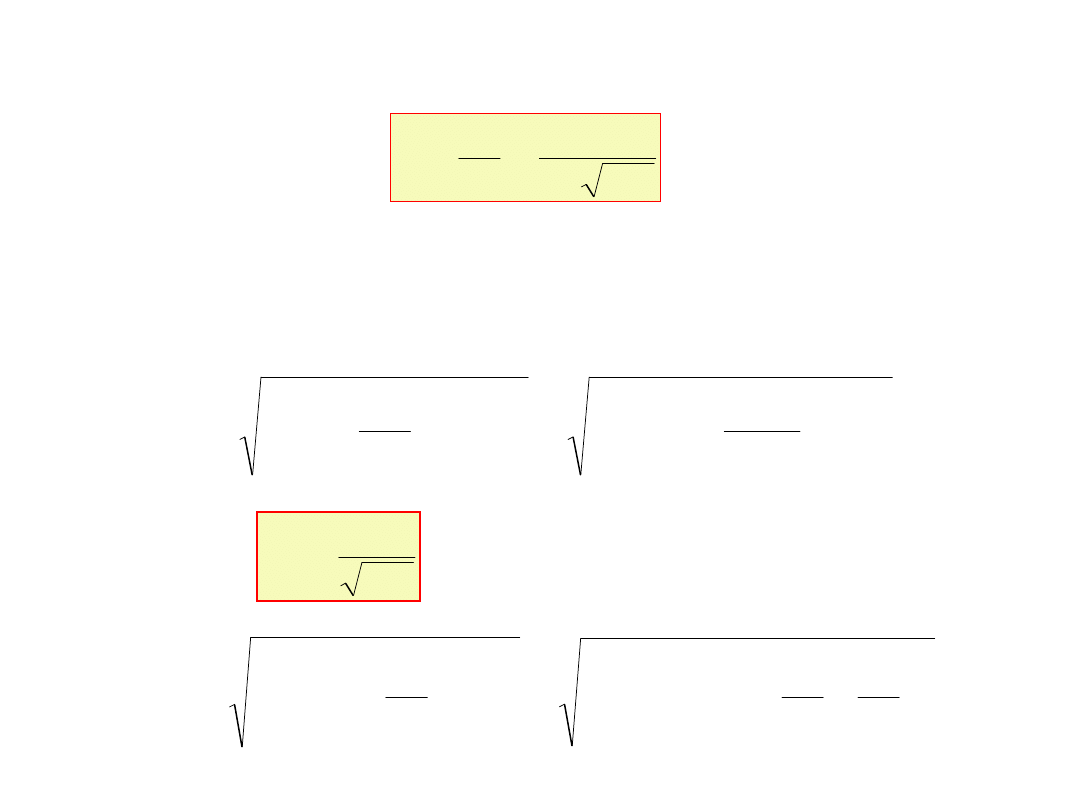
Częstotliwość rezonansowa f

0

obliczamy z zależności:

LC

2

1

2

f

0

0











Korzystając z pulsacji rezonansowej przekształcamy
wyrażenie dla modułu impedancji:

2

2

2

2

2

LC

1

L

R

L

C

1

R

Z













































ponieważ

LC

1

0





więc





2

0

0

2

0

2

2

2

0

2

2

L

R

L

R

Z





















































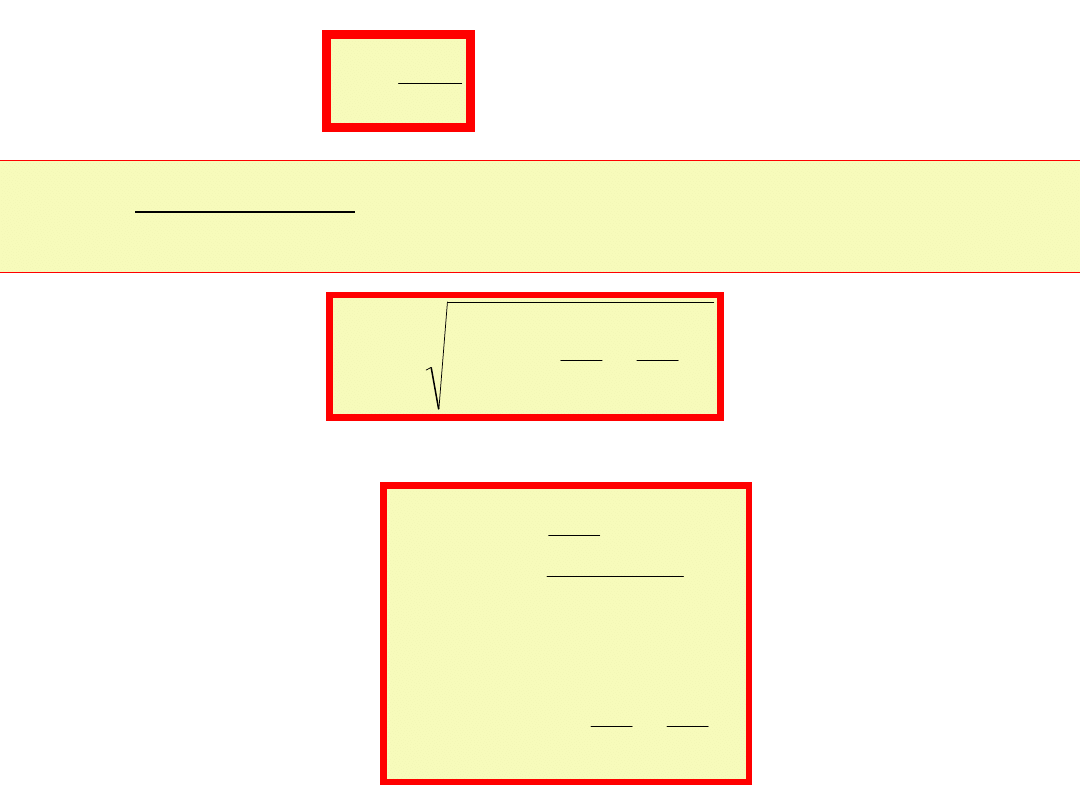
Wielkość:

R

L

Q

0





nazywamy dobrocią szeregowego obwodu rezonansowego
i podstawiając mamy:

2

0

0

2

Q

1

R

Z



























Uwzględniając wprowadzone oznaczenia dla fazy mamy:





































































0

0

Q

arctg

R

L

C

1

arctg

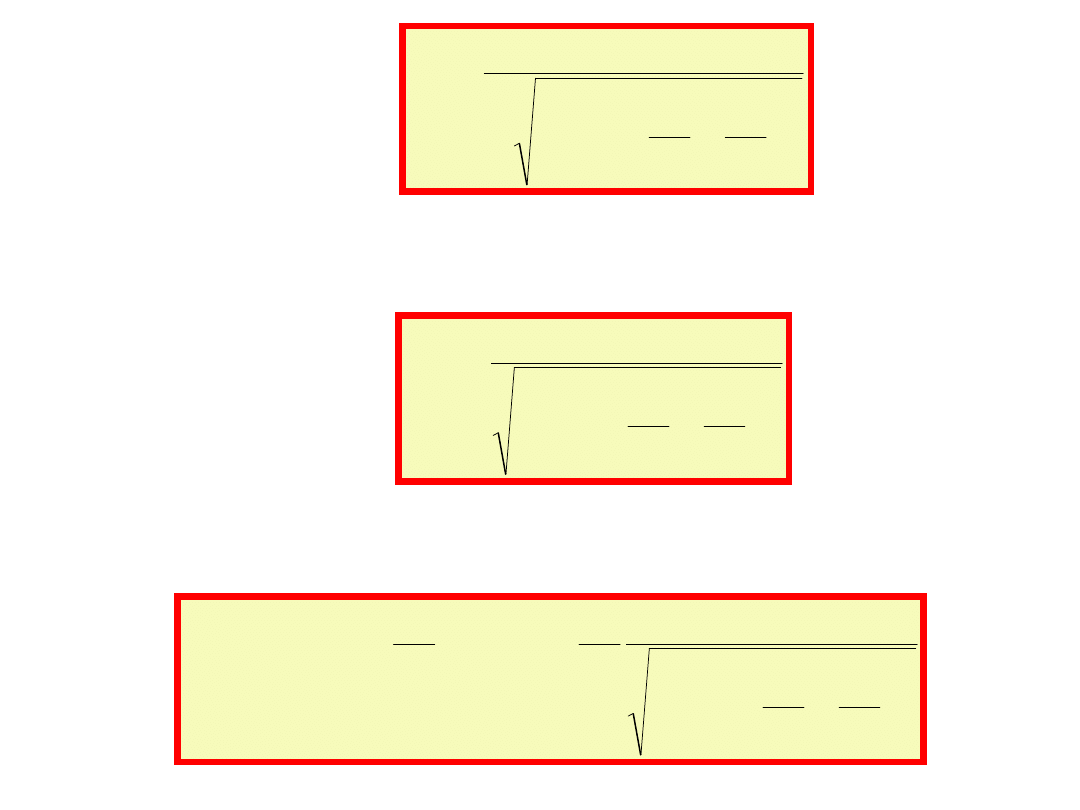
Amplituda prądu:

2

0

0

2

m

m

Q

1

R

E

I



























Amplituda spadku napięcia na rezystancji R jest:

2

0

0

2

m

R

Q

1

E

U



























Amplituda spadku napięcia na indukcyjności jest:

2

0

0

2

m

0

m

0

0

m

L

Q

1

QE

LI

LI

U











































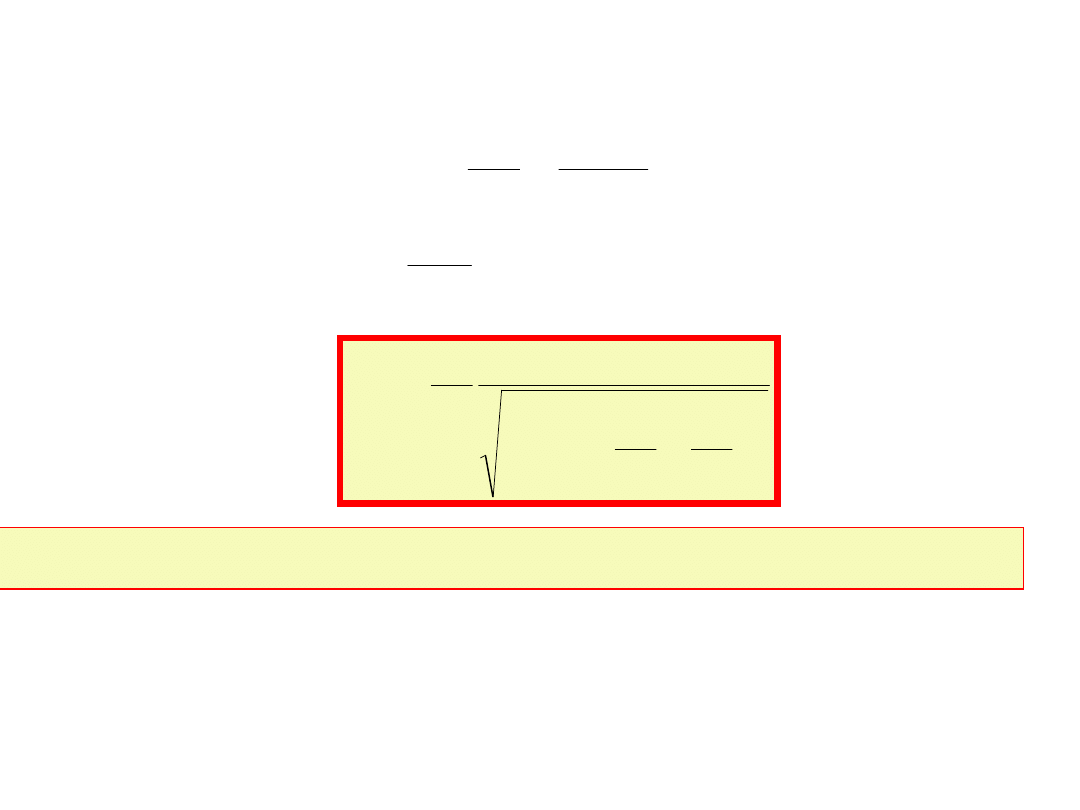
Amplituda spadku napięcia na pojemności jest:

C

I

C

I

U

0

m

0

m

C











ale z definicji:

L

C

1

0

0







i mamy:

2

0

0

2

m

0

C

Q

1

QE

U































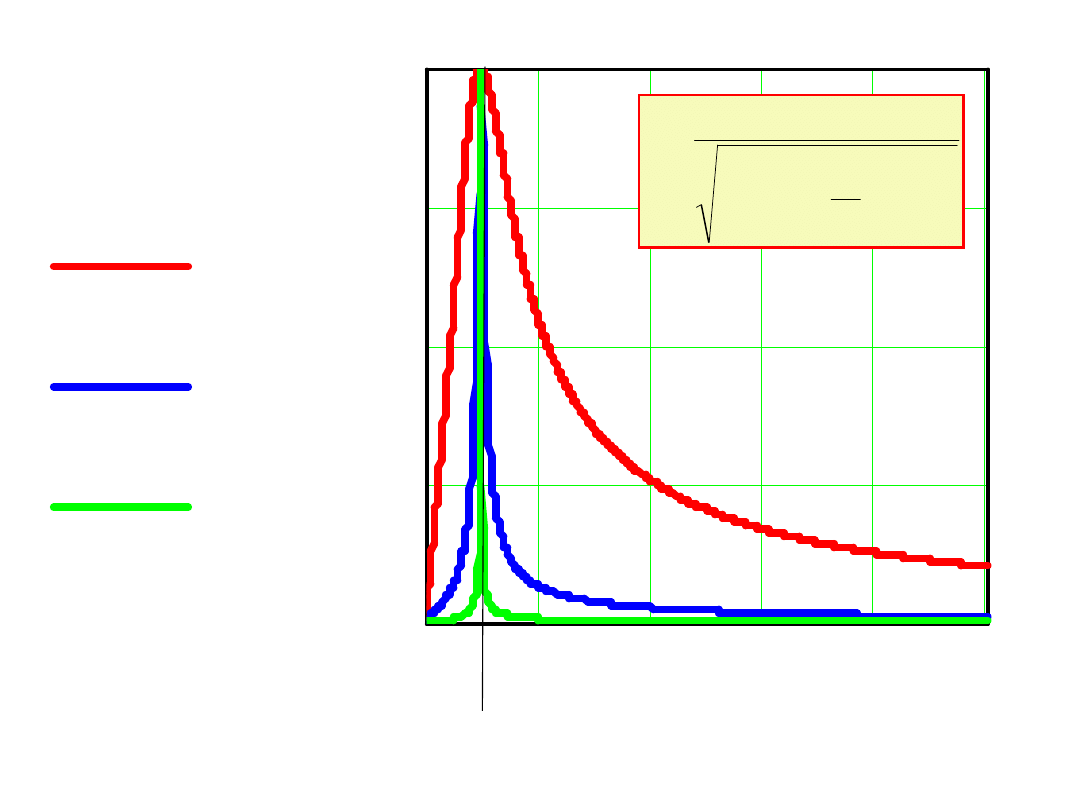
Charakterystyki częstotliwościowe obwodu

Dla otrzymania wyników ogólnych przedstawimy

amplitudę prądu I=I

m

/I

0

, gdzie I

0

=E

m

/R oraz =/

0

0

2

4

6

8 10

0

0.25

0.5

0.75

1

I  1







I  10







I  100









2

2

1

Q

1

1

I























I(,Q=1)

I(,Q=10)

I(,Q=100)



/

0

=1

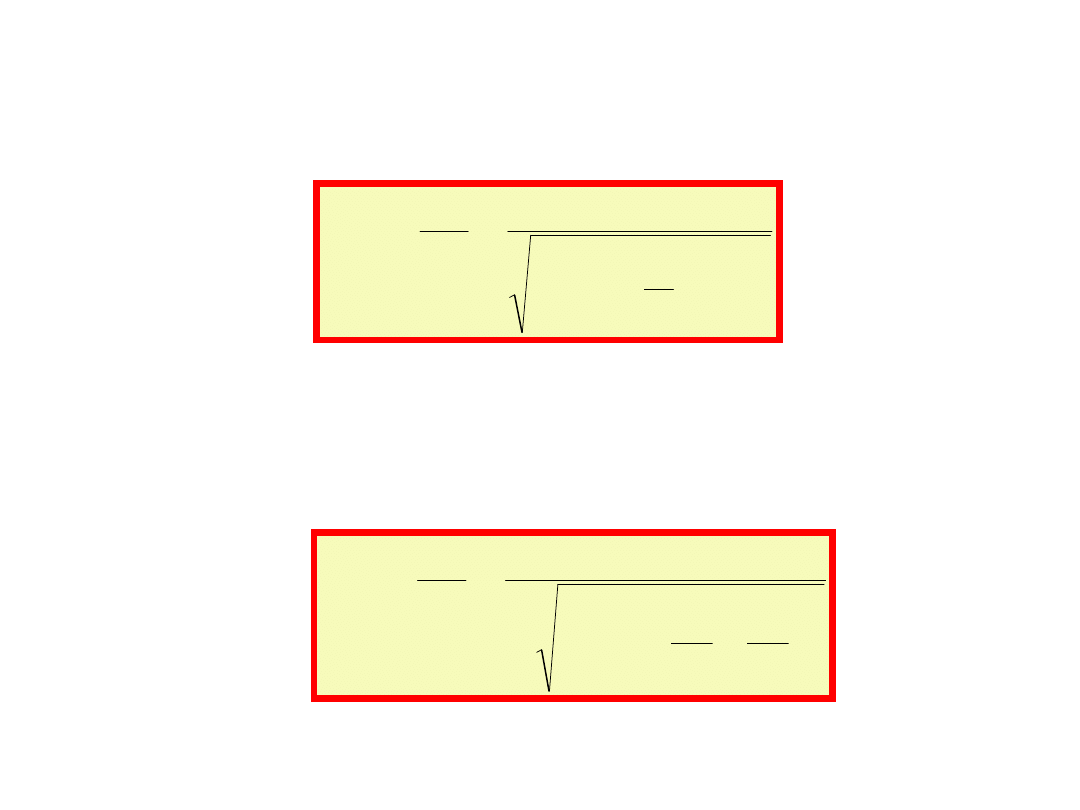
Spadek napięcia na indukcyjności w postaci
bezwymiarowej będzie:

2

2

m

L

0

L

1

Q

1

Q

E

U

U



























i podobnie spadek napięcia na pojemności w postaci
bezwymiarowej jest:

2

0

0

2

m

C

0

C

Q

1

Q

E

U

U































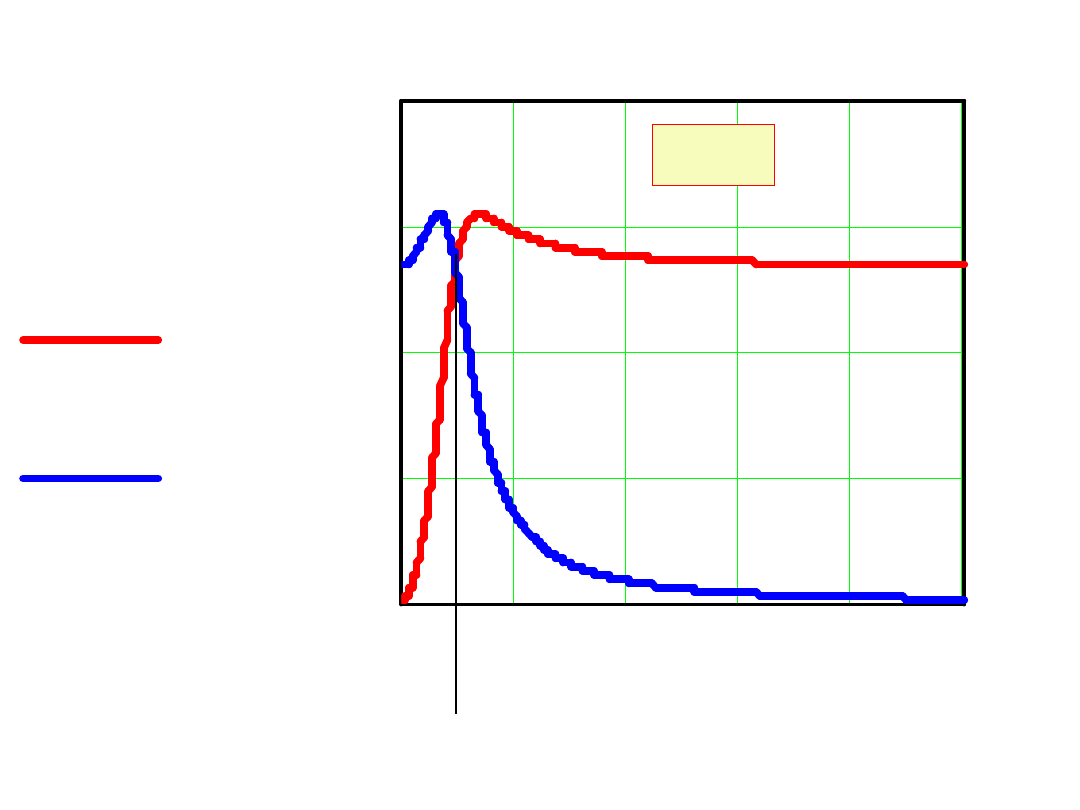
0 2 4 6 8 10

0

0.38

0.75

1.13

1.5

UL  1







UC  1









Q=1

U

L0

()

U

C0

()

=

0



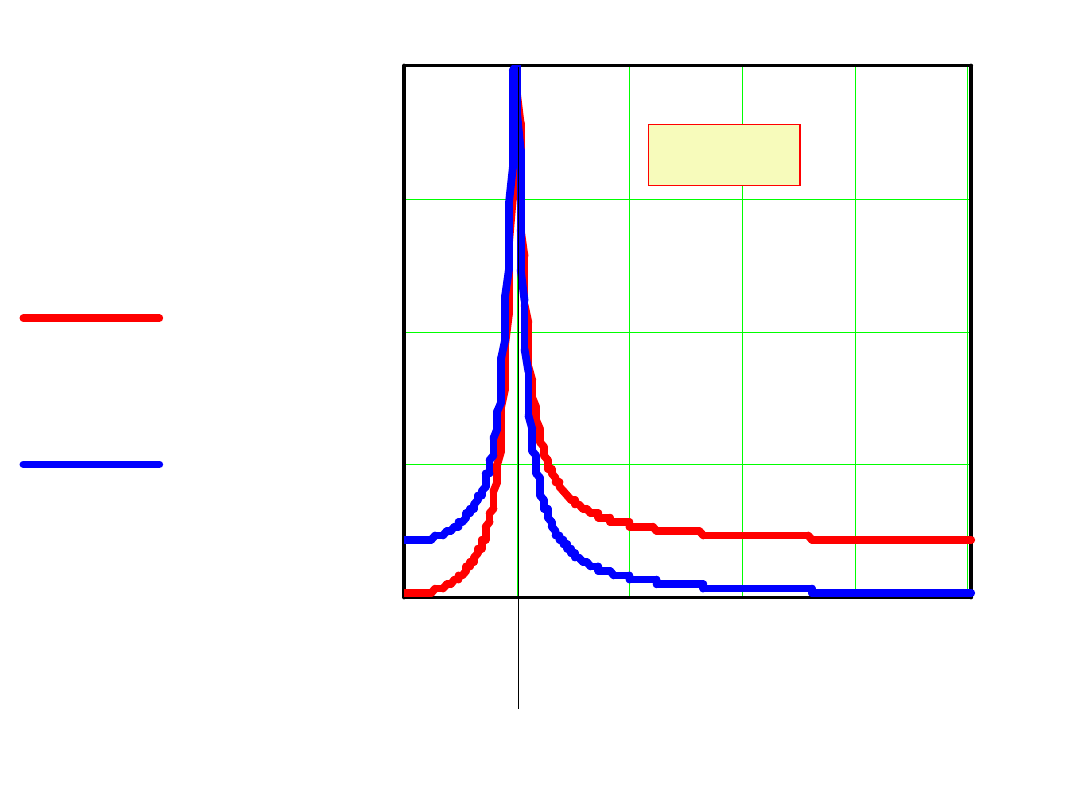
0 1 2 3 4 5

0

2.5

5

7.5

10

UL  10







UC  10









Q=10

U

L0

()

U

C0

()



=

0

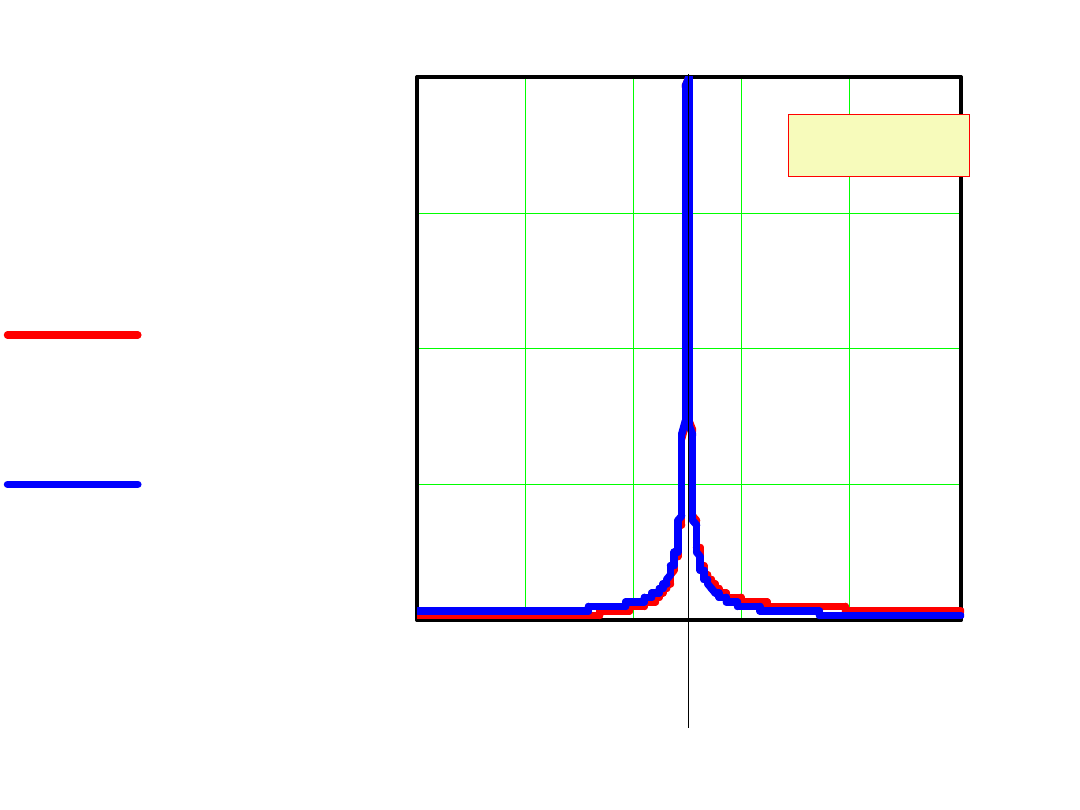
0 0.4 0.8 1.2 1.6 2

0

25

50

75

100

UL  100







UC  100









Q=100

U

L0

()

U

C0

()



=

0

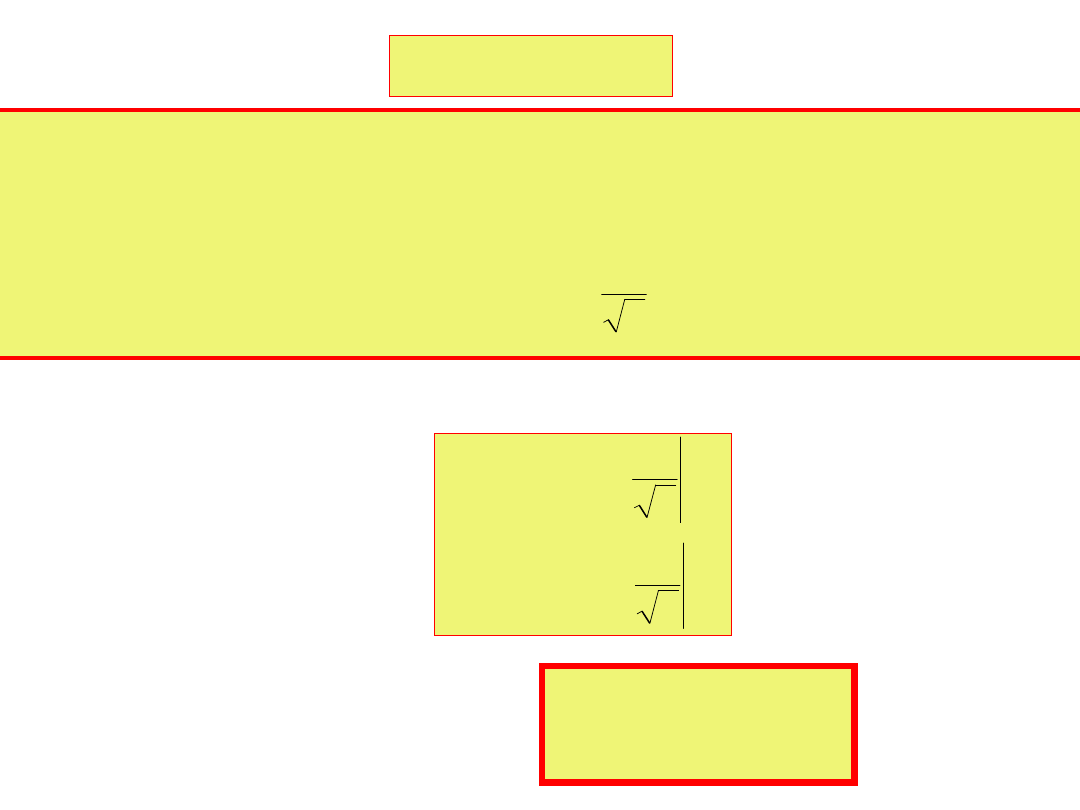
Pasmo 3dB

Jest to szerokość pasma pulsacji bądź częstotliwości

po przekroczeniu, którego amplituda sygnału spada

o 3dB bo .

Szerokość pasma określa zależność dla napięcia
na pojemności:

1

0

C

gór

1

0

C

dol

2

Q

U

2

Q

U





















i ponieważ =/

0

, to

gór

0

dol

0

gór

0

dol

0

f

f

f























01

.

3

2

1

log

20



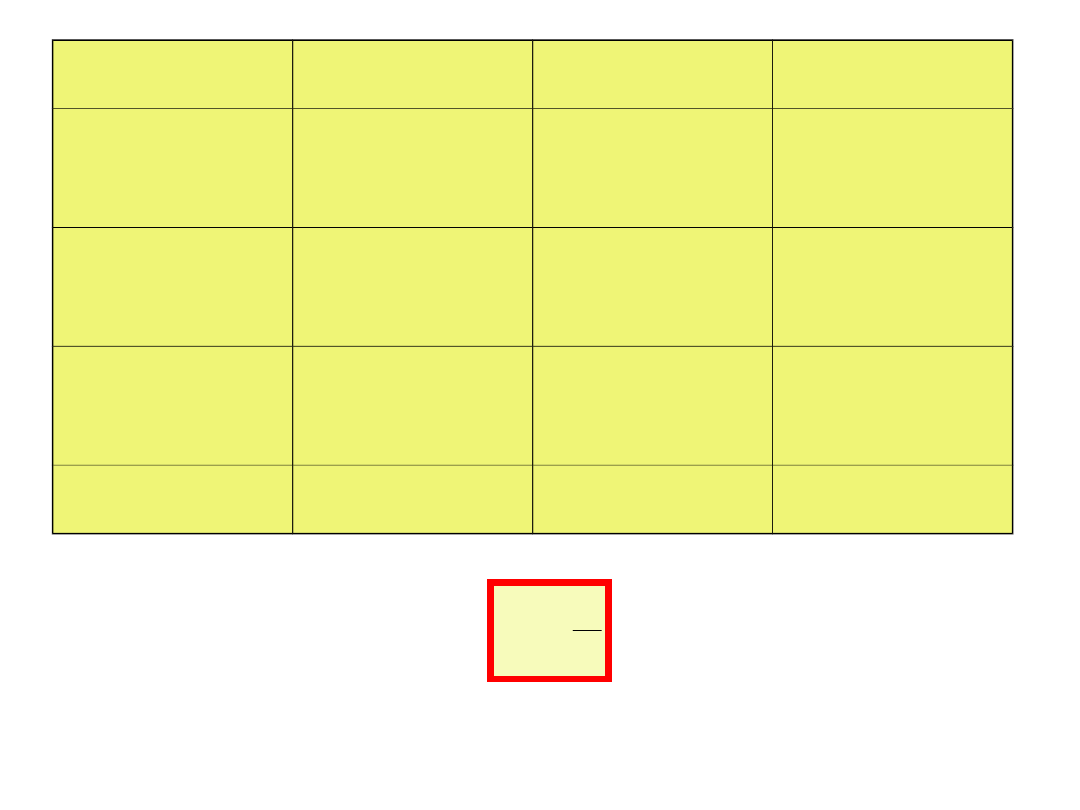
f

dol

Q

f

gór

f

0.882611

f

0

5

1.086737

f

0

0.20413f

0

0.945978

f

0

10

1.046482

f

0

0.10052f

0

0.994962

f

0

100

1.004963

f

0

0.01f

0

0.9995f

0

1000

1.0005f

0

0.001f

0

Mamy dla szerokości pasma 3dB zależność:

Q

f

f

0





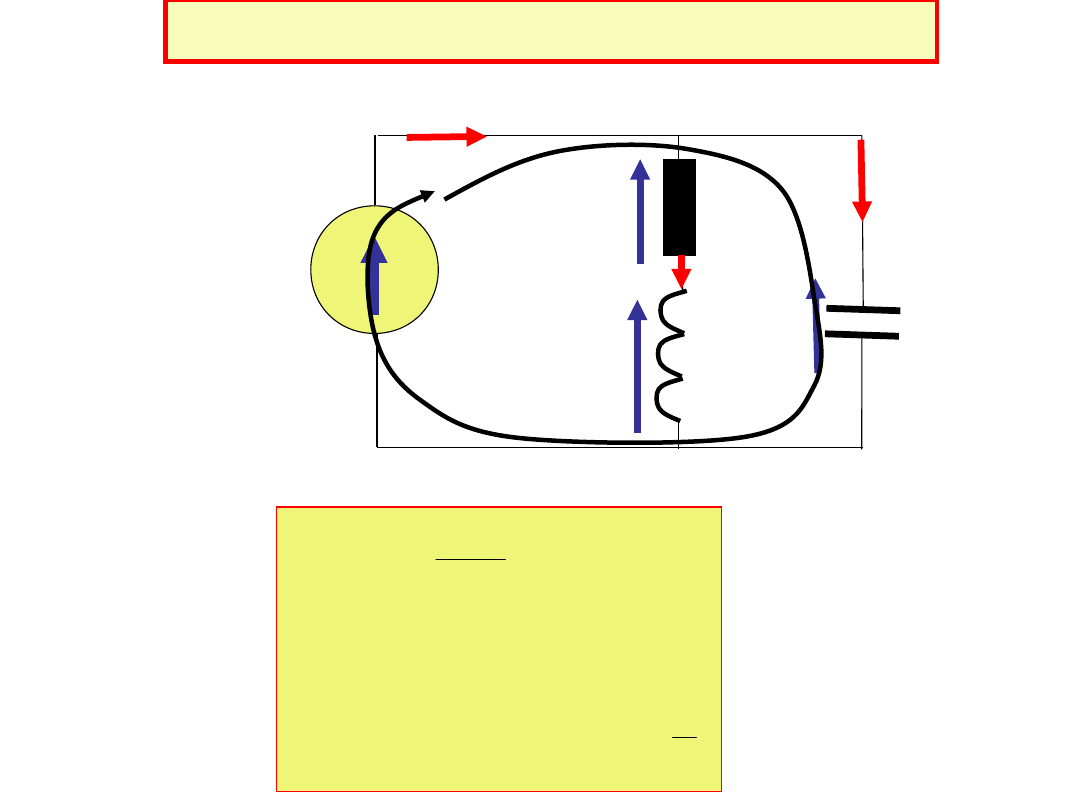
Równoległy obwód rezonansowy

e(t)=E

m

sin(t)

u

R

(t)

u

L

(t)

C

u

c

(t)

i(t)=I

m

sin(ωt+φ)

i

C

(t)

i

LR

(t)

e(t)-u

C

(t)=0 → u

C

(t)=e(t)=E

m

sin(ωt)

 
 

 

 































2

t

sin

CE

t

i

t

cos

CE

t

i

dt

du

C

t

i

m

C

m

C

C

C

 

 









 

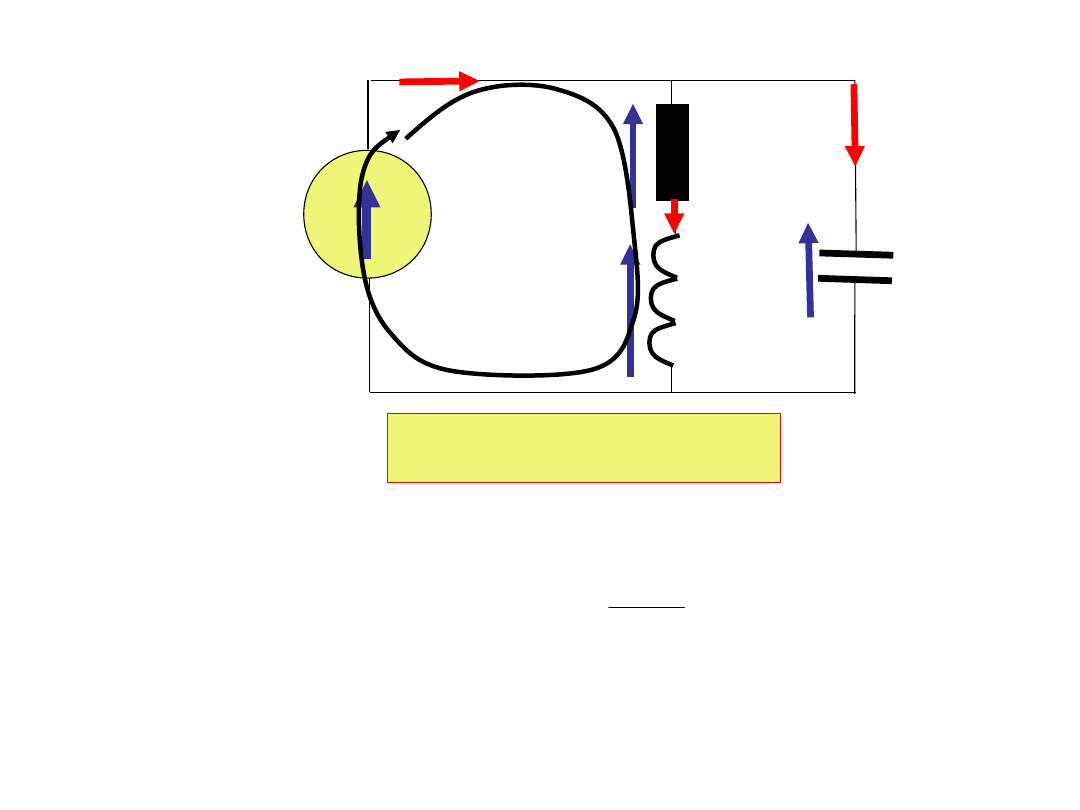
t

sin

E

t

cos

LI

t

sin

RI

t

e

dt

di

L

t

Ri

m

mL

mL

LR

LR

























e(t)=E

m

sin(t)

u

R

(t)

u

L

(t)

C

u

c

(t)

i(t)=I

m

sin(ωt+φ)

i

C

(t)

i

LR

(t)

u

R

(t)+u

L

(t)=e(t)

Przyjmując: i

LR

(t)=I

mL

sin(ωt+)

mamy:

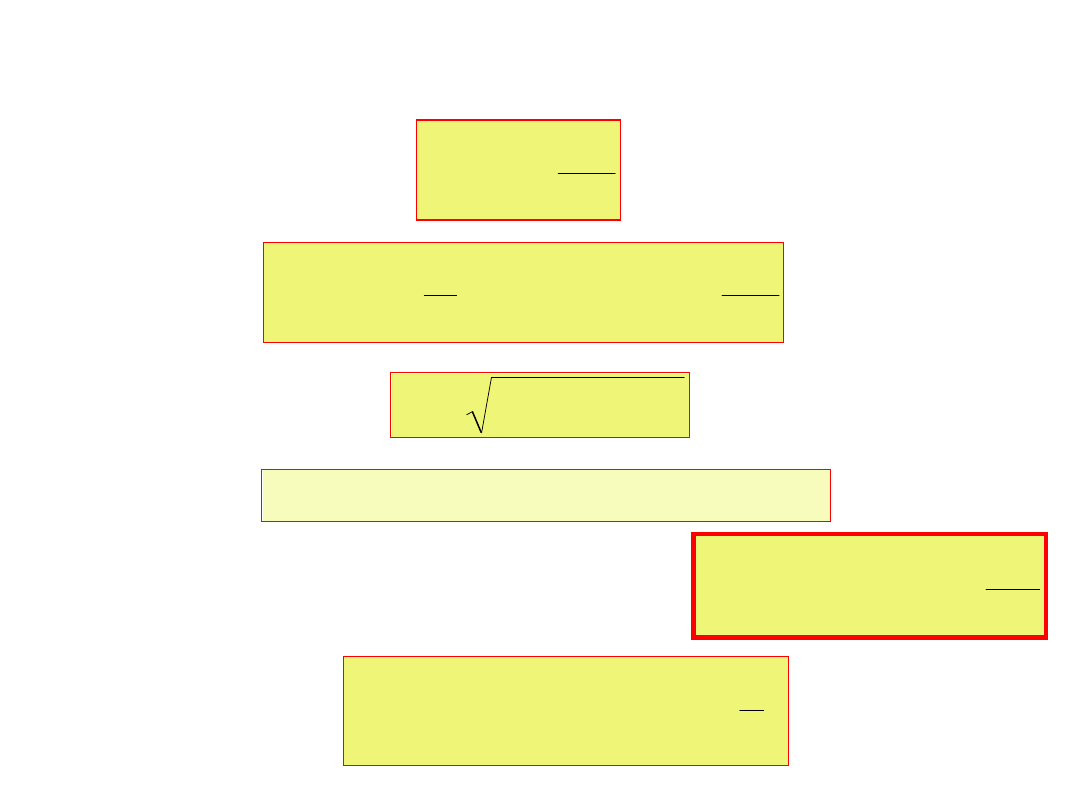
Przyjmując podobnie jak w obwodzie RL:

R

L

tg









lub

 

 

Z

L

sin

Z

R

cos













gdzie

 

2

2

L

R

Z







mamy:





 

t

sin

E

t

sin

Z

I

m

mL















Warunkiem spełnienia równości jest:

Z

E

I

i

m

mL









a więc prądy są:

 























2

t

sin

CE

t

i

m

C

 

 



































t

sin

Z

E

t

i

2

t

sin

CE

t

i

m

LR

m

C

Prąd źródła i(t) jest: i(t)=i

LR

(t)+i

C

(t)

czyli:













































t

sin

Z

E

2

t

sin

CE

t

sin

I

m

m

m





 

   

   

 

 

   









































































t

sin

Z

cos

t

cos

Z

sin

C

E

t

cos

Z

sin

t

sin

Z

cos

t

cos

C

E

t

sin

I

m

m

m

Przekształcamy tak aby otrzymać wyrażenie jak po
stronie lewej:

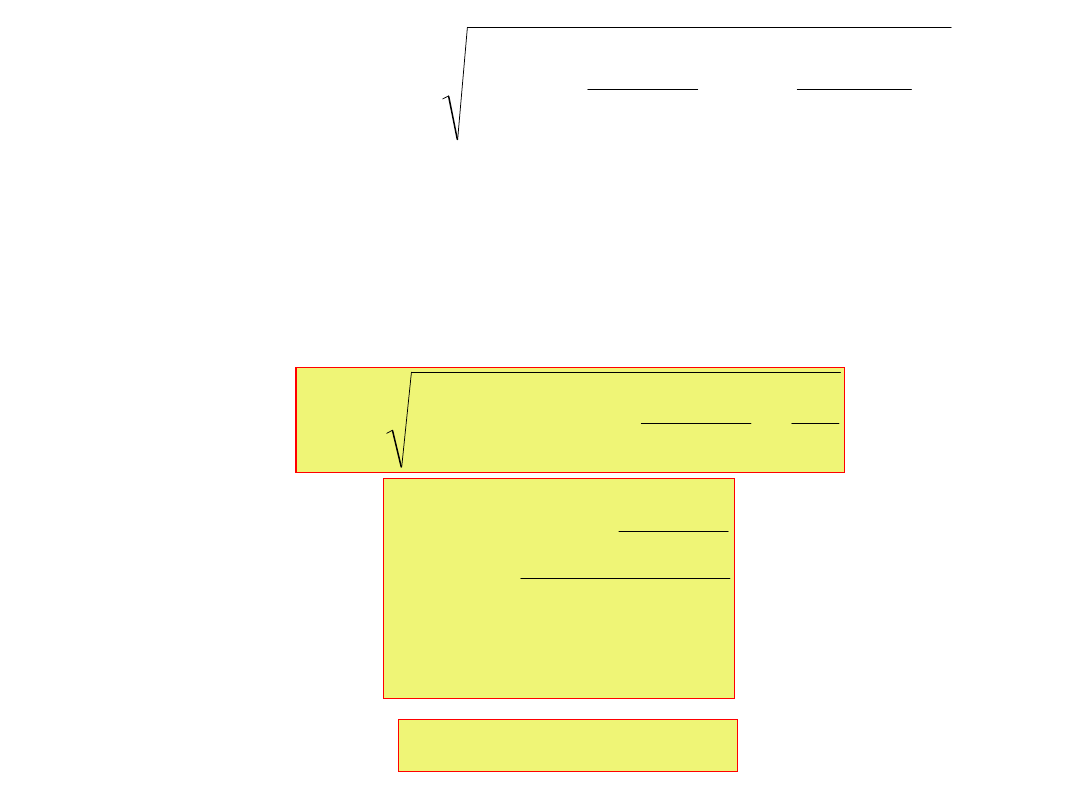
Przyjmując:

 

 

2

2

0

Z

cos

Z

sin

C

Y





































Y

0

– nazywamy modułem admitancji.

Podnosząc do kwadratu i biorąc pod uwagę, że

 

 

1

sin

cos

2

2









mamy:

 

 

2

2

0

Z

1

Z

sin

C

2

C

Y













 

 

 

0

m

m

Y

E

I

cos

Z

sin

C

tg















czyli

 













t

sin

I

t

i

m

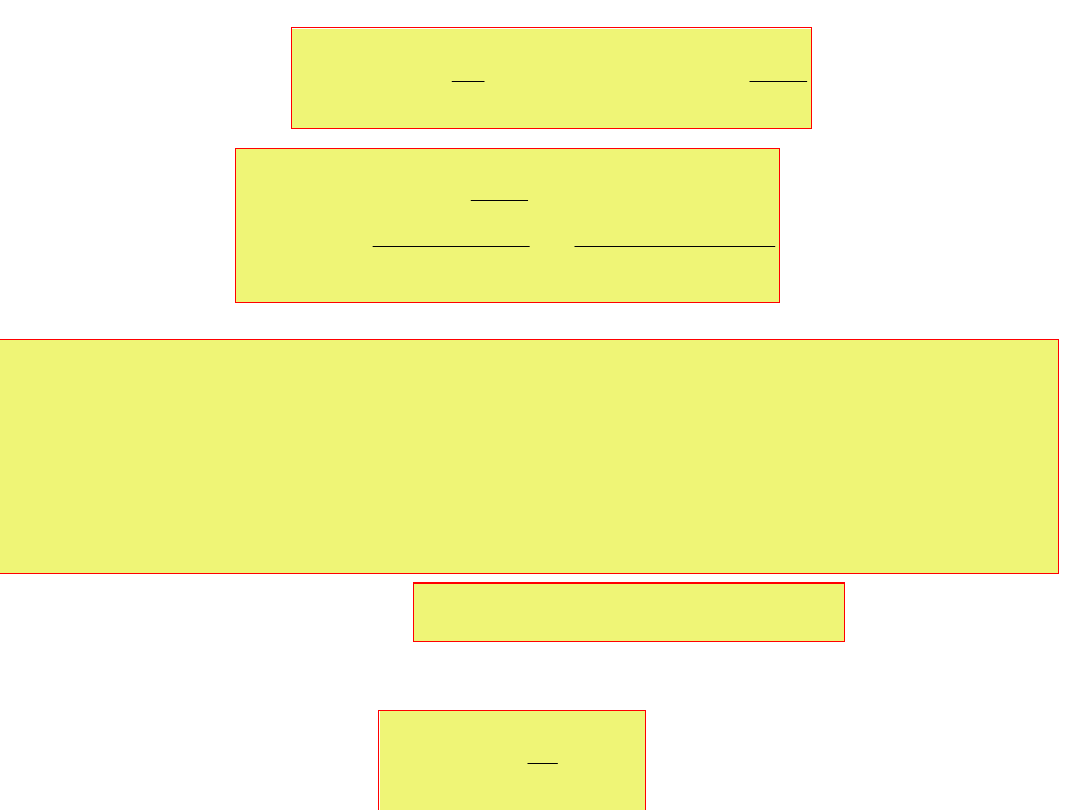
Ponieważ

 

 

Z

L

sin

Z

R

cos













więc

 

 

 























cos

Z

L

CZ

cos

Z

L

C

tg

2

2

2

Jeżeli to φ=0 i wtedy mamy:

e(t)=E

m

sin(ωt) oraz i(t)= EmY

0

sin(ωt)

oznacza to, że prąd i napięcie są w fazie.

Zjawisko takie nazywamy rezonansem.

,

0

L

CZ

2









Zbadajmy kiedy:

 





0

L

L

R

C

2

2













Pulsacja ω=0 jest nie interesująca, więc dzieląc przez ωC
mamy

 

2

2

R

C

L

L







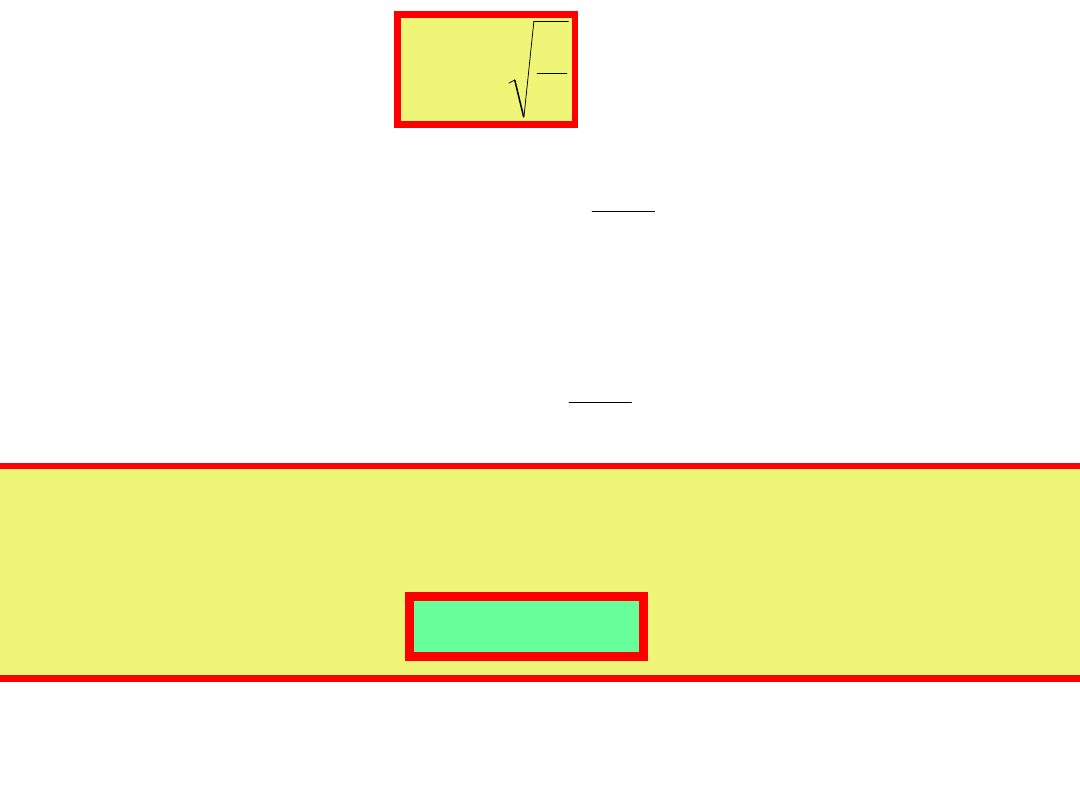
Wprowadzając:

C

L

R

kr

 - oporność krytyczna

mamy:

 



































2

kr

2
kr

2

R

R

1

R

L

Powyższe równanie jest spełnione dla rzeczywistych

wartości pulsacji ω, jeżeli: lub R<R

kr.

1

R

R

kr



Tak więc warunkiem aby w obwodzie równoległym
był możliwy rezonans jest:

kr

R

R 

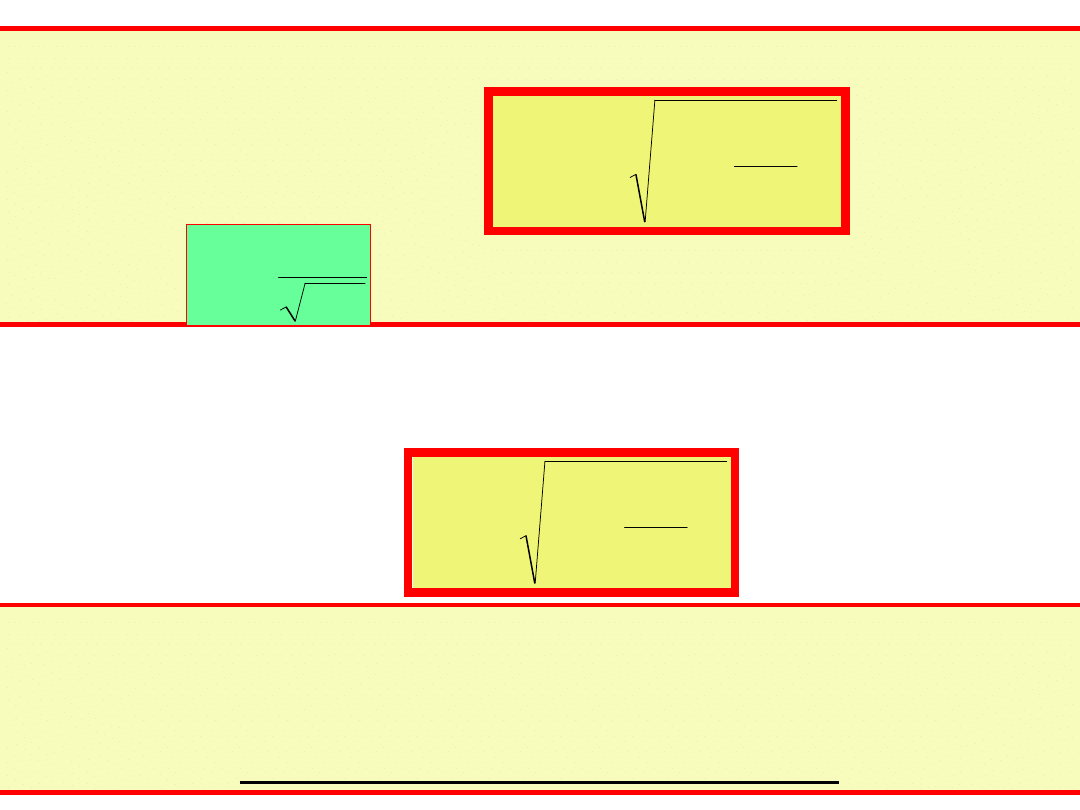
Jeżeli powyższy warunek jest spełniony, to pulsacja

rezonansowa ω

r

jest:

gdzie

2

kr

0

r

R

R

1





















LC

1

0





Częstotliwość rezonansowa f

r

=ω

r

/(2π) jest:

2

kr

0

r

R

R

1

f

f

















Ze względu na fakt, że obwód składa się z dwóch

równoległych gałęzi rezonans nazywa się skrótowo

rezonansem równoległym

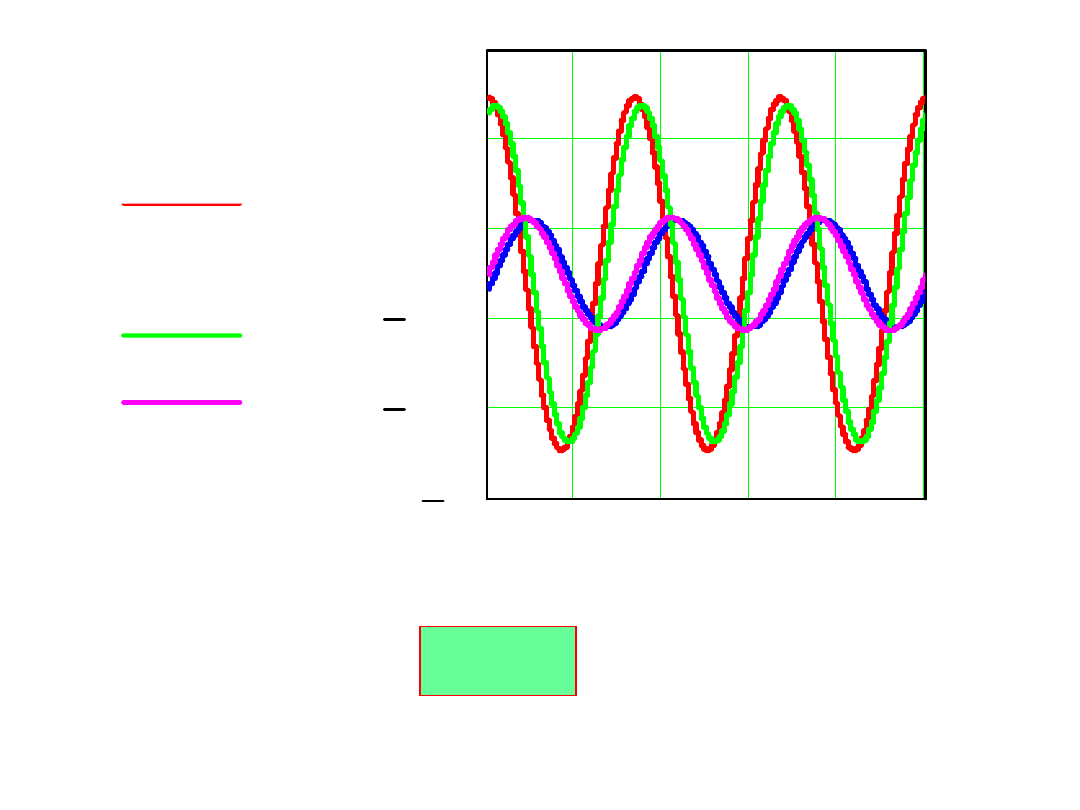
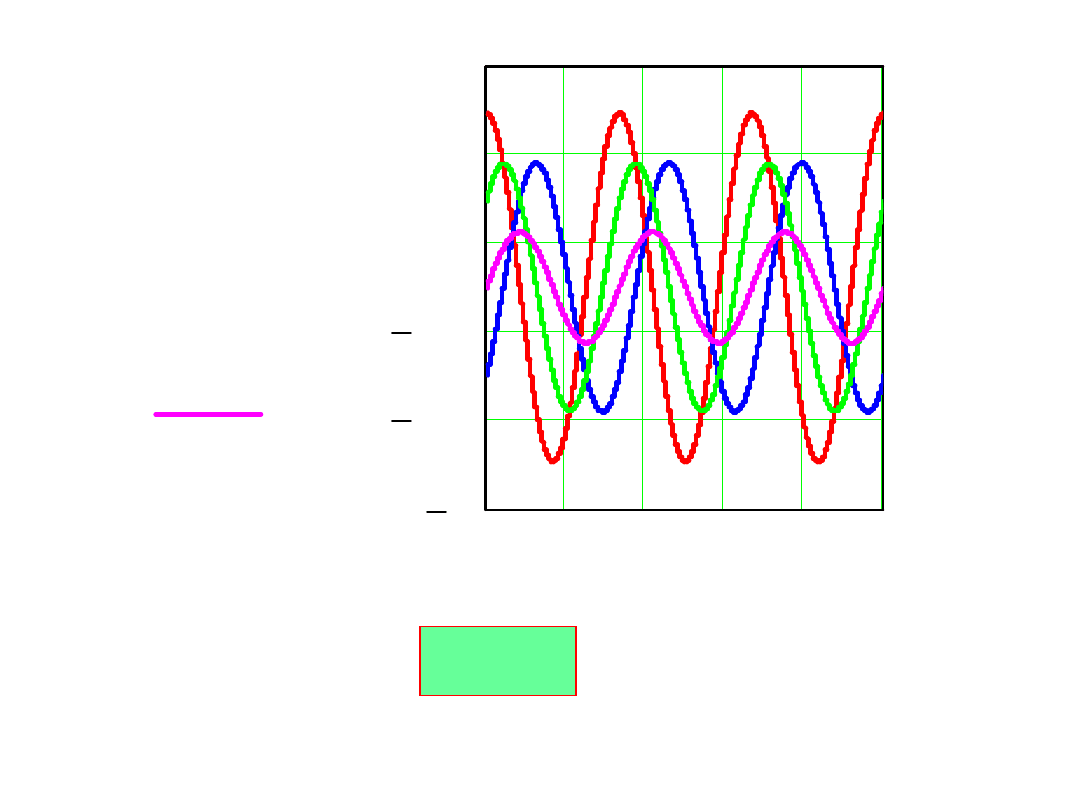
0 0.012

0.024

0.036

0.048

0.06

4

2.4

0.8

0.8

2.4

4

iC t 314



(

)

iLR t 314



(

)

i t 314



(

)

e t 314



(

)

t

R>R

kr

i

C

(t)

i

LR

(t)

i(t)

e(t)

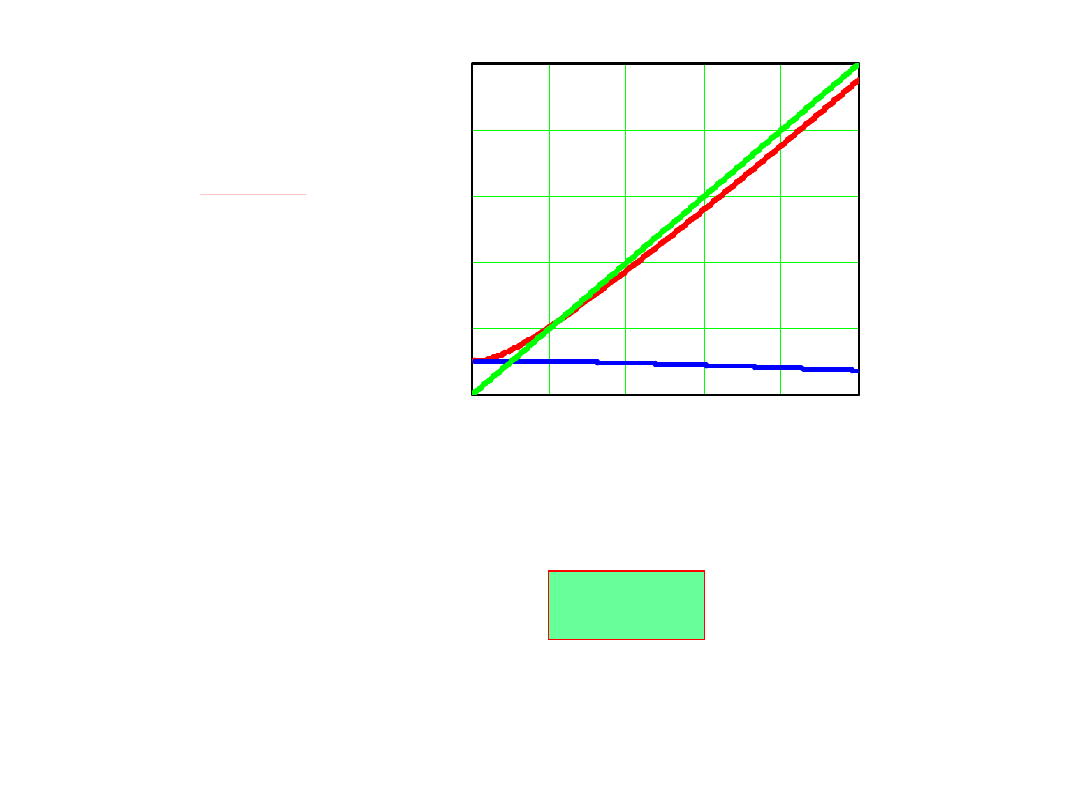
0 200400600800

1000

0

2

4

6

8

10

I0 

 

Im 

 

 C

 Em





R>R

kr

I

m0

(ω)

I

mLR

(ω)

I

mC

(ω)

0 0.012

0.024

0.036

0.048

0.06

4

2.4

0.8

0.8

2.4

4

iC t 314



(

)

iLR t 314



(

)

i t 314



(

)

e t 314



(

)

t

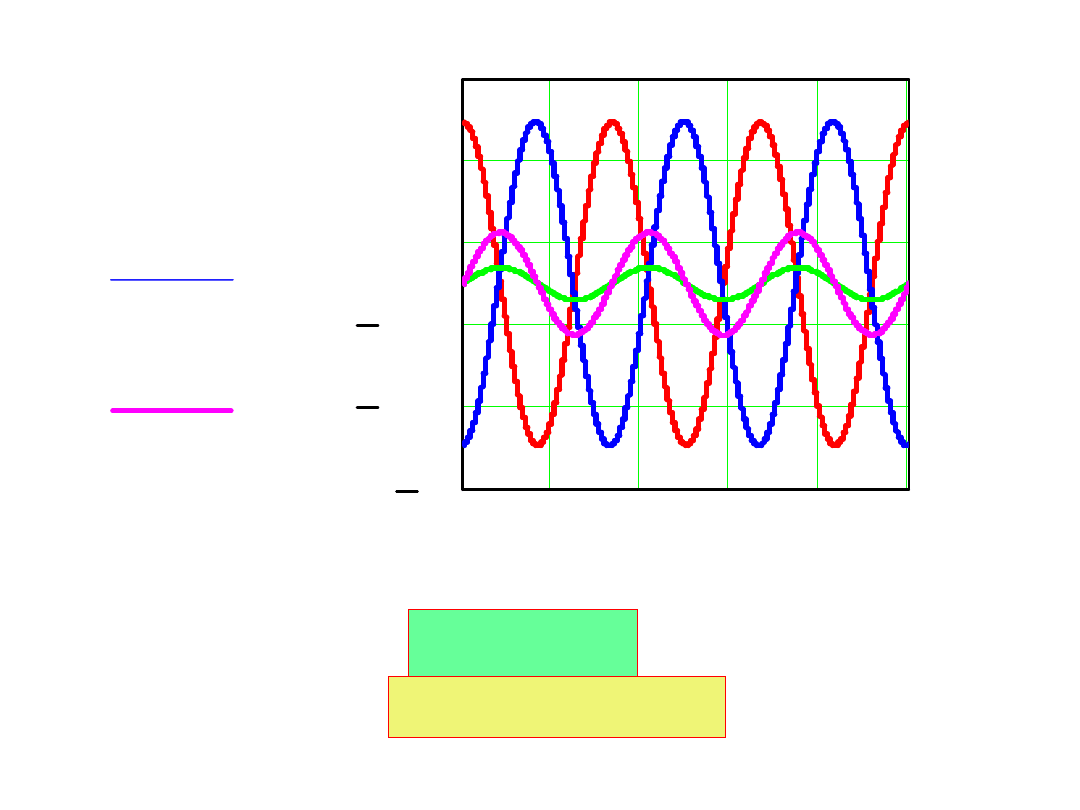
i

C

(t)

i

LR

(t)

i(t)

e(t)

R=R

kr

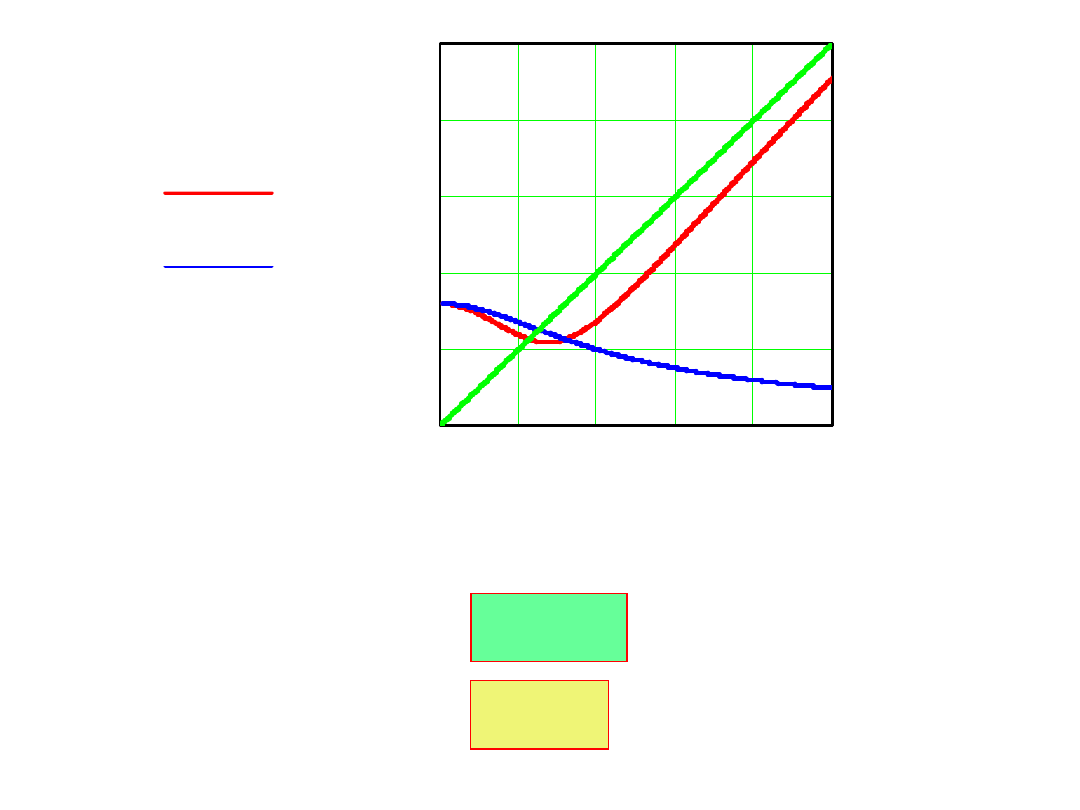
0 200400600800

1000

0

2

4

6

8

10

I0 

 

Im 

 

 C

 Em





I

m0

(ω)

I

mLR

(ω)

I

mC

(ω)

R=R

kr

ω

r

=0

0 0.012

0.024

0.036

0.048

0.06

4

2.4

0.8

0.8

2.4

4

iC t r







iLR t r







i t r







e t r







t

i

C

(t)

i

LR

(t)

i(t)

e(t)

R=0.1R

kr

ω=314.643s

-1

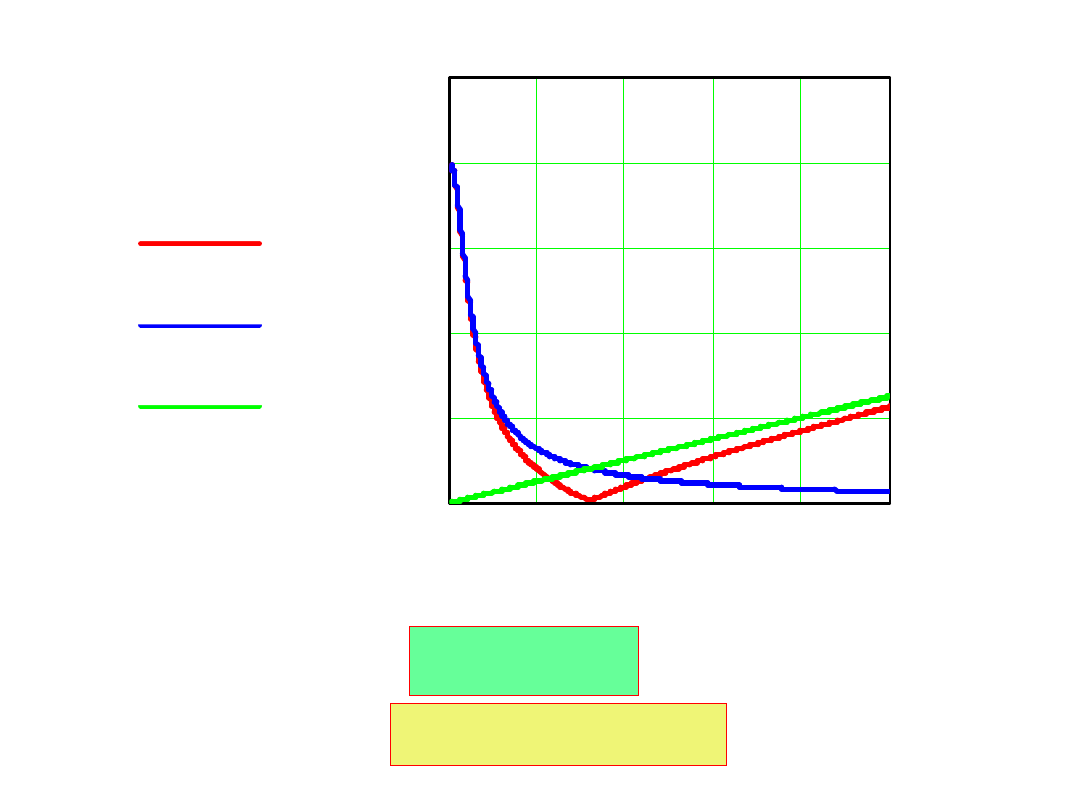
0 200400600800

1000

0

8

16

24

32

40

I0 

 

Im 

 

 C

 Em





I

m0

(ω)

I

mLR

(ω)

I

mC

(ω)

R=0.1R

kr

ω=314.643s

-1

0 0.012

0.024

0.036

0.048

0.06

4

2.4

0.8

0.8

2.4

4

iC t r







iLR t r







i t r







e t r







t

i

C

(t)

i

LR

(t)

i(t)

e(t)

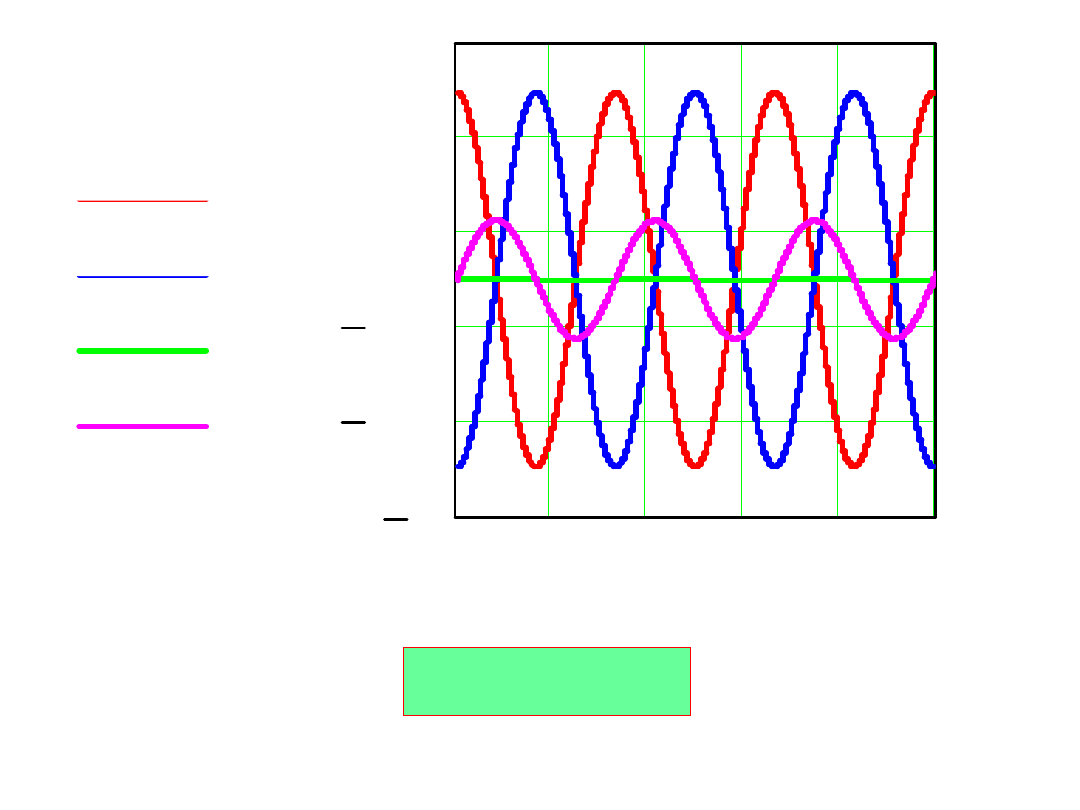
R=0.001R

kr

Dobroć jest zdefiniowana:

R

L

Q

r





Podstawiając:

2

kr

0

r

R

R

1





















mamy:

1

R

R

Q

2

kr

















Jeżeli R

kr

>>1, to i ω

r

=ω

0

.

R

R

Q

kr

