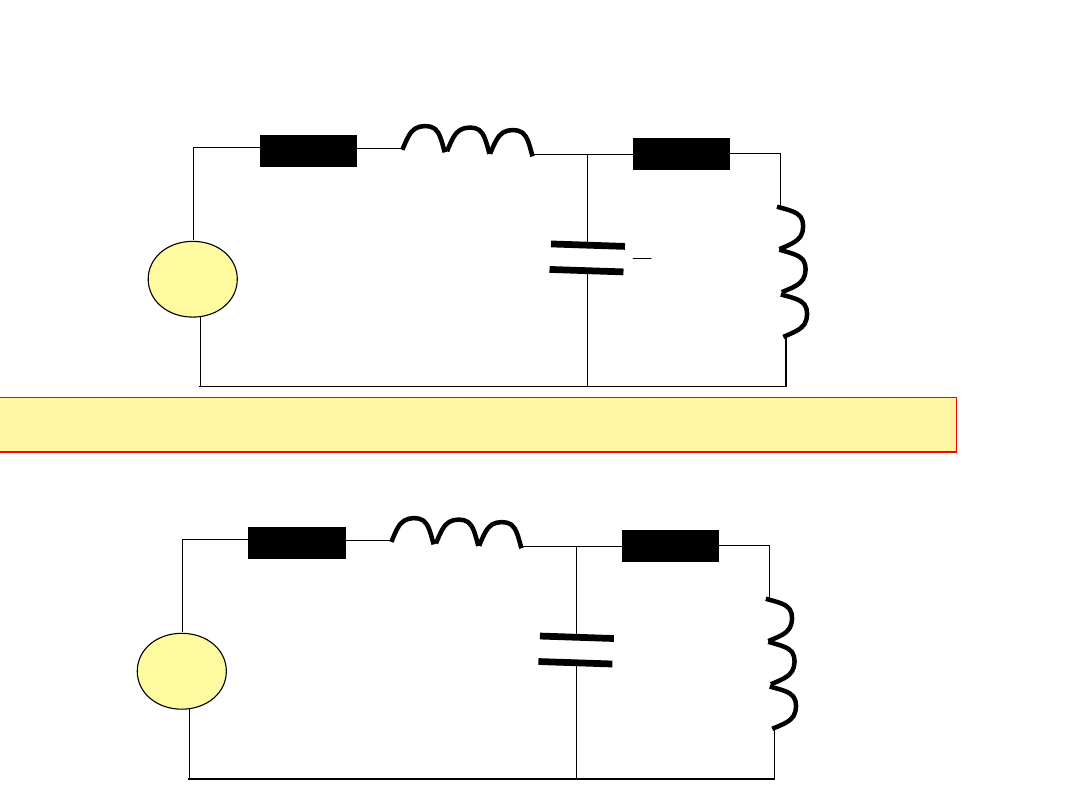
Obliczenia zostaną wykonane dla a =10, b =5

Zadanie: Obliczyć rozpływ prądów w obwodzie i przeprowadzić
bilans mocy:

~

230V, 50Hz

a[Ω]

b[mH]

5b[Ω]

10a[mH]

 

mF

a

1

~

230V, 50Hz

10Ω

5mH

25Ω

100mH

mF

1

.

0

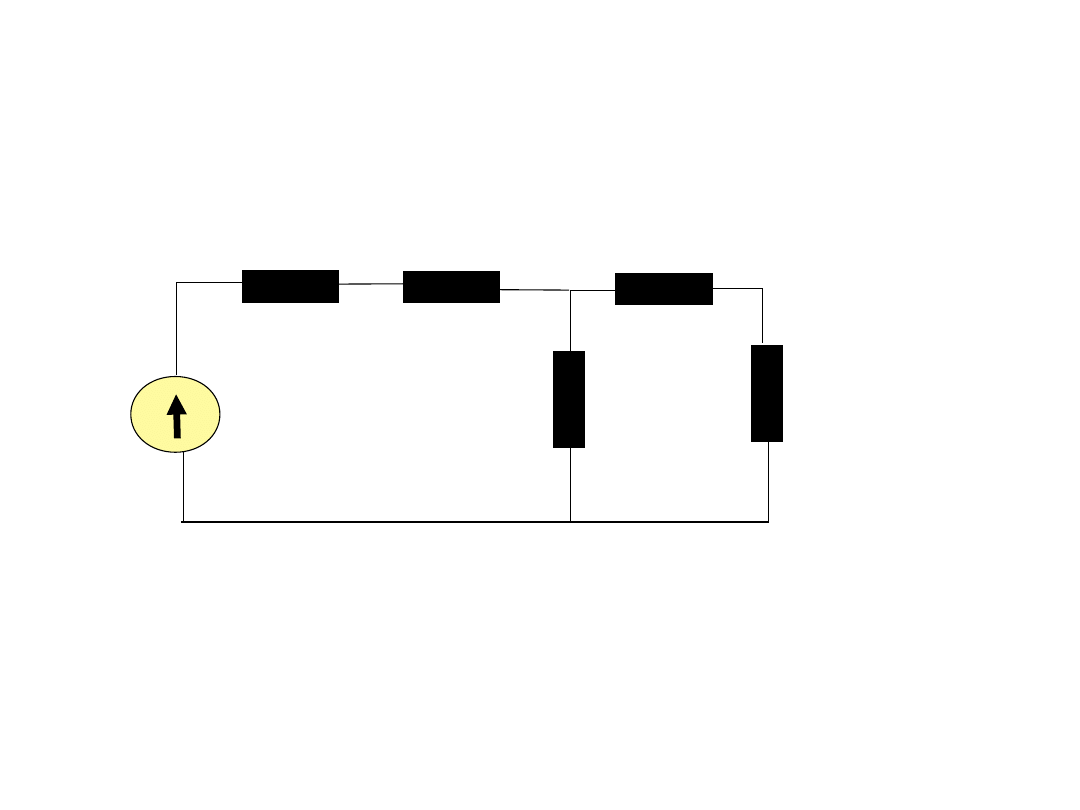
Schemat obwodu dla amplitud zespolonych f=50Hz → ω=314s

-1

.

Wszystkie wielkości w omach.

230V

10

j1.57

25

j31.4

85

.

31

j



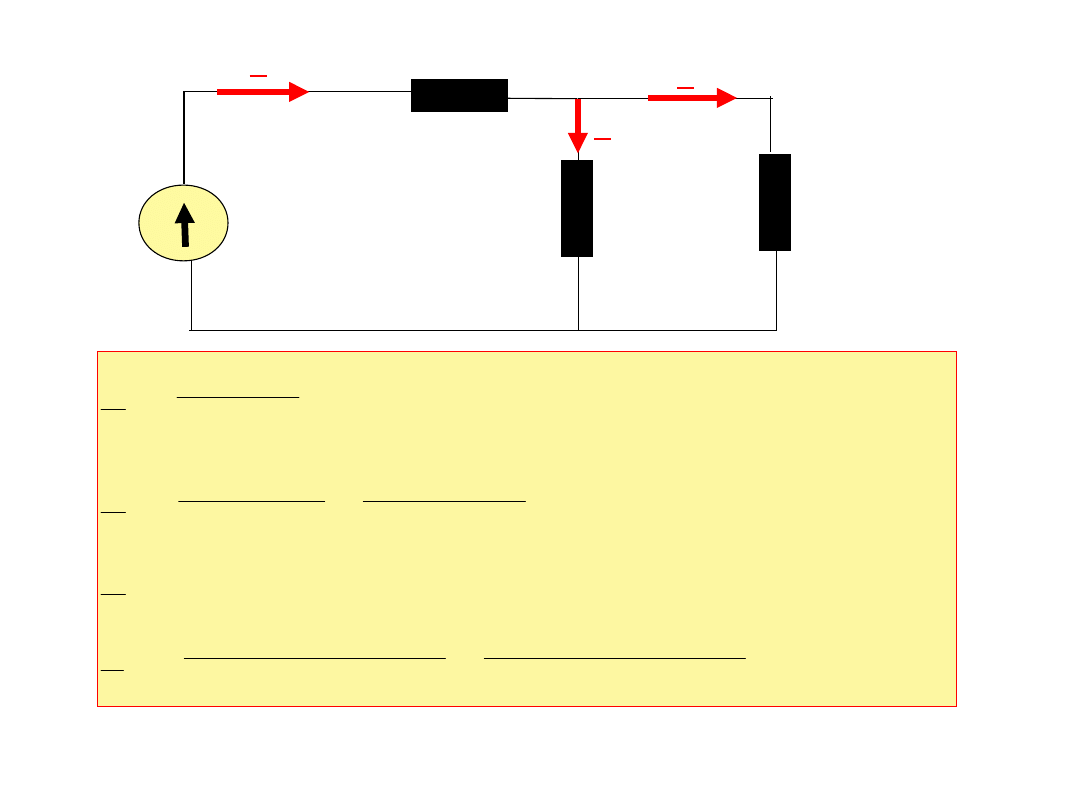
230V

10+j1.57

25+j31.4

85

.

31

j



lub

I

I

1

I

2





2

.

31

j

5

.

40

10

428

.

1

4

.

2

01195

.

0

j

0155

.

0

01195

.

0

j

0155

.

0

1

Z

01195

.

0

j

0155

.

0

Y

01945

.

0

j

0155

.

0

4

.

31

25

4

.

31

j

25

4

.

31

j

25

1

Y

0314

.

0

j

85

.

31

j

1

Y

4

12

12

2

2

2

1











































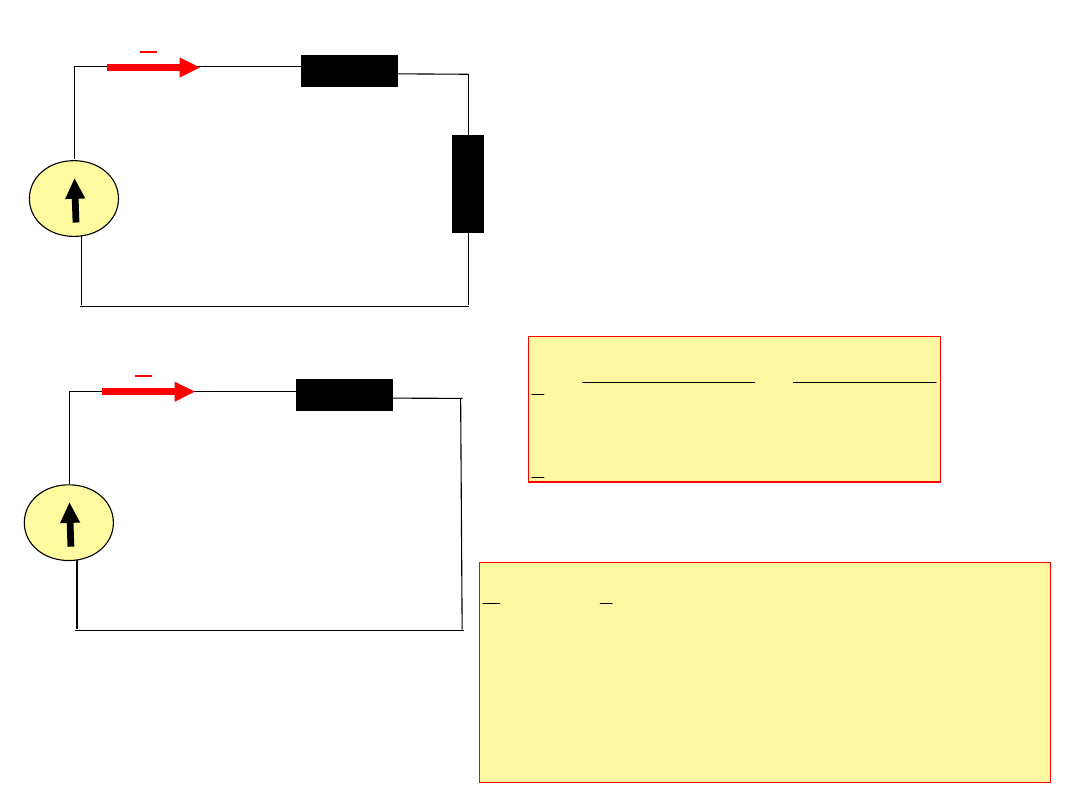
230V

10+j1.57

2

.

31

j

5

.

40 

I

230V

50.5-j29.6

I

62

.

329

j

62

.

329

j

e

93

.

3

I

e

5

.

58

230

6

.

29

j

5

.

50

230

I











Moc dostarczana do obwodu:

kVAr

457

.

0

62

.

9

2

3

sin

0.904

Q

;

kW

78

.

0

62

.

9

2

3

cos

0.904

P

;

kVA

904

.

0

S

e

904

e

93

.

3

230

I

E

S

0

dost

0

dost

dost

62

.

329

j

62

.

329

j

dost

























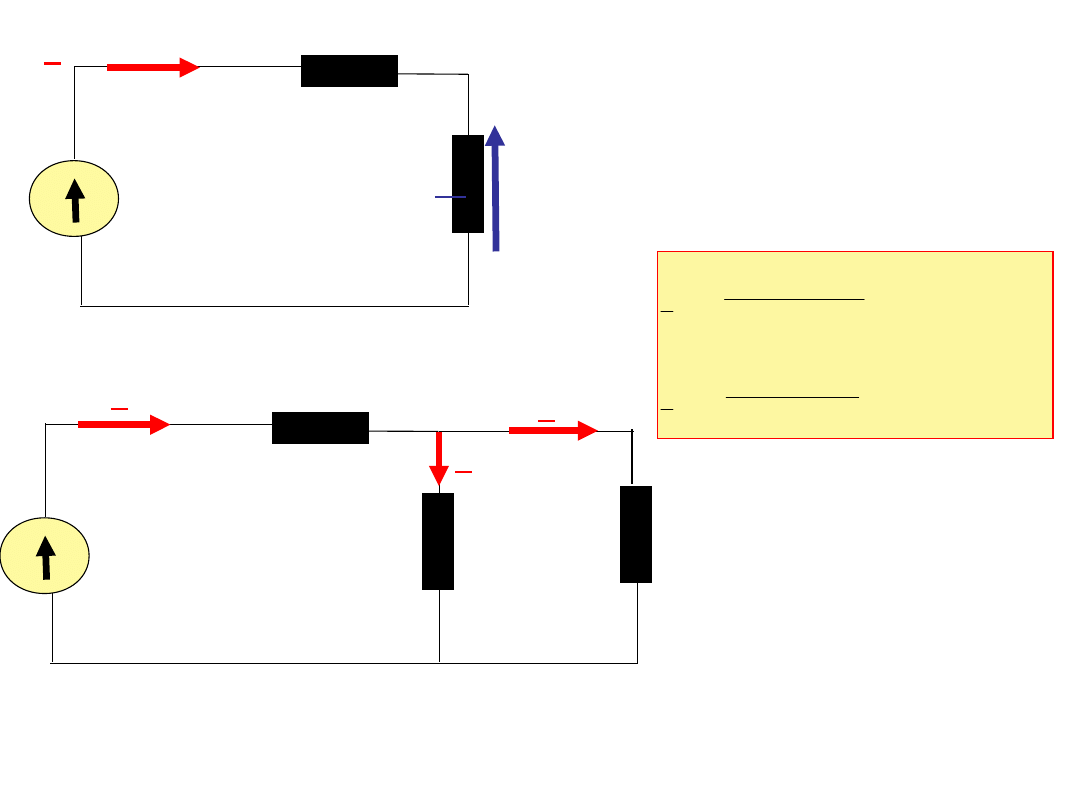
230V

I=3.93e

-j329.62

10+j1.57

51.1e

j32239

U

12

=51.1e

j322.39

·3.93e

-j329.62

=201e

-j7.23

230V

10+j1.57

40.1e

j51.47

85

.

31

j



I

I

1

I

2

7

.

58

j

47

.

51

j

23

.

7

j

2

23

.

277

j

270

j

23

.

7

j

1

e

01

.

5

e

1

.

40

e

201

I

e

31

.

6

e

85

.

31

e

201

I

















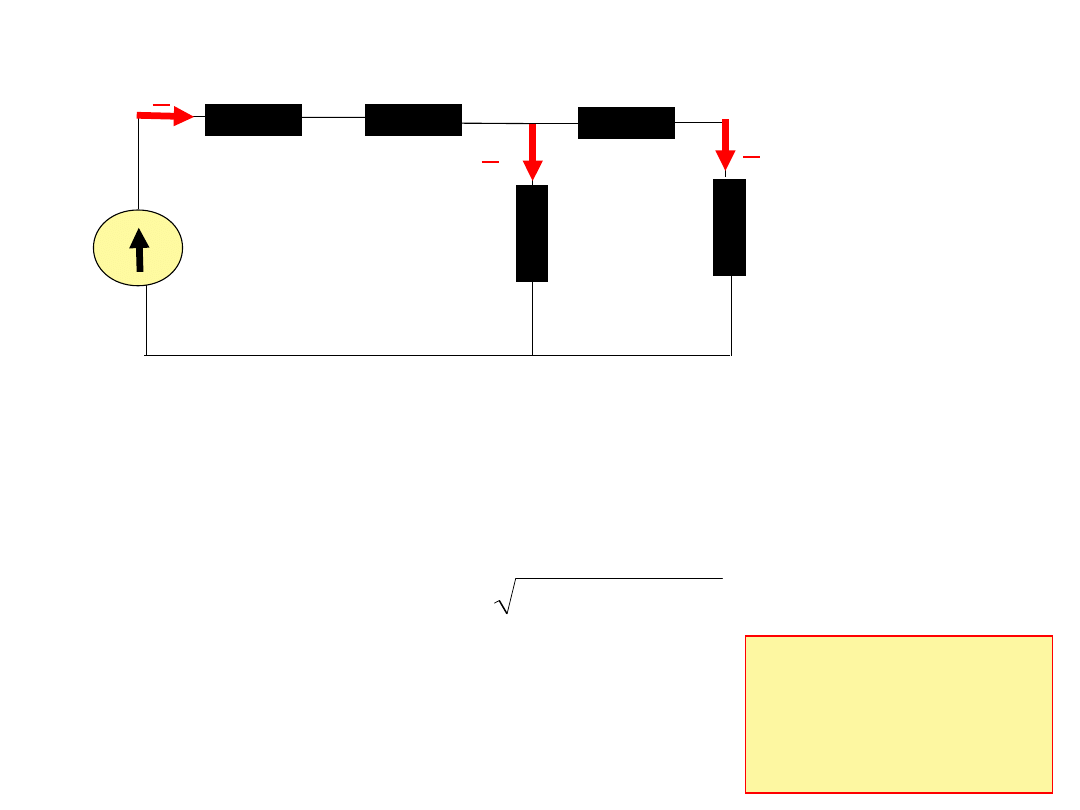
230V

10

j1.57

25

j31.4

85

.

31

j



I

I

1

I

2

Moc czynna pobrana w obwodzie P=10·3.93

2

+25·5.01

2

=0.78kW

Moc bierna pobrana w obwodzie
Q=1.57·3.93

2

+31.4·5.01

2

-31.85·6.31

2

=-0.456kVAr

Moc pozorna pobrana:

kVA

904

.

0

S

456

.

0

78

.

0

S

2

2







kVAr

457

.

0

Q

;

kW

78

.

0

P

;

kVA

904

.

0

S

dost

dost

dost







Z

R

Z

S

Z

T

I

R

I

S

I

T

Po obciążeniu każdej fazy impedancją odpowiednio:

R – Z

R

, S – Z

S

, T – Z

T

i jeżeli impedancje poszczególnych faz są jednakowe, czyli:

Z

R

=Z

S

=Z

T

=Z

to w poszczególnych fazach popłyną prądy o jednakowych

amplitudach I

m

opisane zależnością:

 





 





 

































o

m

T

o

m

S

m

R

240

t

sin

I

t

i

120

t

sin

I

t

i

t

sin

I

t

i

Jeżeli obciążenie we wszystkich fazach jest jednakowe, to mówimy

o obciążeniu symetrycznym.

Jeżeli napięcia zasilające są symetryczne i obciążenia są

symetryczne, to taki układ nazywamy układem trójfazowym

symetrycznym.

W układzie trójfazowym symetrycznym wystarczy wykonać
obliczenia dla jednej fazy R. Prądy i napięcia w pozostałych
dwóch fazach mają identyczne amplitudy i przesunięcia fazowe,
jak w fazie pierwszej, a jedynie należy je dodatkowo przesunąć
o 120

0

i 240

0

odpowiednio dla fazy S i T.

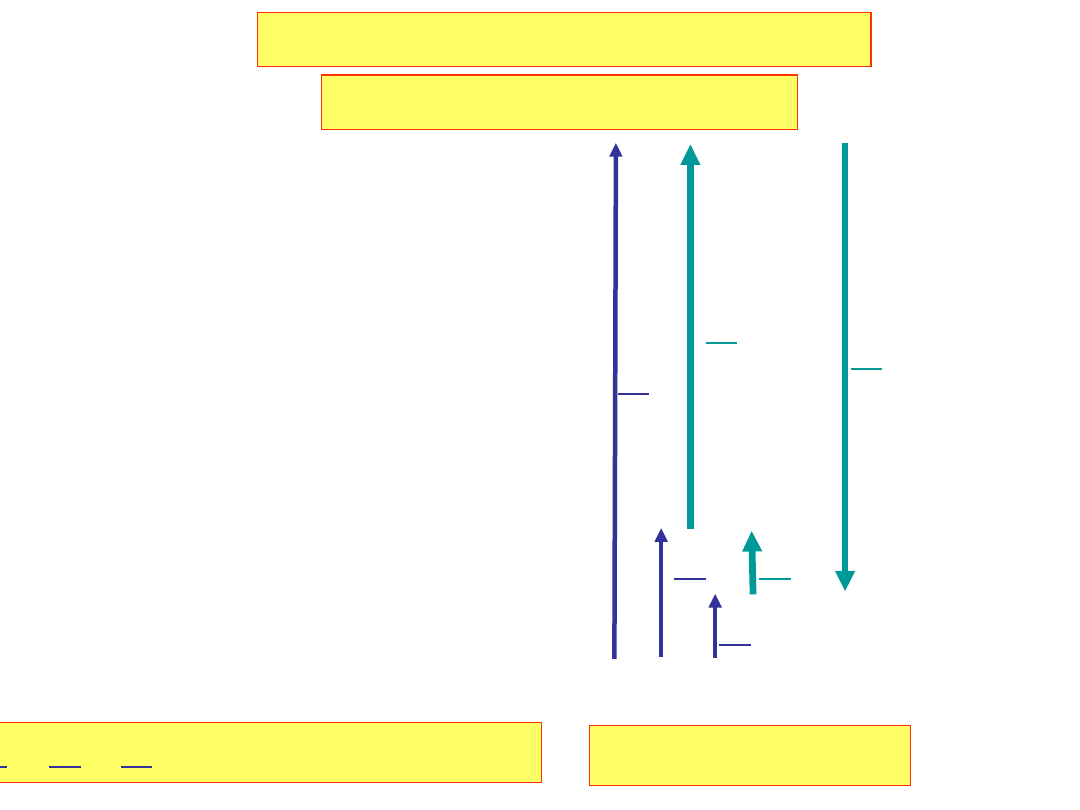
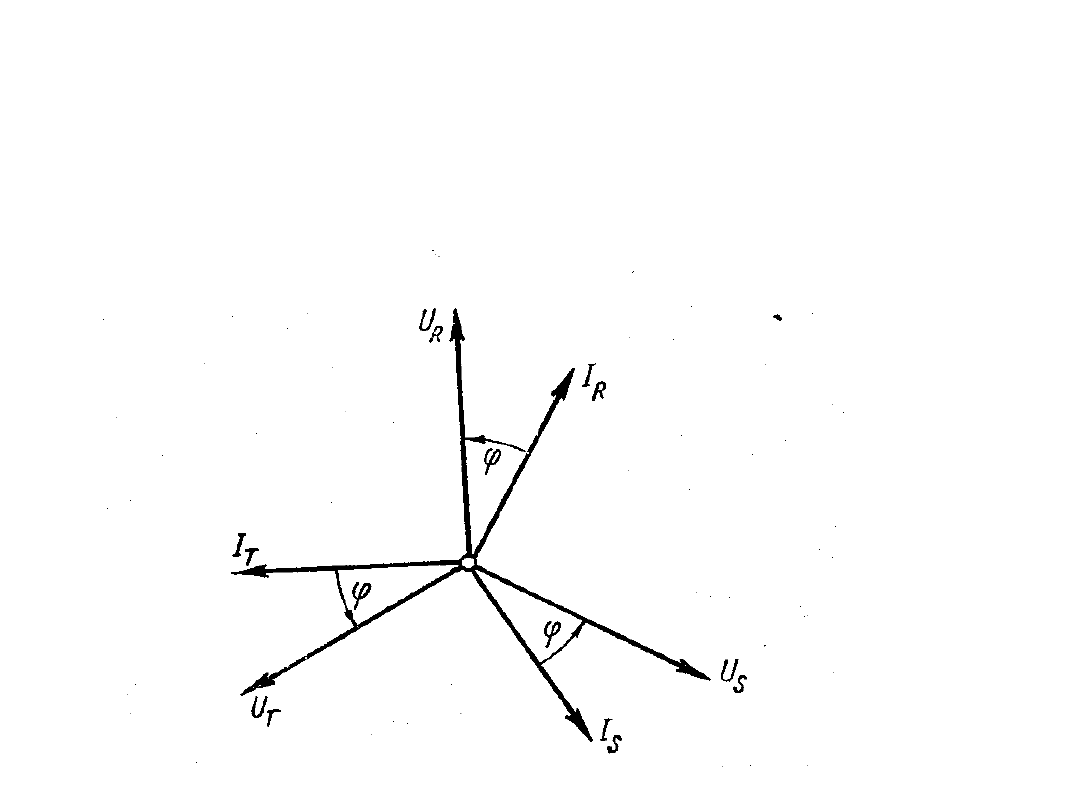
Układy trójfazowe skojarzone

U

R

U

S

U

T

U

R

, U

S

, U

T

– napięcia fazowe

U

RS

U

ST

U

TR

U

R

= U

S

= U

R

=U

f

Skojarzenie w gwiazdę

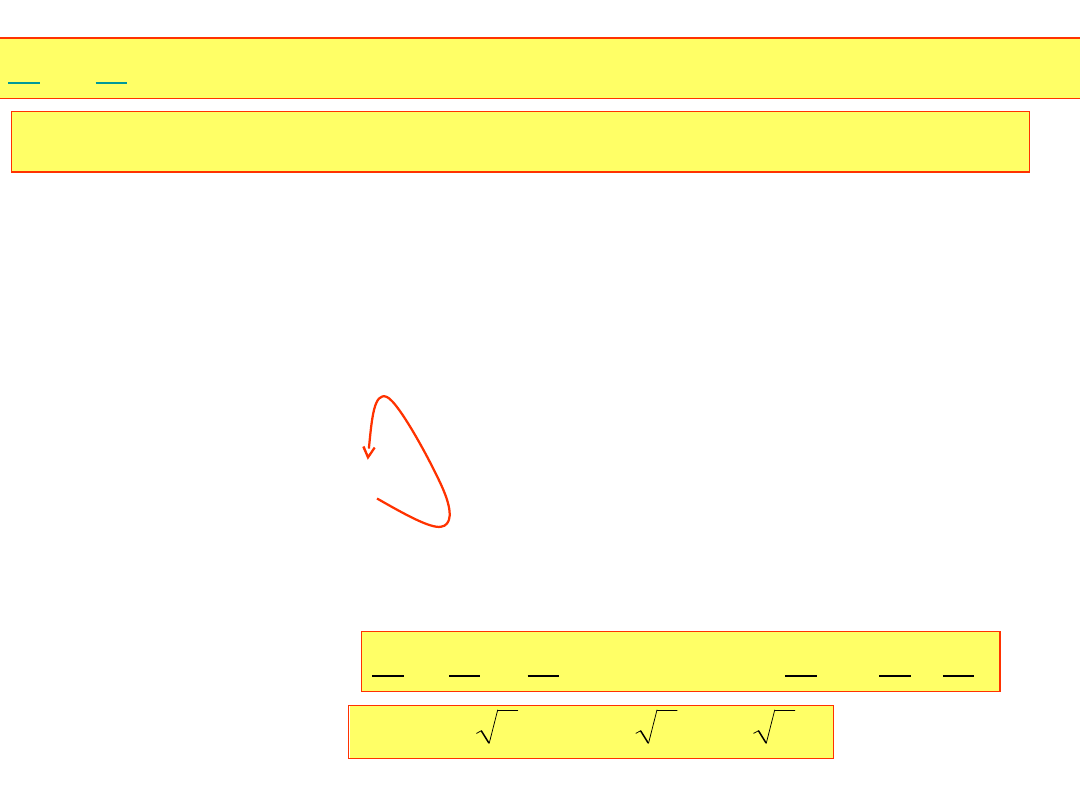
U

RS

, U

ST

, U

RT

– napięcia przewodowe lub międzyprzewodowe

W układzie symetrycznym: U

RS

=U

ST

=U

TR

=U lub U

p

U

S

+U

RS

-U

R

=0 czyli U

RS

=U

R

-U

S

i mamy z trójkąta:

f

f

f

p

U

3

U

3

5

.

0

U

3

5

.

0

U







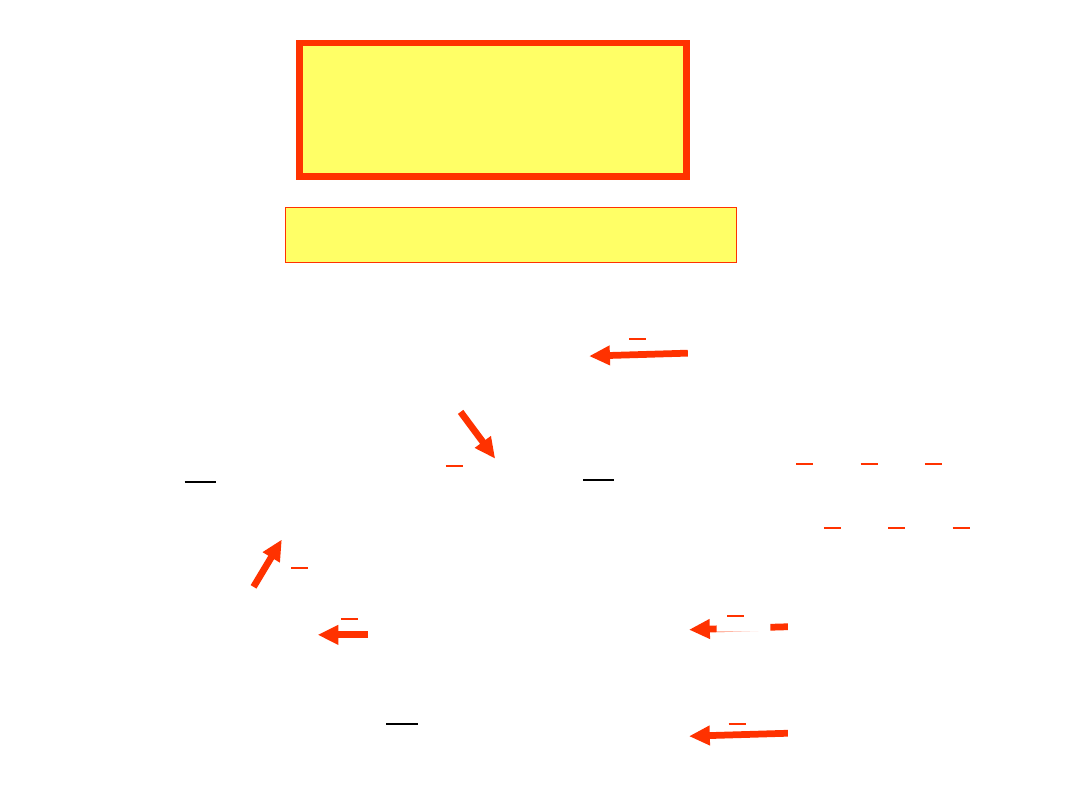
Jeżeli U

f

=230V,

to U

p

=398V≈400V

Skojarzenie w trójkąt

U

RS

U

ST

U

TR

I

R

I

S

I

T

I

SR

I

TS

I

RT

I

R

+I

RT

-I

SR

=0

I

R

=I

SR

-I

RT

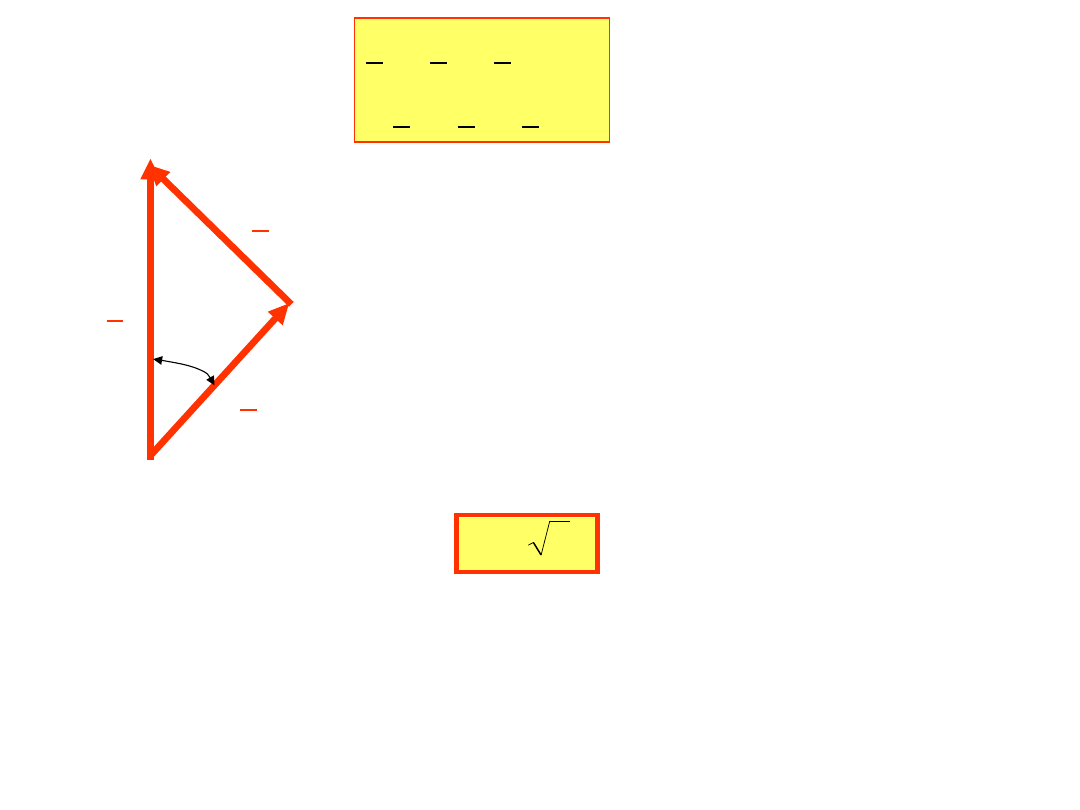
I

R

+I

RT

-I

SR

=0

I

R

=I

SR

-I

RT

30

0

I

R

I

SR

-I

RT

W układzie symetrycznym

amplitudy prądów przewodowych

są jednakowe I

R

=I

S

=I

T

=I

p

i amplitudy prądów fazowych

są jednakowe I

RT

=I

SR

=I

TS

=I

f

f

p

I

3

I 

Sposoby przyłączania odbiorników do 4-ro przewodowej sieci

trójfazowej

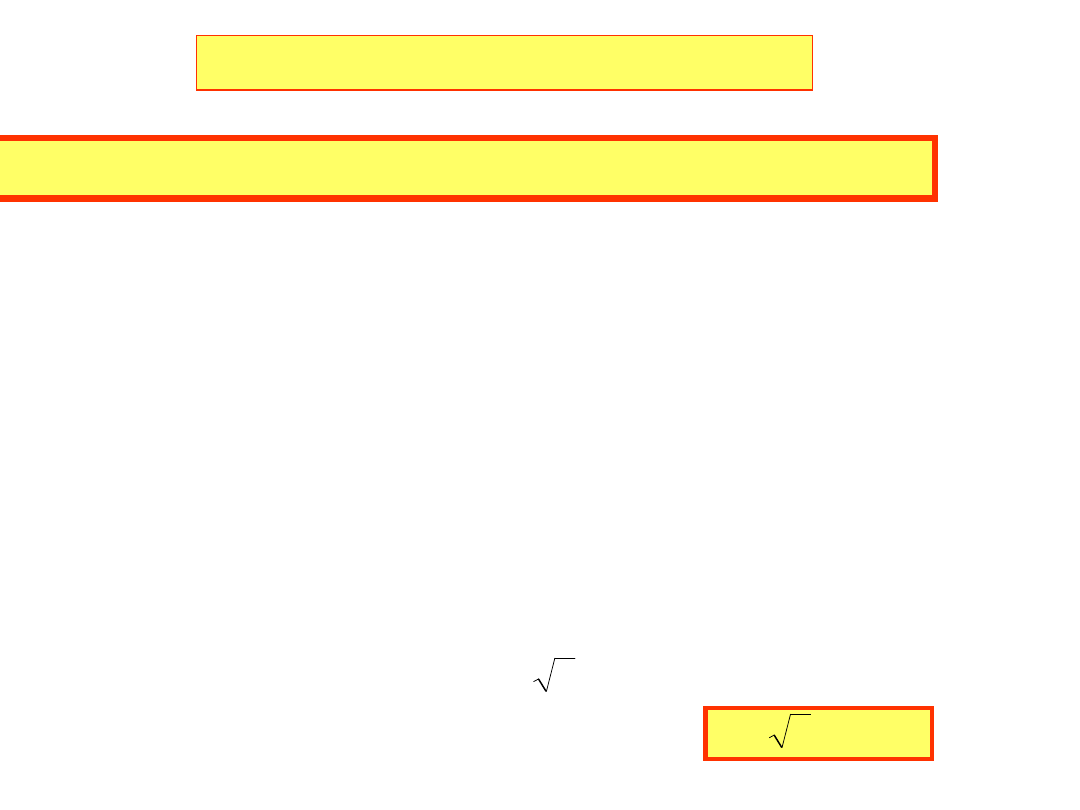
,więc moc wyrażona

za pomocą wielkości przewodowych jest

Moc w układach trójfazowych

Odbiornik połączony w gwiazdę: P=3U

f

I

f

cosφ

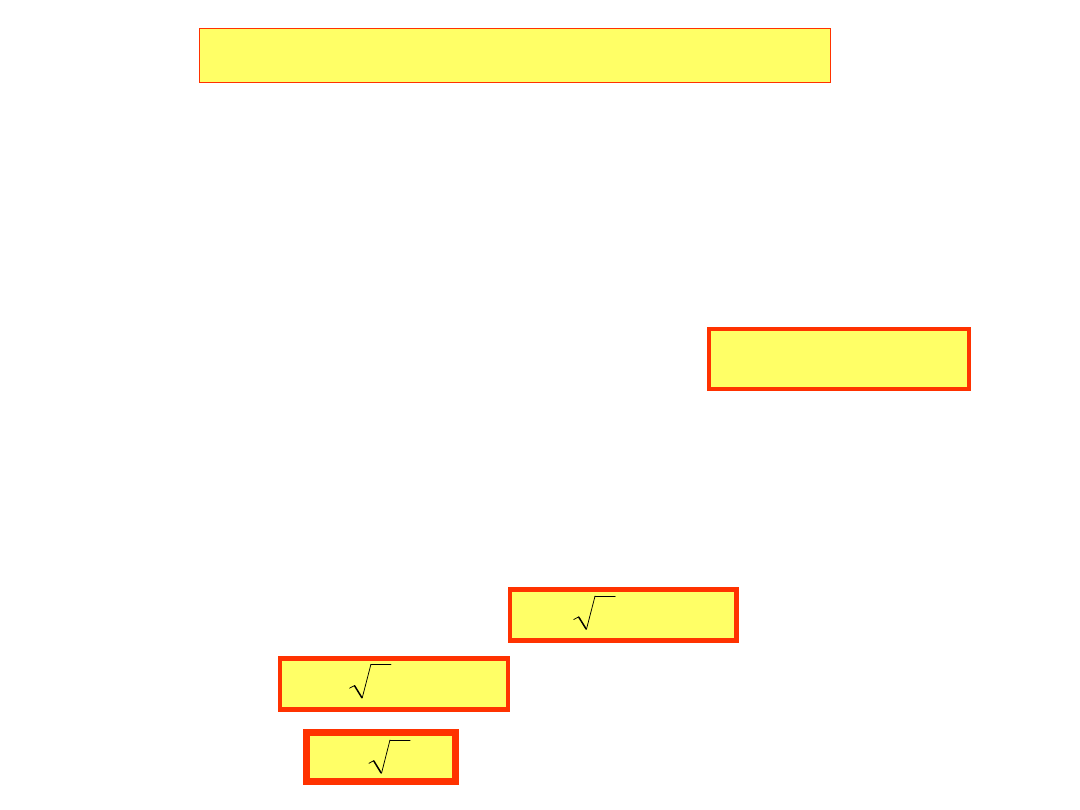
Biorąc pod uwagę, że I=I

f

,

f

U

3

U





cos

UI

3

P

Odbiornik połączony w trójkąt

P=3UI

f

cosφ

dla wielkości przewodowych:





cos

UI

3

P

Moc bierna:





sin

UI

3

Q

Moc pozorna:

UI

3

S

Transformator

Transformator jednofazowy - budowa

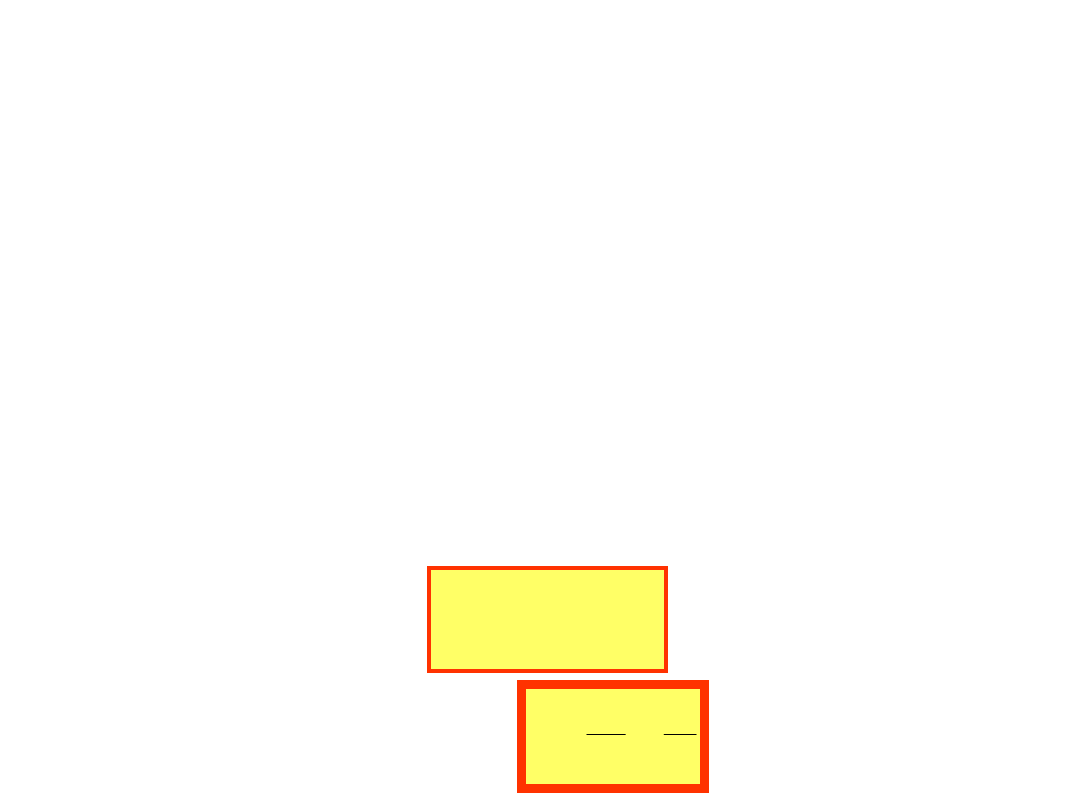
f

z

44

.

4

E

f

z

44

.

4

E

m

2

2

m

1

1









Przekładnia transformatora:

2

1

2

1

z

z

E

E







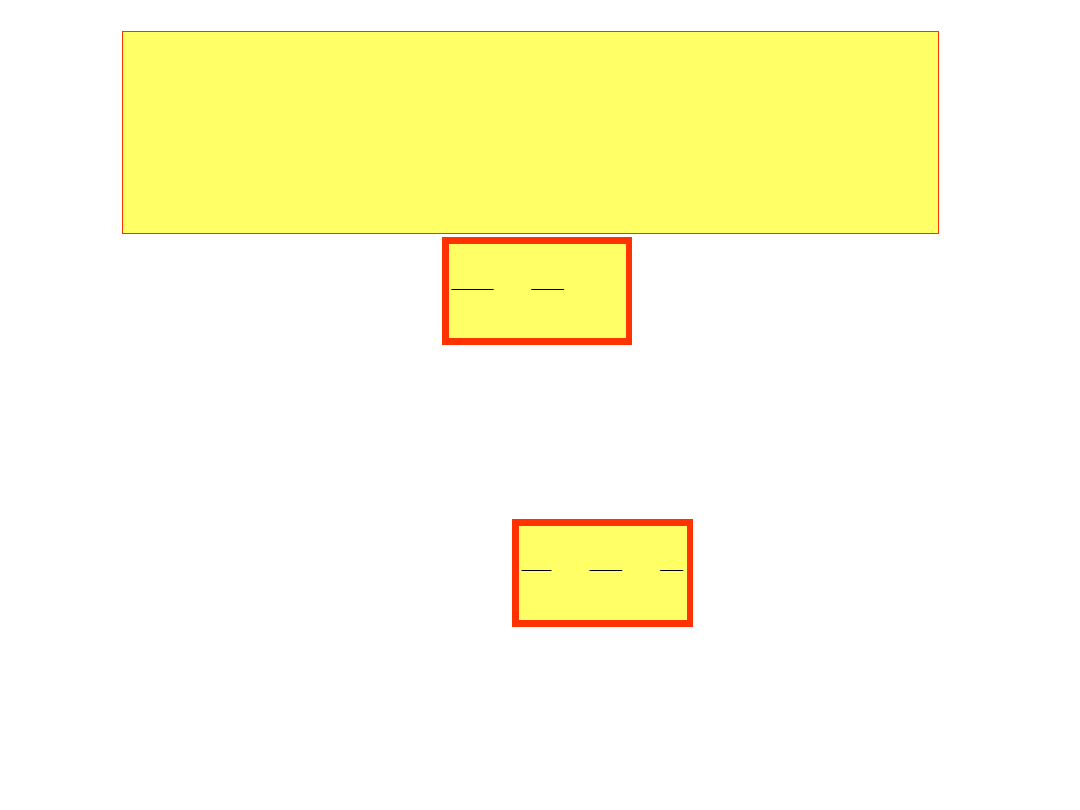
Napięcia na zaciskach transformatora:

U

1

– pierwotne,

U

2

– wtórne







2

1

2

1

z

z

U

U

Ponieważ sprawność transformatora jest bardzo duża 0.95 – 0.99
więc zachodzi U

1

I

1

=U

2

I

2

stąd przekładnia prądowa:







1

z

z

I

I

1

2

2

1

Autotransformator

Transformatory trójfazowe

•

Autotransformator YNa0d11.

•

Moc: 160 MVA

•

Napięcie GN 230 kV, DN 120 kV

•

Częstotliwość znamionowa 50 Hz

•

Prądy znamionowe GN 401,6 A, DN 769,8 A

•

Masa całkowita 150 ton, masa oleju 42 tony, masa części wyjmowanej 85 ton

Maszyny prądu stałego

Maszynę przetwarzającą energię mechaniczną na elektryczną

nazywamy generatorem lub prądnicą.

Maszynę przetwarzającą energię elektryczną na mechaniczną

nazywamy silnikiem lub motorem.

Maszyna elektryczna składa się z dwóch zasadniczych części:

stojana – nieruchoma część maszyny

wirnik – ruchoma część maszyny

Inne nazwy: stojan nazywany magneśnicą,
wirnik nazywany twornikiem

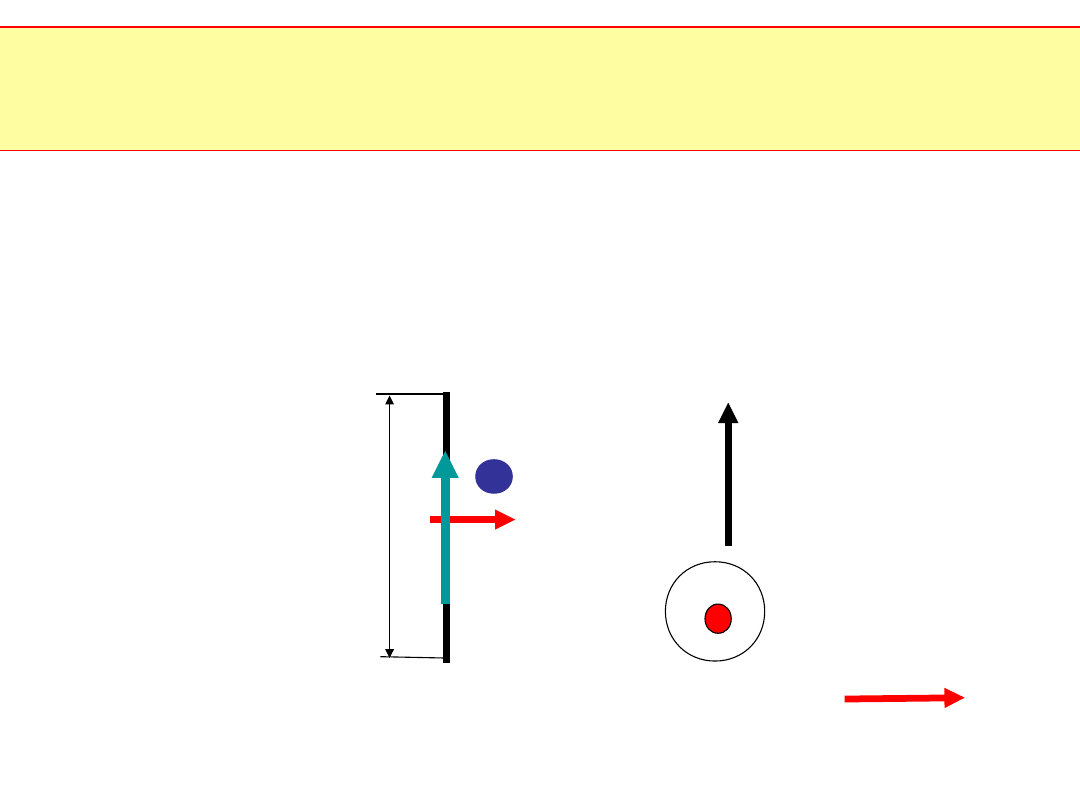
x

W przewodach wirnika generuje się siła elektromotoryczna E:

E=Blv

B – indukcja magnetyczna w teslach [T],
v – prędkość ruchu przewodu w m/s,
l – długość przewodu znajdującego się w polu magnetycznym
w metrach.

l

v

x

B

E

Reguła prawej ręki

x B

v

E

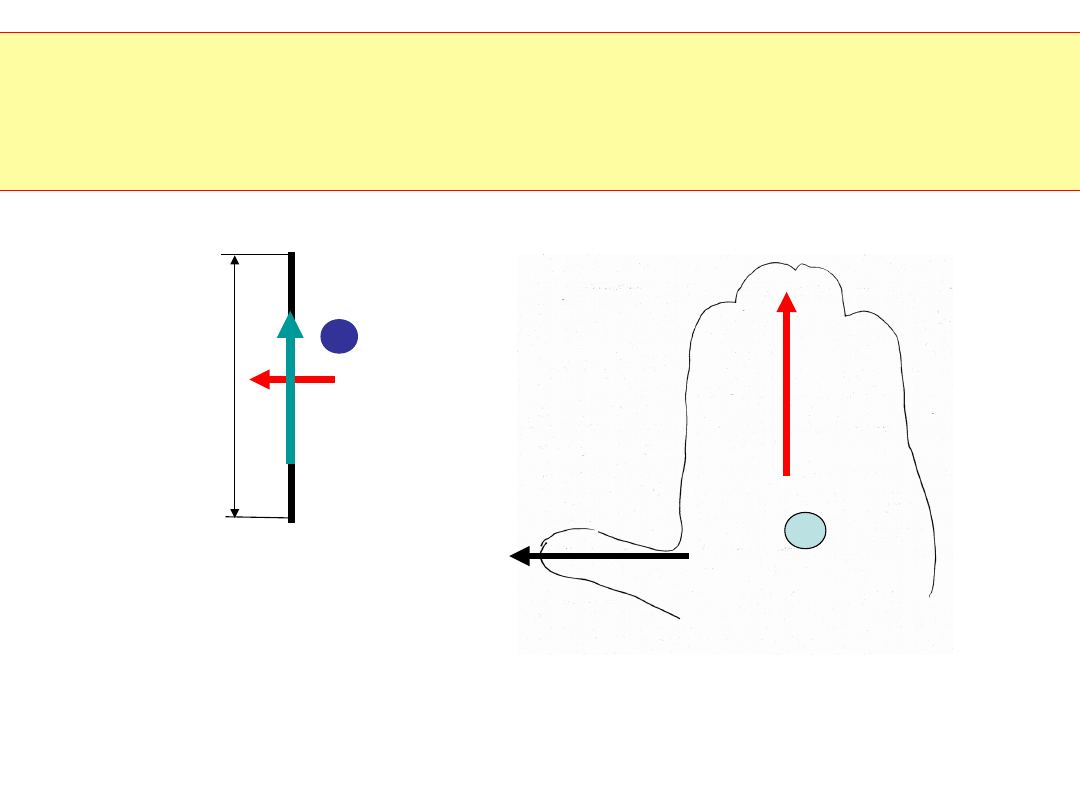
Jeżeli w polu magnetycznym o indukcji B zostanie umieszczony
przewód o długości l, w którym płynie prąd I, to na przewód
działa siła F=BIl

l

F

x

B

I

Reguła lewej ręki

W uzwojeniach wirnika na skutek ruch obrotowego w polu

magnetycznym powstaje zmienna w czasie siła elektromotoryczna

e(t)

X B

I

F

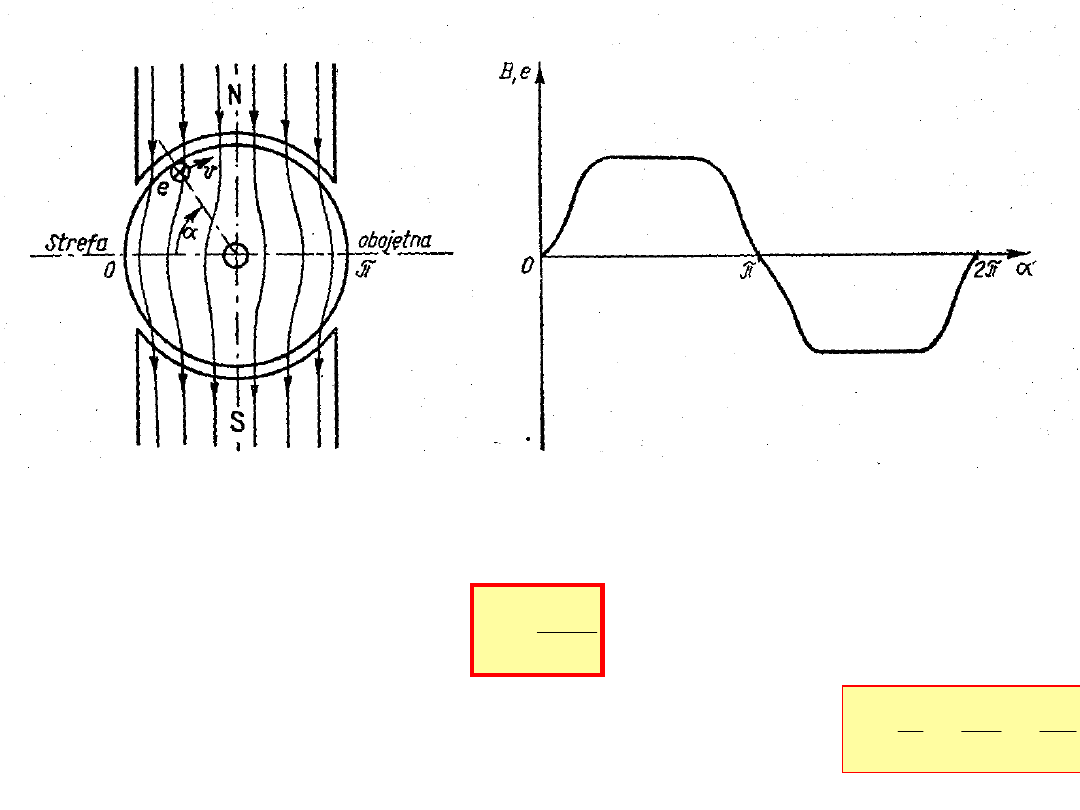
Prędkość kątowa wirowania wirnika ω, często używamy prędkości
obrotowej n liczonej w liczbie obrotów na minutę, czyli:

60

n

2





60

n

2

T

1

f











Dla maszyny o jednej parze biegunów p=1 i mamy:

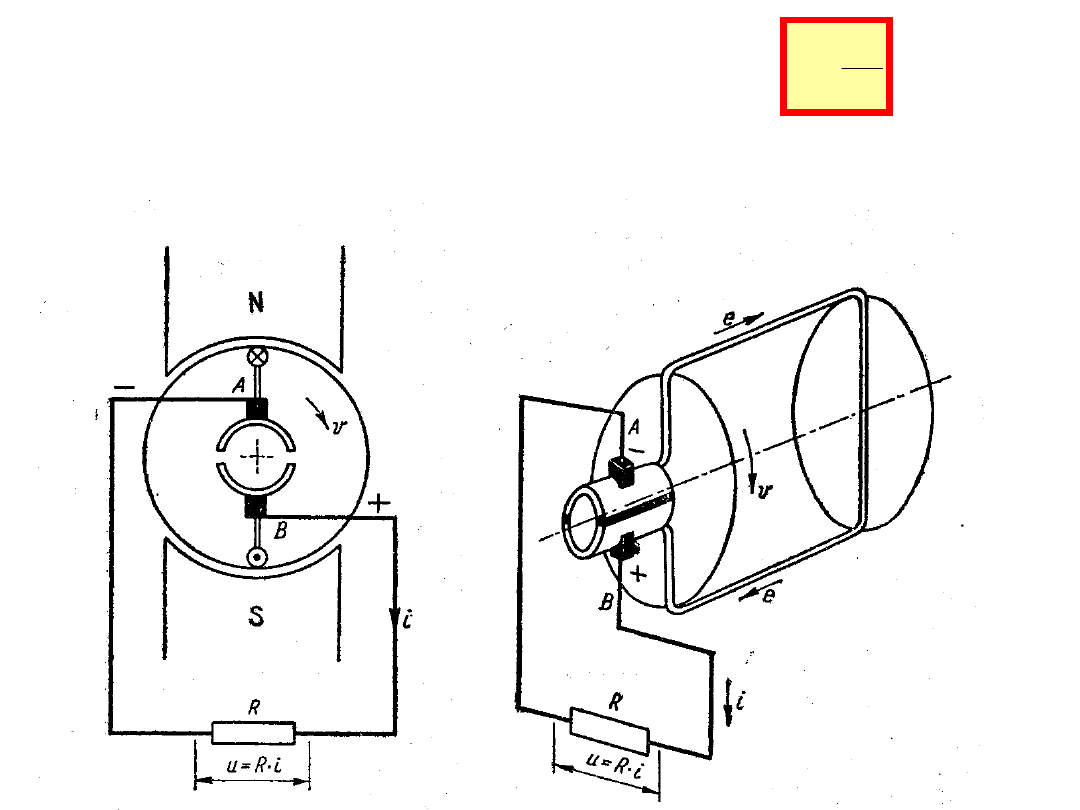
Dla maszyny o p – parach biegunów mamy:

60

pn

f 

Komutator – zamienia zmienną SEM twornika na stałą

Przebieg SEM i prądu cewki

Wykonanie komutatora wielodziałkowego

Przykład wykonania maszyny dwubiegunowej maszyny prądu
stałego.

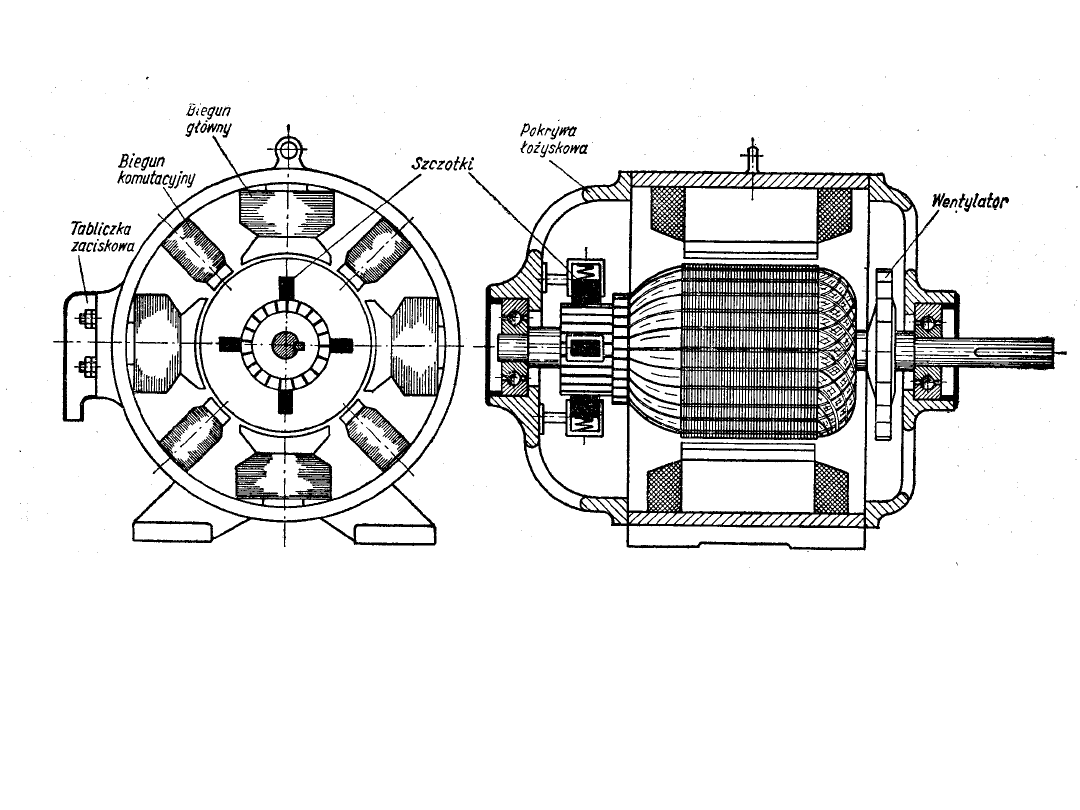
Uzwojenia wirnika są umieszczone w żłobkach

Wirnik

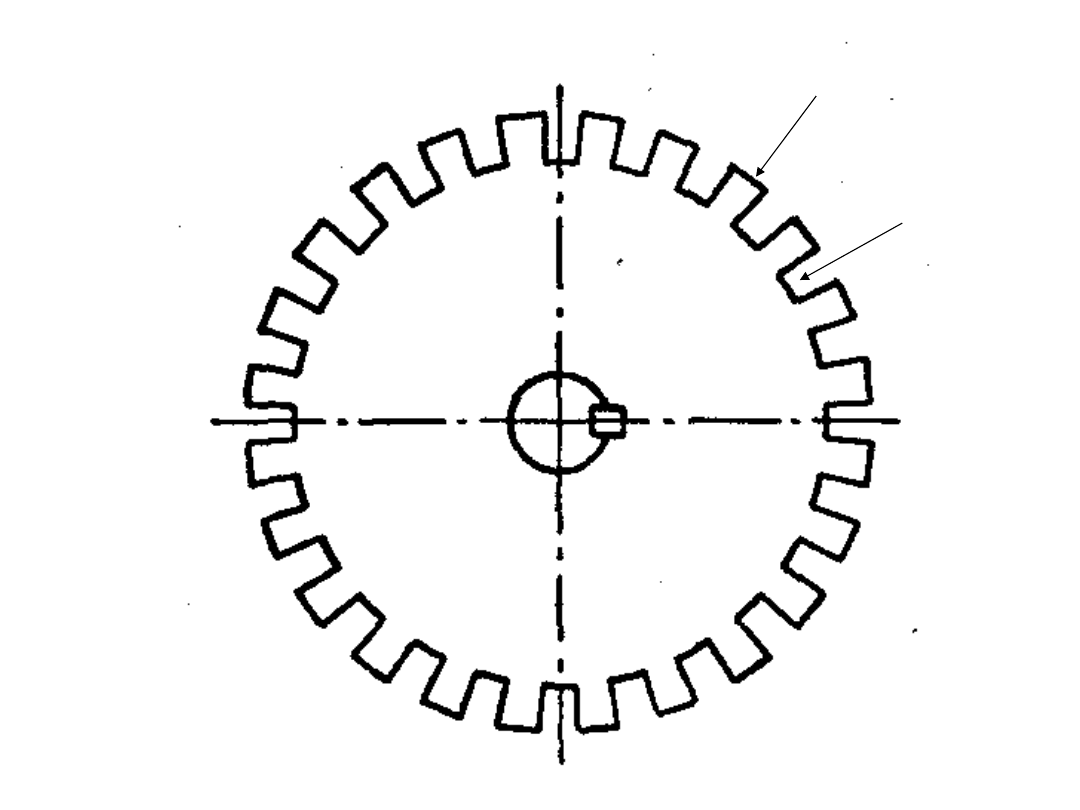
Przekrój poprzeczny wirnika

ząb

żłobek

Stojan

Prądnice prądu stałego ze względu na sposób wzbudzenia
dzielimy na
1.prądnice obcowzbudne
2.prądnice samowzbudne

Siła elektromotoryczna E generowana w maszynie prądu

stałego: E=kΦn

gdzie Φ –strumień główny maszyny w weberach [Wb],

n – prędkość obrotowa,

k – stała konstrukcyjna maszyny.

Prądnica obcowzbudna pracuje w schemacie:

Zależność U(I) przy I

m

=const i n=const jest nazywana

charakterystyką zewnętrzną

Charakterystyka zewnętrzna prądnicy obcowzbudnej U=f(I)
charakterystyka wewnętrzna E=f(I)

Regulację napięcia na zaciskach prądnicy przeprowadzamy
regulując prąd wzbudzenia I

m

zmieniając rezystor R

reg

. Krzywa, która podaje przepis jak

regulować prąd wzbudzenia I

m

w zależności od prądu obciążenia I

podaje charakterystyka regulacyjna.

uzwojenie biegunów
komutacyjnych

Charakterystyka regulacyjna

a – liczba liter w nazwisku, b – liczba liter w imieniu
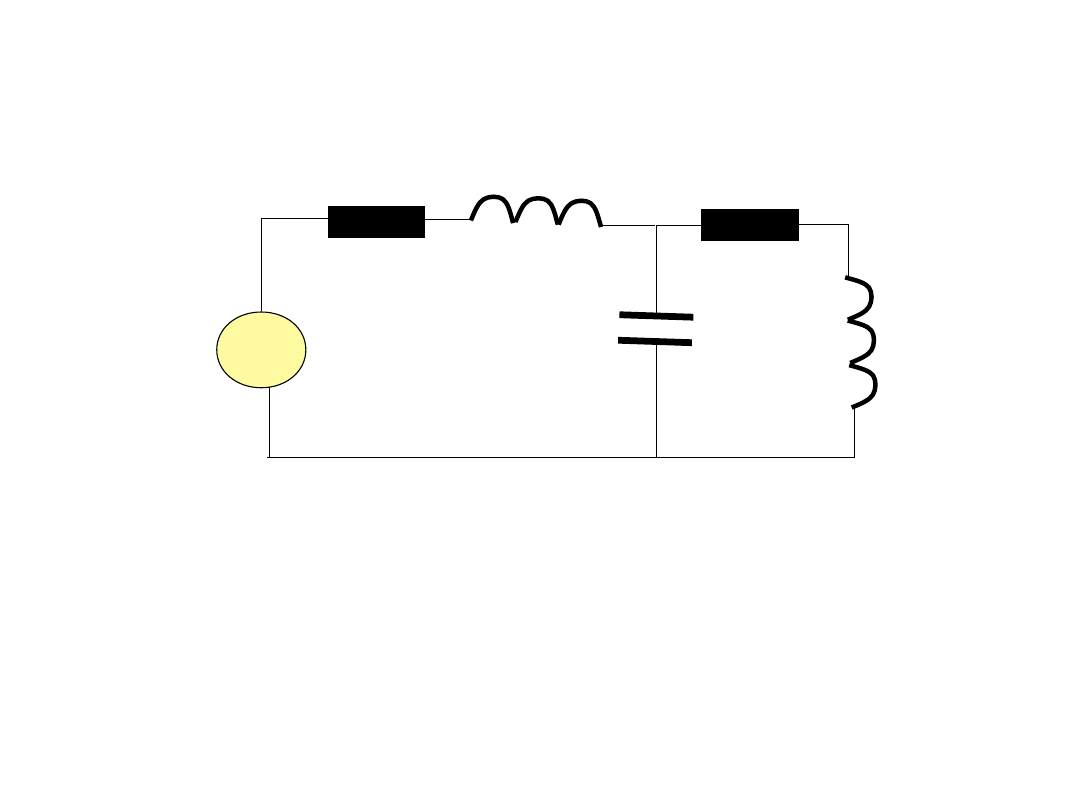
Zadanie 1. (10pktów) Wyznaczyć moc czynną, bierną i pozorną
dostarczaną do obwodu przez źródło.

~

230V, 50Hz

b[Ω]

b[mH]

5a[Ω]

5a[mH]





 

F

b

a

10





Zadanie 2. (5pktów) Napięcie po stronie niskiego napięcia
transformatora wynosi (a+b)[V], a prąd a·b[kA]. Jakie jest
napięcie i prąd po stronie wysokiego napięcia, jeżeli jego
przekładnia wynosi 20?

Maszyny obcowzbudne są rzadko stosowne gdyż wymagają
osobnego źródła zasilania.

Prądnica samowzbudna – warunki wzbudzenia
Maszyna pracuje w układzie:

R

k

– rezystancja krytyczna

1.istnieje magnetyzm szczątkowy,
2.zgodność strumienia wzbudzenia i magnetyzmu szczątkowego,
3.R

m

<R

k

Najczęściej stosowaną prądnicą prądu stałego jest

samowzbudna prądnica bocznikowa

uzwojenie biegunów komutacyjnych

Charakterystyka zewnętrzna prądnicy bocznikowej jest wyznaczana
przy stałej wartości R

reg

i przy stałej prędkości obrotowej n

Prądnica szeregowa

uzwojenie biegunów komutacyjnych

Charakterystyka zewnętrzna

Ze względu na dużą zmienność napięcia w zależności od obciążenia
maszyna nie jest praktycznie stosowana.

Prądnica szeregowo - bocznikowa

Charakterystyka zewnętrzna prądnicy szeregowo - bocznikowej

Stosowana dla uzyskania stabilnego napięcia na wyjściu.

Silniki prądu stałego

F=BIl

Moment maszyny jest:

M=cΦI

t

gdzie
Φ – strumień główny,
I

t

– prąd wirnika,

c – stała konstrukcyjna.

W przewodach wirnika powstaje siła elektromotoryczna E

E=kΦn

Napięcie na zaciskach twornika: U=E+R

tc

I

t

i prędkość obrotową silnika otrzymujemy z zależności:







k

I

R

U

n

t

tc

Rozruch silnika prądu stałego

Bez rezystora rozruchowego

prąd rozruchowy osiąga

bardzo duże wartości około

20I

n

Rozruch z czterostopniowym rozrusznikiem

Silnik bocznikowy prądu stałego

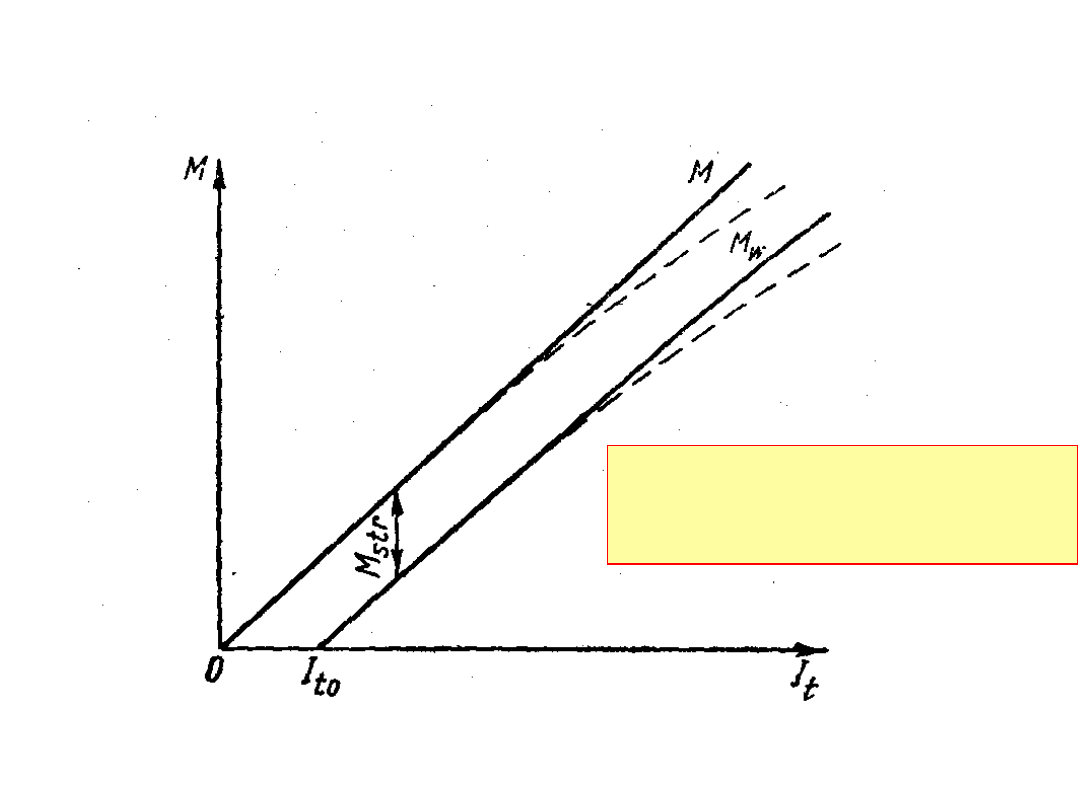
Moment silnika bocznikowego w funkcji prądu twornika

Moment maszyny jest:

M=cΦI

t

Charkterystyka mechaniczna silnika jest to zależność między

prędkością obrotową n a momentem obrotowym

Charakterystyka mechaniczna naturalna silnika bocznikowego.
Silnik przyłączony do sieci bez żadnych rezystorów na napięcie U

n

n

0

- prędkość idealnego

biegu jałowego





k

U

n

0

Spadek prędkości
przy obciążeniu
momentem M

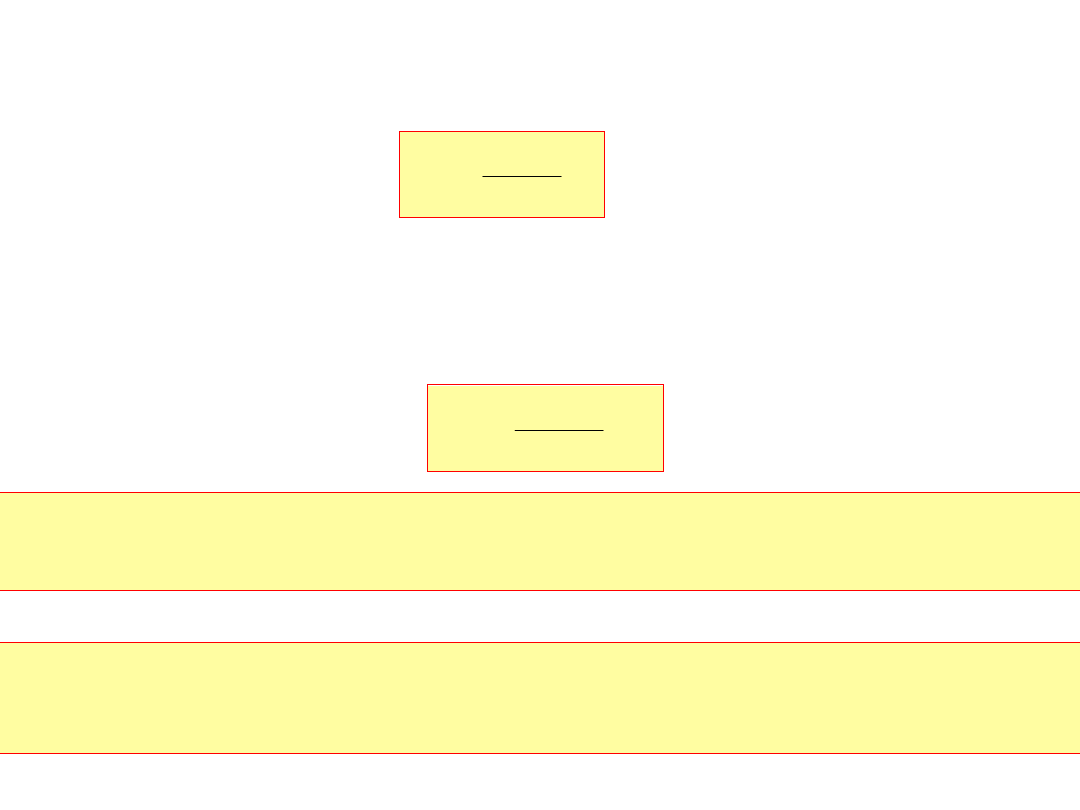
Spadek prędkości Δn przy obciążeniu momentem M jest:

M

ck

R

n

2

tc







W silnikach bocznikowych przy obciążeniu momentem

znamionowym ten spadek prędkości procentowy s jest

rzędu (5 – 10)%

100

n

n

n

%

s

0





Charakterystyka mechaniczna naturalna silnika bocznikowego

jest tzw. charakterystyką sztywną

Jeżeli do obwodu twornika włączymy dodatkowe rezystory,
to otrzymujemy tzw. charakterystyki mechaniczne sztuczne.

Charakterystyki nazywamy charakterystykami miękkimi

Wykorzystujemy je przy rozruchu

dt

d

J

M

M

M

op

d









M

rp

– moment rozruchowy, M

n

– moment znamionowy,

M

op

– moment oporowy

Regulacja prędkości silnika bocznikowego













k

I

R

R

U

n

t

d

tc

Prędkość można regulować na trzy sposoby:
1.Przez zmianę oporu R

d

,

2.Przez zmianę strumienia Φ,
3.Przez zmianę napięcia U.

Regulacja przez zmianę oporu R

d

Wady: Niska sprawność – strata mocy w rezystancji R

d

do 50%,

duża podatność zmian prędkości na zmiany obciążenia.
Ten sposób stosowany rzadko, tylko przy rozruchu.

Przez zmianę strumienia Φ

Regulujemy prąd magnesujący I

m

rezystorem R

d

.

Prąd I

m

jest mały w stosunku

do prądu twornika I

t

(kilka %).

Praktyczny zakres regulacji
prędkości silnika:

3

n

n

min

max



W żadnym przypadku nie można
dopuścić do przerwania obwodu
wzbudzenia, gdyż wtedy Φ≈0 i













k

I

R

R

U

n

t

d

tc

prędkość osiąga bardzo duże wartości

co grozi zniszczeniem silnika. Nazywamy to rozbieganiem silnika.

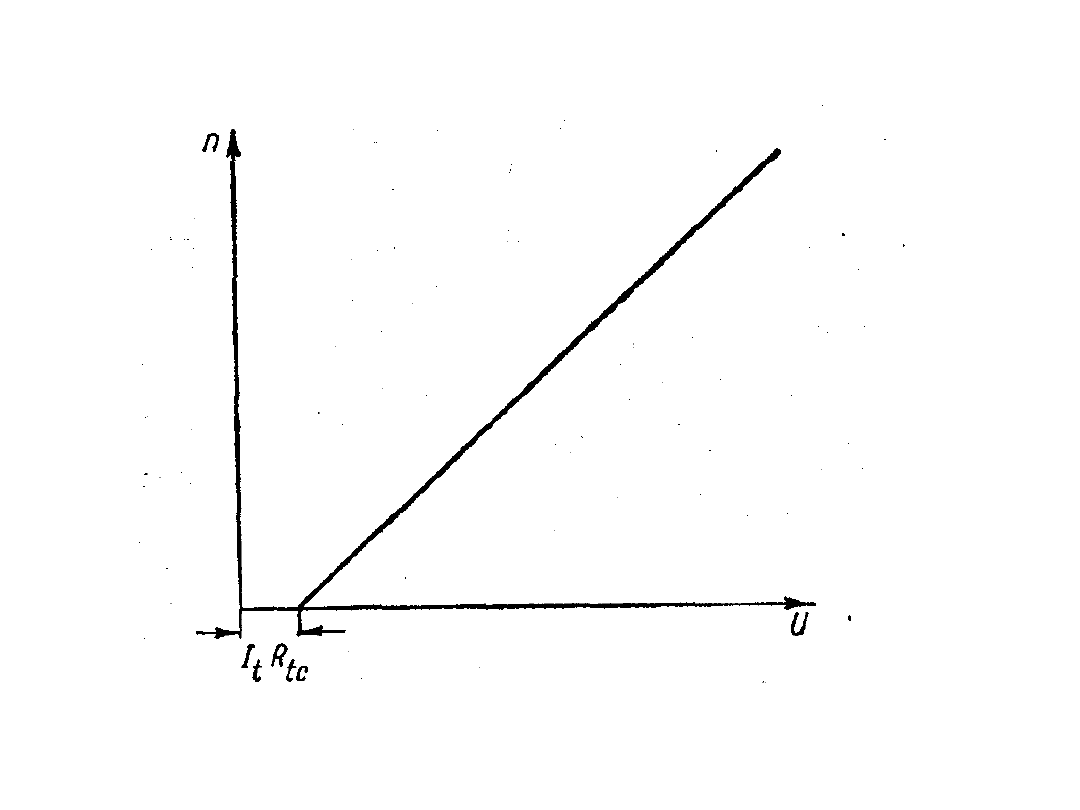
Przez zmianę napięcia U

Napięciem steruje się stosując układy energoelektroniczne.