Wykład 2: Prezentacja danych

Biometria i

Biostatystyka

Zmienne typu atrybuty

i zmienne rangowe



Wykresy słupkowe



Wykresy kołowe

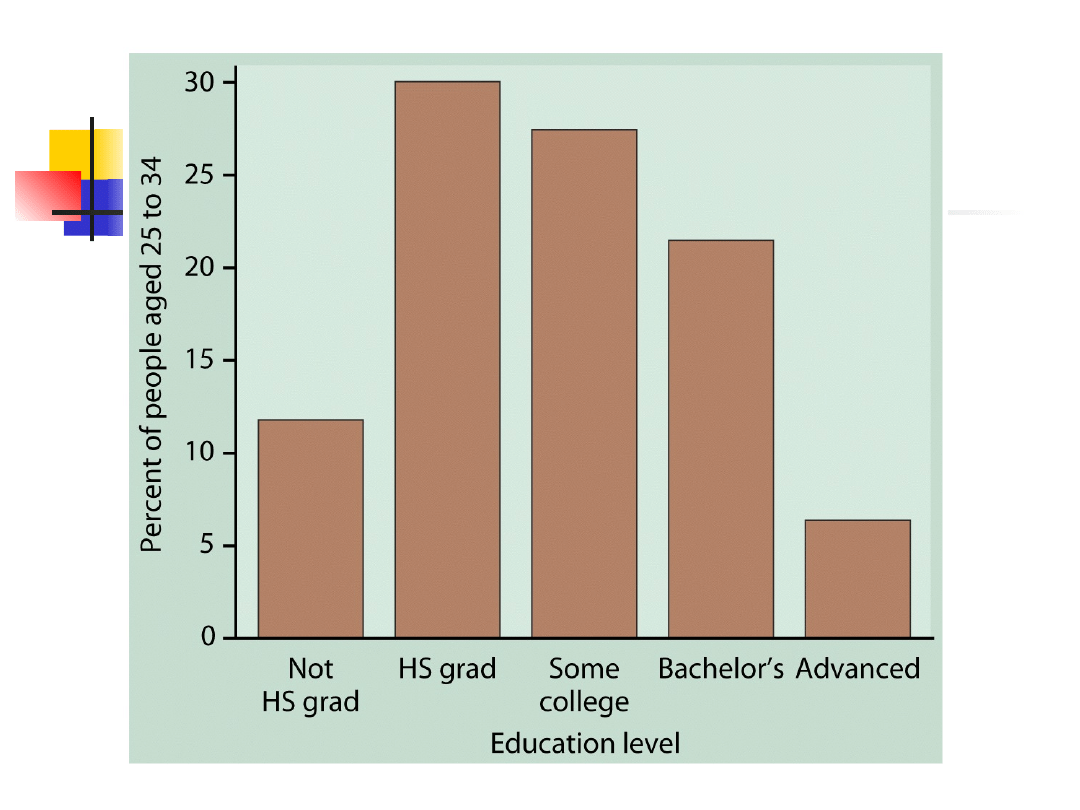
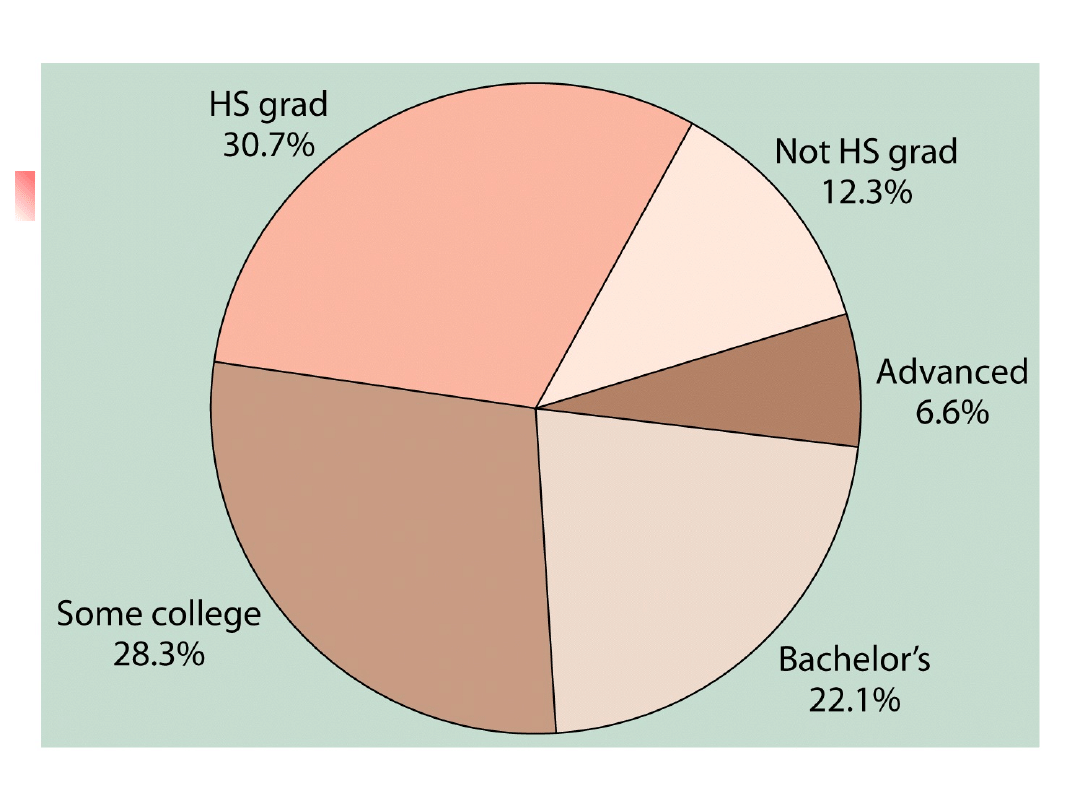
Zmienne pomiarowe

Wykresy „łodygowe” (stem-
leaf)



Obrazują kształt rozkładu,
jednocześnie ukazując na wykresie
wartości numeryczne.



Są najbardziej odpowiednie dla
niewielkiej liczby dodatnich
obserwacji.

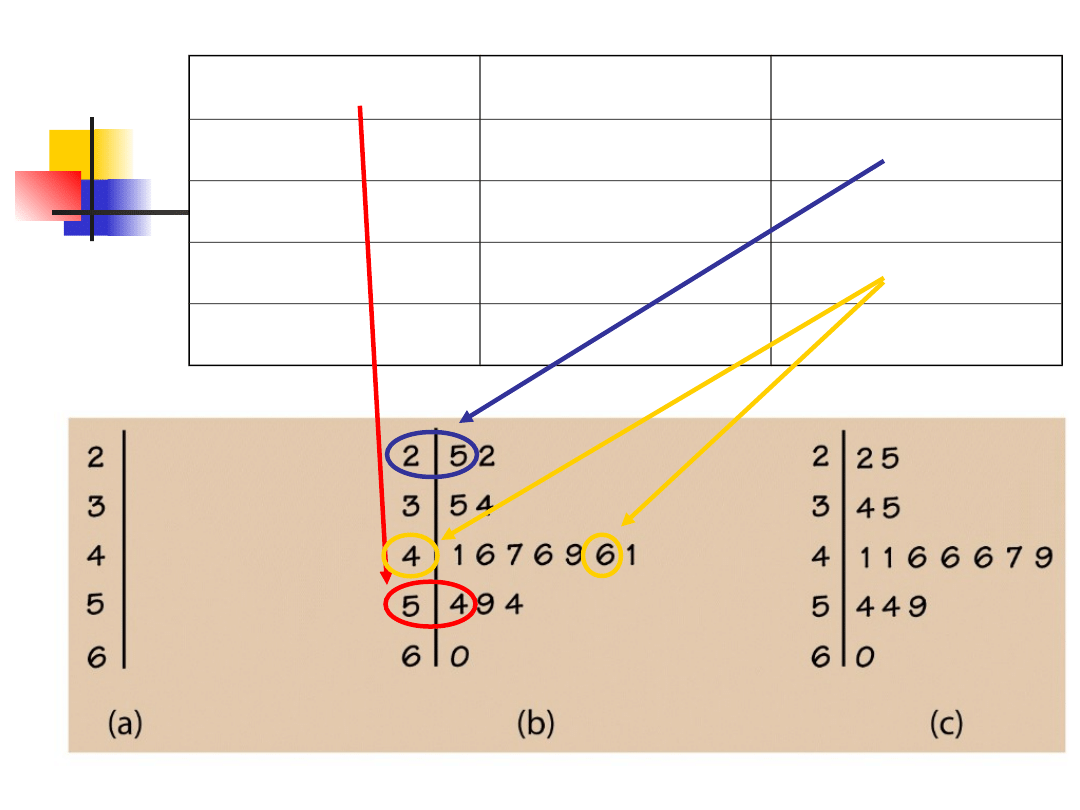
Rysowanie wykresu
łodygowego



Podziel każdy wynik na łodygę (stem) i

listek (leaf).



Łodyga: tyle cyfr ile potrzeba



Listek: pojedyncza cyfra



Wypisz łodygi w pionowej kolumnie

rosnąco w dół. Narysuj pionową linię po

prawej stronie.



Wypisz każdy listek w wierszu po prawej

stronie od jego łodygi, w porządku

rosnącym.

Biuro obsługi klienta
Liczba odwiedzin dziennie

54

59

35

41

46

25

47

60

54

46

49

46

41

34

22

54

59

35

41

46

25

47

60

54

46

49

46

41

34

22

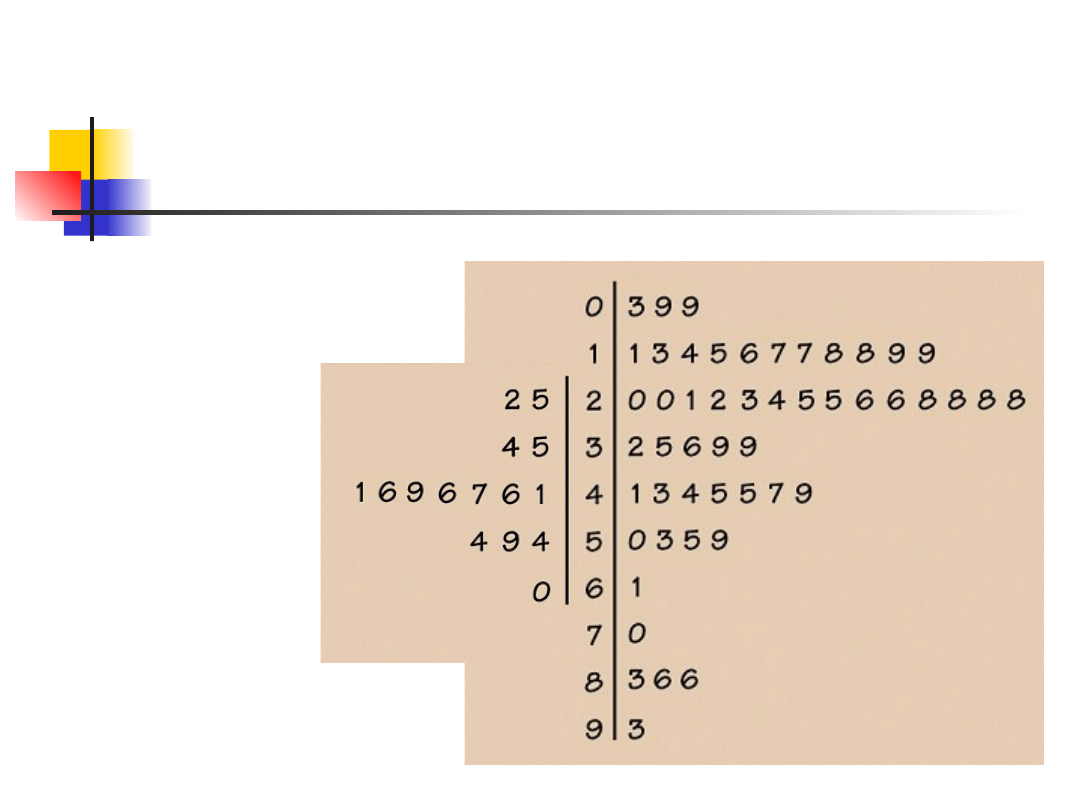
Porównywanie dwóch
rozkładów



Wykresy o
wspólnym
pniu

Wykresy „łodygowe”, cd.



Są nieodpowiednie dla dużych

zestawów danych



Każda łodyga musi zawierać dużą liczbę

listków



Warianty:



Podzielić każdą łodygę na dwie, np.:



Jedna z liśćmi od 0 do 4



Druga z liśćmi od 5 do 9



Mają za zadanie zobrazować kształt

rozkładu zmiennej losowej

Histogramy



Histogramem nazywa się wykreślne
przedstawienie szeregu rozdzielczego
wykonane w sposób następujący: na
osi poziomej odkłada się odpowiednie
przedziały klasowe, zaś na osi
pionowej rzędne odkłada się w ten
sposób, żeby pola odpowiednich
prostokątów były proporcjonalne do
liczebności danych klas.

Histogramy



Nie mają takich ograniczeń jak
wykresy łodygowe



Dzielą zakres obserwowanych wartości
na przedziały, pokazując jedynie
liczności lub udział procentowy
obserwacji w danym przedziale



Można wybrać dowolną liczbę
przedziałów

równej

szerokości

Rysowanie histogramu

1.

Podziel zakres zmienności danych na
przedziały o równej szerokości.

2.

Rozpocznij tak, by pomiar najmniejszy
był mniej więcej w połowie pierwszego
przedziału.

3.

Zlicz liczbę obserwacji w każdym
przedziale. Zrób tabelę częstości
wystąpień.

4.

Narysuj histogram.

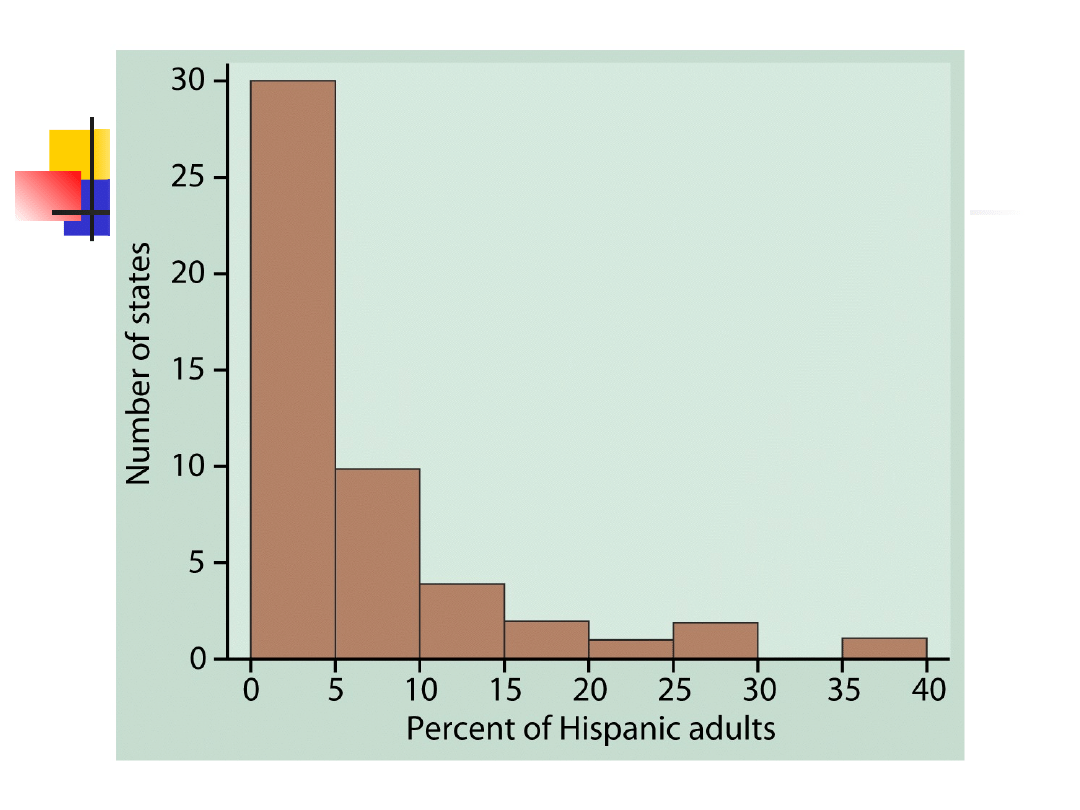
Histogramy, cd.



Częstości względne



Ułamek lub procent obserwacji, które
przypadają na poszczególne przedziały



Poprawnie oznacz „liczba” lub „procent”.



Właściwy wybór przedziałów:



Za mało: wszystkie wartości tylko w kilku
przedziałach



Za dużo: dużo przedziałów ma 1 lub mniej
wyników

Histogramy, cd.



Wzór heurystyczny do oszacowania szerokości

przedziału:



Jeśli szerokość przedziału jest za mała lub za

duża, można ją skorygować przez pomnożenie

lub podzielenie przez a = 1.2 ÷1.5



Sprawdza się przy rozkładach zbliżonych do

rozkładu normalnego oraz przy względnie

dużych ale nie bardzo dużych n (liczność próby)

3

1

n

IQR

64

.

2

h

0









Histogramy, cd.



Jest kilka innych wzorów pomocnych
przy poszukiwaniu liczby przedziałów.
Kilka przykładów:



Żeby znaleźć szerokość, wystarczy
podzielić zakres przez k.

)

n

(

log

3

.

3

1

k

n

k

)

n

(

log

5

k

10

10













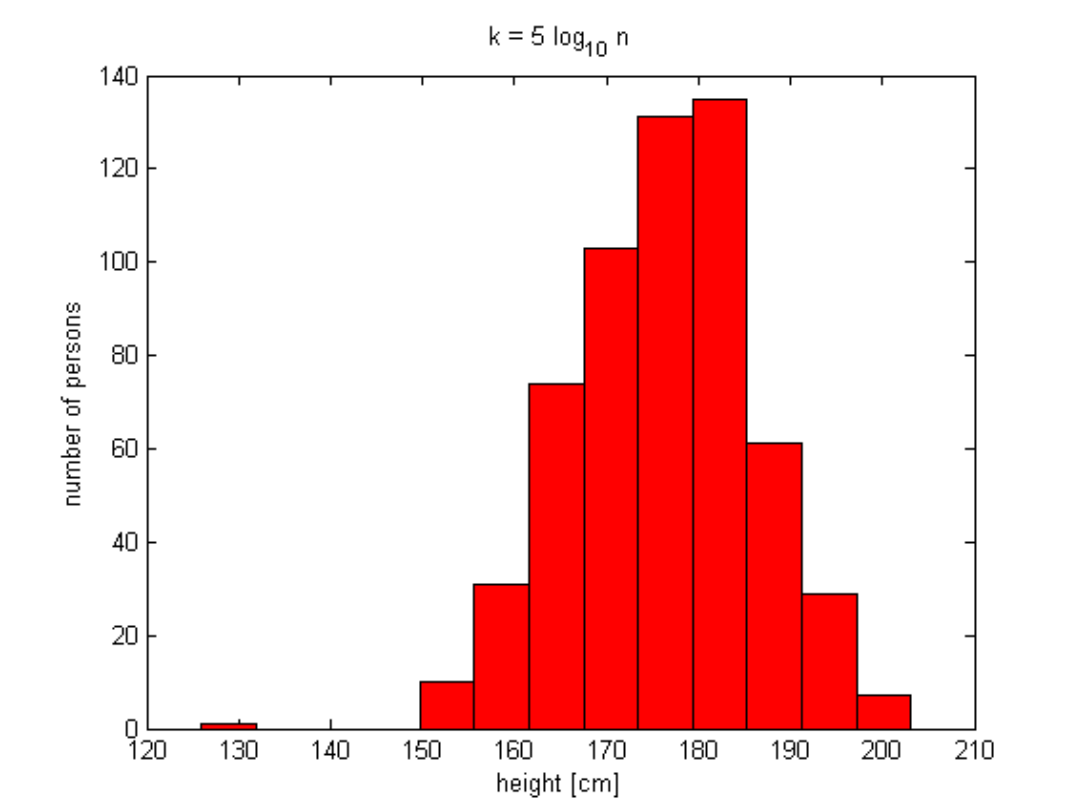
Histograms, cont.

93

.

5

h

14

k

0





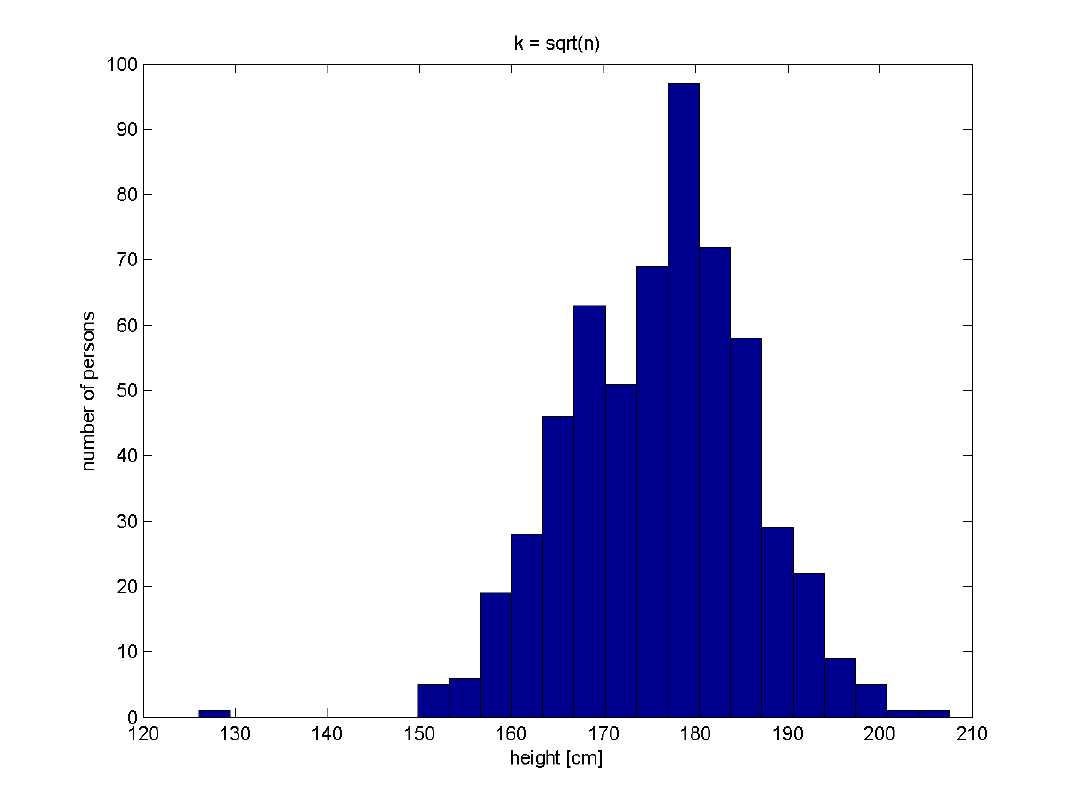
Histograms, cont.

40

.

3

h

24

k

0





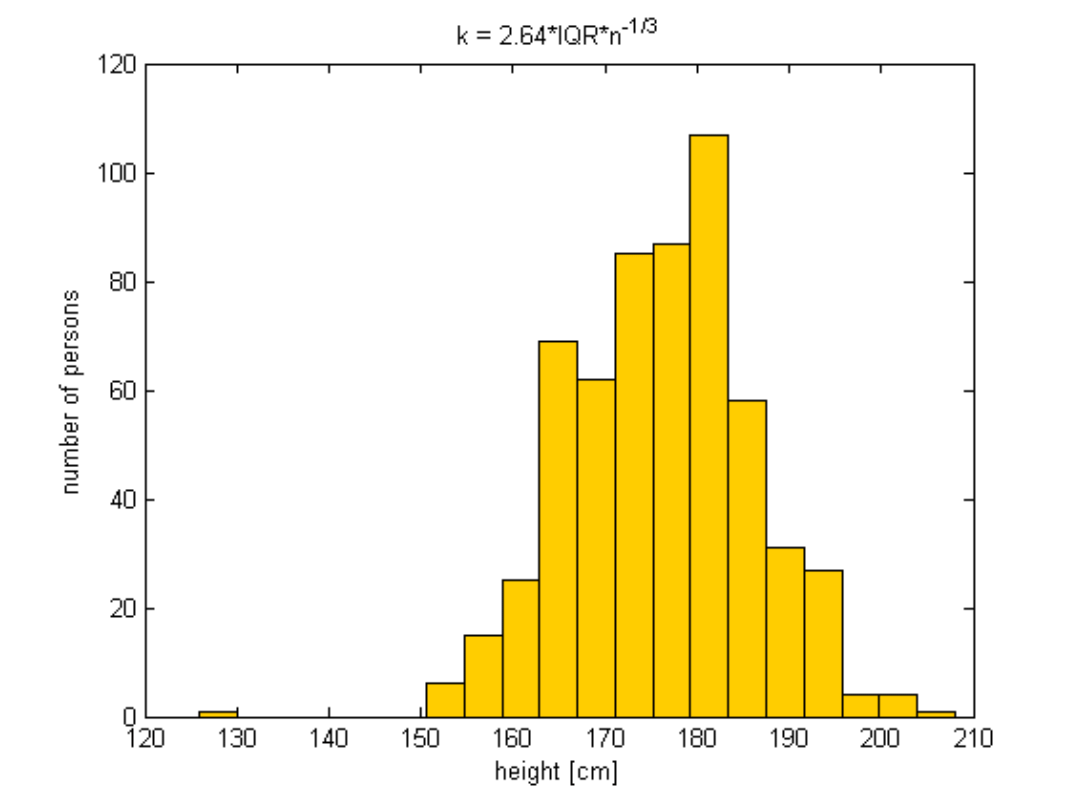
Histograms, cont.

11

.

4

h

20

k

0





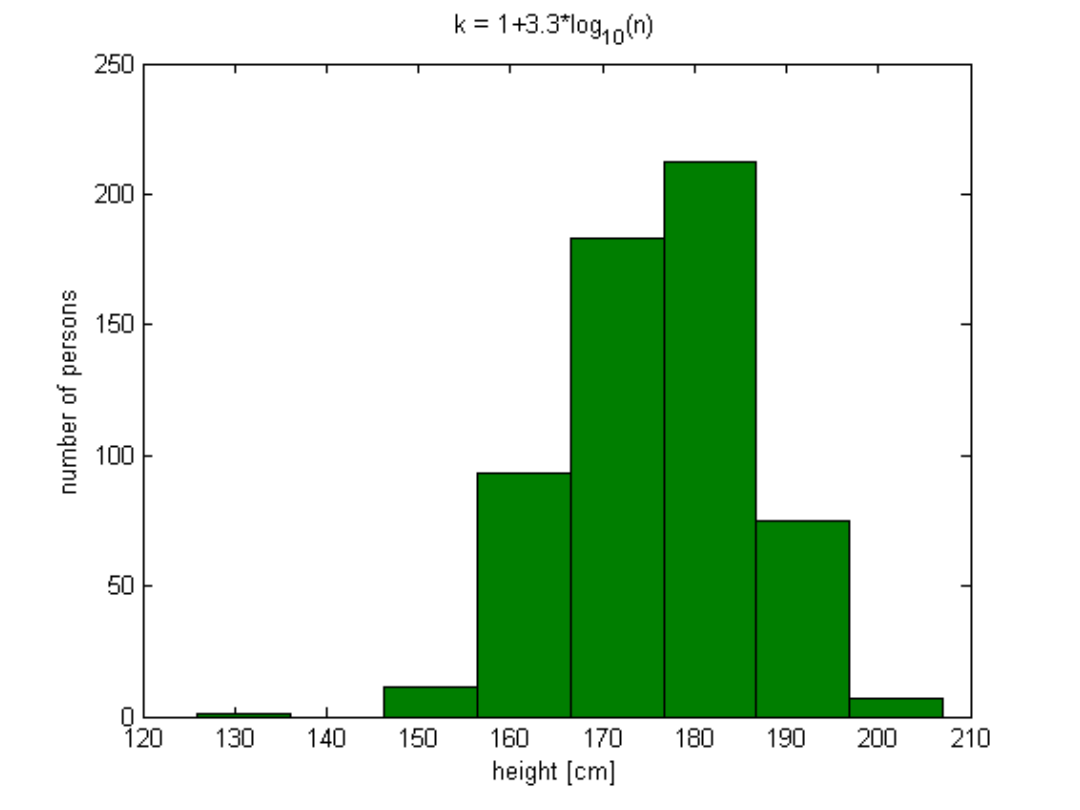
Histograms, cont.

12

.

10

h

8

k

0





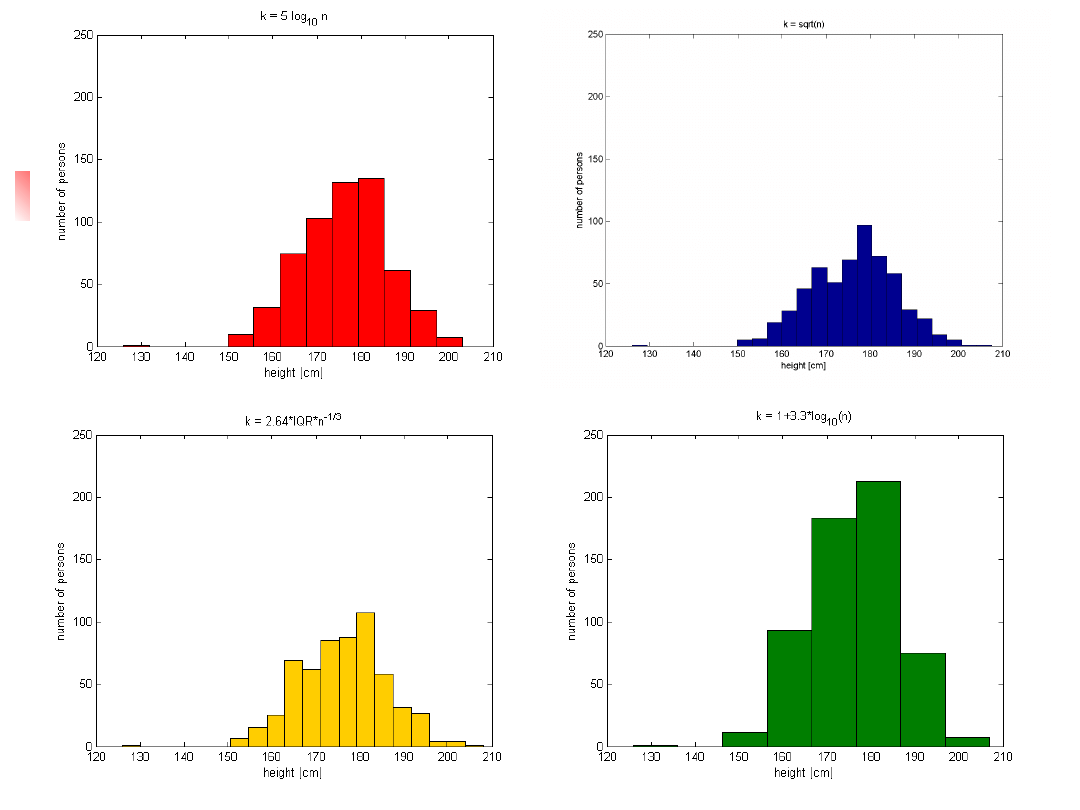
Histograms, cont.

Histogramy, cd.



Wiele zależy od Twojej decyzji odnośnie
szerokości przedziałów.



Pole pod krzywą zmienia się w zależności od h i
jest równe:



Żeby otrzymać eksperymentalną funkcję gęstości
prawdopodobieństwa, musimy sprowadzić pole
powierzchni S do 1. Ponieważ h nie może być
zmienione, musimy skorygować jednostkę na osi
OY.

n

*

h

S

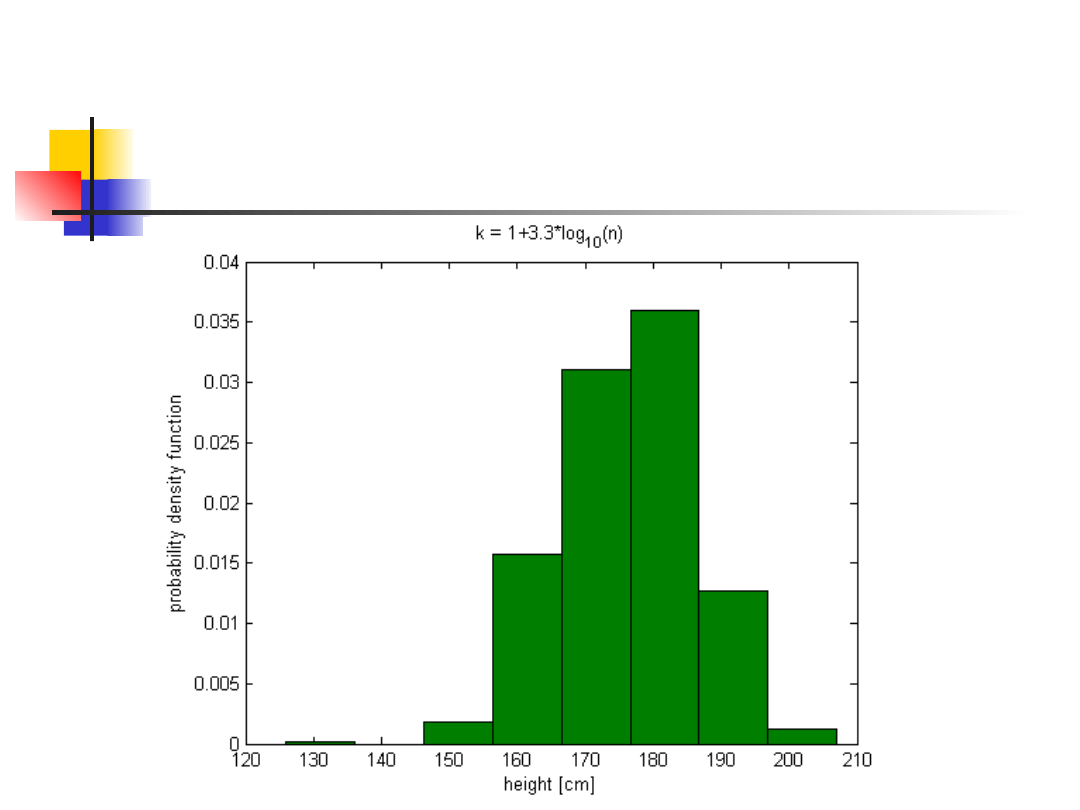
Histogramy, cd.

Symetria i kurtoza



Często obserwujemy odstępstwa
od rozkładu normalnego.
Statystyki, które pozwolą to ocenić
ilościowo bardzo użyteczne.



Zajmiemy się dwoma najczęściej
pojawiającymi się odstępstwami
rozkładów od normalności:

skośnością

i

kurtozą

.

Skośność



Skośność

, inaczej zwana asymetrią, ocenia

na ile jeden z końców krzywej rozkładu
prawdopodobieństwa jest niesymetryczny w
stosunku do drugiego końca.



W takim przypadku brak jest zgodności
wartości średniej i mediany.



W zależności od deformacji, krzywe określa
się mianem prawo- i lewoskośności.

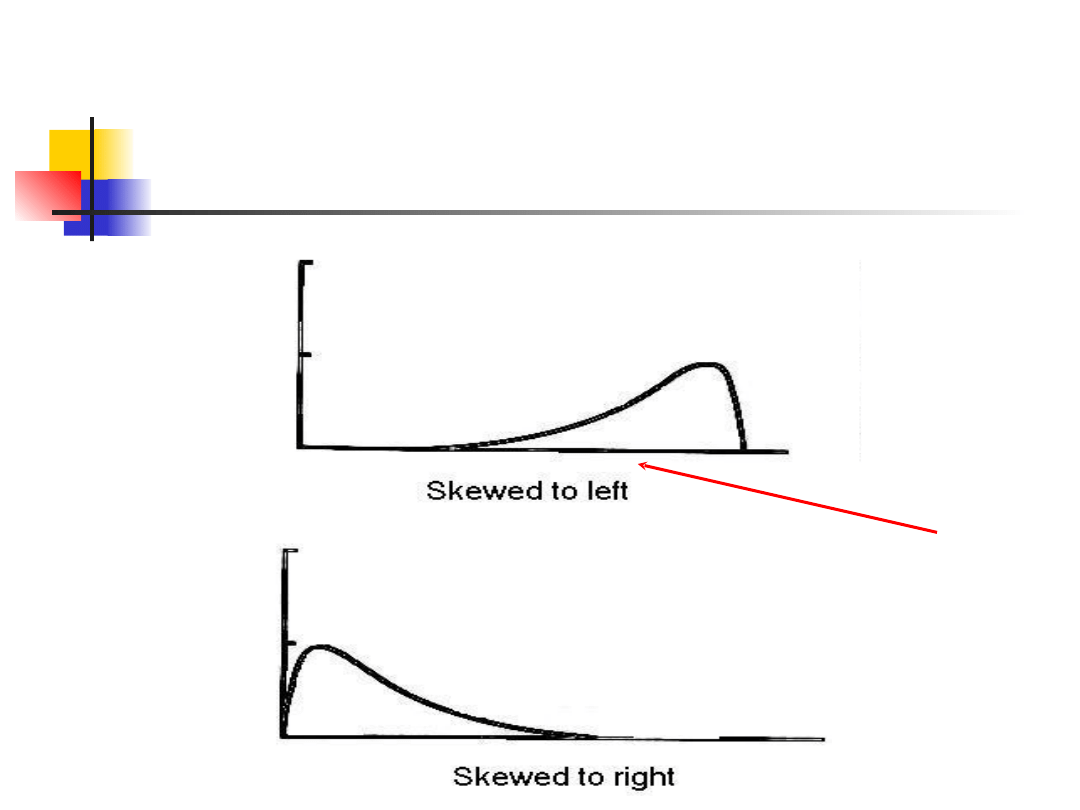
Skośność

Przykład - wzrost: skośność =
-0.26

Kurtoza



Jeśli symetryczny rozkład ma
środek, dwa ramiona i dwa końce,
kurtoza opisuje stosunek między
częścią środkową i końcami w
odniesieniu do ramion.



Definiujemy leptokurtozę
(wyostrzenie krzywej) i platykurtozę
(spłaszczenie krzywej).

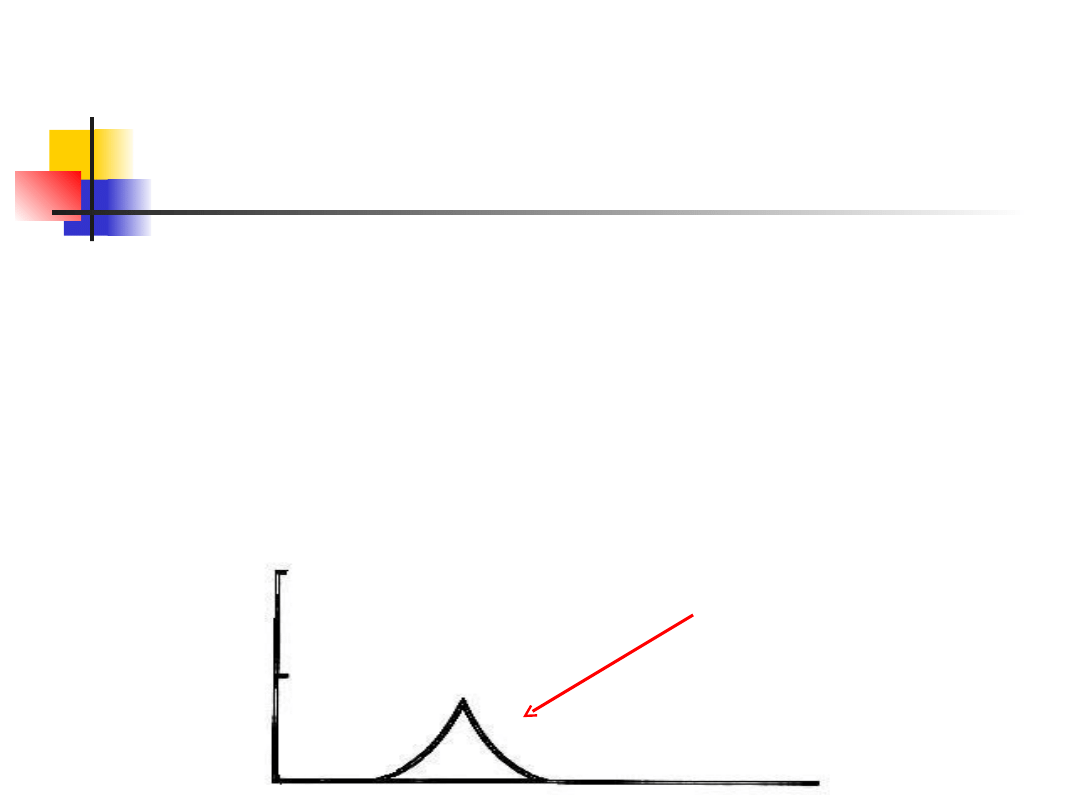
Kurtoza



O leptokurtozie (wyostrzeniu)
mówimy, gdy krzywa ma więcej
obserwacji blisko środka i na końcach a
mniej w ramionach w porównaniu do
rozkładu normalnego, z tą samą średnią i
wariancją

.

Przykład - wzrost: kurtoza = 3.65

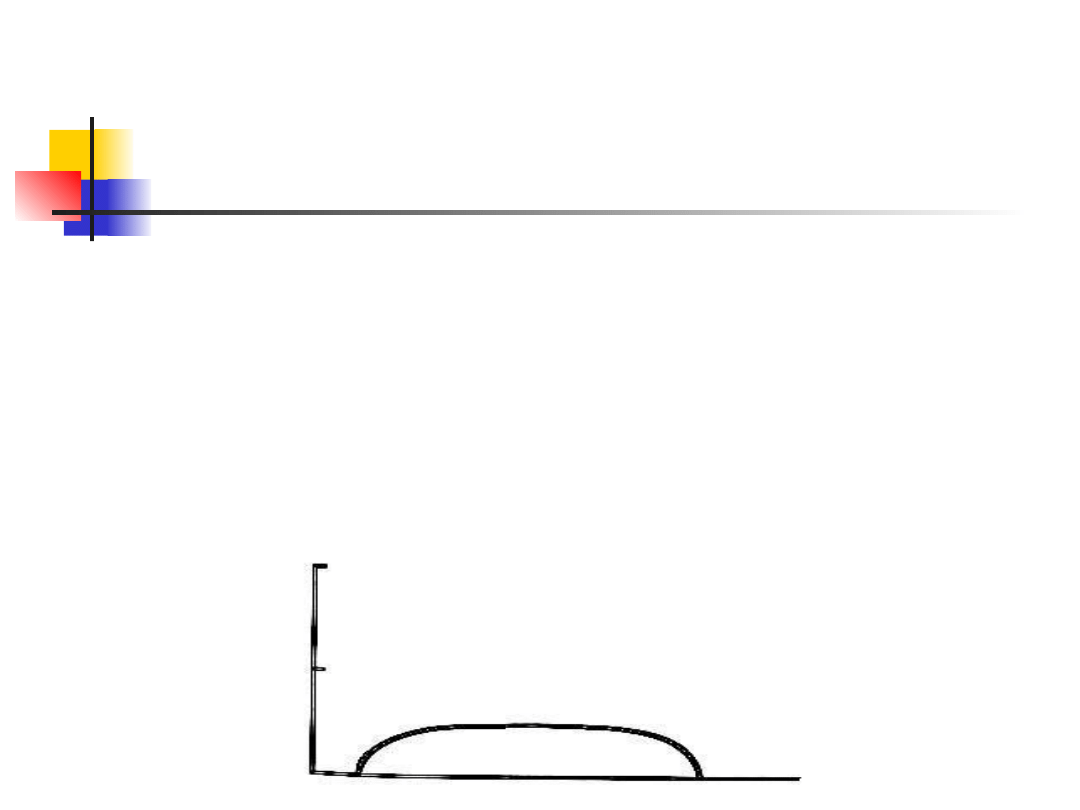
Kurtoza



O platykurtozie (spłaszczeniu)
mówimy, gdy krzywa ma mniej
elementów w środku i końcach, za to
więcej w ramionach niż krzywa
normalna.

Skośność i kurtoza



Przykładowe statystyki mierzące skośność i
kurtozę są zapisywane jako g

1

and g

2

i służą do

reprezentowania parametrów populacji γ

1

i γ

2

.

3

3

1

)

2

)(

1

(

)

(

s

n

n

X

X

n

g

i















4

2

2

4

1

)

1

(

2

)

3

)(

2

(

)

(

3

)

(

s

n

n

X

X

X

X

g

i

i

n

n

n





















Skośność i kurtoza



W normalnym rozkładzie częstości γ

1

i

γ

2

są równe zero.



Ujemne g

1

wskazuje na lewoskośność,

a dodatnie g

1

- prawoskośność.



Ujemne g

2

mówi o wyostrzeniu, zaś

dodatnie g

2

- o spłaszczeniu.



Wartości bezwzględne z g

1

and g

2

nie

mają wielkiego znaczenia.

Ocena skośności i kurtozy za
pomocą kwantyli



Oznaczając i-ty kwartyl jako Q

i

, możemy

zdefiniować współczynnik skośności
Bowley’a (Bowley, 1920):

1

3

2

1

3

2

Q

Q

Q

Q

Q

skewness









wielkość, która może przyjmować
wartości od -1 dla rozkładu ekstremalnie
lewoskośnego, przez 0 dla rozkładu
symetrycznego, do 1 dla rozkładu
prawoskośnego

Ocena skośności i kurtozy za
pomocą kwantyli



Pomiar kurtozy (wyostrzenia) na podstawie
oktyli O

i

(12.5%, 25%, 37.5% itd.) został

zaproponowany przez Moors’a w 1988

1

3

1

3

5

7

)

(

)

(

Q

Q

O

O

O

O

kurtosis













Dla skrajnie spłaszczonego rozkładu
ta wartość wynosi 0; 1.233 dla
normalnego; nieskończoność dla
skrajnie wyostrzonego.

Opisywanie rozkładów
liczbami



Miary położenia



Wartość średnia



Mediana



Miary rozrzutu



Odchylenie standardowe



Kwartyle



Metoda pięciu liczb (wykresy ramkowe)



Poszukiwanie wielkości odstających

Metoda pięciu liczb



Obejmuje najmniejszą obserwację,
pierwszy kwartyl, medianę, trzeci
kwartyl i największą obserwację,
napisane od najmniejszego do
największego:

Minimum Q1 M Q3
Maksimum

Metoda pięciu liczb, cd.



Dostarcza w miarę pełnej informacji o
położeniu i rozrzucie.



Położenie



Mediana



Rozrzut



rozrzut środkowej połowy pomiarów (od
25% do 75%) ukazują kwartyle



Minimum i maksimum pokazują pełny
rozrzut

Wykresy ramkowe
(pudełkowe)



Wykres pięciu liczb



Centralna ramka obejmuje Q1 i Q3



Linia w pudełku to M



Linie wychodzące z ramki dochodzą
do największej i najmniejszej wartości
wśród pomiarów

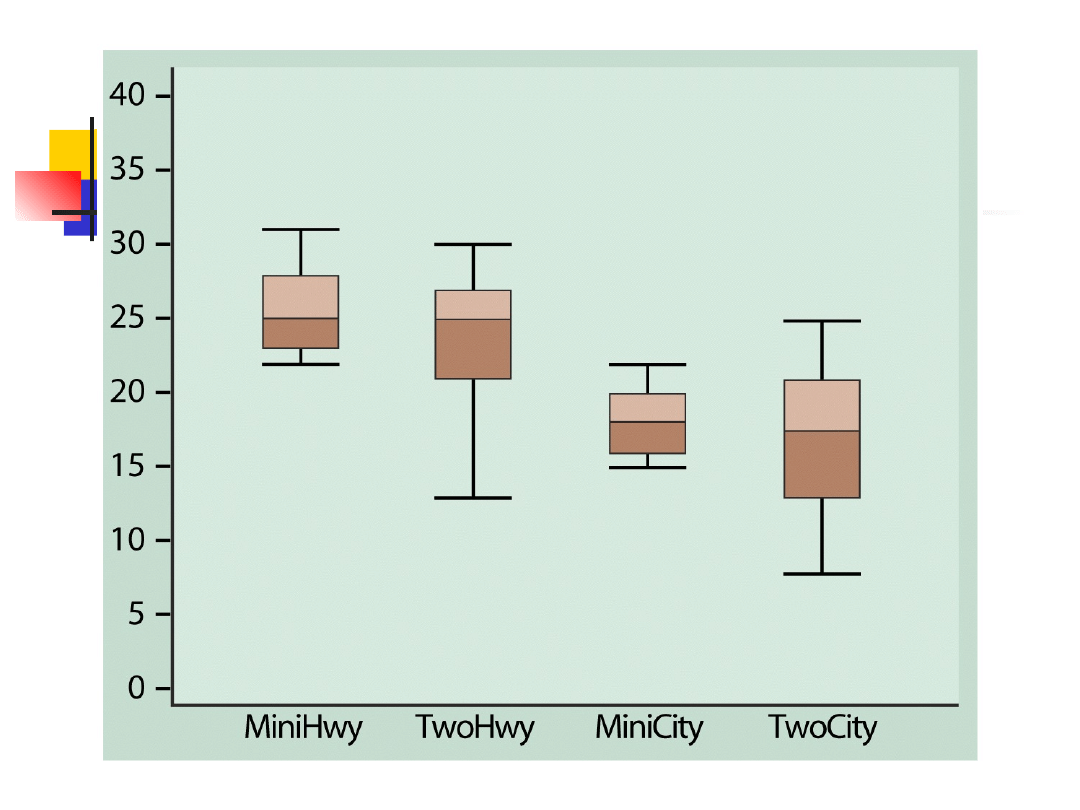
Wykresy ramkowe, cd.



Przedstawiają mniej informacji niż

histogramy i wykresy łodygowe



Używane do porównania więcej niż

jednej serii pomiarów



Analiza wykresu



Znajdź medianę (środek)



Określ rozrzut (między Q1 i Q3;

między min i max)

Punkty odstające



Definicja:



Pomiar odstający to obserwacja, która
istotnie różni się od pozostałych i tym
samym pojawia się podejrzenie, że
pojawiła się jako efekt innego niż
analizowany mechanizmu.

D. Hawkins. Identification of Outliers. Chapman and Hall, London,

1980

Detekcja punktów
odstających



Odległość między kwartylami = zakres
połowy danych = przedział
międzykwartylowy = IQR



IQR = Q3 – Q1



IQR jest odporny na zmiany na końcach
dystrybucji zmiennej losowej.



Wynik może być punktem odstającym,
jeśli ma wartość powyżej Q3+1.5 x IQR
lub poniżej Q1-1.5 x IQR.

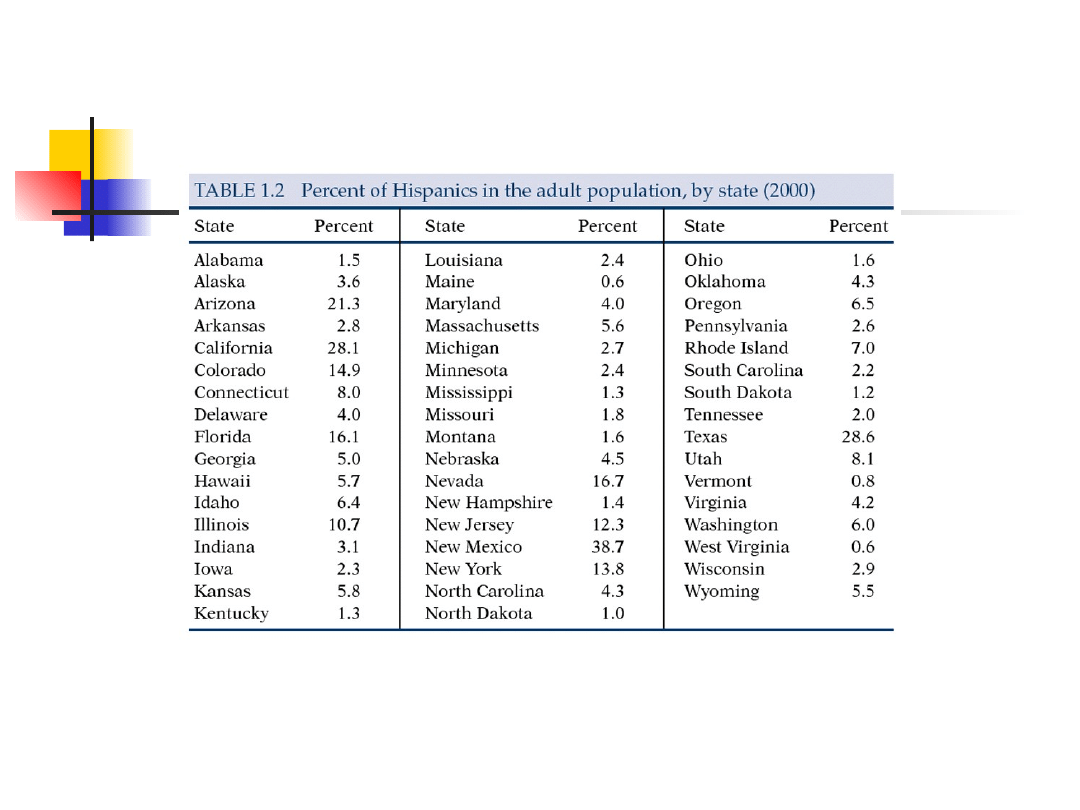
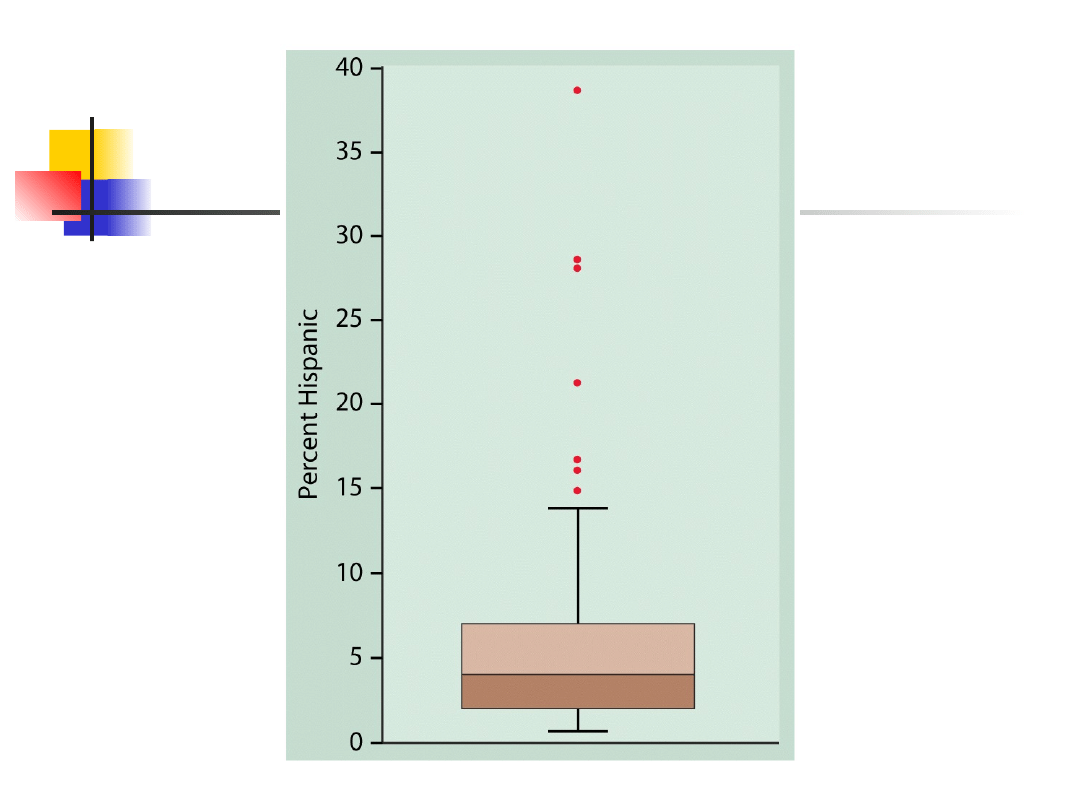
Example: % narodowości
USA



Q1 = 2.0, Q3 = 7.0



IQR = 7.0 – 2.0 = 5.0



Wszystkie wartości poniżej 2.0 – 1.5*5.0 = -5.5 lub

ponad 7.0 + 1.5*5.0 = 14.5 są oznaczone jako

możliwe punkty odstające. Jest 7 takich obserwacji.



To nie zwalnia od własnego osądu – trzeba zerknąć

na dystrybucje i podjąć decyzję o pozostawieniu lub

usunięciu pomiaru z dalszej analizy.



Wygodne narzędzie do oceny dużych zbiorów

danych.

Zmodyfikowany wykres
ramkowy



Zaznacz każdy punkt odstający osobno
używając symboli typu ‘*’ lub ‘o’.



Linie od „pudełka” prowadzą tylko do
największych i najmniejszych pomiarów,
które pozostały po usunięciu punktów
odstających.

Przykład - wzrost



Liczność próbki N = 582



Wartość średnia = 176.16 cm



Mediana = 177 cm



Zakres = 82 cm



Q1 = 170 cm; Q3 = 183 cm



IQR = 13 cm



Odchylenie standardowe = 9.86 cm

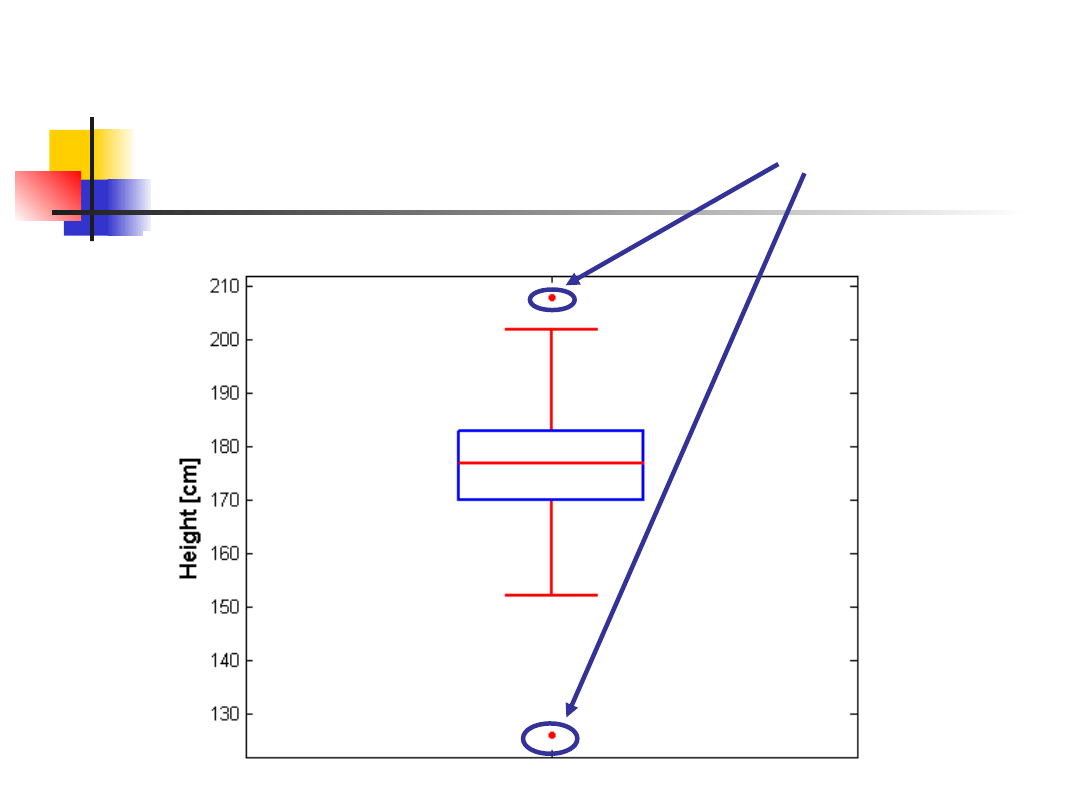
Przykład - wzrost

Dwie wielkości odstające
210 cm i 125 cm

Normalny wykres
kwantylowy



Rozkłady normalne



Dobre modele dla niektórych rozkładów

rzeczywistych danych



Rozkłady niektórych zmiennych są skośne i

dalekie od normalnych



Należy przejrzeć dane!



Sposoby sprawdzenia normalności



Histogramy



Wykresy łodygowe



Normalne wykresy kwantylowe

Konstrukcja normalnego wykresu
kwantylowego

1.

Uporządkuj zaobserwowane dane w porządku

malejącym. Zapisz jakim percentylem danych

jest każda wartość.

2.

Przeprowadź obliczenia dla normalnego rozkładu

żeby znaleźć punkty standardowe z tych

percentyli.

3.

Zaznacz każdy punkt x w zależności od z. Jeśli

rozkład danych jest w przybliżeniu standardowy

normalny, narysowane punkty będą leżały blisko

prostej x=z. Jeśli rozkład danych jest bliski do

innego dowolnego rozkładu normalnego, punkty

będą leżały blisko innej linii, także prostej.

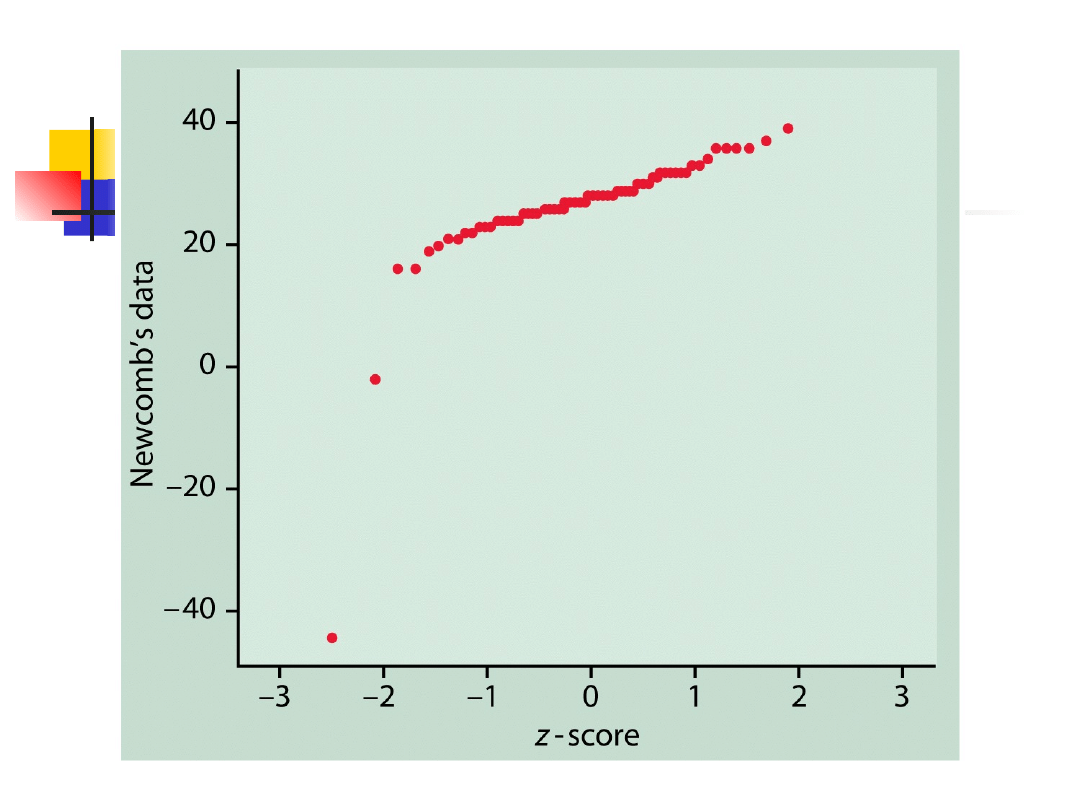
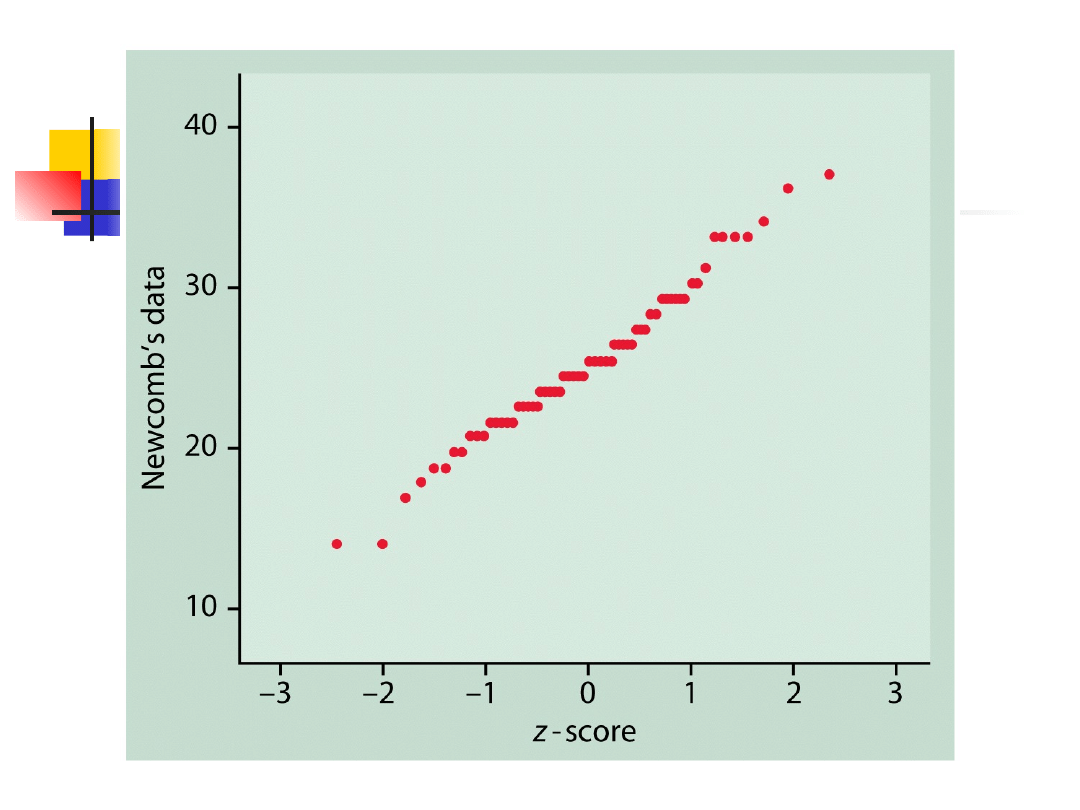
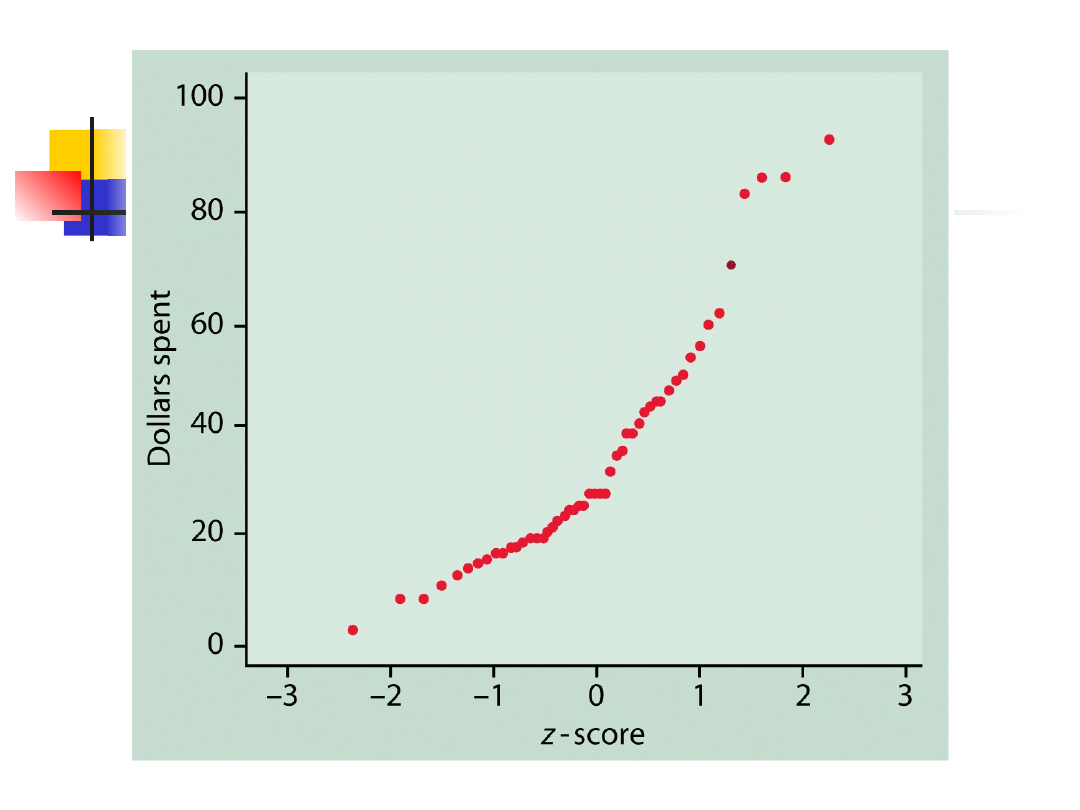
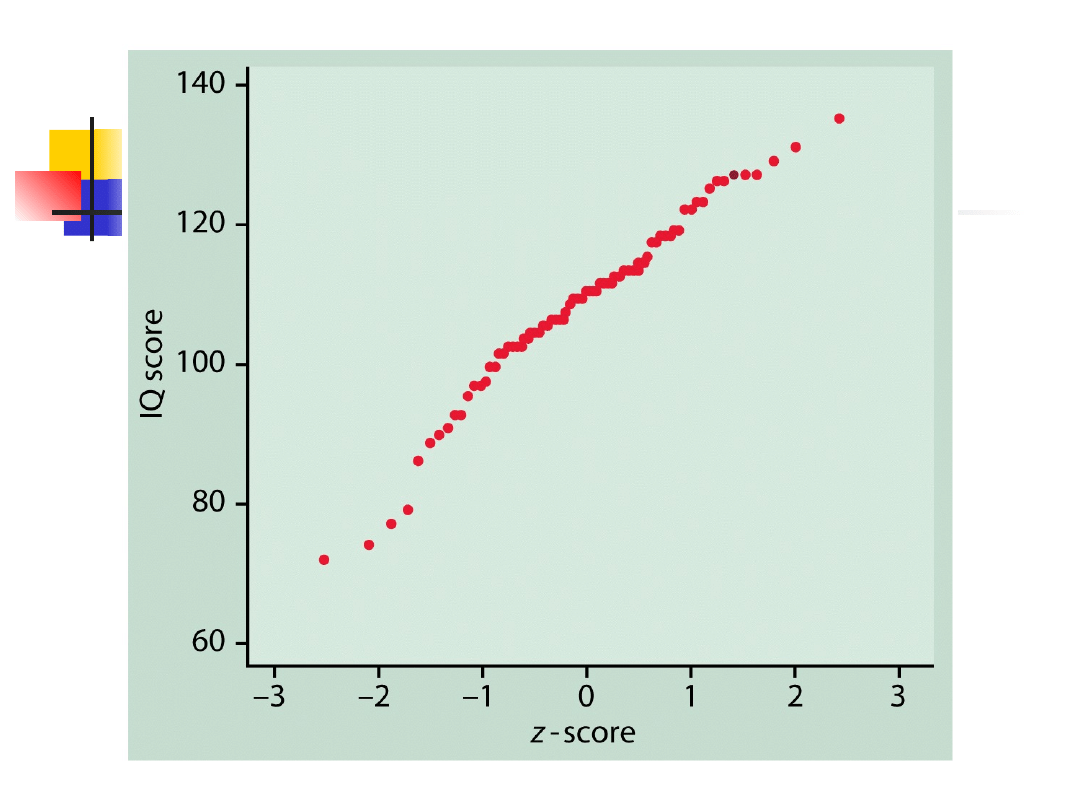
Normalny wykres
kwantylowy



Linia prosta



Dane pochodzą z rozkładu normalnego



Systematyczne odchylenia od linii

prostej



Dane nie pochodzą z rozkładu

normalnego



Punkty odstające ujawniają się jako

punkty leżące daleko od ogólnego

kształtu wykresu.