MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 1

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH -

WYKŁAD 1

Elżbieta Jarzębowska

Zakład Automatyki i Osprzętu Lotniczego

Program wykładu

1. Wprowadzenie – czym jest modelowanie, modele liniowe, nieliniowe, zlinearyzowane.

1.1. Podstawowe reguły i etapy modelowania.
1.2. Skutki założeń modelowych – przykład – koło sztywne i koło ogumione.
1.3. Skutki linearyzacji modelu nieliniowego – przykład.

Spis zalecanej literatury pomocniczej do wykładu. Przewodnik po literaturze.

2.

Klasyfikacje modeli dla układów mechanicznych.

2.1

Modele nieliniowe holonomiczne - przykłady.

2.2

Modele nieliniowe nieholonomiczne – przykłady.

2.2.1 modele kinematyczne
2.2.2 modele dynamiczne.

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 2

3.

Modele nieliniowe holonomiczne.
3.1

Teoria – równania Lagrange’a II rodzaju.

3.2

Teoria – kanoniczne równania Hamiltona.

3.3

Zalety i ograniczenia niektórych równań; ciekawostka – dlaczego stosuje się

równania Routha do symulacji ruchu modelu satelity po orbicie.

3.4

Manipulator wieloczłonowy – przykład wykładowy – zbudować model dynamiki.

Projekt domowy - samodzielne zbudowanie modelu dynamiki dla zadanego przykładu,
wykonanie symulacji numerycznej, animacji ruchu.
Pracochłonność projektu domowego – 10 godzin.

4.

Modele nieliniowe nieholonomiczne.
4.1

Kinematyczne i dynamiczne modele układów nieholonomicznych.

4.2

Więzy – klasyfikacja więzów w mechanice i nie tylko.

4.3

Teoria – równania Lagrange’a z mnożnikami.

4.4

Teoria – równania Maggiego i Kane’a.

4.5

Teoria – równania Boltzmanna-Hamela.

4.6

Manipulator wieloczłonowy z więzami geometrycznymi – przykład wykładowy –

zbudować model dynamiki.

4.7

Pojazd kołowy - przykład wykładowy – zbudować model dynamiki.

4.8

Model układu biomechanicznego - przykład wykładowy – zbudować model

kinematyki skoczka z trampoliny i model dynamiki robaka z łuską.

4.9

Model „pojazdu kosmicznego” - przykład wykładowy – zbudować model dynamiki.

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 3

Projekt domowy – zbudować, dla zadanego przykładu układu technicznego, nieliniowy
model dynamiki, przeprowadzić symulację ruchu, pokazać animację.
Pracochłonność projektu domowego – 10 godzin.

5.

Reprezentacja równań więzów w analizie numerycznej modeli nieliniowych.

6.

Aspekty numeryczne rozwiązywania równań ruchu układów mechanicznych.

7.

Podsumowanie kursu.

Rozdanie projektów domowych końcowych. Pracochłonność projektu domowego – 15
godzin.

Cele kształcenia:

1. Przekazanie porcji wiedzy z zakresu metod modelowania nieliniowego układów mechanicznych,

typowych w zastosowaniach inżynierskich. Zakres przewidzianej porcji wiedzy obejmuje modelowanie
układów holonomicznych i nieholonomicznych, na poziomie kinematyki i dynamiki.

2. Pokazanie, poprzez strukturę wykładu i dobór przykładów, zakresu zastosowań różnych metod

modelowania i sposobu podejścia do budowy i analizy różnych modeli nieliniowych.

3. Pokazanie słuchaczom i nauczenie ich „sposobu podejścia” do modelowania, który będą mogli

wykorzystać w pracy praktycznej jako inżynierowie i w pracy naukowej.

4. Wykład nie jest wykładem z mechaniki analitycznej mimo, że metody mechaniki analitycznej będą

wprowadzane i wykorzystywane w modelowaniu.

5. Pokazanie, że modelowanie jest pewną sztuką opartą jednak na racjonalnych regułach.

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 4

WARUNKI ZALICZENIA: zadania domowe i projekt końcowy.

Zalecana literatura (

możliwa do zdobycia, bez literatury o znaczeniu historycznym

):

1. Bloch, A.M. 2003. Nonholonomic mechanics and control, New York: Springer-Verlag.

2. Brockett, R.W. 1983. Asymptotic stability and feedback stabilization. In Differential

geometric control theory, ed. R.W. Brockett, R.S. Millman and H.J. Sussmann, Boston, MA:

Birkhauser.

3. Chaplygin, S.A. 1897. About a motion of a heavy body on a horizontal plane. In Izbrannye

trudy klassiki nauki, 363-375. Moscow: Nauka (in Russian).

4. de Jalon, J.G. and E. Bayo. 1994. Kinematic and dynamic simulation of multibody systems.

Mech. Eng. Series. Berlin: Springer-Verlag.

5. Dobronravov, V.V. 1970. Foundations of mechanics of non-holonomic systems. Moscow:

Vyschaja Shkola (in Russian).

6. Galiulin, A.C. 1971. Design of systems for programmed motion. Moscow: Nauka (in

Russian).

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 5

7. Gutowski, R. 1971. Analytical mechanics, Warsaw: PWN (in Polish) lub Mechanika

analityczna.

8. Jarzębowska, E. and N. H. McClamroch. 2000. On nonlinear control of the Ishlinsky

problem as an example of a nonholonomic non-Chaplygin system. In Proc. Am. Control

Conf. 3249-3253. Chicago, IL.

9. Jarzębowska, E. 2002. On derivation of motion equations for systems with nonholonomic

high-order program constraints. Multibody System Dynamics 7(3):307-329.

10. Jarzębowska, E. 2005. Dynamics modeling of nonholonomic mechanical systems: theory

and applications. Nonlinear Analysis 63 (5-7):185-197.

11. Jarzębowska, E. 2006. Control oriented dynamic formulation of robotic systems with

program constraints. Robotica 24(1):61-73.

12. Jarzębowska, E. and R. Lewandowski. 2006. Modeling and control design using the

Boltzmann-Hamel equations: a roller-racer example. In Proc. 8th IFAC Symposium on Robot

Control, SYROCO.

13. Jarzębowska, E. 2007. Stabilizability and motion tracking conditions for nonholonomic

control systems. Mathematical Problems in Engineering. Hindawi Publishing Corp.

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 6

14. Kamman, J.W. and R. L. Huston 1984. Dynamics of constrained multibody systems. J.

Appl. Mech. 51:899-903.

15. Kane, T.R. and D. L. Levinson. 1985. Dynamics - theory and applications. McGraw Hill.

16. Kane, T.R. and D. L. Levinson. 1996. The Use of Kane’s Dynamical Equations in

Robotics. Int. J. Robot. Res. 2(3):3-21.

17. Korieniev G.V. 1964. Introduction to mechanics of a controllable body. Moscow: Nauka, (in

Russian).

18. Kwatny, H.G. and G.L. Blankenship. 2000. Nonlinear control and analytical mechanics, a

computational approach. Boston: Birkhauser.

19. Lancos, C. 1986. The variational principles of mechanics. 4th ed. New York: Dover Publ.

20. Layton, R.A. 1998. Principles of analytical system dynamics. New York: Springer-Verlag.

21. Lewis, A.D., J.P. Ostrowski, R.M. Murray and J. Burdick. 1994. Nonholonomic

mechanics and locomotion: The snakeboard example. In IEEE Int. Conf. Robot. Automat.,

2391-2400.

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 7

22. Lewis, F.L., C. T. Abdallah and D. M. Dawson. 1996. Control of robot manipulators. New

York: Macmillan Publ. Comp.

23. Marsden, J.E. and T.S. Ratiu 1992. An introduction to mechanics and symmetry. Texts in

Appl. Math. 17, Springer-Verlag.

24. Moon, F.C. 1998. Applied dynamics. John Wiley & Sons Inc.

25. Murray, R.M., Z.X. Li, and S.S. Sastry. 1994. A mathematical introduction to robotic

manipulation. Boca Raton, Florida: CRC Press.

26. Nejmark, J.I. and N.A. Fufaev. 1972. Dynamics of nonholonomic systems. Providence,

Rhode Island: Am. Math. Society.

27. Nielsen, J. 1935. Vorlesungen uber elementare mechanik. Berlin: Verlag von J. Springer.

28. Nijmeijer, H. and A. van der Schaft. 1990. Nonlinear dynamical control systems. New

York: Springer-Verlag.

29. Papastavridis, J.G. 2002. Analytical mechanics, a comprehensive treatise on the dynamics

of constrained systems; for engineers, physicians, and mathematicians. New York: Oxford

University Press.

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 8

30. Pars, L.A. 1965. Treatise of analytical dynamics. London: W. Heinemann, Ltd.

31. Slotine, J.J. and W. Li. 1991. Applied nonlinear control. New Jersey: Prentice Hall,

Englewood Cliffs.

32. Sontag, E.D. 1990. Mathematical control theory. New York: Springer.

33. Spong, M.W. and M. Vidyasagar. 1989. Robot control and dynamics. New York: Wiley.

34. Udwadia, F. and R. Kalaba. 1996. Analytical dynamics - a new approach. New York:

Cambridge Univ. Press.

35. Yun, X. and N. Sarkar. 1998. Unified formulation of robotic systems with holonomic and

nonholonomic constraints. IEEE Trans. Robot. Automat., 14(4):640-650.

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 9

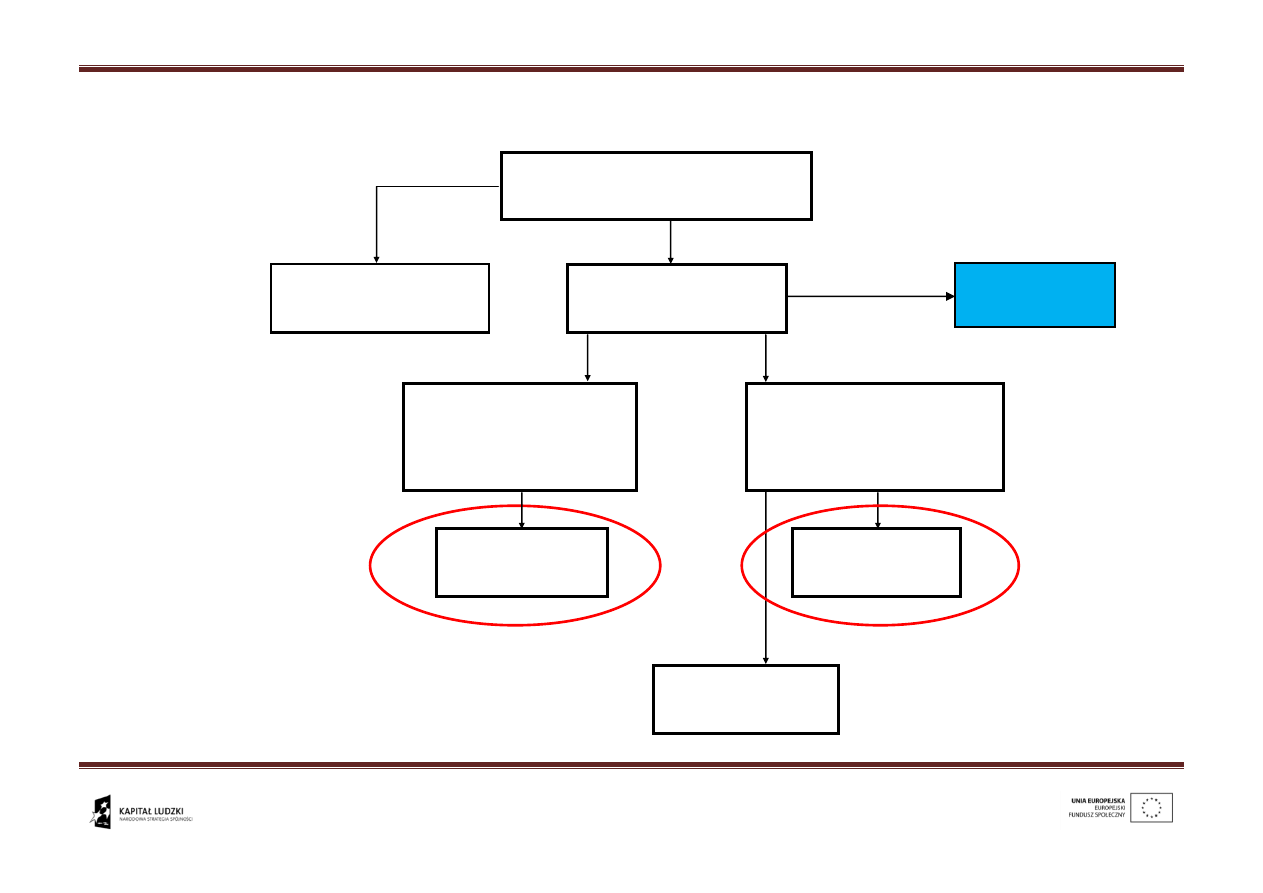
1. Wprowadzenie:

M

ODELE UKŁADÓW

MECHANICZNYCH

Modele liniowe

Modele

nieliniowe

Modele

holonomiczne

(roboty, manipulatory)

Modele

nieholonomiczne

(pojazdy kołowe,

kosmiczne)

Modele

kinematyczne

Modele

dynamiczne

Model

Modele

dynamiczne

Model

linearyzacja

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 10

Dlaczego interesują nas modele nieliniowe? Przecież modele liniowe
są takie proste, przewidywalne (np. badanie stateczności), tanie pod
wieloma względami i jest dla nich rozwiniętych bardzo wiele
narzędzi badania i opisu.......

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 11

Podstawowe „reguły” i etapy modelowania

Modelowanie jest jak uprawianie sportu – im więcej ćwiczysz, tym lepiej ci idzie.....
Modelowanie jest też jak sztuka – wymaga wyczucia, zmysłu obserwacji........

1. Jaki obiekt będzie modelowany? Wyodrębnienie obiektu modelowania.
2. Modelowanie jest procesem celowym – po co buduję model? Do analizy ruchu? Do

sterowania? Do przeprojektowania? Do......?

3. Cel modelowania determinuje model fizyczny.
4. Budowa modelu fizycznego. Ile wersji modelu buduję?
5. Cel modelowania determinuje model matematyczny (współrzędne, model na poziomie

kinematyki, dynamiki.....)

6. Budowa modelu (modeli) matematycznego.
7. Identyfikacja (mamy modelowanie nieliniowe).
8. Symulacja modelu (badania modelu).
9. Weryfikacja z obiektem rzeczywistym. (Powrót do 3?)

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 12

Skutki linearyzacji modelu nieliniowego – przykład

Założenia: rozważmy przykład z zakresu sterowania i zlinearyzujemy model kinematyczny
monocyklu. Model monocyklu jest prosty, lecz jest kinematycznie ekwiwalentny modelowi
platformy dwukołowej lub dwukołowego pojazdu.
Zobaczmy, co z tego wyniknie........



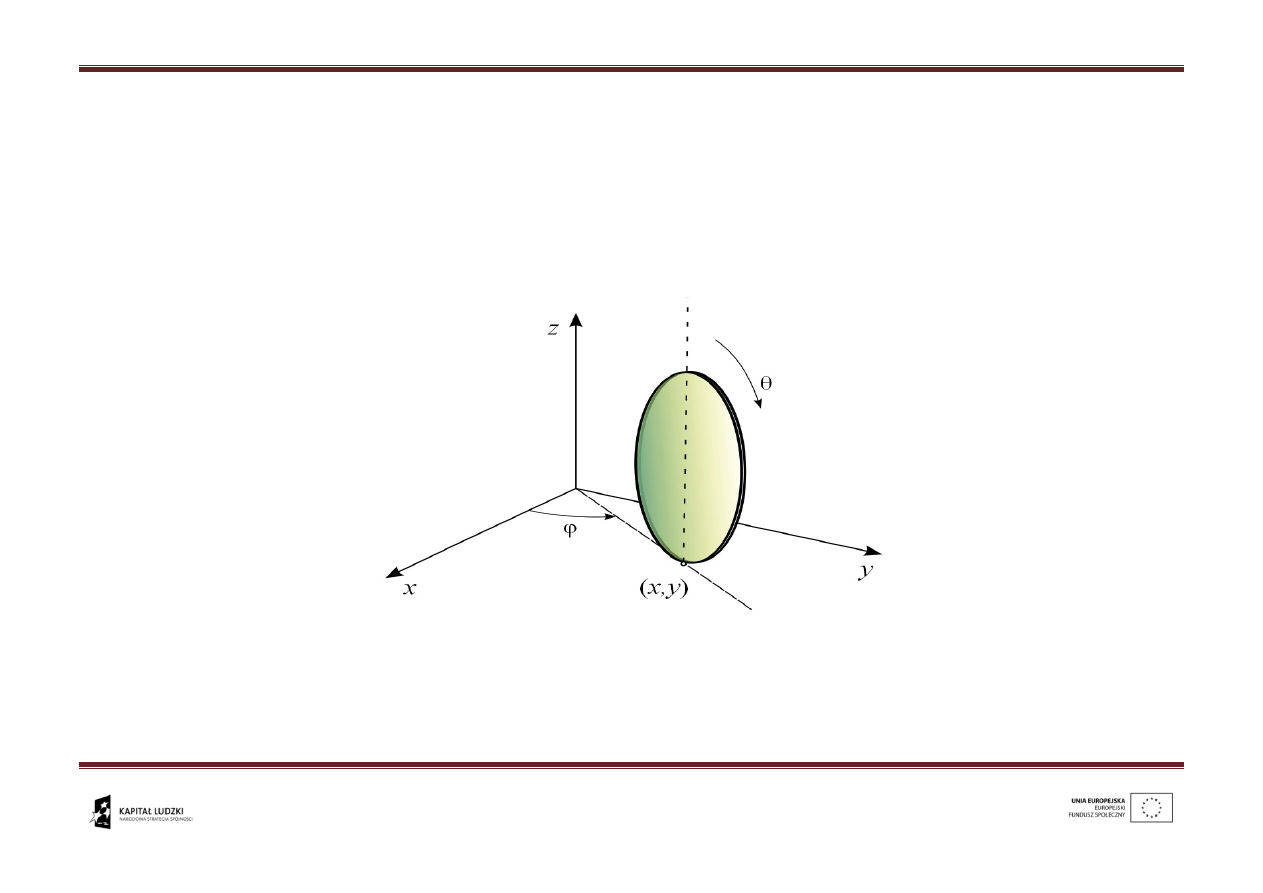
- kąt odchylenia (heading angle) koła, mierzony od osi x,



- kąt obrotu własnego (roll angle) mierzony of ustalonego odniesienia,

(x,y) – współrzędne punktu kontaktu koła z podłożem.

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 13

Warunek toczenia sztywnego koła bez poślizgu (kinematyka, semestr II )
formułujemy w postaci tzw. więzów materialnych nieholonomicznych o
postaci









sin

r

y

,

cos

r

x













Kinematyczny model sterowania ma postać

Ż(q)= g

1

(q)v + g

2

(q)ω,

czyli

v – prędkość liniowa koła,
ω – prędkość kątowa koła wokół osi pionowej,
dwa wejścia sterujące – dwie prędkości.









































































1

0

0

0

v

sin

cos

y

x







MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 14

Każdy wie, że monocyklem można jeździć – można nim sterować i
dostępna jest cała przestrzeń konfiguracji (zajedziemy wszędzie, choć
nie z „każdą” prędkością). Badamy tzw. sterowalność w punkcie
(controllability at a point).

Linearyzacja styczna nieliniowego modelu kinematyki w punkcie q

e

(tangent linearization) pozwala uzyskać model liniowy

gdzie

e

q

q

q~





.

Powyższy model jest niesterowalny! (Teoria sterowania – kryterium
LARC).
Macierz dystrybucji





3

2

1

g

g

g





traci rząd.



















































1

0

0

0

v

sin

cos

q~

e

e



MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 15

Zobaczmy, że tylko w przypadku ogólnym, macierz dystrybucji zbudowana
z wektorów g

1

, g

2

i ich nawiasu Liegu, dla

ma pełny rząd.

Rzeczywiście:











































0

2

1

1

2

2

1

3





cos

sin

g

q

g

g

q

g

g

g

g

Wtedy LARC jest spełnione globalnie( w każdym q

e

), ponieważ





3

2

1

g

g

g





i

rank [g1 g2 [g1, g2] ] = 3 = n.









































































1

0

0

0

v

sin

cos

y

x







g

1

g

2

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 16

WNIOSKI:

1. Model uproszczony jest niesterowalny!
2. Aby zaprojektować sterowanie, trzeba korzystać z modelu

nieliniowego i narzędzi sterowania nieliniowego (żaden algorytm
sterowania liniowego nie jest tu do zastosowania!!).

3. Do innych celów, model zlinearyzowany może byłby dobry.....czyli nie

zawsze można, ot po prostu...., zlinearyzować.....

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 17

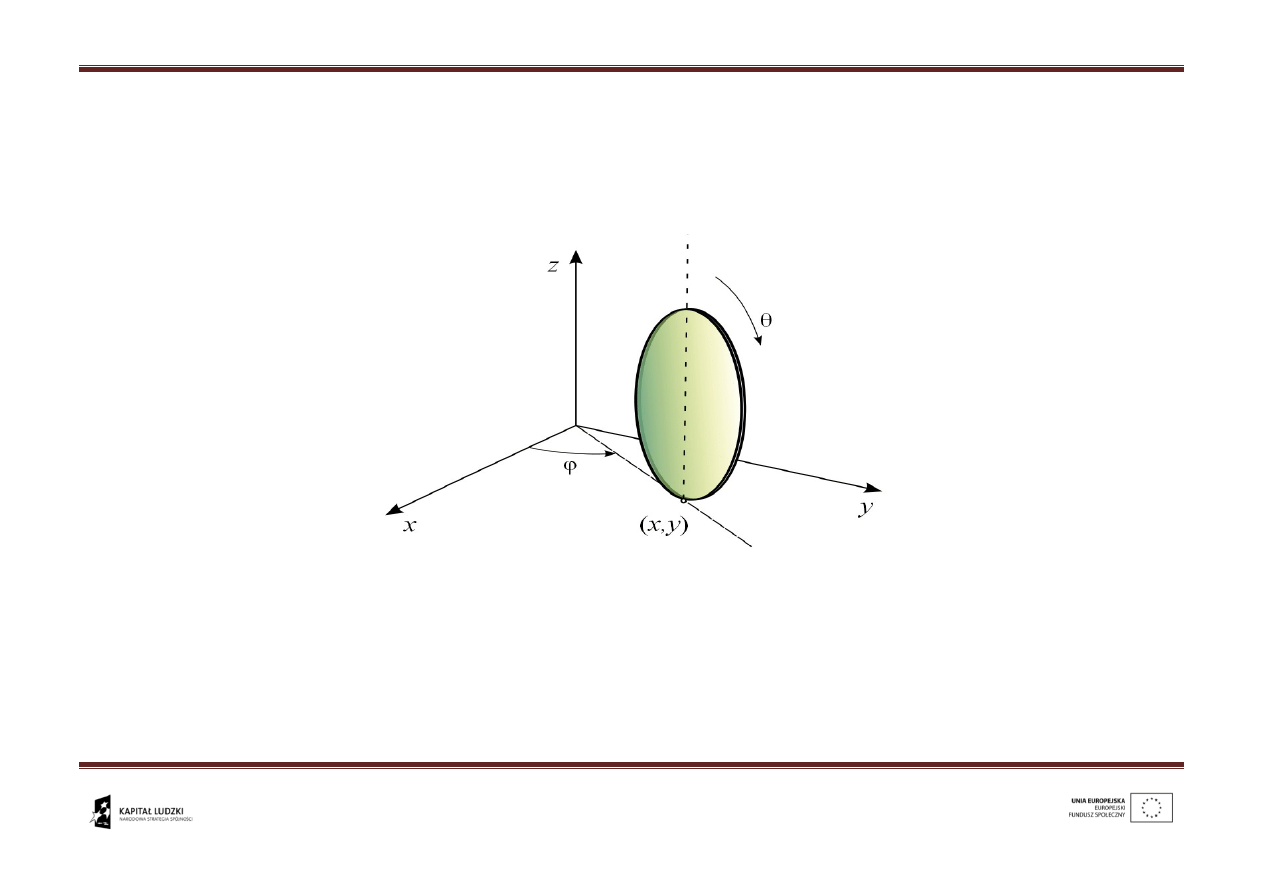
Skutki założeń modelowych – przykład – koło sztywne i koło
ogumione

Weźmy koło sztywne z poprzedniego przykładu

i dodatkowe warunki, które są konsekwencją założenia sztywności koła i
toczenia bez poślizgu, czyli









sin

r

y

,

cos

r

x













.

To założenie czyni

model układu nieholonomicznym.
W dalszej części wykładu zobaczymy, jak zbudować model matematyczny
dla układu nieholonomicznego.

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 18

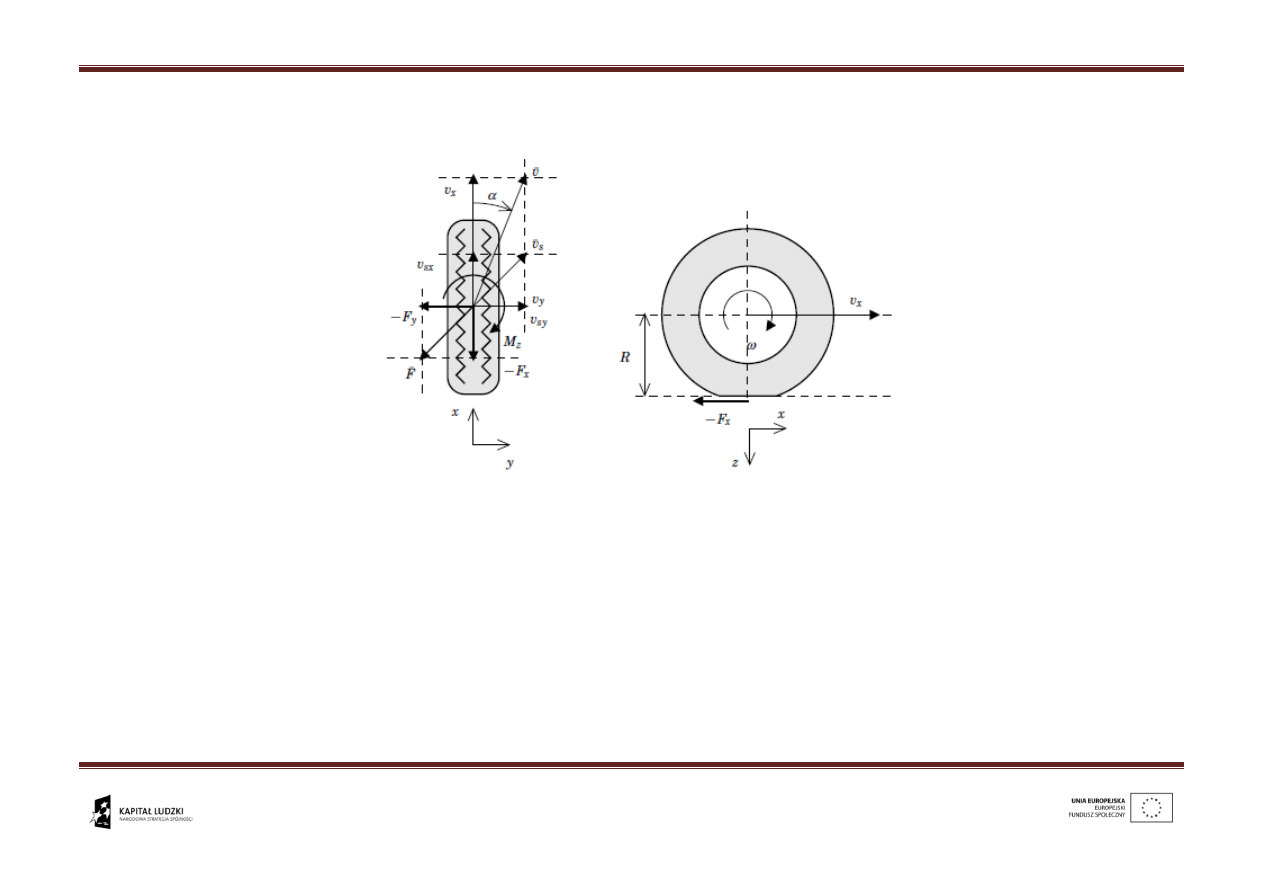
Teraz załóżmy, że koło jest ogumione i wygląda, jak na rys. poniżej.

(

wg. Tire modeling and friction estimation, J. Svendenius, Lund University, Dept. Of Automatic

Control, 2007)

Wyznaczenie F

x

, F

y

, momentów sił jest opisane wg. wielu teorii, np. przez tzw.

magic formula Pacejki. Nie ma już równań więzów nieholonomicznych, jak w
poprzednim modelu.
Koło ogumione jest holonomiczne!

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 19

Prosty przykład wyboru współrzędnych do modelu matematycznego
zdeterminowanych sposobem napędzania manipulatora

Wybierz współrzędnie, gdy:
- dwuczłonowy manipulator napędzany jest jednym silnikiem z podstawy,
- dwuczłonowy manipulator napędzany jest silnikami umieszczonymi w
przegubach

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 20

Spis zalecanej literatury do wykładu 1:

1. Bloch, A.M. 2003. Nonholonomic mechanics and control, New York: Springer-Verlag.

2. de Jalon, J.G. and E. Bayo. 1994. Kinematic and dynamic simulation of multibody

systems. Mech. Eng. Series. Berlin: Springer-Verlag.

3. Dobronravov, V.V. 1970. Foundations of mechanics of non-holonomic systems. Moscow:

Vyschaja Shkola (in Russian).

4. Gutowski, R. 1971. Analytical mechanics, Warsaw: PWN (in Polish) lub Mechanika

analityczna.

5. Jarzębowska, E. Mechanika analitczna, skrypt PW, oficyna wydawnicza PW, 2003.

6. Jarzębowska, E. and R. Lewandowski. 2006. Modeling and control design using the

Boltzmann-Hamel equations: a roller-racer example. In Proc. 8th IFAC Symposium on

Robot Control, SYROCO.

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 21

7. Kane, T.R. and D. L. Levinson. 1985. Dynamics - theory and applications. McGraw Hill.

8. Kane, T.R. and D. L. Levinson. 1996. The Use of Kane’s Dynamical Equations in

Robotics. Int. J. Robot. Res. 2(3):3-21.

9. Kwatny, H.G. and G.L. Blankenship. 2000. Nonlinear control and analytical mechanics, a

computational approach. Boston: Birkhauser.

10.

Lancos, C. 1986. The variational principles of mechanics. 4th ed. New York: Dover

Publ.

11.

Layton, R.A. 1998. Principles of analytical system dynamics. New York: Springer-

Verlag.

12.

Lewis, F.L., C. T. Abdallah and D. M. Dawson. 1996. Control of robot manipulators.

New York: Macmillan Publ. Comp.

13.

Moon, F.C. 1998. Applied dynamics. John Wiley & Sons Inc.

14.

Murray, R.M., Z.X. Li, and S.S. Sastry. 1994. A mathematical introduction to robotic

manipulation. Boca Raton, Florida: CRC Press.

MODELOWANIE NIELINIOWYCH UKŁADÓW MECHANICZNYCH

[Type text]

page 22

15.

Nejmark, J.I. and N.A. Fufaev. 1972. Dynamics of nonholonomic systems. Providence,

Rhode Island: Am. Math. Society.

16.

Papastavridis, J.G. 2002. Analytical mechanics, a comprehensive treatise on the

dynamics of constrained systems; for engineers, physicians, and mathematicians. New

York: Oxford University Press.

17.

Pars, L.A. 1965. Treatise of analytical dynamics. London: W. Heinemann, Ltd.

18.

Spong, M.W. and M. Vidyasagar. 1989. Robot control and dynamics. New York: Wiley.

19.

Udwadia, F. and R. Kalaba. 1996. Analytical dynamics - a new approach. New York:

Cambridge Univ. Press.