Podstawy analizy statystycznej dla potrzeb 

administracji publicznej

Wykład 5

Miary 

asymetrii 

służą 

do 

badania 

kierunku 

zróżnicowania wartości zmiennej

.

Z  punktu  widzenia  potrzeb  analizy  statystycznej 
istotny  jest  nie  tylko  przeciętny  poziom  (miary 
położenia)  i  wewnętrzne  zróżnicowanie  zbiorowości 
(miary 

zróżnicowania), 

ale 

również 

to, 

czy 

przeważająca  liczba  jednostek  znajduje  się  powyżej, 
czy  poniżej  przeciętnego  poziomu  badanej  cechy. 
Problem  ten  wiąże  się  z  oceną  asymetrii  (skośności) 
rozkładu.

x

x

D

M

x





x

i

n

i

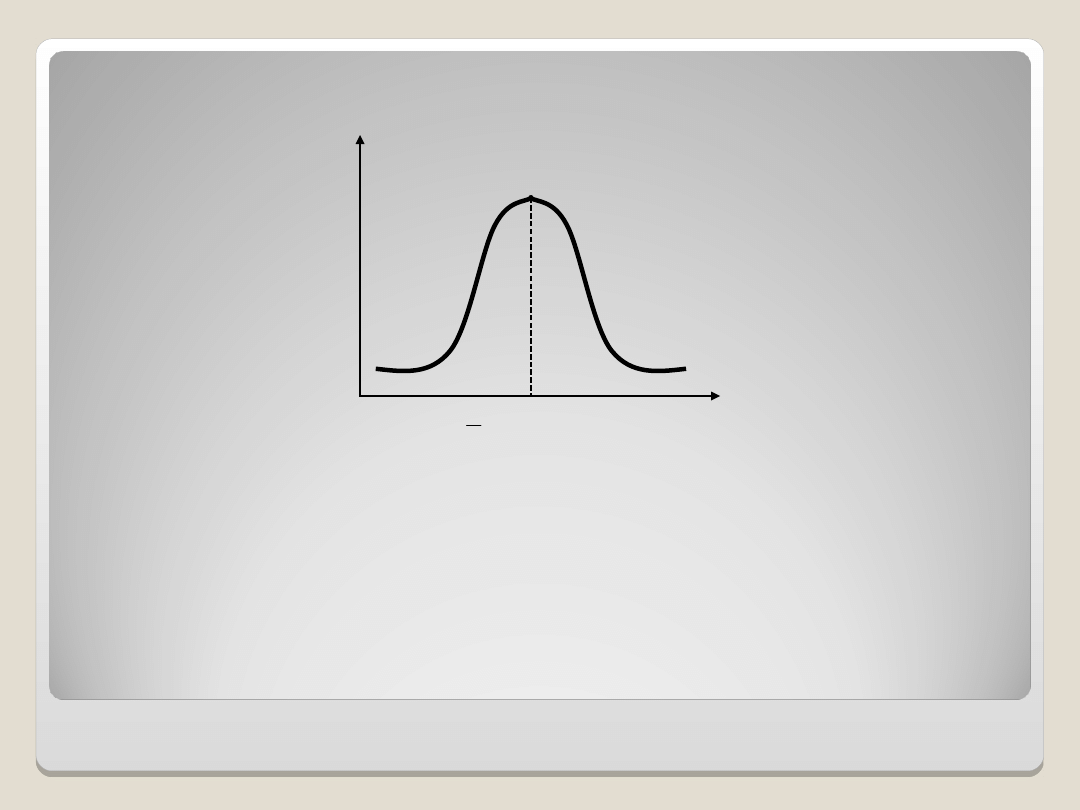
Rozkład symetryczny

Po tyle samo jednostek ma wartości większe

 i mniejsze od poziomu średniego.

x

i

n

i

x

D

x

M

x

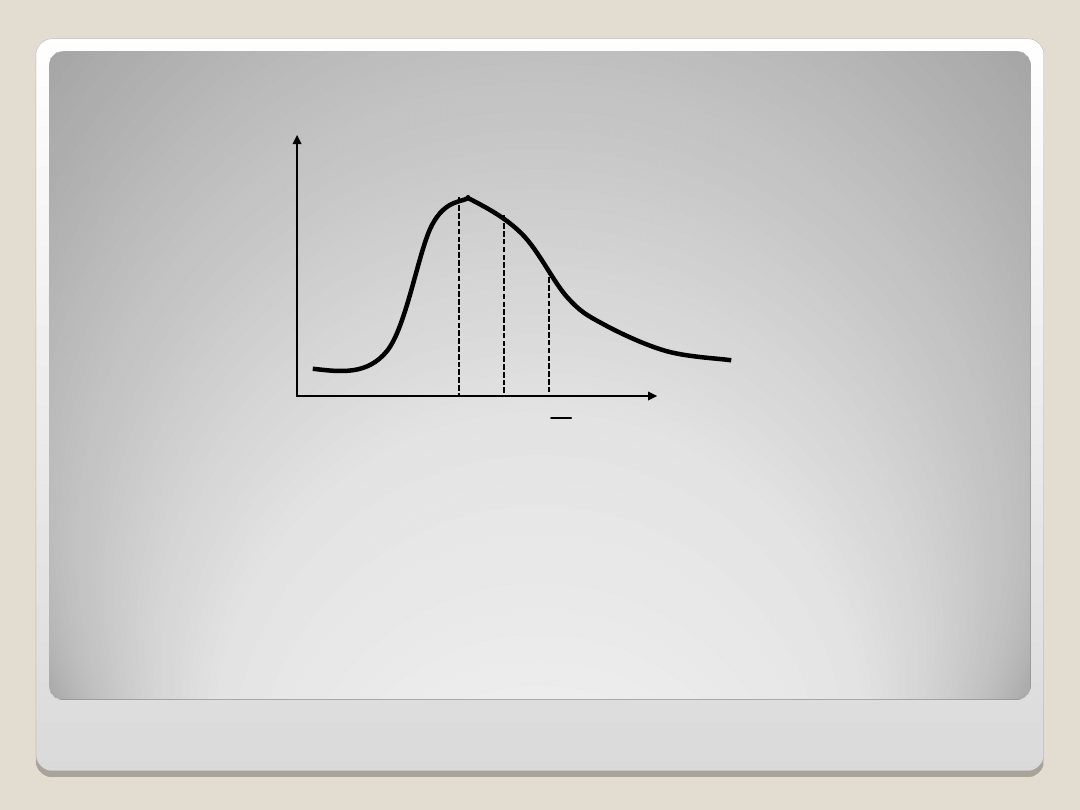
Rozkład o asymetrii prawostronnej

Większość  jednostek ma wartości mniejsze od poziomu 
średniego.

x

i

n

i

x

D

x

M

x

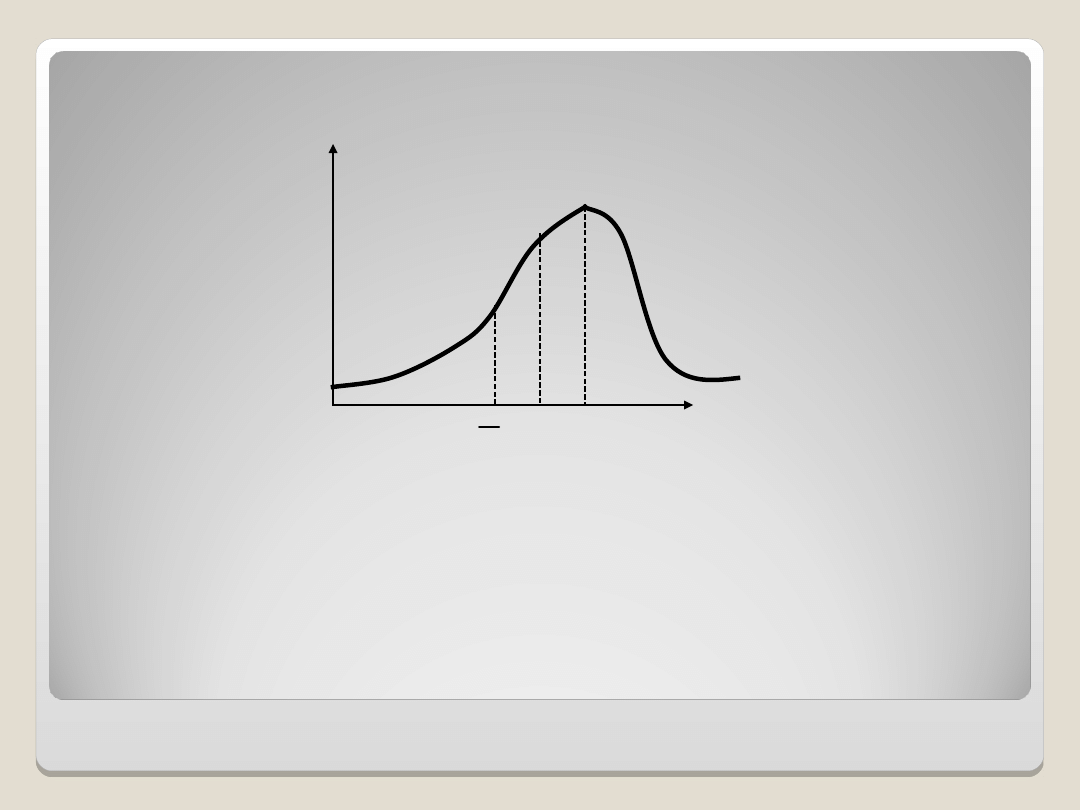
Większość jednostek ma wartości większe

  od poziomu średniego.

Rozkład o asymetrii lewostronnej

Miary asymetrii (skośności)

Miary asymetrii (skośności)

Ocena  asymetrii  to  rozstrzygnięcie  czy 
przeważająca  liczba  jednostek  ma  wartości 
zmiennej  powyżej  czy  poniżej  średniej 
arytmetycznej.

Rozkład symetryczny:

Rozkład o asymetrii  dodatniej 
(prawostronnej):

Rozkład o asymetrii  ujemnej (lewostronnej):

D

Me

x





x

Me

D





D

Me

x





Wskaźniki asymetrii 
(skośności)

D

x

W

__

sk







 



1

3

p

sk

Q

Me

Me

Q

W













N

x

x

W

N

1

i

3

i

3

k

sk













•  mieszany

•  klasyczny

•  pozycyjny

Wskaźniki asymetrii 
(skośności)

0

W

symetria

sk





dodatnia

asymetria

0

W

sk





ujemna

asymetria

0

W

sk





Są to bezwzględne miary asymetrii i określają 
jedynie kierunek asymetrii:

Współczynniki asymetrii (skośności)

0









p

k

s

A

A

A

symetria

dodatnia

asymetria

A

,

A

,

A

p

k

s



 0

ujemna

asymetria

A

,

A

,

A

p

k

s



 0

s

D

x

A

__

s







 



Q

Q

Me

Me

Q

A

p

2

1

3









2

3

2

3

3

3











s

A

k

•  mieszany

•  klasyczny

•  pozycyjny

Są  to  względne  miary  asymetrii  (niemianowane)  i 
określają kierunek i siłę asymetrii, a zatem służą do 
porównań asymetrii różnych rozkładów. Mamy:

Współczynniki asymetrii (skośności)

Siła asymetrii           :
(0,00-0,30> - asymetria słaba,
(0,30-0,70> - asymetria umiarkowana,
(0,70 -1,00> - asymetria silna.

A

Wyznaczanie miar asymetrii dla szeregu 

rozdzielczego punktowego

.

1

Q

,

42

,

1

s

,

3

Q

,

2

Q

,

1

Q

,

2

D

,

09

,

2

x

3

2

1















09

,

0

2

09

,

2

D

x

Wsk











Asymetria rozkładu 
jest dodatnia, oznacza 
to, że liczba napraw 
większości 
komputerów jest 
mniejsza od średniej.

0

)

1

2

(

)

2

3

(

)

Q

Q

(

)

Q

Q

(

W

1

2

2

3

p

sk



















Rozkład jest symetryczny.

06

,

0

42

,

1

2

09

,

2

s

D

x

A











Siła asymetrii jest słaba.

Wyznaczanie miar asymetrii dla 
szeregu rozdzielczo-
przedziałowego 

•Współczynnik mieszany

x

x

s

S

D

x

A





75

86

,

164

88

,

246







x

x

D

S

y

04

,

1

86

,

164

75

88

,

246







s

A

Interpretacja: Asymetria prawostronna, bardzo silna.

Większość komputerów miała koszt napraw mniejszy od średniego 
kosztu napraw.

Wyznaczanie miar asymetrii dla 
szeregu rozdzielczo-przedziałowego 
(c.d.) 

•Współczynnik pozycyjny

1

3

3

1

2

Q

Q

M

Q

Q

A

x

Q









71

,

385

33

,

233

89

,

88

3

1







Q

M

Q

y

03

,

0

89

,

88

71

,

385

33

,

233

2

71

,

385

89

,

88













Q

A

Interpretacja:

Dla komputerów tworzących dwie środkowe ćwiartki zbiorowości koszt 
napraw charakteryzuje się rozkładem o bardzo słabej asymetrii 
prawostronnej.

24. Analizie podlegają subwencje ogólne przypadające na

1 mieszkańca w dwóch województwach. Otrzymano

następujące wyniki: w pierwszym województwie średnia

równa 70 zł/mieszk., dominanta równa 60 zł/mieszk.; w

drugim województwie średnia równa 40 zł/mieszk.,

dominanta równa 50 zł/mieszk.

a)  subwencje ogólne na mieszkańca większości gmin

województwa 1 są większe od średniej,

b)  subwencje ogólne na mieszkańca większości gmin

województwa 2 są większe od średniej,

c)  subwencje ogólne na mieszkańca większości gmin

województwa 2 są mniejsze od średniej.

25. Otrzymano następujące wyniki: kwartyl

pierwszy równy 4, kwartyl drugi równy 5, a

trzeci równy 7. Wyniki te przedstawiają

rozkład:

a)  symetryczny,
b)  asymetryczny, dodatni,
c)  asymetryczny, ujemny.

26.  Otrzymano  następujące  wyniki:  średnia

równa  4,  dominanta  równa  6,  wariancja

równa 16. Wyniki te przedstawiają rozkład:

a)  symetryczny,
b)  ujemny, umiarkowanie asymetryczny,
c)  ujemny o słabej asymetrii.