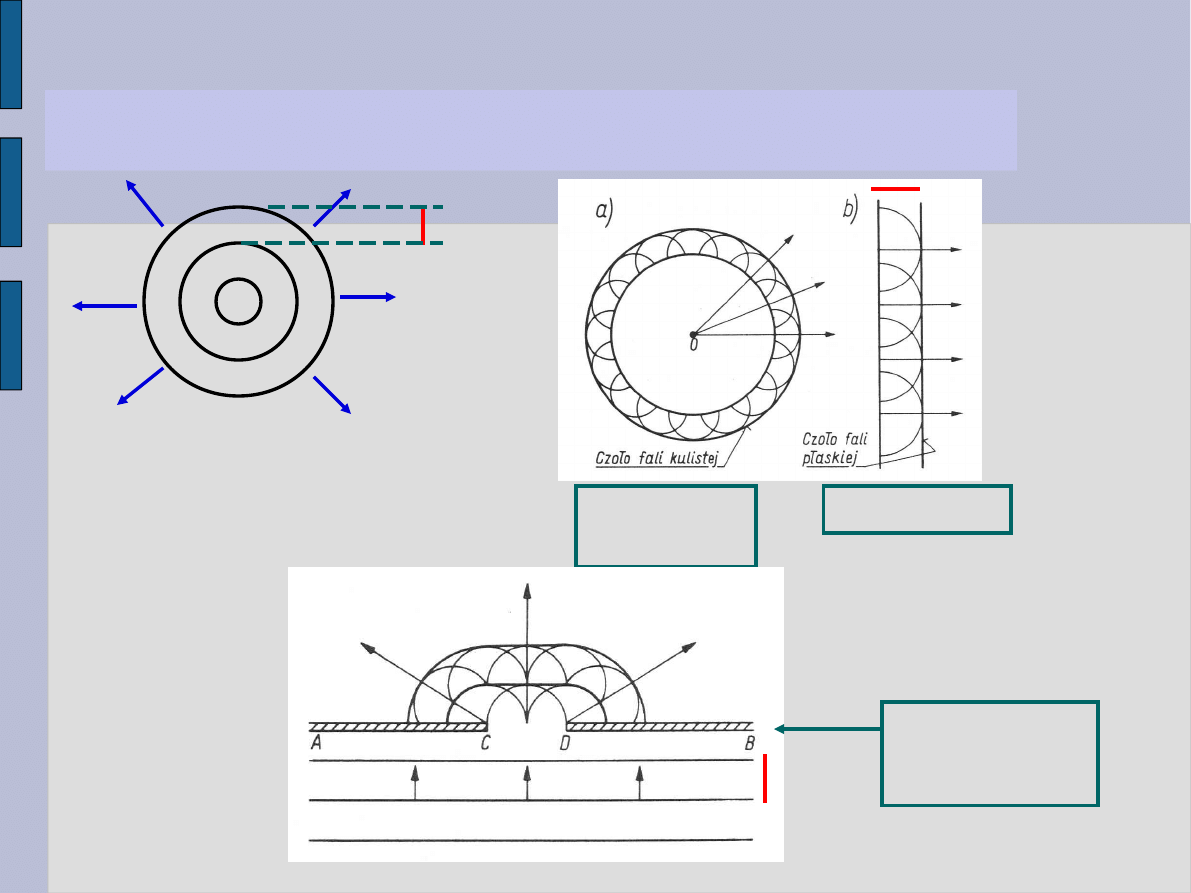
Fala płaska

Fala 

kulista

Każdy punkt ośrodka, do którego dociera czoło fali, zachowuje 

się jako samodzielne źródło wysyłające fale elementarne.

Fale mechaniczne 

– ośrodek 

sprężysty.

Dyfrakcj

a

Zasada 

Huygensa





AB -  

przegroda CD 

- otwór

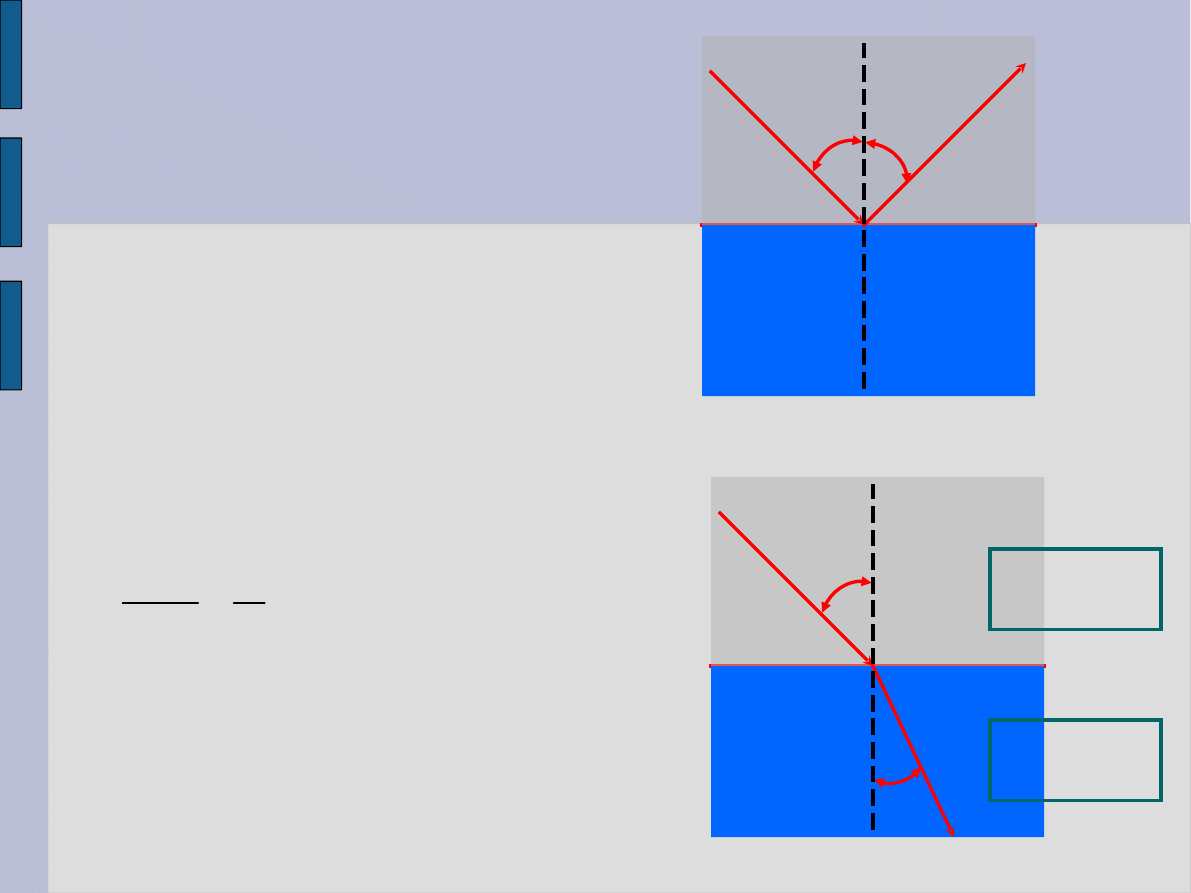
Odbicie 

fal





Załamanie 

fal

 = 

’



Ośrodek 

1

Ośrodek 

2

.

'

sin

sin

21

2

1

n

v

v









n

21

= współczynnik 

załamania 

  ośrodka 2 

względem 1

Współczynnik załamania powietrza 

 1.

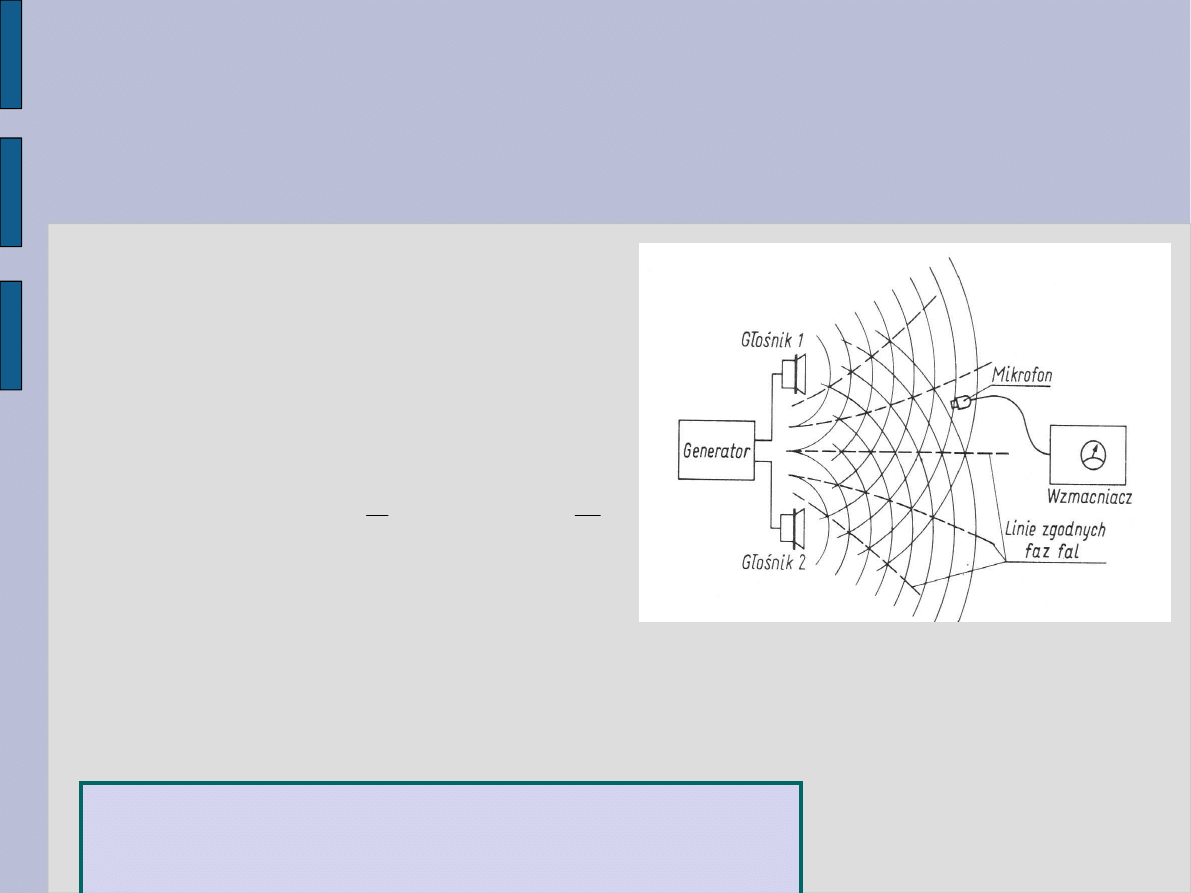
Interferencja 

fal

Nakładanie się dwóch lub więcej fal o tych samych 

długościach (tj. tych samych pulsacjach). 

Rozważmy dwie fale rozchodzące się 

w danym kierunku z taką samą 

prędkością v: 

Długość fal 



 taka sama (tj. tych samych 

pulsacjach), amplitudy A fal takie same, fazy 



 

fal różne o tych

).

sin(

),

sin(

2

1





















t

kx

A

t

kx

A

.

2

cos

2

cos

2

2

1



































t

kx

A

Równanie wypadkowych fal

(1) Gdy 



 = 0, ± 2, ± 4, ..... , fazy fal zgodne. 

(1)

(2)

Wtedy amplituda = 2A,  zachodzi wzmacnianie fal

.

 

(2) Gdy 



 = ± , ± 3, ± 5, ..... , fazy fal niezgodne. 

Wtedy amplituda = 0,  zachodzi zgaśnięcie fal

.

 

Warunek dla interferencji:

 różnica faz musi 

być stała. Fale takie nazywane są falami 

koherentnymi.

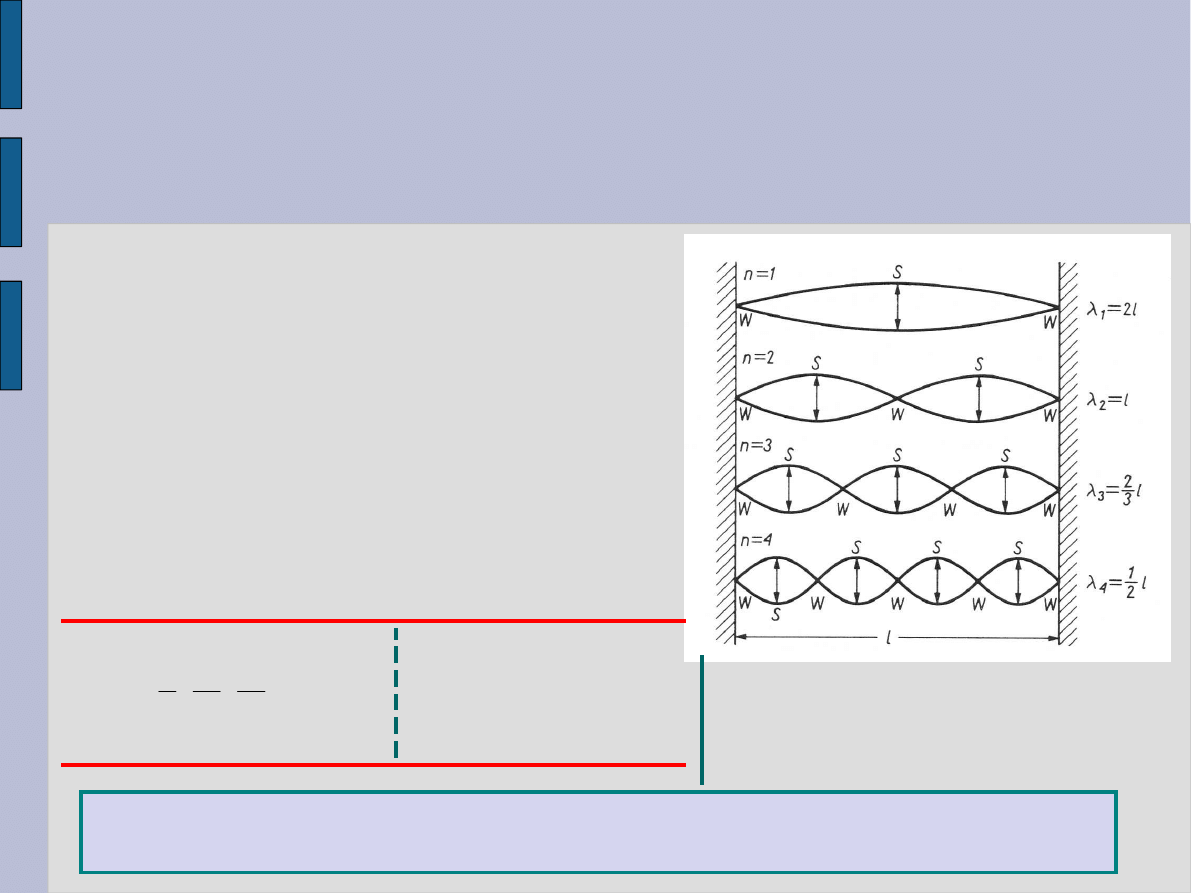
Fale 

stojące

Ponieważ k = 2/, dla 

powstania:

Fale wytworzone w ciele o skończonych rozmiarach.

Ruch falowy ograniczony w przestrzenni. Np. fala wytworzona na 

napiętej strunie. 

Wniosek: Strzałki i węzły są położone na przemianę oraz odległość 

między kolejnymi strzałkami lub węzłami wynosi /2.

Superpozycja fal padających i 

odbitych daje fale stojące.

Równania 

fal:

Fala padająca na powierzchni, fala odbita z tej 

powierzchni;

Kierunki ruchu fali padającej i fali odbitej przeciwne.

).

sin(

)

sin(

odb

pad

t

kx

A

t

kx

A

















(1

)

(2)

Równanie fali stojącej 

(wypadkowej):

.

cos

sin

2

odb

pad

t

kx

A















(3

)

Amplituda 

maksimalna:

Amplituda minimalna:

,....

,

,

2

5

2

3

2









kx

,....

2

,

,

0







kx

Punkty A

max

 – 

strzałki.

Punkty A

min

 – 

węzły.

strzałek: /4, 3/4, 5/4, .....

węzłów: 0, /2, , 3/2, .....