•SYSTEMY
LICZBOWE

•SYSTEMY
LICZENIA

•KODY LICZBOWE

MIARY INFORMACJI -

MAŁE

• Bit (Binary Digit) - najmniejsza jednostka

informacji (0-1) (nie - tak). Binary (ternary) -
element mogący przyjąć 2 (3) wartości.

• Quarter - jednostka informacji zawierająca 2

bity (ćwiartka byte). Dibit - zestaw 2 bitów
spośród 4 możliwych kombinacji: 00, 01, 10,
11.

• Nibble - jednostka informacji zawierająca 4

bity (połowa byte).

• Quadbit - zestaw 4 bitów reprezentujący jedną

z 16 kombinacji nibble.

on

on

yes

yes

true

true

high

high

1

1

of

of

no

no

false

false

low

low

0

0

BITY, BAJTY, SŁOWA

•Bity są podstawową jednostką informacji w

komputerze.

•W każdym z nich można przechowywać

pojedynczą binarną porcję informacji.

•Bity grupuje się w większe jednostki:

- bajt (byte) = 8 bitów,
- słowo (word) = 16 lub 32 lub 64 bitów w

zależności od procesora.

•Bity “01011010” mogą oznaczać:

- liczbę 90
- ASCII znak ‘Z’
- instrukcję DECB procesora Motorola 6800
- po prostu bity

•Zależy to od kontekstu:

- bity same w sobie nie mają określonego

znaczenia

- wartości zależą od tego jak bity zostaną

użyte

- jeżeli są interpretowane jako liczba, to ich

wartość to 90

- jeżeli są interpretowane jako znak, to ich

wartość to ‘Z’

•Dlatego w językach programowania określa

się typy zmiennych.

INTERPRETACJA BITÓW

•Pamięć składa się z bitów

- struktury danych muszą być zakodowane

dla zachowania w pamięci

•Liczby (całkowite)

- kodowane przy użyciu dwójkowego

(binarnego) systemu liczbowego

•Znaki alfanumeryczne

- kodowane jako liczby przy użyci kodu

ASCII

•Kod programu

- instrukcje kodowane jako układ liczb i

bitów

•Inne struktury (structs, floats, ...)

- zwykle konwertowane do liczb

PAMIĘĆ A BITY

•Każdemu bajtowi przypisany jest

unikalny adres

- adres jest liczbą całkowitą
- żadne dwa bajty nie mają tego samego

adresu

•Adresowanie jest ciągłe

- najniższy adres to 0
- sąsiadujące bajty mają kolejne adresy
- najwyższy adres zależy od pojemności

pamięci komputera

•Adresowanie jest niezależne od

zawartości

- zmiana zawartości bajta nie zmienia

jego adresu

ADRESOWANIE
PAMIĘCI

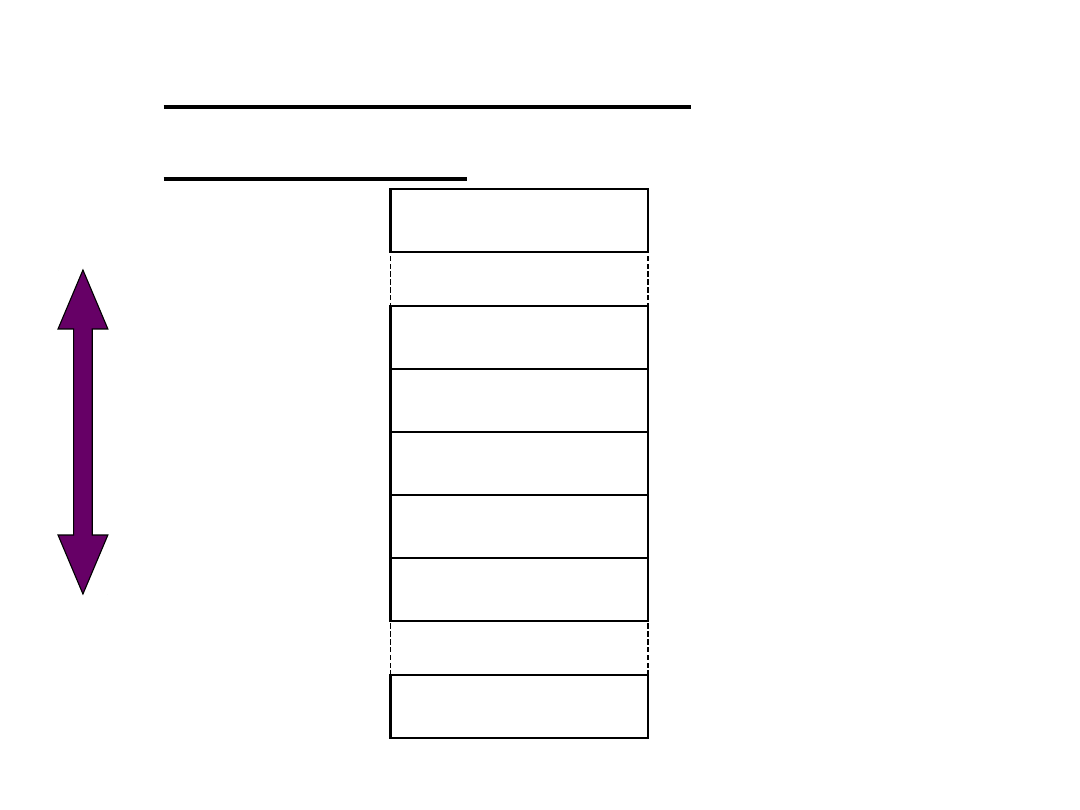
ADRESOWANIE
PAMIĘCI

01101110

01101110

01011010

01011010

00000000

00000000

01011010

01011010

11011110

11011110

11011001

11011001

0

0

10430

10430

10431

10431

10432

10432

10433

10433

10434

10434

16777215

16777215

T

T

en

en

komputer ma

komputer ma

16777216 b

16777216 b

ajtów

ajtów

(16

(16

megabajtów,

megabajtów,

16MB

16MB

)

)

pamięci

pamięci

niższe

niższe

a

a

dresy

dresy

wyższe

wyższe

ad

ad

resy

resy

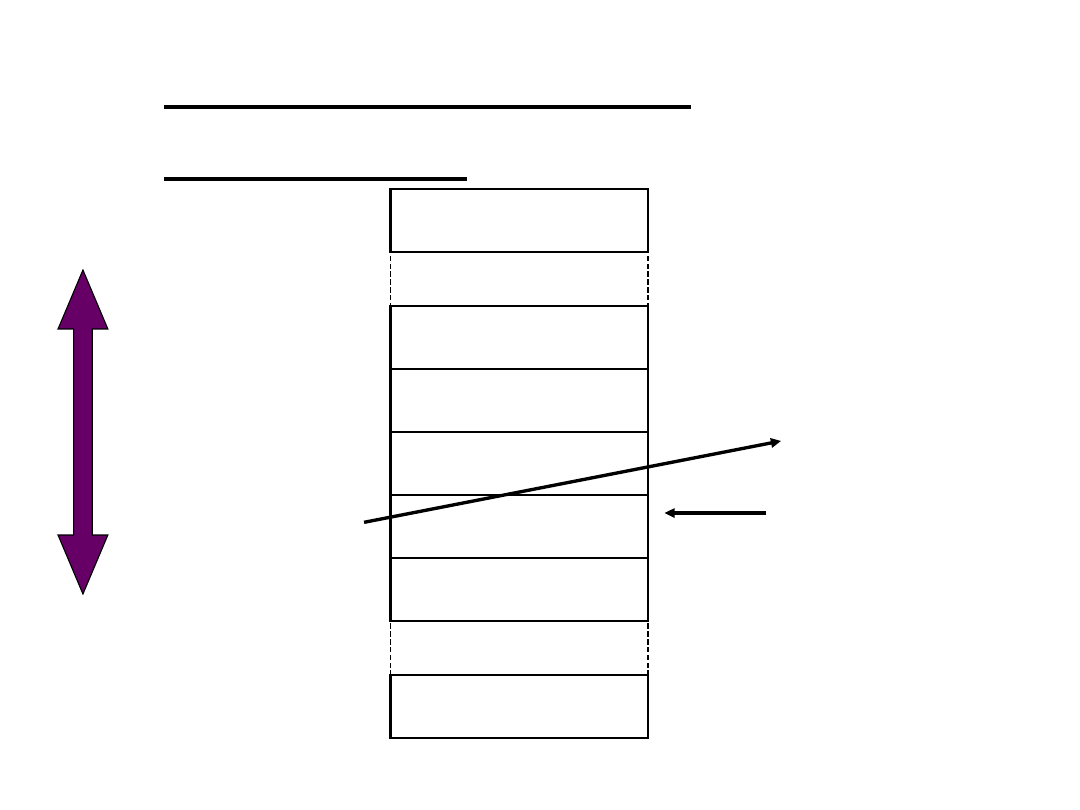
ADRESOWANIE
PAMIĘCI

01101110

01101110

01011010

01011010

00000000

00000000

01011010

01011010

11011110

11011110

11011001

11011001

0

0

10430

10430

10431

10431

10432

10432

10433

10433

10434

10434

16777215

16777215

Bajt

Bajt

o adresie

o adresie

10433

10433

zawiera

zawiera

01011010

01011010

niższe

niższe

a

a

dresy

dresy

wyższe

wyższe

ad

ad

resy

resy

MIARY INFORMACJI -

DUŻE

• Byte (Binary Digit Eight, czyt. bajt) - słowo;

jednostka informacji zawierająca 8 bitów (octet),

reprezentująca jeden znak (literę, cyfrę, znak

specjalny). Za pomocą 1 bajta można zapisać liczbę

równą maks. 255, tj. 2

8

-1.

• Kilobyte (KB) - 2

10

= 1.024 byte. Strona

maszynopisu (30 wierszy x 60 znaków) to ok. 1.8

KB.

• Megabyte (MB) - 2

20

= 1.048.576 byte. Dyskietki -

1.4 MB. CD-ROM - 650 MB.

• Gigabyte (GB) - 2

ł0

= 1.073.741.824 byte. Dyski

twarde. Bazy danych w firmach.

• Terrabyte (TB) - 2

40

= 1.099.511.627.776 byte.

Krajowe bazy danych.

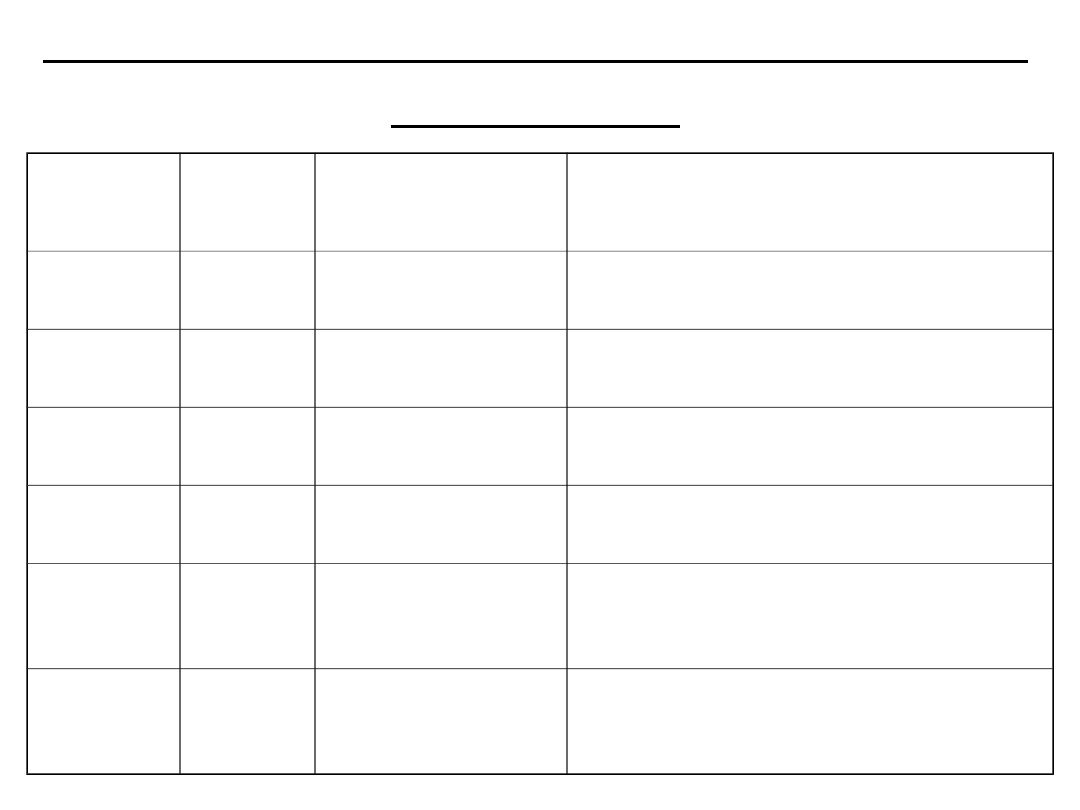
Dziesiętne przedrostki skalujące

(SI-1960)

Symbo

l

Nazw

a

Wykładnic

zo

Dziesiętnie

k

kilo

1000

1

1000

M

mega

1000

2

1000 000

G

giga

1000

3

1000 000 000

T

tera

1000

4

1000 000 000 000

P

peta

1000

5

1000 000 000 000

000

E

egza

1000

6

1000 000 000 000

000 000

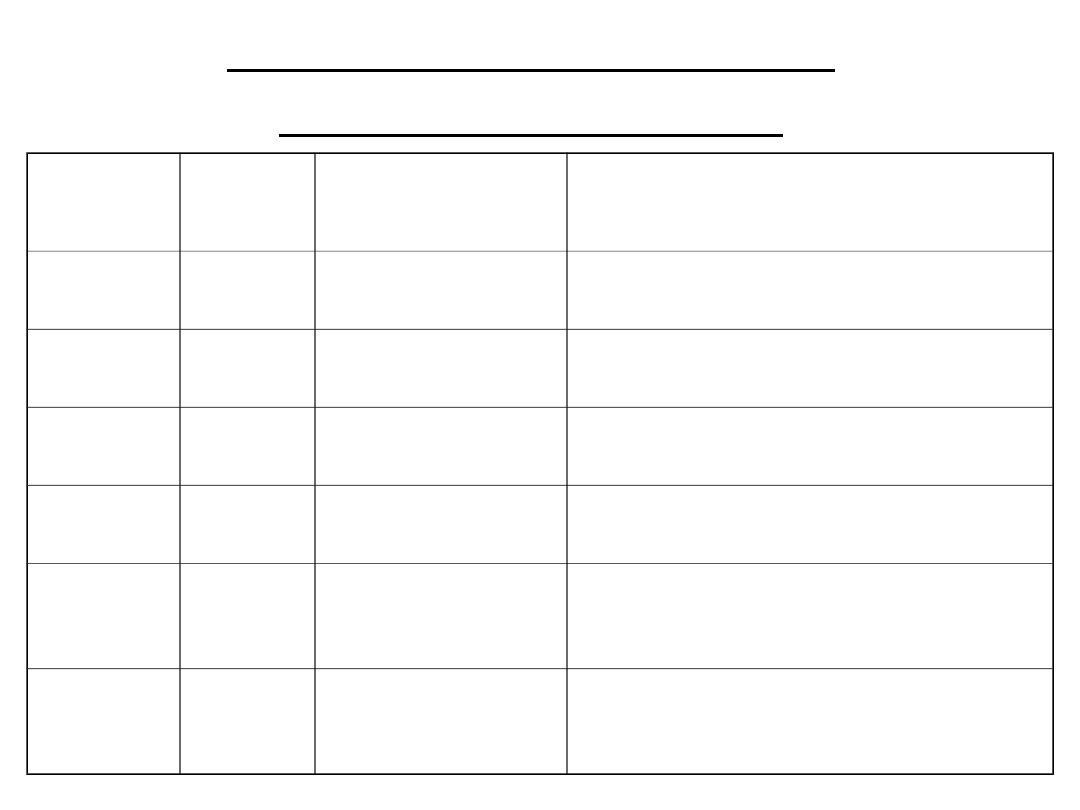
Binarne przedrostki

skalujące (1997)

Symbo

l

Nazw

a

Wykładnic

zo

Dziesiętnie

Ki

kibi

1024

1

1 024

Mi

mebi

1024

2

1 048 576

Gi

gibi

1024

3

1 073 741 824

Ti

tebi

1024

4

1 099 511 627 776

Pi

pebi

1024

5

1 125 899 906 842

624

Ei

exbi

1024

6

1 152 921 504 606

846 976

Skróty miar informacji

• k/K - to 1000 lub 2

10

= 1024

• b/B - to bit lub bajt

– 1 kb=1000 bitów
– 1Kb=1024 bity
– 1kB=1000 bajtów
– 1 KB=1024 bajty

Jak długo trzeba pisać, aby zapełnić dysk
komputera?

•Zakładamy pojemność 10GB i szybkość
pisania 1 znak na sekundę, czyli 60 na minutę,
czyli 3600 na godzinę, czyli około 90000 na
dobę.

•Wówczas:

10 GB /90000 B/dobę = 10

10

B /10

5

B/dobę =

10

5

dób, czyli 10

5

dób /400 dób/rok = 250 lat

•Wynik dokładny:

10 GB /(60 × 60 × 24) B/dobę = 10 · 2

30

B /

86400 B/dobę =. . . = 340 lat

Jednostki czasu w

informatyce

• Sekunda

- odszukanie rekordu na

taśmie magnetycznej.

• Mili- microsekunda 10

-3

, 10

-6

- czas

dostępu do twardego dysku, szybkość
PC.

• Nano- picosekunda 10

-9

, 10

-12

-

szybkość superkomputera IV, V
generacji.

• Femto- octosekunda 10

-15

, 10

-18

-

szybkość komputerów w przyszłości.

Jednostki mocy

obliczeniowej

• MIPS (Million/Mega Instructions Per

Second) - mierzy szybkość w operacjach
podstawowych (rozkazach); miara
zwodnicza, żartobliwie zwana też
Meaningless Indicator of Processor
Speed.

• KIPS, MIPS, GIPS, TIPS
• MFLOPS (Million/Mega of FLoating-

point Operations Per Second) - mierzy
szybkość w operacjach
zmiennoprzecinkowych.

Jednostki awaryjności

• MTBF (Mean Time Between Failure) - średni

czas między kolejnymi awariami (> 1-2 lat).

• MTTR (Mean Time To Repair) - średni czas

reperacji, potrzebny na wykonanie naprawy i
doprowadzenie sprzętu do stanu przed awarią
(< 24 h.)

• MTBDL (Mean Time Between Data Loose) -

średni czas między kolejnymi utratami danych.

• MTDA (Mean Time Data Access) - średni czas

trwałości danych zawartych w pamięciach
masowych; dla dysków twardych > 100 lat.

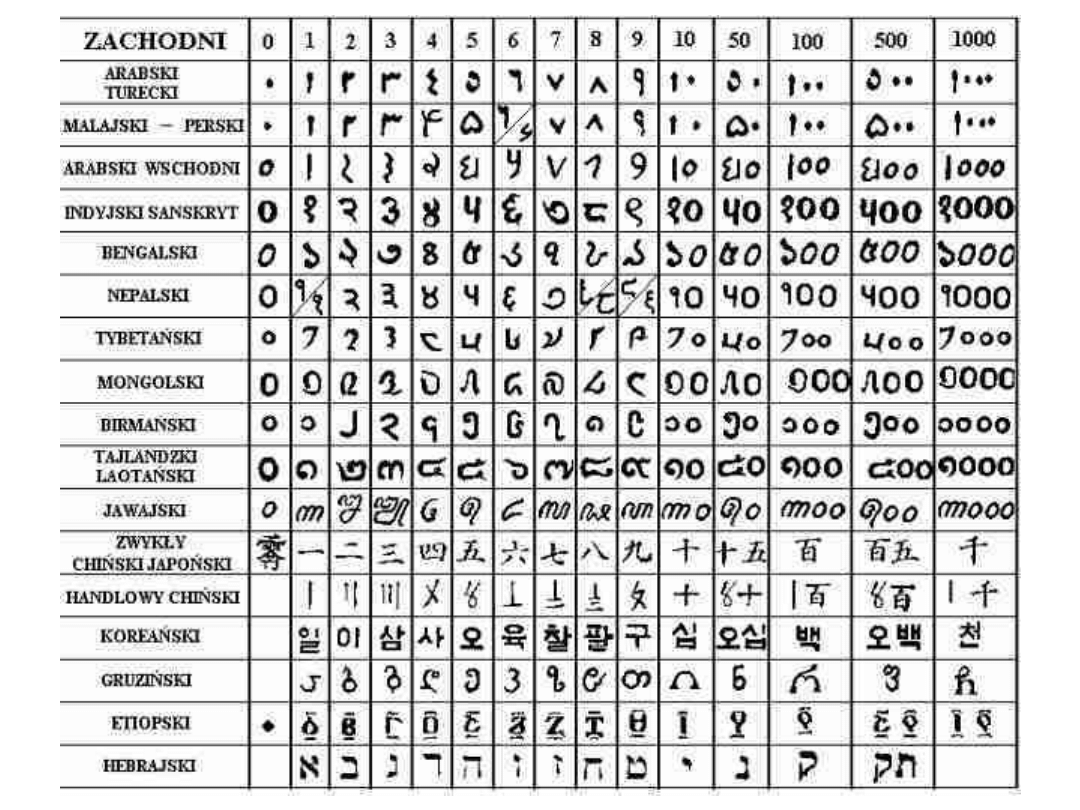
•System liczbowy to sposób tworzenia liczb
ze znaków cyfrowych oraz zbiór reguł
pozwalających na wykonywanie operacji
arytmetycznych na liczbach.

•Systemy niepozycyjne – cyfry zachowują
swoją wartość bez względu na zajmowane
miejsce, np. system rzymski (MMII).

•Systemy pozycyjne – wartość liczbowa
cyfry zależy od jej pozycji (miejsca) w liczbie.

SYSTEMY LICZBOWE

•Podstawa systemu (P) – ilość różnych cyfr
systemu.

•Cyfra (C) – P-elementowy zbiór znaków
graficznych z których tworzymy liczby.

•Waga – wartość liczbowa cyfry zależna od
numeru pozycji.

•Waga danej pozycji jest P-krotnie większa od
wagi poprzedniej pozycji, tzn. waga i-tej
pozycji równa jest podstawie podniesionej do
i-tej potęgi.

•Wagi cyfr wzrastają od prawej strony do
lewej.

ELEMENTY SYSTEMU
LICZBOWEGO

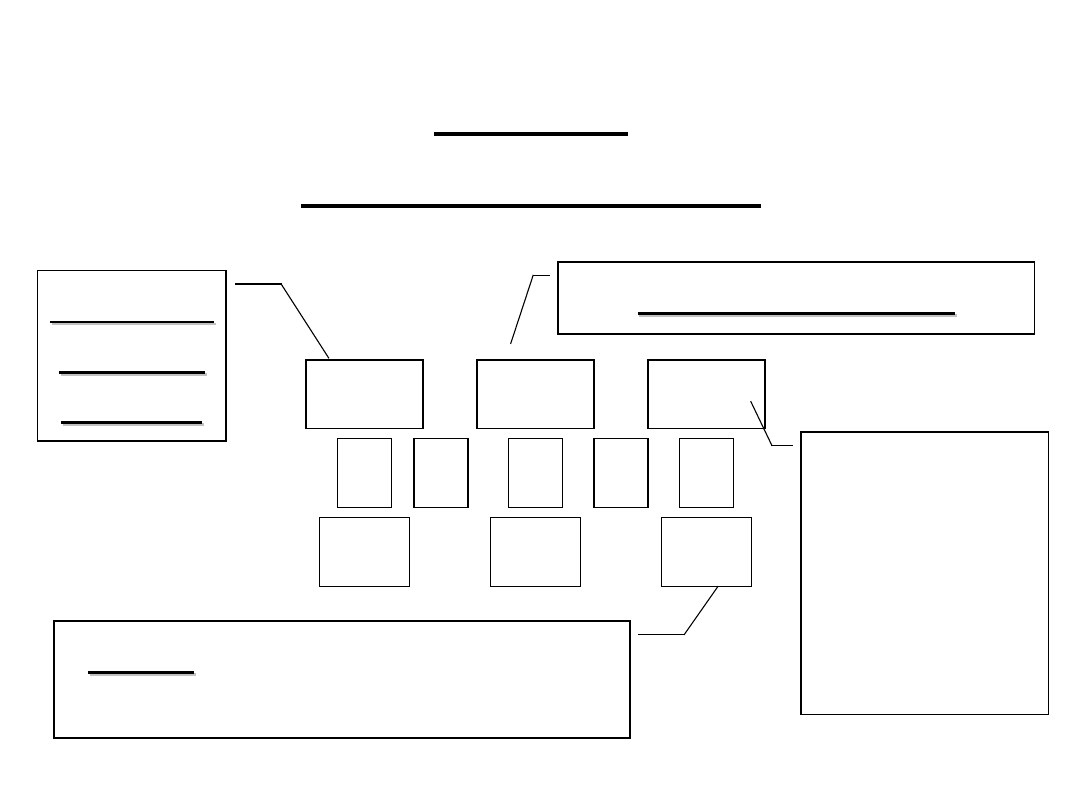
SYSTEM DZIESIĘTNY

(DECYMALNY)

• System pozycyjny zapisu liczb oparty na P=10

cyfrach 0,1,...,9 (l. naturalne), oraz na znaku – l.
całkowite), kropki lub przecinka (l. wymierne).

• Znak + jest opcjonalny.
• Wartość liczby zapisanej jako d

n

...d

1

d

0

to:

• Np. 512,34 = 5*10

2

+1*10

1

+2*10

0

+3*10

-1

+4*10

-

4















n

i

i

i

n

n

d

d

d

d

w

0

1

1

0

10

10

...

10

1

1

2

2

3

3

10

10

2

2

10

10

1

1

10

10

0

0

×

×

×

×

×

×

+

+

+

+

wartość

wartość

pozycji

pozycji

(skala)

(skala)

stała podstawa

stała podstawa

cyfra

cyfra

(

(

mnożnik

mnożnik

)

)

zmienia

zmienia

się

się

od

od

0

0

d

d

o 9 (

o 9 (

podstawa

podstawa

–

–

1)

1)

„123”

DZIESIĘTNIE

wykładnik

(waga)

(waga)

zwiększa

zwiększa

się od

się od

zera w

zera w

lewo

lewo

• System oparty na 2 cyfrach (bitach) 0, 1.
• Wartość liczby zapisanej jako b

n

...b

1

b

0

to:

• Kolejne pozycje mają wartości: 1, 2, 4, 8, 16, 32,

64, 128, ...

• 7

10

=111

2

= 4+2+1 = 1*2

2

+1*2

1

+1*2

0

• 10

10

=1010

2

= 8+0+2+0 = 1*2

3

+ 0*2

2

+1*2

1

+0*2

0

• Liczby całkowite - dodatkowy bit znaku
• 25

10

=011001

2

-25

10

=111001

2

• Ułamki (dla niewymiernych bierze się przybliżenie)
• 0,625

10

= 0,101

2

= 0,5+0,125 = 1*2

-1

+0*2

-2

+1*2

-3

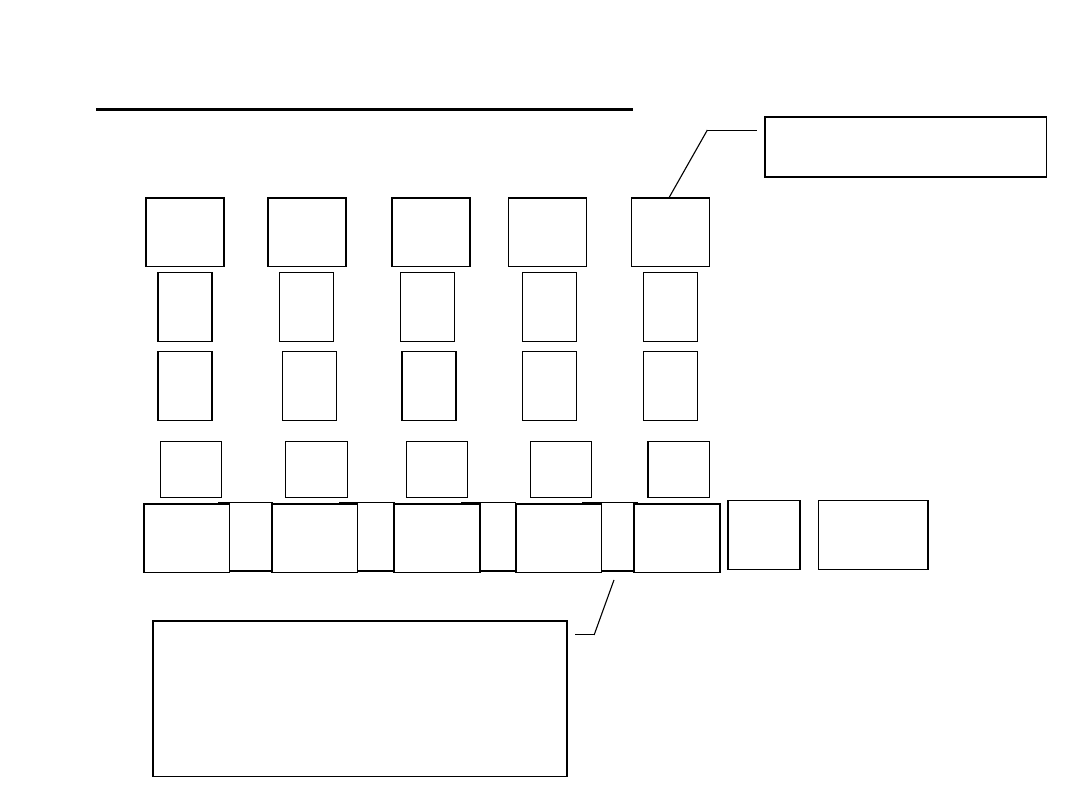
SYSTEM DWÓJKOWY

(BINARNY)















n

i

i

i

n

n

b

b

b

b

w

0

1

1

0

2

2

...

2

podstawa to

podstawa to

2

2

2

2

4

4

2

2

3

3

2

2

2

2

2

2

1

1

2

2

0

0

×

×

×

×

×

×

×

×

×

×

+

+

+

+

+

+

+

+

1

1

1

1

1

1

0

0

0

0

=

=

=

=

=

=

=

=

=

=

16

16

8

8

0

0

2

2

0

0

=

=

26

26

cyfry to

cyfry to

0

0

lub

lub

1

1

(

(

ponieważ podstawa

ponieważ podstawa

to

to

2)

2)

„26” DWÓJKOWO

ALGEBRA BOOLE’A

• Negacja (NOT): !1 = 0, !0 = 1
• Koniunkcja (AND):
• 0&0 = 0, 1&0 = 0, 0&1 = 0, 1&1 =

1

• Alternatywa (OR):
• 0|0 = 0, 1|0 = 1, 0|1 = 1, 1|1 =

1

• Różnica symetryczna (XOR):
• 0^0 = 0, 1^0 = 1, 0^1 = 1, 1^1

= 0

• 1101&1000 = 1000, 1101|1000 = 1101,

1101^1000 = 0101, !1101 = 0010

1

1

0

0

1

0

0

0

0

1

1

0

0

1

0

1

AND

0

1

0

0

0

0

0

0

1

1

0

0

1

0

0

0

0

1

1

0

0

1

0

1

OR

1

1

1

0

1

1

0

1

1

1

0

0

1

0

0

0

0

1

1

0

0

1

0

1

XOR

1

0

1

0

1

1

0

1

1

1

0

0

1

0

0

0

NO

T

0

0

1

1

0

1

1

1

OPERACJE NA BITACH

DODAWANIE I MNOŻENIE

• 1 1

• 1111

• 11111 2

• ------- --

• 1111 15

• + 1001 9

• + 0011 3

• + 1011 11

• + 1110 14

• ======= ==

• 110100 52

• 10101 21

• * 101 * 5

• ===== ===

• 10101 105

• 00000

• 10101

• =======

• 1101001

ZAKRESY LICZB

L.bitów

Bez znaku

Ze znakiem

1

0 1

0 1 2 3

-1 -0 0 1

(00,01,10,11)

(11, 10, 00, 01)

4

0 ... 15

-8 ... 7

8

0 ... 255

-128 ... 127

16

0 ... 65535

-32768..32767

-2.147.483.648...

2.147.483.647

2

32

0...4.294.967.296

Kod uzupełnieniowy do

dwóch (U2)

• Kod dwójkowy do reprezentacji liczb ze znakiem,

liczb całkowitych i rzeczywistych.

• Należy zmienić w liczbie binarnej każdą cyfrę na

przeciwną (0 na 1 i 1 na 0) i do wyniku dodać 1.

• 45

10

= 0010 1101

2

1101 0010 +1=

= 1101 0011

U2

= -45

10

• Najbardziej znaczący bit liczby w kodzie U2

decyduje o znaku liczby (1- ujemna, 0- dodatnia).

• Liczby dodatnie w kodzie U2 i binarnym są

identyczne.

System szesnastkowy

(heksadecymalny)

• P=16 znaków: 0, 1, ..., 9, A, B, C, D, E, F
• Kolejne pozycje mają wartości: 1, 16, 256,

4096, ...

• 1A2

16

= 1*16

2

+ 10*16

1

+ 2*16

0

= 418

10

• 1A2

16

= 0001 1010 0010

2

=

256+128+32+2

10

• FFFF

16

=65535

10

=15*16

3

+15*16

2

+15*16

1

+1

5

10

=(1111) (1111) (1111) (1111)

2

• Liczby szesnastkowe pozwalają na krótszy

zapis długich liczb binarnych.

• Wartość liczby zapisanej jako ciąg h

n

,...,h

1

,h

o







n

i

i

i

h

w

0

16

System ósemkowy (oktalny)

• P=8 cyfr: 0, 1, ..., 7
• Kolejne pozycje mają wartości: 1, 8, 64, 512,

4096, ...

• 777

8

= 7*8

2

+ 7*8

1

+ 7*8

0

= 448+56+7

10

= 511

10

=

(111) (111) (111)

2

• Dowolną ósemkową liczbę jednopozycyjną można

zapisać za pomocą 3 bitów (w systemie „16” to 4
bity).

• Wartość liczby zapisanej jako ciąg q

n

,...,q

1

,q

o

• System obecnie rzadko stosowany, np. prawa

dostępu do plików w systemie UNIX.







n

i

i

i

q

w

0

8

10, 2, 16

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

2

2

3

3

4

4

5

5

6

6

7

7

8

8

9

9

10

10

11

11

12

12

13

13

14

14

15

15

0

0

1

1

0010

0010

0011

0011

0100

0100

0101

0101

0110

0110

0111

0111

1000

1000

1001

1001

1010

1010

1011

1011

1100

1100

1101

1101

1110

1110

1111

1111

0000

0000

0001

0001

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

2

2

3

3

4

4

5

5

6

6

7

7

8

8

9

9

A

A

B

B

C

C

D

D

E

E

F

F

0

0

1

1

wartości w

wartości w

systemie

systemie

dziesiętnym

dziesiętnym

wartości w

wartości w

systemie

systemie

dwójkowym

dwójkowym

wartości w

wartości w

systemie

systemie

szesnastkowym

szesnastkowym

POZYCYJNE SYSTEMY LICZBOWE

2

2

3

3

4

4

5

5

6

6

7

7

8

8

9

9

10

10

11

11

12

12

13

13

14

14

15

15

16

16

10100111100

10100111100

1211122

1211122

110330

110330

20330

20330

10112

10112

3623

3623

2474

2474

1748

1748

1340

1340

1009

1009

938

938

7C1

7C1

6BA

6BA

5E5

5E5

53C

53C

Niższe podstawy

Niższe podstawy

:

:

mniej zwarte

mniej zwarte

,

,

mniejszy

mniejszy

zakres cyfr

zakres cyfr

Wyższe podstawy

Wyższe podstawy

:

:

bardziej zwarte

bardziej zwarte

,

,

większy

większy

zakres cyfr

zakres cyfr

Reprezentacje liczby

Reprezentacje liczby

1340

1340

(

(

dziesiętnie

dziesiętnie

)

)

przy

przy

podstawach od

podstawach od

2

2

do

do

16

16

p

o

d

st

a

w

a

p

o

d

st

a

w

a

SYMBOLE W SYSTEMACH

LICZBOWYCH

2

2

3

3

4

4

5

5

6

6

7

7

8

8

9

9

10

10

11

11

12

12

13

13

14

14

15

15

16

16

10100111100

10100111100

1211122

1211122

110330

110330

20330

20330

10112

10112

3623

3623

2474

2474

1748

1748

1340

1340

1009

1009

938

938

7C1

7C1

6BA

6BA

5E5

5E5

53C

53C

p

o

d

st

a

w

a

p

o

d

st

a

w

a

Cyfry o wartościach

Cyfry o wartościach

większych od 9 mają

większych od 9 mają

symbole liter z alfabetu

symbole liter z alfabetu

:

:

A = 10

A = 10

B = 11

B = 11

C = 12

C = 12

D = 13

D = 13

E = 14

E = 14

F = 15

F = 15

itd

itd

.

.

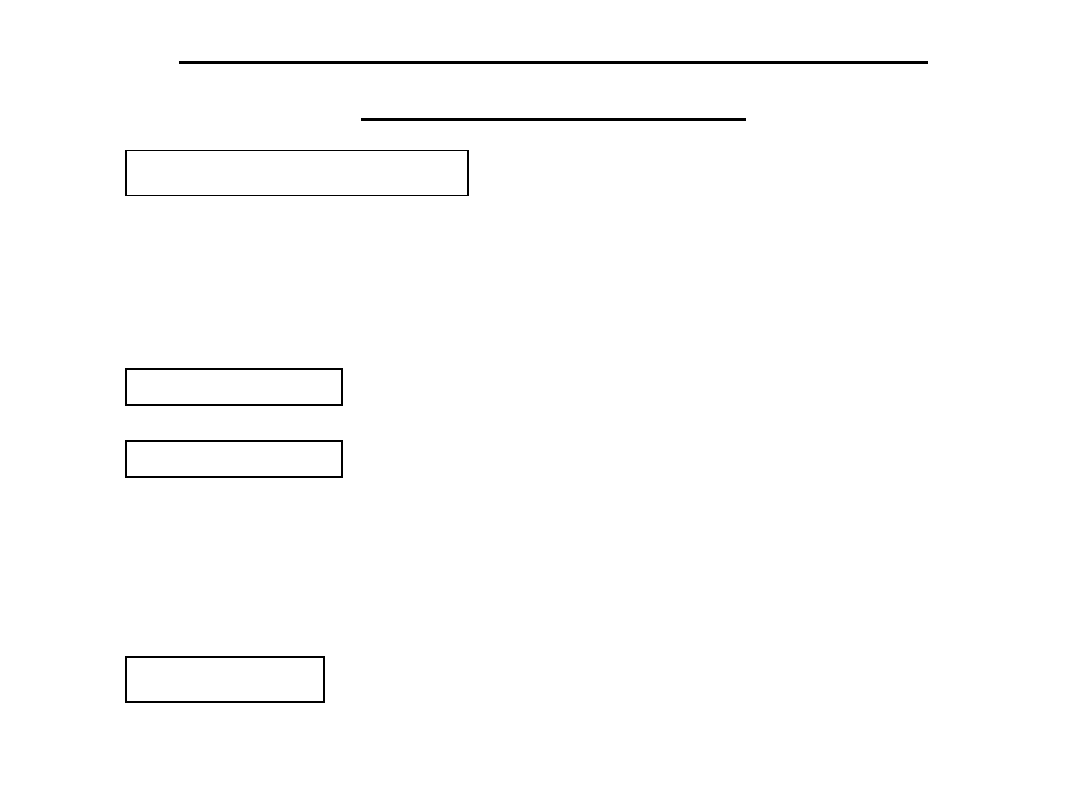
PODSTAWY W SYSTEMACH

LICZBOWYCH

2

2

3

3

4

4

5

5

6

6

7

7

8

8

9

9

10

10

11

11

12

12

13

13

14

14

15

15

16

16

10100111100

10100111100

1211122

1211122

110330

110330

20330

20330

10112

10112

3623

3623

2474

2474

1748

1748

1340

1340

1009

1009

938

938

7C1

7C1

6BA

6BA

5E5

5E5

53C

53C

p

o

d

st

a

w

a

p

o

d

st

a

w

a

dwójkowy (binarny)

dwójkowy (binarny)

ósemkowy

ósemkowy

(

(

octal

octal

)

)

dziesiętny

dziesiętny

(

(

decimal

decimal

)

)

szesnastkowy

szesnastkowy

(

(

hexadecimal

hexadecimal

)

)

(“hex”)

(“hex”)

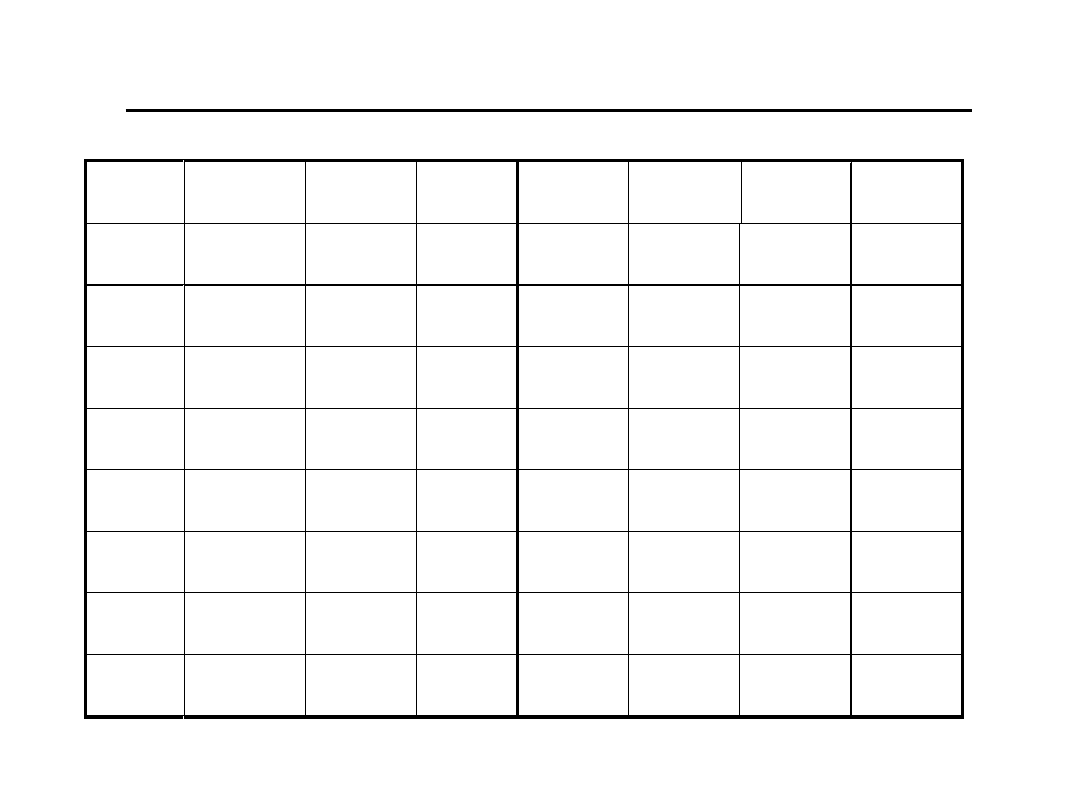
Relacje systemów zapisu

dec bin

oct hex dec bin oct hex

0 0000

0

0

8 1000

10

8

1 0001

1

1

9 1001

11

9

2 0010

2

2

10 1010

12

A

3 0011

3

3

11 1011

13

B

4 0100

4

4

12 1100

14

C

5 0101

5

5

13 1101

15

D

6 0110

6

6

14 1110

16

E

7 0111

7

7

15 1111

17

F

KONWERSJA LICZB

• Zamiana liczb dziesiętnych na liczby w innych

systemach polega na sukcesywnym dzieleniu jej
i kolejnych wyników dzielenia przez
podstawę systemu (2, 8, 16) oraz zapisywaniu
ciągu reszt z dzielenia w uszeregowaniu od
prawej do lewej (znakami „alfabetu” danego
systemu). Dzielenie kończymy gdy wynik jest
mniejszy niż 1, 7, 15.

• 255

10

= 255:16 = 15 r 15 = FF

16

• 255

10

= 255:8 = 31 r 7; 31:8 = 3 r 7 = 377

8

• 15

10

=15:2=7 r 1; 7:2=3 r 1; 3:2=1 r 1 = 1111

2

• 255

10

=FF

16

= 377

8

= 011 111 111

2

= 1111 1111

2

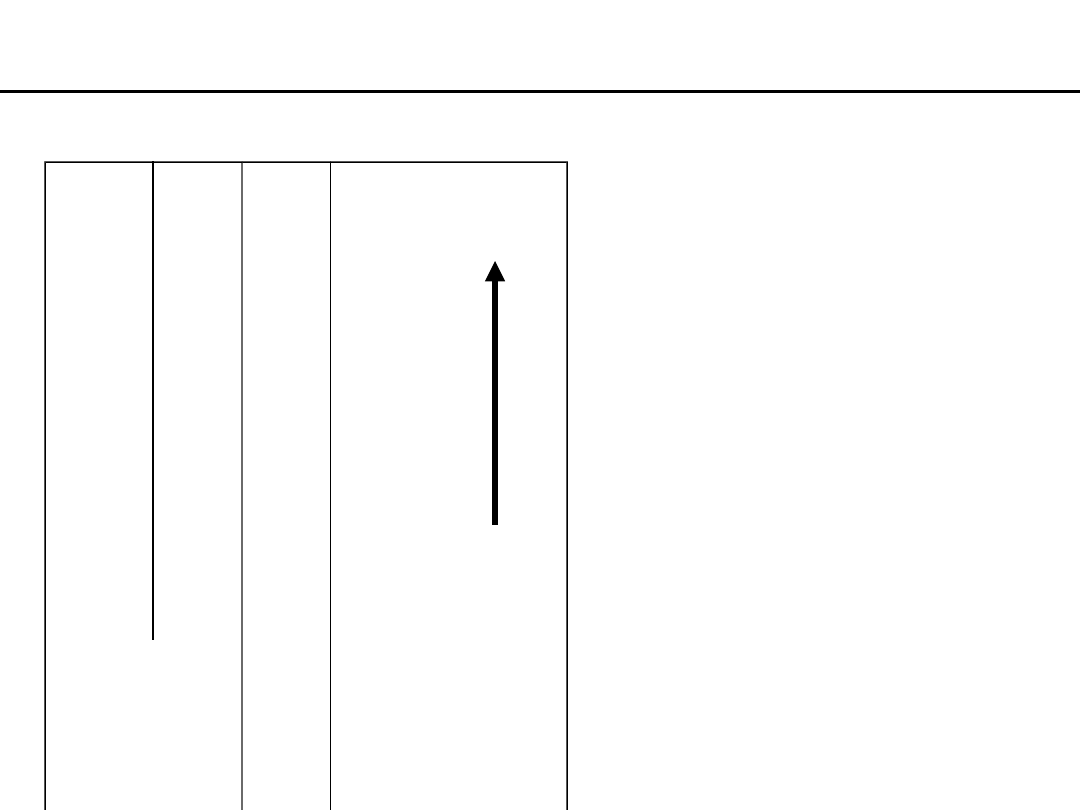
Zamiana liczby dziesiętnej na binarną

69:2

34
34:2

17
17:2

8
8:2

4
4:2

2
2:2

1
1:2

0

r.1
r.0
r.1
r.0
r.0
r.0
r.1

Najmłodsz
y bit

Najstarszy
bit

Kolejno

dzielimy liczbę

dziesiętną

przez 2 z resztą

i zapisujemy

reszty

od

najstarszego

do

najmłodszego

bitu

(od dołu do

góry)

69

(10)

=

1000101

(2)

Każdą pozycję liczby binarnej nazywamy

bitem

(

bi

nary

digi

t

) i jest to najmniejsza jednostka ilości informacji

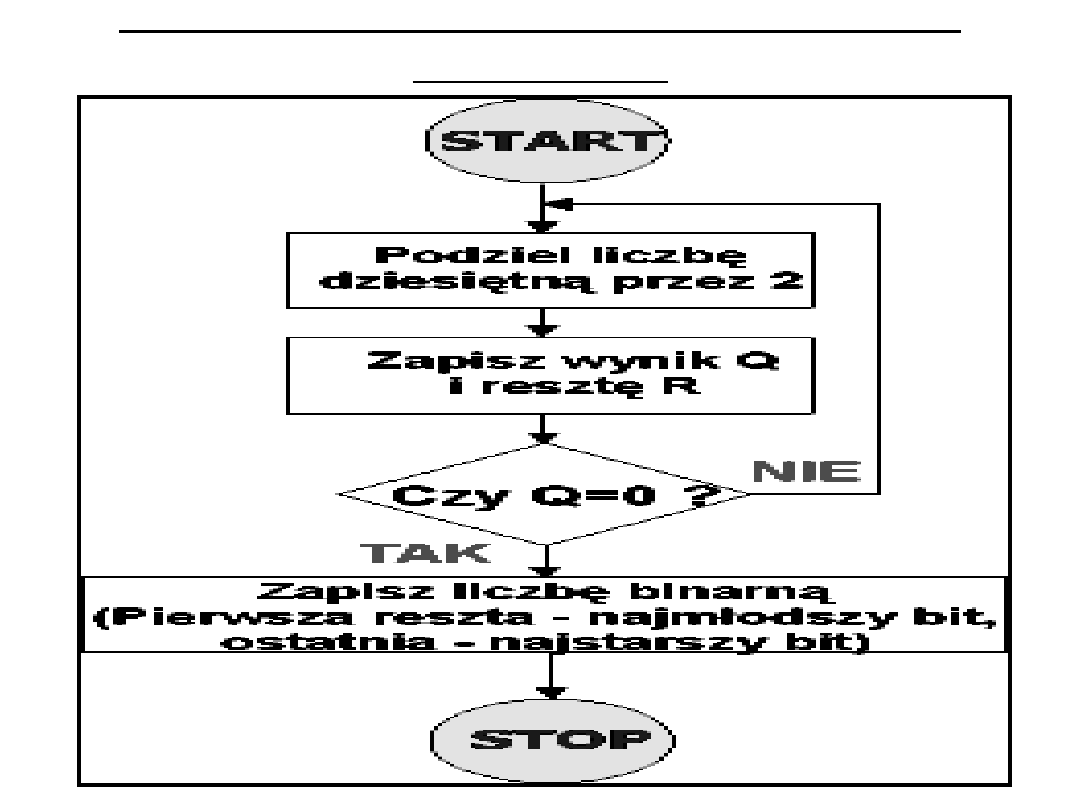
Algorytm zamiany liczby dziesiętnej

na binarną

•Liczba dziesiętna 69 to binarnie 1000101
•Dzielimy liczbę binarną na tzw. kęsy o
długości 4 bitów (licząc od ostatniej pozycji)
czyli: (0100) (0101)
•Dla każdego kęsa znajdujemy wartość
dziesiętną i zapisujemy ją w postaci
heksadecymalnej

binarnie

(0100) (0101)

dziesiętnie

4 5

heksadecymalnie

45

tak więc: 45

(16)

=4*16

1

+

5*16

0

=64+5=69

(10)

DZIESIĘTNY NA SZESNASTKOWY

DWÓJKOWY NA

SZESNASTKOWY

• Rozbijamy liczbę na czteroznakowe kęsy:

10010101111

(2)

=(0100) (1010) (1111)

• Przypisujemy każdej czwórce liczbę dziesiętną:

(0100)

(2)

=4

(10)

(1010)

(2)

=10

(10)

(1111)

(2)

=15

(10)

• Przypisujemy każdej liczbie dziesiętnej liczbę

szesnastkową:
4

(10)

=4

(16)

10

(10)

=A

(16)

15

(10)

=F

(16)

• 10010101111

(2)

= 4AF

(16)

KOD BCD

• BCD - kodowanie dwójkowo-dziesiętne

(Binary Coded Decimal)

• Czterem bitom w kodzie BCD odpowiada

jedna cyfra dziesiętna.

• 94

10

=0101 0100

BCD

• Stosowany do reprezentacji danych w

komputerach, np. w listach rozkazów,
wprowadzania informacji numerycznych,
wyświetlania liczb dziesiętnych.

KODOWANIE
INFORMACJI

ASCII-8 ASCII-7 EBCDIC

Bajt Bity Bity Bity
A 1010 0001

100 0001

1100 0001

B 1010 0010

100 0010

1100 0010

C 1010 0011

100 0011

1100 0011

0 0101 0000

011 0000

1111 0000

1 0101 0001

011 0001

1111 0001

2 0101 0010

011 0010

1111 0010

3 0101 0011

011 0011

1111 0011