Gazy

doskonale

Tytuł zagadnienia w programie:

Termodynamika i fizyka cząsteczkowa.

Termodynamika: ciepło i jego ruch w układach.

Termodynamika fenomenologiczna:

opis makroskopowy przy pomocy

takich wielkości jak: ciśnienie, temperatura, objętość, energia,

entropia itp.

Opiera się na zasadach termodynamiki.

Termodynamika statystyczna:

opis mikroskopowy przy pomocy

prędkości, masy, energii, pędu itp., atomów i cząsteczek układu.

Opiera się na mechanice i rachunkach prawdopodobieństwa.

Fizyka cząsteczkowa:

dotyczy fizycznego opisu zjawisk związanych z

zachowaniem się atomów i cząsteczek układu w określonych

warunkach termodynamicznych.

Opiera się na pojęciu gazu fikcyjnego (doskonałego) i gazu i

par

rzeczywistych.

Równanie stanu gazu doskonałego

Gazy rzeczywiste typu wodoru i helu dobrze spełniają równanie

Clapeyrona przy

wysokich temperaturach T i niskich ciśnieniach p

.

,

nRT

pV 

gdzie: p - ciśnienie, V - objętość, T – temperatura gazu, R – stała

gazowa (8.314 J/molK), n – liczba moli gazu.

(1

)

Doświadczenia nad własnościami gazów wykazały, że zachowują

się one zgodnie z zależnością:

Równanie (1) nazywamy równaniem stanu gaz. Nosi nazwę

równanie Clapeyrona.

Trzy parametry p, V i T jednoznacznie określające stan pewnej

ilości gazu, to parametry stanu gazu.

Gaz doskonały - fikcyjny gaz, który dokładnie spełniałby

równanie (1).

Gaz doskonały,

to taki gaz w którym brak sił wzajemnego

oddziaływania między jego cząsteczkami a cząsteczki zachowują

się jako sprężyste kulki o znikomo małych rozmiarach.
Dla 1 mola dowolnego gazu liczba cząsteczek jest stała równa

liczbie Avogadro i.e. N

A

= 610

23

cząsteczek/mol. Wtedy

,

A

kT

N

pV 

(2

)

gdzie: k = 1.3810

-23

J/K. (k – stała

Boltzmanna)

Energia wewnętrzna i ciepło

Rozważmy pchanie bloku na powierzchni innego

ciała.

.

F

F

F

F

zew

tarcie

zach

wyp







F

zew

– zewnętrzna siła do pchania.

Przyrost energii kinetycznej

.

d

)

F

F

(F

kin

zew

B

A

tar

zach

E

s 











Wypadkowa siła

gdzie F

tar

’ reakcja na tarcie a F

tar

’ds.= praca wykonana, aby

dostarczyć dodatkowej energii kinetycznej i potencjalnej

indywidualnym cząsteczkom. Praca ta powoduje ogrzewanie

siebie i otoczenia.

Energia przekazana układowi w sposób nie mechaniczny to

ciepło Q

; jednostka ciepła J.

F

zew

Tutaj: F

zach

– siła

zachowawcza.

A

B

,

Δ

d

)

d

(

d

(

d

wew

pot

kin

'

tar

pot

kin

tar

zach

kin

zew

E

E

E

E

E

E

B

A

B

A

B

A

B

A

















































s

F

s

F

s)

F

s

F

Stąd mamy

rotacja

oscylacja

(1)

(2)

(3)

Zmiana energii wewnętrznej i I zasada

termodynamiki

Energetyczne oddziaływanie układu z jego otoczeniem przejawia

się jako: wymiana ciepła i wykonanie pracy.

W danym stanie układu energia wewnętrzna U ma określoną

wartość. Jeżeli stan układu ulega zmianie, to energia wewnętrzna

układu tez zmienia się.

.

1

2

W

Q

U

U







Siły zewnętrzne powodują zmianę energii wewnętrznej układu ze stanu 1 do 2:

(1)

W przypadku malej zmiany stanu układu równanie (1) można

zapisać w postaci:

(2)

Zmiana energii wewnętrznej układu termodynamicznego jest

równa sumie ciepła oddanego (lub pobranego) przez układ i pracy

wykonanej nad układem przez siły zewnętrzne.

Równanie (1), to pierwsza zasada termodynamiki. Mówi ona:

.

d

d

d

W

Q

U





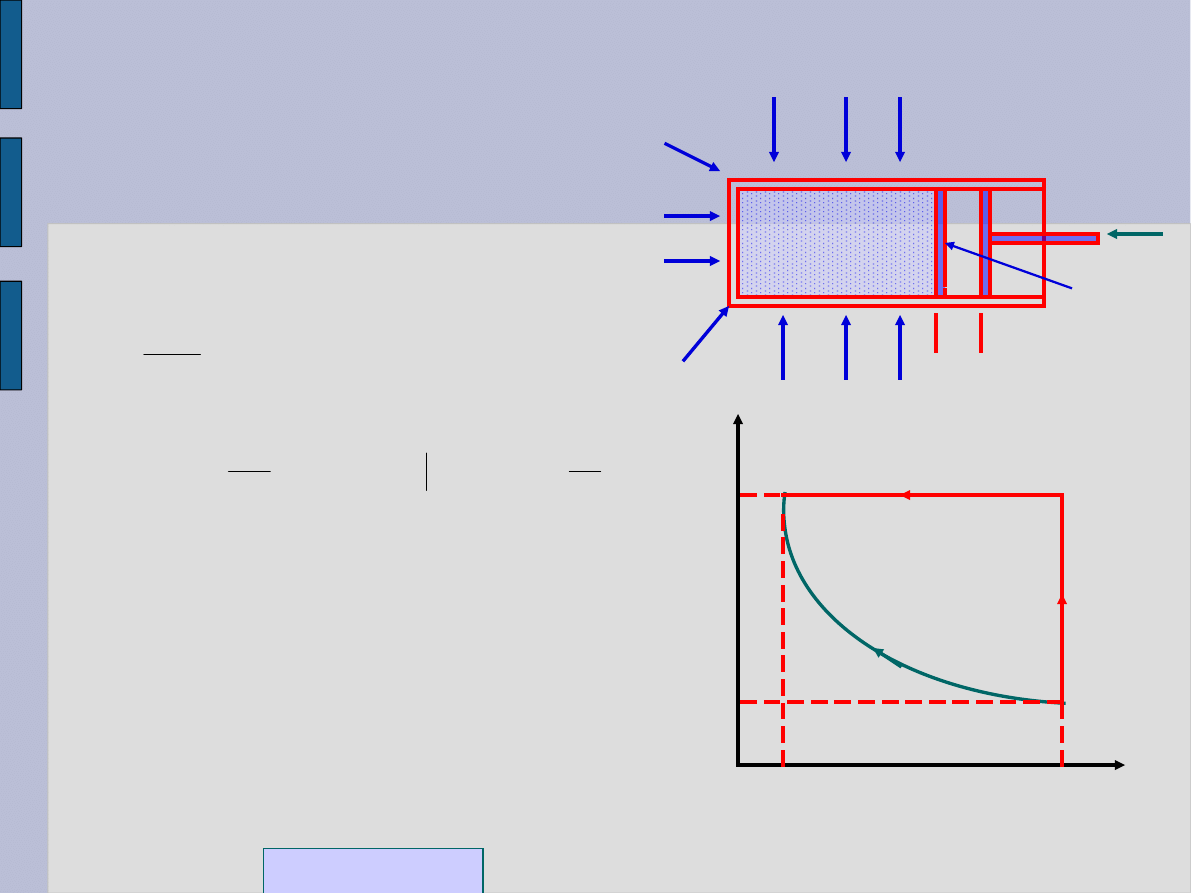
Praca sił ciśnienia gazu

doskonałego

Ciepło Q

Praca wykonana przez siłę

zewnętrzną:

p

V

V

1

V

2

p

2

p

1

F

p

ds

S

W przypadku przemiany

izotermicznej

.

d

d

d

V

p

s

pS

s

F

dW













Praca sił ciśnienia

.

d

2

1







V

V

V

p

W

.

V

nRT

p

Z równań (2) i (3)

mamy

.

ln

ln

d

2

1

2

1

2

1

V

V

nRT

V

nRT

V

V

nRT

W

V
V

V

V













W przemianie izotermicznej

temperatura układu stała; więc nie

ma zmiany w energii wewnętrznej tj.

dU = 0.

(1)

(2)

(3)

(4)

W przypadku przemiany

izobarycznej

.

)

(

d

2

1

2

1











V

V

V

V

p

V

p

W

(5)

Z równań (1) i (3)

otrzymujemy

.

d

d

d

d

Q

T

nR

V

p

W













(6)

Zatem

.

d

const

d

T

Q 