Kurs podstawowy z

Kurs podstawowy z

Zastosowania Komputerów

Zastosowania Komputerów

mgr Marcin Golański

mgr Marcin Golański

•

Statystyka a Karate?

Statystyka a Karate?

•

W obu przypadkach

W obu przypadkach

ważna jest praktyka

ważna jest praktyka

•

Ludzie boją się

Ludzie boją się

karateki i statystyki

karateki i statystyki

•

Od nas zależy czy

Od nas zależy czy

statystyka będzie

statystyka będzie

szamotaniem czy

szamotaniem czy

użytecznym

użytecznym

narzędziem

narzędziem

Morał: praktykować należy
efektywnie a nie efektownie

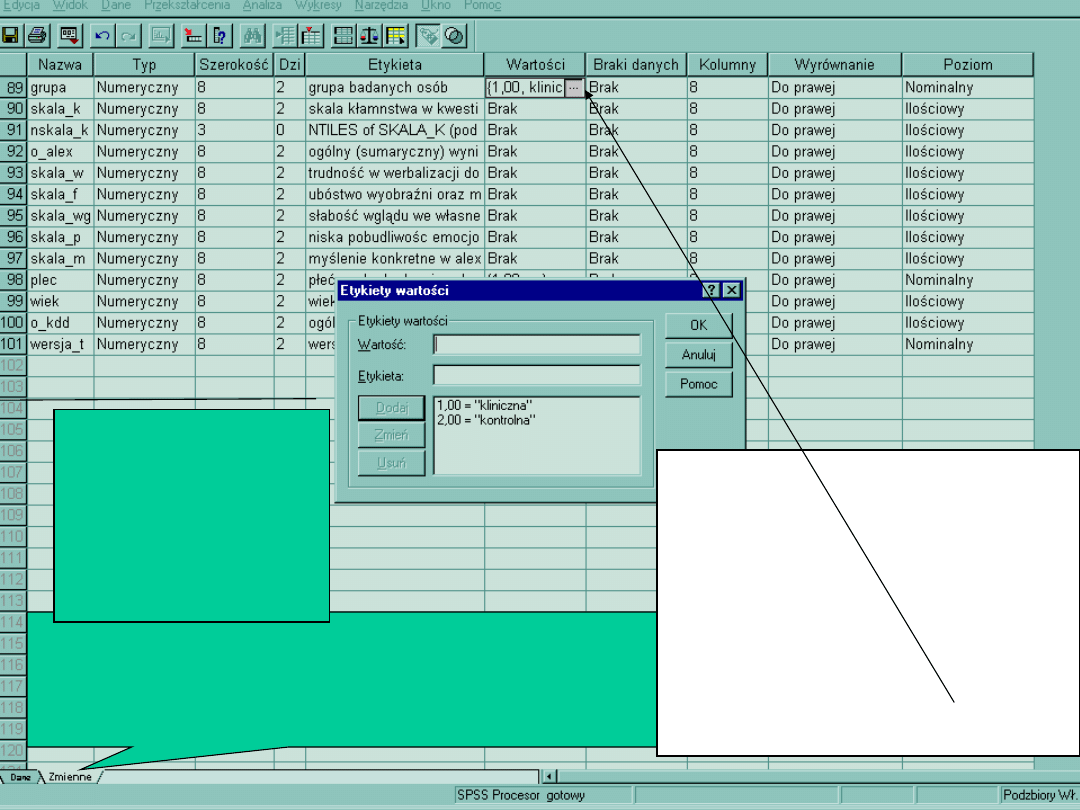
1 Tutaj podobnie jak w Excelu znajdują się zakładki.
Zakładka ‘zmienne’ daje nam informacje o samych zmiennych:
Jak są kodowane? Jakie mają wartości? itp.

3 Otwiera się okno,
w którym wpisujemy
w pierwszym
wierszu wartość, w
drugim etykietę, a
następnie klikami
przycisk DODAJ

2 W polu zmiennych wpisujemy
nazwę zmiennej

(1 kolumna) zawiera max
8znaków, typ zmienne:
numeryczny lub tekstowy,
Etykieta zawierać winna
dokładny opis zmiennej (bez
ograniczeń znaków).wartości
danej zmiennej można opisać w
kolumnie 6. Aby to uczynić
klikamy myszką szary
kwadracik, pojawi się okno...

Zakładka ‘Dane’ informuje nas, że znajdujemy się
w zbiorze danych
gdzie w kolumnach znajdują się zmienne, w
wierszach zaś przypadki

Przed rozpoczęciem
zaawansowanych analiz, naszych,
świeżo wpisanych danych warto
przyjrzeć się ich poprawności zapisu.
Może się zdarzyć, że zamiast 1 w
ankiecie wpisaliśmy 11. W ten
sposób znajdziemy ewentualne błędy.
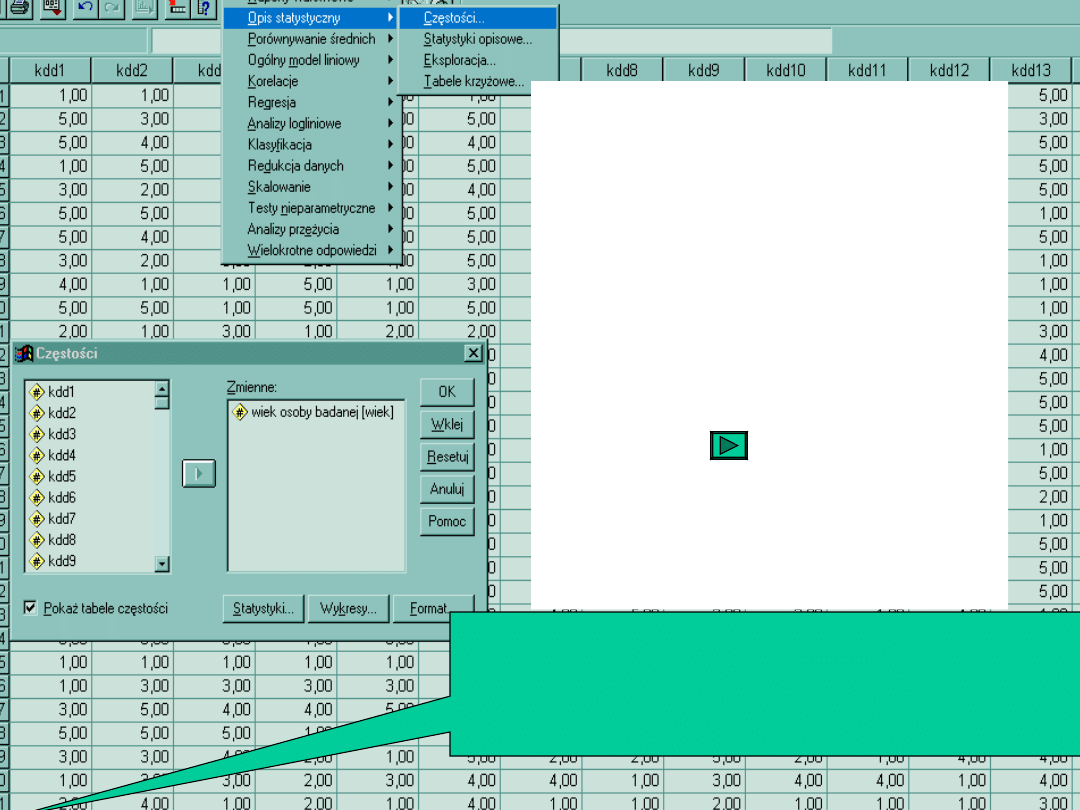
W oknie CZĘSTOŚCI znajdziemy
wiele przydatnych miar do analizy
zmiennej. Wyłapywanie błędów
wystarczy wykonać proste obliczenie
częstości, bez dodatkowych opcji
(średnich, median..). w oknie
CZĘSTOŚCI zaznaczamy żądana
zmienną i przenosimy ją do okna po
prawej stronie, za pomocą strzałki.
Operacje zatwierdzamy przez OK

Edytor Raportów jest
integralną częścią
pakietu SPSS. Ma swoje
własne rozszerzenie
’.spo’. Można zapisać
jego zawartość
niezależnie od edytora
danych jako dowód
naszych obliczeń.
Poprzez Okno w pasku
narzędzi można
przechodzić do edytora
danych

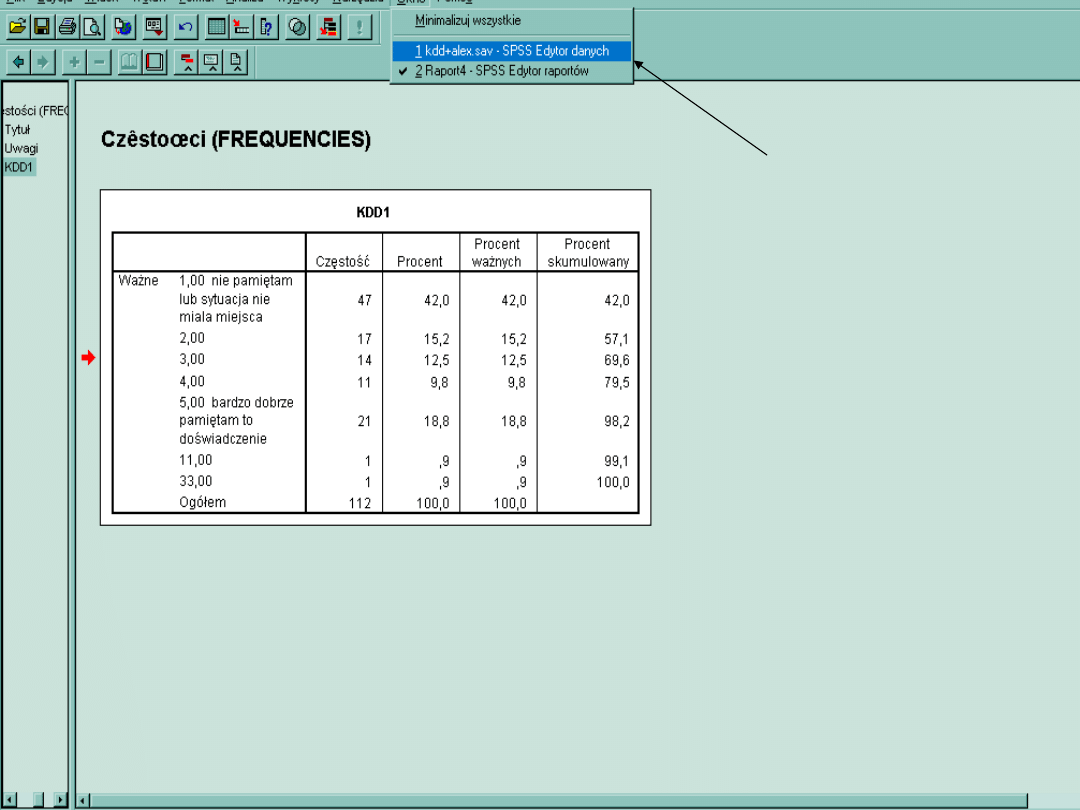
W Edytorze raportów zawsze znajdziemy odbicie naszych wykonywanych
komend.
Powyższa Tabelka to najprostszy z możliwych raportów, czyli zliczenie
częstości.
Kwestionariusz KDD składa się z 36 pozycji. Tabela dotyczy pozycji
pierwszej(KDD1).
Pozycje KDD punktowane są w skali od 1 do 5. Raport Częstości bo przy
każdej wartości zliczone jest jej występowanie. Widzimy, że ogółem
badanych było 112 osób. 47 osób zaznaczyło, że nie pamięta sytuacji z
pozycji 1 kwestionariusza, co stanowi 42 % respondentów.17 uznało, że
słabo pamięta, co stanowi 15,2 % badanych. Osób, które nie pamiętają lub
słabo pamiętają, jest 57,1% . Okazało się też, że w przypadku dwóch osób
popełniono błędy w deklaracji danych .

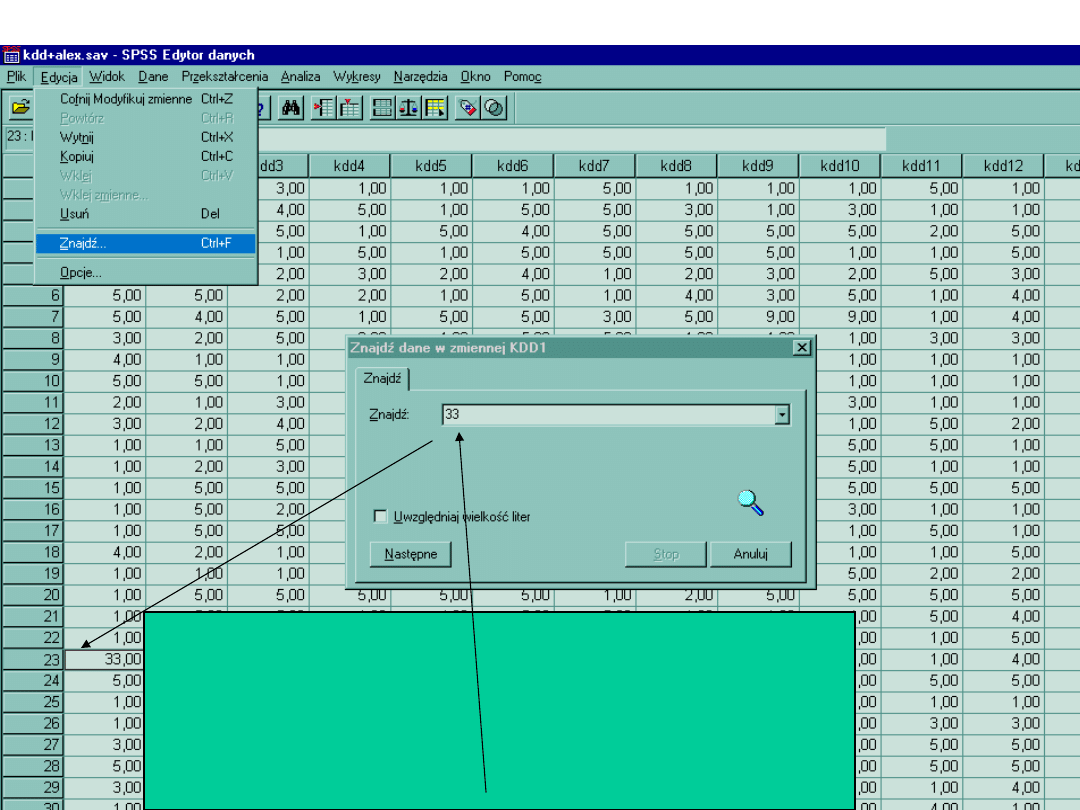
Usuwanie błędów

Jeśli wiemy, że w pozycji 1 KDD wkradł się błąd i znamy
jego wartość, należy go znaleźć i zmienić, aby przy
okazji liczenia nie zaburzył nam wyników.

W tym celu klikamy kursorem na kolumnę zmiennej.
Następnie wchodzimy do paska narzędzi i w Edycji
posługujemy się poleceniem znajdź. Wpisujemy żądaną
wartość

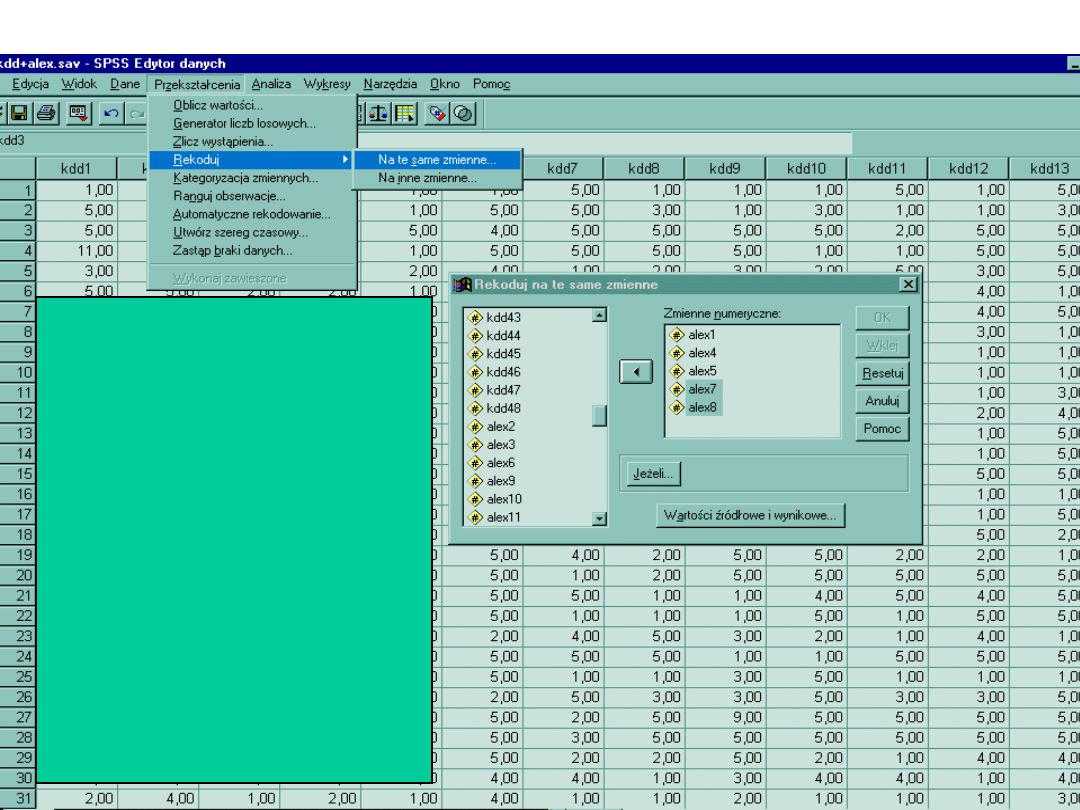
Tworzenie wskaźników zmiennych

Kwestionariusze często
wymagają przekodowania skali
zgodnie z kluczem odpowiedzi
jaką przyjął autor. Inaczej
będziemy otrzymywali
przekłamane wyniki. Wszelkie
operacje zmieniające zbiory
danych wykonujemy w opcji
Przekształcenia.

W tym przypadku dokonujemy
odwrócenia 20 -tu pozycji w
Alex40.

Przekształcenia>rekoduj>n
a te same zmienne>zmienne
do okna>wartości zmienne i
wynikowe.....

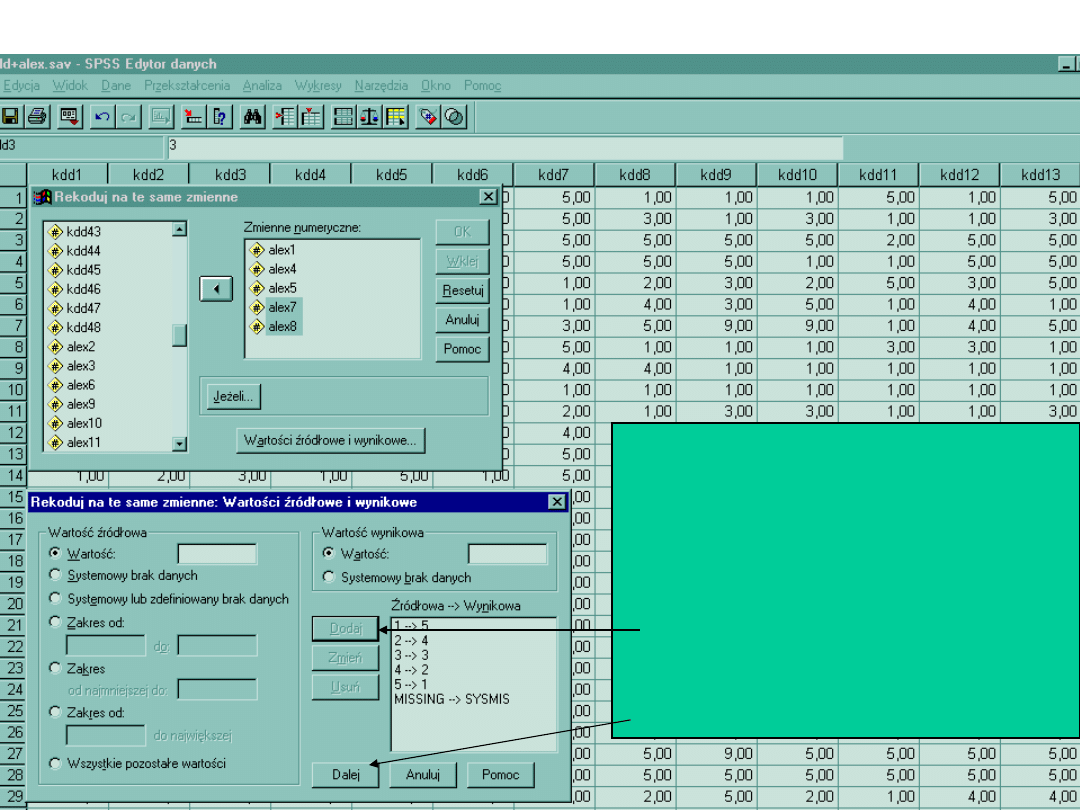
Rekodowanie na te same zmienne

Po wejściu do okna zmienne
wynikowe i źródłowe w
wartościach źródłowych wpisujemy
obecną wartość zmiennej, po
stronie wynikowej zaś wpisujemy
wartość pożądaną.

Każde przekodowanie
zatwierdzamy komendą DODAJ.

Po wpisaniu poleceń dla całej skali,
klikamy DALEJ >OK

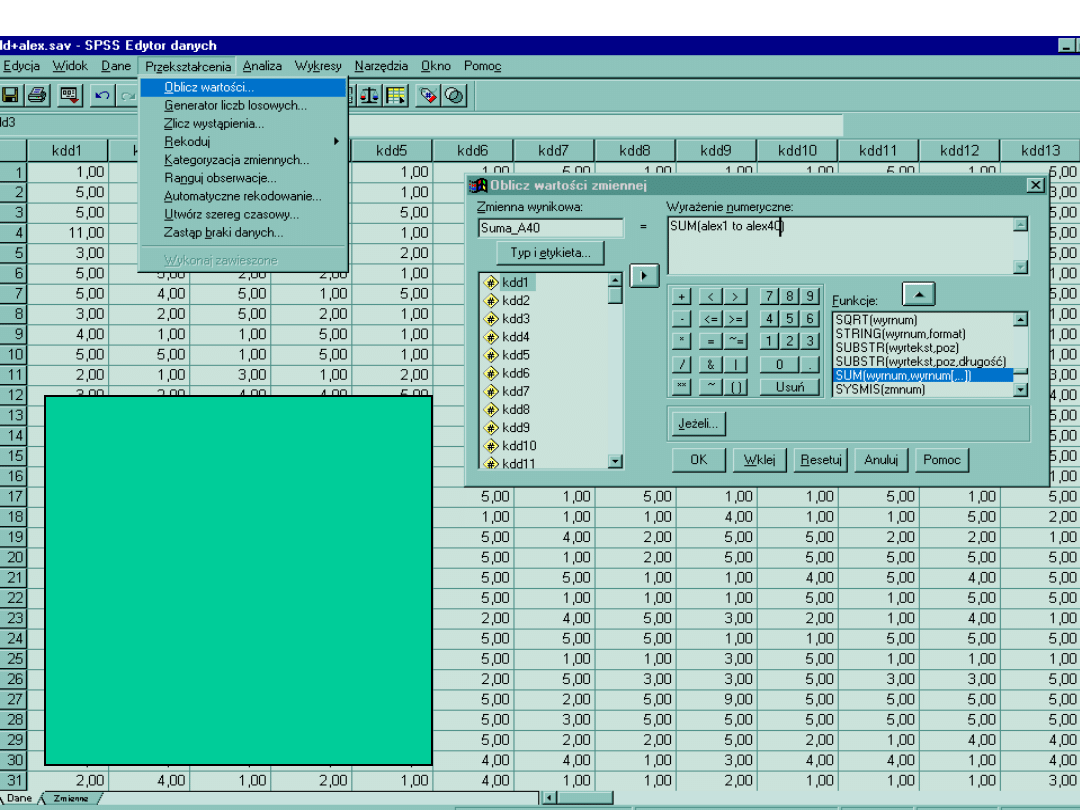
Tworzenie wskaźników zmiennych

Tworzenie zmiennej może się
opierać o sumę, średnią. My
tworzymy zmienną
Likertowską. W okienku
Funkcje odnajdujemy
interesujące nas polecenie.
Następnie wpisujemy jakie
zmienne mają zostać
zsumowane: SUM (alex1 to
alex40).

W oknie zmienna wynikowa
wpisujemy nazwę nowej
zmiennej. W oknie typ i
etykieta, możemy podać
pełną jej nazwę z polskimi
znakami.

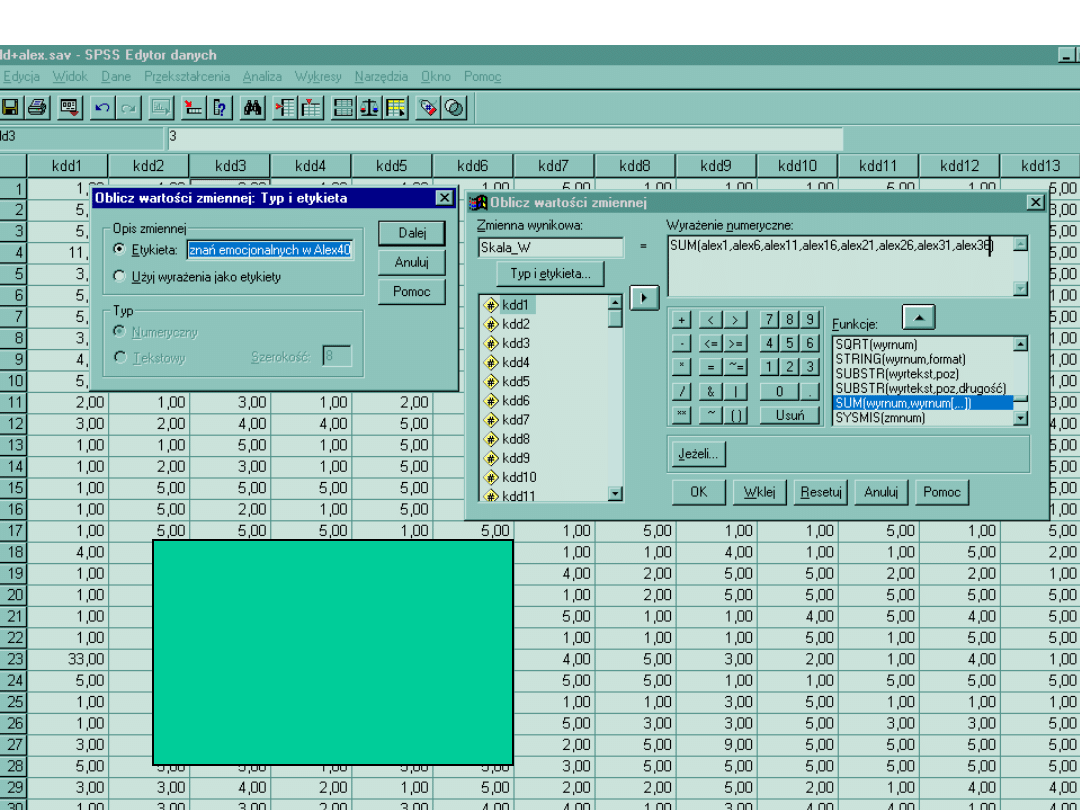
Tworzenie wskaźników Cd..

Jeśli pozycje wchodzące
na skalę nie układają się
w zakresy, wtedy trzeba
je wpisywać pojedynczo,
oddzielając każdą
przecinkiem
SUM(alex1,alex6,...,alex
36)

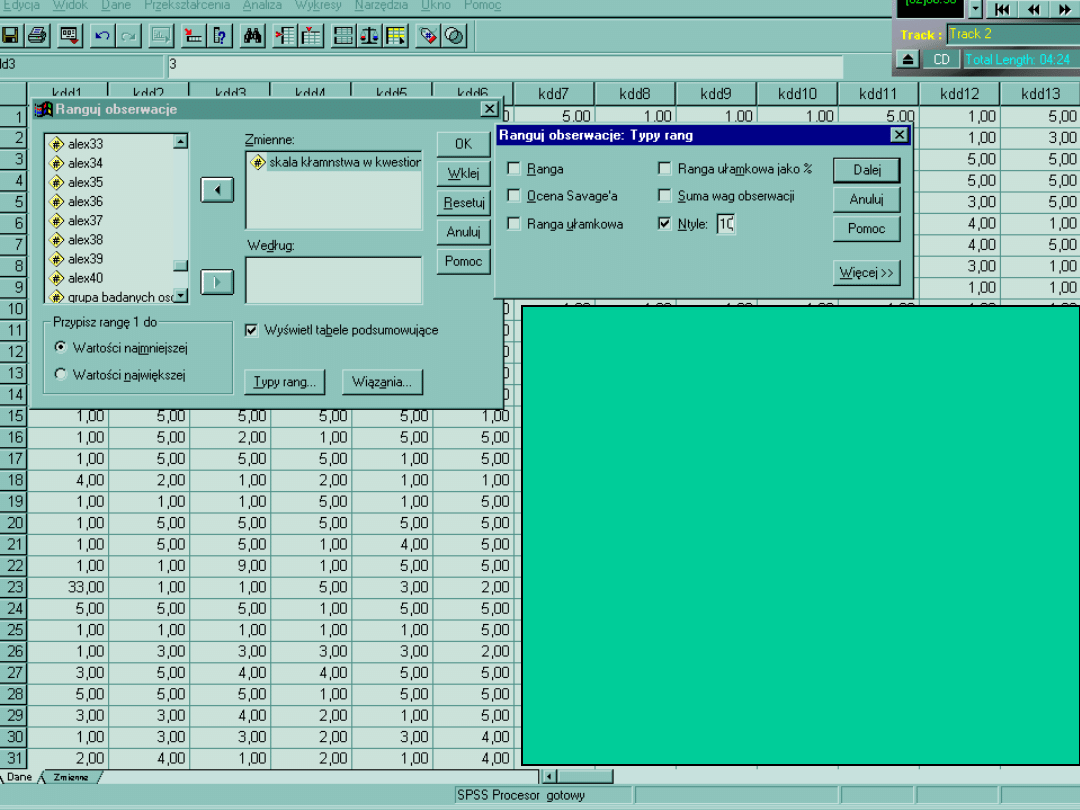
Dzielenie zbioru danych wg kryterium

Spróbujmy praktycznie
wykorzystać utworzoną
Skalę Kłamstwa.

Powiedzmy, że chcemy
odrzucić wyniki badanych,
których wyniki znajdują się
w górnych 10% -ach.

Kolejna operacja
przekształceń> Ranguj
obserwacje >Typy
rang>Ntyle=10

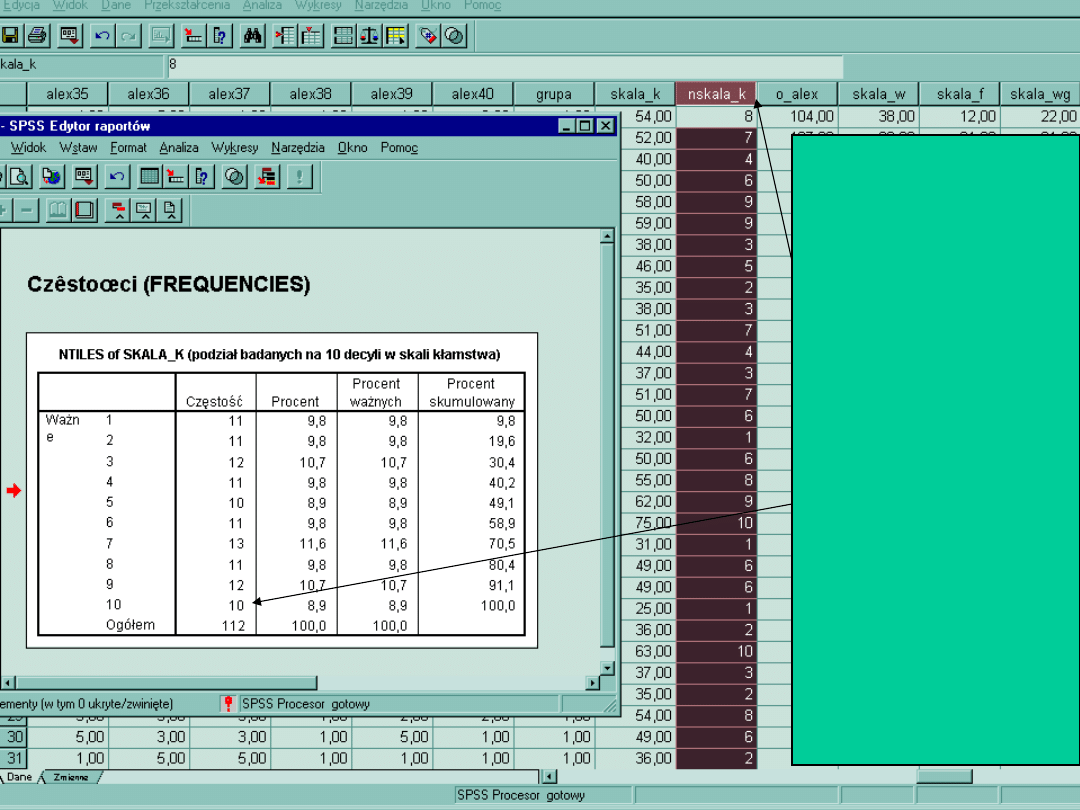
Powstała
nowa zmienna
nskala_k,

Wykonując
częstości z
tej zmiennej
dowiemy się
ile jest takich
osób.
Odszukując je
należy usunąć
wiersze tych
osób z dalszej
analizy

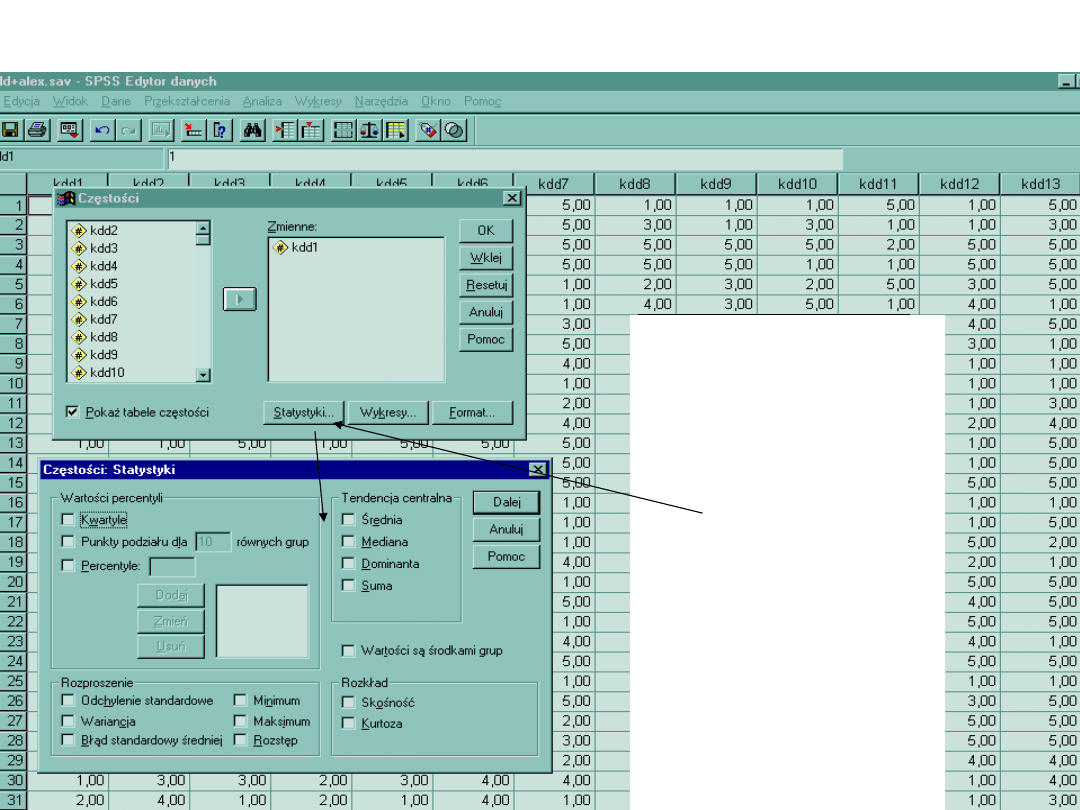
Statystyki Opisowe

1Statystyki opisowe
wykonuje się :
Analiza>Opis
Statystyczny>Często
ści .

2Następnie
wchodząc do okna
Statystyki
zaznaczamy
interesujące nas
miary

Ważne! Komputer
jest bezmyślny i
policzy wszystko
czego zażądamy.
Sensowność zależy
od nas

1

2

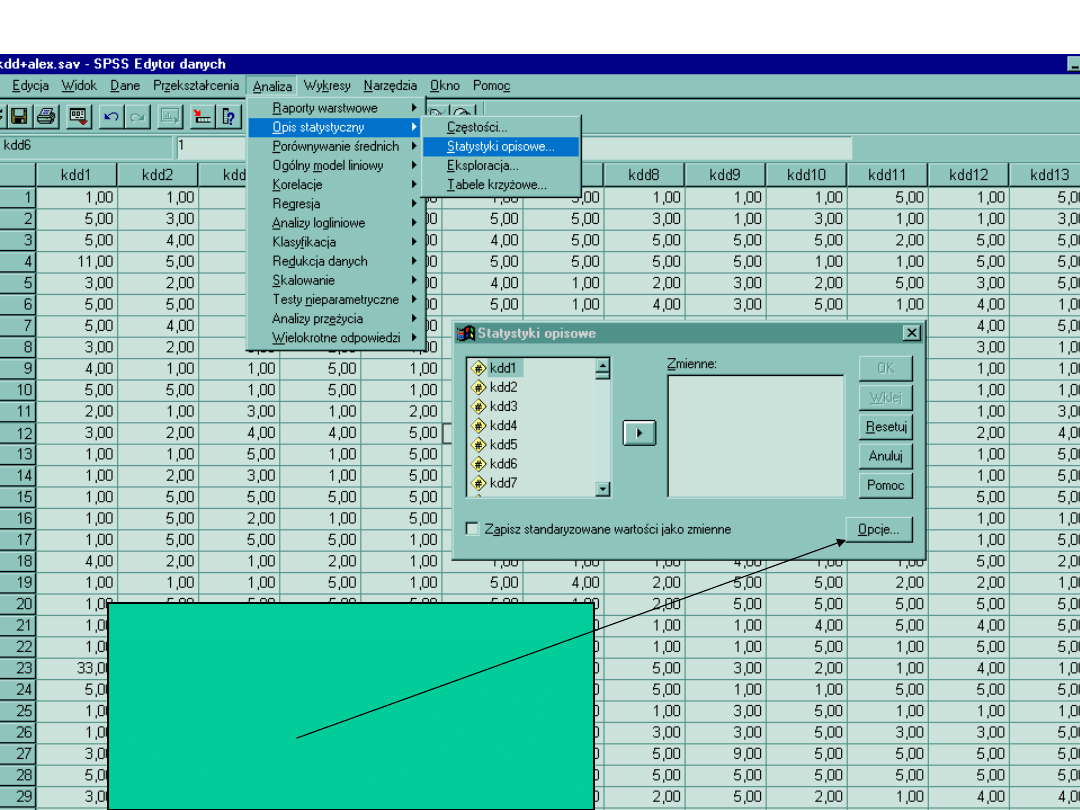
Statystyki opisowe Cd..

Statystyki opisowe można
policzyć inna metodą:

Analiza> Opis Statystyczny>
Statystyki opisowe> Opcje

Zmienne psychologiczne są w większości przypadków nie obserwowalne

Zmienne psychologiczne są w większości przypadków nie obserwowalne

„gołym okiem”. O ich poziomie możemy wnioskować tylko na podstawie

„gołym okiem”. O ich poziomie możemy wnioskować tylko na podstawie

wskaźników uzyskanych dzięki pomiarom np. testowym lub

wskaźników uzyskanych dzięki pomiarom np. testowym lub

manifestującym się zachowaniu świadczącym o danej cesze. Poszczególne

manifestującym się zachowaniu świadczącym o danej cesze. Poszczególne

zmienne w badaniu mogą być mierzone na różnych skalach pomiarowych.

zmienne w badaniu mogą być mierzone na różnych skalach pomiarowych.

Rodzaje skal pomiarowych:

Rodzaje skal pomiarowych:

Skala nominalna

Skala nominalna

– pozwala nam odróżniać dwa obiekty, nie umożliwia

– pozwala nam odróżniać dwa obiekty, nie umożliwia

porównywania obiektów. Zmienną mierzoną na skali nominalnej jest płeć –

porównywania obiektów. Zmienną mierzoną na skali nominalnej jest płeć –

możemy powiedzieć tylko, że kobieta różni się od mężczyzny. Nie możemy

możemy powiedzieć tylko, że kobieta różni się od mężczyzny. Nie możemy

jednak twierdzić, że jedna z tych płci jest lepsza.

jednak twierdzić, że jedna z tych płci jest lepsza.

Skala porządkowa (rangowa)

Skala porządkowa (rangowa)

– pozwala rozróżnić obiekty, ale także

– pozwala rozróżnić obiekty, ale także

uszeregować je w kolejności zależnej od nasilenia danej właściwości np.

uszeregować je w kolejności zależnej od nasilenia danej właściwości np.

poziom wykształcenia: osoba o wykształceniu podstawowym ma niższy

poziom wykształcenia: osoba o wykształceniu podstawowym ma niższy

poziom wykształcenia niż osoba o wykształceniu średnim, czy wyższym.

poziom wykształcenia niż osoba o wykształceniu średnim, czy wyższym.

Skale ilościowe: przedziałowa (interwałowa) i stosunkowa (ilorazowa)

Skale ilościowe: przedziałowa (interwałowa) i stosunkowa (ilorazowa)

– umożliwiają rozróżnienie obiektów, ustawienie ich w kolejności a także

– umożliwiają rozróżnienie obiektów, ustawienie ich w kolejności a także

określenie o ile jeden obiekt jest „lepszy”od drugiego (skala przedziałowa)

określenie o ile jeden obiekt jest „lepszy”od drugiego (skala przedziałowa)

lub też ile razy jeden obiekt jest mniejszy / większy od drugiego (skala

lub też ile razy jeden obiekt jest mniejszy / większy od drugiego (skala

stosunkowa).

stosunkowa).

Skale pomiarowe

Skale pomiarowe

zmiennych

zmiennych

 

Skala

nominalna

Skala

porządkowa

(rangowa)

Skala

przedziałowa

(interwałowa)

Skala

ilorazowa

(stosunkowa)

Czy jeden obiekt różni się
od drugiego?

Tak

Tak

Tak

Tak

Czy jeden obiekt jest
większy od drugiego?

Nie

Tak

Tak

Tak

O ile jeden obiekt jest
większy od drugiego?

Nie

Nie

Tak

Tak

Ile razy jeden obiekt jest
większy od drugiego?

Nie

Nie

Nie

Tak

Jakie informacje uzyskać można posługując się

Jakie informacje uzyskać można posługując się

określonymi skalami?

określonymi skalami?

Miary tendencji centralnej

: średnia, mediana (wartość, która jako pierwsza odcina

co najmniej 50% przypadków), modalna (najczęściej występująca wartość)

Miary rozproszenia:

wariancja, odchylenie standardowe

Miary kształtu rozkładu

:

skośność

(rozkład dodatnio {prawoskośny} i

ujemnieskośny {lewo})
i

kurtoza

(rozkład platy- i leptokurtyczny)

Centyle

– są to wartości,które dzielą wszystkie osoby na równoliczne grupy:

Kwartyle

dzielą osoby badane na cztery równoliczne grupy (po 25 %): drugi kwartyl

to mediana,

Decyle:

dzielą wyniki na dziesięć grup – piąty decyl to mediana,

Percentyle

na 100 grup - 50 percentyl to mediana, 10 percentyl to pierwszy decyl, 25

percentyl to pierwszy kwartyl

Rodzaje statystyk opisowych

Rodzaje statystyk opisowych

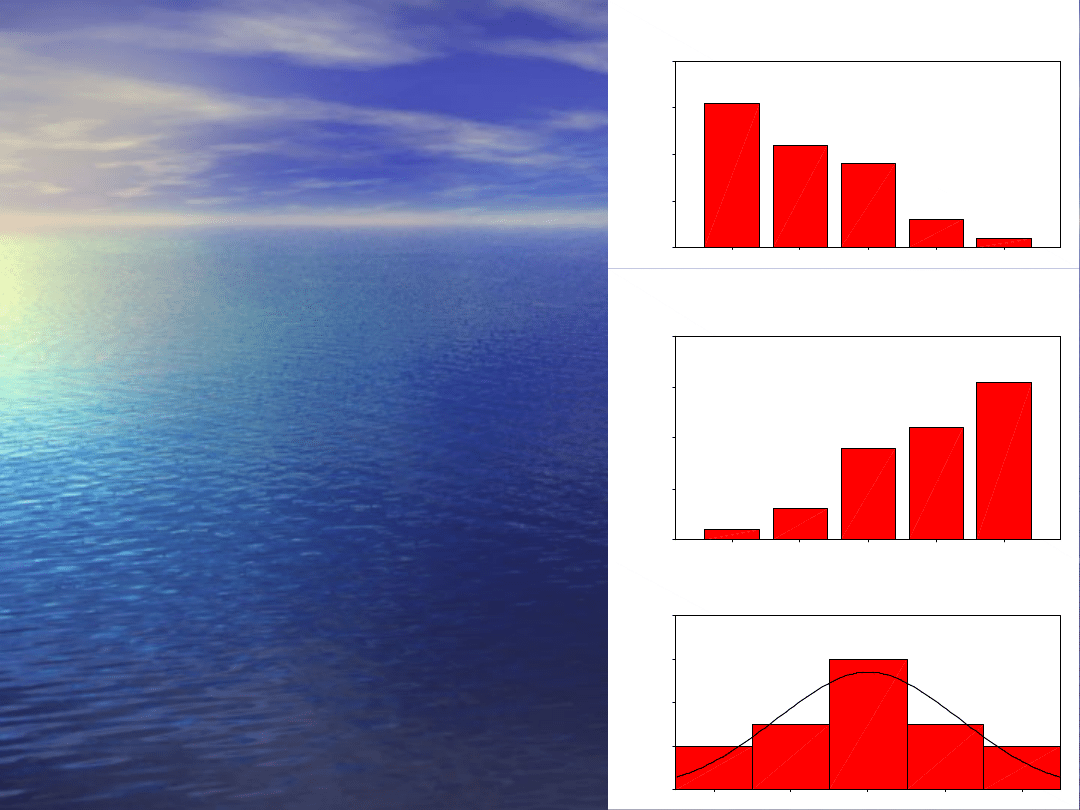
Relacje między

Relacje między

poszczególnymi miarami

poszczególnymi miarami

tendencji centralnej a

tendencji centralnej a

skośnością

skośnością

•

Jeśli rozkład jest

Jeśli rozkład jest dodatnio-skośny,

dodatnio-skośny,

a

a

więc wartości układają się w

więc wartości układają się w

kierunku dodatnim (w prawo) wtedy

kierunku dodatnim (w prawo) wtedy

relacja między miarami tendencji

relacja między miarami tendencji

centralnej jest następująca:

centralnej jest następująca:

Średnia >mediana>modalna

Średnia >mediana>modalna

•

Jeśli rozkład jest

Jeśli rozkład jest ujemnie-skośny

ujemnie-skośny

, a

, a

więc wartości układają się w

więc wartości układają się w

kierunku ujemnym (w lewo) wtedy

kierunku ujemnym (w lewo) wtedy

miary tendencji centralnej układają

miary tendencji centralnej układają

się następująco:

się następująco:

Średnia <mediana<modalna

Średnia <mediana<modalna

•

Gdy

Gdy

rozkład jest normalny

rozkład jest normalny

wartości

wartości

wszystkich miar tendencji

wszystkich miar tendencji

centralnej są równe.

centralnej są równe.

Średnia =mediana=modalna

Średnia =mediana=modalna

Rozk³ad Dodatni

Egzamin Trudny

6,00

5,00

4,00

3,00

2,00

C

zê

st

o

œ

æ

40

30

20

10

0

Rozkład Ujemny

Egzamin łatwy

6,00

5,00

4,00

3,00

2,00

C

zę

st

o

ść

40

30

20

10

0

6,0

5,0

4,0

3,0

2,0

Rozkład Normalny

Egzamin w sam raz

C

zę

st

o

ść

40

30

20

10

0

M=4 ; Me=4 ;
Mo=4

M= 4,9 ; Me=5 ;

M= 4,9 ; Me=5 ;

Mo=6

Mo=6

M=3,06 ; Me=3 ; Mo=2

M=3,06 ; Me=3 ; Mo=2

Przykład

Przykład

– do czego nam miary

– do czego nam miary

skośności?

skośności?

•

Porównajmy wyniki egzaminu z metodologii u

Porównajmy wyniki egzaminu z metodologii u

różnych wykładowców (plik egzamin.sav)

różnych wykładowców (plik egzamin.sav)

•

Żeby to zrobić należy skopiować wyniki ze strony

Żeby to zrobić należy skopiować wyniki ze strony

internetowej

internetowej

•

Następnie wkleić je do SPSS lub najpierw do

Następnie wkleić je do SPSS lub najpierw do

EXCELA

EXCELA

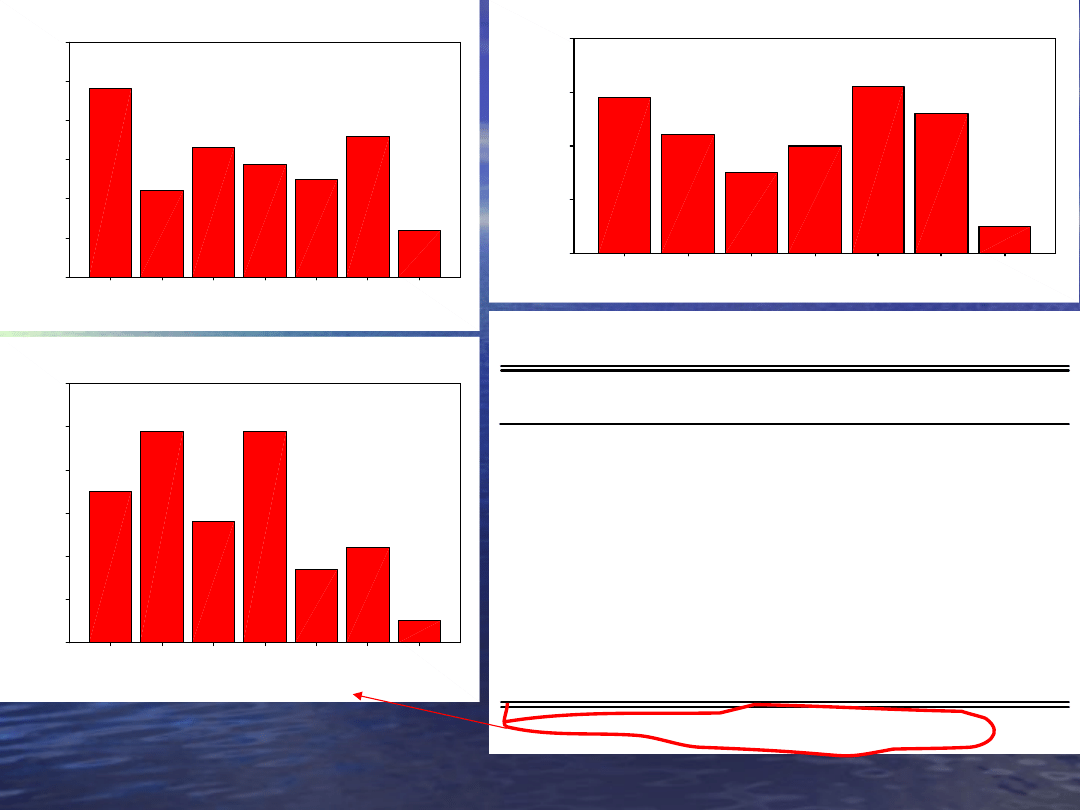
wyniki prof. Sędka

M= 3,55 ; Me = 3,5 ; Mo=3 (4)

6,00

5,00

4,50

4,00

3,50

3,00

2,00

C

zę

st

o

ść

60

50

40

30

20

10

0

wyniki dr Krejtz

M=3,76 ; M=4; M=4,5

6,00

5,00

4,50

4,00

3,50

3,00

2,00

C

zę

st

o

ść

40

30

20

10

0

wyniki prof. Karyłowskiego

M=3,7 ; Me=3,5 ; Mo=2

6,00

5,00

4,50

4,00

3,50

3,00

2,00

C

zę

st

o

ść

60

50

40

30

20

10

0

Statystyki

205

148

205

0

57

0

3,5488

3,7568

3,6976

3,5000

4,0000

3,5000

3,00

a

4,50

2,00

,111

-,229

-,008

,170

,199

,170

-,433

-,947

-,962

,338

,396

,338

Ważne

Braki danych

N

Średnia

Mediana

Dominanta

Skośność

Błąd standardowy skośności

Kurtoza

Błąd standardowy kurtozy

wyniki prof.

Sędka

wyniki dr Krejtz

wyniki prof.

Karyłowskiego

Istnieje wiele wartości modalnych. Podano wartość najmniejszą.

a.

Tak naprawdę jest
to rozkład
bimodalny