ALGORYTM POSTĘPOWANIA

ALGORYTM POSTĘPOWANIA

w doborze metody do

w doborze metody do

zmiennych

zmiennych

Czyli co? Gdzie? kiedy?

Czyli co? Gdzie? kiedy?

Dowiedzieć się będzie można

Dowiedzieć się będzie można

też o Analizie Regresji

też o Analizie Regresji

Jaki test wybrać, kiedy mierzymy siłę związku między
zmiennymi?

Ile
zmiennych

dwi
e

więcej niż
dwie

Na jakiej skali
mierzone?

nominal
na

porządko
wa

ilościow
a

porządko
wa

ilościo
wa

V-
Cramera

Rho-
Spearma
na

R-
Pearsona

Współczynn
ik
wielokrotne
j korelacji
rangowej-
Kendalla

Współczynn
ik korelacji
wielokrotne
j-R-
Pearsona

regresja

Ile grup
porównujemy

dwi
e

więcej niż
dwie

Na jakiej skali zmienna
zależna?

nominalna

porządkow
a

ilościow
a

Chi-
Kwadrat

U-Manna-
Whitneya

t-
Studen
ta

Chi-
Kwadrat

Jaki test wybrać, kiedy sprawdzamy istnienie

różnic między grupami

niezależnymi?

nominalna

porządkow
a

ilościow
a

Kruskal
a-
Wallisa

F-
Fishera
(analiza
wariancji
)

Analiza Regresji

Analiza Regresji

Jest to metoda, którą należy traktować jako

Jest to metoda, którą należy traktować jako

rozwinięcie analizy korelacyjnej

rozwinięcie analizy korelacyjnej

W zwykłych korelacjach mierzymy

W zwykłych korelacjach mierzymy

współwystepowanie zmiennnych ze sobą (inaczej:

współwystepowanie zmiennnych ze sobą (inaczej:

co z czym chodzi w parze) np. związek między

co z czym chodzi w parze) np. związek między

temperatura otoczeniea a agresją

temperatura otoczeniea a agresją

Możemy też sprawdzić na ile te chodzenie w

Możemy też sprawdzić na ile te chodzenie w

parze jest związkiem silnym (R kwadrat)

parze jest związkiem silnym (R kwadrat)

R

R

2

2

to siła związku przyjmująca wartość od 0 do 1,

to siła związku przyjmująca wartość od 0 do 1,

co przekłada się na % - ent wariacji

co przekłada się na % - ent wariacji

wytłumaczonej jednej zemiennej na podsatawie

wytłumaczonej jednej zemiennej na podsatawie

drugiej zmiennej korelowanej. Np.. Jeśli agresja

drugiej zmiennej korelowanej. Np.. Jeśli agresja

jest skorelowana ze wzrostem temperatury r =

jest skorelowana ze wzrostem temperatury r =

0,7 to R

0,7 to R

2 =

2 =

0, 5 co oznacza, że obie zmienne są

0, 5 co oznacza, że obie zmienne są

związane w 50 % - ach

związane w 50 % - ach

Analiza Regresji

Analiza Regresji

Wspomniany przykład jest najprostyrzym

Wspomniany przykład jest najprostyrzym

waraintem analizy regresji, kiedy na

waraintem analizy regresji, kiedy na

podstawie jednej zmiennej przewidujemy

podstawie jednej zmiennej przewidujemy

zachowanie drugiej zmiennej.

zachowanie drugiej zmiennej.

Co się jednak dzieje kiedy chcemy się

Co się jednak dzieje kiedy chcemy się

dowiedzieć na ile inne kielka zmiennych

dowiedzieć na ile inne kielka zmiennych

potrafi wytłumaczyć zmienność

potrafi wytłumaczyć zmienność

(wariancję) jakiejś zmiennej

(wariancję) jakiejś zmiennej

Wtedy dzieki analizie regresji możemy

Wtedy dzieki analizie regresji możemy

sprawdziić jak wszystkie zmiennne

sprawdziić jak wszystkie zmiennne

tłumaczą zmiennośc zmiennej zależnej

tłumaczą zmiennośc zmiennej zależnej

oraz jaki udział mają poszczególne

oraz jaki udział mają poszczególne

zmienne

zmienne

np. W jakim stopniu wariancja zdolnośc do

np. W jakim stopniu wariancja zdolnośc do

kariery jest tłuczona przez zmienne

kariery jest tłuczona przez zmienne

temperamentalne?

temperamentalne?

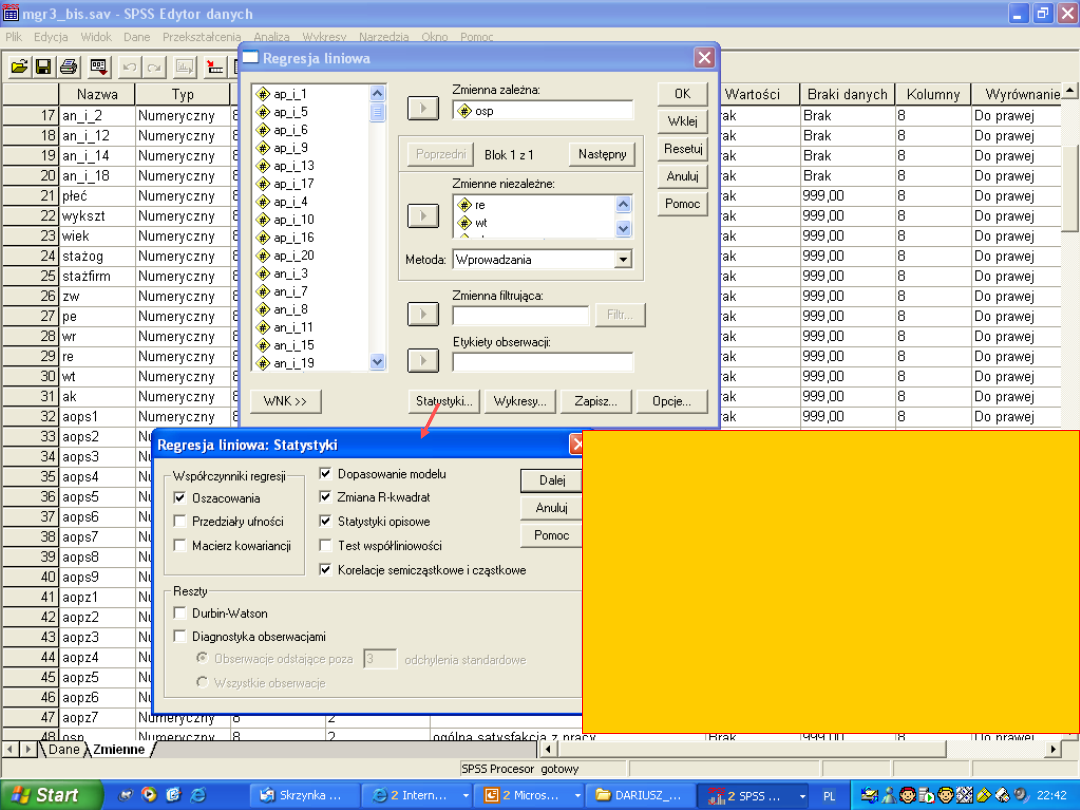
Analiza Regresji PRZYKŁAD

Analiza Regresji PRZYKŁAD

Ścieżka:
ANALIZA > RREGRESJA

LINIOWA

II. Zawsze warto zaznaczyć
statystyki Korelacje
semicząstkowe i cząstkowe

Statystyki opisowe

Dopasowanie modelu i Zmianę R
kwadrat

II

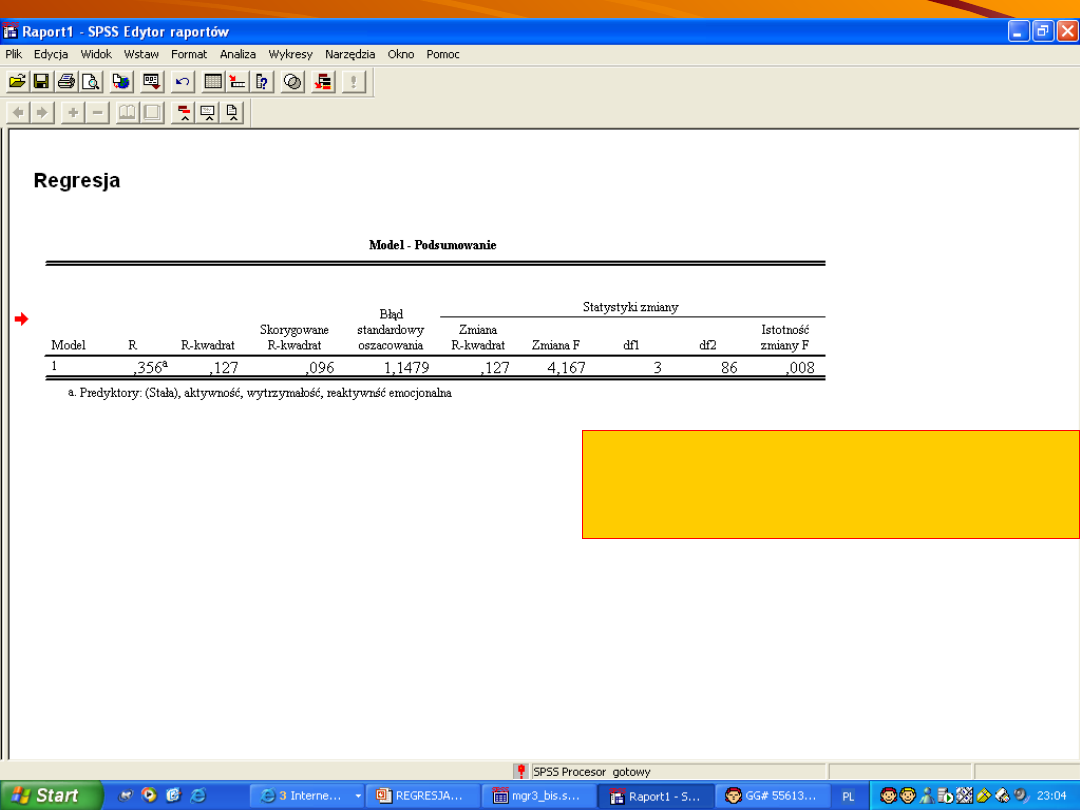
R kw. = 0,127, co oznacza, ze trzy
predyktory łącznie tłumaczą 12,7
% wariancji satysfakcji z pracy.

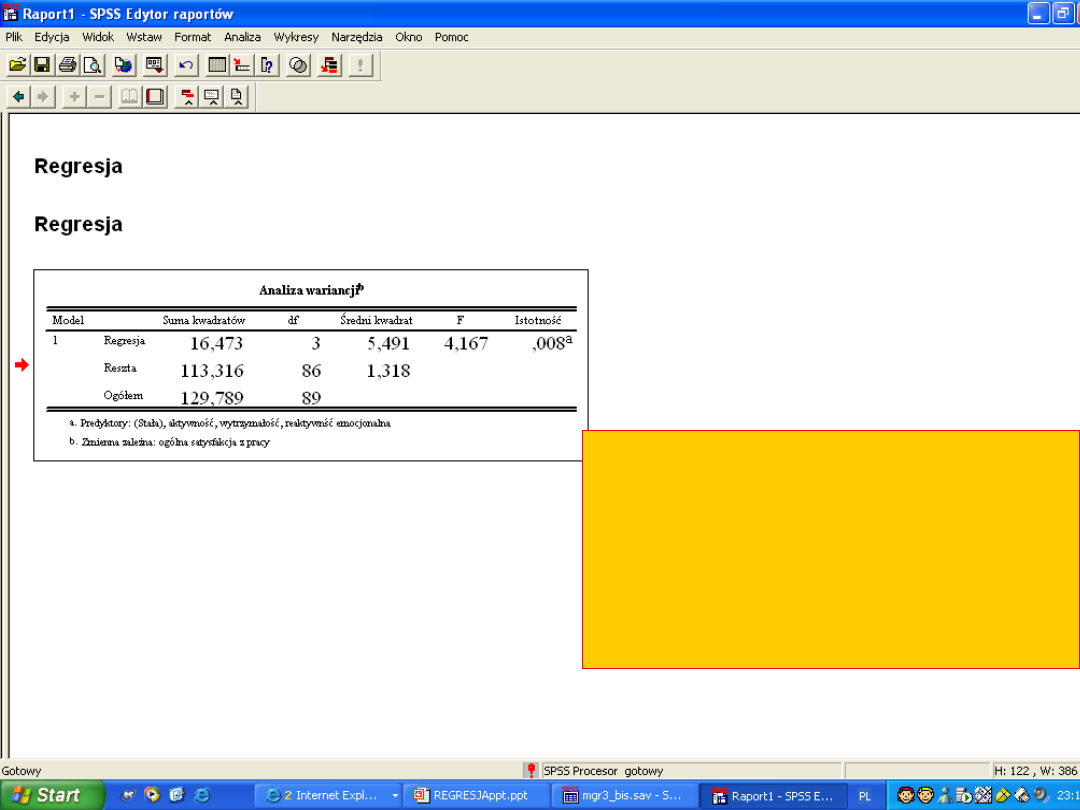
W ramach analizy regresji
wykonuje się analizę wariancji w
celu sprawdzenia dopasowaniu
modelu. Jeśli wynik jest istotny to
OK., oznacza to, że model regresji
jest dobry ( o modelach później
trochę powiemy)

Korelacje miedzy predyktorami

Korelacje miedzy predyktorami

Biorąc pod uwagę korelacje, które

Biorąc pod uwagę korelacje, które

zaznaczyliśmy w statystykach

zaznaczyliśmy w statystykach

sprawdzamy, czy predyktory są ze soba

sprawdzamy, czy predyktory są ze soba

związane istotnie

związane istotnie

Jeśli są okaże się, że tak to wtedy będzie

Jeśli są okaże się, że tak to wtedy będzie

różnica między korelacjami rzędu

różnica między korelacjami rzędu

zerowego i cząstkowymi.

zerowego i cząstkowymi.

oznaczać to będzie, że nawet jeśli każdy z

oznaczać to będzie, że nawet jeśli każdy z

predyktorów wysoko koreluje ze zmienną

predyktorów wysoko koreluje ze zmienną

zależną to wspólnie będą tłumaczyły

zależną to wspólnie będą tłumaczyły

stosunkowo ma ło wariancji

stosunkowo ma ło wariancji

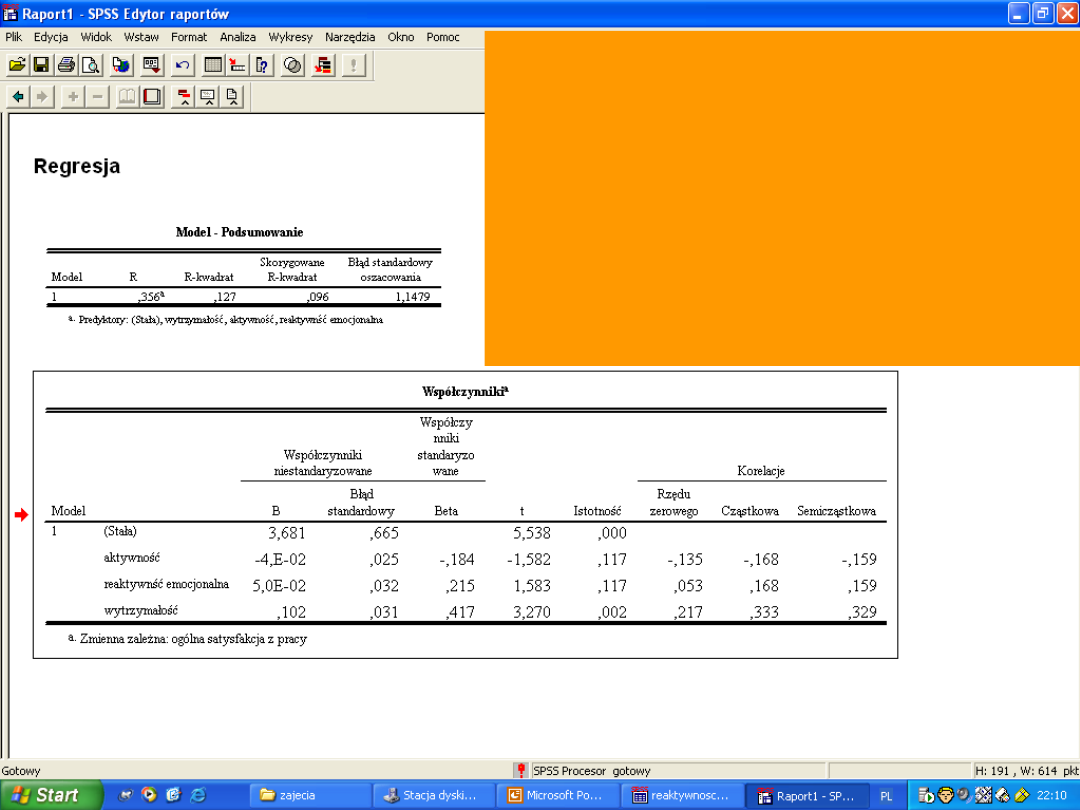
Współczynniki standaryzowane Beta są
dość duże, ale łączna wariancja
tłumaczona w modelu jest mała. Wynika
to z korelacji między predyktorami.
Korelacja rzędu zerowego to korelacja
między predyktorem a zm. Zal.
Korelacja cząstkowa to czysty wpływ
predyktora po wyizolowaniu związku
wynikającego z interkorelacji między
predyktorami

Uprzedziliśmy fakty mówiąc o wsp.

Uprzedziliśmy fakty mówiąc o wsp.

Beta.

Beta.

Generalnie analiza wariancji opiera

Generalnie analiza wariancji opiera

się o równanie regresji

się o równanie regresji

Y = bx + a

Y = bx + a

b to wsp. Regresji zaś „a” to stała

b to wsp. Regresji zaś „a” to stała

Przyjrzyjmy się jak będzie wyglądało

Przyjrzyjmy się jak będzie wyglądało

równanie dla naszych trzech

równanie dla naszych trzech

predyktorów

predyktorów

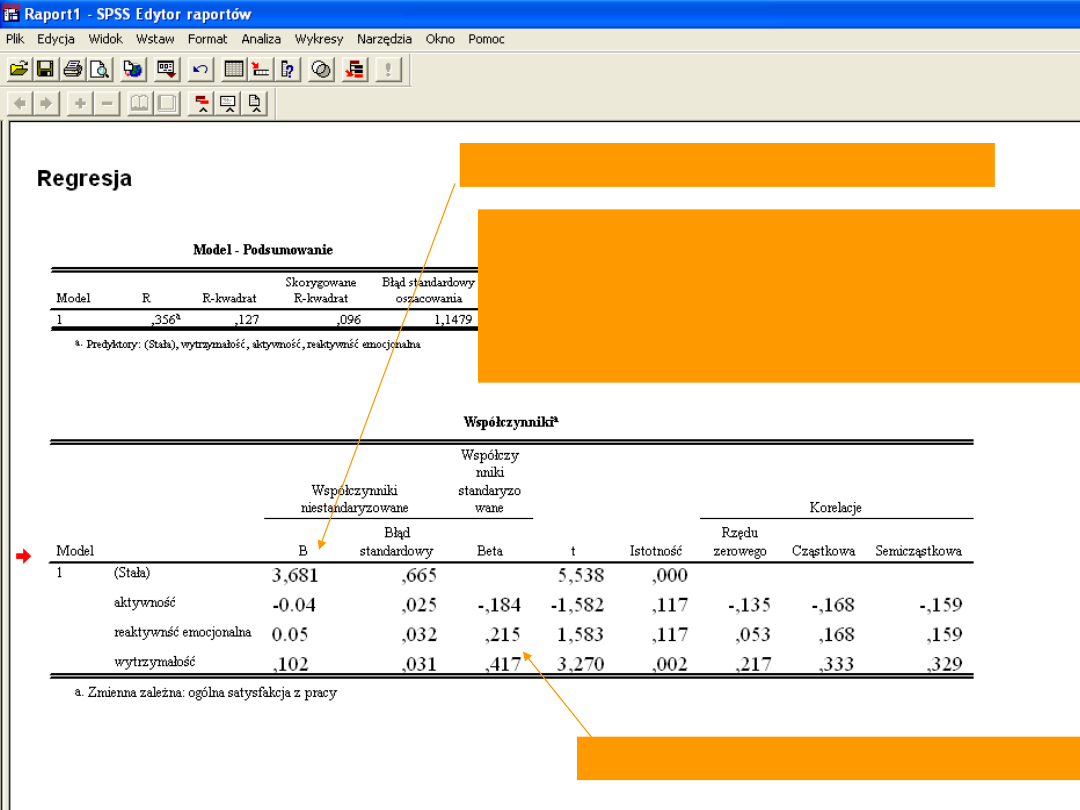
Y = -0,04x + 0,05X + 0,102X + 3,681

ZY = -0,184*Zx + 0,215*ZX + 417*ZX

Y = -0,04x + 0,05X + 0,102X + 3,681

Równanie bez wartości standaryzowanych
należy rozumieć w ten sposób, że wsp. b
oznacza kat nachylenia lini regresji
względem osi X, zaś wsp. a oznacza
przesuniecie modelu na osi Y

Metody wprowadzania

Metody wprowadzania

zmiennych do modelu regresji

zmiennych do modelu regresji

USUWANIA (Backward)

USUWANIA (Backward)

Do modelu wprowadzane są wszystkie

Do modelu wprowadzane są wszystkie

predyktory a potem usuwane są najsłabsze

predyktory a potem usuwane są najsłabsze

p>0,1

p>0,1

SELEKCJI POSTĘPUJACEJ (Forward)

SELEKCJI POSTĘPUJACEJ (Forward)

Do modelu wprowadzane są kolejno

Do modelu wprowadzane są kolejno

najsilniejsze

najsilniejsze

UWAGA! Wybór metody należy

UWAGA! Wybór metody należy

uzależniać od ilości wariancji

uzależniać od ilości wariancji

wytłumaczonej (R kwadrat)

wytłumaczonej (R kwadrat)

Metody wprowadzania

Metody wprowadzania

zmiennych do modelu regresji

zmiennych do modelu regresji

KROKOWA (Stepwise)

KROKOWA (Stepwise)

Połączenie backward i forward

Połączenie backward i forward

Do modelu wprowadzane są

Do modelu wprowadzane są

najsilniejsze (p<0,05) oraz usuwane

najsilniejsze (p<0,05) oraz usuwane

najsłabsze (p>0,1)

najsłabsze (p>0,1)

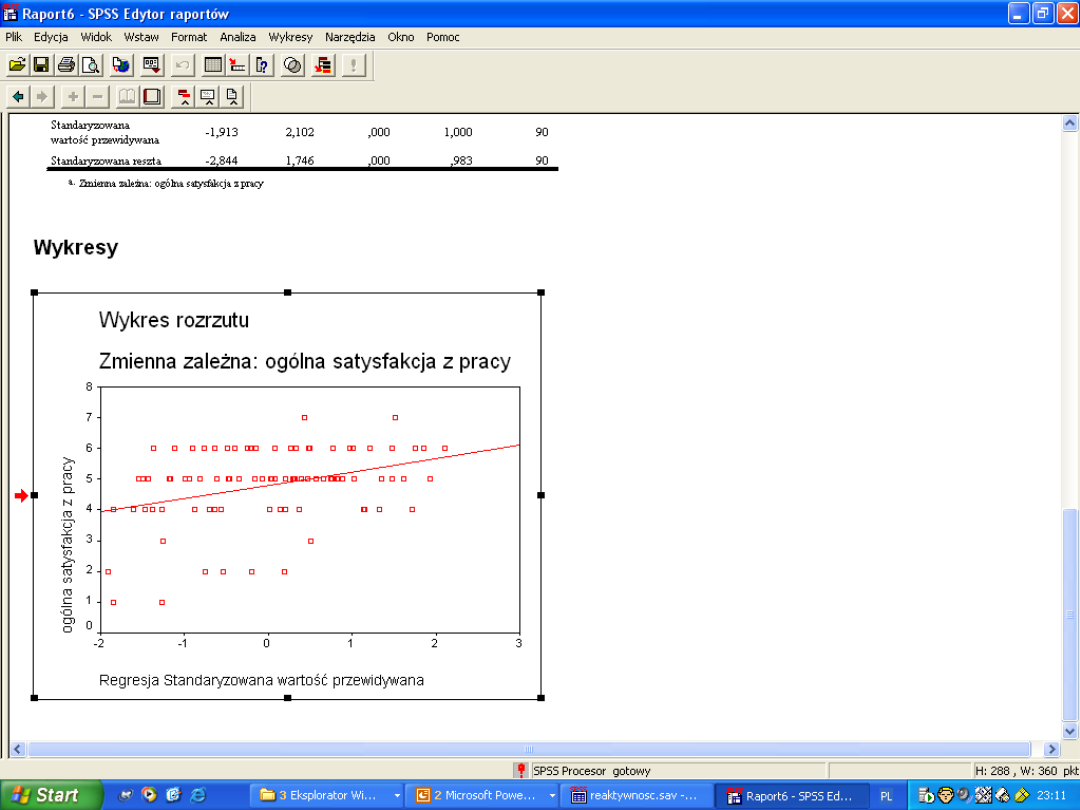
Analiza Regresji PRZYKŁAD

Analiza Regresji PRZYKŁAD

W jakim stopniu wariancja zdolnośc do

W jakim stopniu wariancja zdolnośc do

kariery jest tłuczona przez zmienne

kariery jest tłuczona przez zmienne

temperamentalne? (reaktywność,

temperamentalne? (reaktywność,

wytrzymałość, aktywność)

wytrzymałość, aktywność)

Założenia:

Założenia:

Zm. Zależna rozkład normalny

Zm. Zależna rozkład normalny

Zm. Niezależne: skale ilościowe

Zm. Niezależne: skale ilościowe

Zm. Niezależne (inaczej predyktory)

Zm. Niezależne (inaczej predyktory)

Nie powinny być ze sobą istotnie

Nie powinny być ze sobą istotnie

skorelowane

skorelowane