Podsumowanie

• Prześledziliśmy procedurę standaryzacji wyników, właściwości

rozkładu normalnego

• za pomocą filtrów usunęliśmy wyniki, które zawierały się w

górnych 10 % rozkładu normalnego ( w oparciu o wyniki „Z”)

• przygotowane dane z kwestionariusza poddaliśmy analizie

rzetelności,

• omówione została metoda Alfa Cronbacha oparta o współczynnik

korelacji, od czego zależy rzetelność, jak ją poprawić

• testowanie hipotez, wnioskowanie, istotność statystyczna, błędy
• Model korelacyjny: podstawowe wsp. Korelacji i sposoby ich

stosowania, związek liniowy i krzywoliniowy

• Modele eksperymentalne:testy T do porównywania średnich,

rodzaje i założenia teoretyczne (zmienna zależna na skali
ilościowej, rozkład normalny zmiennej)

• dla testu dla prób niezależnych wariancje powinny być równe w

obu grupach

• stopnie swobody, sposób zapisu i interpretacja.
• ANOVA do porównywania więcej niż dwóch średnich
• oparta na stosunku dwóch wariancji (kontrolowanej / błędu)
•

Zajęcia No 3

ANOVA - ZAŁ

Wariancje w grupach zmiennej niezależnej muszą być
równe (test Levene’a, podobnie jak w teście T dla prób
niezależnych)

Liczebności w grupach powinny być zbliżone.

Zm. Zależna powinna być na skali ilościowej

Powinna mieć rozkład normalny (sprawdzamy za pomocą
testu Kołmogorowa - Smirnova)

Statystyka F jest rozwinięciem testu T dla prób
niezależnych, porównuje więcej niż dwie średnie

2

F = T

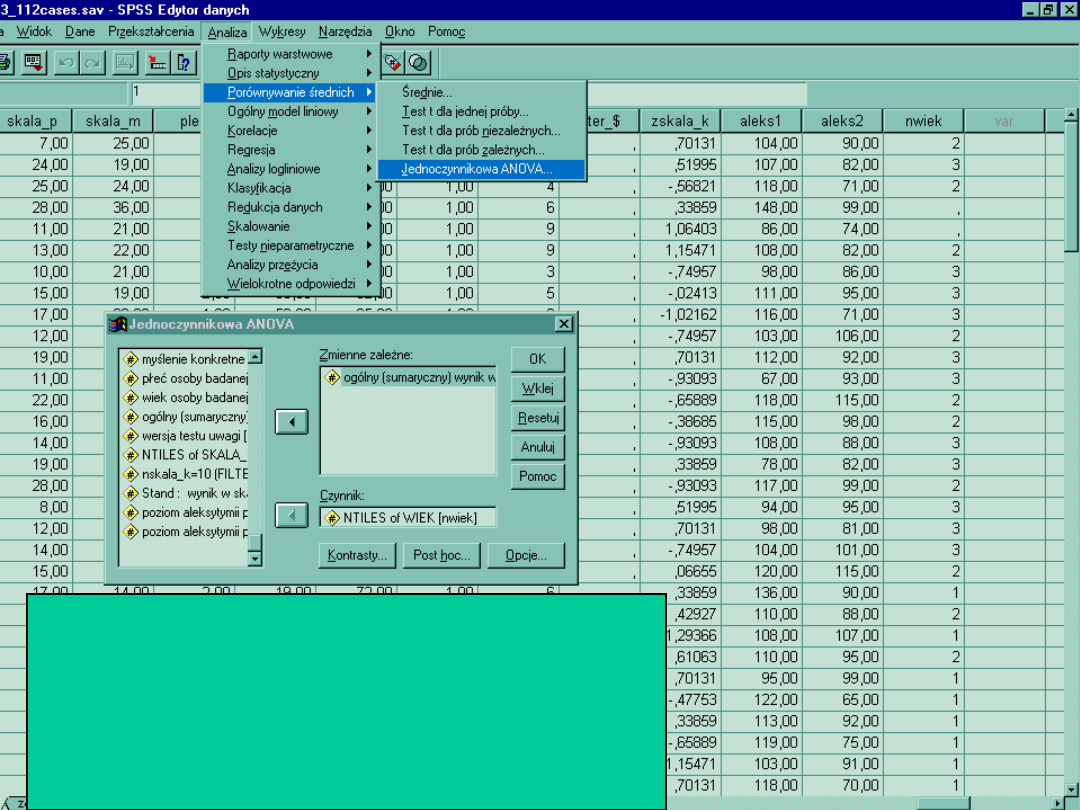
Ze zmiennej wiek za pomocą podziału na trzy równe
części utworzyliśmy zmienną trzykategorialną Nwiek (1-

młodzi, 2 średni, 3- starzy)

.

Chcemy zbadać czy

grupy

różnią się pod względem poziomu aleksytymii (zm.
Zależna!!!)
Jeżeli różnice między grupami mają być istotne to
zróżnicowanie (wariancja) między grupami wiekowymi
powinna być większa niż wewnątrz tych grup(błąd)

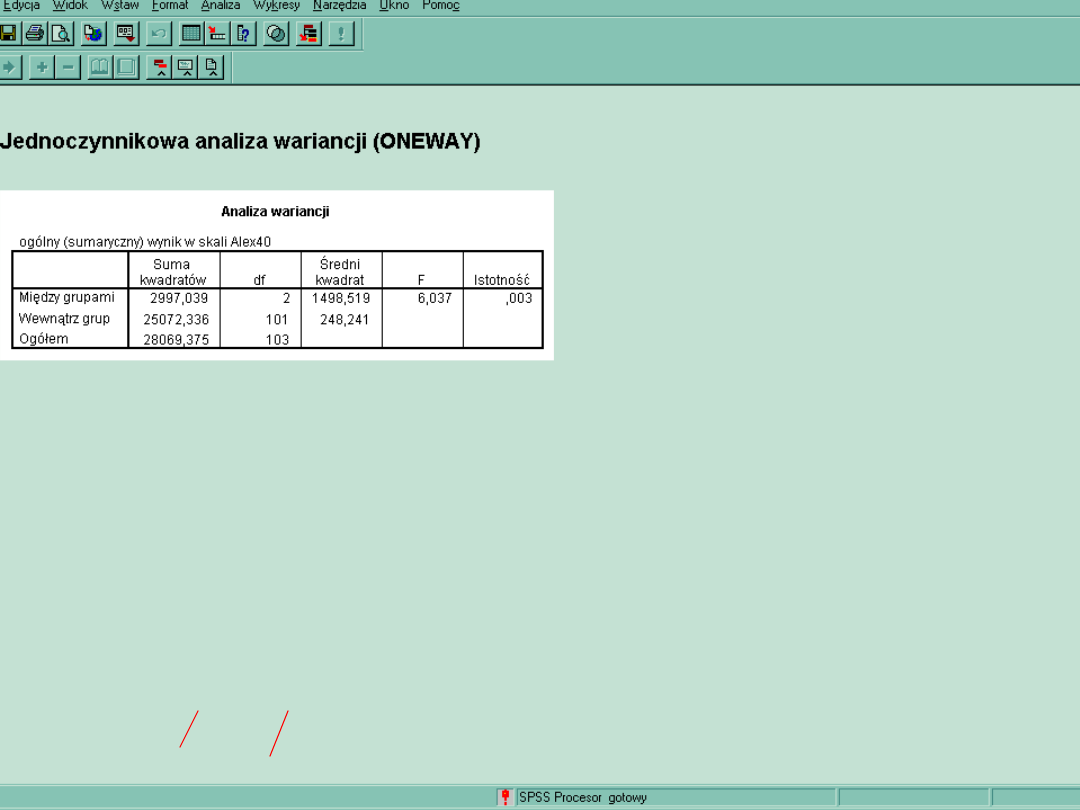
F (dfm, dfw) = X; p< 0,xxx

F(2,101) = 6,037; p < 0,01

Test F wynosi dużo więcej niż 1 i stąd różnice w średnich okazały się istotne.

SS total = SS między + SS wewnątrz

Df total = Df między + Df wewnątrz

czyli N = 104, Df total = N - 1, 103 Df między = k - 1, gdzie k = liczba grup Df wewnątrz = N - k

stąd N -1 = ( k -1) + (N -k)

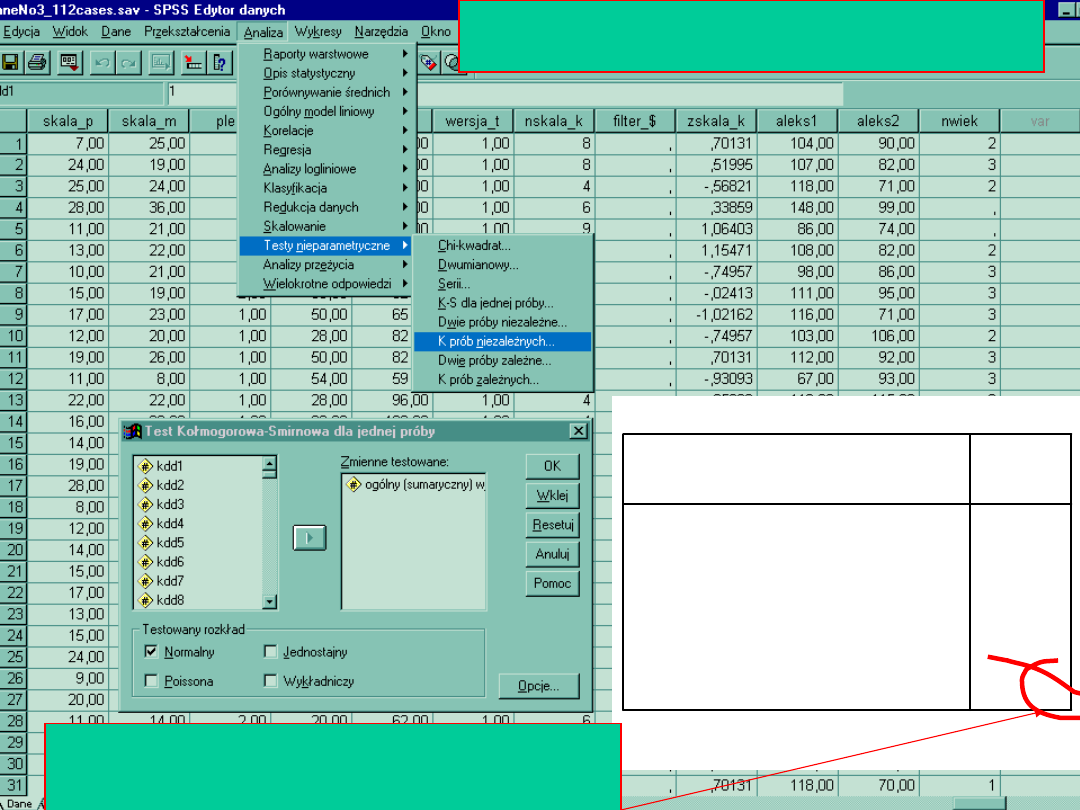
Co jednak z założeniami teoretycznymi, które

decydują o zastosowaniu ANOVY?

1. Zgodność z rozkładem normalnym

Test Kołmogorowa-Smirnowa dla jednej próby

112

101,2321

16,7558

,062
,062

-,045

,655

,784

N

Średnia
Odchylenie standardowe

Parametry rozkładu
normalnego

a,b

Wartość bezwzględna
Dodatnia
Ujemna

Największe różnice

Z Kołmogorowa-Smirnowa

Istotność asymptotyczna (dwustronna)

ogólny

(sumaryczny)

wynik w skali

Alex40

Testowana jest zgodność z rozkładem normalnym.

a.

Obliczono na podstawie danych.

b.

Jeżeli test okaże się istotny, wtedy należy odrzucić
hipotezę o zgodności z rozkładem normalnym i nie
powinno się wykonywać ANOVY

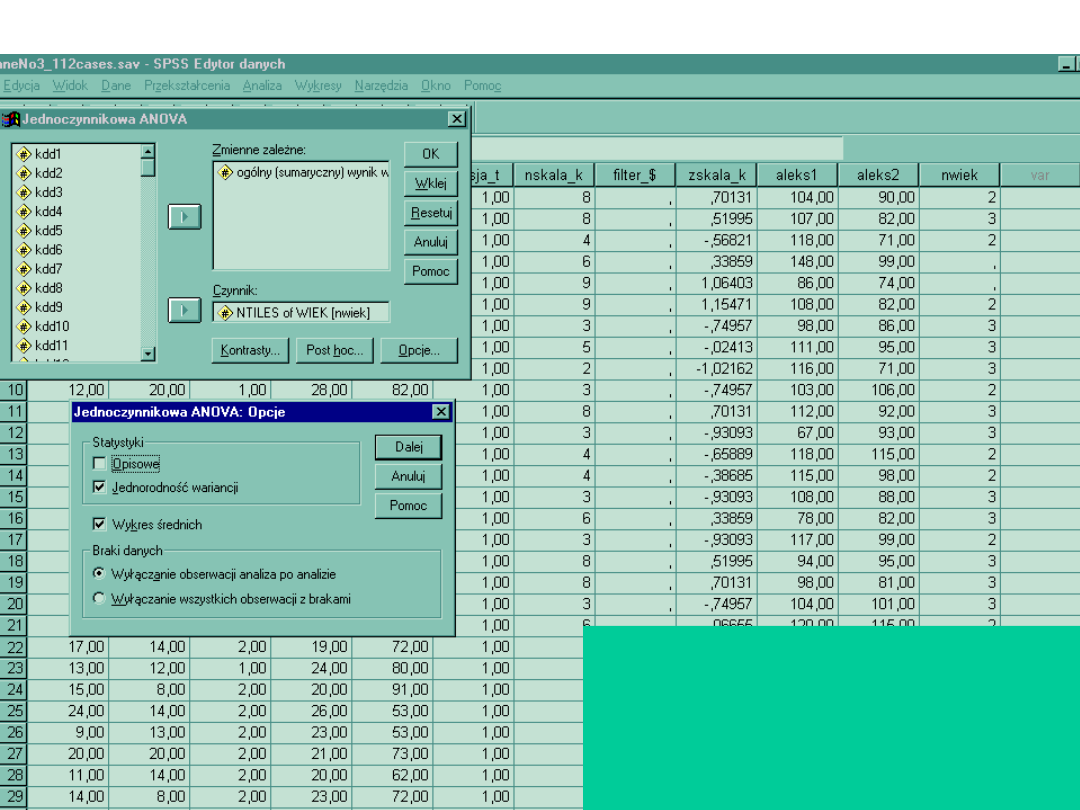
2. Założenie o równości wariancji w grupach

W teście T dla prób niezależnych
mieliśmy niejako wbudowany test
Levene’a. Tutaj o założenia musimy
dbać sami:
Opcje > Jednorodność wariancji
Żeby lepiej zilustrować jak wyglądają
różnice w poziomie aleksytymii
zaznaczamy tez Wykres średnich

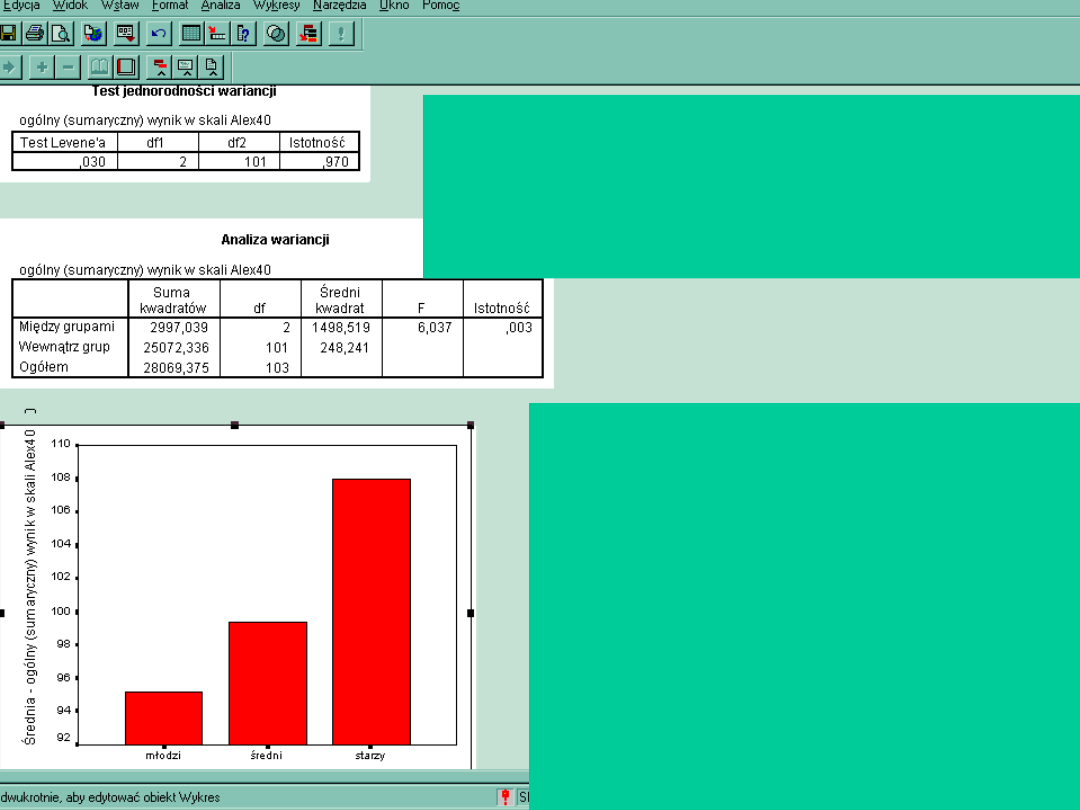
1. Podobnie jak w teście K-S zakłada się równość
wariancji w grupach. Jeśli test okaże się istotny,
oznacza to, że wariancje w grupach są różne, co może
wynikać chociażby z nieproporcjonalnych liczebności
w grupach. Istotny test Levene’a jest
przeciwwskazaniem do stosowania ANOVY

2. Mamy sprawdzone założenia teoretyczne.
Okazało się, że test jest istotny. Na wykresie
widać, że grupy rzeczywiście się różnią.
Powstaje pytanie, które różnice są istotne
statystycznie.
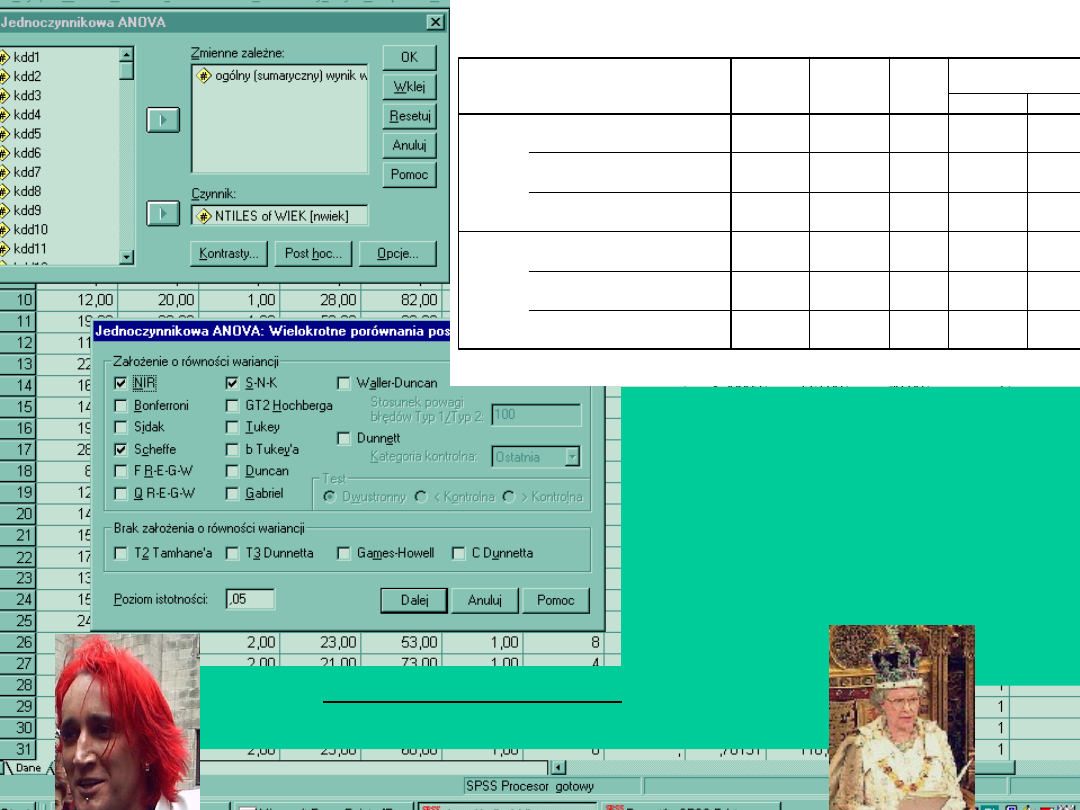
Do tego celu stosujemy testy Post hoc, czyli
analizę postpriori .
Pozwala nam wniknąć w strukturę zmiennej.
Opiera się na porównywaniu średnich w
grupach, każdą z każdym.
Jest często ostatnią deską ratunku, bo jeśli
test F jest nieistotny może okazać się, że
jednak poszczególne grupy się różnią. Verte
>

Porównania wielokrotne

Zmienna zależna: ogólny (sumaryczny) wynik w skali Alex40

-4,1529

3,7939

,551

-13,5789

5,2730

-12,8286*

3,7663

,004

-22,1860

-3,4711

4,1529

3,7939

,551

-5,2730

13,5789

-8,6756

3,7939

,078

-18,1016

,7504

12,8286*

3,7663

,004

3,4711

22,1860

8,6756

3,7939

,078

-,7504

18,1016

-4,1529

3,7939

,276

-11,6791

3,3732

-12,8286*

3,7663

,001

-20,2999

-5,3572

4,1529

3,7939

,276

-3,3732

11,6791

-8,6756*

3,7939

,024

-16,2017

-1,1495

12,8286*

3,7663

,001

5,3572

20,2999

8,6756*

3,7939

,024

1,1495

16,2017

(J) NTILES of WIEK
2 średni
3 starzy
1 młodzi
3 starzy
1 młodzi
2 średni
2 średni
3 starzy
1 młodzi
3 starzy
1 młodzi
2 średni

(I) NTILES of WIEK
1 młodzi

2 średni

3 starzy

1 młodzi

2 średni

3 starzy

Test Scheffe

Test NIR

Różnica

średnich (I-J)

Błąd

standardowy Istotność Dolna granica Górna granica

95% przedział ufności

Różnica średnich jest istotna na poziomie .05.

*.

Post hoc jest multiplikacją testu t,
porównuje każdą grupę z każdą.
Wybór testu zależy od nas i naszych
celów.
Różnią się one wymaganiami, od max.
Liberalności do maksymalnej
konserwatywności, czyli wykrywania
tylko silnie istotnych różnic.
Istotne różnice zaznaczone są
„gwaiazdkami”

< liberalizm

konserwatyzm >

NIR, Duncan

S-N-K

Scheffe

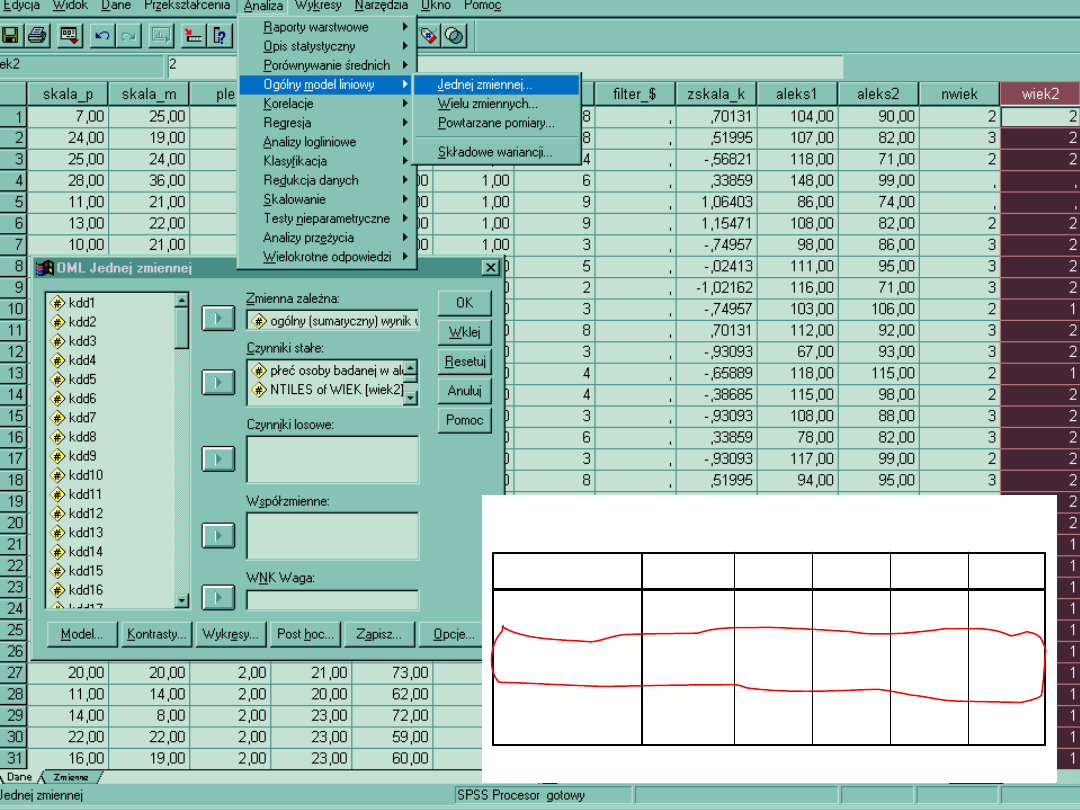
Unianova

Unianova



W praktyce zdarza się, że na zmienną zależną działa więcej niż jeden

W praktyce zdarza się, że na zmienną zależną działa więcej niż jeden

czynnik.

czynnik.



Co jeśli chcieć zbadać wpływ, czy manipulować więcej niż jedną zmienną?

Co jeśli chcieć zbadać wpływ, czy manipulować więcej niż jedną zmienną?



Unianova umożliwia taka analizę, pod warunkiem kontroli pozostałych

Unianova umożliwia taka analizę, pod warunkiem kontroli pozostałych

czynników jako źródła szumu (błędu).

czynników jako źródła szumu (błędu).



Założenia: zmienna zależna na skali ilościowej, dwie zmienne na skali

Założenia: zmienna zależna na skali ilościowej, dwie zmienne na skali

nominalnej

nominalnej



wariancje w grupach zmiennych niezależnych powinny być równe

wariancje w grupach zmiennych niezależnych powinny być równe



liczebności w grupach powinny być takie same

liczebności w grupach powinny być takie same



Uniaanova jest rozwinięciem Anovy. Jest również oparta na statystyce F, z tą

Uniaanova jest rozwinięciem Anovy. Jest również oparta na statystyce F, z tą

różnicą, że statystyk F będzie aż trzy. Dlaczego?

różnicą, że statystyk F będzie aż trzy. Dlaczego?



Unianova weryfikuje hipotezy co do różnic w średnich, wychwytując jakby

Unianova weryfikuje hipotezy co do różnic w średnich, wychwytując jakby

unikalny wpływ czynnika działającego w kolumnie (np. wiek2), będzie to test

unikalny wpływ czynnika działającego w kolumnie (np. wiek2), będzie to test

F dla efektu głównego w kolumnie

F dla efektu głównego w kolumnie



Wychwytuje wpływ czynnika działającego w rzędzie (np. płeć), będzie to test

Wychwytuje wpływ czynnika działającego w rzędzie (np. płeć), będzie to test

F dla efektu głównego zmiennej w rzędzie

F dla efektu głównego zmiennej w rzędzie



jeśli dwie zmienne działają jednocześnie można mówić, że tworzą czasem

jeśli dwie zmienne działają jednocześnie można mówić, że tworzą czasem

nową jakość. Inaczej, wchodzą ze sobą w interakcję - będzie to efekt

nową jakość. Inaczej, wchodzą ze sobą w interakcję - będzie to efekt

interakcyjny

interakcyjny



Oczywiście podobnie jak w przypadku ANOVY chodzi o to, aby wariancja

Oczywiście podobnie jak w przypadku ANOVY chodzi o to, aby wariancja

kontrolowana była jak najwyższa, błąd zaś najmniejszy.

kontrolowana była jak najwyższa, błąd zaś najmniejszy.

Przykład -

Przykład -

Czy płeć i wiek istotnie różnicują poziom

Czy płeć i wiek istotnie różnicują poziom

alekstymii?

alekstymii?

Czy płeć istotnie wpływa na poziom aleksytymii?

Czy płeć istotnie wpływa na poziom aleksytymii?

Czy wiek istotnie wpływa na poziom aleksytymii?

Czy wiek istotnie wpływa na poziom aleksytymii?

Czy starzy mężczyźni istotnie różnią się poziomem

Czy starzy mężczyźni istotnie różnią się poziomem

aleksytymii od starszych kobiet?

aleksytymii od starszych kobiet?

Klasyczny schemat 2 x 2

Klasyczny schemat 2 x 2

Wiek2

1- młodzi

2- starzy

1- M

2- K

52

52

52

52

Testy efektów międzyobiektowych

Zmienna zależna: ogólny (sumaryczny) wynik w skali Alex40

6245,740

a

3 2081,913

9,540

,000

775252,977

1 775253,0 3552,355

,000

1453,780

1 1453,780

6,661

,011

1588,173

1 1588,173

7,277

,008

103,076

1

103,076

,472

,494

21823,635

100

218,236

1086349,000

104

28069,375

103

Źródło zmienności
Model skorygowany
Stała
PLEC
WIEK2
PLEC * WIEK2
Błąd
Ogółem
Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

R kwadrat = ,223 (Skorygowane R kwadrat = ,199)

a.

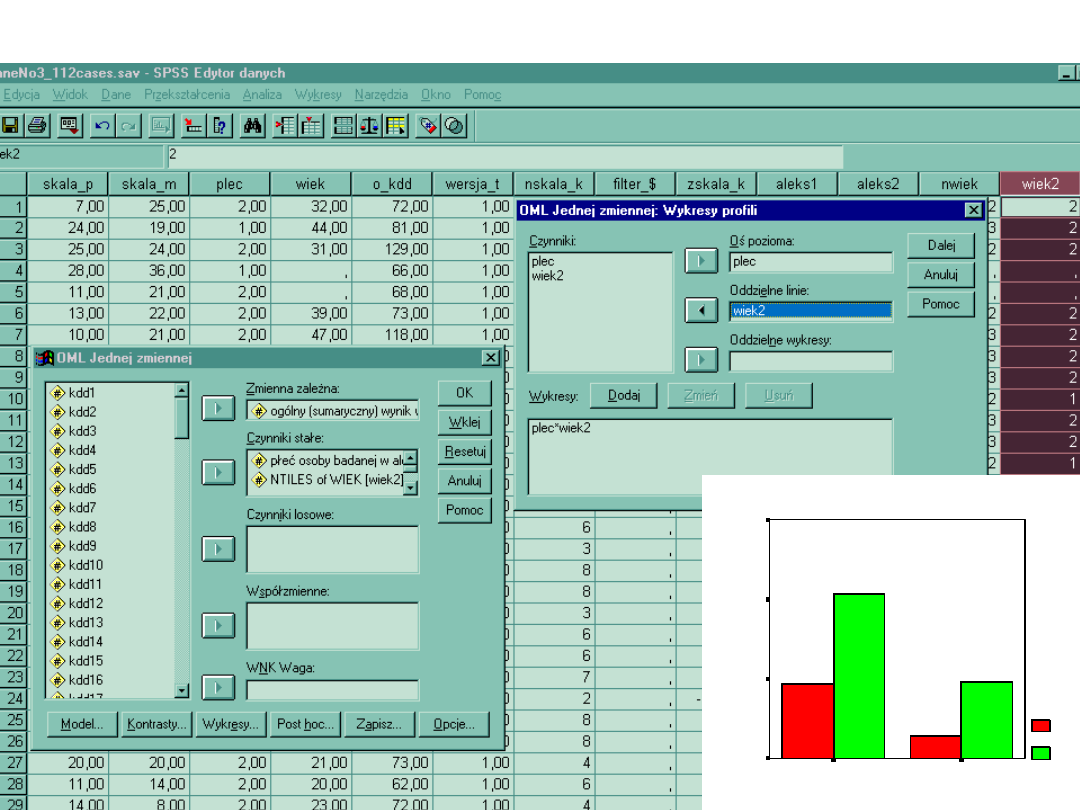
Wykonywanie wykresów

Oszacowane średnie brzegowe - ogólny (sumaryczny) wynik w skali Alex40

płeć osoby badanej w alex 40

k

m

O

sz

ac

ow

an

e

śr

ed

ni

e

br

ze

go

w

e

120

110

100

90

NTILES of WIEK

młodzi

starzy

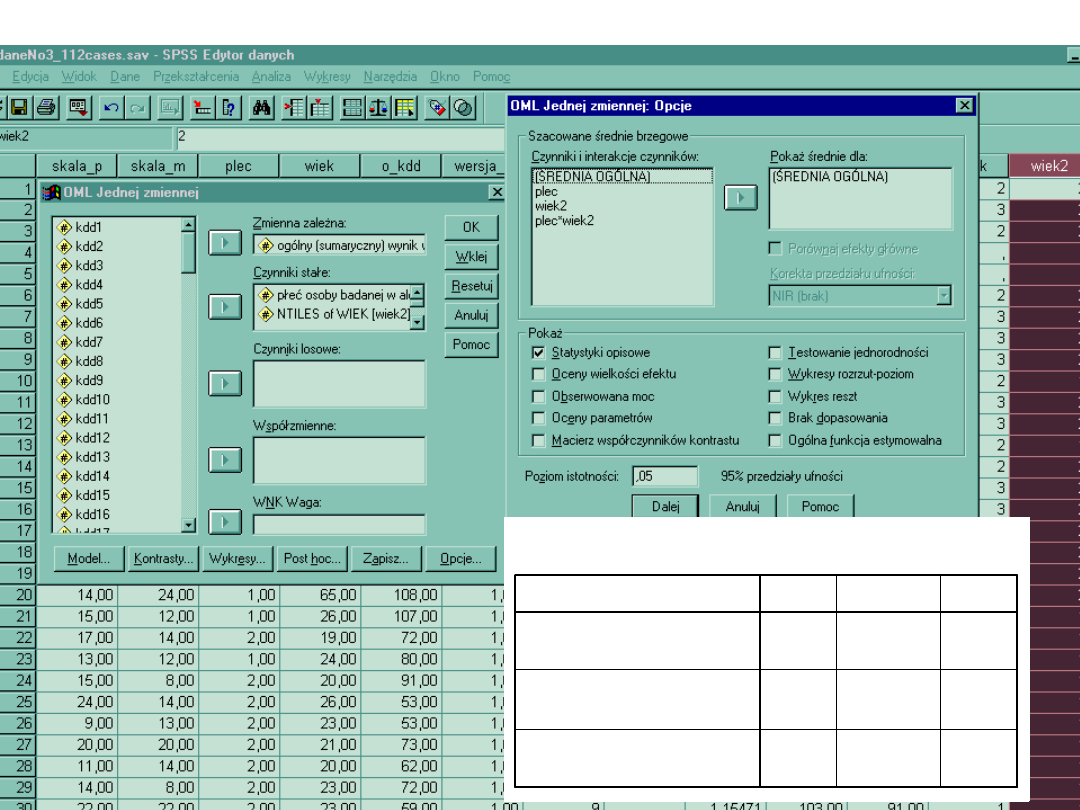
Używanie statystyk opisowych

Statystyki opisowe

Zmienna zależna: ogólny (sumaryczny) wynik w skali Alex40

99,2727

11,4551

11

110,7027

15,4791

37

108,0833

15,3302

48

92,8780

15,4551

41

99,6667

12,9044

15

94,6964

15,0102

56

94,2308

14,8332

52

107,5192

15,5027

52

100,8750

16,5081

104

NTILES of WIEK
1 młodzi
2 starzy
Ogółem
1 młodzi
2 starzy
Ogółem
1 młodzi
2 starzy
Ogółem

płeć osoby
badanej w alex 40
1,00 m

2,00 k

Ogółem

Średnia

Odchylenie

standardowe

N

Przykład 2 edytor danych „suplement”

Badano N= 60 pacjentów psychiatrycznych. Badano

ilość nawrotów psychotycznych po zakończeniu

programu na skali 10 stopniowej.

Badani losowo poddani zostali dwóm rodzajom

oddziaływań eksperymentalnych: psychoterapii lub

farmakoterapii. W obu warunkach połowa badanych

przydzielona została do zespołu sprawującego

opiekę, postrzeganego jako mało empatyczny. Druga

połowa przydzielona została do zespołu

sprawującego opiekę, postrzeganych jako

empatycznych.

Schemat 2 x2

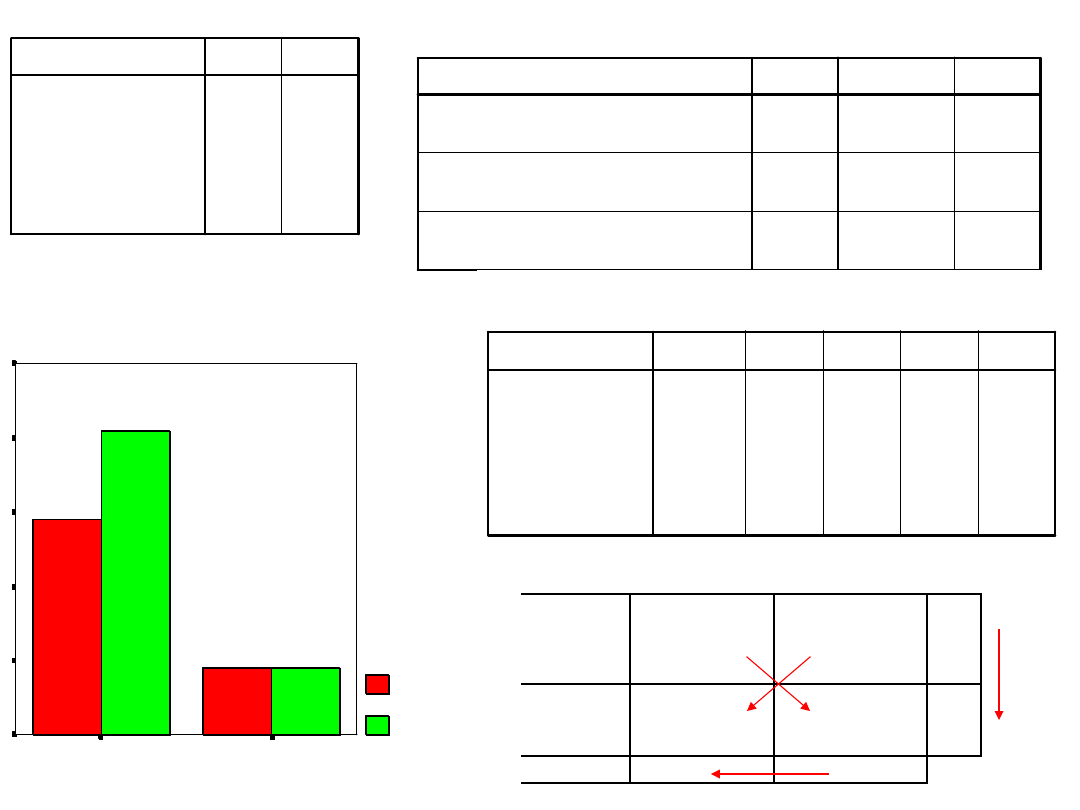
Czynniki międzyobiektowe

mało
empatycz
na

30

empatycz
na

30

farmakote
rapia

30

psychoter
apia

30

1,00

2,00

rodzaj sprawowanej
opieki

1,00

2,00

rodzaj terapii

Etykieta

wartości

N

Statystyki opisowe

Zmienna zależna: ilość nawrotów psychotycznych

5,8000

1,0142

15

8,2000

1,5213

15

7,0000

1,7617

30

1,8000

1,0142

15

1,8000

1,0142

15

1,8000

,9965

30

3,8000

2,2652

30

5,0000

3,4938

30

4,4000

2,9813

60

rodzaj terapii
1,00 farmakoterapia
2,00 psychoterapia
Ogółem
1,00 farmakoterapia
2,00 psychoterapia
Ogółem
1,00 farmakoterapia
2,00 psychoterapia
Ogółem

rodzaj sprawowanej
opieki
1,00 mało empatyczna

2,00 empatyczna

Ogółem

Średnia

Odchylenie

standardowe

N

Testy efektów międzyobiektowych

Zmienna zależna: ilość nawrotów psychotycznych

448,800

a

3

149,600

110,815

,000

1161,600

1 1161,600

860,444

,000

405,600

1

405,600

300,444

,000

21,600

1

21,600

16,000

,000

21,600

1

21,600

16,000

,000

75,600

56

1,350

1686,000

60

524,400

59

Źródło zmienności
Model skorygowany
Intercept
RODZ_OP
RODZ_TER
RODZ_OP * RODZ_TER
Błąd
Ogółem
Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

R kwadrat = ,856 (Skorygowane R kwadrat = ,848)

a.

Oszacowane średnie brzegowe - ilość nawrotów psychotycznych

rodzaj sprawowanej opieki

empatyczna

mało empatyczna

O

sz

ac

ow

an

e

śr

ed

ni

e

br

ze

go

w

e

10

8

6

4

2

0

rodzaj terapii

farmakoterapia

psychoterapia

5,8

1,8

8,2

1,8

psychotera
pia

farmakoterapia

Mało emp.

empatyczna

3,8

5,0

7

1,8

8,8

8,2

5,8

1,8

1,8

Testy nieparametryczne Chi Kwadrat

Testy nieparametryczne Chi Kwadrat



Jeżeli zmienne są na skali nominalnej, wtedy co zrozumiale, nie porównujemy średnich lecz liczebności, czyli rozkłady

Jeżeli zmienne są na skali nominalnej, wtedy co zrozumiale, nie porównujemy średnich lecz liczebności, czyli rozkłady

tych zmiennych. Jeśli chcemy dowiedzieć się czy osoby o różnym stanie cywilnym (zm. nominalna) różnią się między

tych zmiennych. Jeśli chcemy dowiedzieć się czy osoby o różnym stanie cywilnym (zm. nominalna) różnią się między

sobą zadowoleniem z życia (1- zadowolony, 2-niezadowolony). Test taki nazywamy niezależności, bo sprawdzamy czy

sobą zadowoleniem z życia (1- zadowolony, 2-niezadowolony). Test taki nazywamy niezależności, bo sprawdzamy czy

rozkłady obu zmiennych istotnie się różnią pod względem liczebności obserwowanych i teoretycznych

rozkłady obu zmiennych istotnie się różnią pod względem liczebności obserwowanych i teoretycznych



test Chi kwadrat dla dwóch zmiennych porównuje rozkłady tych zmiennych w oparciu i rozkład teoretyczny i

test Chi kwadrat dla dwóch zmiennych porównuje rozkłady tych zmiennych w oparciu i rozkład teoretyczny i

empiryczny (obserwowany)

empiryczny (obserwowany)



X =

X =

2



(O - T)

2

T

T - wartość teoretyczna
O - wartość obserwowana

Przykład- Czy istnieją istotne statystycznie różnice w płci między osobami
alekstymicznymi i nie aleksytymicznymi.
Do tego celu należy dokonać podziału zmiennej O_alex40 wg. mediany na dwie
kategorie, tak, żeby zmienna miała poziom nominalny.
Ho = nie będzie istotnych różnic w płci osób aleksytymicznych i
niealeksytymicznych.
Nie będzie różnic między liczebnościami oczekiwanymi i
obserwowanymi.

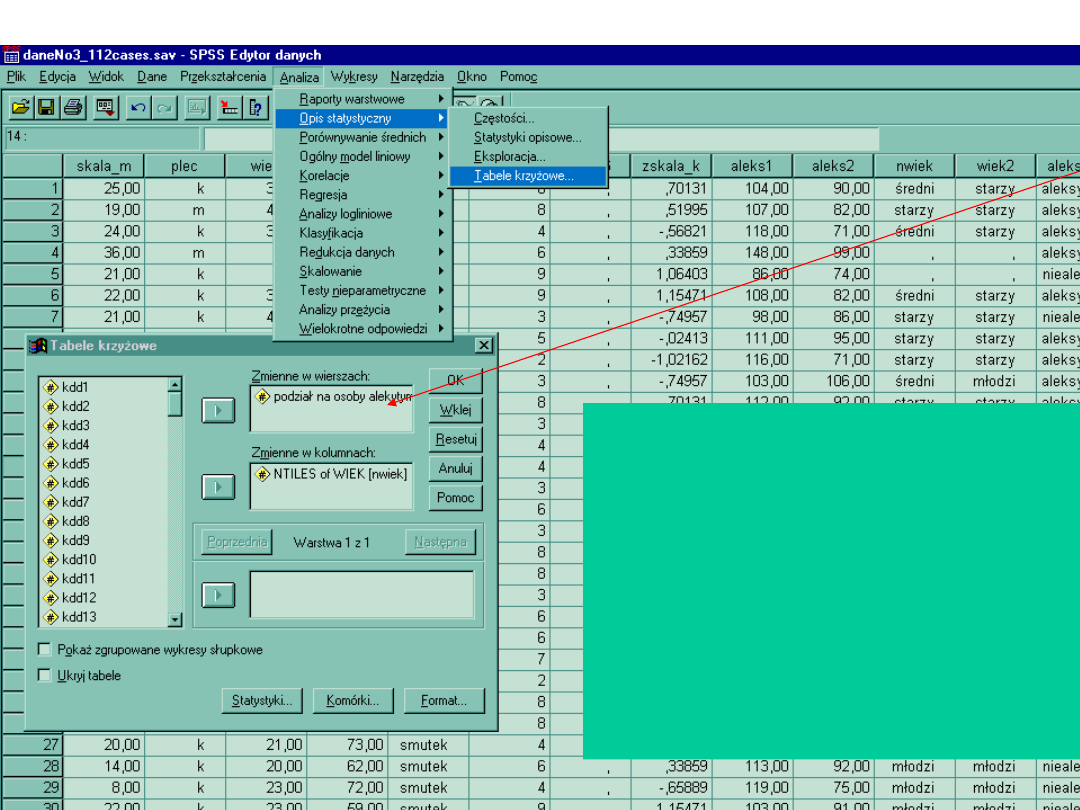
Chi kwadrat dla dwóch zmiennych (test

niezależności)

Chi kwadrat dla dwóch zminnych szukamy w
oknie
Opis statystyczny > tabele krzyżowe.
Nie ma znaczenia wstawienie zmiennych do
kolumn czy wierszy
Jeśli chcemy zastosować Chi kwadrat,
musimy zaznaczyć to jako opcje w oknie
statystyki
W oknie komórki zaznaczamy, dodatkowo
wartości oczekiwane, co ułatwi nam
zrozumienie w jaki sposób wzór Chi kwadrat
znajduje jest skonstruowany.

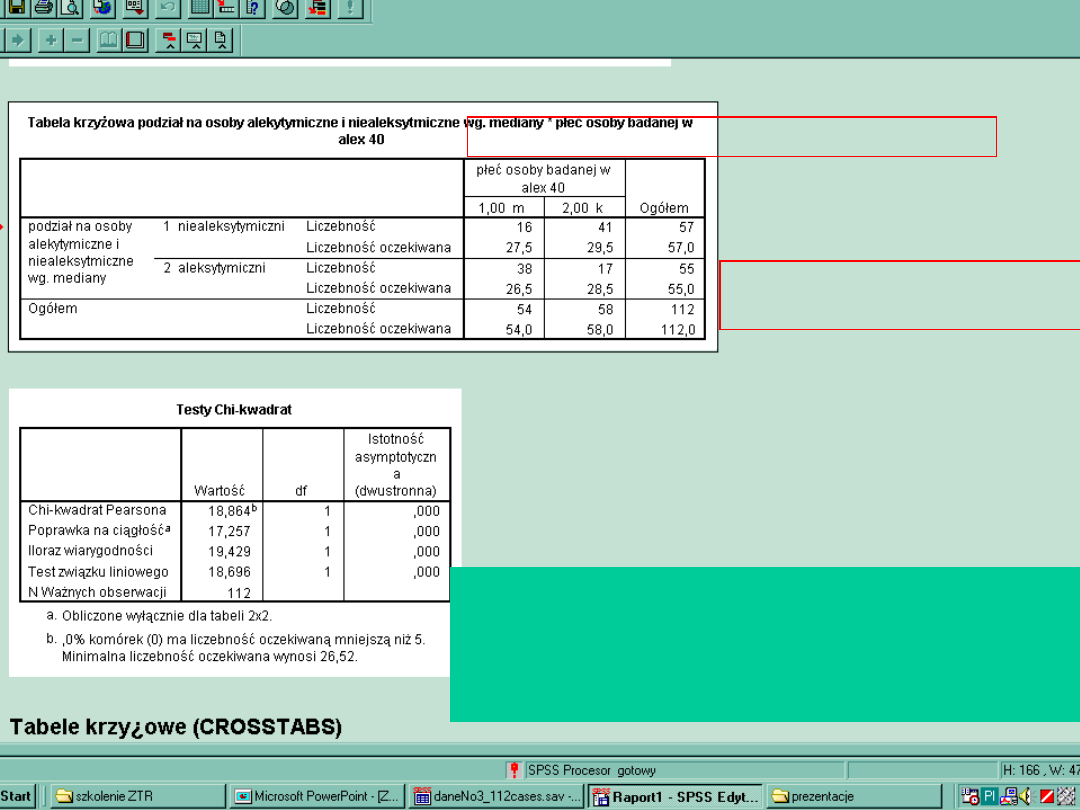
Zapis wg standardów APA:

X

2

(1, 112) = 18,864; p < 0,001

Df = (C - 1) x (R - 1);

C - liczba poziomów zmiennej w kolumnie

R -

-

liczba poziomów zmiennej

w

rzędzie

Chcąc liczyć wartości teoretyczne należy posłużyć
się wartościami brzegowymi i tak np. Dla mężczyzn
niealeksytymicznych 54 x 57 / 112= 27,5
Pozostałe wartości obliczamy analogicznie,
podstawiając do wzoru (patrz. 16)

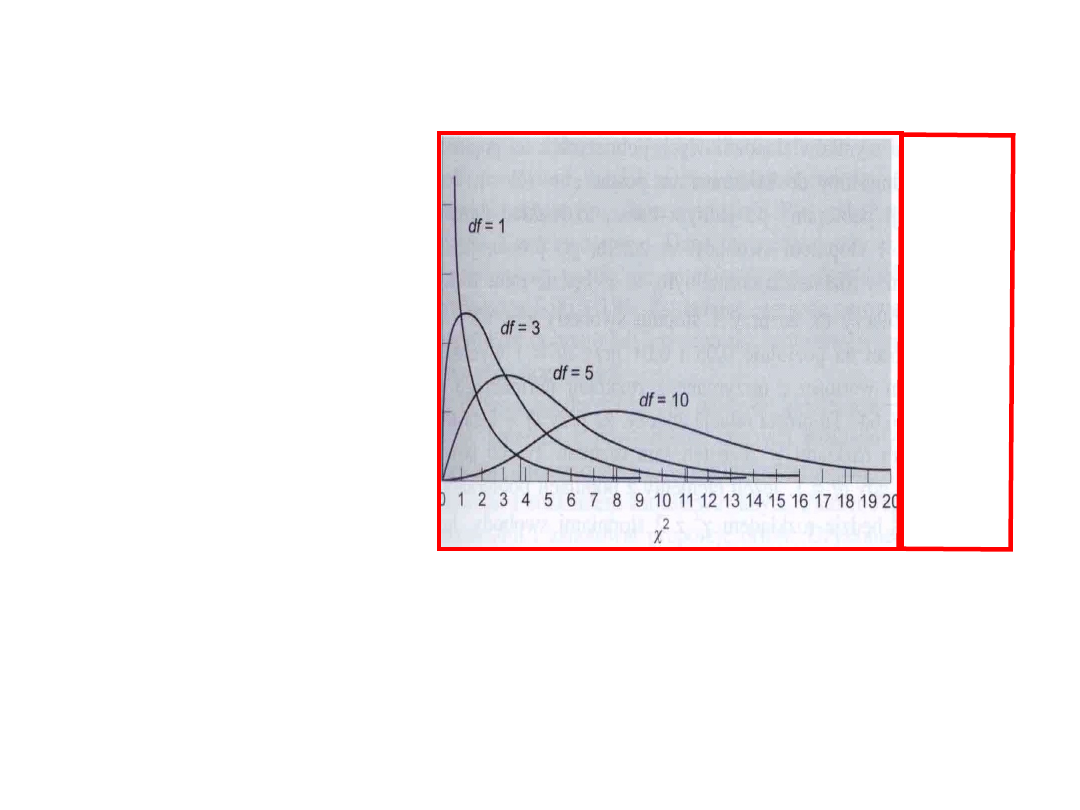
Test Chi kwadrat dla jednej zmiennej (test

zgodności)

• Zmienna nominalna, lub nie spełniająca wymogów normalności
• mała liczebność próby < 30

Ź

ró

d

ło

:

F

e

rg

u

so

n

,

T

a

k

a

n

e

(1

9

9

7

).

A

n

a

li

za

s

ta

ty

st

yc

zn

a

w

p

sy

ch

o

lo

g

ii

i

p

e

d

a

g

o

g

ic

e

.

W

a

rs

za

w

a

:

P

W

N

Sprawdzamy zgodność badanej zmiennej nominalnej z rozkładem teoretycznym.
Nie stosuje się badania testem Chi kwadrat, gdzie obiektów jest więcej niż 30.

Chi kwadrat dla jednej zmiennej- przykład

badając jakąś próbę oczekujemy, zgodnie z przyjętą przez nas teorią, próba będzie
znacząco zróżnicowana przez poziom alekstymii
Chi kwadrat dla jednej próby porówna rozkład rzeczywiście otrzymanych przez nas
wyników z wartościami teoretycznymi.

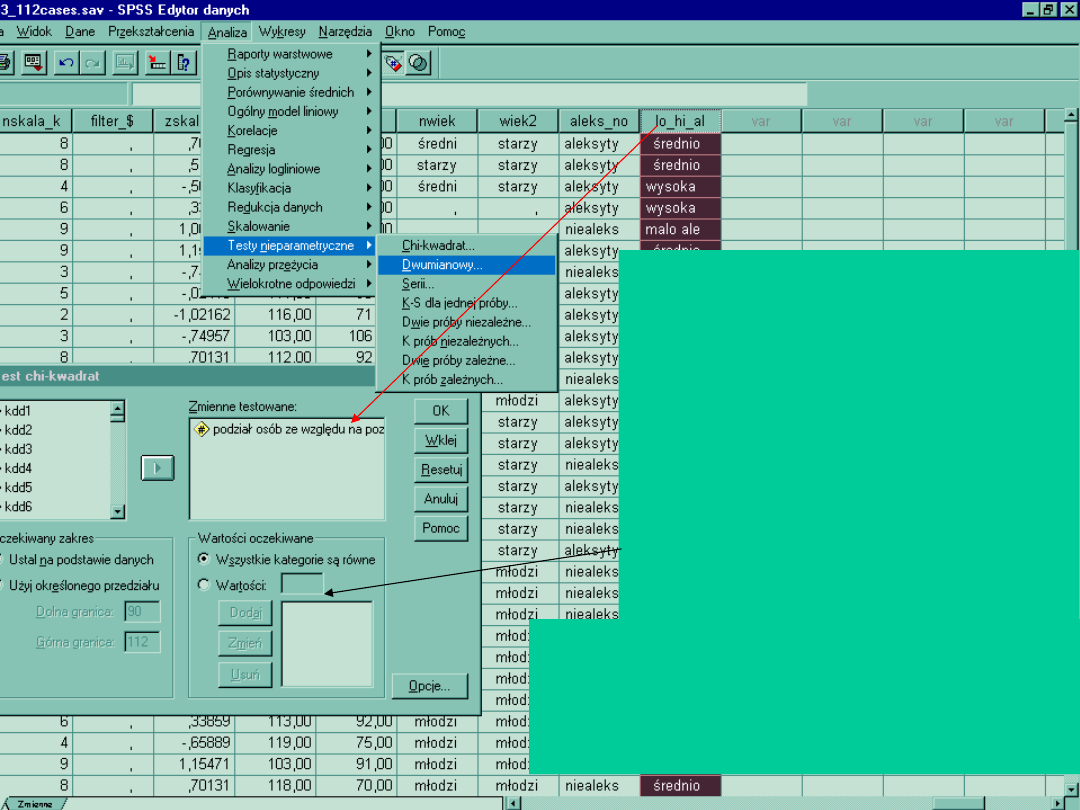
Chi kwadrat dla jednej zmiennej
znajdujemy wśród testów
nieparametrycznych.
W górnym oknie znajdują miejsce
zmienne przeznaczone do analizy.
Ważne jest okno Wartości
oczekiwane. Tutaj program
automatycznie zakłada brak
różnic w liczebnościach naszej
zmiennej. Tzn. będzie tyle samo
aleksytymików co
niealeksytymików. Możemy też,
jeśli mamy taka hipotezę nasze
własne liczebności oczekiwane

Do tego celu utworzyliśmy zmienną
Hi_Lo_al., wyróżniająca trzy poziomy
alekstymii (1-mało alekstymiczne, 2
średnio, 3- wysoka aleksytymia) na
podstawie podziału na 3 równe części.

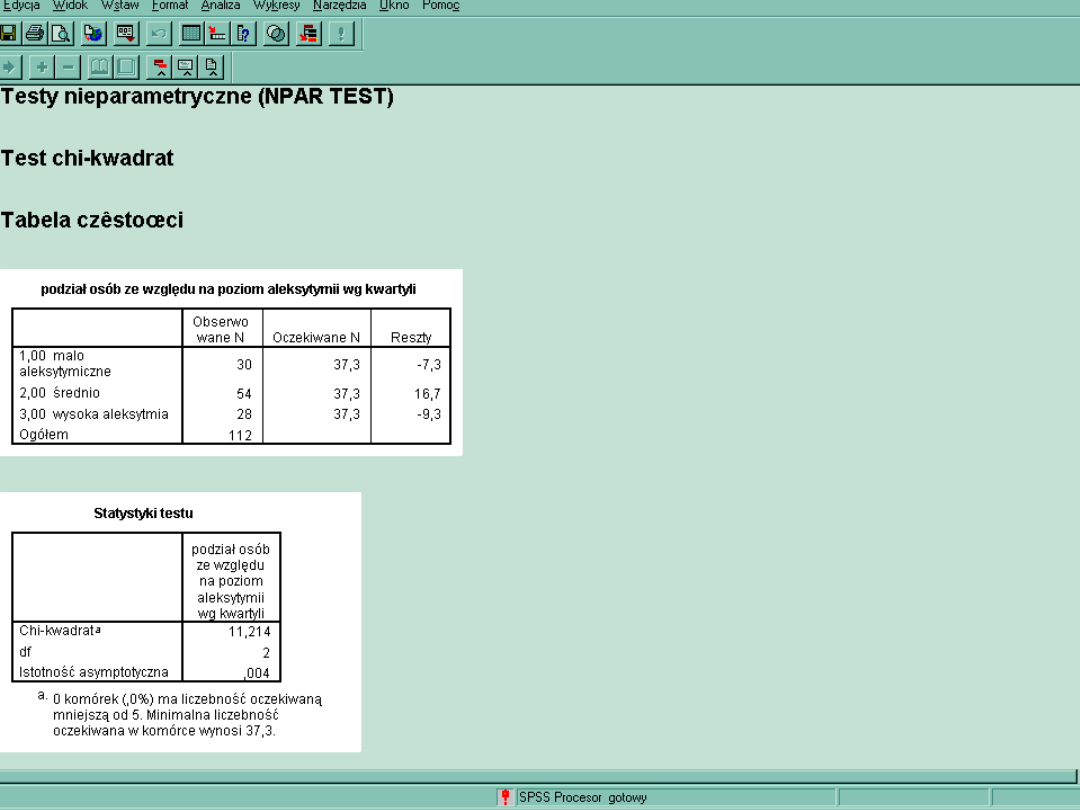
Komputer założył, że w każdej grupie będzie
taka sama liczebność, taj jak mówi to hipoteza
zerowa (H0)
Wartość testu Chi kwadrat okazała się istotna,
tzn. rozkład empiryczny znacząco odbiega od
teoretycznego. Występują istotne różnice w
populacji pod względem poziomu aleksytymii.

Df = C - 1, gdzie C oznacza ilość kategorii
zmiennej testowanej.

X

(2,112) = 11,214; p < 0,01

2