Teoria produkcji

Wydział Zarządzania

Katedra Ekonomii, Finansów i Zarządzania Środowiskiem

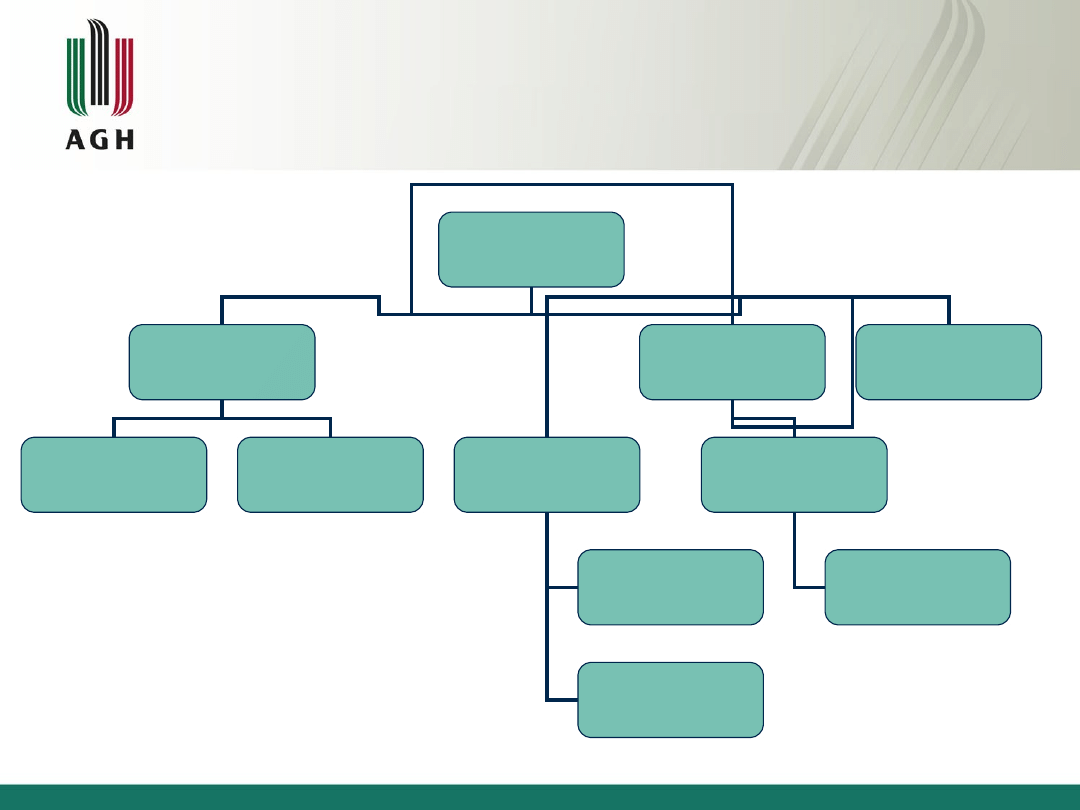
Rodzaje przedsiębiorstw

Str. 147

Rodzaje

przedsiębiorstwa

przedsiębiorstwa

sektora publicznego

spółki

firma

jednoosobowa

przedsiębiorstwo

państwowe

przedsiębiorstwo

komunalne

spółka kapitałowa

spółka osobowa

spółka z o.o.

spółka akcyjna

spółka jawna

22.05.21

2

22.05.21

3

Przedsiębiorstwo jako podmiot
rynku

Przedsiębiorstwo (entrepreneur) – jest podmiotem
gospodarczym prowadzącym działalność produkcyjną
lub usługową, w celu osiągnięcia zysku, przy
wykorzystaniu określonej technologii oraz organizacji
produkcji. Ze względu na to, że podstawowym celem
przedsiębiorstwa jest maksymalizacja zysku, dlatego
też podejmuje ono decyzje w ramach danej technologii
produkcji, środków jakimi dysponuje, cen rynkowych
czynników produkcji, a także kieruje się zasadą
optymalizacji. W gospodarce rynkowej każde
przedsiębiorstwo występuje jako odbiorca różnych
czynników produkcji (pracy, kapitału, ziemi) które są
niezbędne w procesie produkcji, a także dostawca
wytworzonych przez siebie produktów i usług.

Str.147

22.05.21

4

Rodzaje przedsiębiorstw

1. Firmy jednoosobowe (single proprietorship):

-

małe firmy stanowiące własność jednej osoby,

-

właściciel przeważnie zarządza firmą sam i
osobiście może świadczyć w niej usługi, osiągając
korzyści lub ponosząc straty,

-

właściciel ponosi pełną odpowiedzialność za
firmę (osobiście odpowiada za długi spółki
osobistym majątkiem),

-

firmy te zakładane są przeważnie w rzemiośle,
wszelkiego rodzaju usługach oraz handlu
detalicznym.

Str.147

22.05.21

5

Rodzaje przedsiębiorstw

2

. Spółki (corporations):

-

firmy będące w posiadaniu lub kontrolowane
przez dwóch lub więcej wspólników (spółki
kapitałowe mogą mieć jednego właściciela),
którzy dzielą się między sobą zobowiązaniami
oraz zyskami przynoszonymi przez firmę,

-

spółka jest zrzeszeniem osób lub kapitału w
celu prowadzenia działalności gospodarczej,

-

najczęściej spotykane to spółka osobowa i
kapitałowa.

Str.147,148

22.05.21

6

Rodzaje przedsiębiorstw

Spółki osobowe

-

opierają swoją działalność na osobistej pracy

wspólników w spółce, cechą charakterystyczną jest

pełna odpowiedzialność cywilna wspólników za

zobowiązania spółki,

-

przykładem spółki osobowej jest spółka jawna,

która charakteryzuje się odpowiedzialnością

wspólników całym swym majątkiem wraz ze

spółką za długi spółki, nie posiada osobowości

prawnej i zakładana jest najczęściej gdy brak jest

dostatecznie dużej wielkości kapitału aby założyć

spółkę kapitałową ze zdolnością kredytową.

Str.148

22.05.21

7

Rodzaje przedsiębiorstw

Spółki kapitałowe:

- odpowiadają swym kapitałem, czyli

wkładem wspólników,

- spółkami kapitałowymi są spółki z

ograniczoną odpowiedzialnością i spółki
akcyjne.

Str.148

22.05.21

8

Rodzaje przedsiębiorstw

Spółka z ograniczoną odpowiedzialnością
(limited partnership):

-

spółka z o.o. odpowiada za długi całym swoim
majątkiem, wspólnicy zaś (a w zasadzie członkowie
zarządu) są z odpowiedzialności wyłączeni (z
wyjątkami),

-

nabywa osobowość prawną z chwilą jej
zarejestrowania,

-

warunkiem powstania jest wniesienie przez
wspólnika wkładu zakładowego, który stanowi
majątek założycielski spółki, który jest przez cały
czas w posiadaniu spółki i jest gwarancją jej
wypłacalności oraz podstawą do uzyskania kredytu,

Str.148

22.05.21

9

Rodzaje przedsiębiorstw

-

wysokość kapitału zakładowego określa umowa

spółki, lecz nie może być on niższy od minimalnej

wielkości określonej w kodeksie handlowym

(obecnie 5000 zł),

-

na kapitał mogą składać się wkłady pieniężne i

niepieniężne, zwane aportem (tj. meble,

samochód, nieruchomości itp.),

-

kapitał dzieli się na udziały, których nabycie jest

równoznaczne z nabyciem praw członkowskich w

spółce i dających wspólnikowi prawo do zysku,

-

udziały są trudno zbywalne, ponieważ są imienne

i w umowie zaznaczone są obwarowania związane

z ich odsprzedażą.

Str.148

22.05.21

10

Rodzaje przedsiębiorstw

Spółka akcyjna (public corporation):

-

spółka kapitałowa posiadająca osobowość

prawną, której powstanie zależy od zebrania

kapitału zakładowego w formie wkładów

założycieli,

-

proces tworzenia spółki obejmuje

przygotowanie i przyjęcie statutu, objęcie akcji

oraz rejestrację w rejestrze handlowym,

-

najwyższą władzą spółki jest zgromadzenie

akcjonariuszy, które podejmuje decyzje

większością głosów,

-

na walnym zgromadzeniu, akcjonariusze

wybierają zarząd spółki oraz radę nadzorczą,

które bezpośrednio dysponują majątkiem

spółki,

Str.148

22.05.21

11

Rodzaje przedsiębiorstw

-

raz w roku zarząd zwołuje walne
zgromadzenie, któremu składa
sprawozdanie ze swojej działalności i
przedkłada do zatwierdzenia bilans,

-

zatwierdzenie bilansu przez walne
zgromadzenie jest równoznaczne z
przyznaniem wotum ufności dla
zarządu i aprobatą prowadzonej
przez niego polityki.

Str.148

22.05.21

12

Rodzaje przedsiębiorstw

3. Przedsiębiorstwa sektora publicznego:

-

Najczęściej występują w postaci przedsiębiorstw

komunalnych i państwowych.

Przedsiębiorstwa komunalne:
Są własnością społeczności lokalnej (miast, gmin) i

działają dla zaspokojenia potrzeb (np. w zakresie

zaopatrzenia w wodę, gaz komunikację miejską).

Przedsiębiorstwa państwowe:
Są tworzone przez upoważnione organy administracji

państwowej, tzw. organy założycielski (wojewodów,

ministrów) i działają na zasadach ogólnych lub

specjalnych.

Str.149

Każde przedsiębiorstwo decydując się na prowadzenie

określonej działalności gospodarczej zakupuje na
rynku po cenach rynkowych czynniki produkcji,
czyli nakłady, które musi ponieść w celu uruchomienia
lub zwiększenia produkcji.

Każdy proces produkcji powoduje transformację

zakupionych wcześniej czynników w konkretne produkty
lub usługi, które są wynikiem określonego procesu
produkcji. Przedsiębiorca w procesie produkcyjnym
będzie kierował się zasadą racjonalnego
gospodarowania, czyli będzie maksymalizował
produkcję przy danym nakładzie czynników
produkcji lub będzie osiągał założoną wielkość
produkcji przy minimalizacji nakładów. Takie
postępowanie przedsiębiorcy wymusza główny cel, jakim
jest maksymalizacja zysku.

22.05.21

13

Str. 149

Zysk jest kluczowym celem działalności każdego

przedsiębiorstwa związany jest z podstawowymi funkcjami
firmy, ponieważ wpływa na możliwości inwestycyjne,
decyduje o samofinansowaniu, wpływa na wielkość
zatrudnienia oraz pełni rolę motywacyjną, skłaniającą
wszystkich przedsiębiorców do osiągania najlepszych
rezultatów ekonomicznych.

Ponieważ zysk jest powszechnie traktowany jako główny cel

działalności, dlatego też kierownictwo każdego
przedsiębiorstwa:

-

stara się dokonać możliwie najtrafniejszego wyboru
wielkości i struktury produkcji oraz technicznych
metod wytwarzania;

-

pragnie jak najlepiej dostosować swoją produkcję do
wymagań rynku;

-

pragnie wytwarzać produkty po jak najniższych kosztach.

22.05.21

14

Str. 149

Każde przedsiębiorstwo prowadzi ewidencję, w

której rejestruje się wszystkie nakłady i
przychody. Na podstawie tej ewidencji ustala się
na koniec roku, zysk lub stratę finansową. W
przypadku, gdy przedsiębiorstwo ponosi straty
grozi mu bankructwo, ponieważ nie jest ono w
stanie wywiązać się ze wszystkich swoich
zobowiązań. Jeżeli strata ma charakter
przejściowy, to dane przedsiębiorstwo może
uzyskać pomoc w formie subwencji (czyli dopłaty
wyrównawczej do ceny sprzedawanych dóbr i
usług) ze strony władz centralnych lub lokalnych.

22.05.21

15

Str. 149

Funkcjonowanie przedsiębiorstwa może być analizowane w

różnych horyzontach czasowych. Dokonuje się rozróżnienia
między okresem ultrakrótkim (rynkowym) oraz krótkim i
długim okresem.

Okres ultrakrótki utożsamiany jest z bardzo krótkim

okresem, w którym zakłada się, że poziom produkcji
każdego przedsiębiorstwa oraz liczba przedsiębiorstw w
gałęzi są stałe, zaś gałąź produkcji obejmuje
przedsiębiorstwa wytwarzające identyczne (homogeniczne)
produkty.

Okres krótki w ekonomii definiuje się jako okres, w których

rozmiary przedsiębiorstw nie ulegają zmianie, a wielkość
produkcji zmienia się wraz ze zmianami wykorzystania
dostępnych zasobów. W tym okresie nie zmienia się
technologia produkcji, tzn. przedsiębiorstwo wytwarza dany
produkt przy pomocy tej samej technologii produkcji,
niezależnie od tego, czy będzie to trwać kwartał, rok czy
kilka lat.

22.05.21

16

Str. 149,
150

Okres krótki cd:
Na przykład, spółka Forda produkująca samochody może

zwiększyć swoją produkcję w krótkim okresie, zatrudniając
więcej pracowników, zużywając więcej stali, szkła,
elektryczności itd. Krótki okres może być różny w
poszczególnych przemysłach – w jednych, może obejmować
miesiące, a nawet tygodnie (np. przemysł elektroniczny), zaś
w innych lata (np. kopalnie, elektrownie).

Okres długi to okres, w którym zmieniają się rozmiary

przedsiębiorstw w zależności od ponoszonych kosztów
produkcji oraz sytuacji rynkowej. W okresie tym następują
zmiany w technologiach produkcji wynikające z postępu
technicznego. Przykładowo, jeśli spółka Forda zauważy, że
popyt na jej samochody wzrasta, wówczas może decydować
się na powiększenie swojego majątku i zainstalowanie
nowoczesnych urządzeń.

22.05.21

17

Str. 150

Teorie funkcjonowania przedsiębiorstwa

Prekursorami teorii przedsiębiorstwa byli A.

Smith, D. Ricardo i J. S. Mill. Jednakże dopiero
wprowadzenie analizy marginalnej w II
połowie XIX wieku przyczyniło się do
sformułowania podstawowych założeń tzw.
tradycyjnej teorii przedsiębiorstwa.

W latach 70. XIX w. miała miejsce rewolucja

marginalna w teorii ekonomii, która wiązała się
z przyjęciem zasady malejącej użyteczności
marginalnej, jako podstawy zachowania się
konsumenta na rynku. Doprowadziło to do
powstania statycznej teorii przedsiębiorstwa.

22.05.21

18

Str.150

Teorie funkcjonowania przedsiębiorstwa

Statyczna teoria przedsiębiorstwa została oparta

na rachunku marginalnym i przyjęciu założenia
o dążeniu do maksymalizacji zysku jako
poszukiwania wariantu optymalnego w sensie
matematycznym. Podstawową zaletą podejścia
marginalnego jest to, że nie ma konieczności
porównywania wszystkich możliwych czynników
zmiennych. Odpowiednikiem malejącej
użyteczności marginalnej u konsumenta jest
malejąca produkcyjność marginalna u producenta.
Wszystko to ilustruje zastosowanie zasady
ekwimarginalnej, czyli zrównania wielkości
marginalnych przychodu i kosztu (MR=MC)

.

22.05.21

19

Str. 150

Teorie funkcjonowania
przedsiębiorstwa

Przyjęcie zasady ekwimarginalnej pociągnęło za sobą

konieczność przyjęcia trzech kluczowych założeń:

1.

Dany zasób czynnika produkcji (pracy, kapitału,
pieniądza) jest stały w danych warunkach;

2.

Zasoby są mierzalne, dzięki czemu można
optymalizować ich kombinacje;

3.

Przyjęcie zasady ceteris paribus, dzięki której
istnieje możliwość porównywalności różnych
kombinacji rozdziału danego czynnika w różnych
zastosowaniach.

Założenia te odbiegają jednak od faktycznych

warunków działania realnie funkcjonujących
przedsiębiorstw

.

22.05.21

20

Str. 150,
151

22.05.21

21

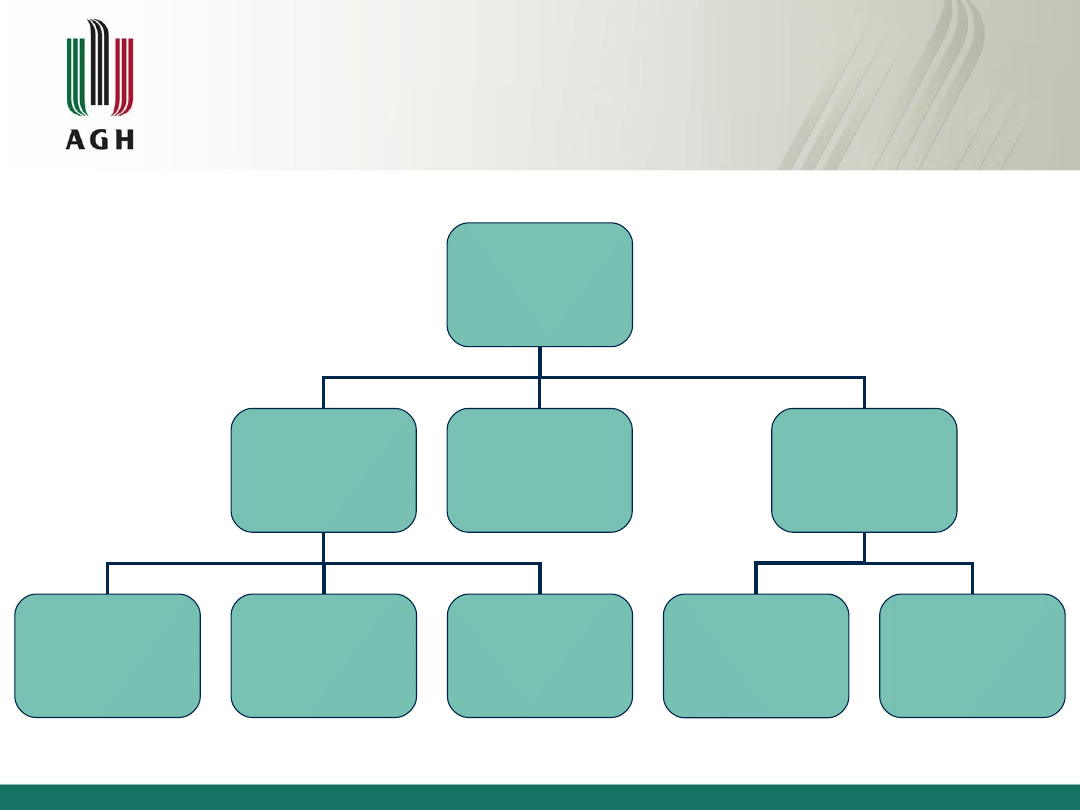
Klasyfikacja teorii
heterodoksyjnych
funkcjonowania
przedsiębiorstwa

Str. 152

Teorie

heterodoksyjne

funkcjonowania

przedsiębiorstwa

teorie

menadżerskie

teoria

behawioralna

teorie

biologiczne

homeostaza

przetrwanie

maksymalizacja

sprzedaży

maksymalizacja

stopy wzrostu

maksymalizacja

użyteczności

22.05.21

22

Teorie funkcjonowania przedsiębiorstwa

Teoria menadżerska:

-

wysuwa na pierwszy plan rozmaicie

zdefiniowane cele menadżerów,

-

kluczową tezą tej teorii jest stwierdzenie

że we współczesnych

przedsiębiorstwach występuje zjawisko

oddzielenia własności od zarządzania,

-

w korporacjach właściciele kapitału

pozbawieni są kontroli nad korporacją,

ponieważ funkcje zarządzania przejmują

menadżerowie, którzy posiadają swobodę i

mogą realizować własne cele.

Str.152

22.05.21

23

Teorie funkcjonowania przedsiębiorstwa

Teoria menadżerska cd:
- W. J. Baumol sformułował pogląd, że w celu

zwiększenia płac i korzyści płacowych,

menadżerowie narzucają firmie cel w postaci

maksymalizacji sprzedaży. Założył on także, że

akcjonariusze przyjmują pewien minimalny

poziom dochodu z kapitału, który jest

jednocześnie ograniczeniem dla menadżerów. W

sytuacji, gdy dochody z kapitału obniżą się poniżej

ustalonego minimum, wówczas mogą oni domagać

się zmiany zarządu. Z tego względu menadżerowie

dokonują takiego wyboru, który przy najwyższym

poziomie produkcji i sprzedaży umożliwia

osiąganie przez akcjonariuszy minimalnego

poziomu dochodu z kapitału.

Str.152

22.05.21

24

Teorie funkcjonowania przedsiębiorstwa

Teoria menadżerska cd:
- kolejną odmianą teorii menadżerskich jest model,

który zakłada że menadżerowie dążą do

maksymalizacji swojej własnej użyteczności,

którą można opisać w kategoriach pieniężnych

(np. zysk, zwiększenie wynagrodzenia pieniężnego)

i niepieniężnych (np. bezpieczeństwo, prestiż,

czas wolny),

-

O. E. Williamson twierdził, że menadżerowie

maksymalizują swoją użyteczność nie tylko przez

wynagrodzenia i dodatkowe korzyści, ale przez

tendencję do powiększania budżetu i zwiększenia

dyskrecjonalnej (nieskrępowanej ograniczeniami)

władzy w wydatkach.

Str.153

22.05.21

25

Teorie funkcjonowania przedsiębiorstwa

Teoria menadżerska cd:

-

inna z teorii menadżerskich zakłada, że kluczowym

celem działania przedsiębiorstwa jest jego wzrost w

ujęciu dynamicznym oraz zmiany wielkości w czasie,

-

wysoka stopa wzrostu wyraża się poprzez wzrost

rozmiarów produkcji i zatrudnienia, co w

konsekwencji oznacza zwiększenie

odpowiedzialności, władzy i prestiżu,

-

zysk jest traktowany jako determinant

ograniczający, a jego zwiększenie jest jednym z

istotnych warunków wzrostu.

-

początkowo cele te są zbieżne, ale problem

pojawia się przy podziale zysku – cele

akcjonariusze i zarządzających są tu odmienne.

Str.153

22.05.21

26

Teorie funkcjonowania przedsiębiorstwa

Teoria behawioralna:

Behawioryzm (

ang

. behavior lub behaviour -

zachowanie

) - kierunek

psychologiczny

, który rozwinął się w

XX wieku

, przede wszystkim w

USA

.

Założenia behawioryzmu:



jakkolwiek kierunek ten nie neguje występowania zjawisk

psychicznych

, twierdzi, że są one swoistymi,

ubocznymi efektami działania

mózgu

, których nie da się skutecznie badać

metodami naukowymi

, gdyż są

one niedostępne obserwacji,



dlatego, jeśli psychologia ma być rzetelną

nauką

, musi się ograniczyć do mierzalnych, jasno

zdefiniowanych

eksperymentów

, w których ludzi poddaje się działaniu określonych

bodźców

i obserwuje

się ich określone reakcje na te bodźce.

Model osobowości według behawiorystów składał się z elementów podstawowych
jakimi były odruchy. Systemy pewnych odruchów, tworzyły struktury nawyków, zaś
grupy nawyków składały się na poszczególne wymiary osobowości. W skrajnej
postaci behawioryzm zakładał, że bardziej złożone zjawiska psychiczne, takie jak np.
uczucia wyższe, czy struktury wpojone kulturowo, nie mają większego wpływu na
działanie ludzi. Ludzie podobnie jak wszystkie inne zwierzęta działają według
stosunkowo prostych zasad opierających się na stałych,

odruchowych

lub

wyuczonych reakcjach na bodźce. Według tego skrajnego poglądu, większość
zdrowych osobników ludzkich, niezależnie od ich "zawartości mózgu" będzie w tych
samych warunkach reagować podobnie na podobne zestawy bodźców. Jedyną zaś
rzeczą, która jest u człowieka wrodzona, jest ogólna zdolność uczenia się.

http://pl.wikipedia.org/wik
i/Behawioryzm

22.05.21

27

Teorie funkcjonowania przedsiębiorstwa

Teoria behawioralna:

Przedsiębiorstwo postrzegane jest jako organizacja

bądź instytucja o charakterze koalicyjnym,

koncentrującym grupy ludzi o podobnych celach i

interesach. Sprzeczność interesów różnych

interesariuszy sprawia trudności w określeniu

właściwej wiązki celów, które zostaną zrealizowane

w poszczególnych przedsiębiorstwach.
Cel rzeczywiście realizowany jest wypadkową

różnych interesów i w praktyce przedsiębiorstwo

może próbować maksymalizować swój zysk,

sprzedaż, wzrost udziału w rynku, wzrost

wynagrodzeń, wzrost inwestycji, wzrost produkcji,

itd., pomimo sprzeczności zachodzących w ramach

realizacji tych celów.

Str.154

22.05.21

28

Teorie funkcjonowania przedsiębiorstwa

Teoria behawioralna (c.d.):

Zgodnie z tą teorią istnieje trudność porównania

korzyści

poszczególnych

przedsiębiorstw

z

korzyściami ogólnogospodarczymi.
Teoria stwarza możliwość głębszego poznania

wnętrza przedsiębiorstwa, jednak z drugiej strony

trudno

za

pomocą

tej

teorii

„wyjść”

z

przedsiębiorstwa,

dokonując

uogólnienia

pozwalającego

na

ocenę

efektów

ogólnogospodarczych

działalności

przedsiębiorstwa.
Relacje pomiędzy właścicielami, przedsiębiorcami,

menedżerami i klientami w przedsiębiorstwie

kształtują się różnorodnie, z różnym wpływem na

działalność przedsiębiorstwa.

Str.154

22.05.21

29

Teorie funkcjonowania przedsiębiorstwa

Teoria biologiczna:

-

wykorzystuje wiele analogii do nauk biologicznych,

-

podstawowymi pojęciami tej teorii jest homeostaza,
tłumacząca zachowania w krótkim czasie oraz
przetrwanie, czyli sprawdzone skuteczne sposoby
postępowania w przeszłości, które stają się wzorami.

-

w teorii homeostazy zakłada się, że przedsiębiorstwo
podobnie jak każdy organizm dąży do osiągnięcia
stanu wewnętrznej równowagi

.

Homeostaza - zdolność utrzymywania stałości parametrów wewnętrznych w

systemie (zamkniętym lub otwartym). Pojęcie to zwykle odnosi się do

samoregulacji

procesów biologicznych

(źródło: http://pl.wikipedia.org/wiki/Homeostaza)

Str.154

22.05.21

30

Jednoczynnikowa funkcja produkcji

Funkcja produkcji (production function):

-

przedstawia związek zachodzący między

wielkością produkcji a ilością

zaangażowanych czynników produkcji,

-

zależności, które funkcja produkcji

wyraża, mają charakter przyczynowo-

skutkowy,

-

przyczyną procesu produkcji są nakłady

(czynniki produkcji) zaś skutkiem
określona wielkość produkcji

.

Str.154

22.05.21

31

Jednoczynnikowa funkcja produkcji

Funkcja produkcji (production function) cd:

-

ze względu na to, że w procesie produkcji zużywa się

wiele czynników, ogólną postać funkcji produkcji

można zapisać jako funkcję wielu zmiennych:

Q = f (n

1

, n

2

, n

3

..., n

n

)

gdzie:
Q – wielkość produkcji,
f – zależność funkcyjna,
n – nakład czynników produkcji.

-

funkcja produkcji wskazuje możliwą wielkość

produkcji, którą można osiągnąć w danym okresie

przy wykorzystywaniu nakładów o określonej

wielkości i strukturze,

-

określona struktura nakładów produkcyjnych

określana jest mianem metody produkcji.

Str.154,155

22.05.21

32

Jednoczynnikowa funkcja produkcji

Funkcja produkcji (production function) cd:

-

w praktyce na nakłady składają się siła robocza i

kapitał,

-

jeżeli zmiany wielkości produkcji uzależnione są od

zmiany obydwóch czynników wówczas funkcję

produkcji można zapisać

Q = f (K, L)

gdzie:
K – kapitał,
L – praca (siła robocza).

- tak zapisaną funkcję określa się mianem

dwuczynnikowej funkcji produkcji, która pokazuje

jaką maksymalną wartość produkcji można osiągnąć

ze wszystkich możliwych kombinacji ilościowych siły

roboczej i kapitału ceteris paribus.

Str.155

22.05.21

33

Jednoczynnikowa funkcja produkcji

Funkcja produkcji (production function) cd:

-

jeżeli natomiast tylko jeden z nakładów wywiera

wpływ na wielkość produkcji, a drugi jest stały,

wówczas otrzymujemy jednoczynnikową funkcję

produkcji, którą można zapisać za pomocą wzoru:

* przy założeniu stałości nakładu kapitału (K =

const.)

Q = f (L)

* przy założeniu stałości nakładu pracy (L = const.)

Q = f (K)

Str.155

22.05.21

34

Jednoczynnikowa funkcja
produkcji

Jednoczynnikowa funkcja produkcji

-

pokazuje, jaką maksymalną wielkość produkcji można

wyprodukować przy różnym poziomie wykorzystania

jednego z czynników produkcji, gdy drugi nie ulega zmianie,

-

w krótkim czasie najczęściej czynnikiem stałym jest

kapitał, dlatego też przedsiębiorstwo aby zwiększyć

rozmiary produkcji musi zaangażować większą ilość siły

roboczej,

-

przyjmując, że czynnikiem zmiennym jest siła robocza,

czyli liczba pracowników, wówczas każdy dodatkowo

zatrudniony nie wytwarza dokładnie takiej samej wielkości

produkcji co poprzedni,

-

ponadto w analizie jednoczynnikowej zakłada się, że

przedsiębiorstwo wykorzystuje w procesie produkcyjnym

daną technologię, czynniki produkcji łączą się ze sobą w

dowolnych proporcjach.

Str.155

22.05.21

35

Jednoczynnikowa funkcja produkcji

Przyporządkowanie poszczególnym

wielkościom produkcji (Q)

odpowiadający im poziom nakładów

czynnika pracy (L), daje w rezultacie

funkcję produkcji całkowitej (TP):

TP = Q * L

Innymi słowy produkt całkowity (total

product - TP) to wielkość produkcji,

czyli ilość dóbr i usług

wyprodukowanych w okresie jednego

roku przez pewną liczbę pracowników.

Str.155,156

22.05.21

36

Jednoczynnikowa funkcja produkcji

Produkt przeciętny (average product – AP) to wielkość

produkcji przypadająca na jednego zatrudnionego

pracownika. Obliczamy go dzieląc wielkość produktu

całkowitego (TP) przez ilość zatrudnionych pracowników (L),

co można zapisać następująco:

Produkt marginalny (krańcowy) (marginal product – MP) to

zmiana produktu całkowitego będąca konsekwencją

zwiększenia (zmniejszenia) nakładu czynnika zmiennego o

jednostkę. W odniesieniu do czynnika pracy będzie to

produktywność kolejnego zatrudnionego pracownika.

Obliczamy go dzieląc zmiany w produkcie całkowitym (TP)

przez zmiany nakładu zaangażowania czynnika pracy (L), co

można zapisać następująco:

Str.156

L

TP

AP

L

TP

MP







22.05.21

37

Jednoczynnikowa funkcja
produkcji

Funkcje produkcji całkowitej, przeciętnej i marginalnej:

Str.157

TP
AP
MP

50

50

40

30

20

10

1

2

4

5

6

3

7

8

9

10

TP
AP
MP

MP

AP

TP

22.05.21

38

Jednoczynnikowa funkcja
produkcji

Zmiany produktu całkowitego, przeciętnego i

marginalnego opierają się na prawidłowości

określanej mianem prawa malejących

przychodów marginalnych, (law of diminishing

reternus) które głosi, że zwiększając nakład

czynnika zmiennego, przy założeniu niezmienności

drugiego czynnika produkcji osiągany jest taki

punkt, po przekroczeniu którego dodatkowa

produkcja otrzymana z kolejnej jednostki

zaangażowania siły roboczej permanentnie maleje.

Innymi słowy po przekroczeniu pewnego punktu

uzyskiwana jest coraz mniejsza wielkość produkcji

z każdej dodatkowej jednostki czynnika zmiennego,

co jednoznacznie wymaga coraz większego

wykorzystania siły roboczej w celu uzyskania

takiego samego przyrostu produkcji co poprzednio.

Str.158

22.05.21

39

Jednoczynnikowa funkcja
produkcji

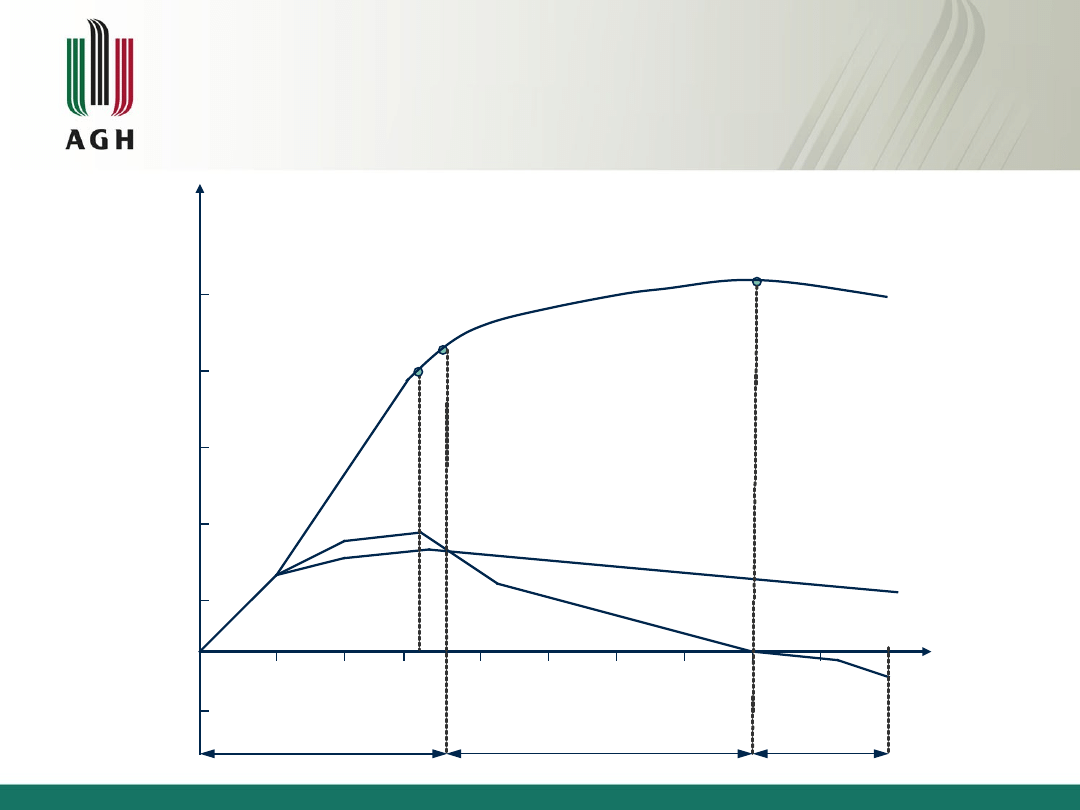
Dokonując krótkiej rekapitulacji odnoszącej się do

jednoczynnikowej funkcji można wyróżnić trzy

etapy produkcji:

-

I etap – produkt całkowity rośnie, zaś produkt

przeciętny rośnie aż do osiągnięcia wielkości

maksymalnej, natomiast produkt marginalny

osiąga wartości większe od produktu przeciętnego;

-

II etap – produkt całkowity rośnie, produkt

przeciętny spada, natomiast produkt marginalny

spada lecz przyjmuje wartości dodatnie;

-

III etap – produkt całkowity i przeciętny spadają,

natomiast produkt marginalny przyjmuje wartości

ujemne.

Str.159

22.05.21

40

Str.159

50

40

30

20

10

1

2

4

5

6

3

7

8

9

10

TP
AP
MP

MP

AP

TP

Etapy produkcji w
przedsiębiorstwie

A

B

C

I etap

II etap

III etap

L

-10

22.05.21

41

Dwuczynnikowa funkcja
produkcji

Dwuczynnikową funkcją produkcji
nazywamy funkcję Q = f(K,L) przy
zmieniających się czynnikach produkcji –
kapitale i pracy.

Technologia produkcji określa proporcje
zastosowania czynników wytwórczych.

Str.160

22.05.21

42

Funkcja Cobba-Douglasa

Założono, że funkcja produkcji jest tzw.

funkcją Cobba –Douglasa postaci:

Q = AL

α

K

β

Gdzie:
Q – wielkość produkcji,
A – stały parametr zależny od jednostek, w

których mierzona jest produkcja i nakłady,

K – nakład czynnika kapitału,
L – nakład czynnika pracy,
α,β – stałe parametry, informujące o względnym

znaczeniu czynnika pracy i kapitału w

procesie produkcji. ( α<1 i β<1)

Str.160

22.05.21

43

Funkcja produkcji

Zakładając, że możemy zapisać:

Na podstawie równania można stwierdzić, że:

jeśli α+β=1, wówczas funkcja Cobba-Douglasa wskazuje

proporcjonalne korzyści skali, co oznacza, że przyrost

produkcji jest proporcjonalny do przyrostu nakładów

czynnika pracy (L) i kapitału (K);
jeśli α+β>1, wówczas funkcja Cobba-Douglasa wskazuje

rosnące korzyści skali, co oznacza, że przyrost produkcji jest

szybszy od przyrostu nakładu L i K;
jeśli α+β<1, wówczas funkcja Cobba-Douglasa wskazuje

malejące korzyści skali, co oznacza, że przyrost produkcji

jest wolniejszy od przyrostu nakładu L i K.

Str.161































K

K

L

L

Q

Q

K

K

L

L







22.05.21

44

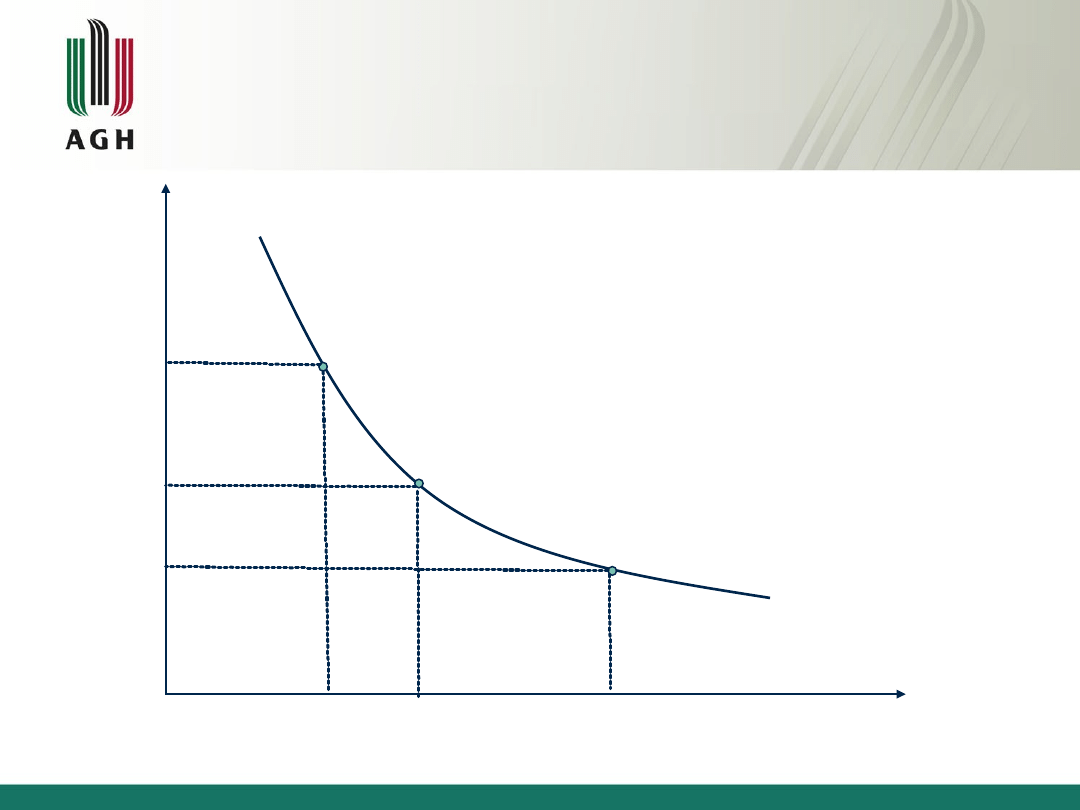
Izokwanta

Zbiór wszystkich kombinacji czynników
produkcji, które umożliwiają osiągnięcie
tego samego poziomu produkcji tworzy
linię jednakowego produktu zwaną
izokwantą (isoquant curve – IQ).

Str. 161

22.05.21

45

Izokwanta produkcji

Str.162

K

K

1

K

2

K

3

0

L

3

L

1

L

2

L

A

B

C

IQ

22.05.21

46

Izokwanta produkcji

Ruch wzdłuż izokwanty produkcji oznacza,

że zmianie ulegają wielkości nakładu
produkcji oraz proporcje miedzy
czynnikami, natomiast nie zmienia się
poziom produkcji.

Rozmiary, w jakich zmiana jednego zasobu

wpływa na zaangażowanie drugiego
czynnika wytwórczego, mierzona jest przy
pomocy nachylenia izokwanty produkcji.

Str.162

22.05.21

47

Izokwanta produkcji

Jeżeli założymy wzrost nakładu czynnika
pracy, któremu odpowiada spadek
zaangażowania czynnika kapitału,
warunkiem osiągnięcia takiego samego
poziomu produkcji jest spełnienie
równości:

Oznacza to, że nachylenie izokwanty w

dowolnym jej punkcie zawsze jest równe
relacji:

Str.162

K

L

MP

K

MP

L













K

L

MP

MP

22.05.21

48

Ilość czynnika pracy (L), która jest niezbędna do

zastąpienia jednostki czynnika kapitału (K) tak, aby poziom

produkcji nie uległ zmianie, określamy mianem

marginalnej (krańcowej) stopy technicznej

substytucji (marginal rate of technical substitution –

MRTS

KL

), którą można zapisać za pomocą wzoru:

Gdzie:
MRTS

KL

– marginalna stopa technicznej substytucji kapitału

pracą,

ΔK – liczba jednostek kapitału zastąpionych jednostką pracy,
ΔL – przyrost zatrudnienia pracy o jednostkę,
MP

L

– produkt marginalny pracy,

MP

K

– produkt marginalny kapitału.

MRST

KL

< 0

Str.163

L

K

MP

MP

MRST

K

L

KL









22.05.21

49

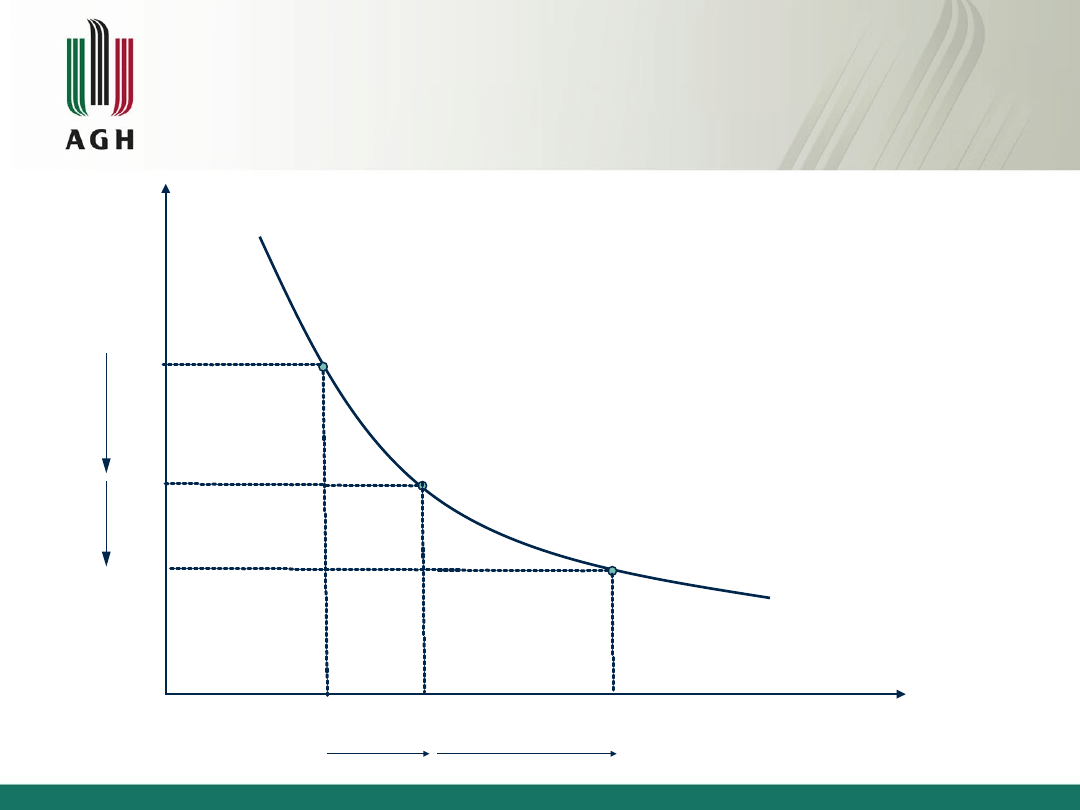
Izokwanta produkcji i

marginalna stopa produkcji

-ΔK

K

1

K

2

K

3

0

L

3

L

1

L

2

L

A

B

C

IQ

K

-ΔK

ΔL

ΔL

Str. 163

22.05.21

50

Izokwanty produkcji

Jedna izokwanta przedstawia

wszystkie możliwe i efektywne
stosunki ilościowe pracy (L) i kapitału
(K), które pozwalają osiągnąć ten sam
poziom produkcji.

Str.164

22.05.21

51

Mapa izokwant produkcji

Str.164

K

0

L

IQ

3

IQ

2

IQ

1

22.05.21

52

Izokwanty produkcji

Najczęściej spotykane izokwanty

produkcji charakteryzują się czterema

podstawowymi właściwościami:

1.

Mają ujemne nachylenie;

2.

Nie przecinają się;

3.

Reprezentują tym większą produkcję, im

dalej od początku układu współrzędnych

się znajdują;

4.

W stosunku do układu współrzędnych są

wypukłe.

Str.164

22.05.21

53

Izokwanty dla czynników zmiennych doskonale
substytucyjnych (gdy zastępowanie jednego
czynnika produkcji drugim zachodzi przy stałej
proporcji)

Str.165

0

L

IQ

3

IQ

2

IQ

1

K

22.05.21

54

Izokwanty dla czynników
zmiennych komplementarnych
stosowanych w ściśle
określonych proporcjach

L

0

L

IQ

3

IQ

2

IQ

1

K

Str.
165

22.05.21

55

Ekonomiczny obszar
produkcji

K

0

L

IQ

1

IQ

2

IQ

3

B

A

Str.
166

22.05.21

56

Ekonomiczny obszar
produkcji

Poniżej linii OB i powyżej linii OA nachylenie izokwant jest

dodatnie. Oznacza to, że w celu utrzymania wielkości

produkcji niezbędne jest zwiększenie nakładu czynnika pracy i

czynnika kapitału. W konsekwencji marginalny produkt

jednego z czynników wytwórczych musi być ujemny. Powyżej

linii 0A ujemny jest marginalny produkt kapitału, w wyniku

czego można zmniejszyć wykorzystanie obu czynników,

utrzymując nie zmienioną wielkość produkcji. Natomiast

poniżej linii 0B ujemny jest marginalny produkt pracy, co

umożliwia ograniczenie nakładu pracy i kapitału bez

zmniejszania produkcji. Obszar zawarty pomiędzy linią 0A i 0B

określany jest mianem ekonomicznego obszaru produkcji,

co oznacza, że każde przedsiębiorstwo chcące

maksymalizować zysk będzie działało w obrębie tego obszaru.

Str.
166

22.05.21

57

Korzyści skali

Korzyści skali (economies to scale) to
zmiany, które zachodzą w wielkości
produkcji, kiedy wszystkie czynniki są
zmieniane profesjonalnie i bez zmian w
metodzie produkcji.

Korzyści te mogą być stałe, rosnące, a także
malejące, co zależne jest od przyrostów
efektów produkcyjnych i przyrostów
nakładów.

Str.166,16
7

22.05.21

58

Stałe korzyści skali dla funkcji
produkcji

K

0

L

IQ

1

IQ

2

IQ

3

Z

D

C

B

A

IQ

4

AB = BC =
CD

Str. 167

22.05.21

59

Rosnące korzyści skali dla
funkcji produkcji

0

L

IQ

1

IQ

2

IQ

3

Z

D

C

B

A

IQ

4

K

AB > BC >
CD

Str.
167

Jeżeli przyrosty
efektów są większe od
przyrostów nakładów,
wówczas mamy do
czynienia z rosnącymi
korzyściami skali.

22.05.21

60

Malejące korzyści skali dla
funkcji produkcji

0

L

IQ

3

IQ

2

IQ

1

K

IQ

4

A

B

C

D

Z

AB < BC < CD

Str. 168

Jeżeli przyrosty
efektów są mniejsze
od przyrostów
nakładów, wówczas
mamy do czynienia z
malejącymi
korzyściami skali.

22.05.21

61

Równanie kosztów

Aby obliczyć całkowity poziom wydatków przedsiębiorcy,
które przeznaczane są na zakup czynników produkcji, stosuje
się tzw. równanie kosztów:

N = P

K

• K + P

L

• L

Gdzie:

N – całkowite wydatki na czynniki produkcji,

P

K

– cena czynnika kapitału,

K – wielkość wykorzystanego czynnika kapitału w procesie
produkcji,

P

L

– cena czynnika pracy,

L – wielkość wykorzystanego czynnika pracy w procesie
produkcji.

Str.168

22.05.21

62

Izokoszta

Izokoszta (isocost curve – IC) to graficzne
odzwierciedlenie równania kosztów,
ukazujące różne kombinacje pracy i
kapitału, które przedsiębiorstwo może
nabyć przy określonych cenach czynników
produkcji i danym poziomie nakładów.

Str.169

22.05.21

63

Izokoszta

0

tgα = P

L

/P

K

IC

N/P

K

N/P

L

L

K

B

A

Str. 169

α

22.05.21

64

Izokoszta

Aby wyznaczyć izokosztę, dzielimy całkowite
wydatki przez cenę czynnika pracy,
otrzymując punkt A. Punkt B otrzymujemy
zaś, dzieląc całkowite wydatki przez cenę
czynnika kapitału, a następnie łączymy oba
punkty.

Nachylenie izokoszty można wyznaczyć ze

wzoru:

Str.170

K

L

L

K

P

P

N

P

P

N









22.05.21

65

Izokoszta

Jako, że izokoszta jest wiązana z budżetem

przedsiębiorcy, jak i z cenami potrzebnych

czynników wytwórczych, izokoszta może ulec

przesunięciu zarówno bliżej początku układu

współrzędnych, jak i dalej.

W przypadku zmiany budżetu, nowa izokoszta jest

zawsze równoległa do poprzedniej.

W przypadku zmian ceny czynnika pracy, punkt

B nie zmienia swojego położenia, a przesuwa się

tylko punkt A (wzdłuż dodatniej osi L układu

współrzędnych).

W przypadku zmian ceny czynnika kapitału

sytuacja jest odwrotna do poprzedniej –

przesunięciu podlega tylko punkt B.

Str.170-
172

22.05.21

66

Przesunięcia izokoszty przy
zmianach budżetu
przedsiębiorcy

K

0

1

P

L

, P

K

= const

IC

3

N/P

K

N/P

K

N/P

K

2

N/P

L

N/P

L

N/P

L

2

1

L

IC

1

IC

2

N

2

< N < N

1

Str. 171

22.05.21

67

Przesunięcie izokoszty przy
zmianie ceny czynnika pracy

0

P

L

, P

K

= const

IC

2

N/P

K

N/P

L

N/P

L

2

1

L

IC

1

N = const

(P

L1

< P

L2

)

K

Str.
171

22.05.21

68

Przesunięcie izokoszty przy
zmianie ceny czynnika kapitału

0

P

K

, P

L

= const

IC

2

N/P

K1

N/P

L

L

IC

1

N = const

(P

K1

< P

K2

)

K

N/P

K2

Str. 172

22.05.21

69

Optimum produkcji

Optimum produkcji (punkt równowagi

przedsiębiorstwa), to punkt styczności

najwyżej położonej osiągalnej izokwanty

produkcji z izokosztą danego

przedsiębiorstwa, czyli najefektywniejsza

kombinacja czynników wytwórczych.
Po wyznaczeniu tego punktu można

odczytać ile należy zaangażować czynnika

pracy i czynnika kapitału, aby przy pełnym

wykorzystaniu budżetu i danych cenach

czynników produkcji osiągnąć najwyższy

poziom produkcji.

Str.172

22.05.21

70

Optimum produkcji

0

IQ

2

N/P

K

N/P

L

L

IC

K

K

1

L

1

IQ

1

IQ

3

E

Str. 173

22.05.21

71

Optimum produkcji

W punkcie równowagi E nachylenie
izokoszty i izokwanty produkcji są równe,
dlatego też optymalna kombinacja obu
czynników wytwórczych możliwa do
osiągnięcia przy danym budżecie
przedsiębiorcy wymaga spełnienia
warunku:

nachylenie izokwanty

:

nachylenie izokoszty:

Str. 173

K

L

KL

MP

MP

MRTS

L

K











K

L

P

P

L

K





22.05.21

72

Ścieżka ekspansji produkcji

Ścieżka ekspansji produkcji

(expansion path – EP) powstaje, gdy

przedsiębiorstwo dokonuje ekspansji

produkcji. Jest to krzywa, która łączy

kolejne punkty równowagi

przedsiębiorstwa.

Dla ścieżki ekspansji produkcji w każdym

jej punkcie współczynnik nachylenia

izokwanty równy jest współczynnikowi

nachylenia izokoszty, co opisuje równość:

Str.174

K

L

K

L

P

P

MP

MP



22.05.21

73

Ścieżka ekspansji produkcji

0

IQ

2

N/P

L

L

IC

1

K

K

3

L

3

IQ

1

IQ

3

E

2

L

1

L

2

K

2

K

1

E

3

E

1

EP

IC

2

IC

3

Str. 174

22.05.21

74

Ścieżka ekspansji produkcji

Ścieżka ekspansji ma kształt zależny od
korzyści skali:

-

Stałe korzyści skali – ścieżka ekspansji jest
prostą linią

- Rosnące i malejące korzyści skali –

ścieżka ekspansji jest parabolą

Str.174-
176

22.05.21

75

Ścieżka ekspansji produkcji dla
funkcji produkcji o stałych
korzyściach skali

0

IQ

2

L

IC

1

K

K

3

L

3

IQ

1

IQ

3

A

L

1

L

2

K

2

K

1

B

EP

IC

2

IC

3

C

Str. 175

22.05.21

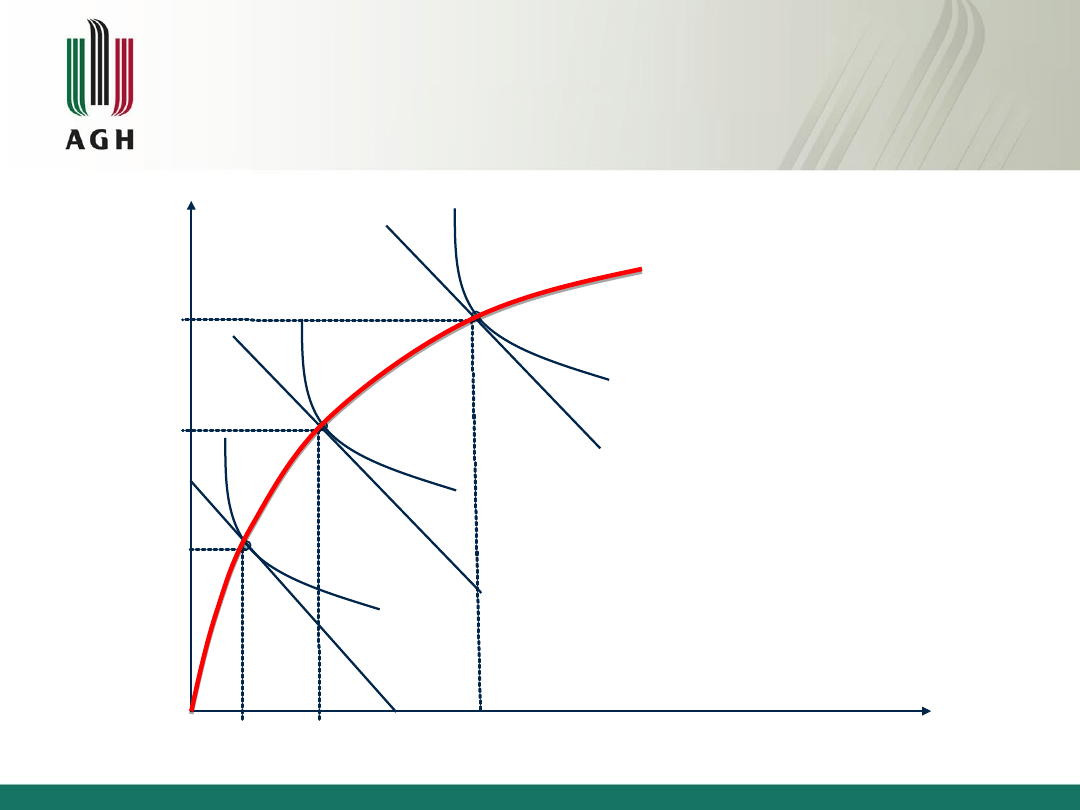
76

Ścieżka ekspansji dla funkcji
produkcji o rosnących korzyściach
skali

0

IQ

2

L

IC

1

K

K

3

L

3

IQ

1

IQ

3

A

L

1

L

2

K

2

K

1

B

EP

IC

2

IC

3

C

Str. 175

22.05.21

77

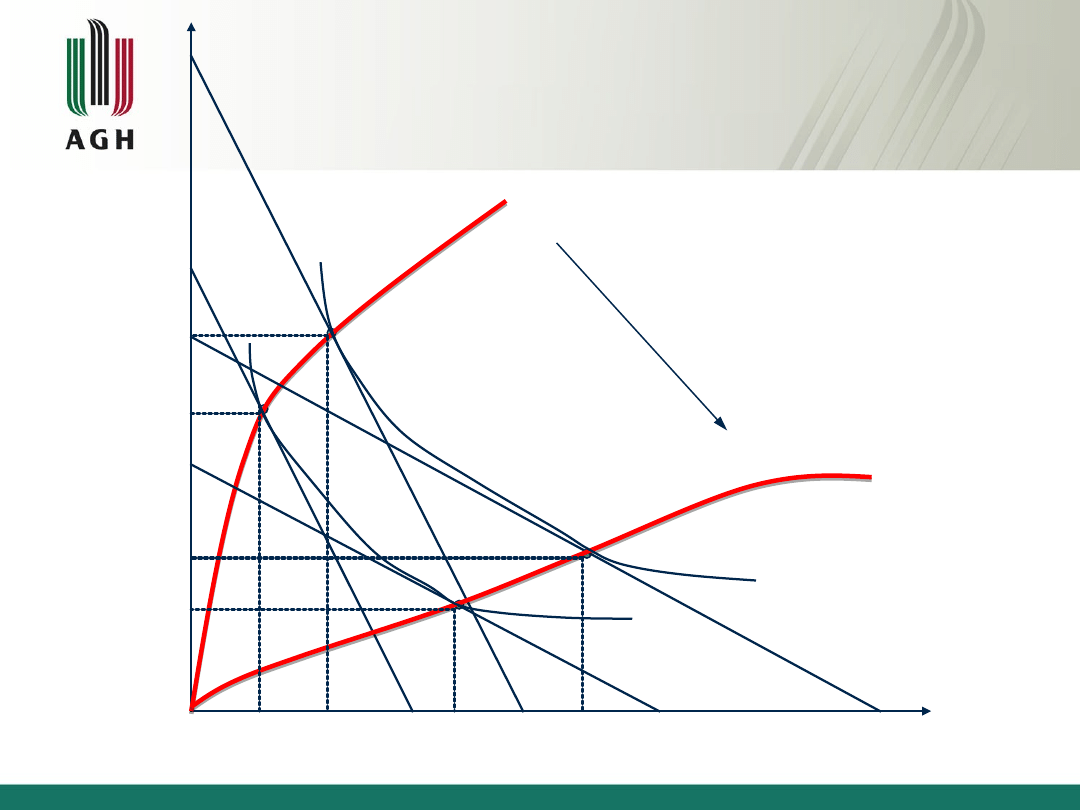
Ścieżka ekspansji dla funkcji
produkcji o malejących
korzyściach skali

0

IQ

2

L

IC

1

K

K

3

L

3

IQ

1

IQ

3

A

L

1

L

2

K

2

K

1

B

EP

IC

2

IC

3

C

Str.
176

22.05.21

78

Zmiana cen
czynników
wytwórczych a
położenie ścieżki
ekspansji
produkcji

0

IQ

2

L

IC

1

K

K

3

L

3

IQ

1

A

L

1

L

2

K

2

K

1

B

EP

1

IC’

2

C

EP

2

IC

2

IC’

1

D

K

4

L

4

N/P

K4

N/P

K2

N/P

K3

N/P

K1

N/P

L1

N/P

L2

N/P

L3

N/P

L4

Str.
176

Zmiana relacji cen czynników a
zmiana położenia ścieżki ekspansji
produkcji

W sytuacji wyjściowej położenie linii jednakowego

kosztu IC

1

wyznaczone jest poziomem ceny czynnika

pracy (P

L

) i czynnika kapitału (P

K

). Wyznaczona dla

tych cen ścieżka ekspansji produkcji (EP

1

) przechodzi

przez dwa punkty A i B. Na skutek zmiany cen

czynników wytwórczych (cena czynnika pracy

obniżyła się, a cena czynnika kapitału wzrosła)

zmieniło się położenie linii jednakowego kosztu

(izokoszty) z IC

1

do IC

2

(izokoszta na skutek zmiany

cen nakładów jest bardziej płaska w stosunku do

początku układu współrzędnych).

22.05.21

79

Str.
177

Efektem zmiany położenia izokoszty jest

również zmiana przebiegu ścieżki

ekspansji produkcji (EP

2

), która

przesunęła się w prawo względem osi

odciętych i przechodzi przez punkty C i D. W

wyniku zaistniałych zmian zwiększyło się

zaangażowanie wykorzystania czynnika

pracy (z L

2

do L

4

), który stał się teraz

nakładem relatywnie tańszym, natomiast

zmniejszył się udział wykorzystania

czynnika kapitału (z K

2

do K

4

), który na

skutek wzrostu jego ceny stał się czynnikiem

relatywnie droższym.

22.05.21

80

Str.
177

22.05.21

81

Źródło: „Podstawy

mikroekonomii”, Tomasz Zalega,

Warszawa 2005