Analizy wielowymiarowe

Wielowymiarowa zmienna
losowa

Model populacji generującej zbiór obiektów
opisanych wieloma cechami statystycznymi
(k>2).

)

,...,

,

(

)

,...,

,

(

2

2

1

1

2

1

k

k

k

x

X

x

X

x

X

P

x

x

x

F









Dystrybuanta wielowymiarowej zmiennej
losowej

Parametry wielowymiarowej
zmiennej losowej





k

,...,μ

,μ

μ

2

1



μ





2

2

2

2

1

k

,...,σ

,σ

σ



2

σ



























1

...

...

...

...

...

...

...

1

...

1

3

2

1

2

23

21

1

13

12

k

k

k

k

k



















ρ

Wektor wartości
przeciętnych

Wektor wariancji

Macierz korelacji

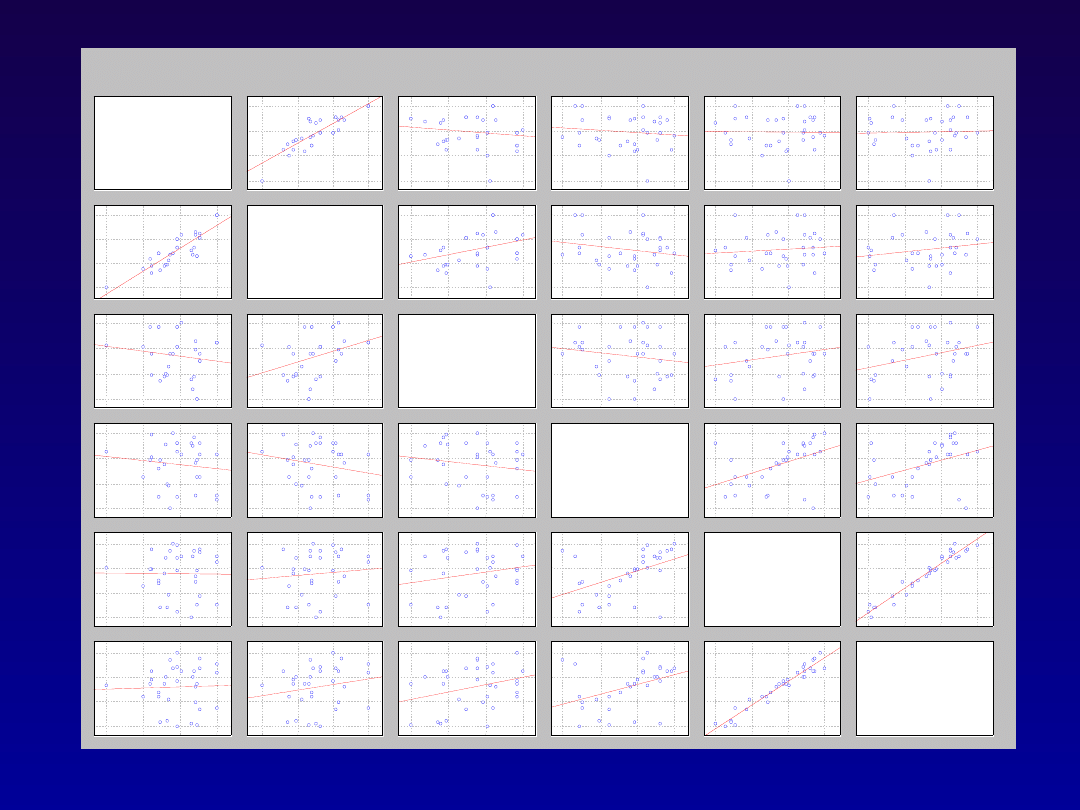
W y k r e s m a c ie r z o w y ( D A N E 1 2 W R Z 4 8 v * 3 2 c )

W Z R O S T

M A S A

W S K R

B I E G _ 5 M

B I E G _ 1 0 M

B I E G _ 1 5 M

Rodzaje korelacji

Rodzaje korelacji

• Prosta – między dwiema zmiennymi
• Cząstkowa – między dwiema

zmiennymi przy wyeliminowaniu
wpływu innych

• Wieloraka – między zestawem

zmiennych objaśniających, a zmienną
objaśnianą

• Kanonicza – Między zestawami

zmiennych

• Prosta – między dwiema zmiennymi
• Cząstkowa – między dwiema

zmiennymi przy wyeliminowaniu
wpływu innych

• Wieloraka – między zestawem

zmiennych objaśniających, a zmienną
objaśnianą

• Kanonicza – Między zestawami

zmiennych

Regresja wieloraka

• Równanie opisujące związek pomiędzy

zmiennymi objaśniającymi
(niezależnymi) a zmienną objaśnianą
(zależną)

• Składnik losowy jest niezależny od

zmiennych

• Składnik losowy podlega rozkładowi

normalnemu o wartości przeciętnej zero i
stałej wariancji

Modele regresji

Modele regresji

• Regresja prosta
• Regresja nieliniowa dwóch zmiennych
• Liniowa regresja wieloraka
• Nieliniowa regresja wieloraka
• Regresja logistyczna
• Regresja wielomianowa
• Model proporcjonalnego hazardu Coxa
• Modele ścieżkowe
• Modele wielorówaniowe

• Regresja prosta
• Regresja nieliniowa dwóch zmiennych
• Liniowa regresja wieloraka
• Nieliniowa regresja wieloraka
• Regresja logistyczna
• Regresja wielomianowa
• Model proporcjonalnego hazardu Coxa
• Modele ścieżkowe
• Modele wielorówaniowe

Regresja wieloraka w
populacji







)

,...,

,

(

2

1

k

X

X

X

f

Y

Y

–

zmienna

objaśniana

(niezależna,

endogeniczna, skutek, odpowiedź)

f – analityczna postać funkcji regresji

X

1

, X

2

, …, X

k

– zmienne objaśniające (niezależne,

egzogeniczne, sterowanie, czynniki, przyczyny)

 - składnik losowy

Liniowa funkcja regresji

wielorakiej w populacji























k

k

X

X

X

Y

...

2

2

1

1

0

β

0

– wyraz wolny regresji (najczęściej nie

interpretujemy go)

β

j

– współczynnik regresji cząstkowej

Współczynnik regresji cząstkowej informuje o ile
przeciętnie zmieni się Y jeżeli zmienna X przy
której stoi ten współczynnik wzrośnie o
jednostkę, a pozostałe zmienne objaśniające nie
ulegną zmianie.

Etapy budowy modelu regresji
wielorakiej

• Określenie zmiennej objaśnianej Y
• Określenie listy potencjalnych zmiennych objaśniających
• Wybór optymalnego zestawu zmiennych objaśniających
• Wybór analitycznej postaci funkcji regresji
• Estymacja równania regresji
• Weryfikacji istotności parametrów strukturalnych modelu
• Regresja krokowa
• Interpretacja modelu
• Ocena dobroci dopasowania
• Analiza reszt
• Prognozowanie i symulacje

Przydatność modeli regresji

Przydatność modeli regresji

• Analiza relacji
• Prognozowanie
• Symulacja
• Wyszukiwanie obserwacji

odstających

• Identyfikacja
• Weryfikacja struktury zjawisk

• Analiza relacji
• Prognozowanie
• Symulacja
• Wyszukiwanie obserwacji

odstających

• Identyfikacja
• Weryfikacja struktury zjawisk

 

WRZY

CZAS UT

0,102

GIBKOŚĆ

0,178

I E

-0,093

KŁAMST

0,076

KPNT

0,26

P O

0,422

PRB

0,44

PSYCHOT

-0,199

RPN

0,42

S „SEKD”

0,406

SPK

0,451

SPRINT 5

-0,304

SPRINT10

0,024

SPRINT15

-0,143

SR

-0,455

T KWADR

0,385

TENIS

0,965

WCZR

-0,053

WSK SPA

-0,052

Badane

Cząstkowa

Cechy

korelacja

CZAS UT

-0,977

GIBKOŚĆ

-0,881

I E

-0,146

KŁAMSTW

0,944

KPNT

-0,871

P O

0,354

PRB

0,756

PSYCHOT

0,987

RPN

-0,961

S„SEKD”

0,893

SNOB

-0,74

SPK

-0,97

SPRINT 10

0,98

SPRINT 15

0,99

SPRINT 5

-0,99

SR

0,91

T KWADR

0,989

TENIS

0,997

WCZR

-0,952

WSK SPA

-0,93

Tabela 6.5.
Parametry strukturalne równania regresji dla zmiennej zależne Y –WRZ

Badane
cechy

Beta

Błąd

st.

beta

B

Błąd

st.

B

T(5)

Poziom

p.

W. wolny

96,49

3

19,707

4,896

0,0045

TENIS

1,289

0,045

1,147

0,040

28,463

0,0000

T KWADR

0,977

0,065

1,177

0,079

14,972

0,0000

SPK

-

0,586

0,065

-

0,757

0,084

-8,969

0,0003

SPRINT1
5

0,656

0,042

17,70

2

1,131

15,646

0,0000

GIBKOŚĆ

-

0,193

0,046

-

0,516

0,124

-4,174

0,0087

SPRINT1
0

0,259

0,023

24,55

2

2,225

11,033

0,0001

SR

0,299

0,061

0,521

0,106

4,918

0,0044

CZAS UT

-

0,363

0,035

-

2,047

0,198

-

10,317

0,0001

SPRINT 5

-

0,711

0,044

-

91,22

5

5,692

-

16,027

0,0000

PSYCHOT

0,643

0,048

1,173

0,087

13,486

0,0000

KŁAMST

0,191

0,030

0,376

0,059

6,422

0,0014

I E

-

0,013

0,039

-

0,037

0,111

-0,331

0,7540

S„SEKD”

0,152

0,034

0,044

0,010

4,434

0,0068

KPNT

-

0,246

0,062

-

0,582

0,147

-3,963

0,0107

RPN

-

0,637

0,082

-

0,833

0,107

-7,757

0,0006

PRB

0,112

0,043

0,203

0,079

2,583

0,0492

P O

0,017

0,020

0,020

0,023

0,845

0,4366

WCZR

-

0,757

0,109

-

1,658

0,238

-6,955

0,0009

WSK SPA

-

0,336

0,060

-

0,756

0,134

-5,640

0,0024

SNOB

-

0,044

0,018

-

0,008

0,003

-2,462

0,0571

Podsumowanie regresji
zmiennej zależnej: Y-WRZ
R= ,999; R2= ,999;
Poprawione R^2= ,998
F(20, 5)=2193,6;
p<,00000; Błąd
standardowy estymacji: ,
21839

DZIĘKUJĘ

Czekam na
pytania …