Materiały dydaktyczne dla studentów IPSiR UW © Beata Gruszczyńska

Analiza współzależności zmiennych mierzalnych

Korelacja i regresja

Część I

Celem analizy współzależności jest badanie związków między zmiennymi
mierzalnymi i prognozowanie jednych zmiennych za pomocą innych zmiennych.

Analiza współzależności między zmiennymi to badanie zbiorowości statystycznej ze
względu na dwie lub więcej zmiennych jednocześnie. Zakładamy, że wszystkie
zmienne są mierzalne.

Warto podkreślić, że terminy współzależność lub współwystępowanie są tu bardzo
zasadne. Należy wyraźnie odróżniać współzależność od zależności, która kojarzy się z
zależnością przyczynowo-skutkową. Statystyka koncentruje się na badaniu liczbowym
związku między zmiennymi, natomiast natura związku, jej przyczynowo-skutkowy
charakter należy ustalać w oparciu o wiedzę, teorię w danej dziedzinie wiedzy
socjologii, psychologii, kryminologii itp.

Umownie, dla ułatwienia będziemy mówić o zmiennej Y – zależna, a o zmiennej X
jako niezależna, ale nie w rozumieniu zależności przyczynowo-skutkowej. Lepszym,
„zgrabniejszym” określeniem dla zmiennej Y jest – zmienna objaśniana, a dla
zmiennej X – objaśniająca.

O współzależności w uproszczeniu mówimy zależność, lecz nie oznacza to związku
przyczynowo-skutkowego.

Korelacja pozorna – oznacza przypadkowe współwystępowanie zmiennych Y i X,
które nie ma potwierdzenia w naturze związku. Przykład: Y – liczba urodzeń i X –
liczba przylatujących bocianów. W interpretacjach związków należy uważać, aby nie
wpaść w pułapkę korelacji pozornych.

Zależność funkcyjna i zależność statystyczna

Zależność funkcyjna, funkcja matematyczna jest to jednoznaczne przyporządkowanie
wartościom jednego zbioru wartości drugiego zbioru [według pewnego przepisu f].

Zależność funkcyjna przedstawia się następująco: y = f(x)

Np. y=2x+4 (funkcja liniowa) oznacza, że gdy x=4 to y=12, a gdy x=10 to y=24.

Zależność (współzależność) statystyczna nie jest jednoznaczna. Dotyczy zmiennych
empirycznych i związku empirycznego. Mówimy o prawidłowościach (najczęściej
występujących tendencjach), i mogą pojawić się wyjątki (stąd zależność nie
jednoznaczna).

Materiały dydaktyczne dla studentów IPSiR UW © Beata Gruszczyńska

Zależność statystyczną między zmiennymi Y i X przedstawiamy jako:

Y= f (X, e)

gdzie:

Y - zmienna objaśniana,
X - zmienna objaśniająca,
e – składnik losowy, który reprezentuje wpływ na Y czynników losowych oraz innych
zmiennych objaśniających, nie uwzględnionych w modelu.

Y – może być np. wynik testu z logiki (musi być mierzalne), a X – liczba godzin nauki.

W ogólnym podejściu możemy przyjąć, że zmienna Y (objaśniająca) jest współzależna
z wieloma zmiennymi objaśniającymi: X1, X2, ….Xk, co możemy zapisać jako:

Y= f (X1, X2, …., Xk, e)

Uwzględnienie wielu zmiennych jest domeną analizy wielowymiarowej, w której
obserwujemy wpływ zmiennych objaśniających na zmienną objaśnianą, a także
wzajemną zależność zmiennych objaśniających.

W analizie związków empirycznych (statystycznych) wskazujemy na prawidłowości
współwystępowania zmiennych np. Y i X (przeciętny trend) oraz rozbieżności od
prawidłowości (rozrzut punktów empirycznych).

Współwystępowanie tych dwóch zmiennych Y i X przedstawiamy na wykresie
zwanym diagramem korelacyjnym, w którym na osi X – poziomej (odciętych)
przedstawiamy zmienną niezależną (objaśniającą), a na osi rzędnych Y – pionowej
(rzędnych) zmienną zależną (objaśnianą).

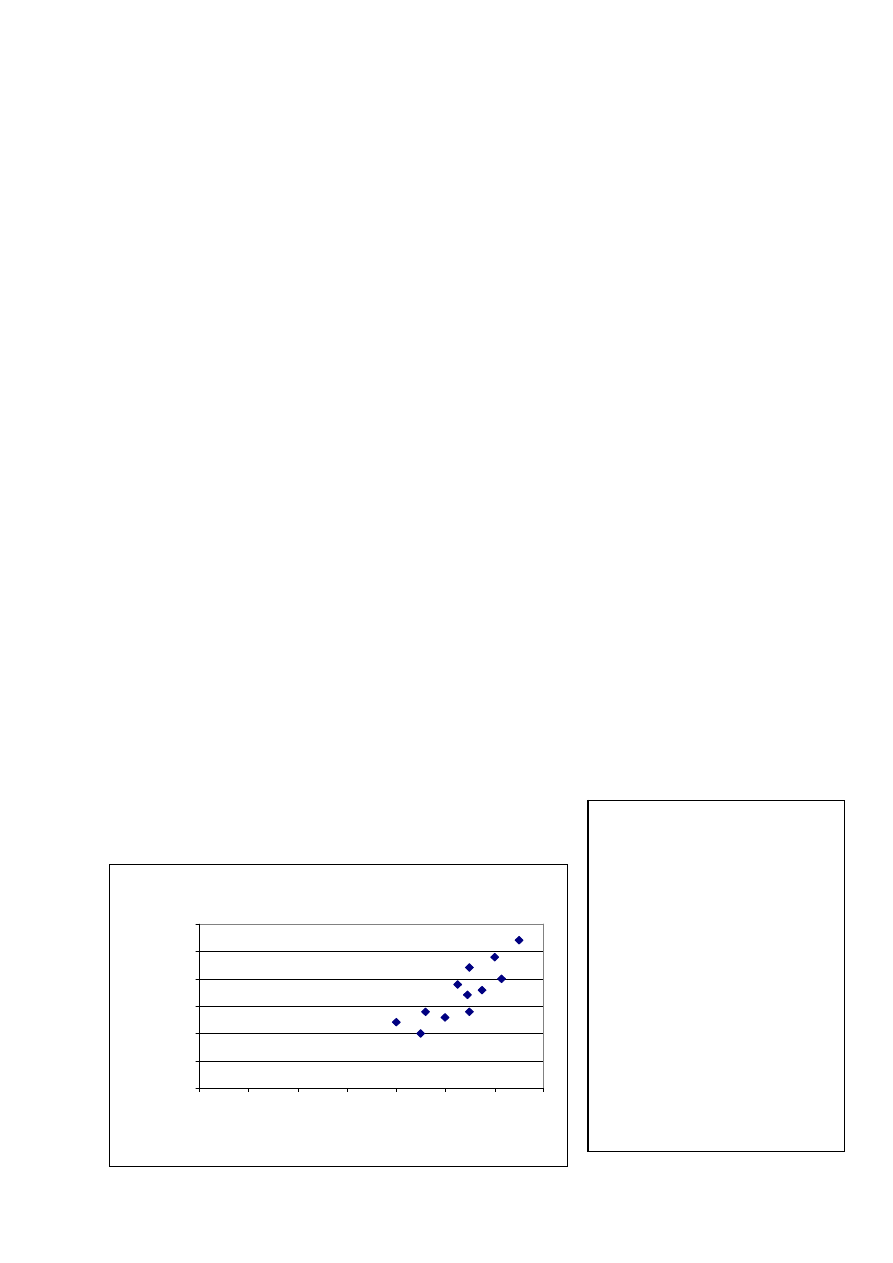
Przykład 1. Związek między dwiema zmiennymi: Y – szybkość czytania i X – iloraz
inteligencji (IQ):

Diagram korelacyjny:

Diagram korelacyjny

(Y - szybkość czytania; X - IQ)

0

50

100

150

200

250

300

0

20

40

60

80

100

120

140

Inne przykłady
współzależności:

1) X cena produktu A;
Y popyt na produkt A

2) X ilość spożywanych
kalorii; Y – waga

3) X liczba godzin treningu;
Y sprawność

Materiały dydaktyczne dla studentów IPSiR UW © Beata Gruszczyńska

Elementy korelacji i regresji

Korelacja

• Mówi o tym jaki jest kierunek związku Y i X

• Mówi o tym jaka jest siła związku Y i X

Warto podkreślić, że siła związku jest domeną wyłącznie związków statystycznych.
Ta charakterystyka – siła nie występuję w przypadku związków matematycznych, które
są jednoznaczne.

Regresja

• Mówi o tym jaki jest kierunek związku

• Mówi o tym jaki jest kształt

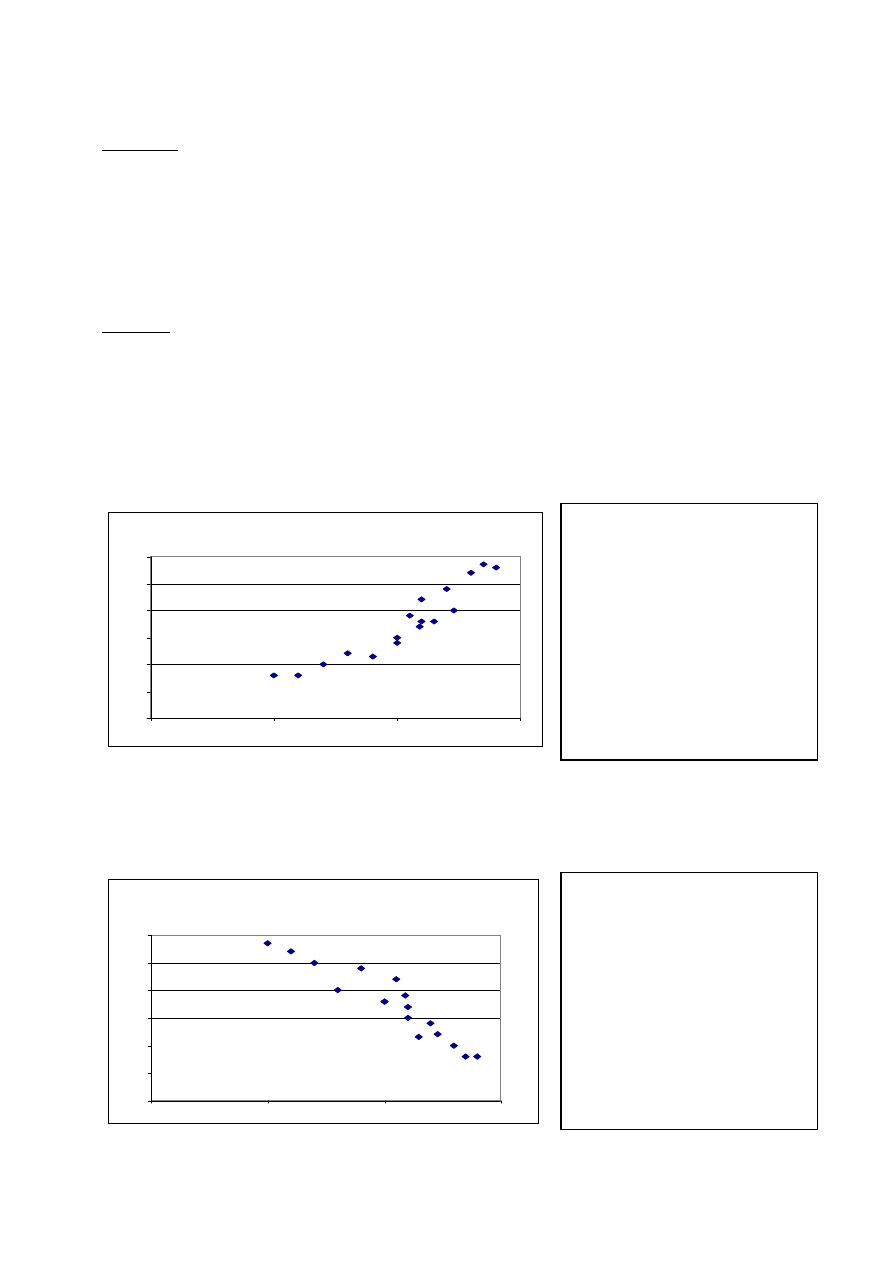
Kierunek związku może być dodatni lub ujemny.

Związek między Y i X jest dodatni, jeśli rosnącym wartością zmiennej X odpowiadają
rosnące wartości zmiennej Y.

Współzależność dodatnia

0

50

100

150

200

250

300

0

50

100

150

Związek między Y i X jest ujemny jeśli rosnącym wartością zmiennej X odpowiadają
malejące wartości zmiennej Y.

Współzależność ujemna

0

50

100

150

200

250

300

0

50

100

150

UWAGA: proszę podać
przykłady zmiennych,
między którymi zachodzi
współzależność ujemna

Y – zmienna objaśniana:

…………………………..

X – zmienna objaśniająca

……………………………

UWAGA: proszę podać
przykłady zmiennych,
między którymi zachodzi
współzależność dodatnia

Y – zmienna objaśniana:

…………………………..

X – zmienna objaśniająca

Materiały dydaktyczne dla studentów IPSiR UW © Beata Gruszczyńska

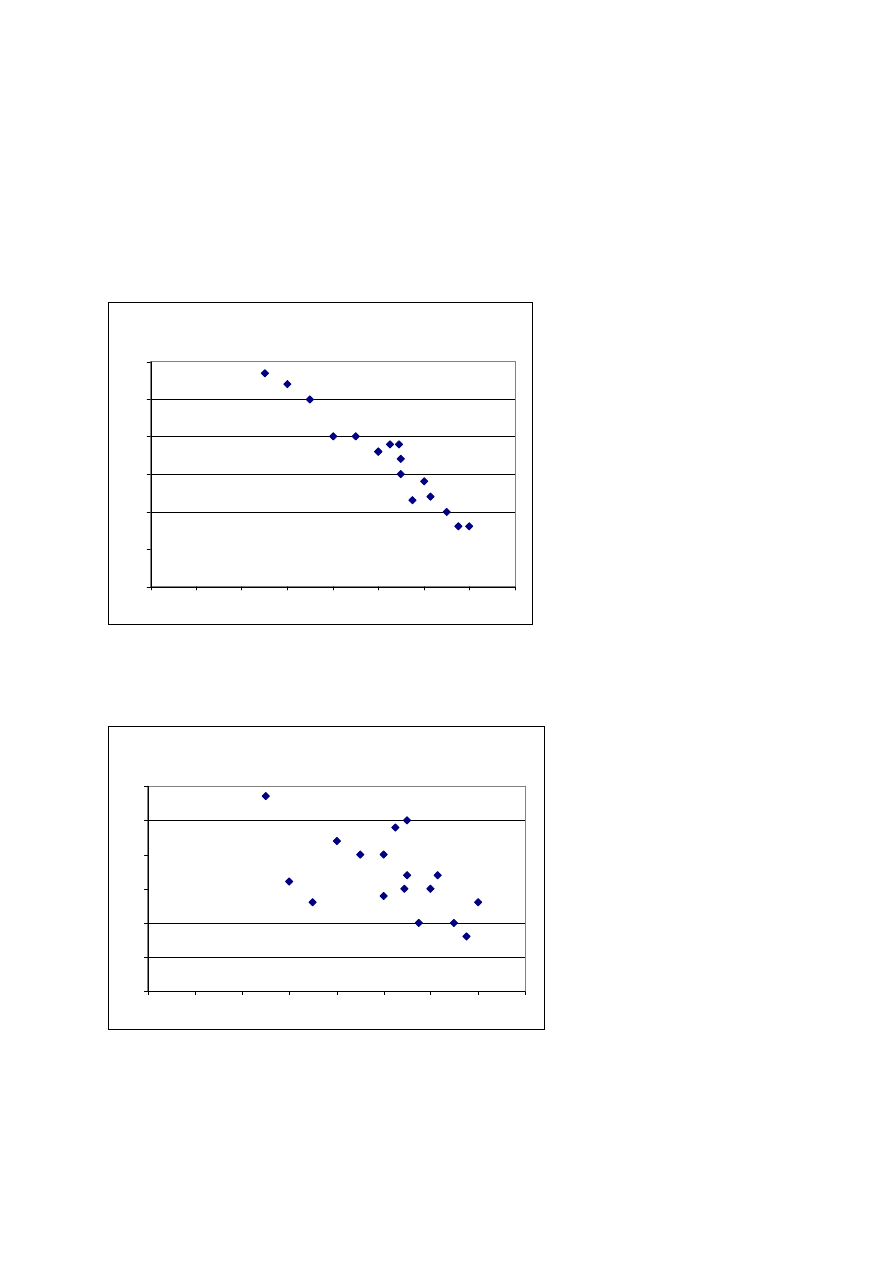
Siła współzależności może być duża i mała.

Jeśli punkty skupione są np. blisko linii – oznacza to silną współzależność. Jeśli punkty
empiryczne są bardzo rozproszone – związek określamy jako słaby.

Przykład związku silnego i ujemnego:

Współzależność silna (ujemna)

0

50

100

150

200

250

300

0

20

40

60

80

100

120

140

160

Przykład związku słabego i ujemnego:

Współzależność słaba (ujemna)

0

50

100

150

200

250

300

0

20

40

60

80

100

120

140

160

Kształt związku: współzależność może mieć kształt liniowy lub nieliniowy
(logarytmiczny, wykładniczy itp.).

Materiały dydaktyczne dla studentów IPSiR UW © Beata Gruszczyńska

Współczynnik korelacji liniowej Pearsona

Do określenia siły korelacji stosuje się współczynnik korelacji liniowej Pearsona r,
który oblicza się według wzoru:

∑

∑

∑

−

−

−

−

=

2

2

)

(

)

(

)

)(

(

y

y

x

x

y

y

x

x

r

i

i

i

i

Współczynnik korelacji Pearsona mierzy siłę zależności tylko w przypadku
współzależności liniowej.

Właściwości współczynnika r Pearsona.

1. Współczynnik r przyjmuje wartości od -1 do +1,

czyli: -1 ≤ r ≤ 1

2. Wartość współczynnika korelacji określa siłę i kierunek współzależności

a) moduł r (

I

r

I

) – określa siłę współzależności

b) znak (+ –) – określa kierunek związku

3. Interpretacja siły współzależności:

a) r=0: brak związku między zmiennymi YX
b) r= –1 lub r=+1: związek funkcyjny („najsilniejszy”)
c)

I

r

I

bliskie 1: związek między YX silny

d)

I

r

I

bliskie 0: związek słaby

4. Współczynnik korelacji r Pearsona ma własność symetryczności,

czyli:

r

yx

= r

xy

oznacza to, że siła zależności między Y i X jest taka sama jak między X i Y.

5. Kwadrat r (r

2

) określa się mianem współczynnika determinacji i oznacza %

zmienności Y wyjaśniony zmiennością X.
Np.

r

2

=0,67 oznacza, że zróżnicowanie Y można w 67% wyjaśnić

zróżnicowaniem X.

Materiały dydaktyczne dla studentów IPSiR UW © Beata Gruszczyńska

Przykład 1.

Obliczyć współczynnik korelacji między Y i X (Y – szybkość czytania i X – iloraz
inteligencji (IQ).

lp

x

i

y

i

x

i

- x

y

i

- y (x

i

- x )*( y

i

- y )

(x

i

- x )

2

( y

i

- y )

2

1 80

120

-27

-55

1485

729

3025

2 92

140

-15

-35

525

225

1225

3 90

100

-17

-75

1275

289

5625

4 109

170 2

-5

-10

4 25

5 100

130 -7

-45

315

49

2025

6 105

190 -2

15

-30

4 225

7 110

220

3

45

135

9

2025

8 110

140

3

-35

-105

9

1225

9 115

180 8

5

40

64 25

10 120

240 13

65

845

169

4225

11 123

200

16

25

400

256

625

12 130

270 23

95

2185

529 9025

Suma

1284 2100

X X

7060

2336

29300

Średnia X= 107 Średnia Y= 175
UWAGA: Proszę uzupełnić pola zacienione w tabeli!

85

,

0

*

)

(

)

(

)

)(

(

29300

2336

7060

.

..........

..........

..........

.

..........

..........

.

..........

..........

2

2

=

=

−

−

−

−

=

∑

∑

∑

y

y

x

x

y

y

x

x

r

i

i

i

i

r

2

= 0,73 – Współczynnik determinacji

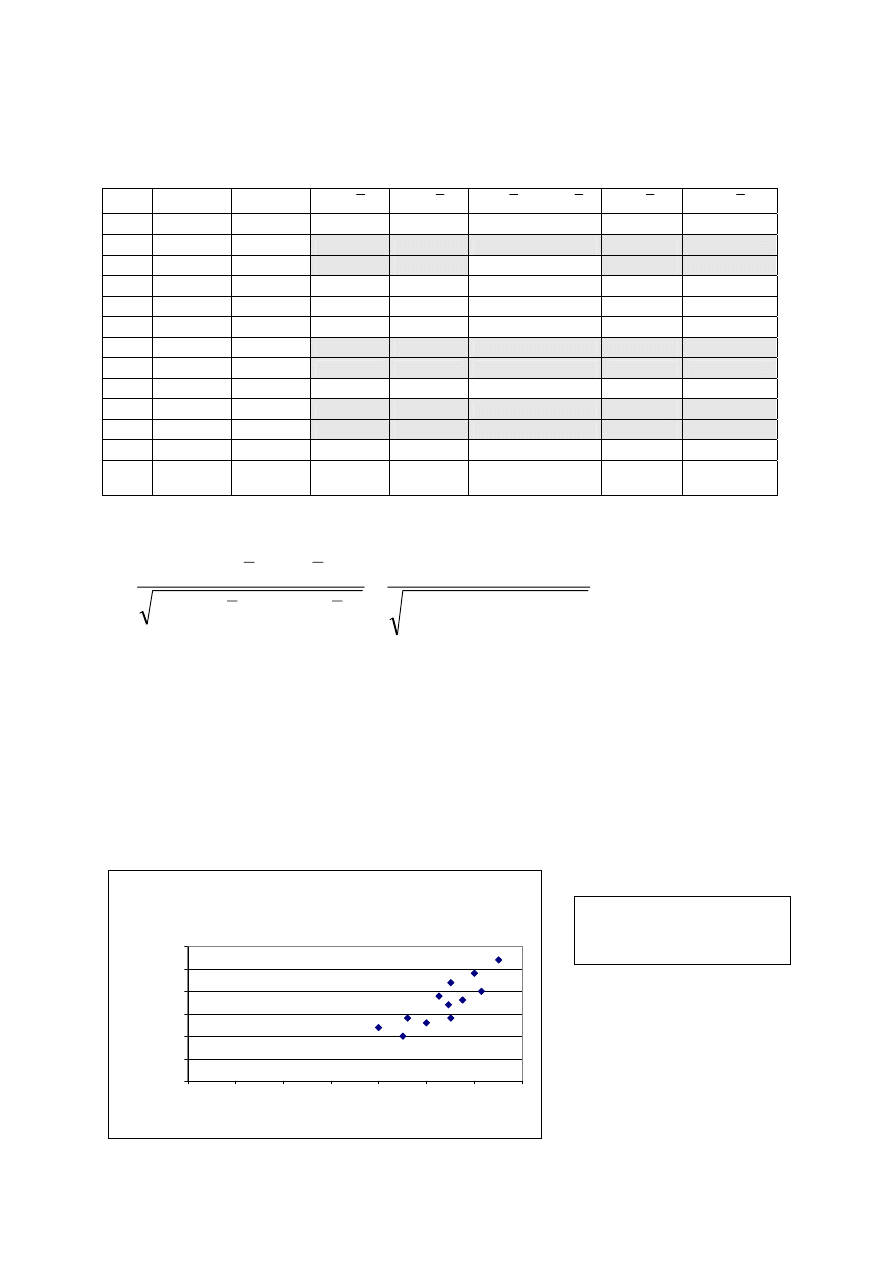
Interpretacja:
Związek między Y i X jest silny i dodatni, co oznacza, że osoby o wyższym IQ szybciej

czytają. Współczynnik determinacji 0,73 oznacza, że zróżnicowanie szybkości czytania

można w 73% wyjaśnić zróżnicowaniem IQ.

Wykres – diagram korelacyjny

Diagram korelacyjny

(Y - szybkość czytania; X - IQ)

0

50

100

150

200

250

300

0

20

40

60

80

100

120

140

Oś X – IQ
Oś Y – Szybkość czytania