Estymacja parametrów 

Estymacja parametrów 

modelu regresji liniowej z 

modelu regresji liniowej z 

wykorzystaniem opcji 

wykorzystaniem opcji 

„Regresja” arkusza 

„Regresja” arkusza 

kalkulacyjnego Excel

kalkulacyjnego Excel

Weryfikacja modelu

Weryfikacja modelu

Przykład

Stwierdzono, że najlepszymi 

zmiennymi objaśniającymi zmienną 

Y (rozmiary produkcji w mln zł) są 

zmienne X

1

, (wartość 

zainstalowanych maszyn i urządzeń 

w mln zł.) oraz X

2

 (średni czas 

przestoju maszyn i urządzeń w 

setkach godz.).

Oszacować  parametry modelu 

ekonometrycznego

 i przeprowadzić weryfikację modelu 

na podstawie danych zaczerpniętych 

z tabeli:

Y

Y

X

X

1

1

X

X

2

2

3

3

2

2

5

5

4

4

2

2

4

4

3

3

1

1

5

5

2

2

1

1

5

5

5

5

3

3

4

4

7

7

4

4

3

3

8

8

4

4

2

2

10

10

5

5

1

1

5

5

3

3

4

4

12

12

6

6

1

1

















2

2

1

1

0

X

X

Y

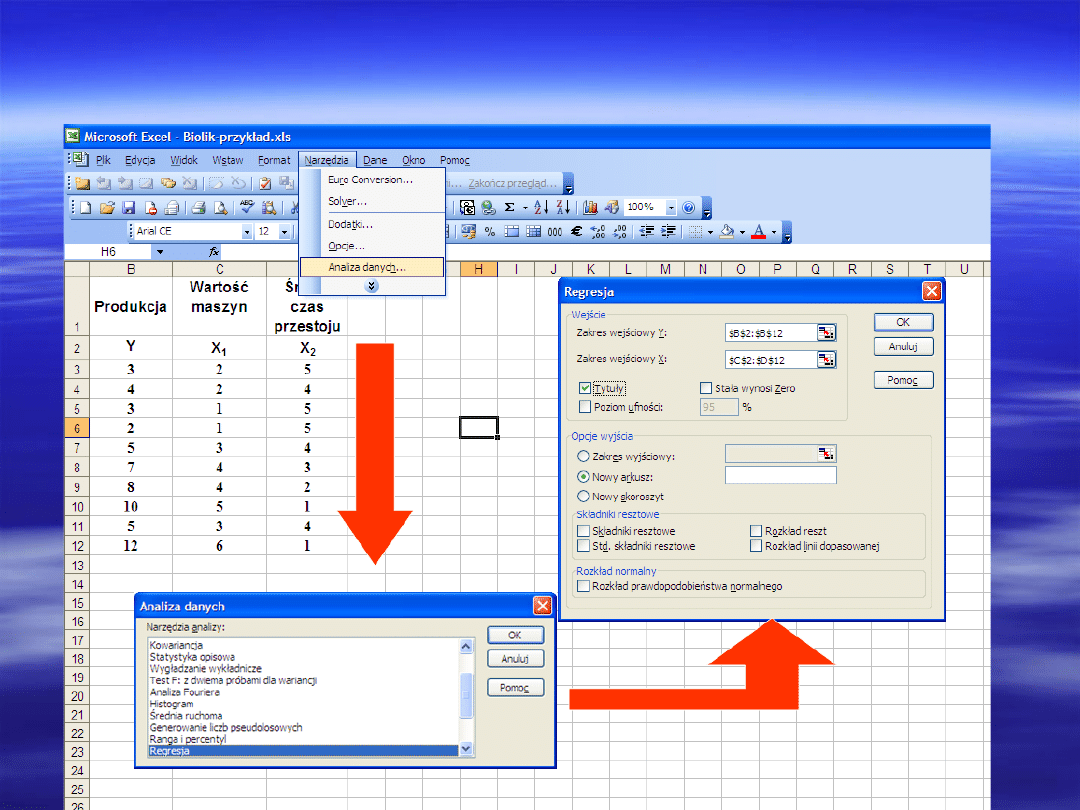
Oszacowanie parametrów modelu regresji liniowej umożliwia opcja 
„Regresja”. W aktywnym oknie z wprowadzonymi danymi wykonujemy 
polecenia:

                       

Narzędzia/ Analiza danych/Regresja  lub Dane/ Analiza 

danych/Regresja 

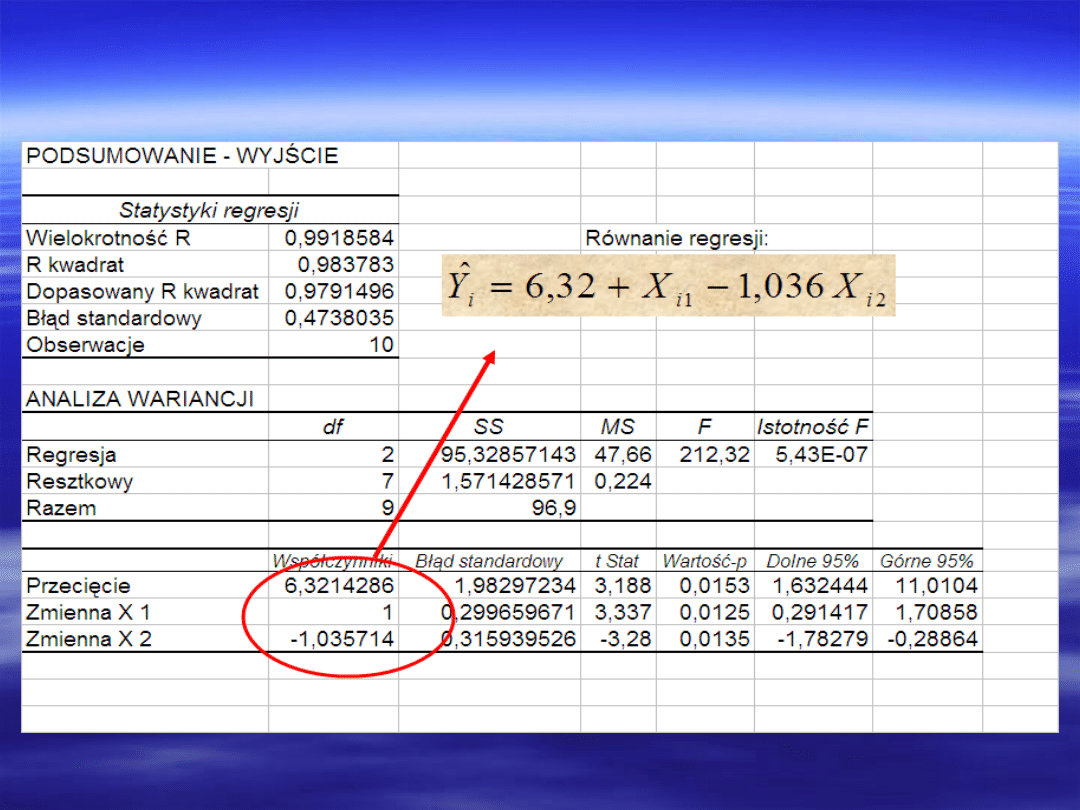
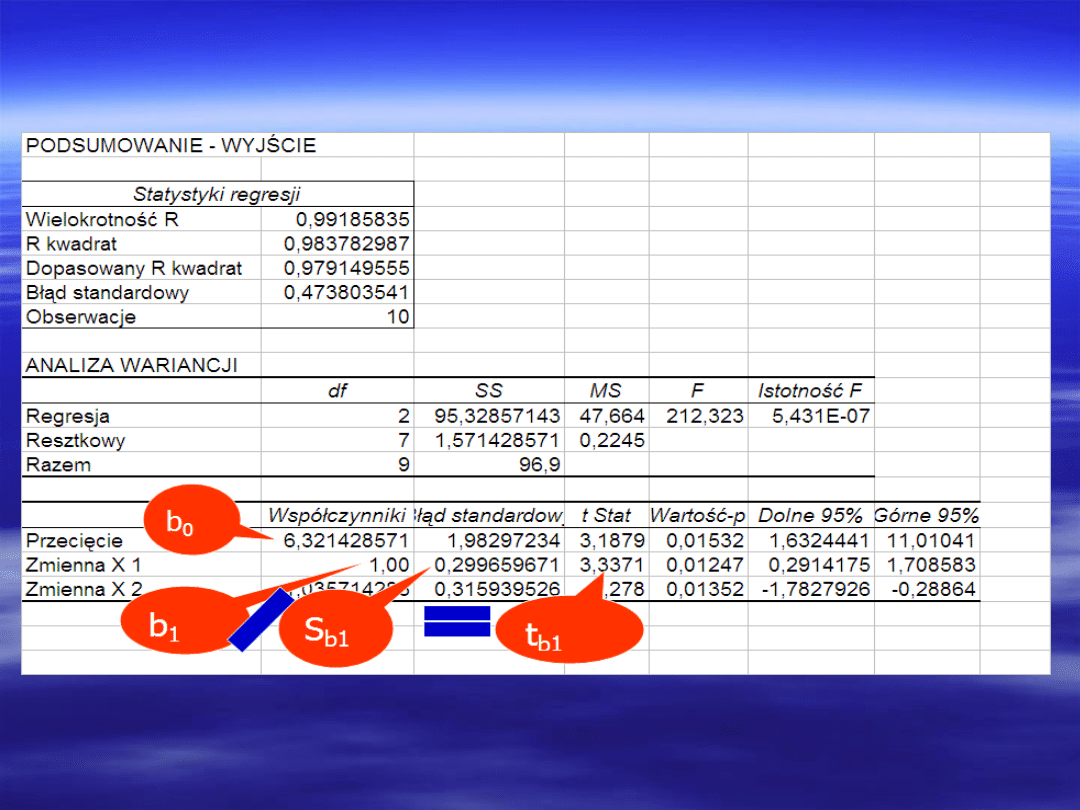
Wyniki opcji 
„Regresja”

Analiza wariancji









n

i

i

Y

Y

SST

1

2

)

(









n

i

i

i

Y

Y

SSE

1

2

)

ˆ

(









n

i

i

Y

Y

SSR

1

2

)

ˆ

(

     SST     =           SSR            +            SSE

odchylenie     odchylenie 

   odchylenie

całkowite 

 wyjaśnione regresją

 niewyjaśnione 

regresją

SS – Sum of Squares

SS – Sum of Squares

T – Total

T – Total

R – Regression

R – Regression

E – Error

E – Error

Interpretacja oznaczeń 

Interpretacja oznaczeń 

wyników analizy wariancji w 

wyników analizy wariancji w 

Excelu

Excelu

1 =       SSR/SST          +            SSE/SST

R

2

Współczynnik 
zbieżności φ2

Miary dopasowania modelu do 

danych

Dopasowany R kwadrat jest to skorygowany o liczbę 

zmiennych objaśniających w modelu współczynnik determinacji, 
który obliczamy ze wzoru:

gdzie: 
 n- liczba obserwacji zmiennej objaśnianej
k– liczba zmiennych objaśniających występujących w modelu

)

2

R

(1

1

k

n

1

k

1

2

R













~

Współczynnik determinacji: 











 n

1

t

2

)

t

y

t

(y

n

1

t

2

)

t

y

-

t

yˆ

(

2

R

Wartość współczynnika determinacji R

2 

zawiera się w 

przedziale <0,1> i informuje jaka część zaobserwowanej, 
całkowitej zmienności y została wyjaśniona przez model. 

Miary dopasowania modelu do danych

Miary dopasowania modelu do 

danych

Odchylenie standardowe reszt:

1

-

k

n

n

1

t

2

t

u

1

-

k

n

n

1

t

2

)

t

y

t

(y

u

S



















ˆ

Wielkość  odchylenia  standardowego  reszt  interpretujemy 

jako  przeciętne  odchylenie  zaobserwowanych  wartości  zmiennej 
y

i

  od  odpowiadających  im  wartości  obliczonych  na  podstawie 

oszacowanego modelu regresji.

Miary dopasowania modelu do 

danych

Dodatkowo obliczamy współczynnik zmienności (V) :

%

100

Y

u

S

V 

Współczynnik  ten  informuje,  jaki  procent  średniej  arytmetycznej 

zmiennej  objaśnianej  modelu  stanowi  odchylenie  standardowe  reszt. 

Mniejsze  wartości  współczynnika  zmienności  losowej  wskazują  na 

lepsze dopasowanie modelu do danych empirycznych.

 

Stopnie 

Stopnie 

swobody

swobody









n

i

i

Y

Y

SST

1

2

)

(















n

i

i

n

i

i

e

Y

Y

SSE

1

2

1

2

)

ˆ

(









n

i

i

Y

Y

SSR

1

2

)

ˆ

(

degree of freedom

liczba stopni 

swobody

Stopnie swobody

Stopnie swobody

Wartość średnia 

Wartość średnia 

kwadratów reszt

kwadratów reszt



Wartość średnia kwadratów reszt 

Wartość średnia kwadratów reszt 

(wariancja składnika losowego) MSE 

(wariancja składnika losowego) MSE 

mówi o 

mówi o 

zgodności z danymi obserwowanymi w modelu.

zgodności z danymi obserwowanymi w modelu.

(informuje o zmienności składnika losowego)

(informuje o zmienności składnika losowego)

1

1

1

)

ˆ

(

1

2

1

2





























k

n

SSE

k

n

u

k

n

Y

Y

MSE

n

i

i

n

i

i

i

Wartość średnia 

Wartość średnia 

kwadratów reszt

kwadratów reszt

Suma 

Suma 

kwadrató

kwadrató

w

w

Stopnie 

Stopnie 

swobod

swobod

y

y

Wartość średnia 

Wartość średnia 

kwadratów

kwadratów

Regresja

Regresja

SSR

SSR

k

k

MSR = SSR / k

MSR = SSR / k

Resztkow

Resztkow

y

y

SSE

SSE

n-k-1

n-k-1

MSE = SSE /(n-k-1)

MSE = SSE /(n-k-1)

Razem

Razem

SST

SST

n-1

n-1

SSE

n-k-1

1

1

2













k

n

u

MSE

S

n

i

i

u

Zachodzi następująca równość:

Wartość średnia kwadratów 

Wartość średnia kwadratów 

reszt

reszt

Weryfikacja modelu regresji 

Weryfikacja modelu regresji 

liniowej

liniowej

 

 

z Excelem

z Excelem

Badanie istotności parametrów 

Badanie istotności parametrów 

strukturalnych 

strukturalnych 

modelu

modelu

 

 

:

:



test F 

test F 



 

 

t-Studenta

t-Studenta

Badanie istotności 

Badanie istotności 

parametrów 

parametrów 

strukturalnych modelu

strukturalnych modelu

i

ik

k

i

i

i

X

X

X

Y





















...

2

2

1

1

0

,  i=1, 2, 
…n



Pierwszym krokiem weryfikacji oszacowanego modelu jest badanie 

Pierwszym krokiem weryfikacji oszacowanego modelu jest badanie 

istotności parametrów strukturalnych w celu sprawdzenia, które ze 

istotności parametrów strukturalnych w celu sprawdzenia, które ze 

zmiennych objaśniających istotnie wpływają na zmienną objaśnianą y

zmiennych objaśniających istotnie wpływają na zmienną objaśnianą y



Wymaganie jest, aby wszystkie zmienne objaśniające modelu były 

Wymaganie jest, aby wszystkie zmienne objaśniające modelu były 

istotne

istotne



Zazwyczaj nie bada się istotności wyrazu wolnego 

Zazwyczaj nie bada się istotności wyrazu wolnego 

β

β

0

0

Istotność parametrów strukturalnych 

Istotność parametrów strukturalnych 

modelu:

modelu:

H

0

 : R=0 (lub, 

β

i

 =0, dla i=1,2,.. 

k)

H

1

: R > 0 (lub przynajmniej 

jedno 

β

i

0)

Najpierw 

badamy, 

czy 

zbiór 

zmiennych 

objaśniających wpływa istotnie na zmienną y. 

Test F (przypomnienie)

Sprawdzianem tej hipotezy jest statystyka:

o rozkładzie Fishera - Snedecora  o k i n-k-1 stopniach 
swobody.

Wartość średnia 

kwadratów regresji

Wartość średnia 

kwadratów reszt

MSE

MSR

R

k

R

k

n

F











)

1

(

)

1

(

2

2

MSR

MSR

Test F

Test F

MSE

MSE

F

F

Test F

Decyzję  odnośnie  przyjęcia  bądź  odrzucenia  hipotezy  H

0 

podejmujemy  na  podstawie  wartości  prawdopodobieństwa  p  = 

P(F>F

obl

).  Wartość  F

obl

  znajduje  się  w  kolumnie  o  tytule  F, 

natomiast  wartość  prawdopodobieństwa  p  znajduje  się  w 

ostatniej  kolumnie  tablicy  i  nosi  nazwę  „Istotność  F”.  Jeśli 

prawdopodobieństwo  p  jest  nie    większe  od  przyjętego  poziomu 

istotności,  to  sprawdzaną  hipotezę  odrzucamy,  czyli  wartość 

współczynnika korelacji wielorakiej jest istotnie większa od zera.

 

Test F

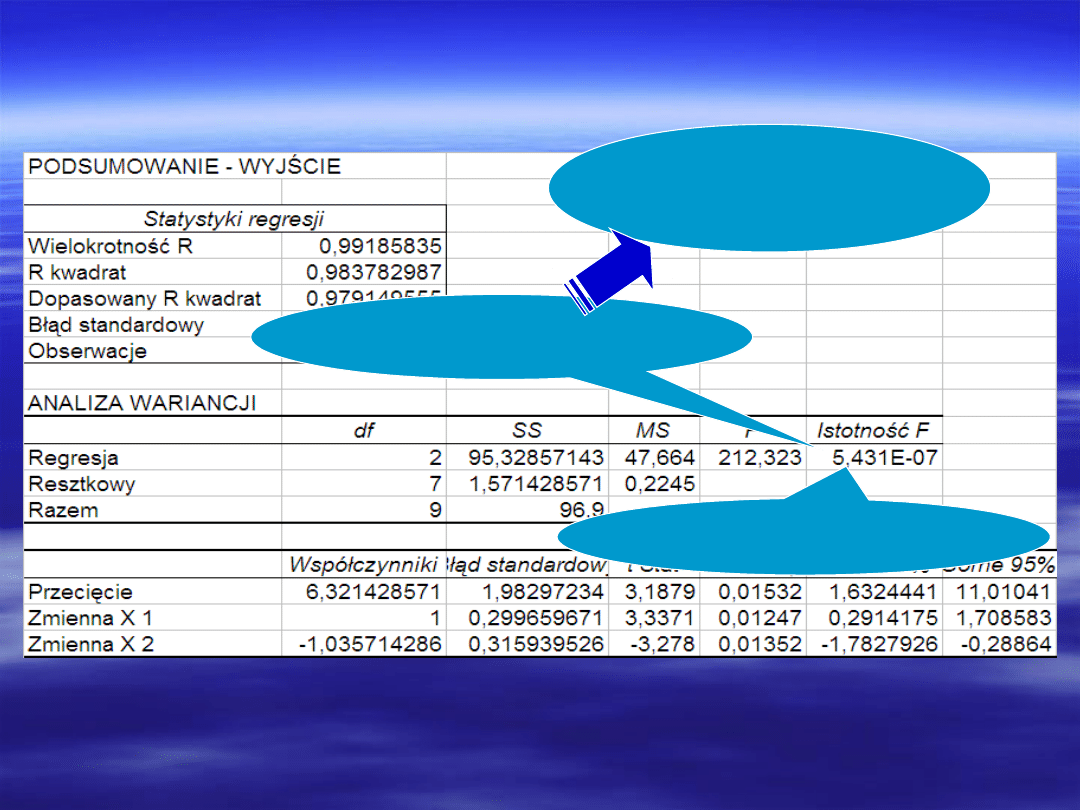
5,43*10

5,43*10

-7

-7

 ≤ 0,05

 ≤ 0,05

Istotność F ≤ 

Istotność F ≤ 

0,05

0,05

Hipotezę H

o 

odrzucamy

Test F

Test 

Test 

t-Studenta 

t-Studenta 

(przypomnienie)

(przypomnienie)



Badanie istotności parametrów strukturalnych modelu 

Badanie istotności parametrów strukturalnych modelu 

polega na weryfikacji hipotez postaci

polega na weryfikacji hipotez postaci

H

H

0

0

 : 

 : 

β

β

j

j

 = 0

 = 0

H

H

A

A

 : 

 : 

β

β

j

j

 ≠ 0

 ≠ 0



parametr 

parametr 

β

β

j

j

 nieistotnie różni się od zera

 nieistotnie różni się od zera



zmienna objaśniająca X

zmienna objaśniająca X

j

j

 nieistotnie wpływa 

 nieistotnie wpływa 

na zmienną objaśnianą Y

na zmienną objaśnianą Y



parametr 

parametr 

β

β

j

j

 istotnie różni się istotnie od zera

 istotnie różni się istotnie od zera



zmienna objaśniająca X

zmienna objaśniająca X

j

j

 istotnie wpływa na 

 istotnie wpływa na 

zmienną objaśnianą Y

zmienną objaśnianą Y

Sprawdzianem hipotezy zerowej jest

 

jak 

wiadomo

 

statystyka t-Studenta o n-k-1 

stopniach swobody równa ilorazowi oceny 
danego parametru i jego średniego  błędu 
szacunku: 

)

(

j

j

bj

b

S

b

t 

Test 

Test 

t-Studenta

t-Studenta

Test 

Test 

t-

t-

Student

Student

a

a

Wartość 

Wartość 

p

p

      Jeżeli wartość prawdopodobieństwa p = P(t>T-
stat) jest nie  większa od przyjętego poziomu 
istotności ( najczęściej przyjmujemy  = 0,05) to 
sprawdzaną hipotezę odrzucamy, czyli wartość 
oceny danego parametru jest istotnie różna od zera. 
Innymi słowy, jeżeli wszystkie wartości p w tablicy 
są mniejsze od przyjętego poziomu istotności np. 
0,05, to parametry przy wszystkich zmiennych 
uwzględnionych w modelu są istotnie różne od zera 
i zmienne wpływają istotnie na kształtowanie się 
zmiennej zależnej Y. 

0,012 ≤ 

0,012 ≤ 

0,05

0,05

p ≤ 

p ≤ 

0,05

0,05

Hipotezę H

o 

odrzucamy

Test 

Test 

t-

t-

Studenta

Studenta