Kwantyzacja sygnału

2

Kwantyzacja

Kwantyzacja (def.) – sprowadzenie zbioru
wartości, przyjmowanych przez sygnał x(t),
najczęściej nieskończonego zbioru liczb
rzeczywistych, do jego skończonego podzbioru.

W wyniku kwantyzacji powstaje sygnał ,
czyli sygnał przyjmujący wartości z określonego
zbioru.

)

(

)

(

t

x

t

x

q



)

(t

x

q

3

Cechy:
• kwantyzacji podlegają sygnały dyskretne
(spróbkowane w czasie),
• sygnał uzyskany w wyniku kwantowania
sygnału dyskretnego jest nazywany sygnałem
cyfrowym,
• kwantyzacja wynika z konieczności
zastosowania przetwornika analogowo-
cyfrowego przed umieszczeniem danych w
komputerze,
• przechowywane dane muszą się zawierać w
skończonym zbiorze wartości, gdyż możliwe jest
użycie określonej ilości bitów do jej
przechowywania.

Kwantyzacja c.d.

4

• Przykładowe źródło może generować wartości

rzeczywiste z przedziału [–200, 200].
• Uzyskiwane wartości liczbowe można

reprezentować np. jako najbliższą liczbę

całkowitą, czyli można otrzymać 401 możliwych

wartości.
• W ten sposób tracona jest część informacji, w

tym przypadku po kwantyzacji każda z liczb

rzeczywistych: 14,201; 13,831; 14,23 uzyska

taką samą wartość: 14.
• Utracone informacje, są tracone bezpowrotnie.

Kwantyzacja – przykład 1

5

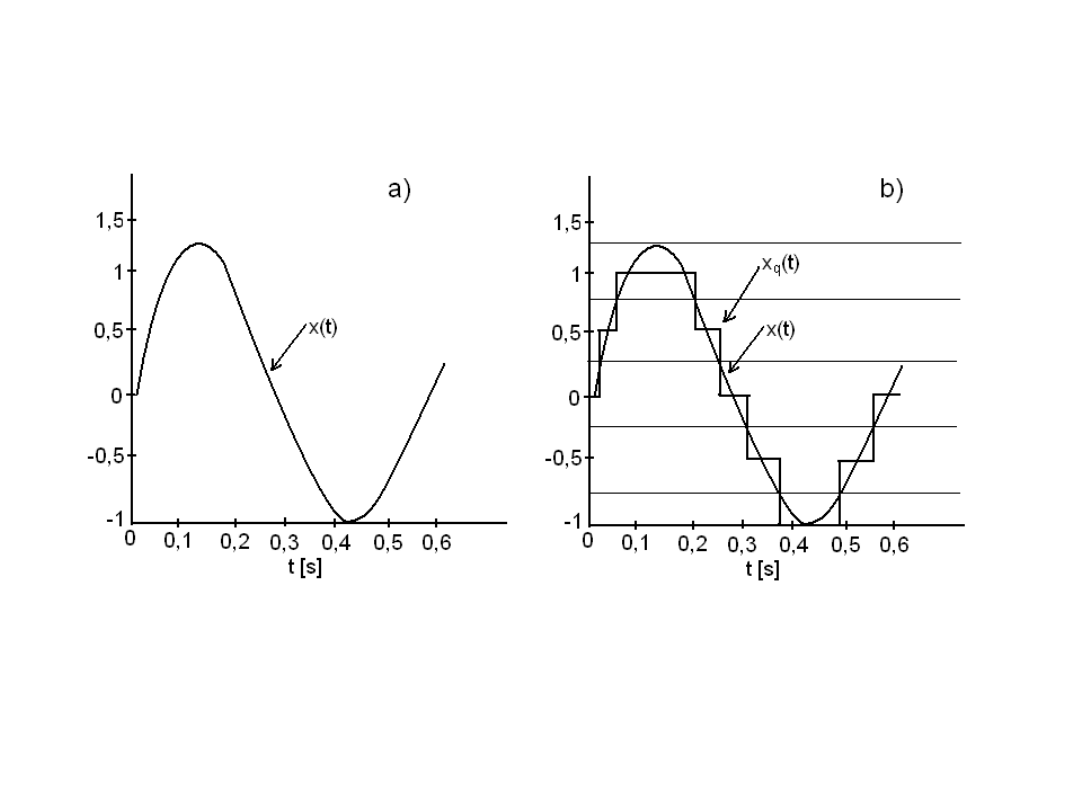
Kwantyzacja – przykład 2

Rys.1.1. Sygnał: a) ciągły, b) skwantowany
(dyskretny w wartościach).

6

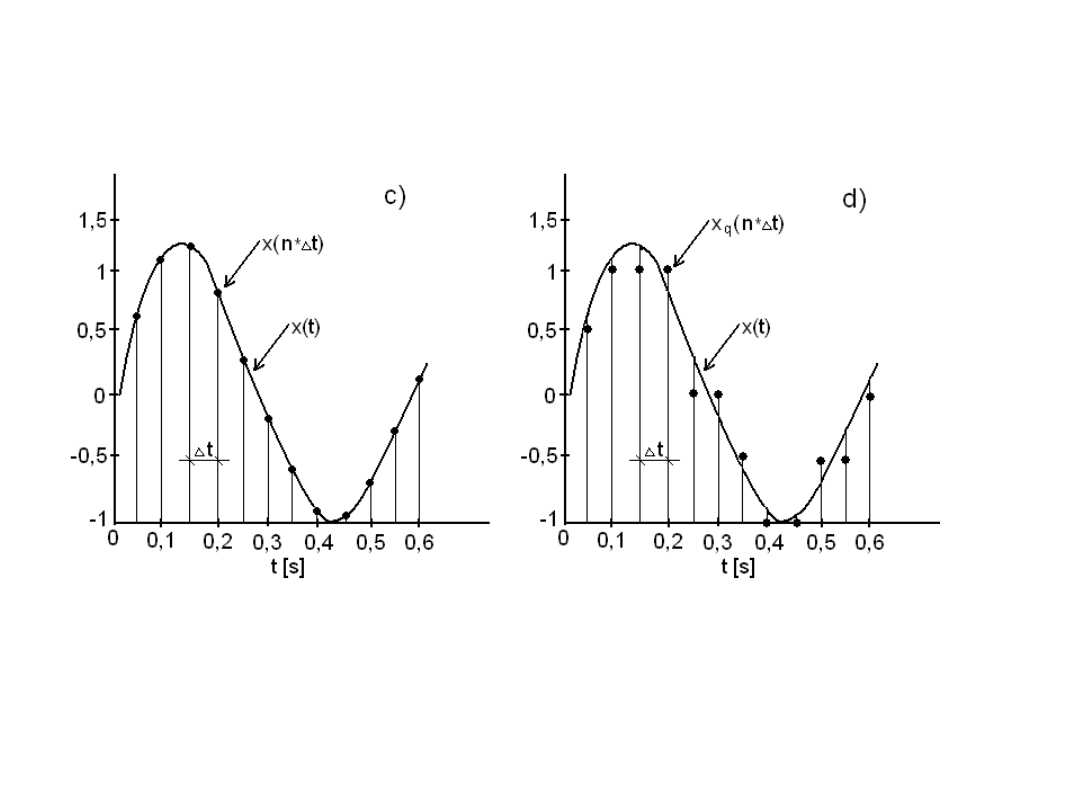
Kwantyzacja – przykład 3

Rys.1.2. Sygnał: a) spróbkowany (dyskretny w
czasie),
b) spróbkowany i skwantowany (cyfrowy).

7

Reprezentacje danych cyfrowych

Reprezentacją danych cyfrowych nazywamy
format zapisu liczb przedstawiony na określonej
ilości bitów.
• Liczba bitów jest ograniczona (najczęściej 8,
16, 32, 64).
• Liczba bitów w danym formacie wynika często,
z wielkości rejestrów sprzętowych maszyny
wykorzystującej dany format.
• Zbiór wartości możliwych do przedstawienia w
danym formacie jest ograniczony.
• Wyróżniamy:

– reprezentacje stałoprzecinkowe,
– reprezentacje zmiennoprzecinkowe.

8

Reprezentacje stałoprzecinkowe

binarne

• W sprzęcie cyfrowym liczby są reprezentowane za

pomocą cyfr dwójkowych znanych jako bity.
• Liczba bitów określa długość słowa.
• Zakłada wagę stowarzyszoną z każdą cyfrą w

liczbie stanowiącą podstawę systemu.
• W systemie binarnym wagą jest liczba 2, wobec

czego na N-bitach możemy zapisać 2 do potęgi N

różnych liczb o wartościach od 0 do .
• Stosuje się dwa typy:

– msb (most significant bit) – gdy bit najbardziej

znaczący leży skrajnie po lewej stronie,
– lsb (least significant bit) – gdy bit najmniej

znaczący leży skrlajnie po lewej stronie.

1

2



N

9

Reprezentacje stałoprzecinkowe binarne

c.d.

Wartość reprezentacji stałoprzecinkowej binarnej
jest obliczana na podstawie poniższej zależności:





















1

0

0

0

1

1

1

1

2

2

2

...

2

N

i

i

i

N

N

b

b

b

b

x

,gdzie:
• N jest liczbą bitów,
• bity przyjmują tylko dwie
wartości, ze zbioru {0,1},

0

1

1

,

,..., b

b

b

N

10

Reprezentacje stałoprzecinkowe binarne

c.d.

Przykład:
• liczba binarna 100101 (msb) reprezentuje w
systemie dziesiętnym wartość x:

37

2

1

2

0

2

1

2

0

2

0

2

1

6

6

5

6

4

6

3

6

2

6

1

6







































x

Należy zauważyć, że w przykładzie zastosowano
typ msb, czyli skrajnie leżący bit po lewej stronie
był mnożony przez wagę o najwyższej potędze
(N-1).

11

Reprezentacja dwójkowa znak -

moduł

• Jeden bit w słowie dwójkowym reprezentuje
znak liczby.
• Zerowy bit znaku oznacza wartości dodatnie,
a jedynkowy wartości ujemne.
• Pozostałe bity stanowią moduł tej liczby,
który jest zapisany w reprezentacji binarnej.
• Zazwyczaj stosuje się zapis msb, czyli
skrajnie lewy bit jest bitem znaku.
• Użycie jednego z bitów jako bitu znaku
zmniejsza zakres wartości liczb jakie możemy
reprezentować.

12

Reprezentacja dwójkowa znak – moduł

c.d.

Wartość dziesiętna reprezentacji dwójkowej znak-
moduł jest obliczana na podstawie poniższej
zależności:

































2

0

0

0

1

1

2

2

2

)

1

(

]

2

2

...

2

[

)

1

(

1

1

N

i

i

i

b

N

N

b

b

b

b

b

x

N

N

,gdzie:
• N jest liczbą bitów,
• bity przyjmują tylko dwie
wartości, ze zbioru {0,1}.

0

1

1

,

,..., b

b

b

N

13

Reprezentacja dwójkowa znak – moduł

c.d.

Przykład:
liczba binarna 100101 (msb) reprezentuje w
systemie dziesiętnym wartość x:

5

]

2

1

2

0

2

1

2

0

2

0

[

2

)

1

(

6

6

5

6

4

6

3

6

2

6

1

6











































x

Problem:
00000110 = 6
[phone] = -5
----------------------------
10001011 = -11
• Suma i różnica liczb dwóch liczb tak zapisanych
nie zawsze daje wynik poprawny, wobec czego
trzeba stosować dodatkowe operacje, co jest
niepożądane.

14

Reprezentacja dwójkowa znak–moduł

- ułamki.

Wartość reprezentacji dwójkowej znak-moduł
może reprezentować wartości ułamkowe,
wówczas:



















































2

1

1

0

0

1

1

2

2

2

)

1

(

]

2

...

2

2

2

...

2

[

)

1

(

1

1

M

K

i

i

i

b

K

K

M

M

b

b

b

b

b

b

b

x

M

M

,gdzie:
• M – liczba bitów przed przecinkiem
(reprezentujące wartości całkowite w formacie
znak-moduł),
• K – liczba bitów części ułamkowej,
• K + M – długość słowa.
• Wartości K i M muszą być znane przed
dekodowaniem.

15

Reprezentacja dwójkowa znak–moduł

- ułamki c.d.

Przykład:
Liczba 10010101 jest liczbą zapisaną w kodzie
znak-moduł, w którym dwa bity przeznaczone są
na część ułamkową (M=6, K=2)

Wartość dziesiętna tej liczby wynosi:

25

,

5

]

2

1

2

0

2

1

2

0

2

1

2

0

2

0

[

2

)

1

(

0

2

1

2

6

6

5

6

4

6

3

6

2

6

1

6





























































x

16

Reprezentacja U2

• Powszechnie znana jako reprezentacja
uzupełnienia do dwóch.
• Pierwszy bit pełni funkcję bitu znaku, ale także
jest bitem wartości w przypadku liczby ujemnej.
• Wygodny sposób kodowania z punktu widzenia
sprzętu – możliwość realizacji dodawania i
odejmowania używając tej samej logiki sumatora
sprzętowego.
• Liczby zapisane w kodzie U2 mogą być
wartościami całkowitymi jak i ułamkowymi.

17

Reprezentacja U2 c.d.

Ogólny wzór na wyznaczanie wartości w kodzie
dziesiętnym z kodu U2:























































2

1

1

1

1

0

0

1

1

2

2

1

1

2

2

2

...

2

2

2

...

2

2

M

K

i

i

i

M

M

K

K

M

M

M

M

b

b

b

b

b

b

b

b

x

,gdzie:
• M – liczba bitów przed przecinkiem
(reprezentujące wartości całkowite w formacie
znak-moduł),
• K – liczba bitów części ułamkowej,
• K + M – długość słowa.
• Wartości K i M muszą być znane przed
dekodowaniem.

18

Reprezentacja U2 c.d.

Kodowanie liczb w U2:
• liczby dodatnie są kodowane jak w reprezentacji
znak moduł czyli pierwszym bitem jest zawsze 0, a
pozostałe bity to wartość liczby,
• liczby ujemne kodowane są w sposób
następujący:

– krok 1: kodujemy liczbę przeciwną, czyli moduł z liczby
ujemnej,
– krok 2: negujemy wszystkie bity słowa,
– krok 3: dodajemy wartość 1,
– w wyniku otrzymujemy słowo stanowiące reprezentację
U2 liczby ujemnej.

19

Reprezentacja U2 c.d.

Kodowanie liczb w U2 - przykład:
• Kodowanie liczby -11 przy użyciu 8-bitowego
słowa.

Krok 1: +8 w kodzie U2 to:

00001000

Krok 2: negacja bitów:

11110111

Krok 3: dodanie 1:

+1

Wynik to -8 w U2:

11111000

• Sprawdzenie:

8

2

1

2

1

2

1

2

0

2

1

2

1

2

1

2

)

1

(

8

8

7

8

6

8

5

8

4

8

3

8

2

8

1

8

























































x

20

Reprezentacja U2 - problemy

Dodawanie liczb w U2 o różnych długościach słowa

(przykład):
• Należy dodać liczbę -3 (zapisaną na 4 bitach) do

liczby 15 (zapisaną na 8 bitach).

+15 w U2:

00001111

-3 w U2:

+1101
--------------

= 00010010 (+20 – błędny wynik!!)

• Rozwiązanie problemy to stosowanie rozszerzenia bitowego dla

liczby o mniejszej długości słowa:

+15 w U2:

00001111

-3 w U2: 11111101 (rozszerzenie to uzupełnienie)

-------------- (liczby bitami o wartości bitu

znaku)

= 100001100 ( +12, gdyż bit przeniesienia

jest

ignorowany)

21

Zakres dynamiki liczb dwójkowych

Zakres dynamiki jest określany jako stosunek

największej możliwej wartości słowa do najmniejszej

możliwej wartości słowa, wyrażony w decybelach:

)

_

_

_

_

_

_

(

log

20

_

10

slowa

dlugosc

mozliwa

a

najmniejsz

slowa

dlugosc

mozliwa

najwieksza

dynamiczny

zakres





Dla całkowitej długości słowa dwójkowego ze

znakiem, wynoszącej b+1 bitów (jeden bit znaku i b-

bitów wartości), zakres dynamiczny w decybelach

jest określany:

)

1

2

(

log

20

)

1

1

2

(

log

20

_

10

10















b

b

dB

dynamiczny

zakres

22

Zakres dynamiki liczb dwójkowych

c.d.

W przypadku, gdy : , wówczas:

• Zakres dynamiki liczb dwójkowych jest wprost

proporcjonalny do długości słowa.
• Dla ośmiobitowego słowa w U2, z siedmioma

bitami dostępnymi dla wartości sygnału:

Zakres_dynamiczny = 6,02 * 7 = 42,14 [dB]

• Często przyjmuje się uproszczenie, zakładające, że

zakres dynamiczny jest równy „6dB/bit”

]

[

02

,

6

)

2

(

log

20

)

2

(

log

20

_

10

10

dB

b

b

dynamiczny

zakres

b

dB

















1

2 

b

23

Skończona długość

stałoprzecinkowego słowa – skutki.

• Skończony zbiór reprezentowanych wartości.
• Zwiększenie szumu tła w technikach widmowych.
• Nieidealne odpowiedzi filtrów cyfrowych.
• Powstawanie szumu w wartościach wyjściowych
przetworników analogowo - cyfrowych.
• Prowadzi często do niedokładnych wyników
arytmetycznych.
• Powyższe skutki są znane i muszą być
eliminowane.

24

Reprezentacje zmiennoprzecinkowe

binarne

• Umożliwiają zwiększenie precyzji oraz dynamiki w
stosunku do reprezentacji stałoprzecinkowych.
• Występuje w nich podział słowa na dwie części:

– mantysa m,
– wykładnik e.

• Mantysa oraz wykładnik mogą być liczbami
ujemnymi jak i dodatnimi.
• Ogólna postać liczb zmiennoprzecinkowych
binarnych jest wyrażona wzorem:

e

m

n

2





25

Reprezentacje zmiennoprzecinkowe

binarne c.d.

• Istnieje kilka formatów reprezentacji

zmiennoprzecinkowych, różniących się długością

mantys i wykładników, a także sposobem ich

kodowania, np.:

– IEEE P754 Format,
– IBM Format,
– DEC Format,
– MIL-STD 1750A Format.

• Zazwyczaj stosuje się normalizację,

umożliwiającą wykorzystanie pełnego zakresu

dynamicznego mantysy.
• Normalizacja polega na przesuwaniu bitów

mantysy tak aby pierwszym bitem była jedynka i

dopasowaniu następnie wykładniku.
• Zazwyczaj jedynka, będąca pierwszym bitem, jest

ukryta, występuje umownie poza zakresem.

26

Reprezentacje zmiennoprzecinkowe

binarne – standard IEEE P754

• Najpopularniejszy ze standardów

zmiennoprzecinkowych.
• Słowo bitowe składa się z bitu znaku, wykładnika,

ułamka.
• Wykładnik e jest 8 bitową liczbą w reprezentacji z

przesunięciem.
• Ułamek f to liczba 23 bitowa zapisana w kodzie

znak-moduł z bitem ukrytym.
• Bit znaku S jest skrajnym lewym bitem, po którym

jest 8 bitów wykładnika i następnie 23 bity ułamka.
• Wartość dziesiętna liczby jest obliczana z

zależności:

127

754

2

,

1

)

1

(











e

S

IEEEP

f

wartosc

27

Zakres dynamiki liczb

zmiennoprzecinkowych

Jest elementem bardzo złożonym bowiem zależy od

następujących czynników:
• pozycji kropki dwójkowej,
• czy bit ukryty jest używany, czy nie,
• wartości podstawy reprezentacji liczby

zmiennoprzecinkowej,
• typu kodowania wykładnika i ułamka,
• sposobu traktowania ułamków nieunormowanych,
• sposobu traktowania wykładników, gdy są tylko

jedynkami lub tylko zerami.

28

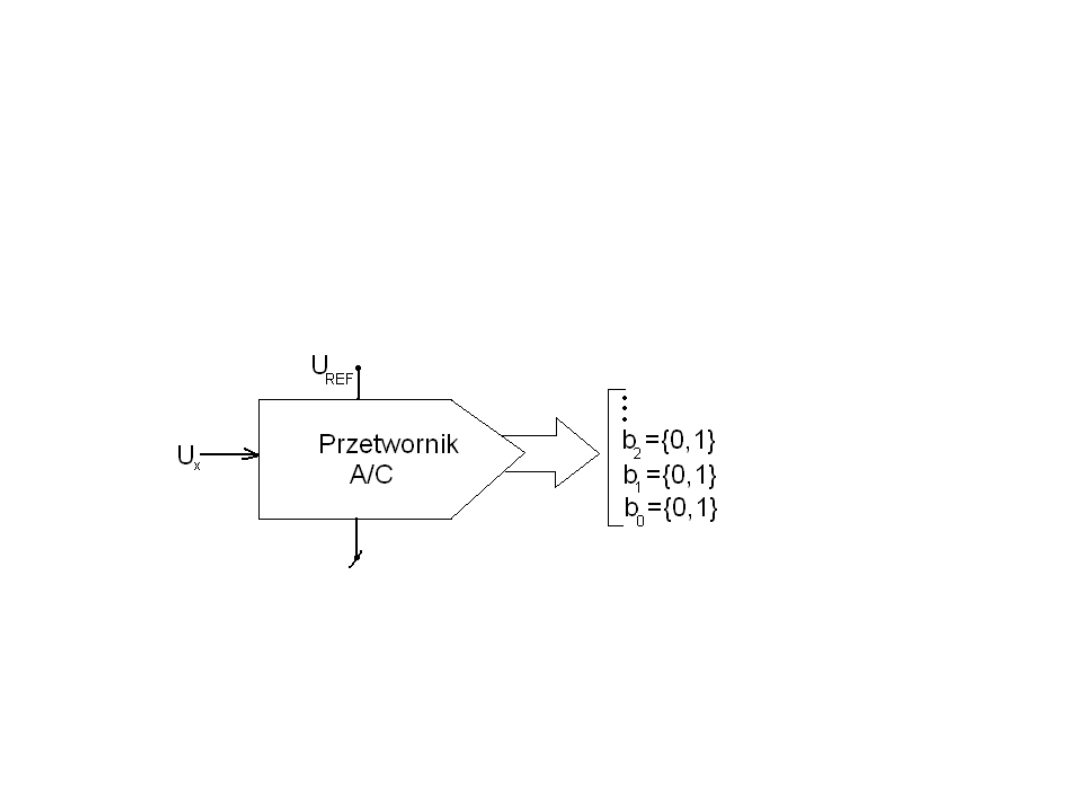
Przetworniki A/C

• Przetwornik A/C (analogowo-cyfrowy), jest

układem elektronicznym mającym jedno wejście, na

które jest podawany sygnał analogowy, oraz n

wyjść, na których pojawia się informacja cyfrowa o

sygnale wejściowym.

• Przetworniki A/C zamieniają wejściowe napięcie

analogowe na odpowiadającą mu liczbę całkowitą ze

znakiem, zapisaną na określonej ilości bitów.

29

Przetworniki A/C c.d.

•Zazwyczaj przetwornik A/C posiada 2 sygnały

wejściowe:

– sygnał mierzony,
– sygnał referencyjny.

• Można przyjąć, że liczba uzyskana na wyjściu,

stanowi numer przedziału kwantowania.
• Można je podzielić ze względu na:

– długość słowa wyjściowego (ilość bitów wyjścia np.:

8-bitowe, 12-bitowe, 16-bitowe itd..),
– budowę wewnętrzną i sposób uzyskiwania wartości

wyjściowej.

30

Przetworniki A/C c.d.

Przykładowe typy przetworników A/C (

różnią się

budową i sposobem uzyskiwania wartości

wyjściowej

):

• bezpośredniego porównania,
• kompensacyjne równomierne,
• kompensacyjne wagowe,
• typu sigma-delta,
• całkujące,

– najczęściej podwójnie całkujący.

31

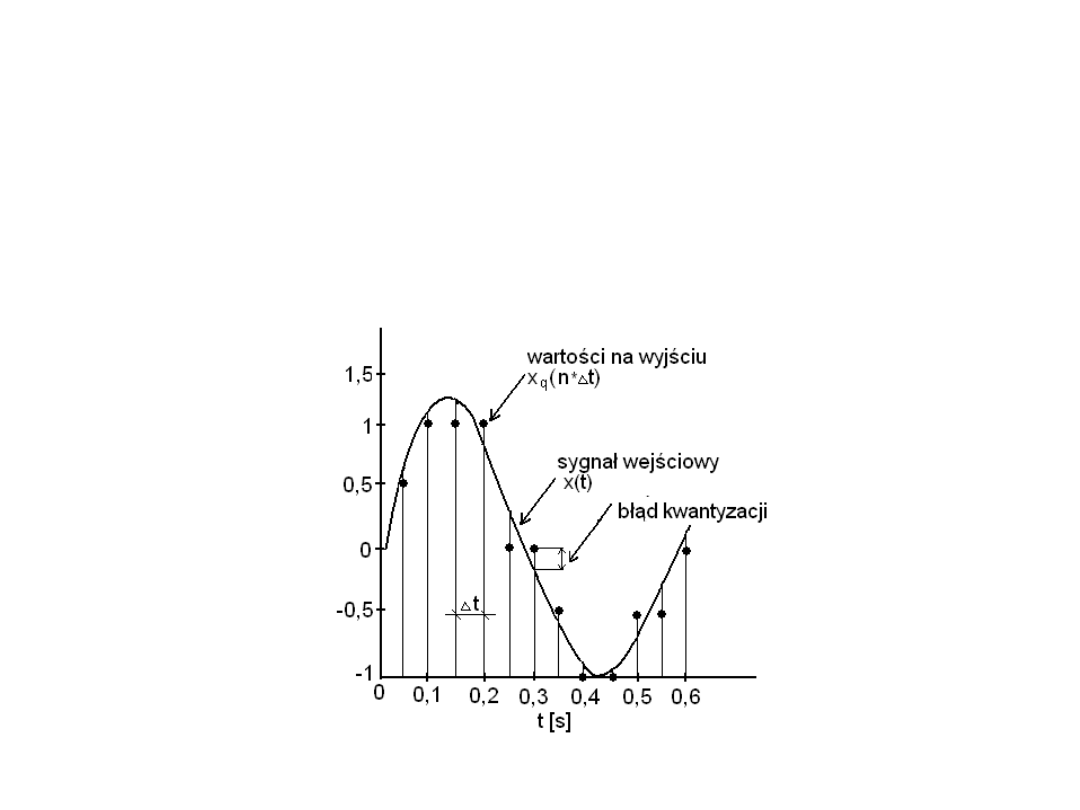
Przetworniki A/C – błędy kwantyzacji

• Błędem kwantyzacji nazywamy różnice pomiędzy

wartością sygnału na wejściu przetwornika,

wartością uzyskiwaną na wyjściu przetwornika.

32

Przetworniki A/C – błędy kwantyzacji

• Maksymalny błąd kwantyzacji określany jest jako,

połowa najmniejszej wartości jaką można uzyskać

na wyjściu danego przetwornika A/C (lsb):

slowa

dlugosc

MAX

napiecia

zakres

caly

lsb

kwant

blad

_

2

_

_

2

1

2

1

_









• Błąd kwantyzacji wynika ze skończonego zbioru

wartości jaki możemy uzyskać na wyjściu

przetwornika.
• Błąd kwantyzacji nie występuje jedynie, gdy

podawany na wejście przetwornika A/C sygnał jest

wielokrotnością wartości lsb danego przetwornika.
• Charakterystyka wartości błędów kwantyzacji w

czasie nazywany jest szumem kwantyzacji.

33

Współczynnik SNR

• Współczynnik SNR jest to stosunek sygnału

wejściowego do szumu.

• Charakteryzuje jakość sygnału wyjściowego.
• Pozwala ocenić użyteczność procesu

przetwarzania lub urządzenia.

szumu

moc

sygnalu

moc

SNR

_

_



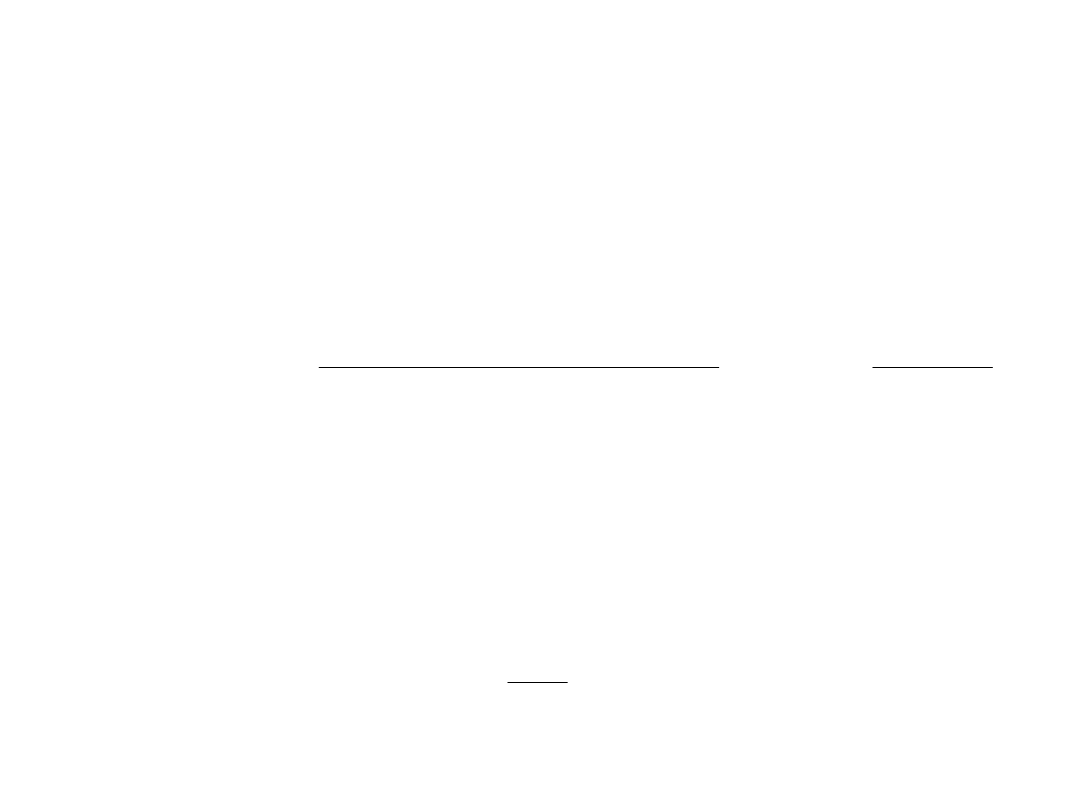
34

Współczynnik SNR c.d.

• Szum kwantyzacji jest przypadkowy, więc nie

można jawnie reprezentować poziomu jego mocy,

ale można użyć statycznego odpowiednika wariancji,

aby wyznaczyć współczynnik SNR wyrażony w dB.

• Zakładamy, że jest to przetwornik b-bitowy o

maksymalnym napięciu Vp (zakres sygnału

wejściowego wynosi 2Vp).
• Szum kwantyzacji wyznaczamy względem napięcia

Vp, wobec czego pojedynczy poziom kwantyzacji q

wynosi:

)

(

log

10

)

_

_

_

_

_

(

log

10

2

/

_

2

10

10

/

C

A

szumu

sygnalu

C

A

AC

kwant

szumu

wariancja

wej

sygnalu

wariancja

SNR













b

p

V

q

2

2



35

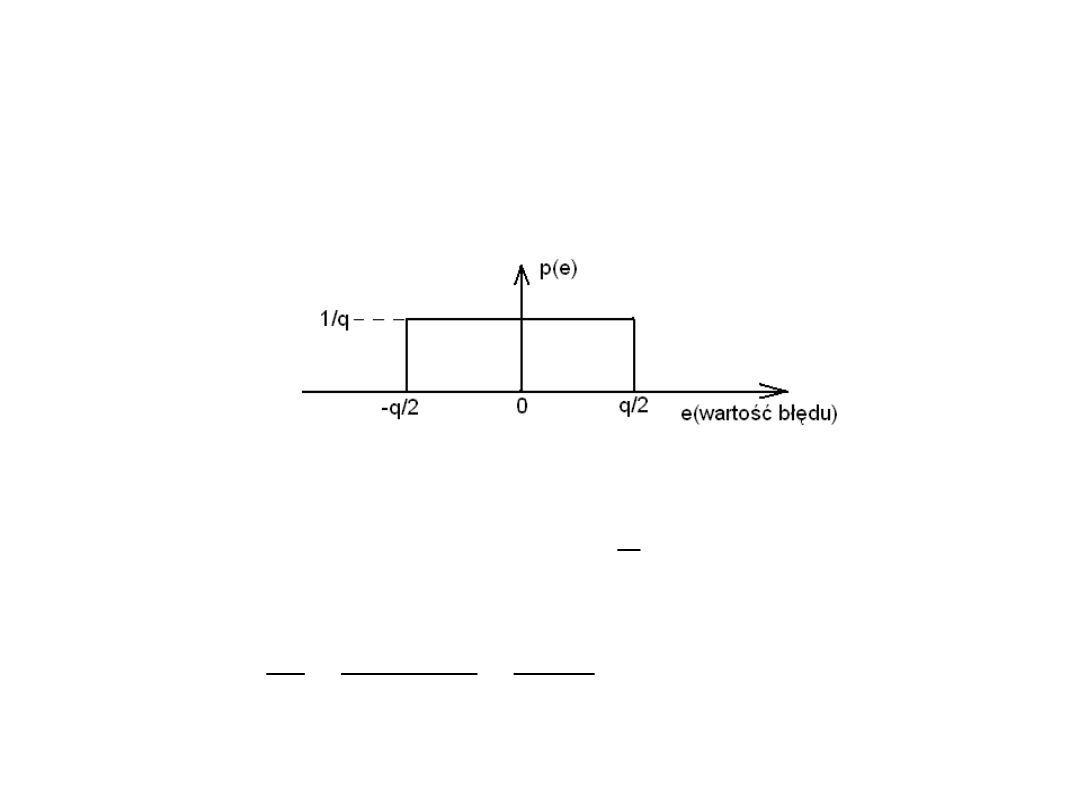
Współczynnik SNR c.d.

• Funkcja gęstości prawdopodobieństwa pojawienia

się dowolnej wartości błędu kwantyzacji p(e) na

postać:

 

b

p

b

p

q

q

q

q

C

A

szumu

V

V

q

ds

e

q

de

e

p

e

2

2

2

2

2

2

2

/

2

/

2

/

2

/

2

2

2

/

_

2

3

)

2

(

12

2

12

1

)

(





























• Obliczamy, więc wariancję szumu:

36

Współczynnik SNR c.d.

• Znając wartość wariancji szumu kwantyzacji,

należy z kolei określić wariancje sygnału

wejściowego.
• Najpierw wprowadzamy pojęcie współczynnika

obciążenia LF zależnego od wartości skutecznej

sygnału:

P

sygnalu

P

V

V

wej

sygnalu

rms

LF







_

_

• Stąd możemy określić wariancję szumu:

2

2

2

)

(

P

sygnalu

V

LF





37

Współczynnik SNR c.d.

• Znając zarówno licznik jak i mianownik

zależności określającej SNR otrzymujemy:

)

(

log

20

77

,

4

02

,

6

)]

2

3

(

)

[(

log

10

)

)

2

3

/(

)

(

(

log

10

10

2

2

10

2

2

2

2

10

LF

b

LF

V

V

LF

SNR

b

b

P

P

AC





























• Możemy teraz określić maksymalny

współczynnik SNR, określamy go przy założeniu,

że wartość amplitudy sygnału wejściowego jest

równa:

2

1

2

/

_





P

P

skali

calej

V

V

LF

38

Współczynnik SNR c.d.

• Wyznaczamy maksymalny współczynnik SNR:

]

[

76

,

1

02

,

6

_

/

dB

b

SNR

MAX

C

A







• Współczynnik SNR dla przetworników A/C

wyrażony w dB jest wprost proporcjonalny do

ilości bitów słowa uzyskiwanego na wyjściu

przetwornika.
• Należy pamiętać o odpowiednim wysterowaniu

przetwornika:

– zalecane jest wysterowanie przetwornika do

pewnego poziomu poniżej wartości maksymalnej,
– przesterowanie przetwornika powoduje wzrost

szumu, a tym samym gwałtowny spadek wartości

współczynnika SNR.

39

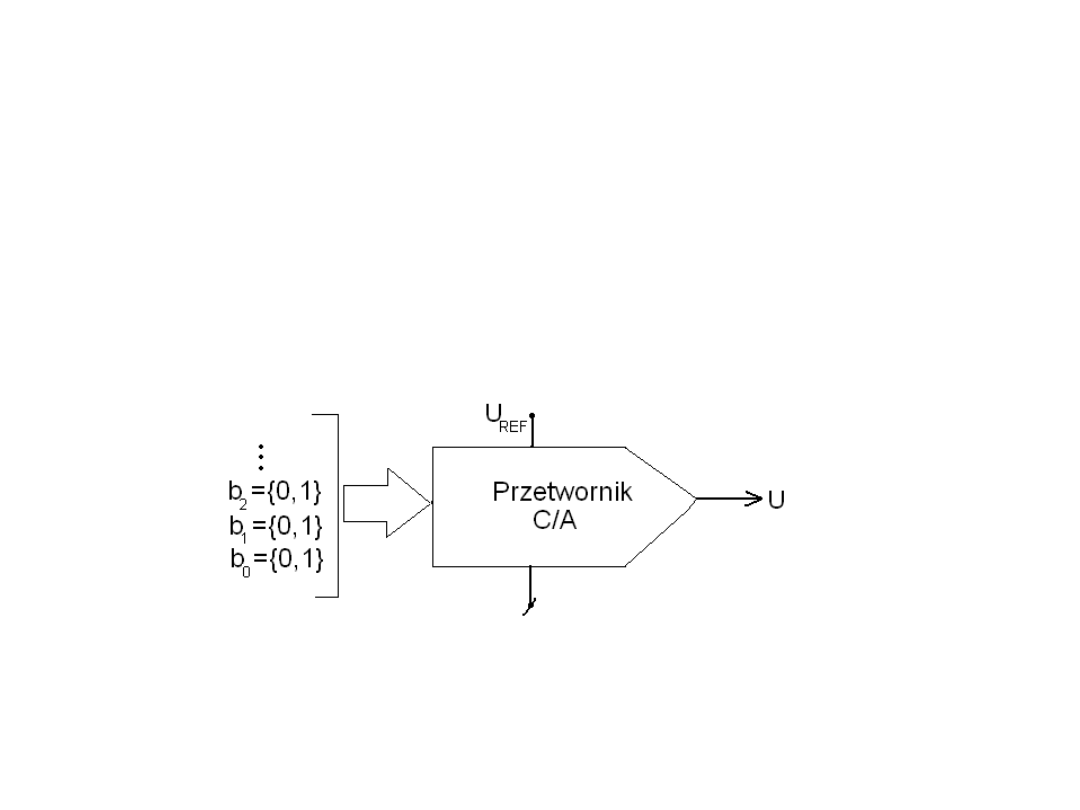
Przetworniki C/A

• Przetwornik C/A (cyfrowo – analogowy) jest

układem elektronicznym o n wejściach, do których

doprowadzane jest n - bitowe słowo cyfrowe, będące

informacją przetwarzaną, oraz o jednym wyjściu, na

którym jest otrzymywana przetworzona informacja

analogowa.

40

Przetworniki C/A

• Przetworniki C/A zamieniają liczbę całkowitą ze

znakiem, zapisaną na n – bitach, na analogowe

napięcie wyjściowe.
• Przetworniki C/A są charakteryzowane przez

następujące parametry:

– rozdzielczość, wyrażona w woltach, jest to

najmniejsza wartość

zmiany napięcia wyjściowego,

– błąd bezwzględny, wyrażona w woltach, jest największą

różnicą między napięciem wyjściowym zmierzonym a

idealnym,
– błąd względny jest błędem odniesionym do całej skali

przetwornika,
– często błąd względny odnosi się do rozdzielczości.

41

Przetworniki C/A

• Przetworniki C/A ze względu na sposób

uzyskiwania napięcia wyjściowego dzielimy na:

– z przełączaniem prądowym,
– z przełączaniem napięciowym.

• Istotne parametry charakteryzujące przetworniki

C/A (opracowanie sprzętowe):

– stałość charakterystyki przy zmianach temperatury i

zasilania,
– czas ustalania się odpowiedzi będący opóźnieniem

uzyskania sygnału analogowego na wyjściu względem

zmiany na wejściu cyfrowym,
– przepięcia będące wyskokami wartości napięcia

wyjściowego w czasie ustalania odpowiedzi.