Poruszające się ciało traktujemy jako

punkt materialny a wtedy możemy
opisać jego ruch a co więcej
konstruować równania ruchu

Kinematyka punktu
materialnego

Mając układ współrzędnych i przyjmując, że

ciała są punktami materialnymi (koncepcja
środka masy) możemy opisać ich ruch.
Będzie to oznaczało, że w każdej chwili
czasu mamy dane położenie prędkość i
przyspieszenie. Poruszające się ciało będzie
wykonywać obroty (oczywiście wokół środka
masy) ale to już zupełnie inna historia czyli
kinematyka i dynamika ruchu obrotowego

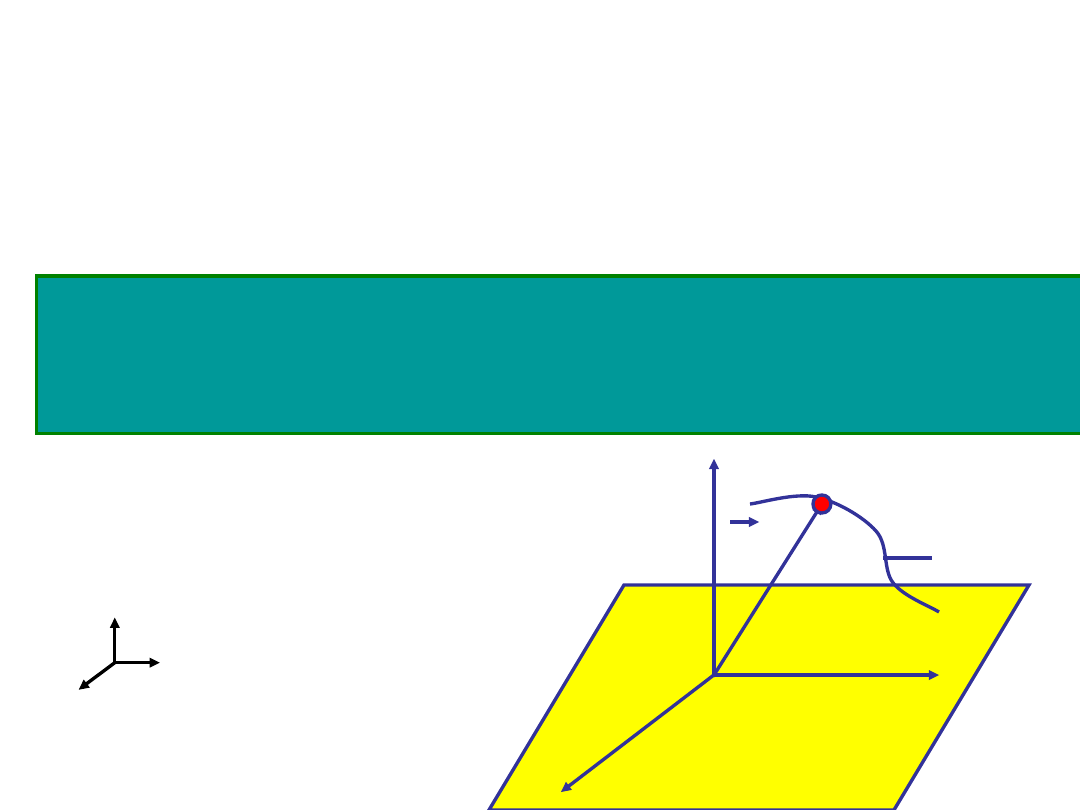
Jeżeli położenie punktu zmienia się

w czasie to
w układzie współrzędnych
prostokątnych
ruch ten możemy opisać w
następujący sposób

)

)

(

ˆ

)

(

ˆ

)

(

ˆ

)

(

t

z

k

t

y

j

t

x

i

t

r









ˆk

ˆi

ˆj

Zakładamy, że układ jest prawoskrętny
ale może nie być : )

tor ruchu

x

y

r(t)

P(x(t),y(t),z(t))

Wersory możemy zapisywać na różne sposoby.
W trakcie ćwiczeń używać będziemy wersji
trzeciej.

x, y i z są współrzędnymi kartezjańskimi.
Współrzędne punktu P możemy również
zapisać we współrzędnych sferycznych.

k

k

i

z

j

j

i

y

i

i

i

x

z

y

x

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

0

0

0









































cos

sin

sin

cos

sin

r

z

r

y

r

x







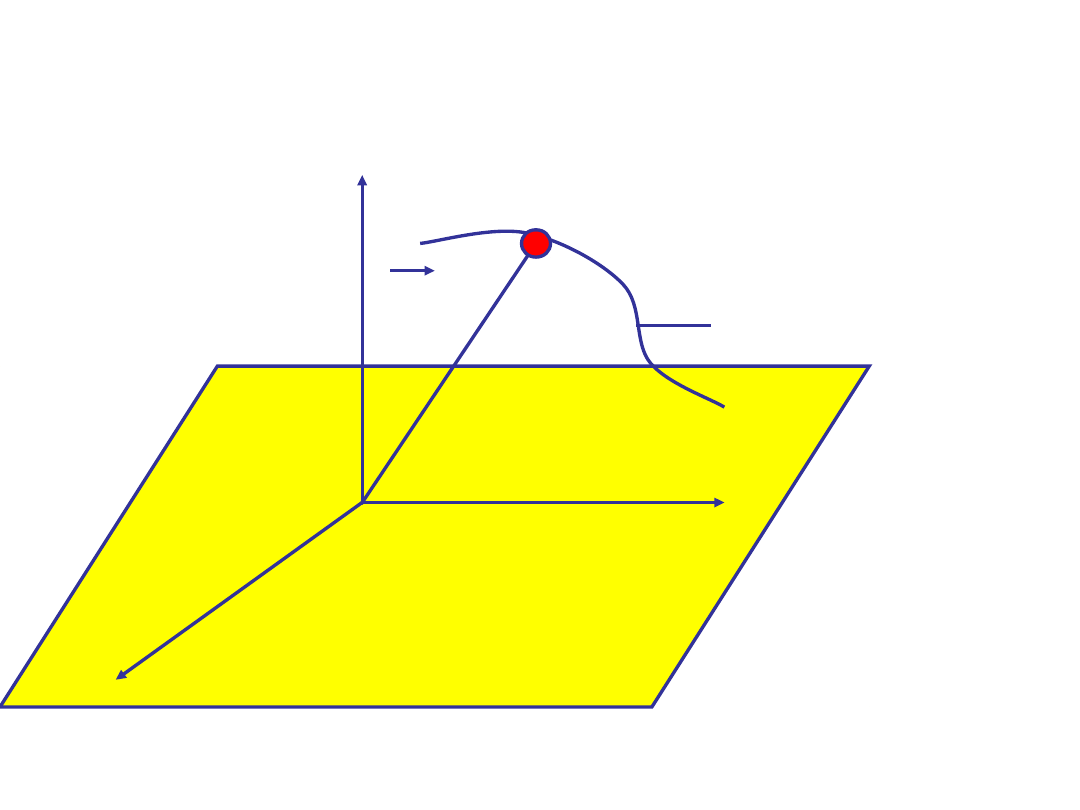
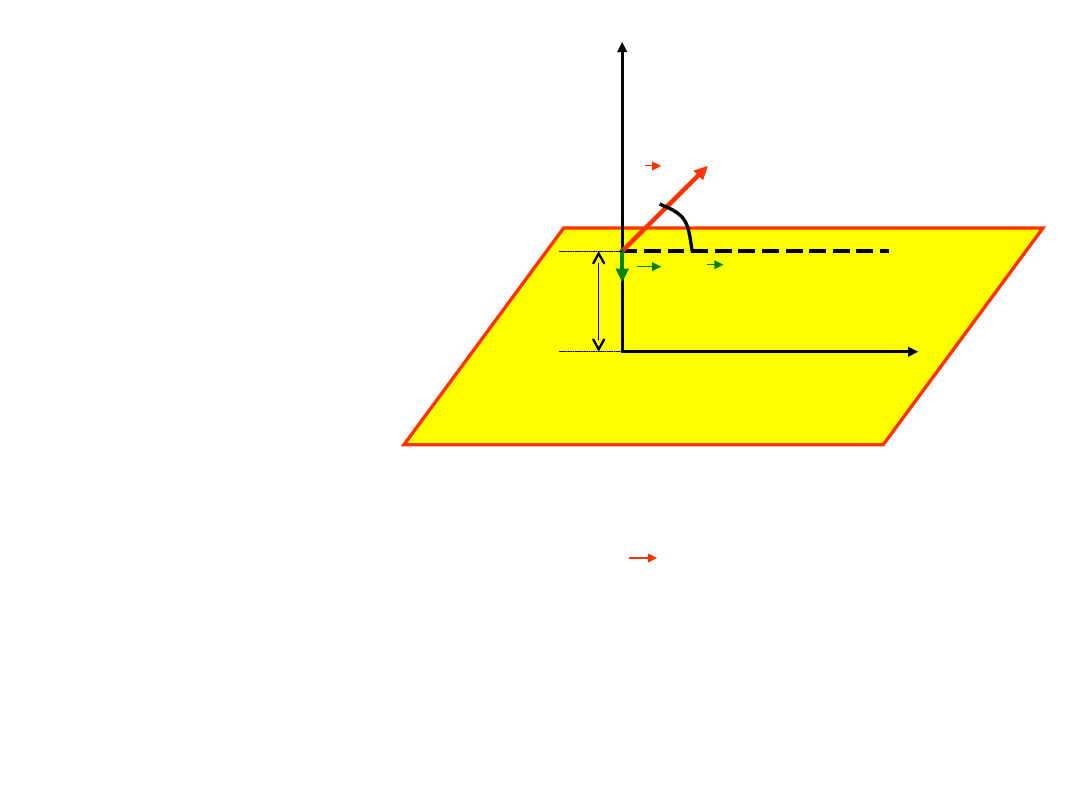
W zależności od tego, czy tor jest linią krzywą
czy prostą, mówimy o

ruchu krzywoliniowym

lub

prostoliniowym.

P(x(t),y(t),z(t))

z

tor

x

y

r(t)

.

Prędkość i przyśpieszenie

jako pochodna

wektora położenia

i prędkości

Interesuje nas prędkość jakiegoś ciała w
konkretnym punkcie P. W jaki sposób możemy ją
obliczyć?

r

1

r

2

r

3

P

1

P

2

P

3

P

x

y

z

r

r

1

r

3

r

2

t

1

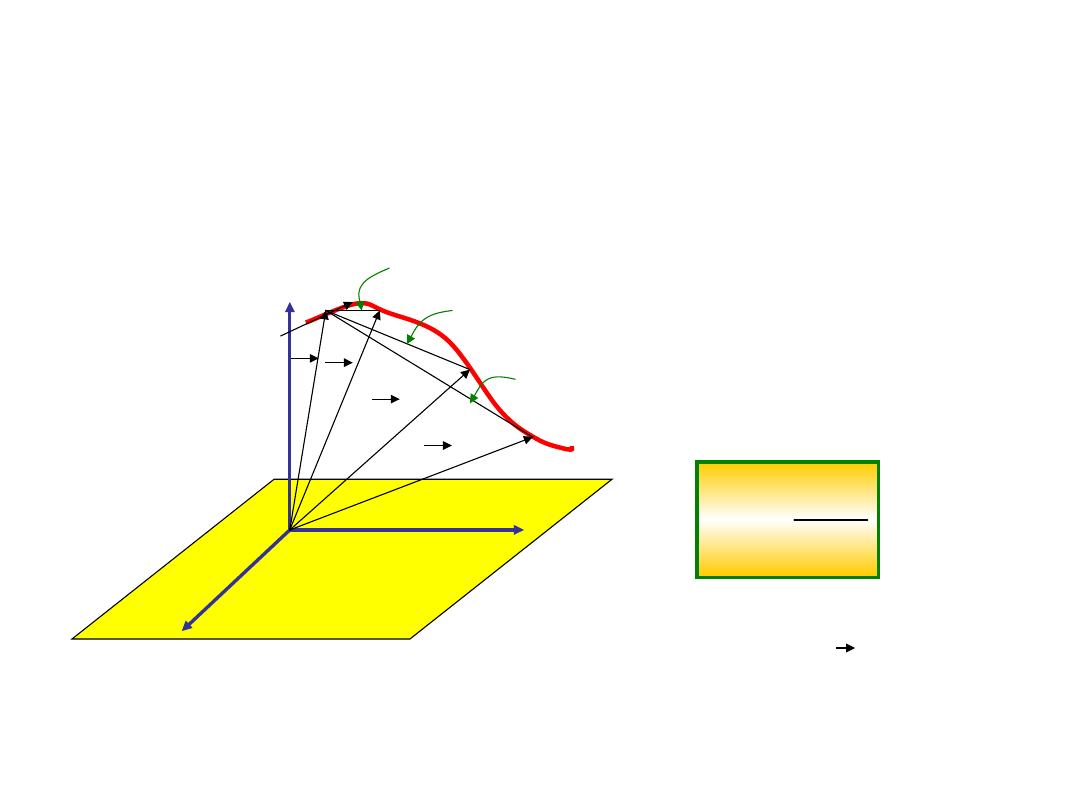
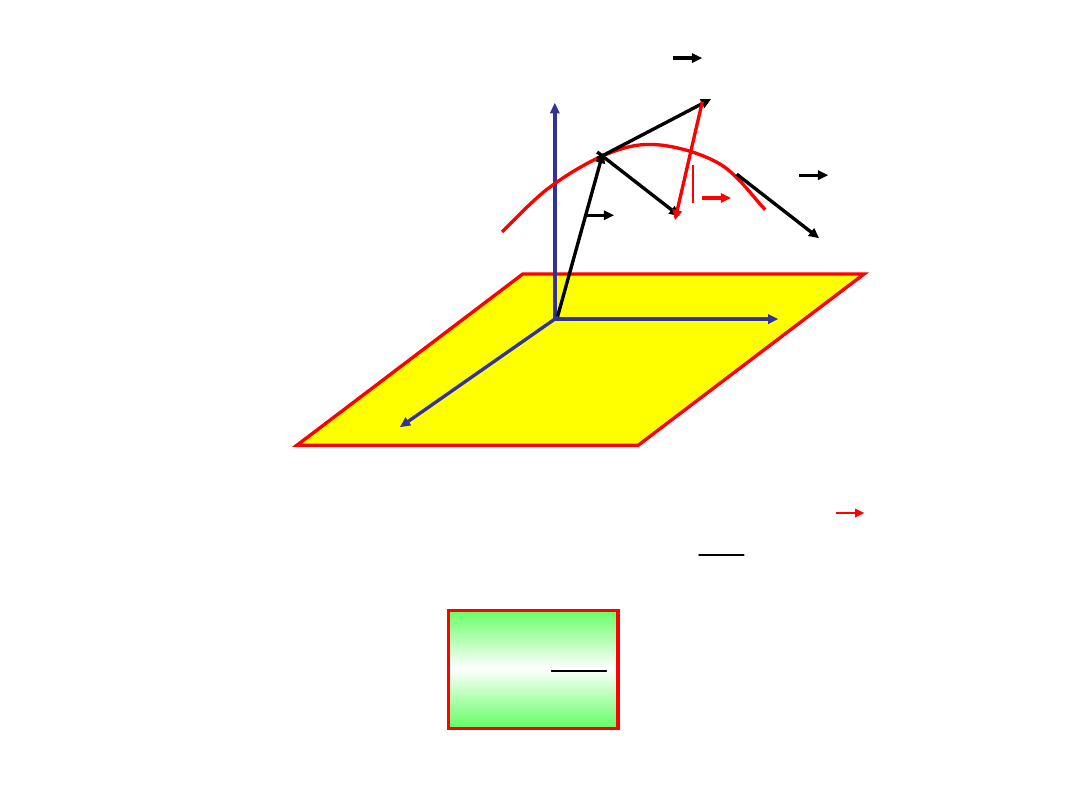
Zacznijmy skracać odstępy
czasu w których określamy
położenie ciała.
Każdorazowo konstruujemy
wektor prędkości średniej

n

n

n

t

r











v

Gdy skracamy
nieograniczenie

odstęp czasu t  0, wartość bezwzględna wektora

r / t dąży do

pewnej wartości granicznej.

z

v

1

x

y

tor

P

1

P

2

v

2



v

r

1

Z rysunku widzimy, że w stosunku do
punktu P

1

w punkcie P

2

nastąpiła zmiana

prędkości

w czasie t.

Średnie

przyśpieszenie definiujemy jako

:

t

a

śr







v



v



Ruch prostoliniowy

Jeżeli tor ruchu ciała jest linią prostą, to
zawsze możemy tak dobrać układ
współrzędnych, aby jedna z jego osi
pokrywała się z torem. Zwykle wybiera się oś
x.

x

r

x

i

t

x

t

x

t

r

ˆ

)

(

)

(

)

(











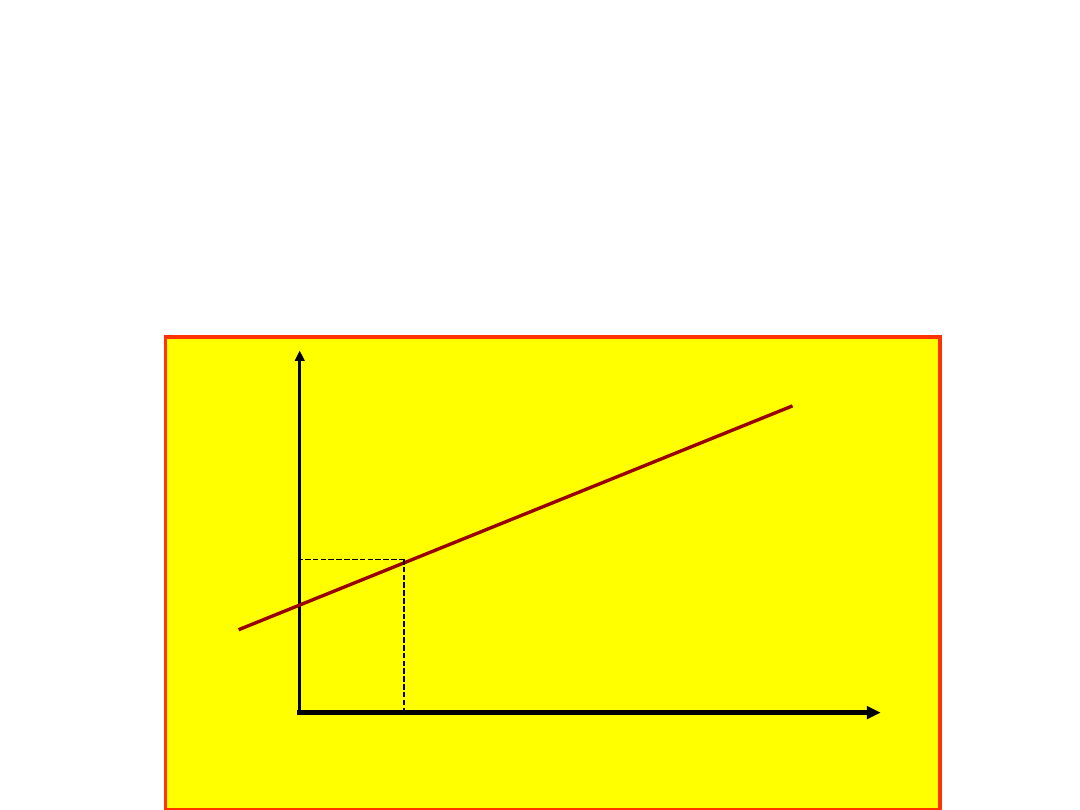
Ruch jednostajny

Ruch jednostajny, jest to taki ruch, w którym
prędkość jest stała, v=const.

.

x jest przebytą przez ciało drogą, którą zwykle
oznaczaliśmy przez s. Wykres drogi od czasu
ma więc postać:

s

t

x=x

0

+

v(t

-t

0

)

t

0

x

0

Ruch jednostajnie zmienny jest to ruch ze
stałym przyśpieszeniem a = const. Gdy a > 0
ruch nazywamy przyśpieszonym, a gdy a < 0
ruch jest opóźniony.

Ruch jednostajnie

zmienny

W celu wyliczenia prędkości z jaką porusza się ciało
musimy rozwiązać równanie:

nie martwcie się to dla

Orłów

)

t

(t

a

v

v

dt

a

dv

dt

a

dv

0

0

t

t

v

v

0

0



















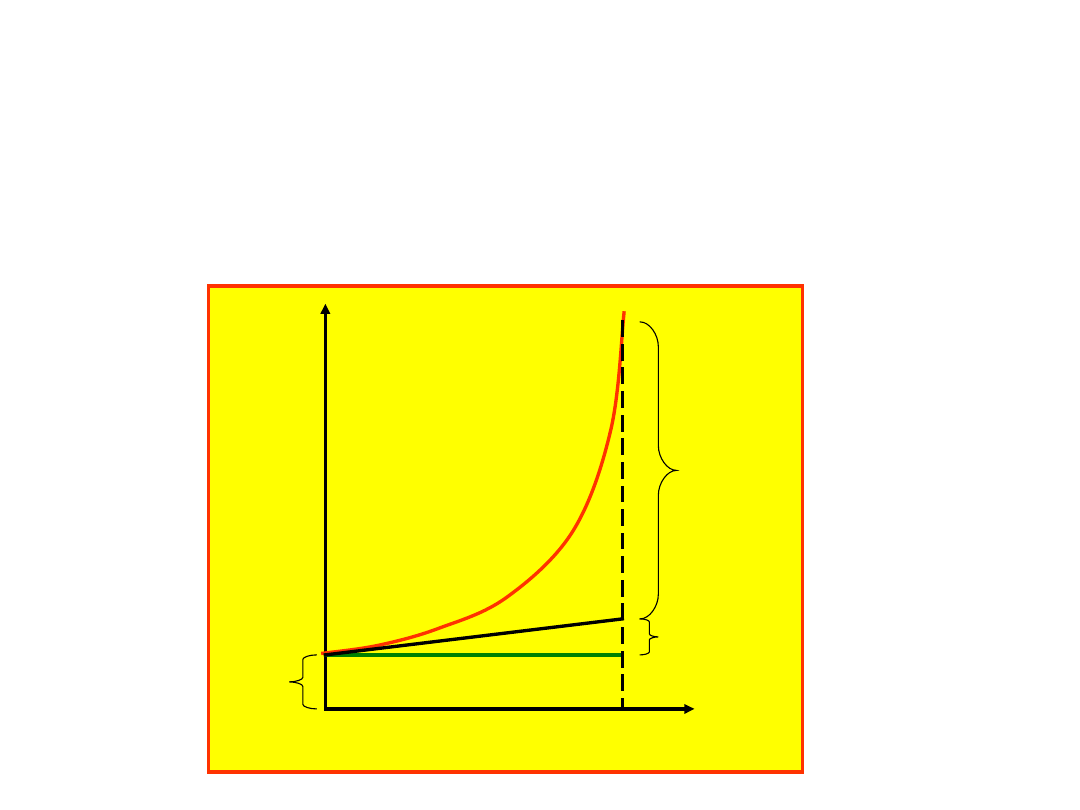
t

s=x

x

0

v

0

t

1/2at

2

Narysujmy drogę
którą ciało przebywa w czasie t
przy założeniu, że t

o

= 0.

x

y

g = -g i

y

v

0

h



W polu ciężkości na wysokości h
wyrzucamy pod kątem  do poziomu z

prędkością

v

0

jakieś ciało.

Możemy tu rozróżnić następujące przypadki:

Rozważmy
następujący ruch.

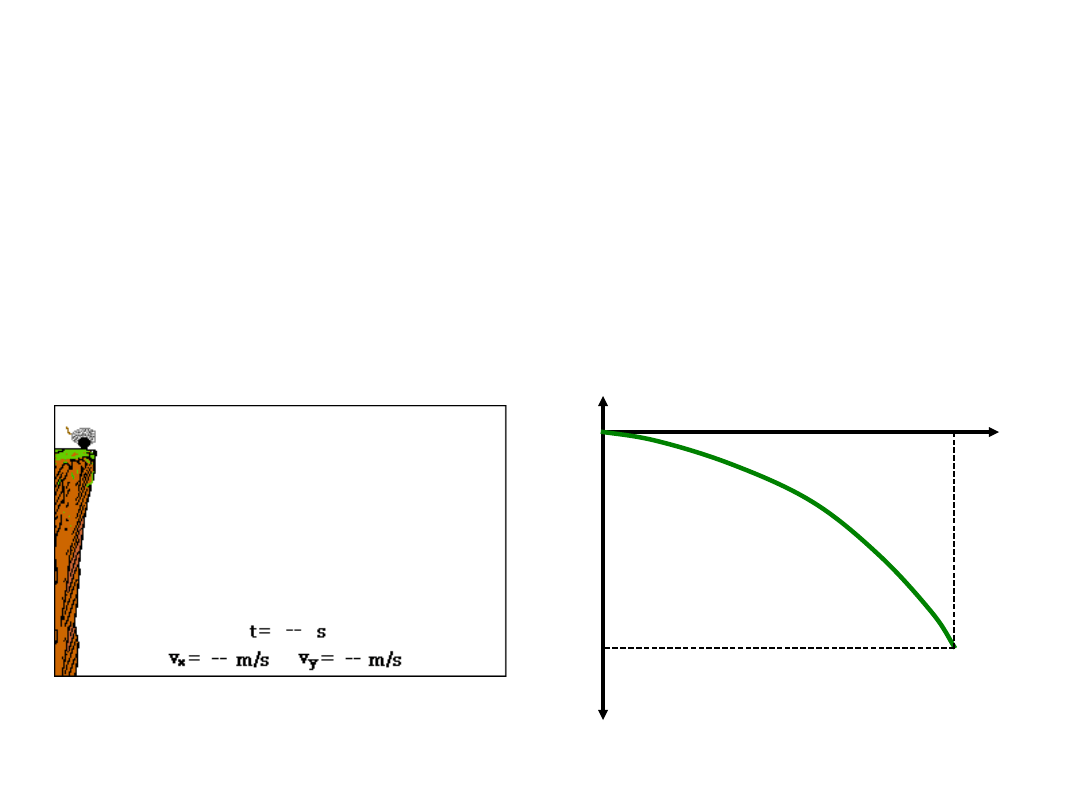
Rzut poziomy

Rzut ten jest przypadkiem 2 w Tabeli 1.

Zajmijmy się następującym problemem. Kula
armatnia została wystrzelona poziomo ze stałą
prędkością v

0x

=100 m/s. Kula spadła na ziemię

w odległości 1200 m od miejsca wystrzelenia .
Pytamy się o długość drogi pionowej jaką
przebyła kula przy zaniedbaniu oporu
powietrza.

x

y

x = 1200 m

y = ?

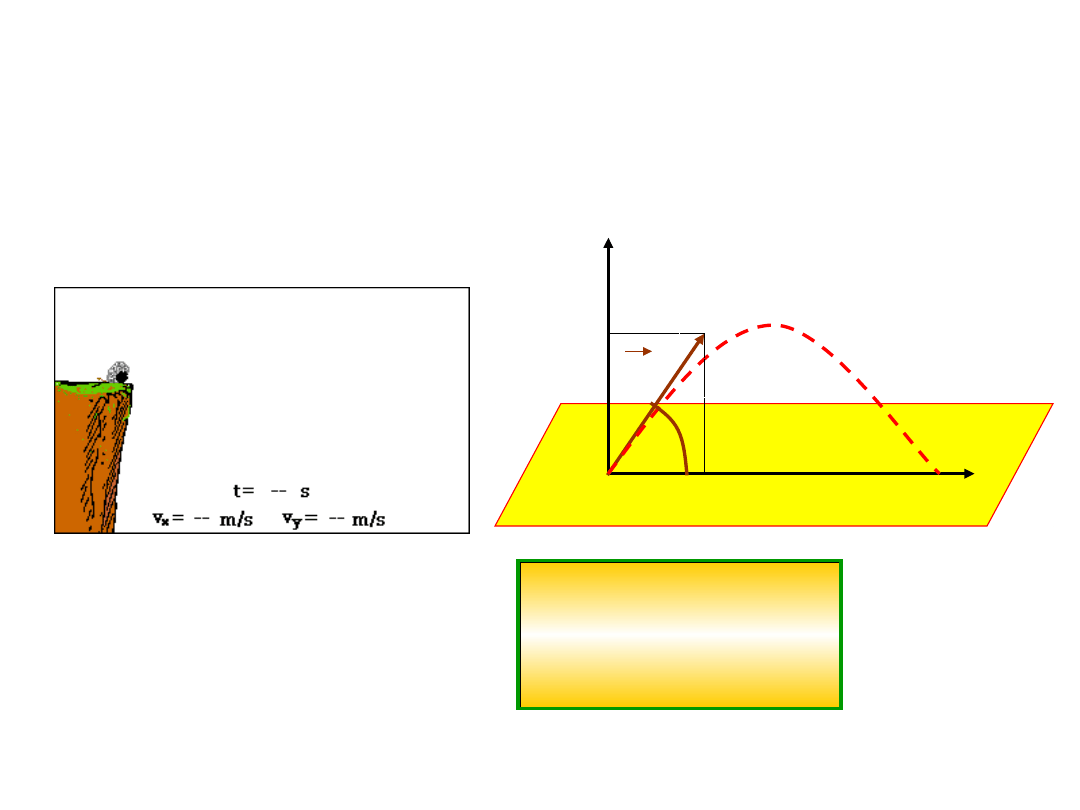
Rzut
ukośny

Jest to przypadek, dla którego:

h = 0 lub h  0, 0 <  < 90

0

, v

0

 0.

y

x

v

0



Składowe prędkości
początkowej
wynoszą:

sinθ

v

v

cosθ

v

v

0

0y

0

0x





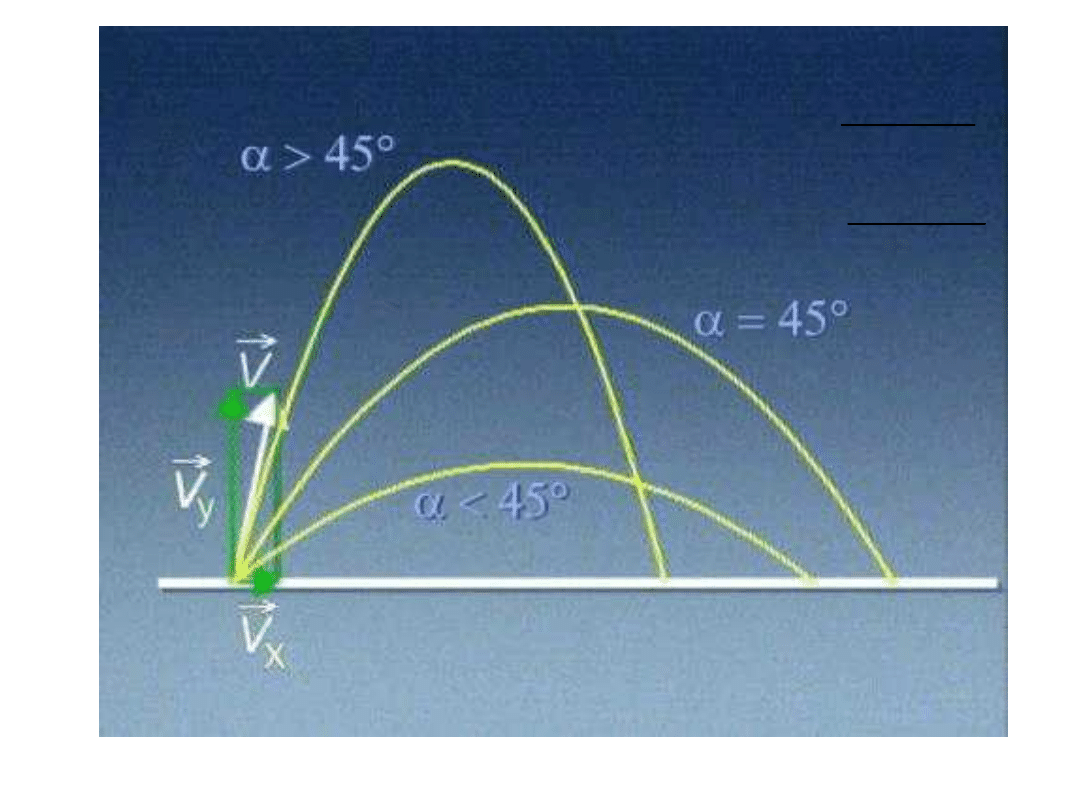
Wysokość rz.:

g

y

2

sin

v

2

2

0

max





Zasięg rz.:

g

x



2

sin

v

2

0

max



Tor ruchu

przedstawia

przesunięta parabola

Rzut ukośny

Należy jeszcze wspomnieć o szczególnym
przypadku rzutu ukośnego, a mianowicie

rzutu pod kątem  = 90

0

z prędkością

początkową v

0

. Taki przypadek nazywamy

rzutem pionowym

.

v

0

v = g
t

Przebywana w czasie t
droga wynosi:

2

0

2

1

gt

t

v

s





Maksymalną wysokość
uzyskamy z warunku

0

v

0







gt

dt

ds

.

Czas ruchu ciała do maksymalnej wysokości h
wynosi więc:
, a uzyskana maksymalna wysokość
.

g

t

0

v



g

h

2

v

2
0



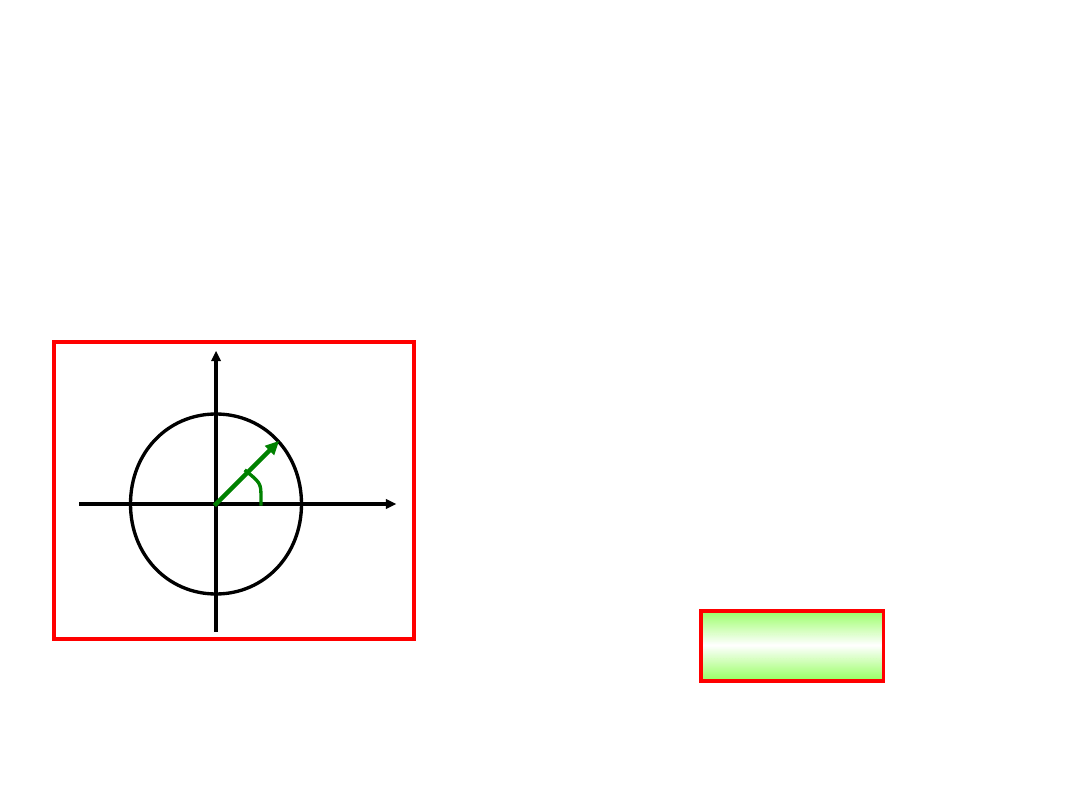
Ruch jednostajny po
okręgu

Początek układu współrzędnych wybieramy w środku
koła, po którym odbywa się ruch. Położenie punktu
na na kole możemy podać jednoznacznie przez
podanie kąta biegunowego  i odległości r od

początku układu.

y

x

r



s

Ruch ciała określony jest
przez funkcję

 = (t),

definiująca tzw. drogę
kątową.

Jeśli przez s oznaczymy
drogę, którą ciało przebyło
po okręgu w czasie gdy
przebyło ono drogę kątową
, to

r

s







Różniczkując to równanie obustronnie,
otrzymujemy;

.