1

Value at risk
przypadek hrabstwa
Orange

Philippe Jorion's

Orange County Case:

Using Value at Risk

to Control Financial Risk

2

Value at risk



Celem prezentacji jest wyjaśnienie w jaki sposób władze hrabstwa Orange

w Kaliforni straciły na rynku finansowym $1.6 billiona na rynku

finansowym.



Case również prezentuje "Value at Risk" (VAR) wartości zagrozonej, która

jest prostą metodą pomiaru ryzyka na rynku finansowym.



Metoda VaR została wprowadzona do systemu finansowego w wyniku

wielu przypadków niepowodzeń na rynku instytucji inwestujących w

instrumenty pochodne



Case ilustruje jak możnaby było wykorzystać VaR do ochrony portfela

inwestycyjnego utrzymywanego przez hrabstwo



This Web case can be used by academic institutions free of charge;

other users should contact Professor Jorion.

The case is also subject to continuous improvements.

© 2008- Philippe Jorion

3

Value at risk – case
Orange County



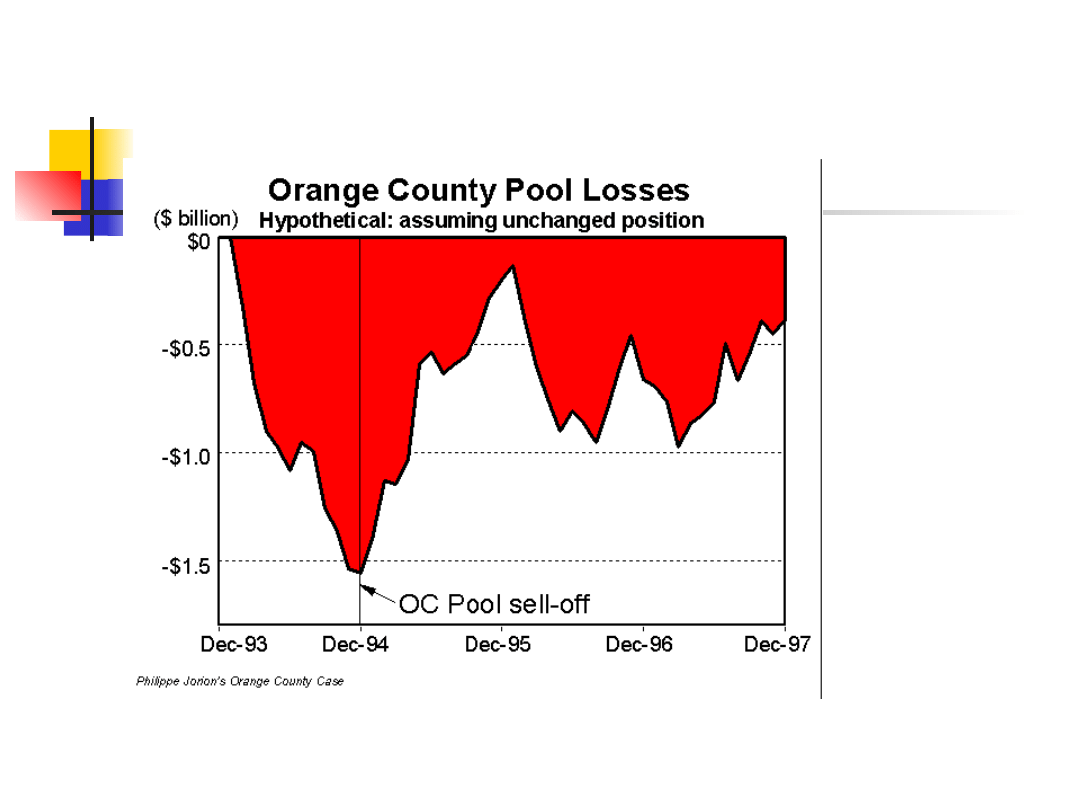
Grudzień 1994 – Orange County zaskoczył rynek informacją,

zainwestowane przez nich środki przyniosły stratę 1,6 mld

USD.



Była to największa strata zanotowana w inwestycjach

prowadzonych przez rządy lokalne w USA i doprowadziła

wkrótcer do bankructwa lokalnych funduszy.



Strata była efektem działalności Boba Citrona – skarbnika

hrabstwa, który do inwestycji wykorzystał ok. 5,7 mld USD

przeznaczonych na cele szkół, miast samego hrabstwa.



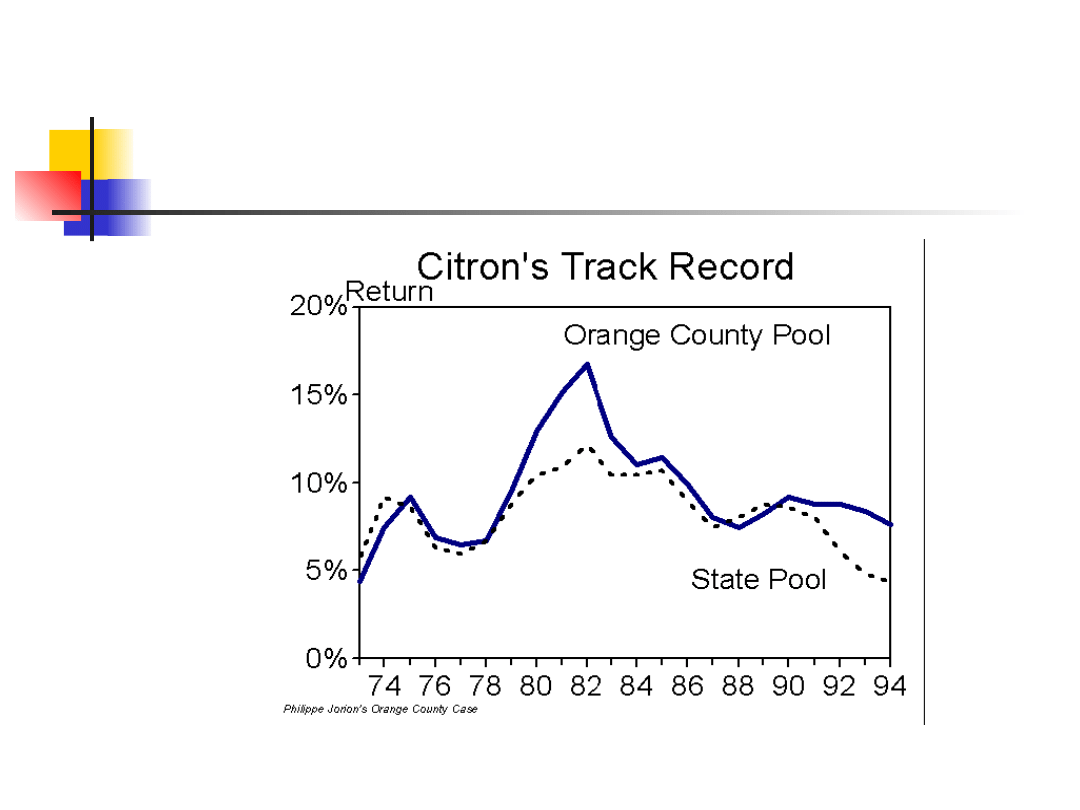
Citron był postrzegany jak czarnoksiężnik, gdyż poprzez swoja

działalność inwestycyjna w okresach wcześniejszych

realizował dochód o ok.. 2 % wyższy niż osiągano na podobnej

działalności w innych hrabstwach.

4

Value at risk – case
Orange County

5

Value at risk – case
Orange County



Wyższy wzrost z inwestycji był możliwy dzięki inwestycjom w

instrumenty pochodne i lewarowanie portfela jak tylko było

to możliwe



Duży poziom dźwigni finansowej wynikał z reinwestowania do

portfela utrzymywanego przez hrabstwo środków

przeznaczonych na bieżącą działalność lokalnych szkół i

miast.



Poziom portfela wzrósł dzięki lewarowaniu z 7,5 mld do 20,5

mld. Citron pod zastaw swoich papierów dłużnych pozyskiwał

finansowanie na nowe inwestycje (emisja collateral), głównie

w 5 letnie obligacje (notes) emitowane przez sponsorowane

przez rzad federalny agencje. (Federal National Mortgage

Association, znana jako ``Fannie Mae'‘).

6

Value at risk – case
Orange County



Strategia Citrona była kontynuowana z

powodzeniem do 1994 roku



W tym roku FED dokonał kilku znaczących

podwyżek stóp procentowych.



Podwyżki wpłynęły na obniżenie wartości portfela

obligacji.



Efekt ten jest określany jako wrażliwość portfela

papierów dłużnych na stopę procentową i jest

mierzony przez średni czas trwania (duration)

7

Wrażliwość obligacji



Duration jest cechą charakterystyczna obligacji. Dla stałokuponowych

obligacji można intuicyjnie ja definiować jako średni okres

zapadalności wszystkich płatności wynikających z obligacji, gdzie

każda płatność jest ważona relacją jej wartości bieżącej do całkowitej

wartości obligacji (NPV)



Dla instrumentów o stałym oprocentowaniu duration jest ważnym

narzędziem zarządzania ryzykiem stopy procentowej i służy do

pomiaru wrażliwości ceny obligacji na zmianę stopy zwrotu (yield)



Rozpatrzmy obligację, która przynosi dochód 50 w pierwszym roku i 50

w drugim roku.



Zapadalność obligacji wynosi 2 lata, ale to odnosi się tylko do drugiej

płatności. Średnia zapadalność obu płatności wynosi 1,5 roku, ale

duration koryguje czas trwania w kierunku okresu 1, gdyż wartość

bieżąca płatności pierwszej jest wyższa niż płatności drugiej (zgodnie z

rachunkiem pieniądza w czasie)

8

Wrażliwość obligacji



Duration jest ważna gdyż opisuje

wrażliwość ceny obligacji na zmianę stopy

procentowej :



Stopa zwrotu z obligacji = - Duration x

1/(1+stopa procentowa) x zmiana

stopy procentowej



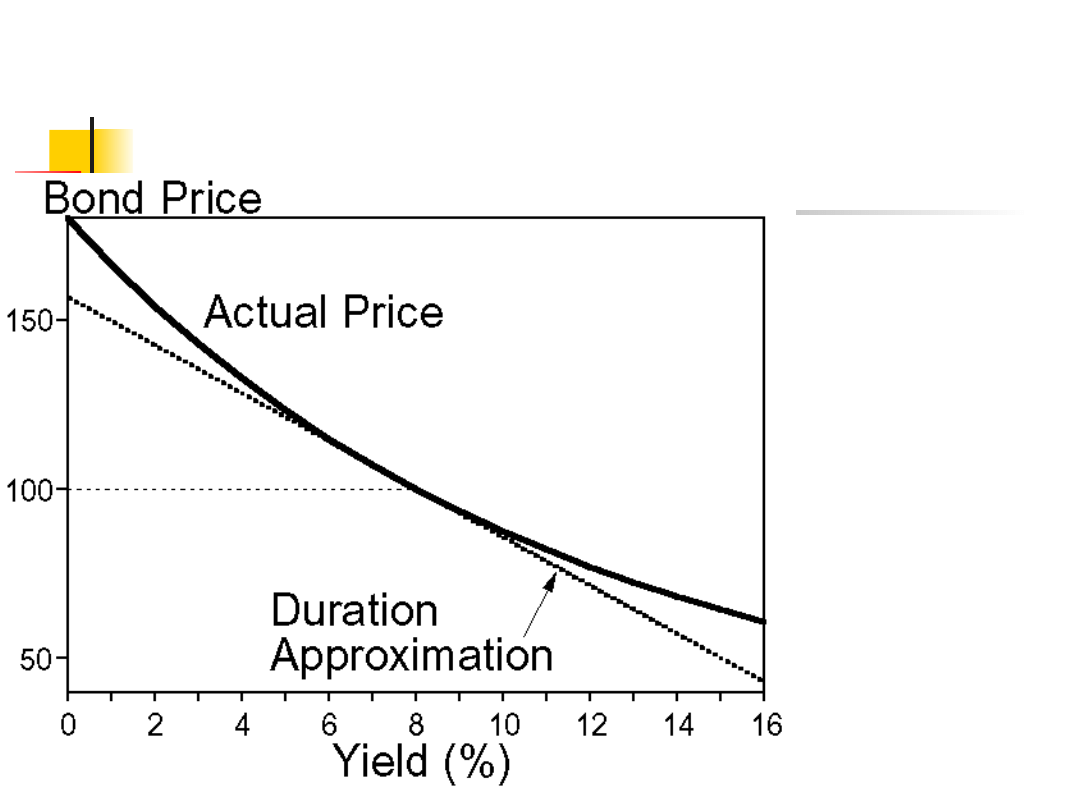
Duration jest tylko aproksymacją, gdyż jest

liniowa, natomiast zmiany cen są nieliniowe

9

Wrażliwość obligacji

10

Wrażliwość obligacji



Duration oraz oprocentowanie obligacji wzrastają

wraz ze wzrostem okresu życia obligacji oraz wraz

ze wzrostem poziomu lewarowania portfela



W poniższej tablicy zaprezentowano wyniki obliczenia

duration dla obligacji om różnym terminie wykupu.

Założono płatność 8 % kuponu od obligacji oraz 8 %

stopę zwrotu.



Można zaobserwować, że wraz ze wzrostem

zapadalności rośnie duration : dla obligacji 5 letniej

wynosi 4.0, dla obligacji 30 letniej 11,3 lat.

11

Wrażliwość obligacji



Table 1. Maturity and Duration



8% Yield,



8% Coupon Bonds



Maturity Duration



(Years) (Years)



1 0.93



2 1.78



3 2.59



5 3.99



7 5.21



10 6.71



30 11.26

12

Wrażliwość obligacji



Wzrost zapadalności aktywów zwiększa duration, a więc

zwiększa wrażliwość ceny obligacji na zmianę stopy

procentowej



Podobnie działa lewarowanie przy wykorzystaniu

instrumentu o krótszym terminie zapadalności.



Załóżmy, że inwestor stworzył portfel 100 milionów.

Zakupił 5 letnie obligacje. Następnie te obligacje zostały

zastawione i otrzymał gotówkę. Gotówka musi być

wykorzystana do wykupu obligacji za 5 lat.



W międzyczasie można ją wykorzystać do zakupu

następnych obligacji za 100 mln.



Proces może być powtórzony jeszcze raz, przez co poziom

lewarowania wzrośnie do 3:1

13

Wrażliwość obligacji



W tej sytuacji każdy ruch cen obligacji będzie w portfelu

multiplikowany przez 3. Jest to równoznaczne ze

wzrostem duration :



Zmiana ceny portfela = - 4 x $300 millionów x 1/

(1+stopa procentowa) x zmiana stopy

procentowej

Zmiana ceny portfela = - 12 x $100 million x 1/(1+

stopy procentowe) x zmiana stopy procentowej



W stosunku do pierwotnej duration portfela wzrosła ona

3 krotnie do 12

14

VaR wracamy do Citrona



Głównym celem Citrona była maksymalizacja

dochodu wykorzystując fakt, że

instrumenty średnioterminowe miały

wyższe oprocentowanie niż instrumenty

krótkoterminowe



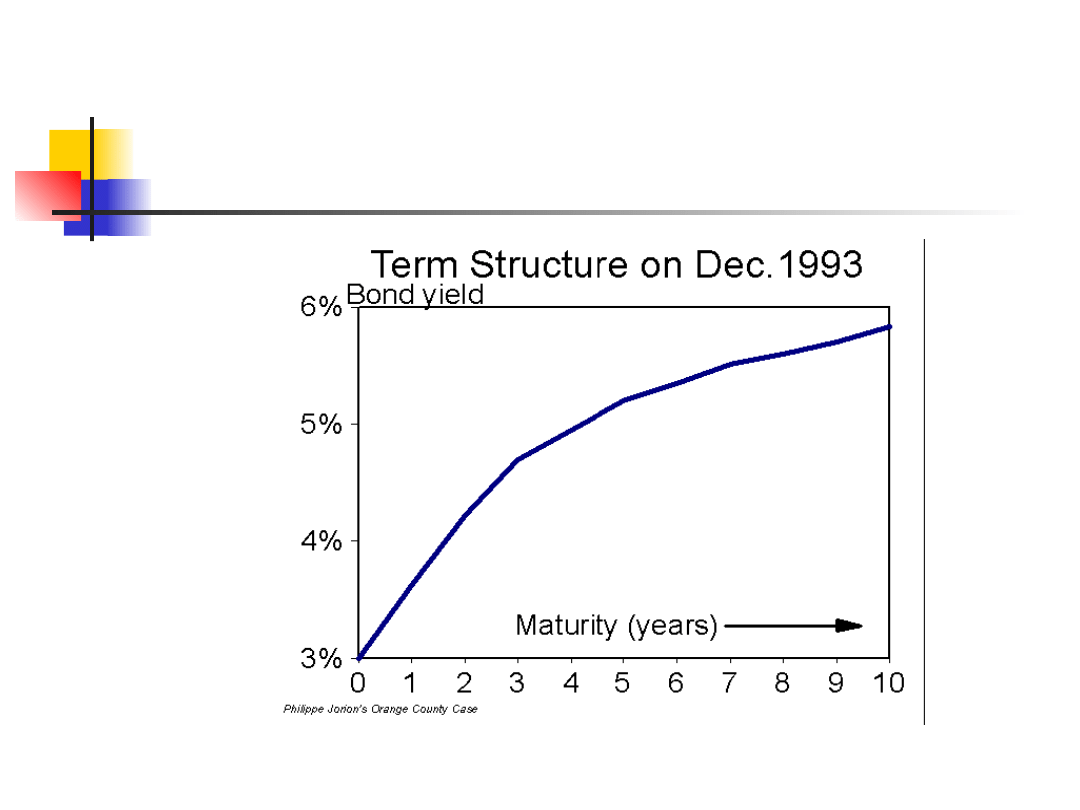
W grudniu 1993 roku krótkoterminowe instrumenty

były oprocentowane poniżej 3 %, natomiast 5 letnie

na poziomie 5,2 %



Taka sytuacja spowodowała tendencję do wzrostu

duration, gdyż to dawało extra zysk.



Ale rosła duration (i wrażliwość na stopę procentową

aktywów) oraz mniejsza wrażliwość na zmianę stóp

procentowych zobowiązań.



Efekt – większe ryzyko

15

VaR wracamy do Citrona

16

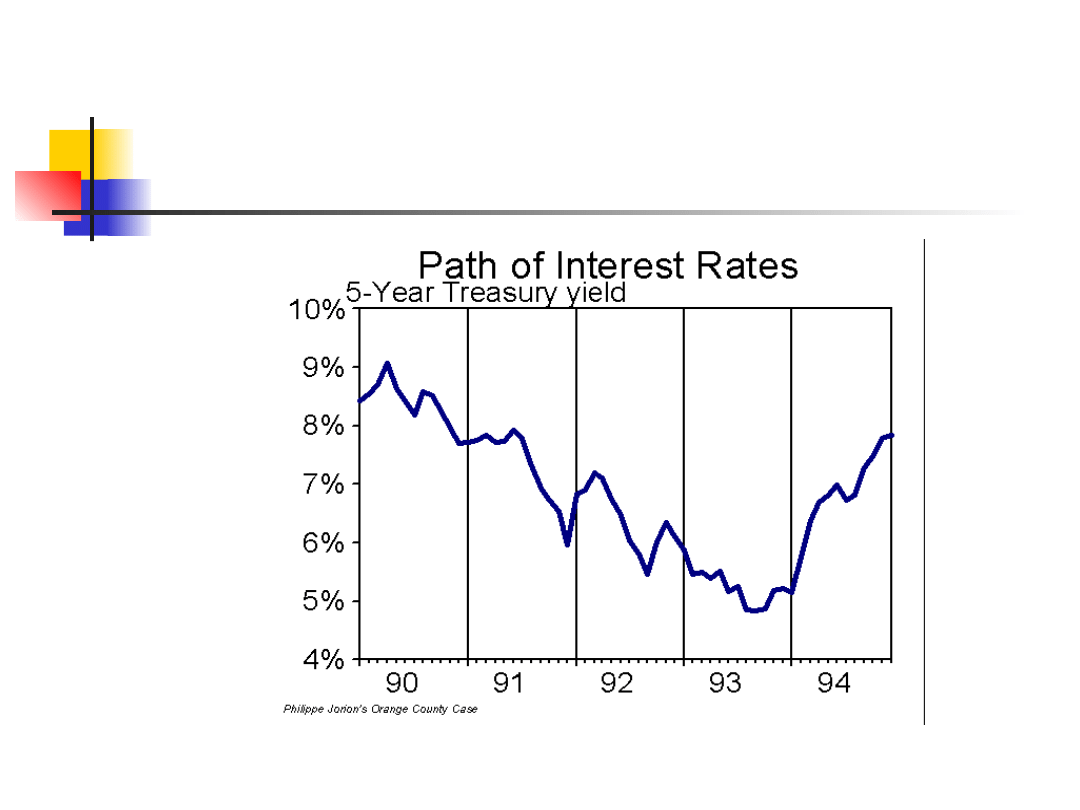
Strategia działała w sytuacji spadku stóp procentowych. W lutym 94 FED
rozpoczął serię 6 kolejnych podwyżek stóp procentowych, co
spowodowało spadki na rynku obligacji.

Wydłużanie okresu duration doprowadziło do 1,6

mld strat

17

Value at Risk



VaR jest metodą szacowania zysku wykorzystującą

standardowe statystyczne metody do szacowania ryzyka



Formalnie :



VaR wyznacza maximum strat możliwych do

poniesienia w określonym horyzoncie czasowym. W

metodzie zakłada się, że poniesienia strat wyższych

niż VaR określone jest bardzo masłym

prawdopodobieństwem (np. 1 %, 5 %)



W oparciu o ocenę sytuacji portfela VaR dostarcza

sumarycznej informacji o ryzyku rynkowym.



Np.. Bank może oszacować dzienne VaR dla portfela handlowego na

poziomie 35 milionów, przy przedziale ufności 99 %. Można to

zinterpretować, że prawdopodobieństwo straty wyższej niż 35

milionów wynosi 1 %. Ta liczba informuje wszystkich o ekspozycji

banku na ryzyko i może być konfrontowana z kapitałami, rezerwami,

aktywami, gdyż jest wyrażona w jednostkach pieniężnych

18

Value at Risk



Jak wyliczyć VaR ?



Załóżmy, że mamy portfel 100 milionów w

średniookresowych obligacjach. Jak wiele możemy

stracić w ciągu miesiąca ?



100 000 ?



1 000 000 ?



10 000 000 ?



Bez odpowiedzi na to pytanie inwestorzy nie mają

możliwości odpowiedzieć na pytanie, czy zwrot

skompensuje skalę ryzyka



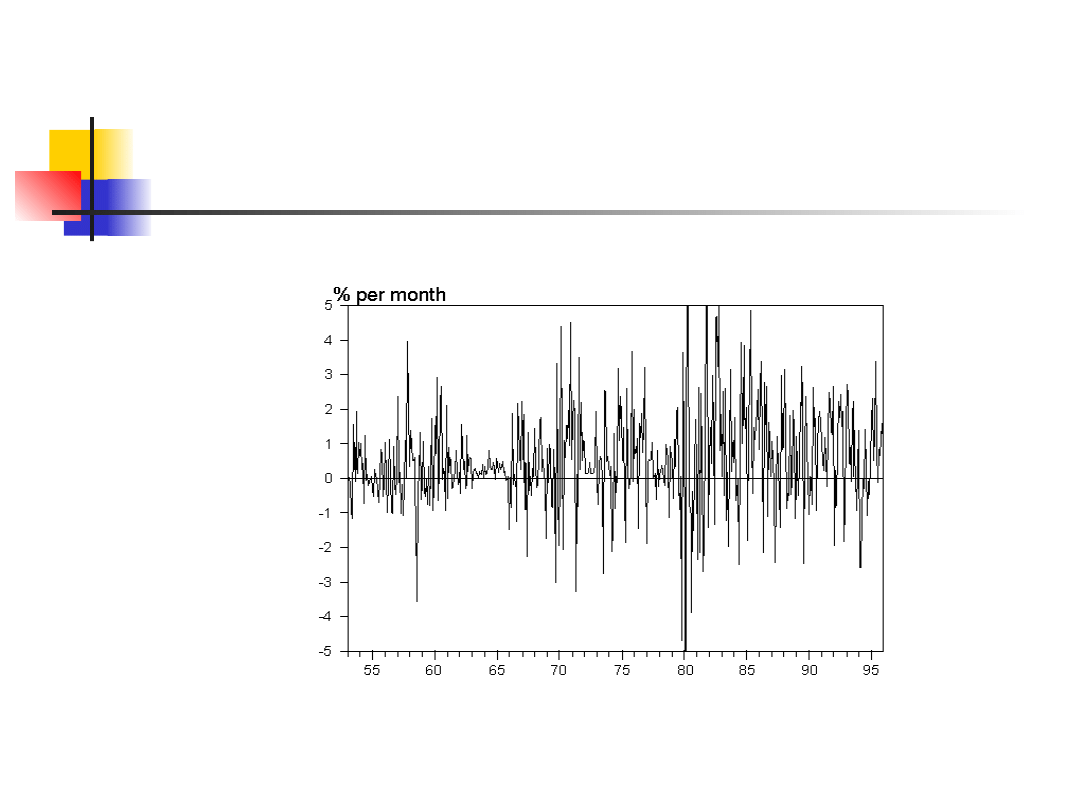
Aby odpowiedzieć na to pytanie należy przeanalizować

charakterystykę średniookresowych obligacji poprzez

obserwację miesięcznej stopy zwrotu z tego typu obligacji.

Dane z okres 1953-1995

19

Value at Risk –

historyczne zwroty z obligacji

20

Value at Risk



Stopy zwrotu zmieniały się w zakresie -6,5 %

(najniższa) do + 12 % (najwyższa)



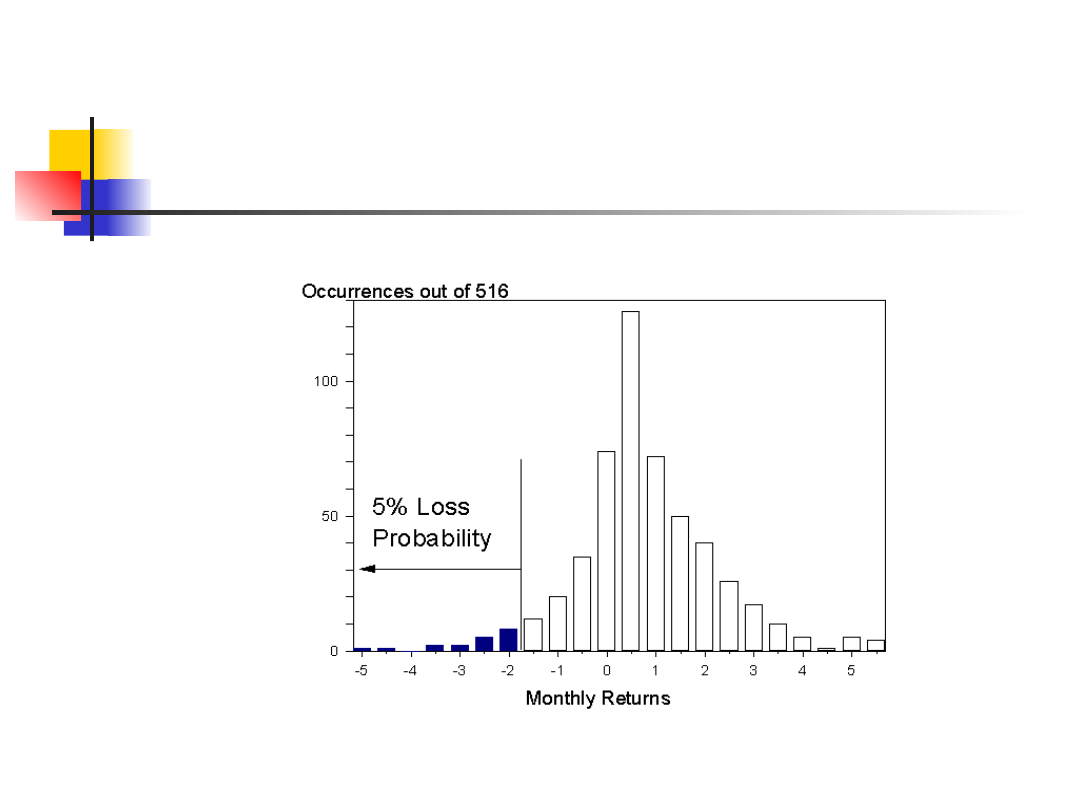
Skonstruujmy empiryczny rozkład

kształtowania się stóp zwrotu porządkując je

od najniższej do najwyższej w przedziałach co

0,5 %, a następnie policzmy częstości

występowania wyników z przedziałów w całej

próbie.



Otrzymamy rozkład gęstości stopy zwrotu

21

Value at Risk

22

Value at Risk



Dla każdej stopy zwrotu możemy obliczyć prawdopodobieństwo

wystąpienia niższych stóp zwrotu (dystrybuantę)



Przyjmując poziom ufności 95 % możemy odszukać punkt dla

którego z prawdopodobieństwem 5 % znajdziemy stopy zwrotu

niższe . Ta graniczna stopa wynosi (-1,7 %)



Jeżeli policzymy prawdopodobieństwo wystąpienia stóp zwrotu

mniejszych lub równych (– 1,7 %), to będzie ono wynosiło 5 %.



Jeśli byśmy założyli, że rozkład stóp zwrotu jest normalny, to do

obliczenia wartości granicznej moglibyśmy wykorzystać

odchylenie standardowe z próby.

23

Value at Risk



Mając powyższe informacje jesteśmy gotowi

policzyć VaR dla portfela zawierającego 100

mln obligacji.



Z prawdopodobieństwem 95 % możemy stwierdzić,

że strata z portfela w ciągu miesiąca nie przekroczy :



VaR = 100 mln x (-1,7 %) = -1,7 mln



W normalnych warunkach rynkowych i dla większości

portfeli obligacji średnioterminowych istnieje 5 %

prawdopodobieństwo, że strata będzie większa niż

1,7 mln

24

Value at Risk



Dwa subiektywne założenia przy wyliczaniu VaR



(1) Horyzont



Dla portfela handlowego banku składającego się z wysoko płynnych

aktywów może być do przyjęcia jednodniowy horyzont czasowy. Dla

inwestora rozliczanego w okresach np.. Miesięcznych horyzont może

mieć dłuższy okres. Okres horyzontu powinien być dopasowany do

momentu zamiaru likwidacji portfela.



(2) Poziom ufności



Wybór poziomu ufności zależy od poziomu awersji do ryzyka oraz od

kosztów straty przewyższającej VaR. Przy większej awersji do ryzyka

oraz wyższych kosztach straty przyjmuje się wyższe poziomy ufności

25

Konwertowanie parametrów
VaR



Jeśli zakładamy kształtowanie się dochodu z portfela zgodnie z

rozkładem normalnym, to konwertowanie parametru

horyzontu lub poziomu ufności jest dość łatwe



Przy założeniu braku korelacji pomiędzy dochodami z różnych okresów

wariancja T – dni okresu będzie równa T x wariancja ze stopy zwrotu

jednodniowej. Co implikuje :



VaR(T days) = VaR(1 day) x (Jednodniowe odchylenie x T)



Konwersja w zakresie poziomu ufności opiera się na tym samym

założeniu. Z rozkładu normalnego N(0,1) wiemy, że dystrybuanta

liczona od jednego ogona dla poziomu ufności 95 % 1,645, natomiast

dla poziomu ufności 99 % wynosi 2,326 odchylenia standardowego.



Chcąc konwertować VaR z poziomu 99 % na poziom 95 %

mamy :



VAR(95%) = VAR(99%) x 1.645 / 2.326.

26

Wykorzystanie duration do szacowania ryzyka

związanego ze zmianą stopy procentowej



Na poziomie ufności 95 % VaR wynosiło
dla portfela 100 mln obligacji 1,7 mln



O ile powinny się zmieniać miesięczne
stopy procentowe, aby realizować tę
stratę?



Wykorzystanie duration 4,5 ; stopy
procentowe na poziomie 5 %

27

Wykorzystanie duration do szacowania
ryzyka związanego ze zmianą stopy
procentowej



Strata na poziomie VaR = Duration x
1/(1+stopa procentowa) x wartość
portfela x miesięczny wzrost stopy
procentowej



1,7 mln = 4,5 x 1/(1+0,05)x100x (wzrost
stopy procentowej przez miesiąc = ?)



? = 0,40 %

28