Podstawy

Metrologii

Wykład 3

Teoria błędów

Program na dziś



Definicja i rodzaje błędów;



Charakterystyka

metrologiczna;



Funkcja błędu.



Niepewność pomiarowa



Rodzaje niepewności Typ A i B



Rozkład Gaussa



Wykresy danych pomiarowych

Wprowadzenie

Przy omawianiu błędów wygodnie jest
przypomnieć na wzór terminologii
stosowanej w literaturze zachodniej
rozróżnienie pomiędzy pojęciami

dokładność

i

precyzja

.

Wynik pomiaru określamy wówczas jako

dokładny

, gdy jest on wolny od błędów

systematycznych, natomiast jako

precyzyjny

, gdy jego błąd przypadkowy

jest bardzo mały.

Wprowadzenie

Każdy eksperyment, każdy pomiar i

prawie każda operacja składowa
pomiaru daje wyniki obarczone
różnymi typami błędów

Wprowadzenie

Teoria błędów

- dział matematyki stosowanej

zajmujący się metodami oceny dokładności
pomiarów lub rachunków przybliżonych.

Teoria błędów umożliwia m.in. określenie

dopuszczalnych wartości błędów
popełnianych przy pomiarach lub rachunkach,
tak aby wynik całości obliczeń (czy też
pomiarów) zapewniał wymaganą dokładność
(tzw. dyskusja błędu).

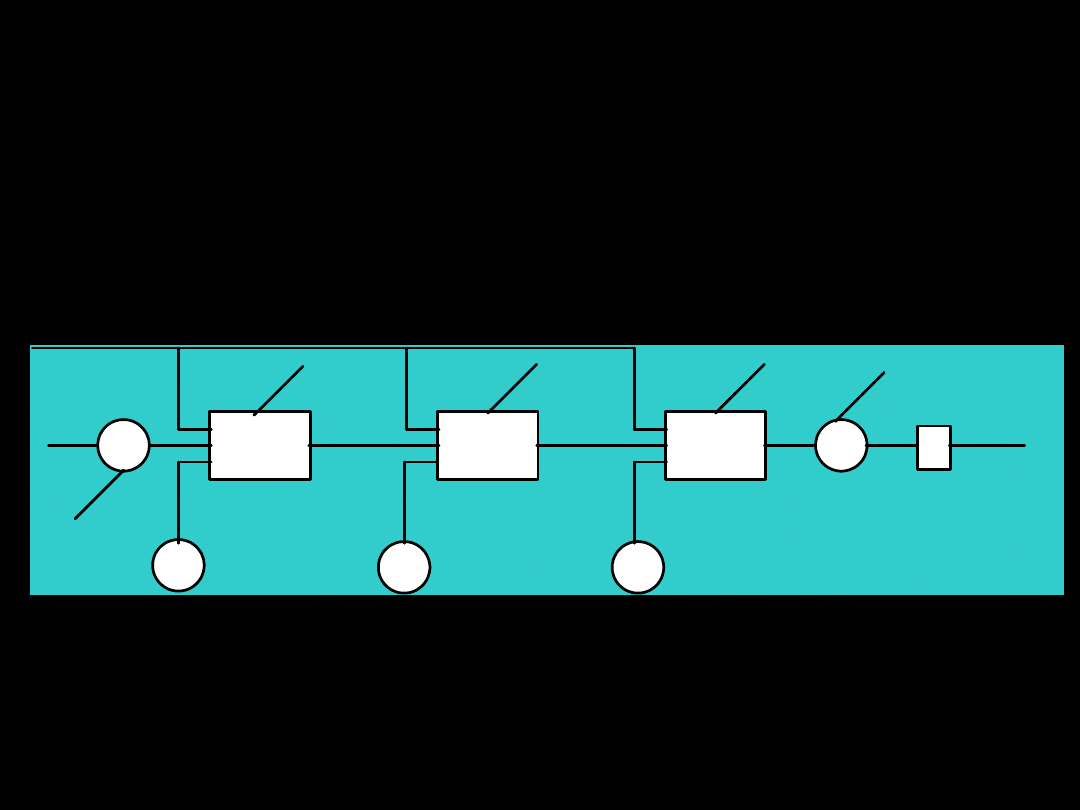
Wprowadzenie

a

a

a

F1

F2

F3

x

i

z

z

z

z

z

x

x"



Pomiar



Pomiar

— pewna sekwencja czynności

doświadczalnych i obliczeniowych,
prowadząca do wyznaczenia liczbowej
wartości wielkości fizycznej.

Ta wybrana sekwencja powinna

minimalizować wpływ oddziaływań
zewnętrznych na badane zjawisko i
przyrządy.

Wynik pomiaru

wartość pomiaru

±

błąd

pomiarowy

Błąd pomiaru

Błąd pomiarowy niepewność pomiarowa,
dokładność pomiaru

Błąd w pomiarach = pomyłka

.

Definicja błędu

Jeżeli wartość wielkości wynosi

x

, a

przyjęto wartość

x`

, to różnica

Δx = x`-x

jest błędem - jest to najlepsza definicja w

przypadku eksperymentów myślowych;

Definicja błędu

Błąd jest to różnica między

wartością wielkości a wartością

poprawną tej samej wielkości

– definicja ta wyraża błąd w dziedzinie

abstrakcji

Definicja błędu

Błąd jest to różnica między

stanem danej wielkości a stanem

rzeczywistym jej wielkości

- definicja ta wyraża błąd w dziedzinie

rzeczywistości powstający przy tworzeniu
obrazu rzeczywistości za pomocą pomiarów.

Rodzaje błędów

Rozróżnia się trzy rodzaje miar
błędu:



błędy prawdziwe,



błędy umownie prawdziwe



błędy graniczne

Podział błędów

Wyniki pomiarów podlegają pewnym

prawidłowościom, tzw. rozkładom typowym dla

zmiennej losowej. Z tego względu błędy

dzielimy na:

•

Błędy grube

(pomyłki), które należy

eliminować

•

Błędy systematyczne

, które można

ograniczyć udoskonaląjąc pomiar

•

Błędy przypadkowe

, które podlegają prawom

statystyki i rachunku prawdopodobieństwa,

wynikają z wielu losowych przyczynków i nie

dają się wyeliminować

Krzywe rozkładu

błędu

Błąd systematyczny Błąd przypadkowy

Błędy grube



Są wynikiem pomyłki eksperymentatora

np. przy

odczytywaniu wartości mierzonych, przy

przeliczaniu jednostek etc., nieprawidłowego

stosowania przyrządu pomiarowego, poważnego

i nieuświadomionego uszkodzenia przyrządu

pomiarowego, zastosowania nieodpowiedniej

metody pomiaru lub niewłaściwych wzorów

teoretycznych do opracowania wyników.



Fakt zaistnienia błędu grubego należy sobie jak

najszybciej uświadomić a wynik obarczony takim

błędem wykluczyć z dalszych analiz.



Jeśli to możliwe, pomiar powtórzyć.

Rodzaje błędów

Wartość oczekiwana błędu

przypadkowego jest równa
zeru

,

- właściwość ta nie zawsze jest zgodna z

sensem fizycznym błędów przypadkowych.

Rodzaje błędów

Błąd może być przedstawiany w

trzech postaciach:



błędu bezwzględnego,



błędu względnego,



błędu unormowanego

(czyli

zakresowego lub sprawdzonego)

Rodzaje błędów

Podział błędów ze względu na warunki

pomiaru:



w warunkach odniesienia popełniany
błąd nazywa się

błędem podstawowym

,



w innych warunkach występują ponadto

błędy dodatkowe

.

Rodzaje błędów



Podział błędów ze względu na

charakter mierzonej

wielkości:

-

błędy statyczne

- błędy dynamiczne

Błąd dynamiczny można zdefiniować dwojako:

a)

jest to błąd spowodowany odmiennymi niż idealne

właściwościami dynamicznymi układu pomiarowego;

b) jest to błąd spowodowany zastosowaniem statycznej

procedury wzorcowania dla układu przy pomocy
którego dokonujemy pomiarów dynamicznych
mierzonej wielkości.

Rodzaje błędów

Podział błędów ze względu na fizyczne

przyczyny powstawania błędu - wyróżnia
się tu m.in.:



błąd wzorcowania,



błąd niestałości,



błędy kwantowania,



błędy próbkowania,



błędy zliczania,



itd.

Rodzaje błędów



Podział błędów ze względu na charakter błędu -
wyróżnia się tu:



błąd systematyczny



błąd przypadkowy (błąd losowy)

- Błąd systematyczny jest to błąd, który przy

wielokrotnym wykonywaniu pomiaru tej samej
wielkości w tych samych warunkach ma wartość
stałą lub zmienia się według znanego prawa.

- Wszystkie pozostałe błędy określa się jako

przypadkowe.

Błąd

systematyczny



Błąd pomiarowy systematyczny

jest to

stała, nieznana, wartość zmiany wyniku

pomiaru, wynikająca z ograniczoności

modelu fizycznego zjawiska, którym się (w

danej chwili) posługujemy, ograniczoności

metody pomiaru, czy też niewłaściwej

kalibracji przyrządu pomiarowego; błąd ten

ujawnia się zwykle dopiero po zmianie

metody pomiaru lub modelu fizycznego

zjawiska.



Błąd systematyczny

o znanej wartości

nazywamy

poprawką.

Błędy

systematyczne



Błędy systematyczne

zawsze w ten sam

sposób wpływają na wyniki pomiarów
wykonanych za pomocą tej samej metody i
aparatury pomiarowej.



Minimalna wartość błędu
systematycznego

jest określona

dokładnością stosowanego przyrządu (lub
klasą w przypadku analogowych mierników
elektrycznych).

Źródłem błędu systematycznego

są:

-

skale mierników

(np. niewłaściwe ustawienie

„zera”),

- nieuświadomiony

wpływ czynników

zewnętrznych

(temperatura, wilgotność) na

wartość wielkości mierzonej,

- niewłaściwy

sposób odczytu

(błąd paralaksy)

lub pomiaru,

- przybliżony

charakter wzorów

stosowanych do

wyznaczenia wielkości złożonej.

Błąd

przypadkowy



Błąd pomiarowy przypadkowy

(statystyczny)

jest to średnia wartość

zmiennych zaburzeń mierzonej wielkości
fizycznej, pochodzących od wielu słabych
oddziaływań zewnętrznych, lub skutek tzw.
nieokreśloności obiektu.

Błąd ten jest najczęściej nieznany, a wyznacza

się go w pomiarach (razem z wartością
pomiaru, jako tzw. błąd pojedynczego pomiaru).

Błędy

przypadkowe

Błędy przypadkowe

zawsze występują w

eksperymencie powodują rozrzut kolejnych
odczytów wokół rzeczywiste wartości mierzonej
wielkości (oczywiście, gdy występuje błąd
systematyczny, pomiary układają się wokół
pewnej, przesuniętej względem rzeczywistej,
wartości).

Błędy przypadkowe

można wykryć drogą

powtarzania pomiarów, przy okazji poprawiając
precyzję pomiarów, korzystając ze średniej
wartości serii pomiarów.

Błędy

przypadkowe

Błędy przypadkowe zawsze towarzyszą
eksperymentowi, nawet jeśli inne błędy

zostaną wyeliminowane.

W przeciwieństwie do błędu systematycznego,

ich wpływ na wynik ostateczny pomiaru nie

można ściśle określić.

Błędy

przypadkowe

Występują zawsze

w pomiarach, lecz

ujawniają się,

gdy wielokrotnie dokonujemy pomiaru przyrządem

,

którego dokładność jest bardzo duża a błędy
systematyczne wynikające z innych przyczyn są
bardzo małe.

Wynikają one z własności obiektu mierzonego

(np.

wahania średnicy drutu na całej jego długości),
własności przyrządu pomiarowego (np. wskazania
przyrządu zależą od przypadkowych drgań budynku,
fluktuacji ciśnienia czy temperatury, docisku dla
suwmiarki), lub mają podłoże fizjologiczne (refleks
eksperymentatora, subiektywność oceny maksimum
natężenia dźwięku czy równomierności oświetlenia
poszczególnych części pola widzenia)

Błąd

przypadkowy

Błąd przypadkowy

manifestuje się rozrzutem

wartości pomiaru przy jego powtarzaniu ( pomiar

wielokrotny).

Małe a liczne zaburzenia pomiaru: efekty mechaniczne

(zmienne tarcie, kurczliwość, wstrząsy), wahania

napięcia zasilania przyrządów, prądy powietrza,

zmienne pola elektromagnetyczne, itp.

•

Błędy przypadkowe metody

(np. błąd

paralaksy)

•

Błędy przypadkowe przyrządu

Błąd (dokładność) przyrządu

jest w błędem

przypadkowym pod warunkiem, że przyrząd jest

dobrze wykalibrowany, w przeciwnym razie, do błędu

przypadkowego dochodzi jeszcze błąd systematyczny.

•

Błąd przypadkowy obiektu

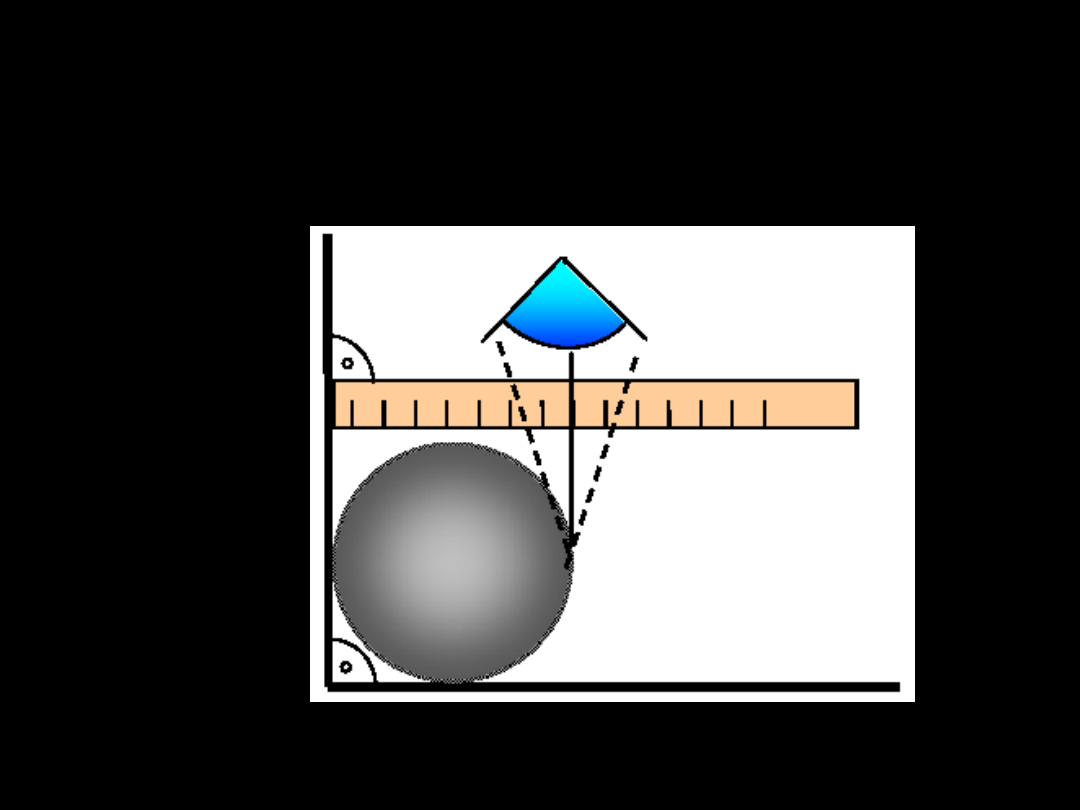
Błąd - paralaksa

Błąd przypadkowy metody
pomiarowej

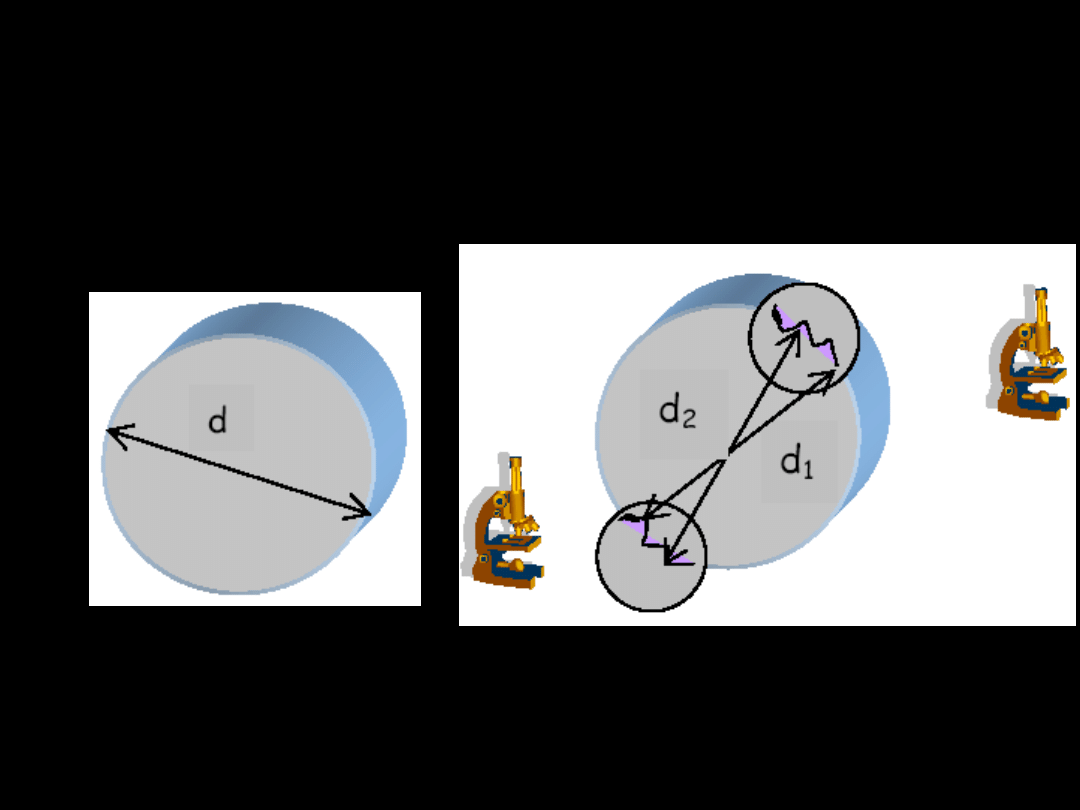
pomiar suwmiarką

pomiar dokładniejszy
Δd = 0.05 mm = 50 µm Δ d

=0.001mm = 1 µm

Pomiar wielokrotny:



20.15, 20.15, 20.15, 20.15 mm ... 20.12, 20.19, 20.11, 20.21, 20.09

mm, ...

Obliczenia błędu

przypadkowego

x

– wielkość fizyczna mierzona,

x

i

– wartości zmierzone, gdzie:

i = 1, ...n

,

n

– liczba pomiarów.



Szukamy tzw.

„wartości prawdziwej”

µ

wielkości fizycznej

x

, dysponując

n

liczbami

– wynikami

pomiarów.



Poszukujemy również wartości błędu
pomiarowego pojedynczego pomiaru

σ

,

charakteryzującej warunki pomiaru (liczba,

„ukryta”

w rozrzucie wartości

x

i

).



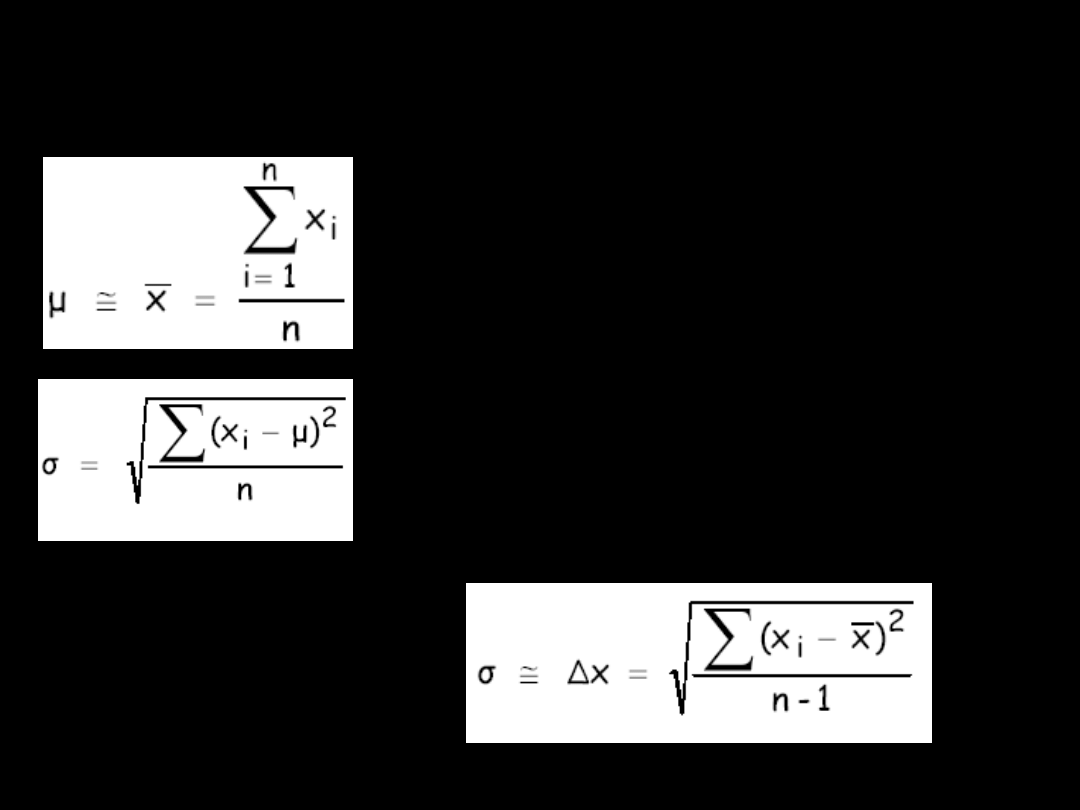
średnia wyników pomiaru („wynik
pomiaru”),



błąd (średni kwadratowy)
pojedynczego pomiaru

-

odchylenie standardowe

lub

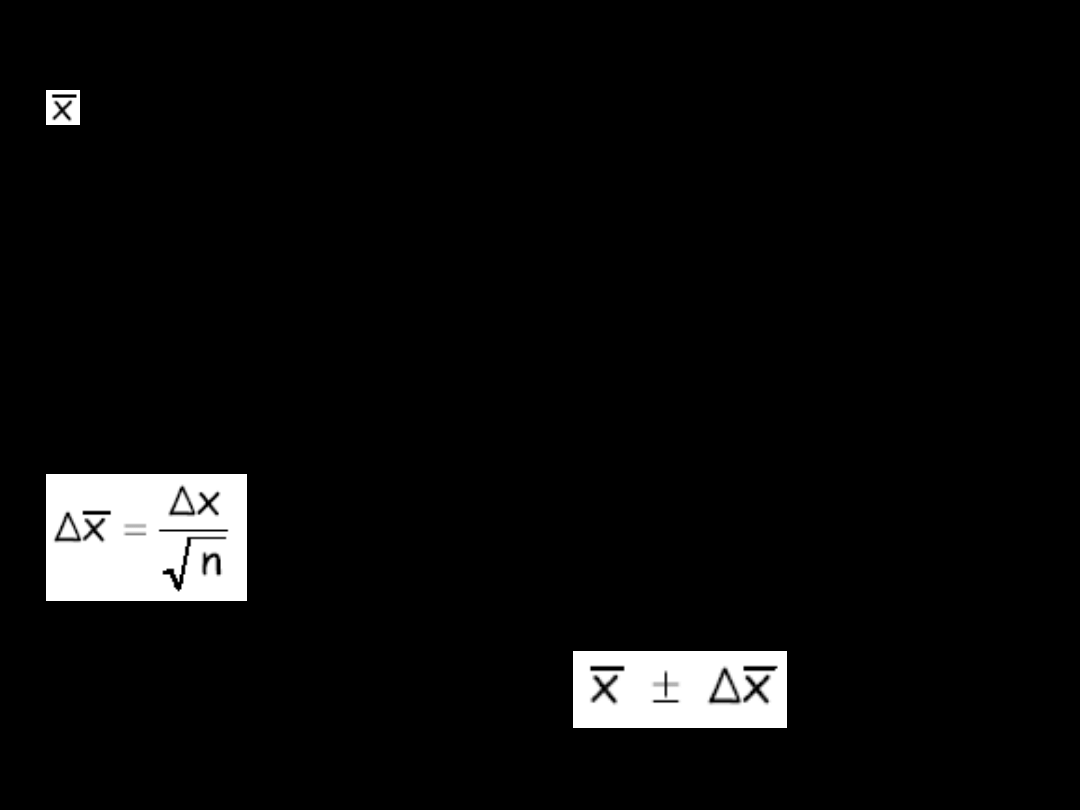
przyjmowane jest za „wartość pomiaru” Δx

nie jest „błędem pomiarowym” („błędem

wartości pomiaru”); jest to

błąd pojedynczego

pomiaru

, charakteryzujący takie same warunki

pomiaru.

Błąd wartości pomiaru będzie zależny

również od krotności pomiarów

n

:

-

błąd wartości średniej („błąd

pomiarowy”).

Ostatecznie:

Charakterystyka

metrologiczna

Pod pojęciem charakterystyka

metrologiczna rozumie się ogół

wiadomości o błędach układu

pomiarowego przedstawionych w

pewien uporządkowany sposób.

Różnorodność przyrządów i

rozmaitość ich zastosowań
powodują, że nie istnieje jednolity
sposób opracowywania
charakterystyk metrologicznych.

Istnieją pewne zalecenia normatywne,

producenci aparatury korzystają z
różnych wariantów charakterystyk,
upraszczając je w dość dowolny
sposób.

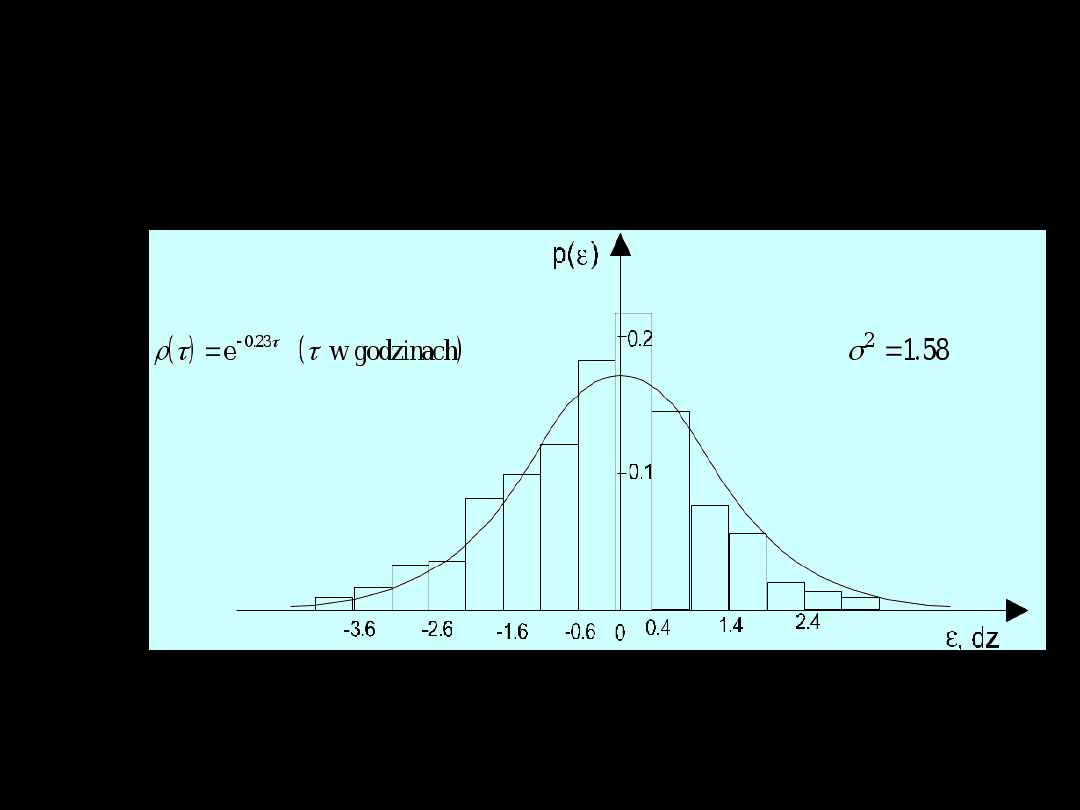
Charakterystyka

metrologiczna

Rozkład prawdopodobieństwa błędu
niestałości

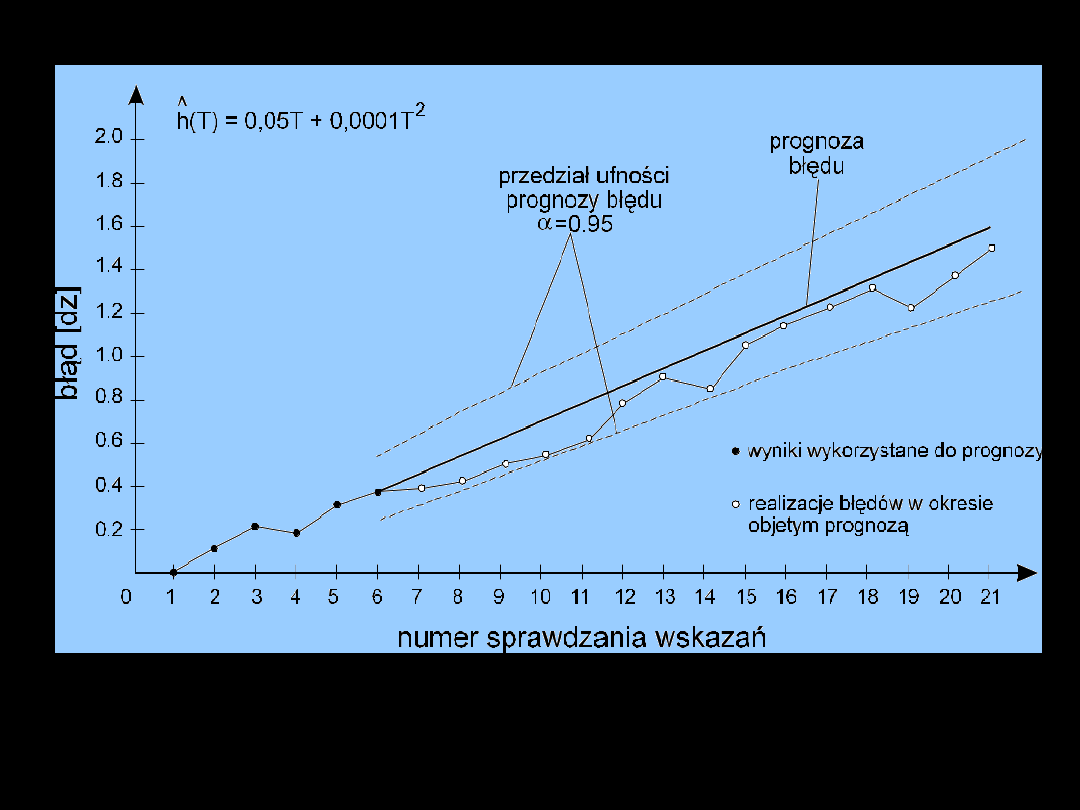
Przebieg błędu niestałości i jego
prognoza

Klasa

niedokładności

Klasa niedokładności przyrządu

(systemu

pomiarowego) określa nam zakres, którego nie
może przekroczyć błąd podstawowy w całym
zakresie pomiarowym.

Sprawdzanie wskazań przeprowadza się w

warunkach odniesienia w punktach skali
przyrządu opisanych cyframi. Punkty te oznacza
się

x

j

, j = 1, ..., k

. Wynikiem sprawdzania jest

zbiór błędów

{D

j

}.

Układ pomiarowy spełnia

wymagania klasy niedokładności, gdy

|D

j

|  D

dop

dla

j = 1, ..., k

.

Adiustacją

nazywa się wykonanie ściśle

określonych stosowną instrukcją
czynności regulacji (kalibrowania) układu
pomiarowego, przy wykorzystaniu
wzorca jako niezbędnego elementu
pomocniczego, sprowadzające błąd do
zadanej wartości (najczęściej do zera).

Oczywiście, gdy np. przyrząd nie ma
możliwości regulacji zamiast adiustacji
można przeprowadzić zwykłe
wzorcowanie.

Wzorcowanie

, jest to zbiór operacji

ustalających relację między
wartościami wielkości mierzonej
wskazanymi przez przyrząd
pomiarowy a odpowiednimi
wartościami wielkości, realizowanymi
przez wzorce jednostki miary.

- legalizacja

jest sprawdzeniem,

stwierdzeniem i poświadczeniem przez organ

administracji miar (wyłącznie), że przyrząd

pomiarowy spełnia wymagania przepisów

metrologicznych,

- uwierzytelnienie

jest to sprawdzenie,

stwierdzenie i poświadczenie, że przyrząd

pomiarowy spełnia wymagania metrologiczne

i ustalone w przepisach, normach i

zaleceniach międzynarodowych lub innych

właściwych dokumentach, a jego wskazania

zostały odniesione do państwowych wzorców

jednostek miar i są z nimi zgodne w

granicach określonych błędów pomiarów.

- Legalizacja i uwierzytelnienie,

ma na

celu sporządzenie oficjalnego dowodu

potwierdzającego możliwość stosowania

danego przyrządu pomiarowego. Jeżeli

wymaga tego przepis nadrzędny lub

kontrakt z klientem (umowa, zamówienie,

zlecenie), wówczas legalizacji/

uwierzytelnienia dokonać musi uprawniona

jednostka i ta jednostka "wystawia"

stosowny

dokument: legalizujący

(np. pod

rygorem spełnienia ściśle określonych

warunków eksploatacyjnych) użytkowanie

przyrządu, oraz

zapewniający

wiarygodność

wyników pomiaru (i

oczywiście monitorowania).

Funkcja błędu

Jeżeli pomiary pewnej wielkości x narażone są na
wpływ wielu niewielkich i przypadkowych zaburzeń, to
rozkład wyników jest rozkładem normalnym.
Całka funkcji gęstości prawdopodobieństwa opisującej
rozkład normalny, oznaczana czasem jako erf(t) i
obliczana zgodnie ze wzorem:

nosi nazwę

funkcji błędu

lub

normalnej całki błędu

i

określa prawdopodobieństwo tego, że wartość
pomiaru znajdzie się w promieniu t odchyleń
standardowych od wartości prawdziwej X.















t

X

t

X

X

x

x

f

t

d

)

(

)

erf(

,

Niepewność

pomiaru

Podstawowe terminy i

definicje

•

wartość oczekiwana

– wartość

zgodna ze zdefiniowana, jest nazywana

często wartością rzeczywista; jest to

wartość, która może być uzyskana w

wyniku doskonałego pomiaru;

•

wartość oznaczana

– wartość

uzyskana w wyniku zastosowania danej

procedury analitycznej; wynik pomiaru

to najczęściej średnia arytmetyczna z

uzyskanych wartości oznaczanych;

•

dokładność pomiaru

– stopień zgodności

pomiędzy wynikiem pojedynczego
pomiaru a wartością rzeczywista;

•

poprawność pomiaru

– stopień

zgodności pomiędzy wynikiem analizy
(średnią) a wartością rzeczywistą;

•

precyzja pomiaru

– zgodność pomiędzy

uzyskiwanymi niezależnymi pomiarami;



niepewność pomiaru

(uncertainty) –

parametr związany z wynikiem pomiaru,
który określa przedział wokół wartości
średniej, w którym może (na założonym
poziomie istotności) znaleźć się wartość
oczekiwana;



standardowa niepewność pomiaru

(standard uncertainty) –

u(xi)

-

niepewność pomiaru przedstawiona i
obliczona jako odchylenie standardowe;



złożona standardowa niepewność

(combined standard uncertainty) –

uc(y)

–

standardowa niepewność wyniku

y

pomiaru,

której wartość jest obliczona na podstawie
niepewności parametrów wpływąjących na
wartość wyniku analizy z zastosowaniem prawa
propagacji niepewności;



rozszerzona niepewność

(expanded

uncertainty) -

U

– wielkość określająca przedział

wokół uzyskanego wyniku analizy, w którym
można, na odpowiednim, przyjętym poziomie
istotności (prawdopodobieństwa) oczekiwać
wystąpienia wartości rzeczywistej;

•

współczynnik rozszerzenia

(coverage

factor) –

k

– wartość liczbowa użyta do

wymnożenia złożonej standardowej
niepewności pomiaru w celu uzyskania
rozszerzonej niepewności, wartość
współczynnika zależy od przyjętego
poziomu prawdopodobieństwa (np.: dla 95
% wynosi 2) i najczęściej jest wybierana z
przedziału liczb 2-3;

Niepewność



W praktyce nie znamy wartości rzeczywistych
wielkości mierzonych i szacujemy
niepewności pomiarowe wynikające ze
statystycznych praw rozrzutu pomiarów

.



Niepewność pomiaru jest związanym
rezultatem pomiaru parametrem,
charakteryzującym rozrzut wyników, który
można w uzasadniony sposób przypisać
wartości mierzonej.



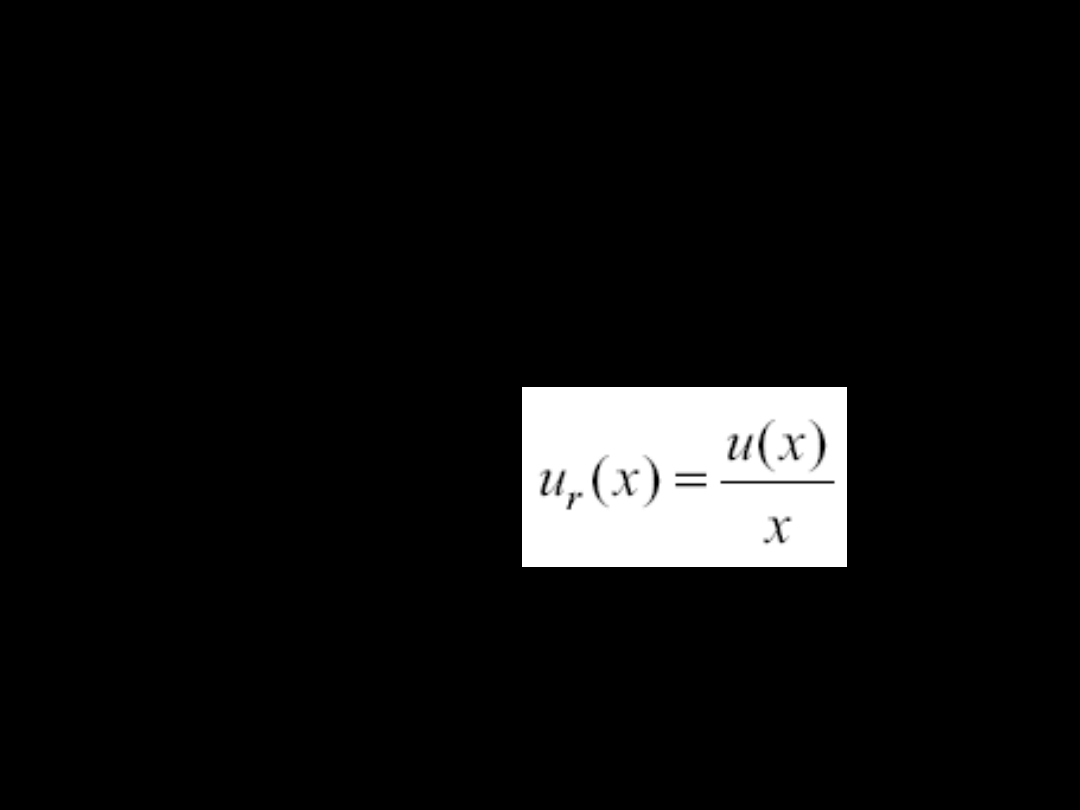
Niepewność u

lub

u(x)

(ang.

uncertainty) posiada wymiar, taki sam
jak wielkość mierzona



Niepewność względna ur(x)

to

stosunek niepewności (bezwzględnej) do
wielkości mierzonej:



Niepewność względna

jest wielkością

bezwymiarową i może być wyrażona w %

Niepewność

Istnieją dwie miary niepewności

pomiaru:



niepewność standardowa

u(x)



niepewność maksymalna
Δx

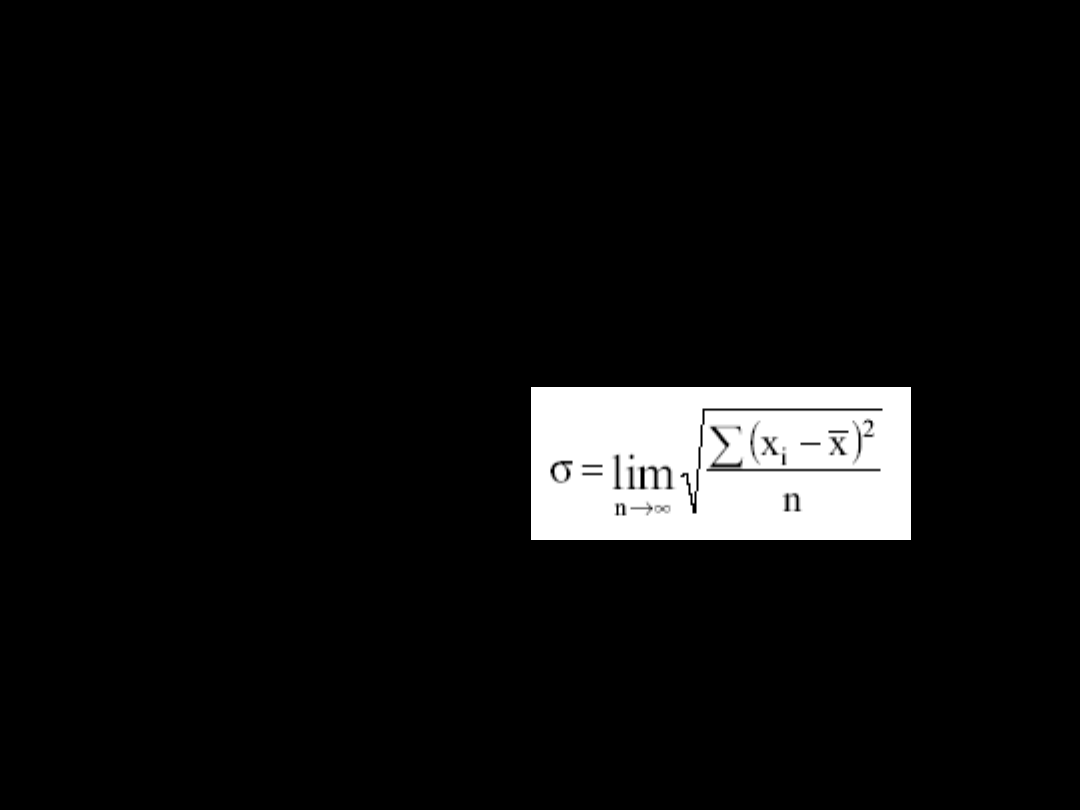
Niepewność

standardowa

1. Rezultat pomiaru jest zmienną losową

x

i

, której rozrzut wokół wartości średniej

x

charakteryzuje parametr zwany

odchyleniem standardowym

2. Dokładnej wartości odchylenia

standardowego nie znamy. Niepewność

standardowa jest jego niezbyt dokładnym

oszacowaniem (estymatorem, oceną).

Niepewność

maksymalna

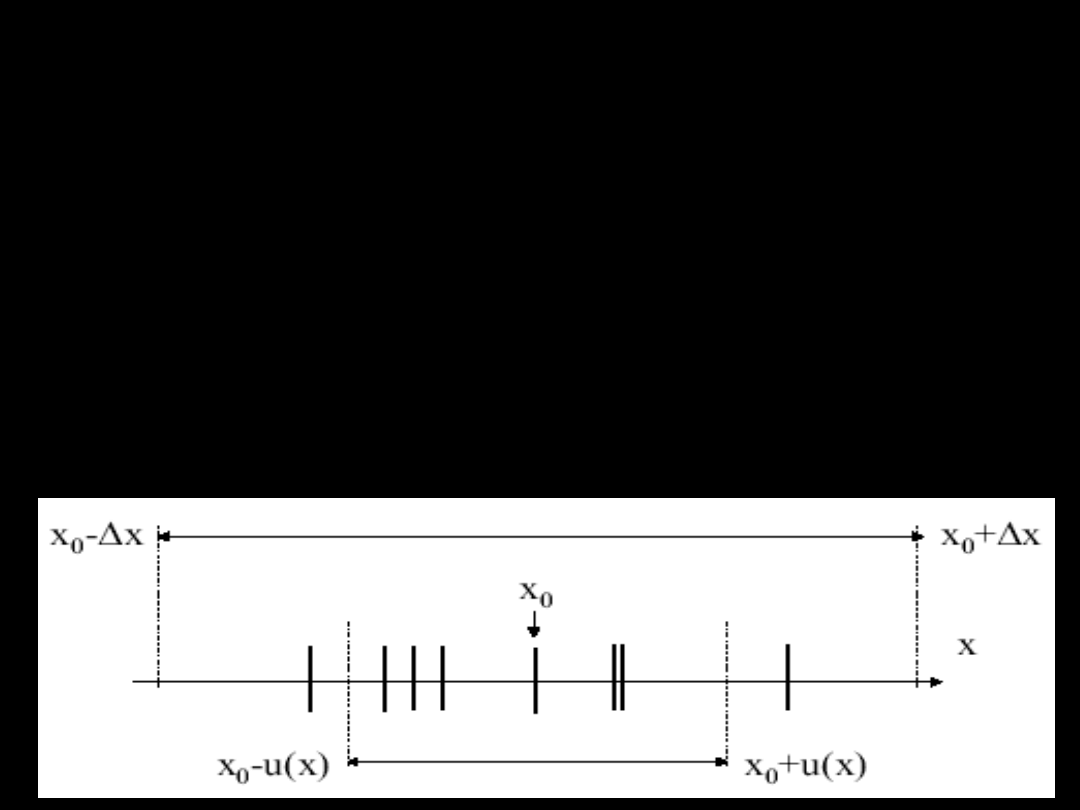
Jest miarą deterministyczną, gdyż zakłada, że można

określić przedział wielkości mierzonej x, w którym
na pewno znajdzie się wielkość rzeczywista.

W tym przypadku staramy się określić przedział,

x

o

- Δx < x

i

< x

o

+ Δx

w którym mieszczą się wszystkie wyniki pomiaru xi,
aktualnie wykonane i przyszłe.
Zaleca się obecnie niepewność maksymalną

specyfikowaną przez producenta zamieniać na
niepewność standardową wg wzoru:

Typy oceny

niepewności

Typ A

Metody wykorzystujące statystyczną analizę serii

pomiarów:

•wymaga odpowiednio dużej liczby powtórzeń pomiaru
• ma zastosowanie do błędów przypadkowych

Typ B

Opiera się na naukowym osądzie eksperymentatora

wykorzystującym wszystkie informacje o pomiarze i

źródłach jego niepewności

•

stosuje się gdy statystyczna analiza nie jest możliwa

•dla błędu systematycznego lub dla jednego wyniku

pomiaru

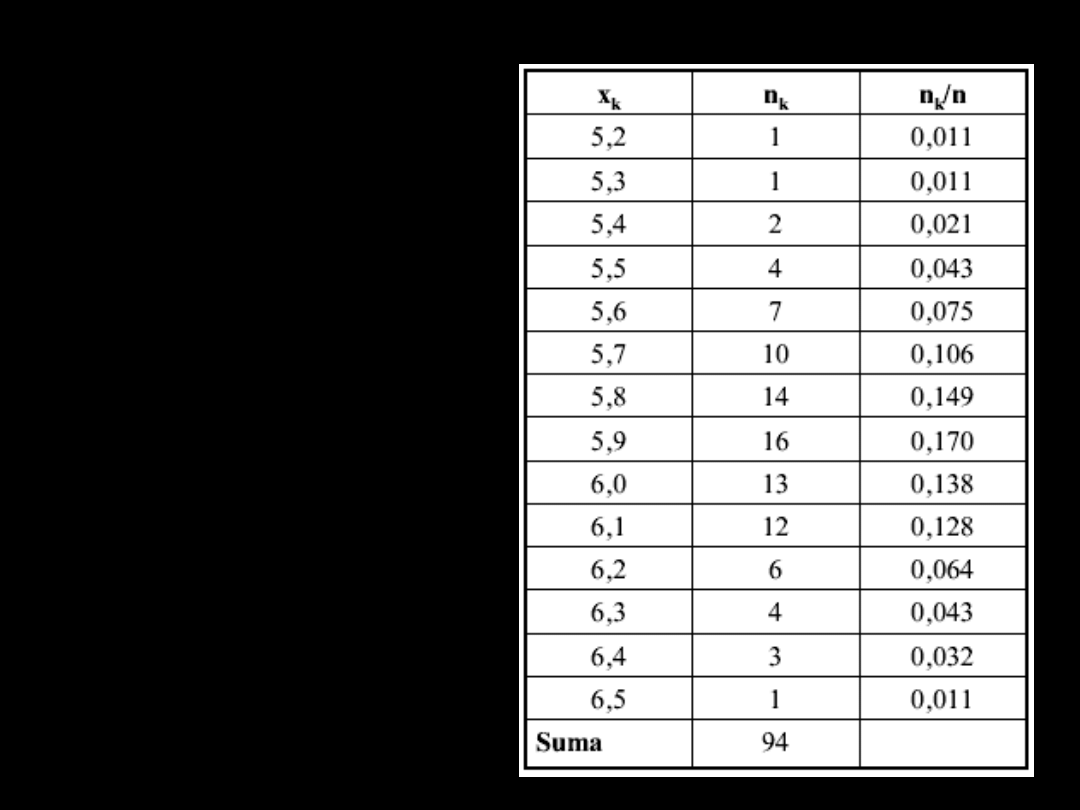
Typ A

Seria wyników (próba)

x

1

,x

2

, ….x

n

obarczonych

niepewnością
przypadkową jest duża
gdy 30<n<100. W
próbie takiej wyniki się
powtarzają:

n

k

jest

liczbą pomiarów, w
których wystąpił wynik

x

k

,

n

k

/n

jest częstością

występowania wyniku

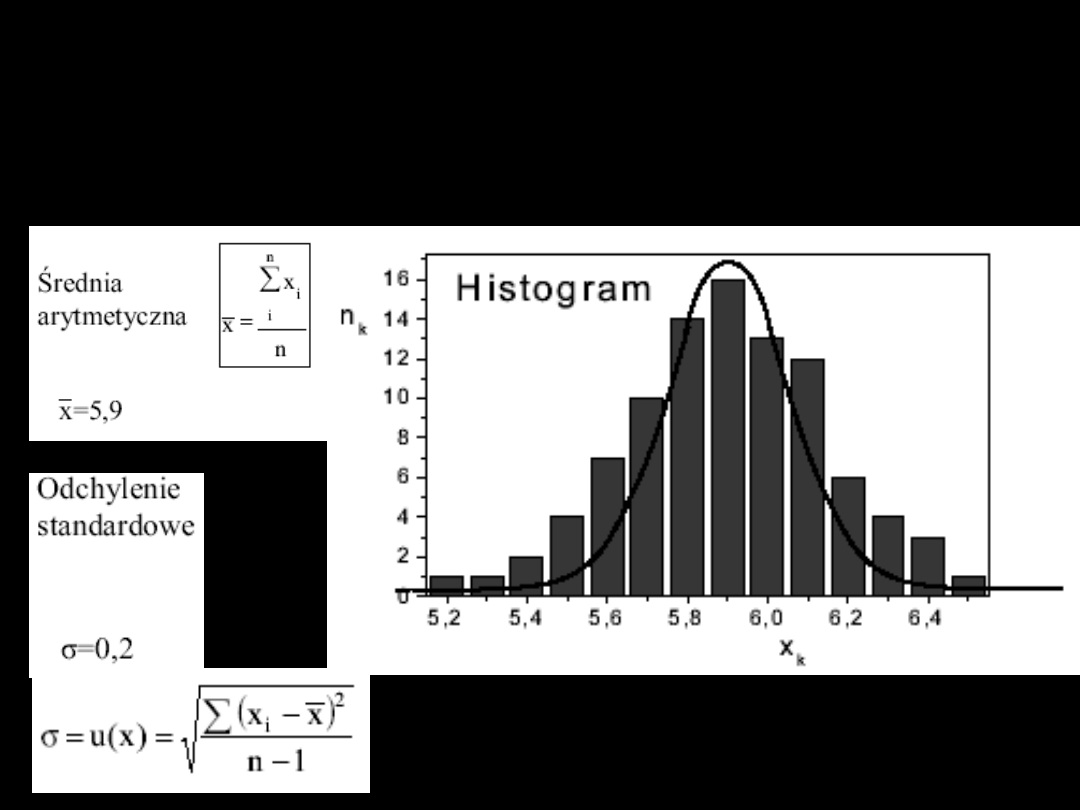
Opracowanie serii

pomiarów

bezpośrednich dużej

próby

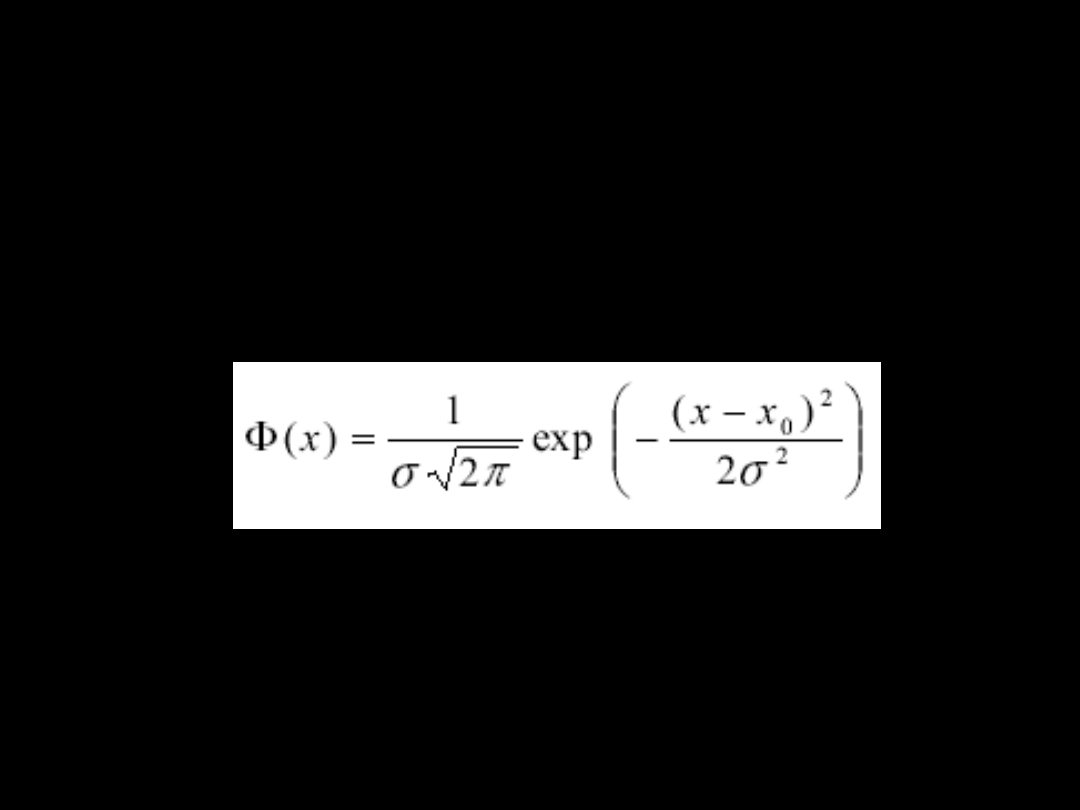
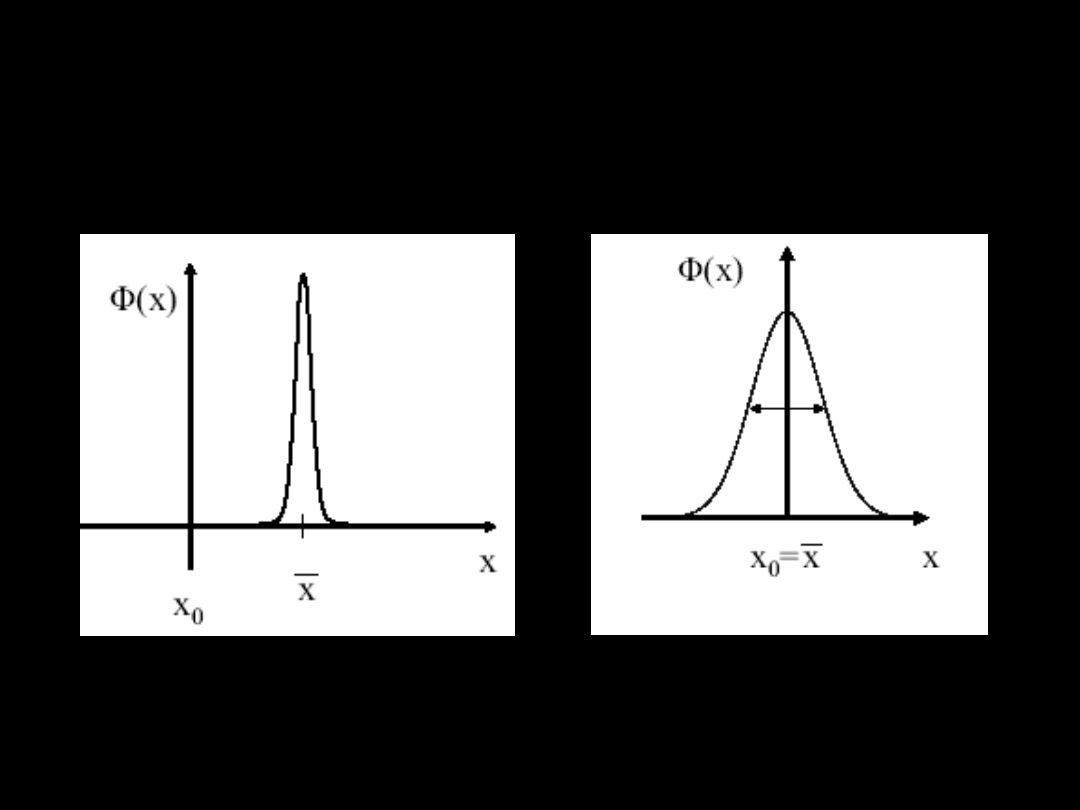
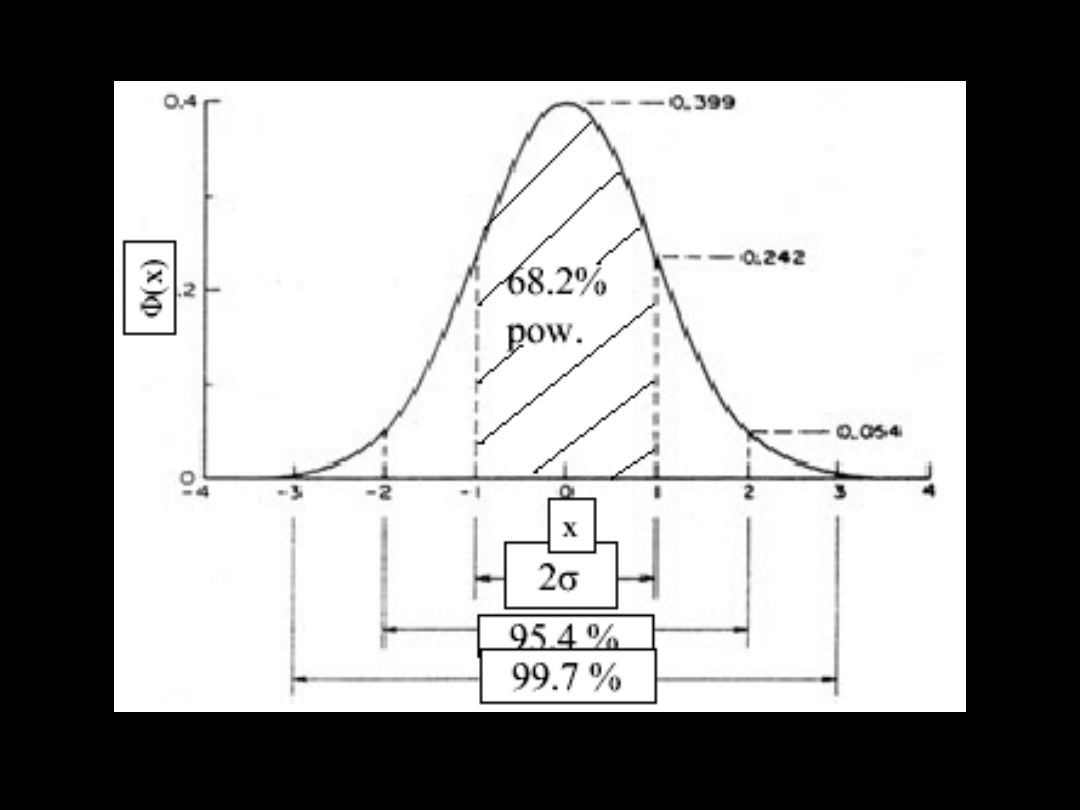
Rozkład normalny

Gaussa

Gęstość prawdopodobieństwa wystąpienia

wielkości x lub jej błędu Δx podlega rozkładowi

Gaussa

x

0

jest wartością najbardziej prawdopodobną i

może być nią średnia arytmetyczna, jest

odchyleniem standardowym, jest wariancją

rozkładu



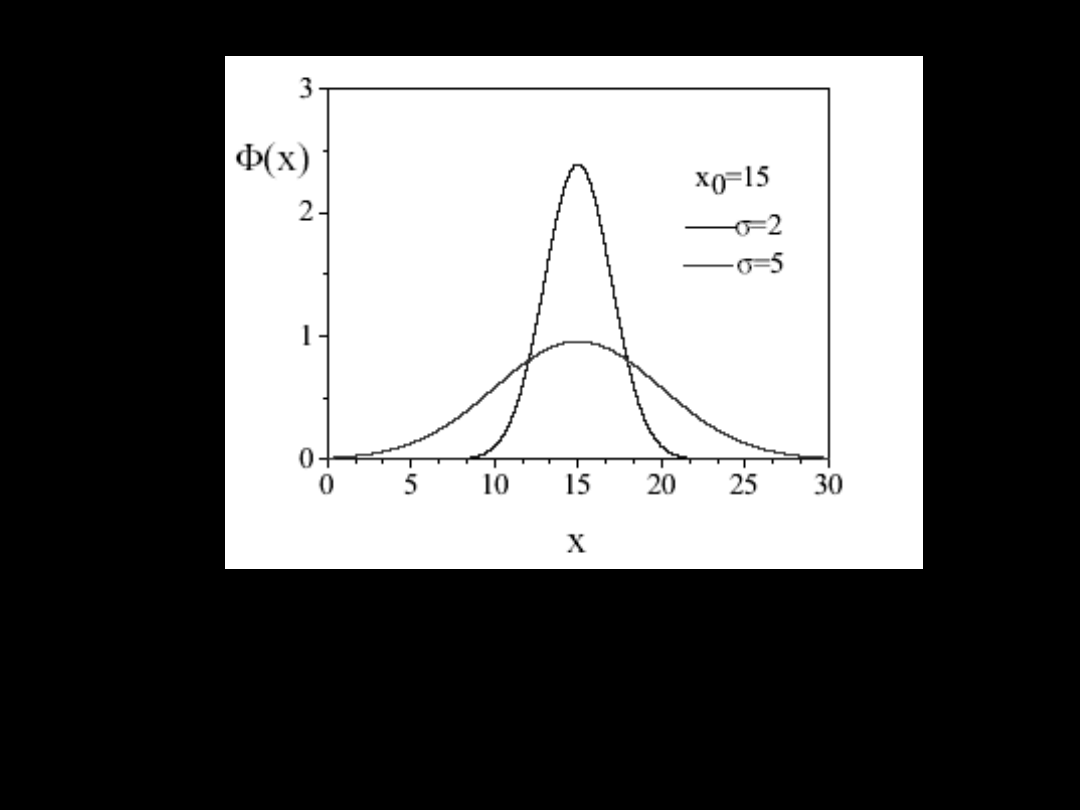
Pomiar o większym

σ

charakteryzuje się

większym rozrzutem wyników wokół
wartości średniej a zatem mniejszą
precyzją

Typ B

Dla oceny typu B wykorzystać można

m.in.:

•

dane z pomiarów poprzednich,

• doświadczenie i wiedzę na temat

przyrządów i obiektów mierzonych,

• informacje producenta przyrządów,
• niepewności przypisane danym

zaczerpniętym z literatury

Gdy informacja o pomiarze i źródle jego niepewności

jest dobra, dokładność oceny typu B jest

porównywalna z dokładnością oceny typu A.

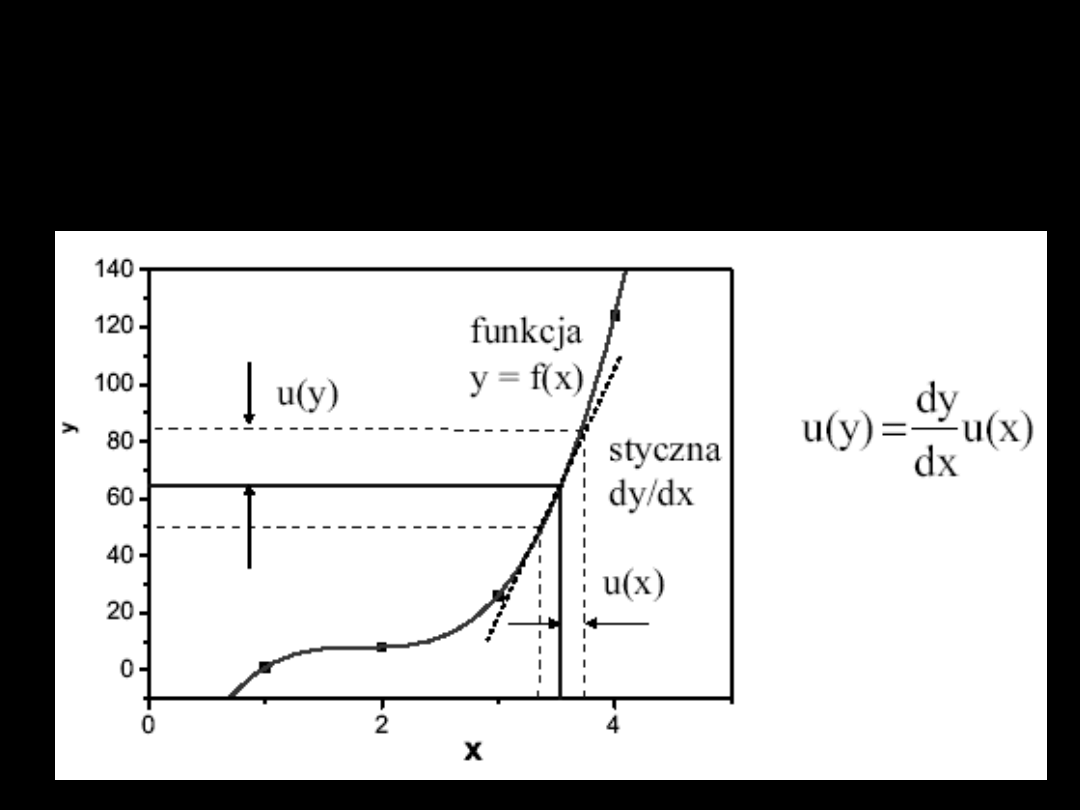
NIEPEWNOŚĆ WIELKOŚCI

ZŁO

ż

ONEJ

–

PRAWO PRZENOSZENIA

BŁĘDU

Metoda różniczki

zupełnej

Dla wielkości złożonej y=f(x

1

,x

2

,...x

n

)

gdy niepewności maksymalne Δx

1

,

Δx

2

, ... Δx

n

są małe w porównaniu z

wartościami zmiennych x

1

,x

2

, ... x

n

niepewność maksymalną wielkości y
wyliczamy z praw rachunku
różniczkowego:

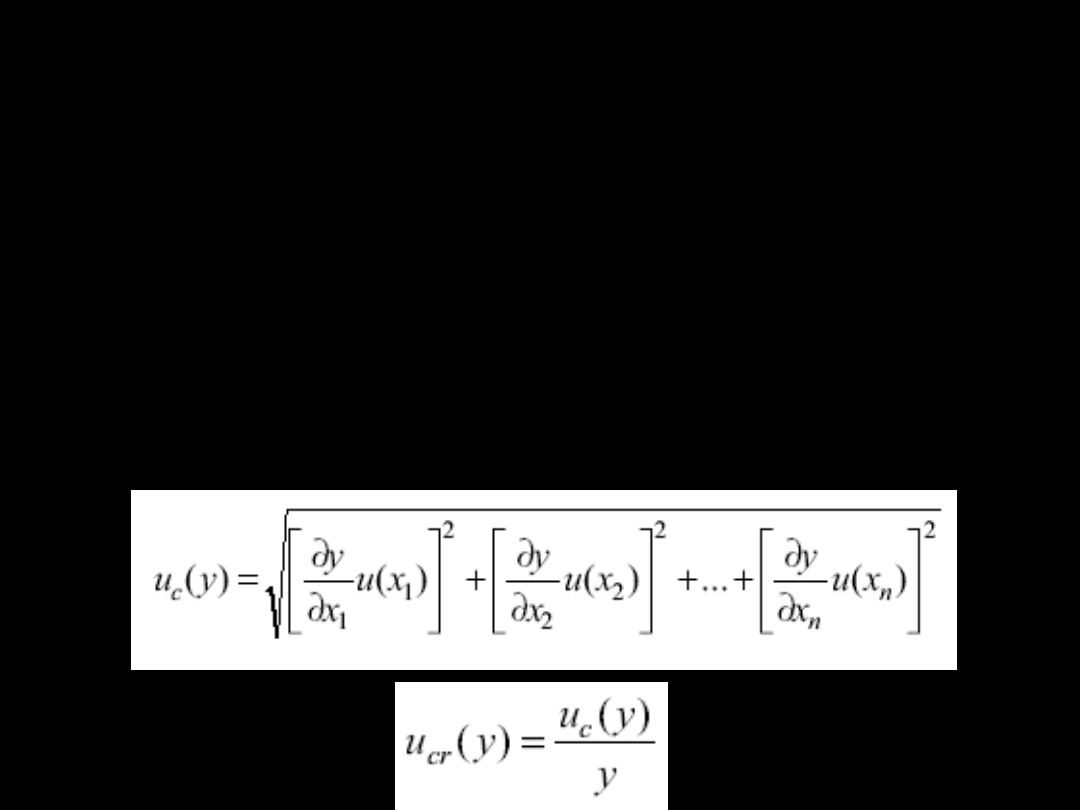
Prawo przenoszenia

niepewności

Niepewność standardową wielkości złożonej
y=f(x

1

,x

2

,...x

n

) obliczamy z tzw.

prawa

przenoszenia niepewności

jako sumę

geometryczną różniczek cząstkowych

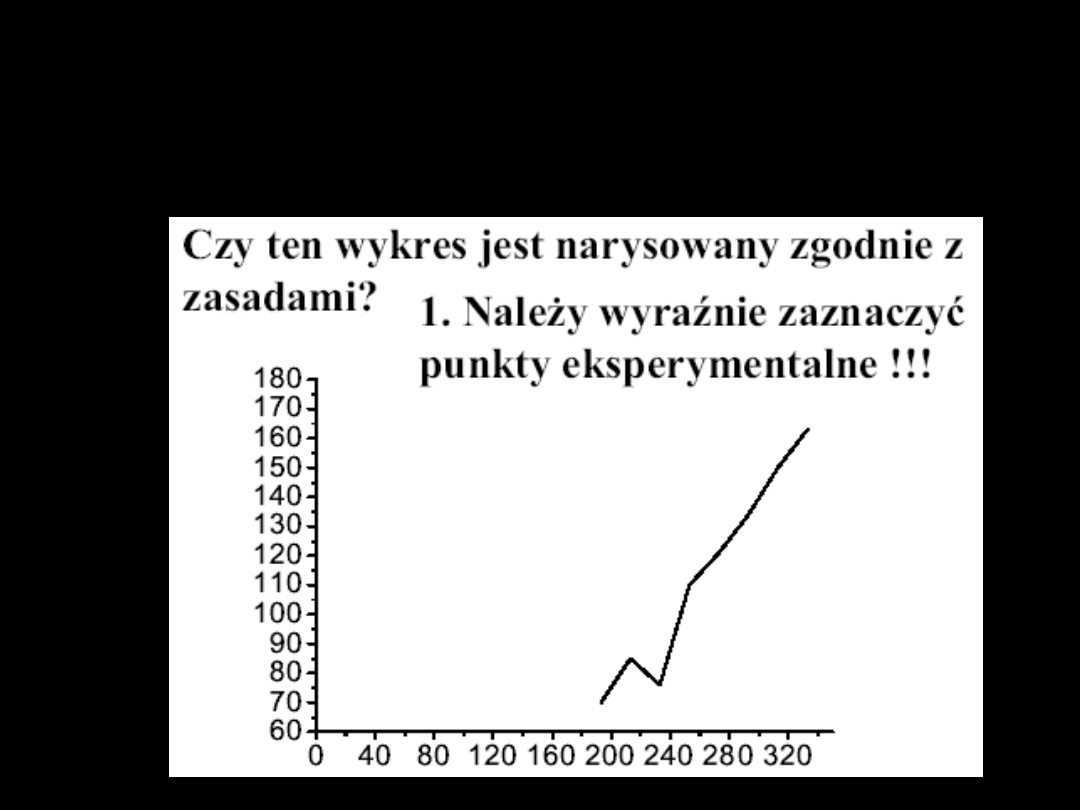
Zasada rysowania

wykresów

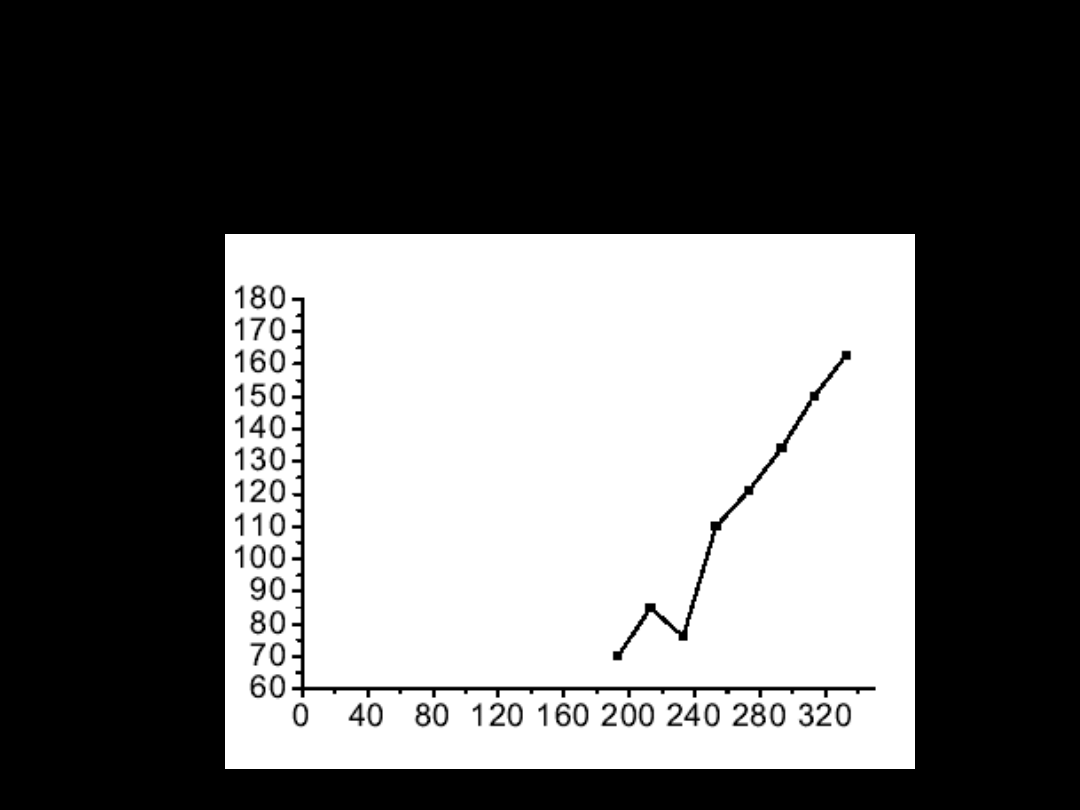
2. Trzeba nanieść błąd pomiaru

3. Dobrać zakresy osi współrzędnych

odpowiednio do zakresu zmienności danych
pomiarowych !!!

4. Właściwie opisać osie współrzędnych i

dobrać skalę, tak aby łatwo można było
odczytać wartości zmierzone.

5. Nie łączyć punktów eksperymentalnych

linią łamaną!!! Jeśli znany jest przebieg
teoretyczny to dokonać dopasowania teorii
do doświadczenia

6. Zadbać o aspekt estetyczny wykresu (opis,

zamknięcie ramką, itp.)

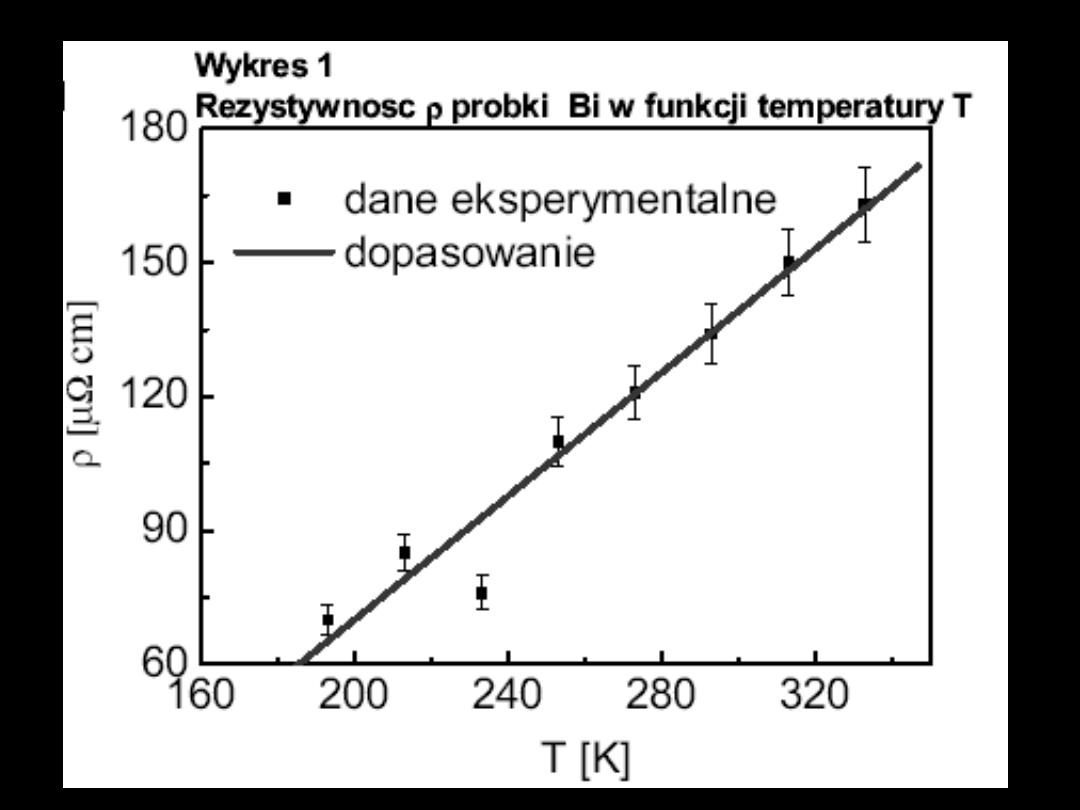
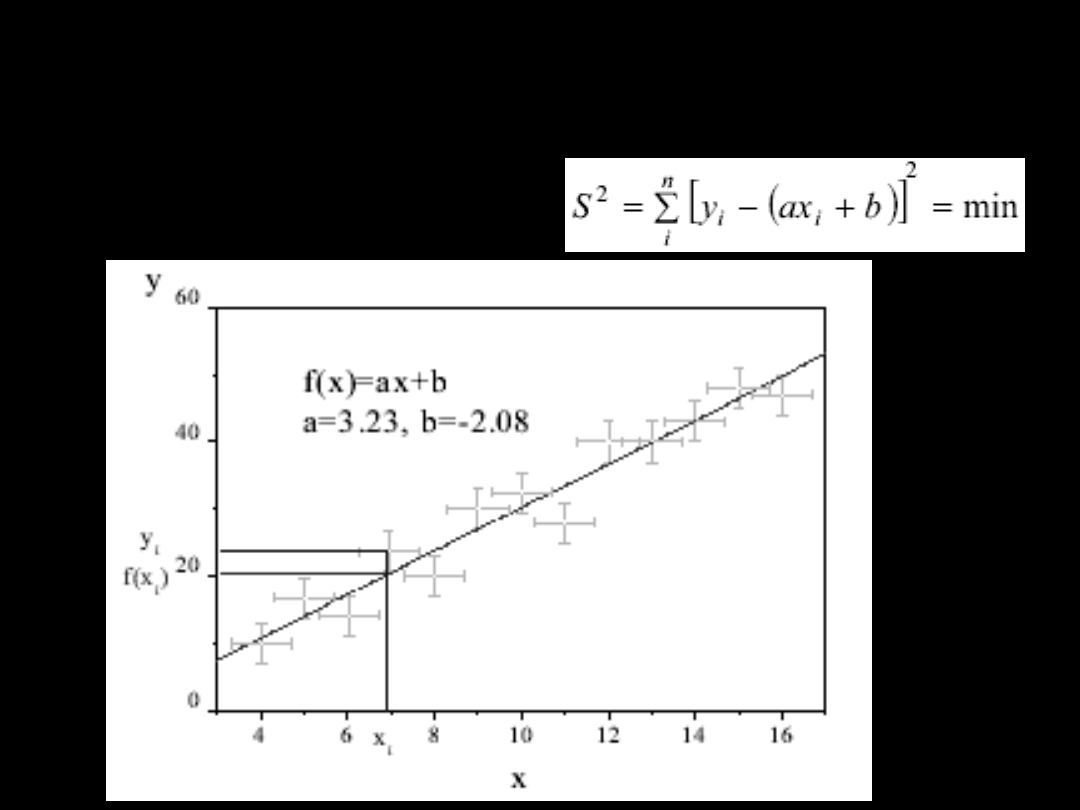
Metoda najmniejszych

kwadratów

Regresja liniowa

Warunek minimum funkcji dwu zmiennych:



Otrzymuje się układ równań liniowych dla
niewiadomych a i b



Rozwiązując ten układ równań otrzymuje
się wyrażenia na a i b

Z praw statystyki można wyprowadzić

wyrażenia na odchylenia standardowe obu
parametrów prostej:

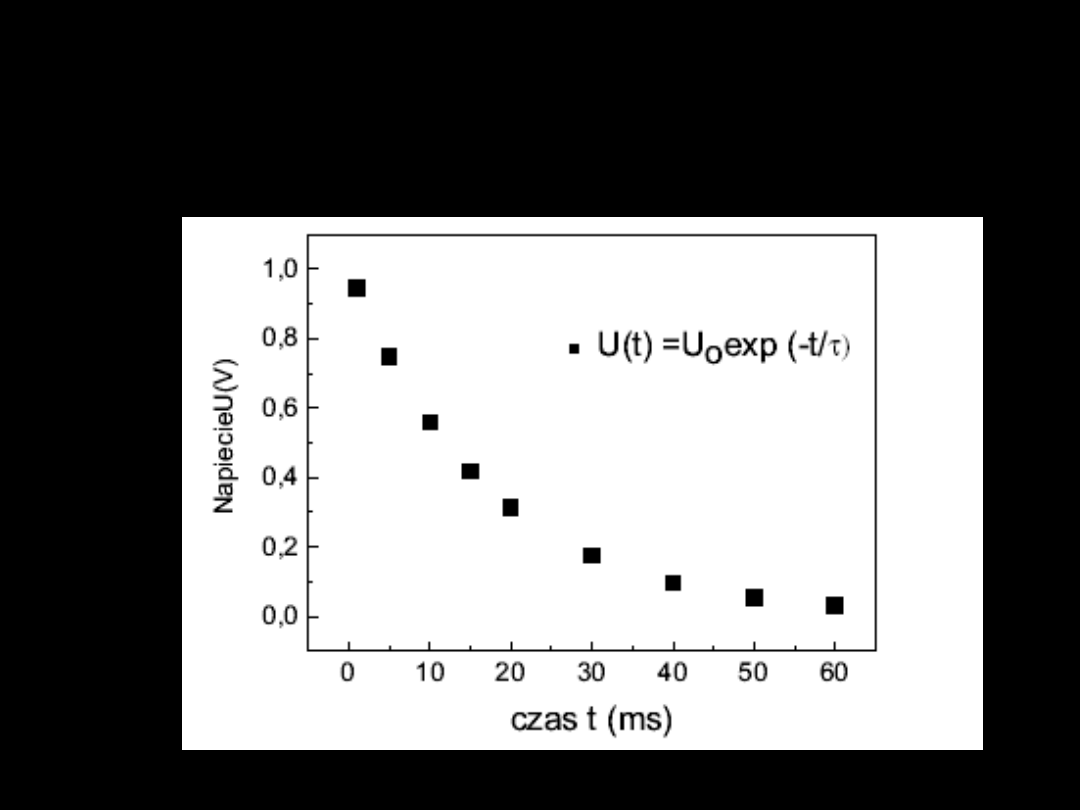
Linearyzacja danych

eksperymentalnych

PODSUMOWANIE

• Każdy pomiar w laboratorium jest obarczony

niepewnością pomiarową, którą eksperymentator

musi określić zgodnie z pewnymi zasadami.

• W pierwszej kolejności należy przeanalizować

źródła błędów, pamiętając, aby wyeliminować

wyniki obarczone błędem grubym. W

laboratorium studenckim błędy systematyczne z

reguły przewyższają błędy przypadkowe.

•

Wielokrotne powtarzanie pomiarów, gdy

dominuje błąd systematyczny, nie ma

sensu. W takim przypadku dokonujemy tylko

3-5 pomiarów w tych warunkach w celu

sprawdzenia powtarzalności.

• Gdy błąd przypadkowy dominuje w

eksperymencie, należy sprawdzić czy

rozkład wyników może być opisany funkcją

Gaussa czy też należy spodziewać się

innego rozkładu. W tym celu dokonujemy

wielokrotnego (np. 100 razy) pomiaru w

tych samych warunkach, obliczamy średnią i

wariancję rozkładu, rysujemy histogram,

etc.)

•

Jako miarę niepewności stosujemy raczej

niepewność standardową, rzadziej

niepewność maksymalną.

• W przypadku wielkości złożonej, stosujemy

prawo przenoszenia błędu. Staramy się

przeprowadzić analizę niepewności wielkości

złożonej tak, aby uzyskać informacje

dotyczące wagi przyczynków, jakie wnoszą do

całkowitej niepewności pomiary

poszczególnych wielkości prostych. W tym

celu należy analizować niepewności

względne.

•

Ważnym elementem sprawozdania z

przebiegu eksperymentu (i to nie tylko w

laboratorium studenckim) jest wykres.

Wykresy sporządzamy zgodnie z dobrymi

zasadami, pamiętając o jednoznacznym

opisie.

• Zawsze, gdy to możliwe, dokonujemy

linearyzacji danych eksperymentalnych, np.

rysując y i ln (x), lub log y i log x, lub y i 1/x

itp. Do tak przygotowanych danych można

zastosować metodę regresji liniowej

•

Jeżeli znane są podstawy teoretyczne

badanego zjawiska, na wykresie
zamieszczamy krzywą teoretyczną (linia
ciągła) na tle wyraźnych punktów
eksperymentalnych (dobieramy
odpowiednie symbole i nanosimy
niepewności eksperymentalne). Możemy
wcześniej dokonać dopasowania
parametrów przebiegu teoretycznego w
oparciu o znane metody „dopasowania”