DOMINOWANIE W

GRAFACH

Magdalena Lemańska

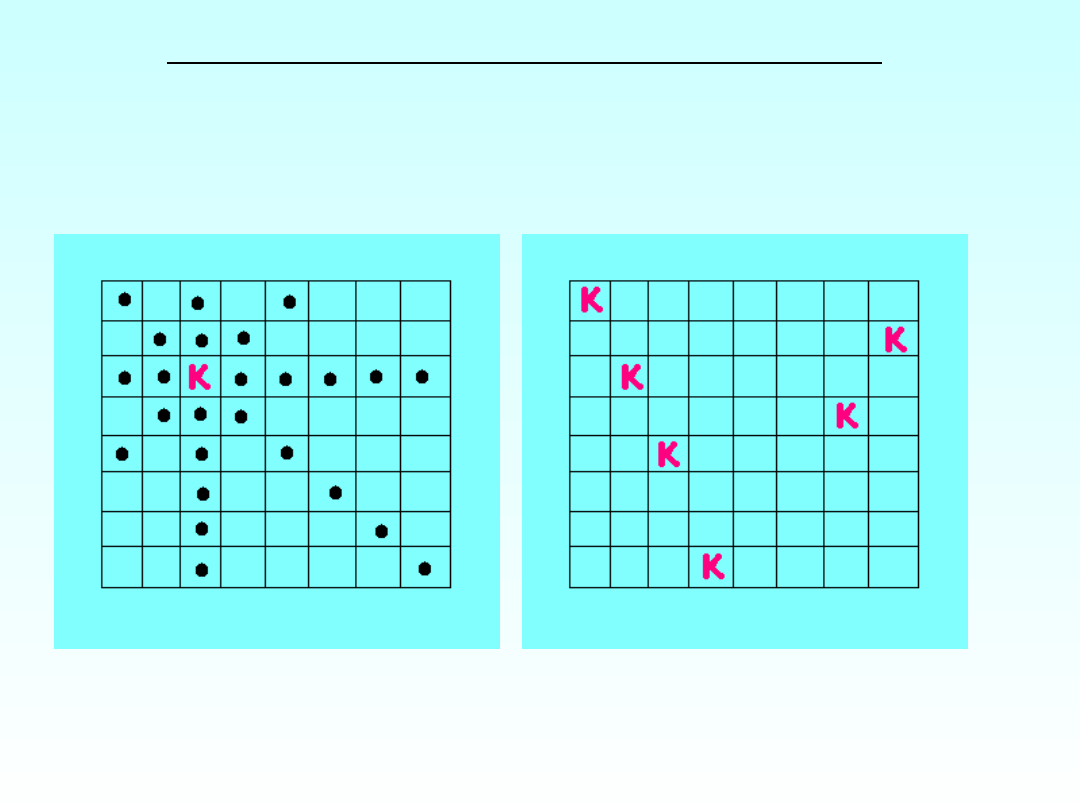
Problem pięciu królowych (1850 r).

Jaka jest najmniejsza liczba królowych jaka może być
rozmieszczona na szachownicy 8 x 8 tak, by każde pole było
w zasięgu jakiejś królowej?

Problem pięciu królowych-problem znalezienia „zbioru
dominującego” o mocy 5.

G=(V,E);
V=V(G)- zbiór wierzchołków, |V(G)|=n(G);
E=E(G)- zbiór krawędzi.

Zbiór D



V(G) jest zbiorem dominującym w

grafie G, jeśli każdy wierzchołek ze zbioru
V(G)-D w grafie G jest dominowany przez
wierzchołek ze zbioru D.

Dla danych wierzchołków x,y grafu G mówimy, że x dominuje y,
jeśli x=y albo jeśli xy



E(G). W takim razie x dominuje siebie

i wszystkie wierzchołki sąsiednie z wierzchołkiem x.

Otwarte sąsiedztwo wierzchołka v: N

G

(v) –

zbiór wszystkich wierzchołków
połączonych krawędzią z v;

Domknięte sąsiedztwo wierzchołka v: N

G

[v]=

N

G

(v)



{v}

Otwarte sąsiedztwo zbioru X



V: N

G

(X) =U

v

X

N

G

(v);

Domknięte sąsiedztwo zbioru:

N

G

[X]=N

G

(X)



X.

Jest kilka sposobów zdefiniowania zbioru dominującego,
każdy z nich ilustruje różne aspekty pojęcia dominowania.

d

G

(u,v) – odległość między u i v - długość

najkrótszej
(u-v)- ścieżki w G

Zbiór D



V(G) wierzchołków grafu G=(V,E) jest zbiorem

dominującym wtedy i tylko wtedy, gdy:

(i) dla każdego wierzchołka v



V-D istnieje wierzchołek u



D

taki, że v jest sąsiedni do u;

(ii) dla każdego wierzchołka v



V-D, d

G

(v,D)



1;

(iii) N

G

[D]=V;

(iv) dla każdego wierzchołka v



V-D, |N

G

(v)



D|



1, czyli

każdy wierzchołek v



V-D jest sąsiedni do przynajmniej

jednego wierzchołka z D;

(v) dla każdego wierzchołka v



V, |N

G

[v]



D|



1.

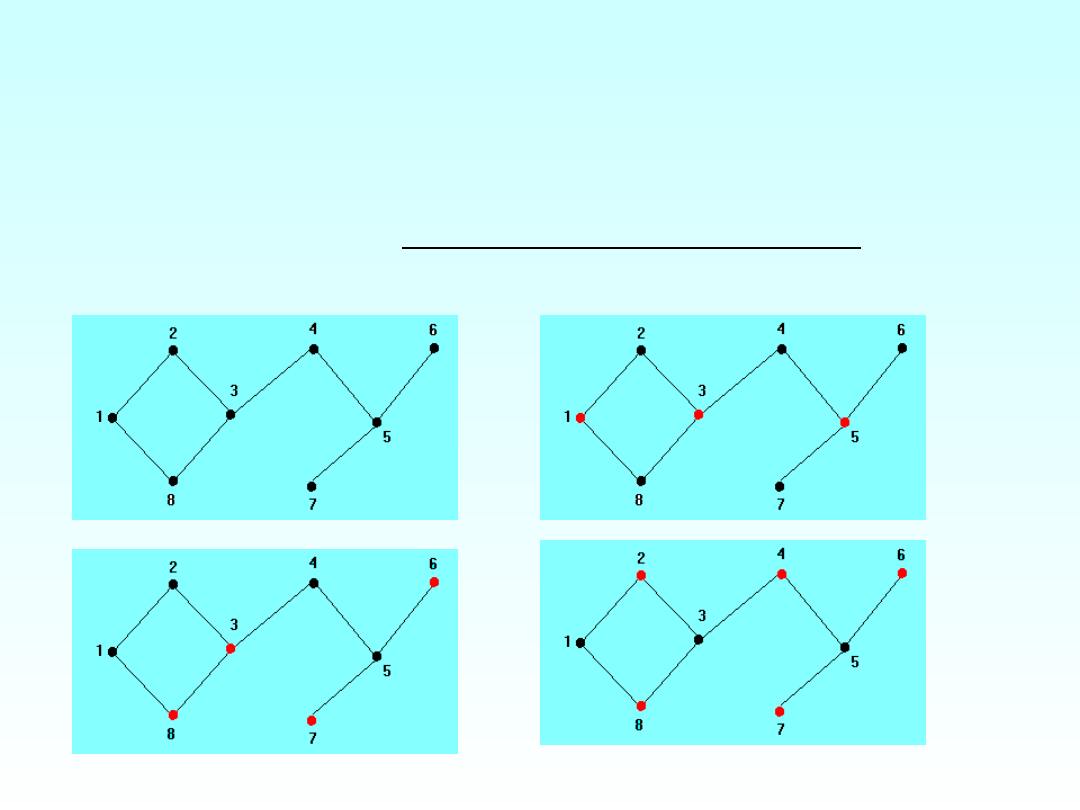
Jeśli D jest dominujący w G, to każdy nadzbiór D’



D też jest

dominujący.

Z drugiej strony, nie każdy podzbiór D”



D jest dominujący w G.

Zbiór dominujący D jest minimalny dominujący, jeśli żaden
podzbiór właściwy D”



D nie jest dominujący.

Twierdzenie 1. Zbiór dominujący D jest minimalnym zbiorem
dominującym wtedy i tylko wtedy, gdy dla każdego wierzchołka
u



D zachodzi jeden z dwóch warunków:

a) u jest izolowany w D;
b) istnieje v



V-D, dla którego N

G

(v)



D = {u}.

Niech D - zbiór dominujący i niech u



D. Mówimy, że

wierzchołek v jest prywatnym sąsiadem wierzchołka u
(w odniesieniu do D), jeśli N

G

[v]



D = {u}.

Zbiór prywatnych sąsiadów wierzchołka u:
PN[u,D]={v : N

G

[v]



D = {u} }.

u



PN[u,D], jeśli jest izolowany w podgrafie indukowanym

G[D], wtedy mówimy, że u jest swoim własnym prywatnym
sąsiadem.

Zbiór dominujący D jest minimalny dominujący wtedy i tylko
wtedy, gdy każdy wierzchołek z D ma przynajmniej jednego
prywatnego sąsiada.

Twierdzenie 2. Każdy spójny graf G rzędu co najmniej dwa
posiada zbiór dominujący D, którego dopełnienie V-D też jest
zbiorem dominującym.

Twierdzenie 3. Jeśli G jest grafem bez wierzchołków izolowanych,
to dopełnienie V-D każdego minimalnego zbioru dominującego D
jest zbiorem dominującym w G.

Moc najmniejszego zbioru dominującego w grafie G nazywamy
liczbą dominowania grafu G i oznaczamy



(G).

Moc największego zbioru minimalnego dominującego w grafie G
nazywamy górną liczbą dominowania grafu G i oznaczamy



(G).



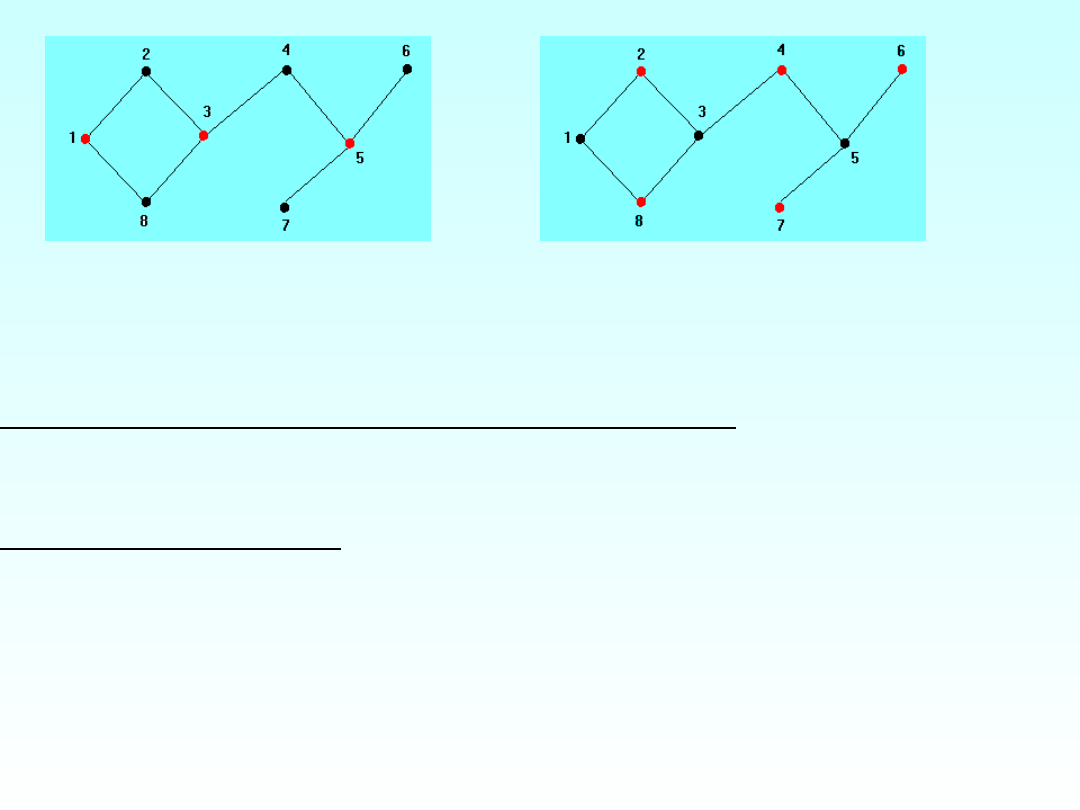
(G)=3



(G)=5

Ograniczenia na liczbę dominowania.

Twierdzenie 4 (Ore) Jeśli graf G nie ma wierzchołków
izolowanych, to



(G)



n/2.

Twierdzenie 5. Dla grafu G bez wierzchołków izolowanych,
rzędu n, gdzie n jest parzyste,



(G) = n/2 wtedy i tylko wtedy,

gdy składowymi grafu G są cykl C

4

albo korona H



K

1

dla

dowolnego grafu spójnego H.

Korona dwóch grafów G

1

i G

2

jest to graf G = G

1



G

2

powstały

z jednej kopii G

1

oraz |V(G

1

)| kopii G

2

gdzie i-ty wierzchołek G

1

jest sąsiedni do każdego wierzchołka w i-tej kopii G

2

.

W szczególności, G = H



K

1

jest grafem powstałym z kopii H

gdzie do każdego wierzchołka v



V(H) dodajemy nowy

wierzchołek v’ i krawędź wiszącą vv’.

Twierdzenie 6. Dla każdego grafu G,



(G)



n -



(G).

Podział krawędzi uv w grafie G otrzymujemy przez usunięcie
krawędzi uv, dodanie nowego wierzchołka w oraz dodanie
krawędzi uw i vw.

Ranny pająk jest to graf powstały przez podział co najwyżej
t-1 krawędzi gwiazdy K

1,t

dla t



0.

Twierdzenie 7. Dla każdego drzewa T,



(T) = n -



(T) wtedy

i tylko wtedy, gdy T jest rannym pająkiem.

Twierdzenie 8. Jeśli graf G nie ma wierzchołków izolowanych
oraz diam(G)



3, to



(Gd) = 2, gdzie Gd jest dopełnieniem grafu G.

Twierdzenie 9. Jeśli



(Gd)



3, to diam(G)



2.

Obwód grafu G, ozn. g(G) jest to długość najkrótszego cyklu
w G (jeśli graf posiada cykl).

Twierdzenie 10. Dla każdego grafu G,
(a)jeśli g(G)



5, to



(G)





(G),

(b)jeśli g(G)



6, to



(G)



2(



(G)-1).

Zbiory niezależne.

Niech i(G) oznacza moc najmniejszego maksymalnego zbioru
niezależnego w grafie G;



0

– moc największego zbioru niezależnego w G.

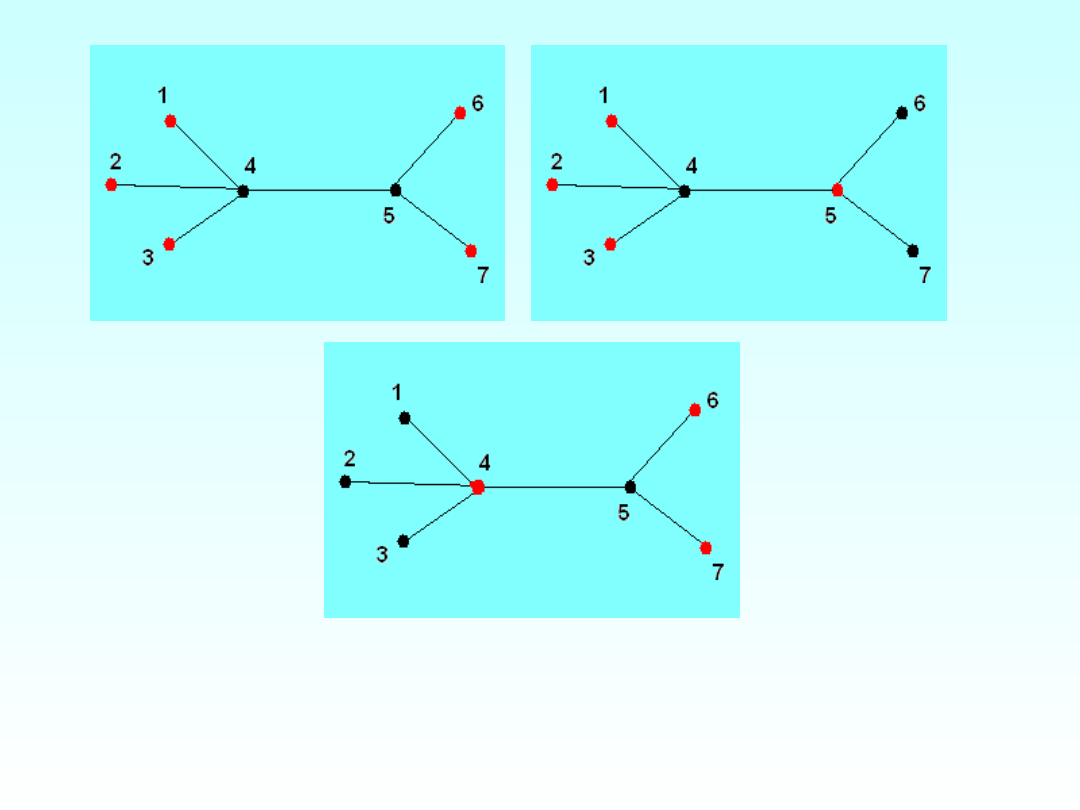
Drzewo T ma zbiory maksymalne niezależne o trzech rozmiarach.

i(T)=3



0

(T)=5

Twierdzenie 11. Niezależny zbiór S jest maksymalny niezależny
wtedy i tylko wtedy, gdy jest niezależny i dominujący.

Zbiory dominujące.

Drzewo T ma zbiory minimalne dominujące o czterech rozmiarach.



(T)=2



(T)=5

Wniosek: Każdy zbiór maksymalny niezależny jest zbiorem
dominującym.

Twierdzenie 12. Każdy zbiór maksymalny niezależny w G jest
minimalnym zbiorem dominującym w G.

Wniosek: Dla każdego grafu G,



(G)



i(G)





0

(G)





(G).

Zbiory nienadmierne.

Możemy powiedzieć, że zbiór D jest zbiorem minimalnym
dominującym w G wtedy i tylko wtedy, gdy:
(*) dla każdego wierzchołka v



D, istnieje wierzchołek

w



V-(D-{v}), który nie jest dominowany przez D-{v}.

Warunek (*) można wyrazić w języku „prywatnych sąsiadów”.

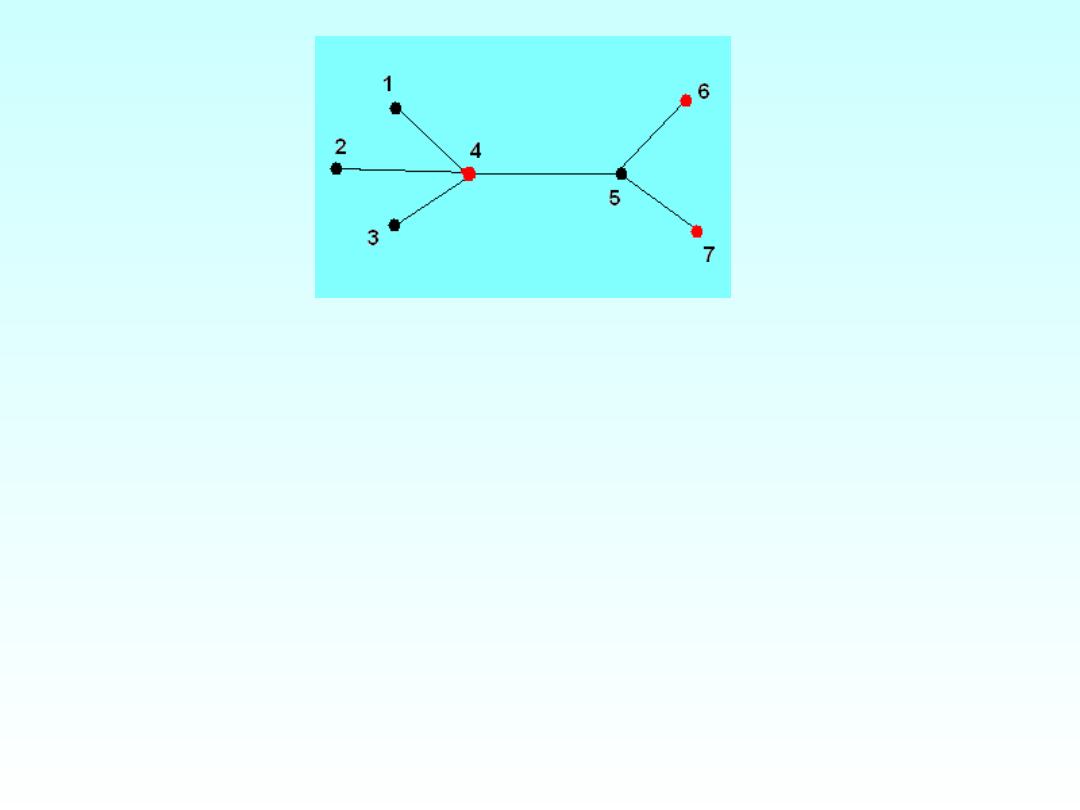
PN[4,D]={1,2,3,4}PN[6,D]={6} PN[7,D]={7}

PN[v,D]=N

G

[v]-N

G

[D-{v}]

W warunku (*) wierzchołek w musi być prywatnym sąsiadem
wierzchołka v w odniesieniu do D (możliwe jest w=v).

(**) zbiór D jest zbiorem minimalnym dominującym w G wtedy
i tylko wtedy, gdy dla każdego wierzchołka v



D, PN[v,D]





,

czyli każdy wierzchołek v



D ma przynajmniej jednego

prywatnego sąsiada.

Jeśli jest spełniony warunek (**), to mówimy, że zbiór D jest
zbiorem nienadmiernym.

Twierdzenie 13. Zbiór dominujący D jest minimalny dominujący
wtedy i tylko wtedy, gdy jest dominujący i nienadmierny.

Rozważmy maksymalne zbiory nienadmierne w grafie G.

Zbiór nienadmierny S jest maksymalny nienadmierny, jeśli
dla każdego wierzchołka u



V-S, zbiór S



{u} nie jest

nienadmierny, czyli istnieje przynajmniej jeden wierzchołek
w



S



{u}, który nie ma prywatnego sąsiada.

W takim razie, nienadmierny zbiór S jest maksymalny
nienadmierny, jeśli zachodzi następujący warunek:

(***) dla każdego wierzchołka w



V-S istnieje wierzchołek

v



S



{w}, dla którego PN[v, S



{w}] =



.

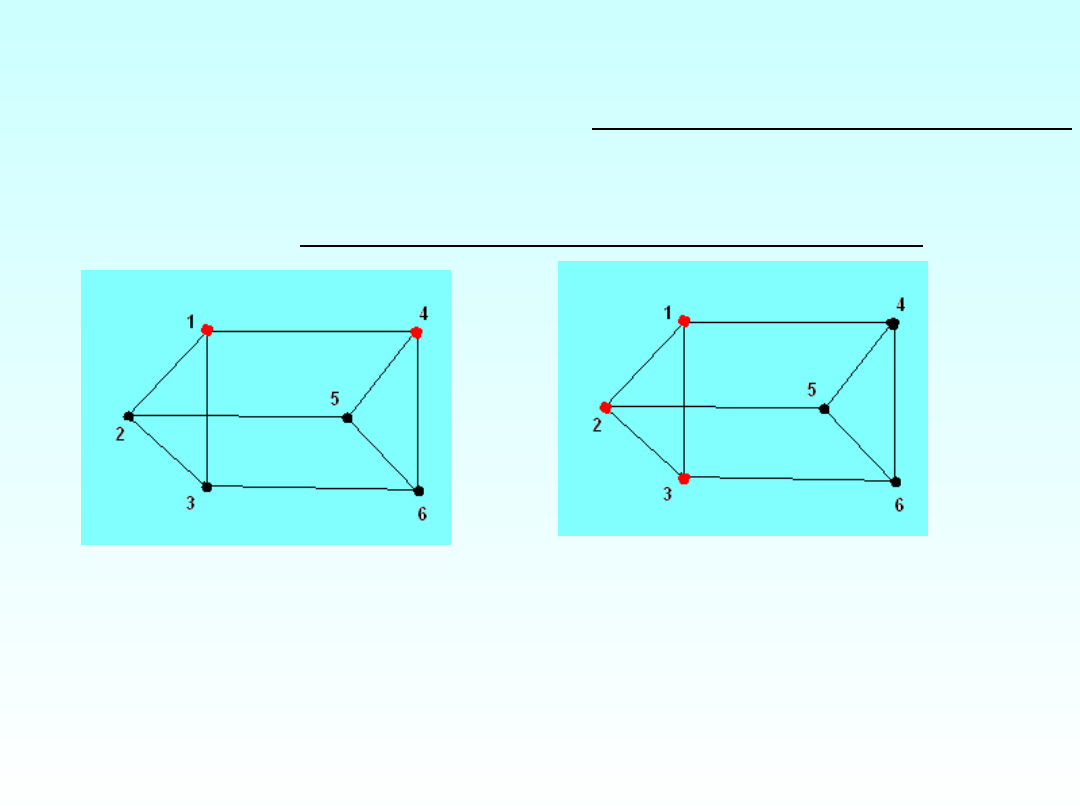
Moc najmniejszego zbioru maksymalnego nienadmiernego
w G oznaczamy ir(G) i nazywamy liczbą nienadmierności.

Moc największego zbioru nienadmiernego w G oznaczamy
IR(G) i nazywamy górną liczbą nienadmierności.

Na czerwono zaznaczone są zbiory maksymalne nienadmierne.

ir(G)=2

IR(G)=3

Twierdzenie 14. Każdy zbiór minimalny dominujący w G jest
zbiorem maksymalnym nienadmiernym w G.

Twierdzenie 15. Dla każdego grafu G,
ir(G)





(G)



i(G)





0

(G)





(G)



IR(G) .

ir(G)=4



(G)=5

Twierdzenie 16. Dla każdego grafu G,



(G)/2 < ir(G)





(G)



2ir(G)-1.

Twierdzenie 17. Dla każdego grafu G, IR(G)



n -



(G).

Inne rodzaje dominowania.

Oprócz dominowania, rozważa się dodatkowe własności zbiorów
wierzchołków, rozważając własności podgrafów indukowanych
przez te zbiory.

Dominowanie spójne

(Sampathkumar, Walikar, 1979)

Zbiór dominujący D nazywamy zbiorem spójnie dominującym,
jeśli D jest dominujący i G[D] jest spójny.

Moc najmniejszego zbioru spójnie dominującego w G
nazywamy liczbą dominowania spójnego grafu G i oznaczamy



c

(G).

Każdy zbiór spójnie dominujący jest dominujący, więc dla
każdego grafu spójnego G mamy



(G)





c

(G).

Twierdzenie 18. W każdym grafie spójnym G istnieje zbiór
spójnie dominujący S taki, że |S|



2



0

(G) – 1.

Wniosek: Dla każdego grafu spójnego G,



c

(G)



2



0

(G) – 1.

Twierdzenie 19. (Duchet, Meyniel)
Dla każdego grafu spójnego G,



c

(G)



3



(G)-2.

Lemat 20. Jeśli w grafie spójnym G istnieje najmniejszy
maksymalny zbiór nienadmierny, który jest zbiorem niezależnym,
to ir(G) =



(G) = i(G).

Twierdzenie 21. Jeśli G jest spójny, to ir(G)





c

(G)



3ir (G)- 2.

Wniosek: Jeśli G jest spójny, to



c

(G)



3i (G)- 2.

Nierówności są najlepsze z możliwych. Przedstawimy przykłady,
dla których zachodzą równości.

Twierdzenie 22. Jeśli G jest grafem, który nie zawiera K

1,3

ani

A-L-grafu jako podgrafów indukowanych, to ir(G) =



(G) = i(G).

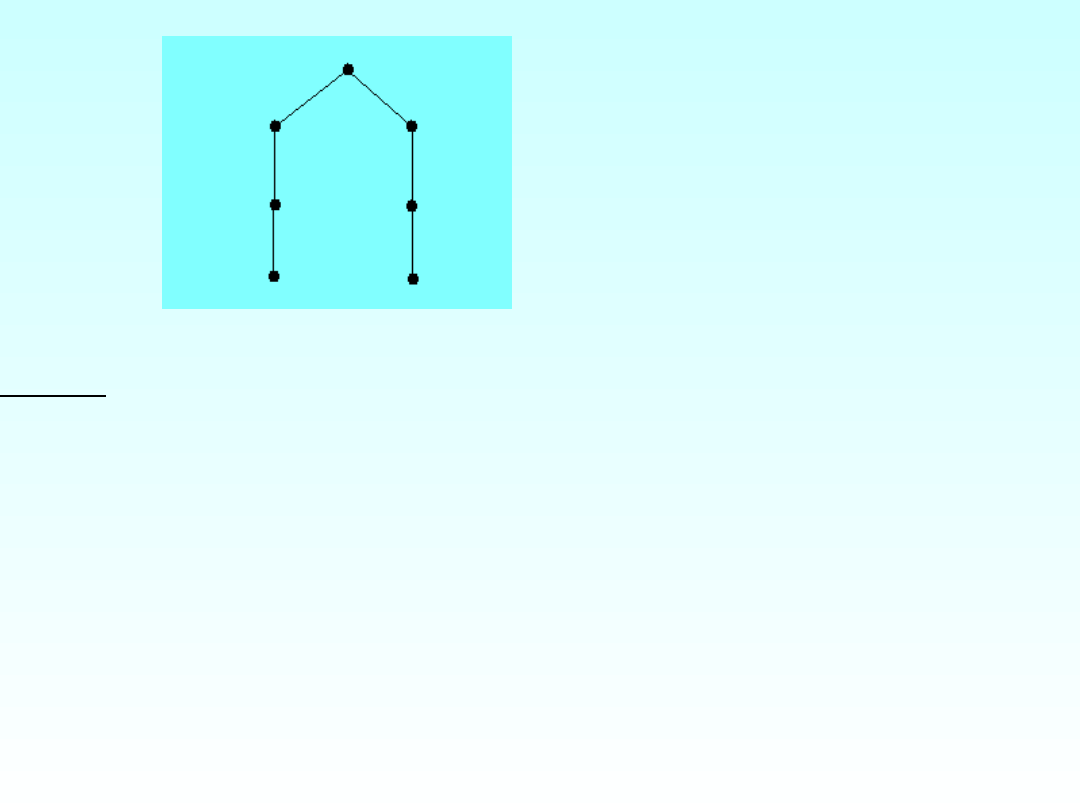
A-L- graf

Przykład 1. Dla dowolnej liczby naturalnej p rozważmy graf
G=C

3p

. W takim grafie



c

(C

3p

) = 3p-2. Zbiór D, do którego należy

co trzeci wierzchołek cyklu jest niezależnym zbiorem
nienadmiernym i dominującym, |D|=p. Widać, że taki graf nie
zawiera K

1,3

ani A-L-grafu jako podgrafu indukowanego, więc

ir(C

3p

) =



(C

3p

) = i(C

3p

)= p.

Przykład 2. Dla dowolnych liczb naturalnych s i t rozważmy graf H
otrzymany przez utożsamienie ze sobą jednego z wierzchołków
każdego z cykli C

3s

,C

3t .

W takim grafie jest 3(s+t)-1 wierzchołków

oraz



c

(H) = 3(s+t)-5.

W grafie tym znajdziemy najmniejszy maksymalny zbiór
nienadmierny, który jest również zbiorem niezależnym (do zbioru
tego musi należeć wierzchołek powstały przez utożsamienie), wiec
zgodnie z lematem 20 mamy ir(H) =



(H) = i(H) = s + t – 1.

Na rysunku jest przedstawiony graf G, dla którego s = t = 2,
a wierzchołek v z jednego cyklu jest utożsamiony z wierzchołkiem u
z drugiego. Widać, ze ilość wierzchołków w tym grafie
n = 11;



c

(G) =3(2 + 2) - 5 = 7; ir(G) =



(G) = i(G) = 2 + 2 - 1 = 3.

Z łańcucha dominowania oraz z tego, że



c

(G)



2



0

(G) – 1 wynika również, że



c

(G)



2



(G) – 1

oraz



c

(G)



2IR(G) – 1 Ograniczenia te sa

najlepsze z możliwych. Na przykład w cyklu C

5

mamy



0

(C

5

) =



(C

5

) = IR(C

5

) = 2;



c

(C

5

) = 3.

Dla każdego grafu spójnego G istnieje drzewo spinające T grafu G
takie, że



c

(G) =



c

(T) = n(G) – n

1

(T), gdzie n

1

oznacza ilość

wierzchołków końcowych w T. Drzewo to ma największą z możliwych
ilość wierzchołków końcowych.

(Sampathkumar, Walikar) Dla każdego spójnego podgrafu
spinającego H grafu G mamy



c

(H)





c

(G).

Twierdzenie 23. Dla każdego grafu spójnego G z n wierzchołkami
zachodzi równość



c

(G) +



(G) = n, gdzie



(G) oznacza

największą ilość wierzchołków końcowych w drzewie spinającym
grafu G.

Twierdzenie 24. Dla każdego grafu spójnego G z n wierzchołkami
i największym stopniem wierzchołka



(G) zachodzi nierówność



c

(G)



n -



(G).

W roku 1956 E.A. Nordhaus oraz J.W. Gaddum
znaleźli ograniczenia dla sumy i iloczynu liczb
chromatycznych grafu G i jego dopełnienia Gd:



(G)+



(Gd)



n+1, n





(G)



(Gd)



(n+1)(n+1)/4

Podobnych ograniczeń szuka się również dla
różnych liczb dominowania.

Ogólnie zagadnienia typu Nordhausa-Gadduma
polegają na znalezieniu podobnych ograniczeń
dla sumy i iloczynu pewnego niezmiennika grafu
G i tego samego niezmiennika dopełnienia Gd
grafu G. Hedetniemi i Laskar znaleźli górne
ograniczenie dla sumy liczb spójnego
dominowania dla grafu G i jego dopełnienia.

Twierdzenie 25. Jeśli G i jego dopełnienie Gd są spójne, to



c

(G)+



c

(Gd)



n+1.

Twierdzenie 26. Dla każdego drzewa T z co najmniej dwoma
wierzchołkami, różnego od gwiazdy, mamy



c

(T)+



c

(Td)



n.

Dominowanie wypukłe i słabo wypukłe.

(prof. Topp)

Zbiór X



V jest wypukły w G, jeśli wszystkie wierzchołki

każdej najkrótszej (x-y)-ścieżki należą do X dla każdych
x,y należących do zbioru X.

Zbiór X



V nazywamy słabo wypukłym w G, jeśli dla każdych

dwóch wierzchołków x,y należących do zbioru X istnieje
najkrótsza (x-y)-ścieżka, której wierzchołki należą do X.

Liczba dominowania słabo wypukłego w G,
oznaczana



wcon

(G), jest to moc najmniejszego zbioru słabo

wypukłego dominującego w G, natomiast liczba
dominowania wypukłego
w G, oznaczana



con

(G), jest to moc

najmniejszego zbioru
wypukłego w G.

Dominowanie spójne: dla każdych dwóch wierzchołków u,v
należących do zbioru dominującego D, istnieje (u-v)- ścieżka, której
wierzchołki należą do D;

Dominowanie słabo wypukłe: dla każdych dwóch wierzchołków u,v
należących do zbioru dominującego D, istnieje najkrótsza (u-v)- ścieżka,
której wierzchołki należą do D;

Dominowanie wypukłe: dla każdych dwóch wierzchołków u,v
należących do zbioru dominującego D, wierzchołki ze wszystkich
najkrótszych (u-v)- ścieżek należą do D.

Obserwacja 28: Dla każdego grafu spójnego G jest



(G)





c

(G)





wcon

(G)





con

(G).

Twierdzenie29 Dla dowolnych k,r



N, r



3, istnieje graf G taki,

że



c

(G) -



wcon

(G) = r oraz



con

(G) -



c

(G) =



con

(G) -



wcon

(G) =k.

Twierdzenie 30 Każda z różnic



con

(G) -



0

oraz



con

(G) -



może

być dowolnie duża.

Twierdzenie 31 Jeśli G jest spójny, nie posiada wierzchołków
końcowych oraz nie istnieje w G cykl indukowany długości
mniejszej niż 6, to



con

(G) = n.

Lemat 27 Dla każdej liczby naturalnej n



7 i dla każdej

liczby naturalnej k, 7



k



n, istnieje graf G rzędu n

taki, że



con

(G)=



wcon

(G) = k.

Hipoteza Vizinga: Dla każdych dwóch grafów G, H jest



(G)



(H)





(G



H )

Twierdzenie 32 (Canoy, Garces) Zbiór D



V(G



H ) jest

wypukły w G



H wtedy i tylko wtedy, gdy D=D

G



D

H

, gdzie

D

G

jest wypukły w G i D

H

jest wypukły w H.

Twierdzenie 33 Jeśli D jest dominujący w G



H, to D

G

jest

dominujący w G i D

H

jest dominujący w H.

Twierdzenie 34 Dla dowolnych grafów spójnych G i H jest



con

(G)



con

(H)





con

(G



H).

Niech G



H będzie iloczynem kartezjańskim grafów spójnych

G i H. Dla zbioru D



V(G



H ) oznaczmy:

D

G

= {u



V(G): (u,v)



D dla pewnego v



V(H)};

D

H

= {u



V(H): (u,v)



D dla pewnego v



V(G)}.

Dominowanie słabo spójne

(Dunbar, Grossman, Hedetniemi, Hatting, 1997)

Podgraf słabo indukowany przez D



V(G) -

graf G[D]

w

=(N

G

[D],E

w

); e



E

w

jeśli e ma

przynajmniej jeden koniec w D;

D



V(G) – zbiór słabo spójny dominujący, jeśli D jest

dominujący oraz G[D]

w

(<D>

w

) jest spójny;

Liczba dominowania słabo spójnego grafu G, ozn.



w

(G)-

moc najmniejszego zbioru słabo spójnego dominującego w G.

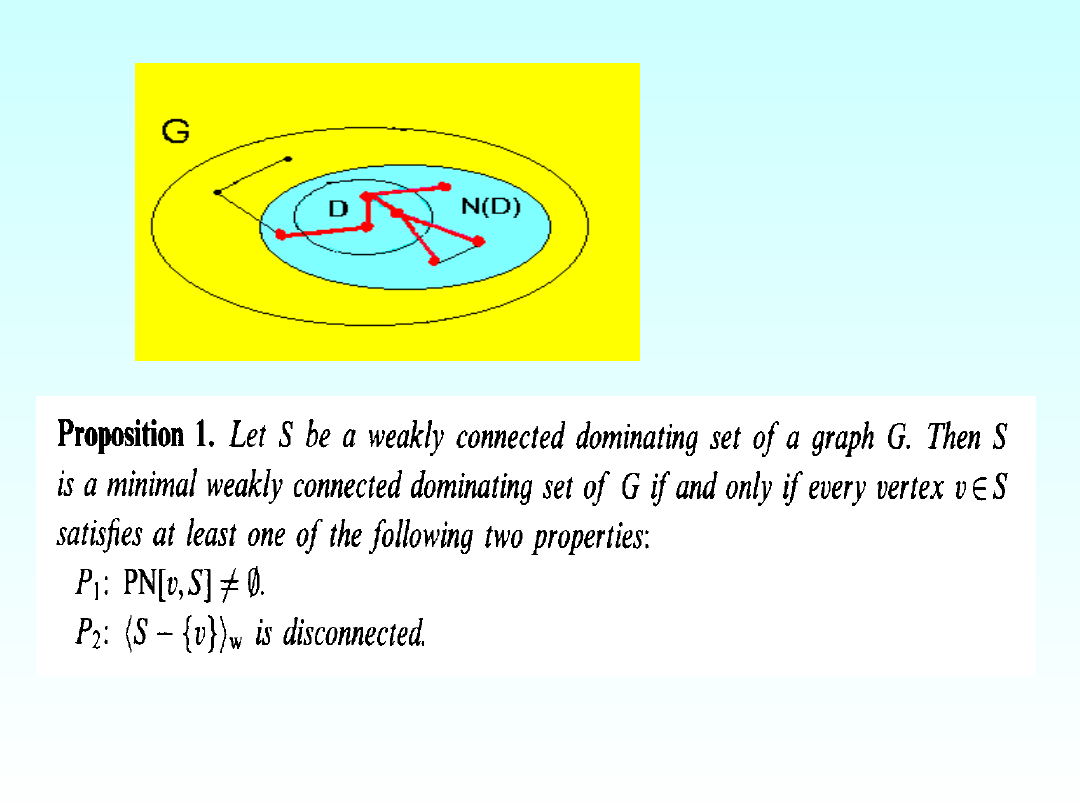
G[D]

w

= (

N

G

[D], E

w

)

Równości między liczbami dominowania.