
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
Macierzowa metoda przemieszczeń
materiały do wykładu nr 2

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
2
Macierzowa metoda przemieszczeń
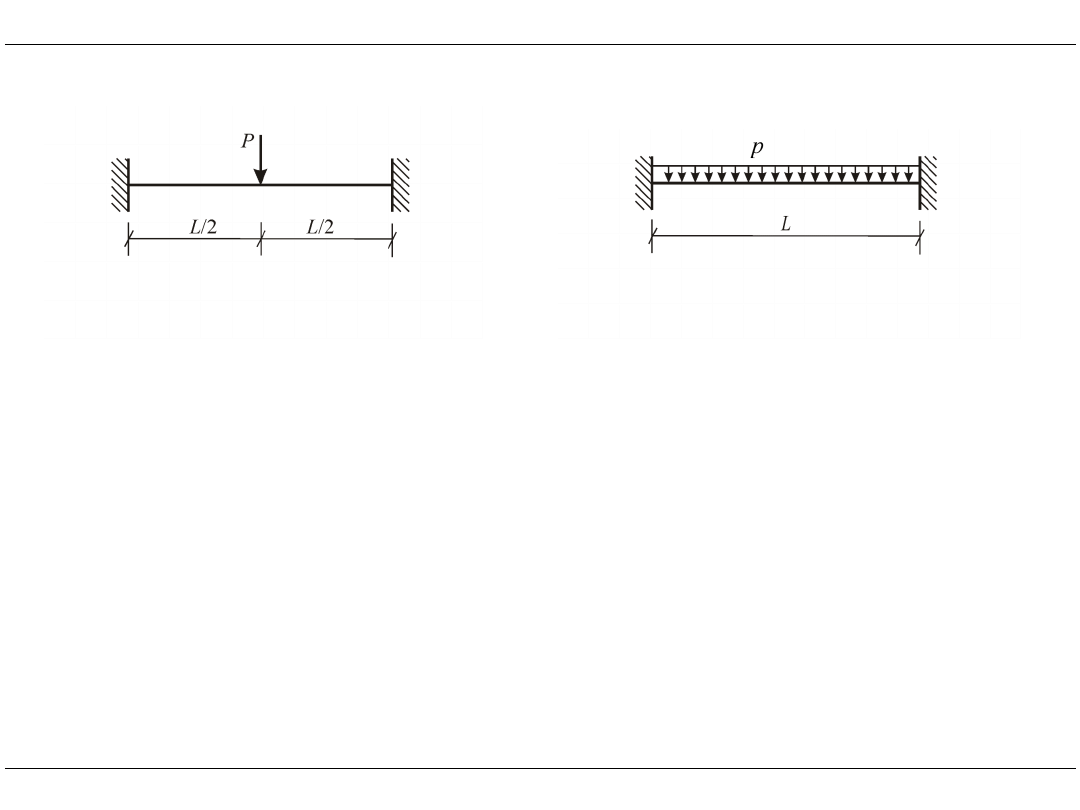
Wpływ obciążeń przęsłowych na wektor obciążenia
0
el
j
j
j
j
S
k D
S
Siły przywęzłowe w elemencie powstają:
• na skutek przemieszczeń końców elementu
• jako reakcje od obciążeń przęsłowych
T
j
ik
ik
ki
ki
T
M
T
M
S
0
0
0
0
0
T
j
ik
ik
ki
ki
T
M
T
M
S
Równanie równowagi dla elementu obciążonego w przęśle:
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
3
Macierzowa metoda przemieszczeń

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
4
Macierzowa metoda przemieszczeń
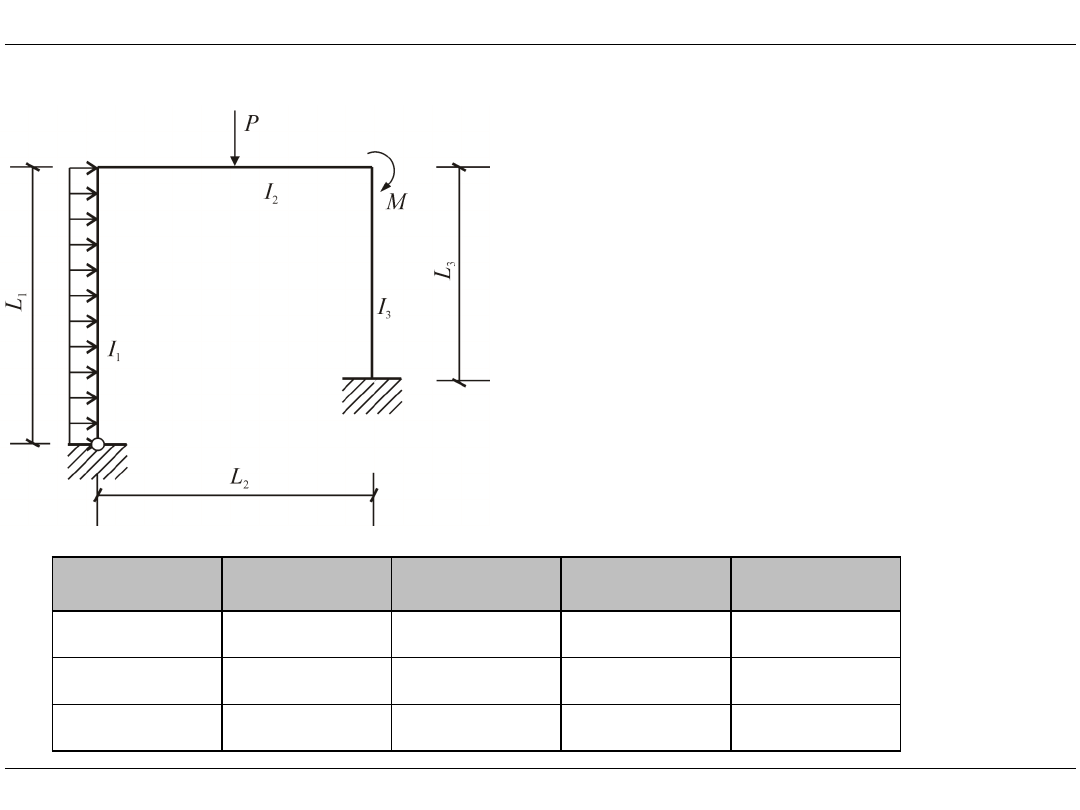
Agregacja macierzy sztywności
• Proces budowy globalnej macierzy sztywności układu z macierzy sztywności
poszczególnych elementów.
• W procesie agregacji wykorzystuje się wektory alokacji.
• W wektorach alokacji pamiętane są adresy poszczególnych przemieszczeń
lokalnych.
• W wektorach alokacji uwzględnione są warunki brzegowe.
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
5
Macierzowa metoda przemieszczeń
Agregacja macierzy sztywności i wektora obciążeń
v
i
j
i
v
k
j
k
Element 1
Element 2
Element 3
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
6
Macierzowa metoda przemieszczeń
Agregacja globalnej macierzy sztywności
1
1
1
1
3
2
3
2
1
1
1
1
1
1
1
1
2
2
1
1
1
1
1
1
1
1
1
3
2
3
2
1
1
1
1
1
1
1
1
2
2
1
1
1
1
12
6
12
6
6
4
6
2
12
6
12
6
6
2
6
4
el
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
k
2
2
2
2
3
2
3
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
3
2
3
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
12
6
12
6
6
4
6
2
12
6
12
6
6
2
6
4
el
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
k
3
3
3
3
3
2
3
2
3
3
3
3
3
3
3
3
2
2
3
3
3
3
3
3
3
3
3
3
2
3
2
3
3
3
3
3
3
3
3
2
2
3
3
3
3
12
6
12
6
6
4
6
2
12
6
12
6
6
2
6
4
el
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
k
𝐤
1
𝑒𝑙
=
𝐤
2
𝑒𝑙
=
𝐤
3
𝑒𝑙
=
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
7
Macierzowa metoda przemieszczeń
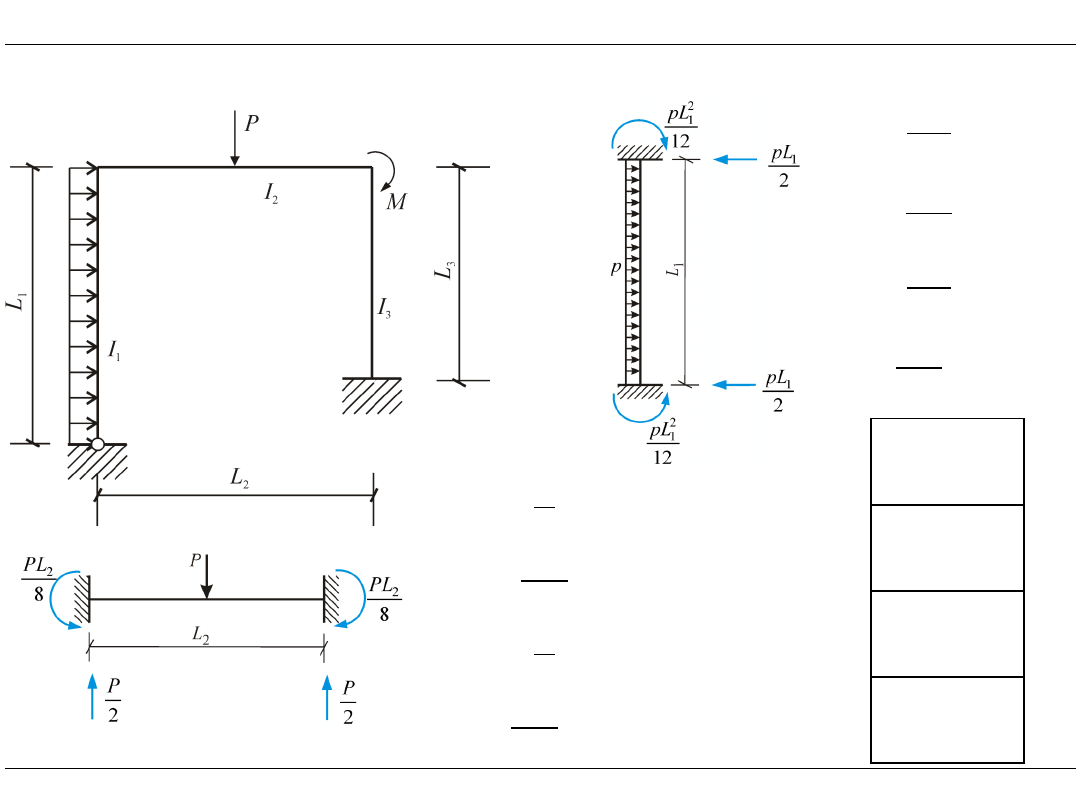
Agregacja globalnego wektora sił przywęzłowych od obciążeń przęsłowych
1
2
1
0
1
1
2
1
2
12
2
12
pL
pL
pL
pL
S
2
0
2
2
2
8
2
8
P
PL
P
PL
S
0
3
0
0
0
0
S
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
8
Macierzowa metoda przemieszczeń
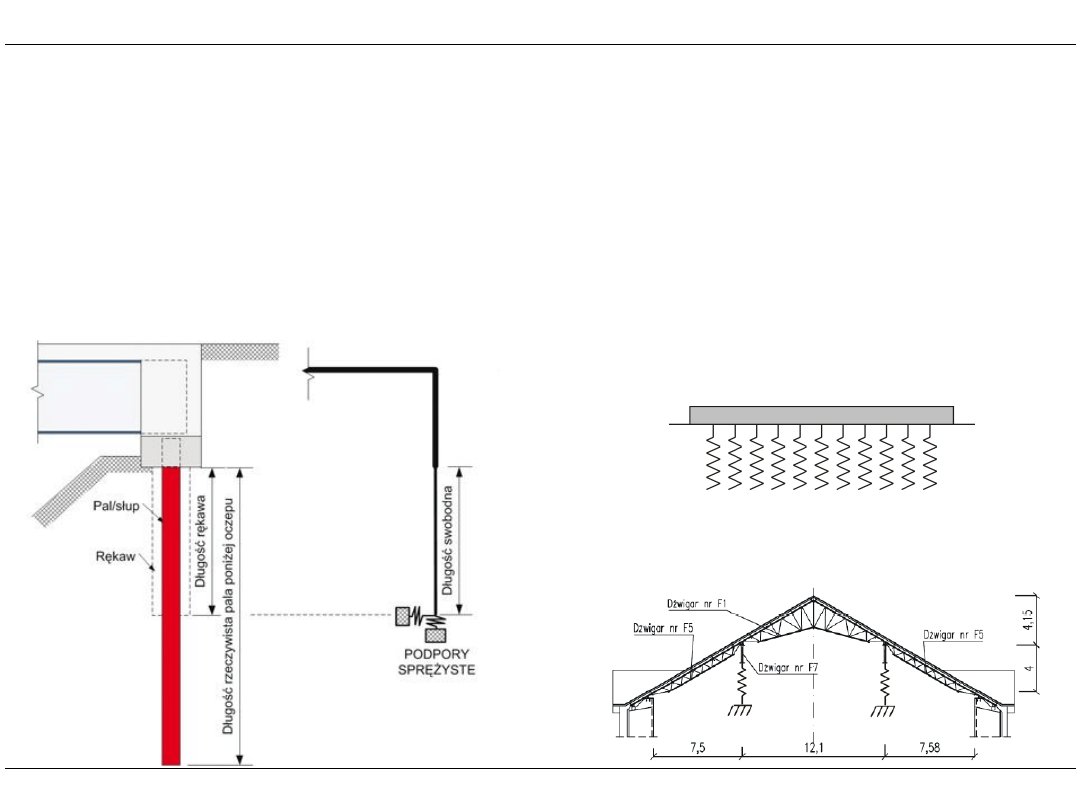
Uwzględnianie więzi sprężystych
• W układach konstrukcyjnych oprócz podpór sztywnych występują podpory sprężyste.
• Zwykle zakłada się, że siła w podporze sprężystej jest wprost proporcjonalna
do przemieszczenia.
• Podpory sprężyste charakteryzuje sztywność:
sztywność podpór liniowych k
x
, k
y
[kN/m],
sztywność podpór obrotowych k
j
[kNm/rad].
Rys. Tomasz Musiał
Obiekty mostowe z przyczółkami zintegrowanymi - cz. I
Inżynier budownictwa, 2012-05-10
Rys. Piotr Iwicki
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
9
Macierzowa metoda przemieszczeń
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
10
Macierzowa metoda przemieszczeń
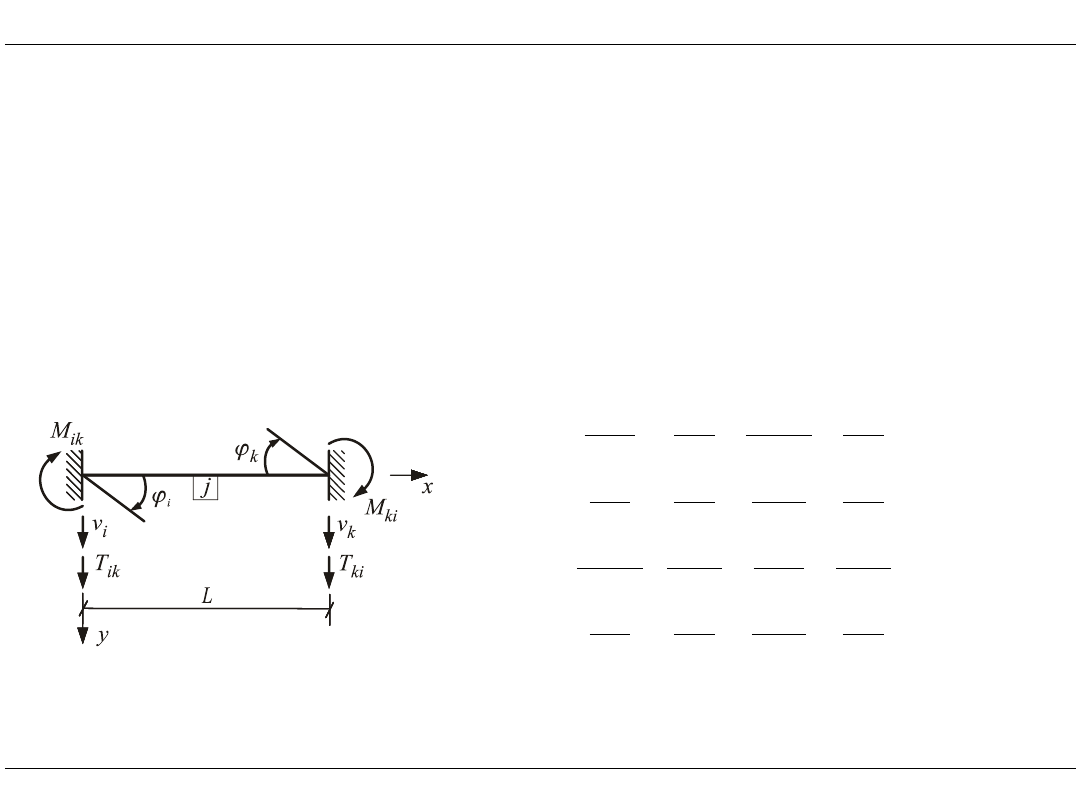
Macierzowa metoda przemieszczeń (MMP)
• Niewiadomymi są uogólnione przemieszczenia
• Najprostszym przypadkiem MMP jest Bezpośrednia Metoda Przemieszczeń
(BMP), w której stosuje się element belkowy macierzy sztywności o pełnym
komplecie więzów, co wiąże się z koniecznością zakwalifikowania obrotów
w przegubach wewnętrznych oraz podporach przegubowych jako
niewiadomych.
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
6
4
6
2
12
6
12
6
6
2
6
4
el
j
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
k
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
11
Macierzowa metoda przemieszczeń
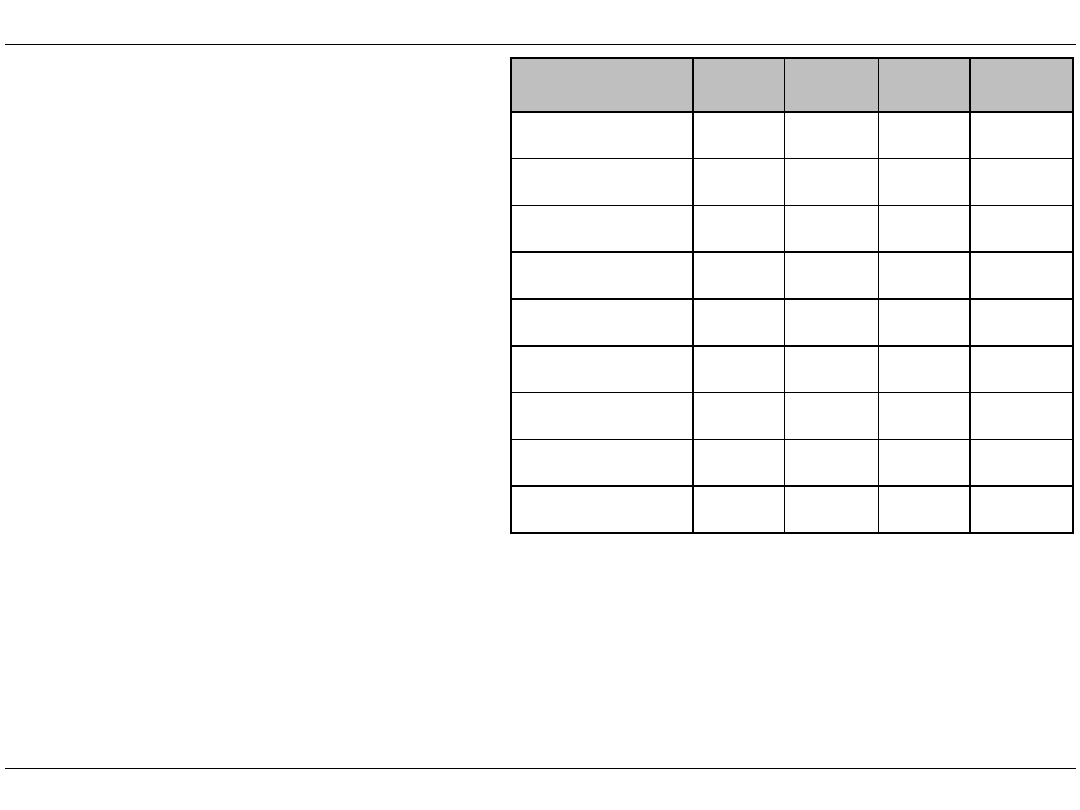
Algorytm MMP
1. Dyskretyzacja układu
2. Określenie wektora przemieszczeń węzłowych
3. Określenie wektora obciążeń węzłowych
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
12
Macierzowa metoda przemieszczeń
Algorytm MMP
4. Zestawienie wektorów alokacji
v
i
j
i
v
k
j
k
Element 1
Element 2
Element 3
Element 4
Element 5
Element 6
Element 7
Element 8
Element 9

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
13
Macierzowa metoda przemieszczeń
Algorytm MMP
5. Utworzenie dla każdego elementu j
macierzy sztywności
wektorów sił przywęzłowych od obciążeń przęsłowych
6. Agregacja globalnej macierzy sztywności układu z macierzy sztywności
poszczególnych elementów
7. Agregacja globalnego wektora obciążeń węzłowych od obciążeń
przęsłowych z poszczególnych wektorów sił przywęzłowych od obciążeń
przęsłowych
8. Obliczenie sumarycznego wektora obciążeń węzłowych

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
14
Macierzowa metoda przemieszczeń
Algorytm MMP
9. Rozwiązanie macierzowego równania równowagi
10. Wykonanie dla każdego elementu j
utworzenie wektora przemieszczeń przywęzłowych
z odpowiednich elementów globalnego wektora przemieszczeń
obliczenie sił przywęzłowych
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
15
Macierzowa metoda przemieszczeń
Kondensacja i modyfikacja macierzy sztywności
W praktycznych zadaniach dla określonych elementów mogą wystąpić:
• zerowe elementy wektora
przemieszeń przywęzłowych
• zerowe elementy wektora sił
przywęzłowych
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
16
Macierzowa metoda przemieszczeń
Modyfikacja macierzy sztywności
Proces modyfikacji:
• ma miejsce przy występowaniu w węzłach więzów geometrycznych
• polega na usunięciu z wyjściowej macierzy sztywności wierszy i kolumn
odpowiadających zerowym przemieszczeniom końców elementu
j
j
j
S
k D
*
*
*
r
T
r
r
rr
r
S
k
k
D
S
k
k
D
*
*
*
S
k D
*
T
r
r
S
k D

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
17
Macierzowa metoda przemieszczeń
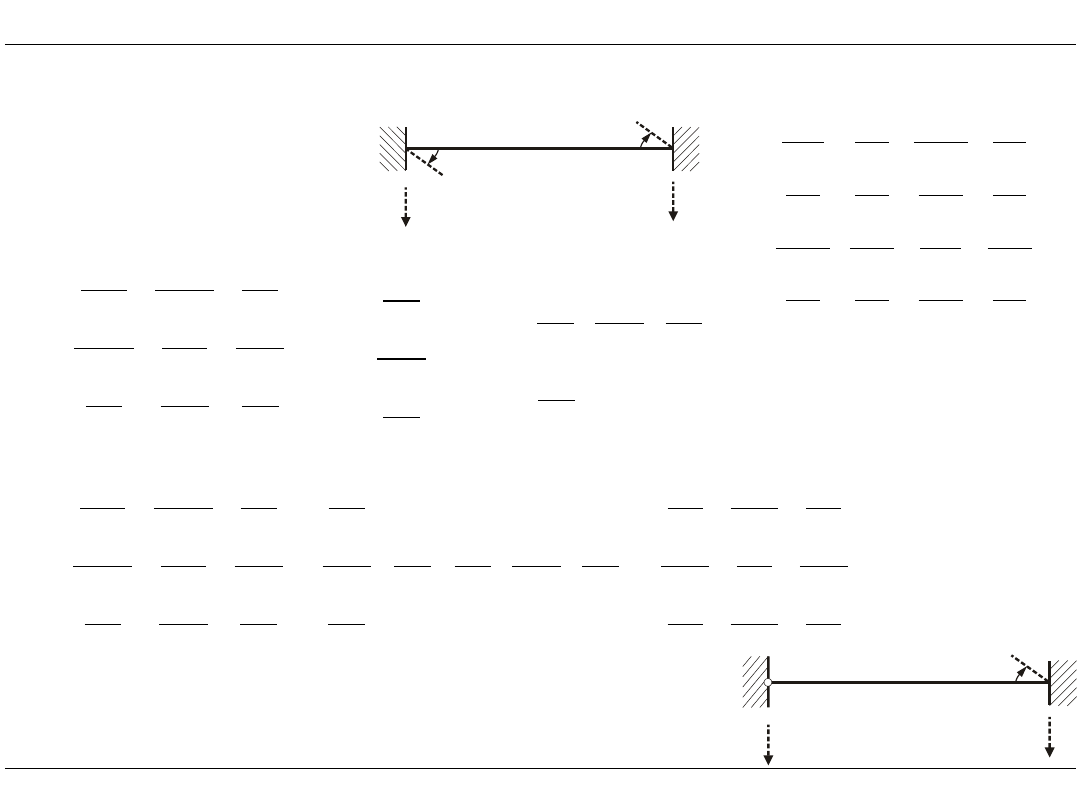
Kondensacja macierzy sztywności
Proces kondensacji:
• ma miejsce przy występowaniu zerowych sił wewnętrznych w węzłach
• proces wyznaczania macierzy sztywności elementu o niektórych więzach
zwolnionych polegający na przekształceniu macierzy sztywności pręta
o komplecie więzów łączących go z węzłami
j
j
j
S
k D
'
'
11
12
2
21
22
2
S
k
k
D
S
k
k
D
'
'
11
12
2
'
2
21
22
2
S
k D
k D
S
k D
k D
0
1
'
2
22
21
D
k k D
'
'
1
'
11
12
22
21
S
k D
k k k D
'
1
'
11
12
22
21
S
k
k k k
D
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
18
Macierzowa metoda przemieszczeń
Kondensacja macierzy sztywności
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
6
4
6
2
12
6
12
6
6
2
6
4
EI
EI
EI
EI
l
l
l
l
EI
EI
EI
EI
l
l
l
l
EI
EI
EI
EI
l
l
l
l
EI
EI
EI
EI
l
l
l
l
k
Kondensacja względem
i
j
1
11
12
22
21
'
k
k
k k k
3
3
2
11
3
3
2
2
2
12
12
6
12
12
6
6
6
4
EI
EI
EI
l
l
l
EI
EI
EI
l
l
l
EI
EI
EI
l
l
l
k
2
12
2
6
6
2
EI
l
EI
l
EI
l
k
21
2
2
6
6
2
EI
EI
EI
l
l
l
k
22
4EI
l
k
3
3
2
2
3
3
2
3
3
2
2
2
2
3
3
2
2
2
2
2
12
12
6
6
3
3
3
12
12
6
6
6
6
2
3
3
3
'
4
6
6
4
2
3
3
3
EI
EI
EI
EI
EI
EI
EI
l
l
l
l
l
l
l
EI
EI
EI
EI
l
EI
EI
EI
EI
EI
EI
l
l
l
l
EI
l
l
l
l
l
l
EI
EI
EI
EI
EI
EI
EI
l
l
l
l
l
l
l
k
v
k
f
k
f
i
v
i
v
k
f
i
v
i
v
k
f
k
v
i
v
k
f
k
f
i
v
i
v
k
f
i
v
i
v
k
f
k
v
i
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
19
Macierzowa metoda przemieszczeń
Modyfikacja i kondensacja macierzy – podsumowanie
kondensacja
modyfikacja
*
*
*
S
k D
'
'
'
S
k D
3
2
3
2
2
3
2
3
3
3
3
3
3
3
3
3
3
ik
i
ik
i
ki
k
EI
EI
EI
l
l
l
T
v
EI
EI
EI
M
l
l
l
T
v
EI
EI
EI
l
l
l
j
3
2
2
2
2
12
6
6
6
4
2
6
2
4
ik
i
ik
i
ki
k
EI
EI
EI
l
l
l
T
v
EI
EI
EI
M
l
l
l
M
EI
EI
EI
l
l
l
j
j
Wyszukiwarka
Podobne podstrony:
PSYCHOLOGIA SPOLECZNA materiały na wykłady, WSFiZ, psychlogia społeczna
materiały na wykład 4a
materiały na wykład 3
Grzyby uprawne + materiały na wykłady, wydział leśny, UBOT
materialy na wyklad 6a id 28522 Nieznany
materiały na wykład 5
materialy na wyklad 6b id 28523 Nieznany
materialy na wyklad 1 id 285225 Nieznany
popityka stabilizacyjna, uczelnia WSEI Lublin, UCZELNIA WSEI 2 1, ekonomia 2rok 4 semestr, makro, po
materiały na wykład 4b
Inzynieria środowiska zaoczne materiały na wykład
materialy na diagnoze, Wyklad VI diagnoza
POLITYKA SPOLECZNA wyklad 8 maja, uczelnia WSEI Lublin, UCZELNIA WSEI, MATERIAŁY NA EGZAMIN 2 semest
Rezerwy na świadczenia pracownicze - materiały do wykladu 2014, UE KATOWICE ROND, I stopień, VI seme
Pytania na Bilskiego, Podręczniki i materiały dydaktyczne, wykłądy, finanse międzynarodowe
fin i rach wyklady letni 2012 LISTA 4, Materiały na studia ZIP, I Rok, Finanse
Zagadnienia na egzamin z Gutka, ZUT-Energetyka-inżynier, III Semestr, Wytrzymałość materiałów II, Wy
Zaliczenie z biofizyki- wykłady 2008, far, biofizyka, egzamin, materiały na ćwiczenia
więcej podobnych podstron