
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
Macierzowa metoda przemieszczeń
materiały do wykładu nr 3

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
2
Macierzowa metoda przemieszczeń
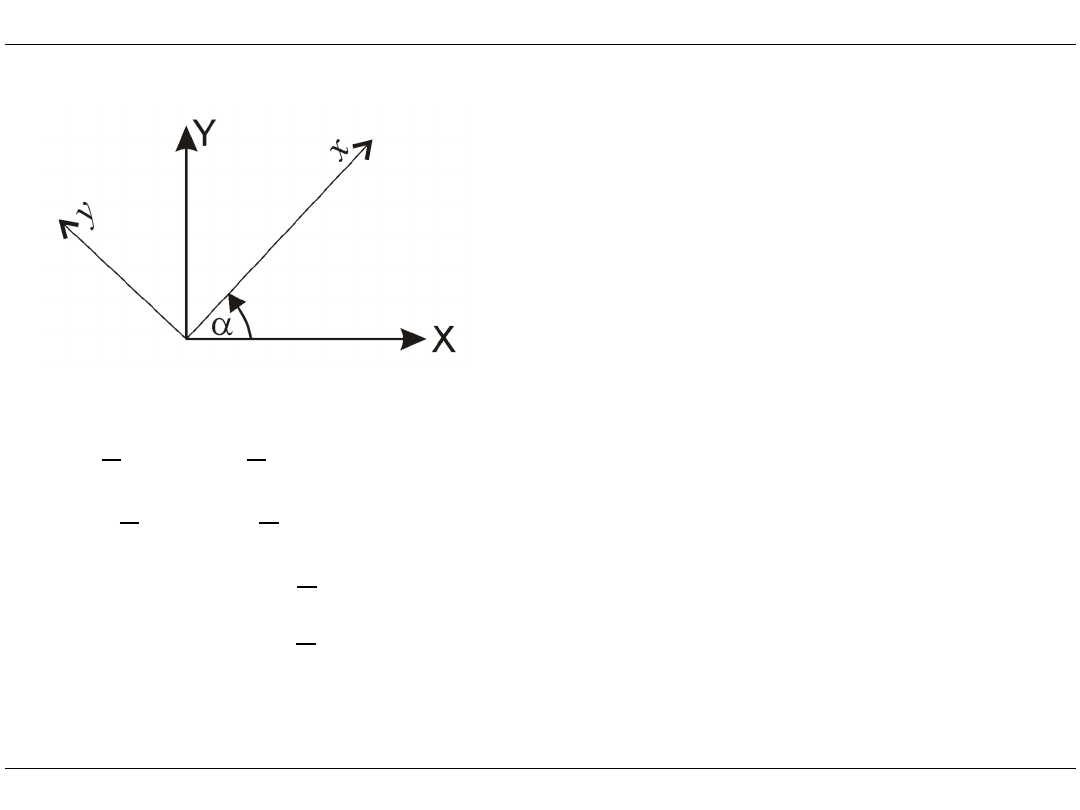
Transformacja układu współrzędnych
• Dla elementów nachylonych pod dowolnym kątem konieczna jest ich
transformacja do globalnego układu współrzędnych
• Macierzowe równanie równowagi dla elementu
zapisane jest w lokalnym układzie współrzędnych
• Macierzowe równanie równowagi układu
zapisane jest w globalnym układzie współrzędnych
• Zamiana układu lokalnego na globalny na poziome elementu wiąże się
z transformacją macierzy sztywności i wektorów obciążeń
• Transformację wykonuje się poprzez macierz transformacji z układu
globalnego do lokalnego
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
3
Macierzowa metoda przemieszczeń
cos
sin
u
u
v
XY
– układ globalny
x
y
– układy lokalny
sin
cos
v
u
v
u
c
s
u
v
s
c
v
cos
sin
c
s
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
4
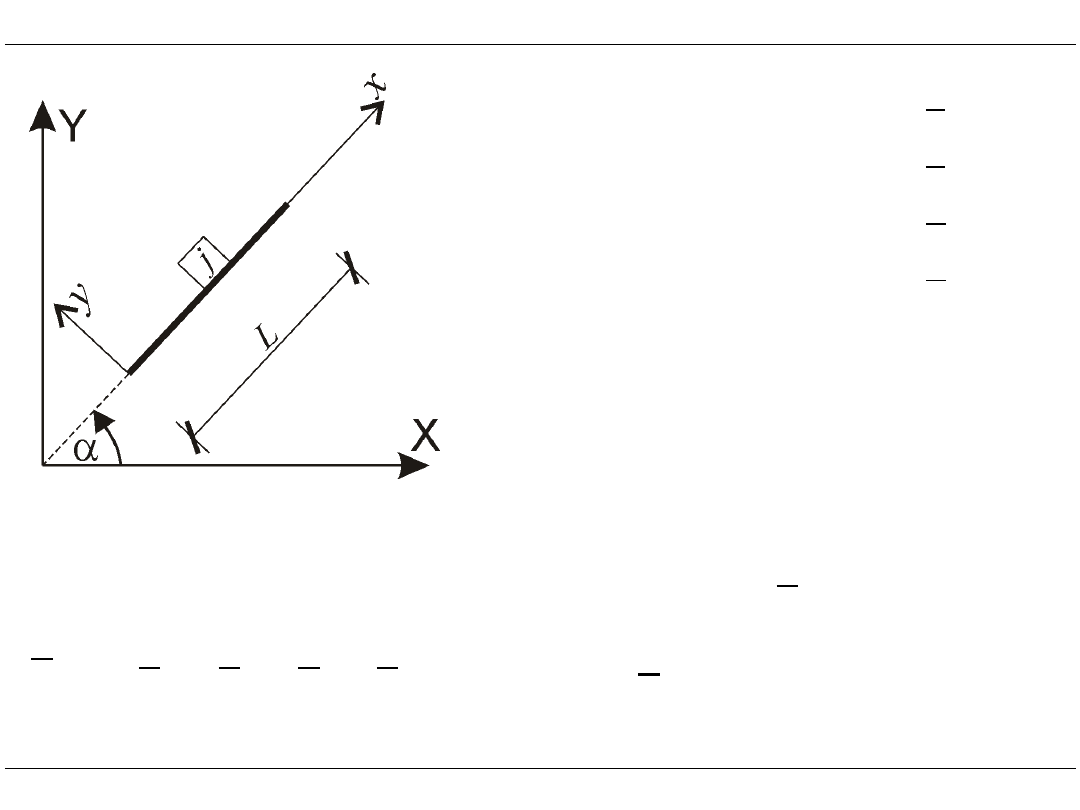
Macierzowa metoda przemieszczeń
T
j
a
a
b
b
u
v
u
v
D
T
j
a
a
b
b
u
v
u
v
D
0
0
0
0
0
0
0
0
a
a
a
a
b
b
b
b
u
u
c
s
v
v
s
c
u
u
c
s
v
v
s
c
j
j
j
D
L D
T
j
j
j
D
L D

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
5
Macierzowa metoda przemieszczeń
j
j
j
S
L S
0
j
j
j
j
S
k D
S
0
j
j
j
j
j
L S
k D
S
j
j
j
D
L D
0
j
j
j
j
j
j
j
L S
k L D
L S
1
1
1
0
j
j
j
j
j
j
j
j
j
j
L L S
L k L D
L L S
0
T
j
j
j
j
j
j
S
L k L D
S
0
j
j
j
j
S
k D
S

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
6
Macierzowa metoda przemieszczeń
Algorytm BMP – ogólny
1. Dyskretyzacja układu
2. Zestawienie wektora przemieszczeń węzłowych
3. Zestawienie wektora obciążeń węzłowych
4. Zestawienie cech elementów, wektorów alokacji
5. Utworzenie dla każdego elementu j
lokalnej macierzy sztywności
wektorów sił przywęzłowych od obciążeń przęsłowych
transformacja macierzy sztywności do układu globalnego
transformacja wektorów sił do układu globalnego
T
j
j
j
j
k
L k L
j
k
0
j
S
0
0
T
j
j
j
S
L S
R
q

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
7
Macierzowa metoda przemieszczeń
Algorytm BMP – ogólny
6. Agregacja macierzy do macierzy globalnej
7. Agregacja wektora do wektora
8. Rozwiązanie macierzowego układu równowagi
9. Obliczenia dla każdego elementu j
ekstrakcja z globalnego wektora przemieszczeń
wektora przemieszczeń końców elementów
transformacja do układu lokalnego
obliczenie sił przywęzłowych
0
Kq
P
R
R
j
D
j
j
j
D
L D
0
j
j
j
j
S
k D
S
j
k
K
0
j
S
0
R
1
q
K P
q
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
8
Macierzowa metoda przemieszczeń
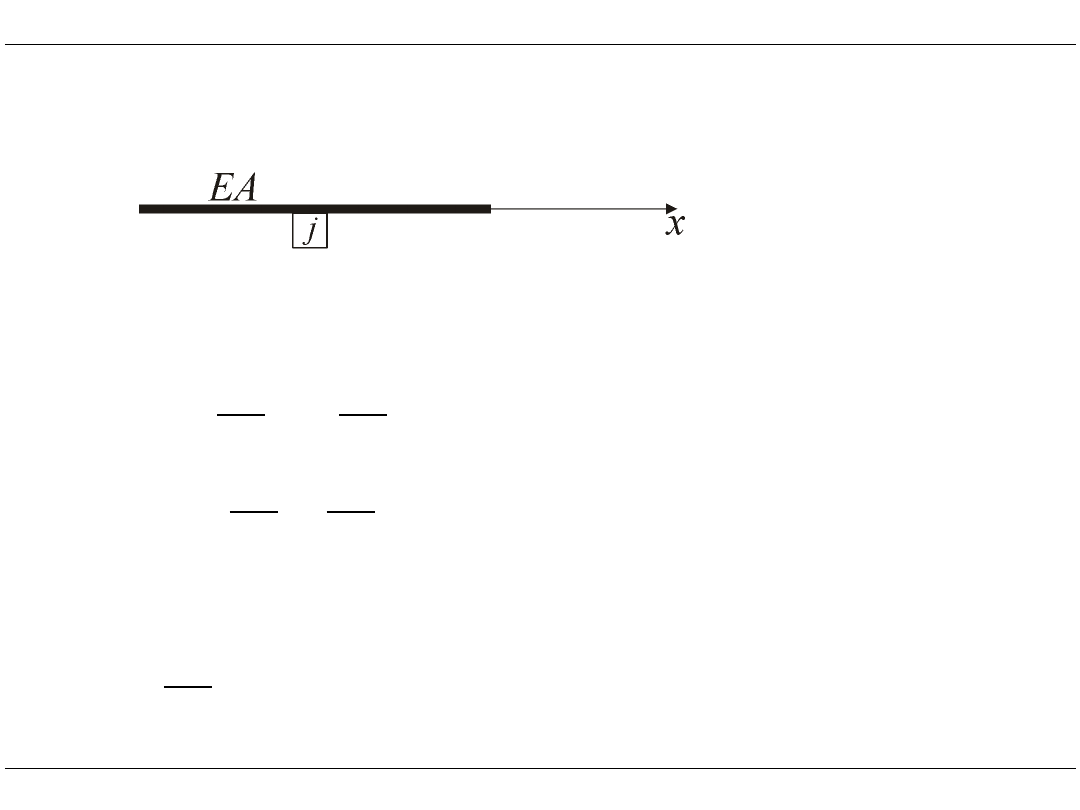
Element prętowy
i
i
k
k
EA
EA
N
u
L
L
N
u
EA
EA
L
L
1
1
1
1
j
EA
L
k
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
9
Macierzowa metoda przemieszczeń
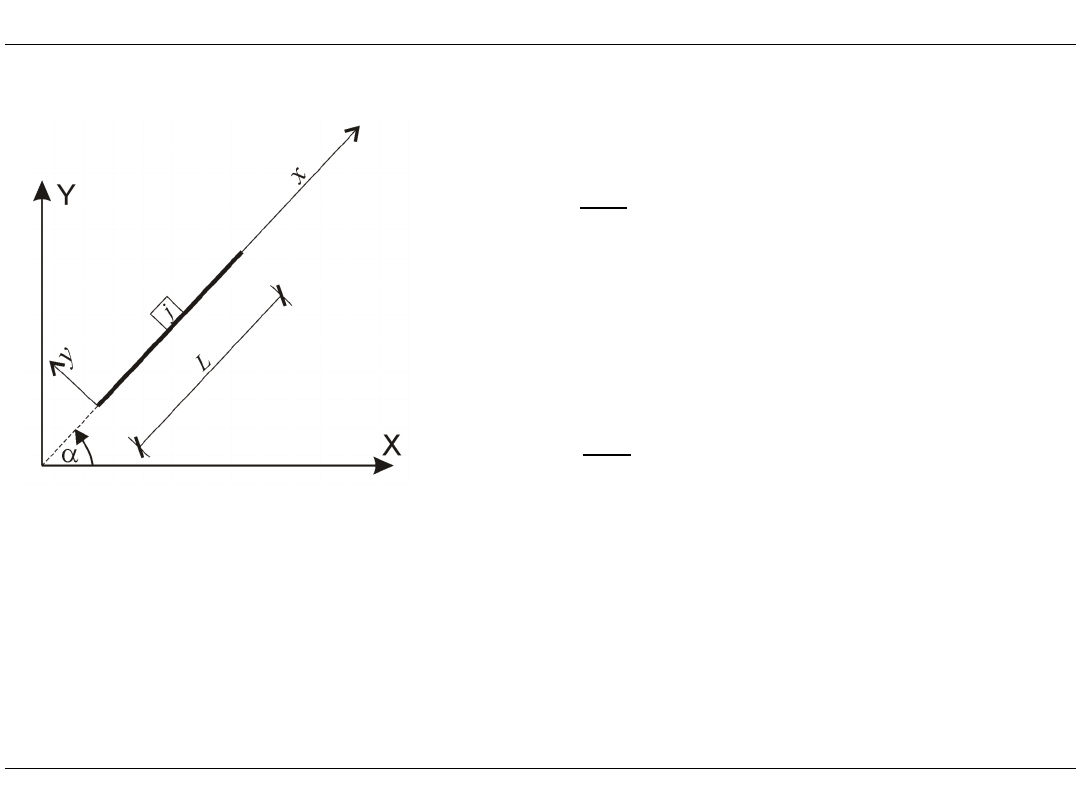
Element kratownicy 2D
1
0
1 0
0
0
0
0
0
1 0
1
0
0
0
0
0
0
a
a
a
a
a
b
b
b
b
b
N
u
N
T
v
EA
N
u
N
L
T
v
1
0
1 0
0
0
0
0
1 0
1
0
0
0
0
0
j
EA
L
k
0
0
0
0
0
0
0
0
j
c
s
s
c
c
s
s
c
L
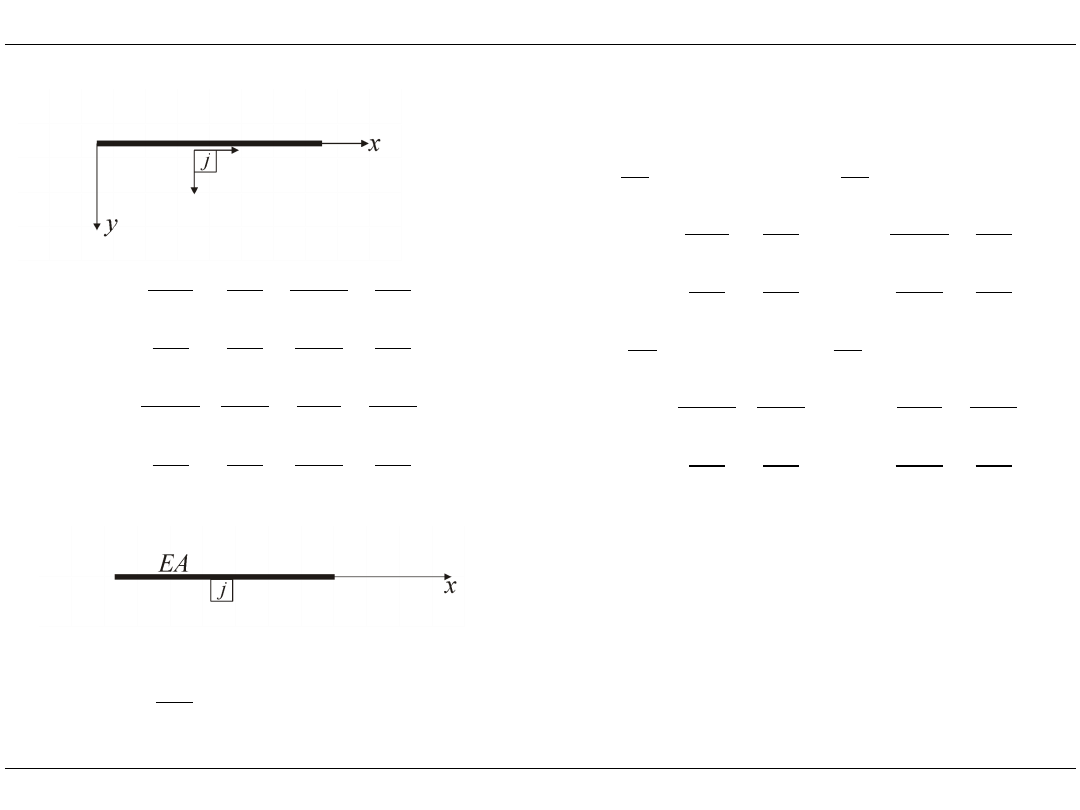
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
10
Macierzowa metoda przemieszczeń
1
1
1
1
j
EA
L
k
3
2
3
2
2
2
3
2
3
2
2
2
0
0
0
0
12
6
12
6
0
0
6
4
6
2
0
0
0
0
0
0
12
6
12
6
0
0
6
2
6
4
0
0
j
EA
EA
L
L
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
EA
EA
L
L
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
k
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
6
4
6
2
12
6
12
6
6
2
6
4
j
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
k
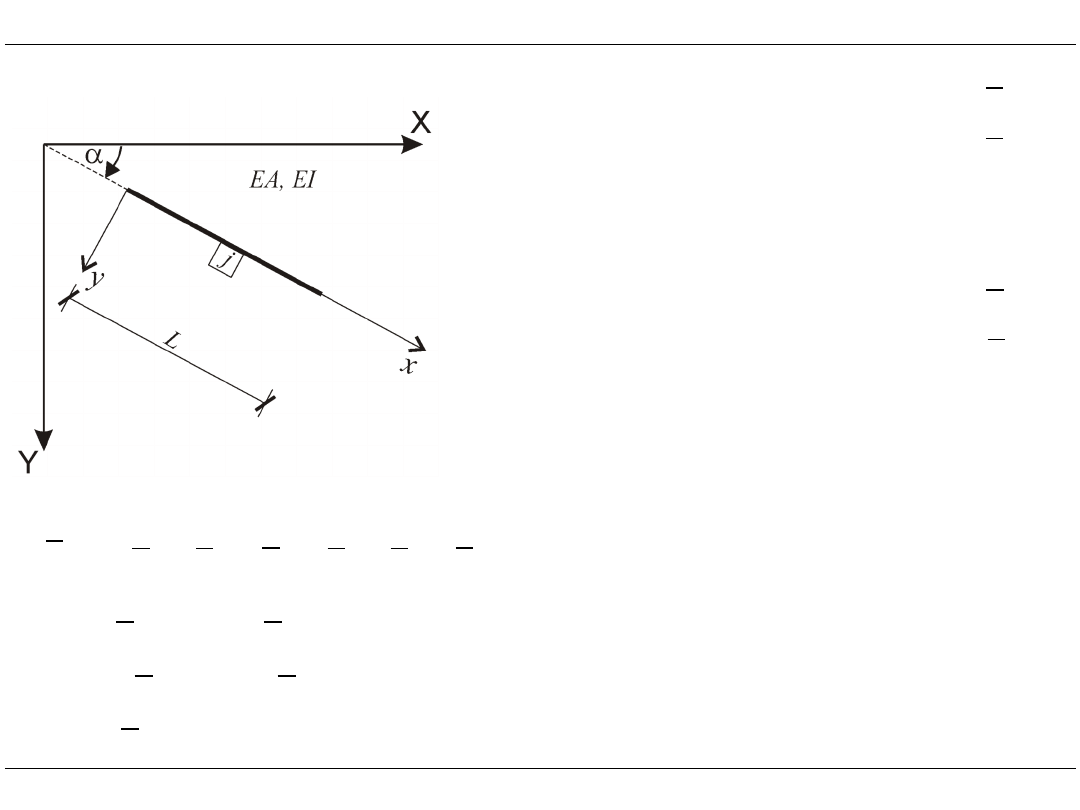
Element ramowy 2D
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
11
Macierzowa metoda przemieszczeń
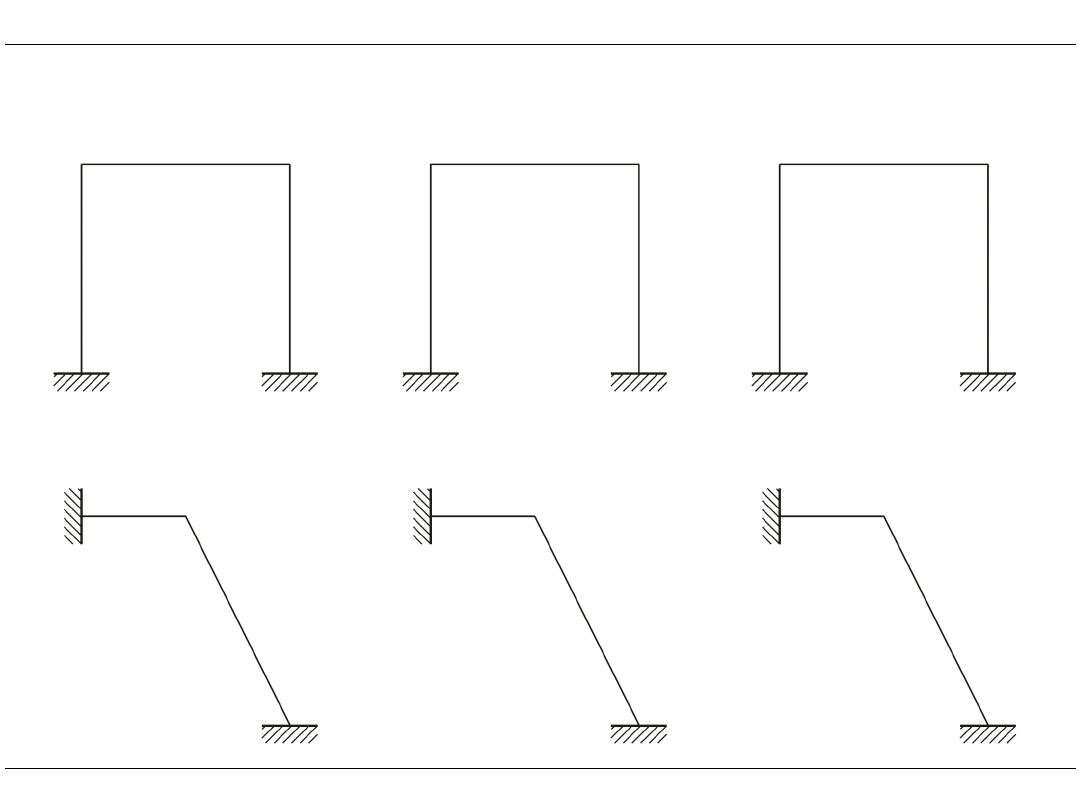
Element ramowy 2D
T
j
a
a
a
b
b
b
u
v
u
v
D
T
j
a
a
a
b
b
b
u
v
u
v
D
cos
sin
sin
cos
a
a
a
a
a
a
a
a
u
u
v
v
u
v
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
a
a
a
a
a
a
b
b
b
b
b
b
u
u
c
s
v
v
s
c
u
u
c
s
v
v
s
c
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
12
Macierzowa metoda przemieszczeń
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
13
Macierzowa metoda przemieszczeń
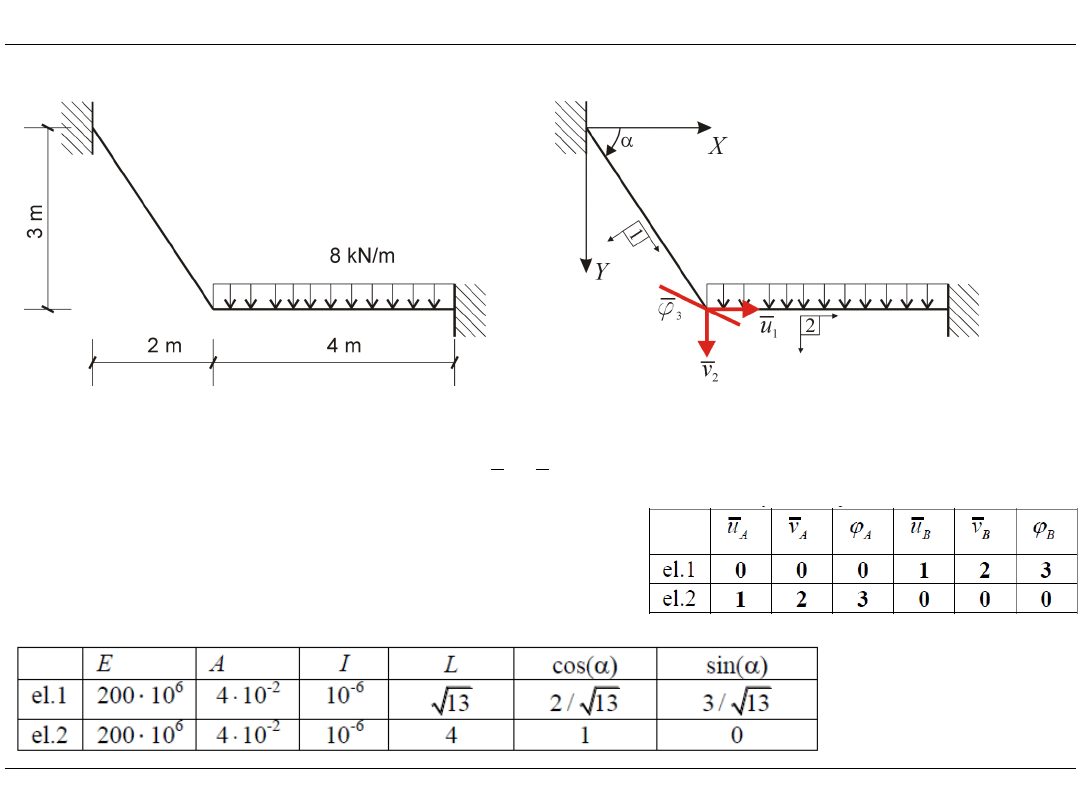
Element ramowy 2D – przykład
wektor przemieszczeń węzłowych
1
2
3
T
u
v
q
wektor obciążeń węzłowych
0
0
0
T
R
tablica cech elementów
wektory alokacji
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
14
Macierzowa metoda przemieszczeń
lokalne macierze sztywności poszczególnych elementów
(ke_frame)
1
1
3
2
3
2
1
1
1
1
2
2
1
1
1
1
1
1
1
3
2
3
2
1
1
1
1
2
2
1
1
1
1
0
0
0
0
12
6
12
6
0
0
6
4
6
2
0
0
0
0
0
0
12
6
12
6
0
0
6
2
6
4
0
0
EA
EA
L
L
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
EA
EA
L
L
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
k
2
2
3
2
3
2
2
2
2
2
2
2
2
2
2
2
2
2
2
3
2
3
2
2
2
2
2
2
2
2
2
2
2
0
0
0
0
12
6
12
6
0
0
6
4
6
2
0
0
0
0
0
0
12
6
12
6
0
0
6
2
6
4
0
0
EA
EA
L
L
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
EA
EA
L
L
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
k
0 0 0 1 2 3
1 2 3 0 0 0
k1 =
2.2188e+006 0 0 -2.2188e+006 0 0
0 51.203 92.308 0 -51.203 92.308
0 92.308 221.88 0 -92.308 110.94
-2.2188e+006 0 0 2.2188e+006 0 0
0 -51.203 -92.308 0 51.203 -92.308
0 92.308 110.94 0 -92.308 221.88
k2 =
2e+006 0 0 -2e+006 0 0
0 37.5 75 0 -37.5 75
0 75 200 0 -75 100
-2e+006 0 0 2e+006 0 0
0 -37.5 -75 0 37.5 -75
0 75 100 0 -75 200

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
15
Macierzowa metoda przemieszczeń
macierze transformacji
(LT)
T1 =
0.5547 0.83205 0 0 0 0
-0.83205 0.5547 0 0 0 0
0 0 1 0 0 0
0 0 0 0.5547 0.83205 0
0 0 0 -0.83205 0.5547 0
0 0 0 0 0 1
T2 =
1 0 0 0 0 0
0 1 0 0 0 0
0 0 1 0 0 0
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1
1
1
1
1
1
1
1
1
1
cos(
)
sin(
)
0
0
0
0
sin(
)
cos(
)
0
0
0
0
0
0
1
0
0
0
0
0
0
cos(
)
sin(
)
0
0
0
0
sin(
)
cos(
)
0
0
0
0
0
0
1
T
2
2
2
2
2
2
2
2
2
cos(
)
sin(
)
0
0
0
0
sin(
)
cos(
)
0
0
0
0
0
0
1
0
0
0
0
0
0
cos(
)
sin(
)
0
0
0
0
sin(
)
cos(
)
0
0
0
0
0
0
1
T

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
16
transformacja macierzy elementowych do układu globalnego
1
1
1 1
T
k
T
k T
2
2
2
2
T
k
T
k T
k1_g =
6.8274e+005 1.024e+006 -76.805 -6.8274e+005 -1.024e+006 -76.805
1.024e+006 1.5361e+006 51.203 -1.024e+006 -1.5361e+006 51.203
-76.805 51.203 221.88 76.805 -51.203 110.94
-6.8274e+005 -1.024e+006 76.805 6.8274e+005 1.024e+006 76.805
-1.024e+006 -1.5361e+006 -51.203 1.024e+006 1.5361e+006 -51.203
-76.805 51.203 110.94 76.805 -51.203 221.88
k2_g =
2e+006 0 0 -2e+006 0 0
0 37.5 75 0 -37.5 75
0 75 200 0 -75 100
-2e+006 0 0 2e+006 0 0
0 -37.5 -75 0 37.5 -75
0 75 100 0 -75 200
agregacja macierzy elementowych do globalnej macierzy sztywności
2
1
j
j
K
k
K =
2.6827e+006 1.024e+006 76.805
1.024e+006 1.5361e+006 23.797
76.805 23.797 421.88
Macierzowa metoda przemieszczeń

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
17
wektory sił przywęzłowych od obciążeń przęsłowych
S10 =
0
0
0
0
0
0
S20 =
0
-16
-10.667
0
-16
10.667
0
1
0
0
0
0
0
0
T
S
2
2
0
2
2
2
2
2
0
0
2
12
2
12
T
pL
pL
pL
pL
S
Macierzowa metoda przemieszczeń
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
18
transformacja wektorów sił przywęzłowych od obciążeń przęsłowych do układu globalnego
S10_g =
0
0
0
0
0
0
S20_g =
0
-16
-10.667
0
-16
10.667
0
0
1
1
1
T
S
T
S
0
0
2
2
2
T
S
T
S
agregacja wektora sił przywęzłowych od obciążeń przęsłowych do globalnego wektora R
0
2
2
0
0
0
1
1
T
j
j
j
j
j
R
T S
S
Ro =
0
-16
-10.667
Macierzowa metoda przemieszczeń

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
19
rozwiązanie układu równań Bezpośredniej Metody Przemieszczeń
0
1
=
Kq
P
P R
R
q
K P
q =
-6.1032e-006
1.4093e-005
0.025284
ekstrakcja wektorów przemieszczeń końców elementu z wektora przemieszczeń globalnych q
1
1
2
3
0
0
0
T
u
v
D
2
1
2
3
0
0
0
T
u
v
D
D1_g =
0
0
0
-6.1032e-006
1.4093e-005
0.025284
D2_g =
-6.1032e-006
1.4093e-005
0.025284
0
0
0
Macierzowa metoda przemieszczeń

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
20
transformacja wektorów przemieszczeń końców elementów do układów lokalnych
1
1
1
D
T D
2
2
2
D
T D
D1 =
0
0
0
8.3403e-006
1.2895e-005
0.025284
D2 =
-6.1032e-006
1.4093e-005
0.025284
0
0
0
Macierzowa metoda przemieszczeń

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
21
przywęzłowe siły przekrojowe w poszczególnych elementach
0
1
1
1
1
S
k D
S
0
2
2
2
2
S
k
D
S
S1 =
-18.505
2.3332
2.8038
18.505
-2.3332
5.6088
S2 =
-12.206
-14.103
-5.6088
12.206
-17.897
13.196
Macierzowa metoda przemieszczeń
Wyszukiwarka
Podobne podstrony:
PSYCHOLOGIA SPOLECZNA materiały na wykłady, WSFiZ, psychlogia społeczna
materiały na wykład 4a
materiały na wykład 2
Grzyby uprawne + materiały na wykłady, wydział leśny, UBOT
materialy na wyklad 6a id 28522 Nieznany
materiały na wykład 5
materialy na wyklad 6b id 28523 Nieznany
materialy na wyklad 1 id 285225 Nieznany
popityka stabilizacyjna, uczelnia WSEI Lublin, UCZELNIA WSEI 2 1, ekonomia 2rok 4 semestr, makro, po
materiały na wykład 4b
Inzynieria środowiska zaoczne materiały na wykład
materialy na diagnoze, Wyklad VI diagnoza
POLITYKA SPOLECZNA wyklad 8 maja, uczelnia WSEI Lublin, UCZELNIA WSEI, MATERIAŁY NA EGZAMIN 2 semest
Rezerwy na świadczenia pracownicze - materiały do wykladu 2014, UE KATOWICE ROND, I stopień, VI seme
Pytania na Bilskiego, Podręczniki i materiały dydaktyczne, wykłądy, finanse międzynarodowe
fin i rach wyklady letni 2012 LISTA 4, Materiały na studia ZIP, I Rok, Finanse
Zagadnienia na egzamin z Gutka, ZUT-Energetyka-inżynier, III Semestr, Wytrzymałość materiałów II, Wy
Zaliczenie z biofizyki- wykłady 2008, far, biofizyka, egzamin, materiały na ćwiczenia
więcej podobnych podstron