Wyznaczanie długości frontu

załadunkowo-wyładunkowego

placów składowych

dla wybranych sytuacji

decyzyjnych

Front załadunkowo - wyładunkowy

• Jest to najczęściej jeden z boków placu

składowego, przeważnie dłuższy bok (może

być jego część), a jego wielkość powinna być

tak dobrana, aby jednocześnie przybywające

środki transportowe mogły być przyjęte w

celu rozładowania materiałów budowlanych,

• Na placach budowy mają zastosowanie

najczęściej tzw. fronty wyładunkowe, które

powinny zabezpieczać sprawny odbiór

dostaw materiałów budowlanych.

Front załadunkowo – wyładunkowy

może być wyznaczany na dwa

sposoby:

• deterministycznie,
• losowo.

Front załadunkowo – wyładunkowy

wyznaczany w sposób

deterministyczny:

Długość frontu „L” zależy od następujących

czynników:

• ilości materiału dostarczanego na budowę w

ciągu doby, wyrażonej w t, m3 lub sztukach
(według harmonogramu dostawy materiału),

• ładowności jednostki transportowej,

wyrażonej w t, m3 lub sztukach,

• długości frontu wyładunkowego jednostki

transportowej, wyrażonej w metrach,

Długość frontu „L” zależy od następujących

czynników : (cd.)

• współczynnika nierównomierności dostawy

(uwzględnia w niewielkim stopniu wpływ
czynników losowych, stopień jest tak
niewielki że metodę uznaje się za
deterministyczną),

• współczynnika uwzględniającego niezbędne

odstępy, które należy zachować między
poszczególnymi środkami transportowymi

Zastosowanie „Teorii kolejek”

• W przypadku silnego oddziaływania

czynników losowych, długość boku placu

składowego, który ma pełnić funkcję frontu

wyładunkowego można wyznaczyć na

podstawie wybranych modeli teorii kolejek

(masowej obsługi). W zależności jednak od

istniejącej sytuacji decyzyjnej, dotyczącej

dostępności miejsca na placu budowy,

można stosować wielokanałowe modele

systemów masowej obsługi "ze stratami" lub

"z ograniczoną kolejką".

Model wielokanałowego systemu

masowej obsługi M/M/c ze

stratami

Założenia ogólne:
• Taki system obsługi nie przyjmuje

zgłoszenia wtedy, gdy wszystkie kanały
obsługi są zajęte,

• W systemie nie może tworzyć się kolejka i

dlatego, jeżeli wszystkie kanały obsługi są
zajęte, to nadchodzące zgłoszenia muszą
opuścić system bez uzyskania obsługi,

Założenia ogólne: (cd.)

• System posiada „c” kanałów obsługi.

Można przyjąć, że są nimi wolne miejsca

postojowe środków transportowych

podczas ich rozładunku,

• Długość samochodu (lub szerokość, w

przypadku samochodów z tylnym

rozładunkiem) powiększona o pewną

wielkość potrzebną do manewrowania

pojazdów może stanowić kanał obsługi,

• Za czas obsługi można uważać czas

postoju samochodu podczas rozładunku,

Założenia ogólne: (cd.)

• W rozpatrywanym przypadku dostarczany

będzie tylko jeden rodzaj materiału tak

więc regulamin kolejki przyjmuję obsługę

według kolejności zgłoszeń,

• Przyjęcie do wyznaczenia długości frontu

wyładunkowego systemu "ze stratami",

czyli systemu, w którym nie może

wystąpić kolejka, można uzasadnić

brakiem miejsca na placu budowy poza

frontem załadunkowo-wyładunkowym,

Postępowanie w metodzie M/M/c ze stratami

• Aby uniknąć nie przyjęcia środków

transportowych przyjeżdżających z

określonymi materiałami budowlanymi w

celu rozładunku, konieczne jest ustalenie

właściwej liczby stanowisk (kanałów

obsługi) wzdłuż placu składowego.

• Liczbę tą dla przyjętego systemu masowej

obsługi można wyznaczyć na podstawie

zależności określającej

prawdopodobieństwo odmowy obsługi, czyli

prawdopodobieństwo tego, że wszystkie

miejsca (kanały obsługi) są zajęte.

Prawdopodobieństwo to wyraża się wzorem:

0

!

P

c

P

c

n







Wielkość występująca we wzorze
wyznacza się z zależności:



s

t

t

0





ts - średni odstęp czasu między
przybyciami

samochodów,

to - czas rozładunku (obsługi)
samochodu.

Wielkość Po ze wzoru oznacza natomiast

prawdopodobieństwo tego, że wszystkie miejsca

(kanały) są wolne. Prawdopodobieństwo to

określa się przy zastosowaniu wzoru:







c

i

i

i

P

0

0

!

1



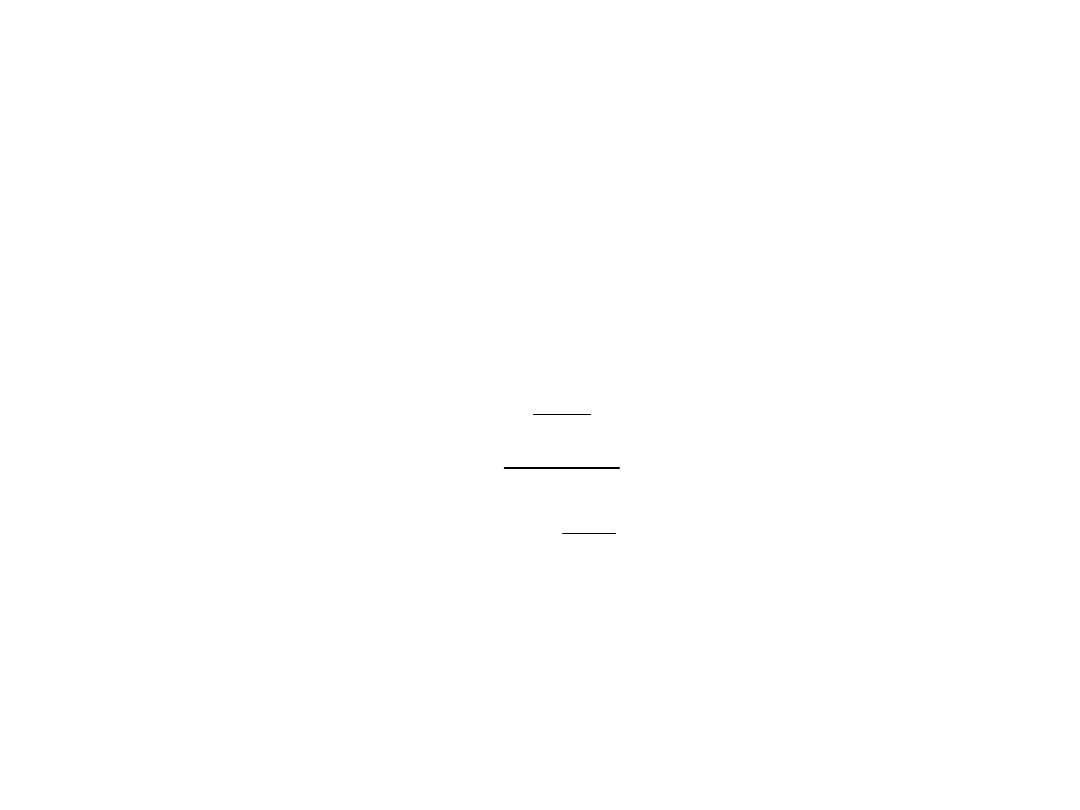
Po podstawieniu prawdopodobieństwo odmowy

obsługi Pn=c przybiera następującą postać:









c

i

i

c

c

n

i

c

P

0

!

!





Dla ułatwienia obliczeń licznik i mianownik tego

prawdopodobieństwa można pomnożyć przez

.

Otrzyma się wtedy zależność:





e













c

i

i

c

c

n

e

i

c

e

P

0

!

!









W liczniku zależności występuje wzór
rozkładu Poissona, a w mianowniku wzór
dystrybuanty tego rozkładu

Wystarczy więc odczytać z tablic odpowiednie

wartości i podzielić licznik przez mianownik,

aby otrzymać wynik. Tablice wartości funkcji

rozkładu Poissona oraz wartości dystrybuanty

tej funkcji można znaleźć m.in. w pracy:

• J. Wolszczan: „Zastosowanie teorii masowej

obsługi w transporcie samochodowym”,

WKiK, Warszawa, 1970.

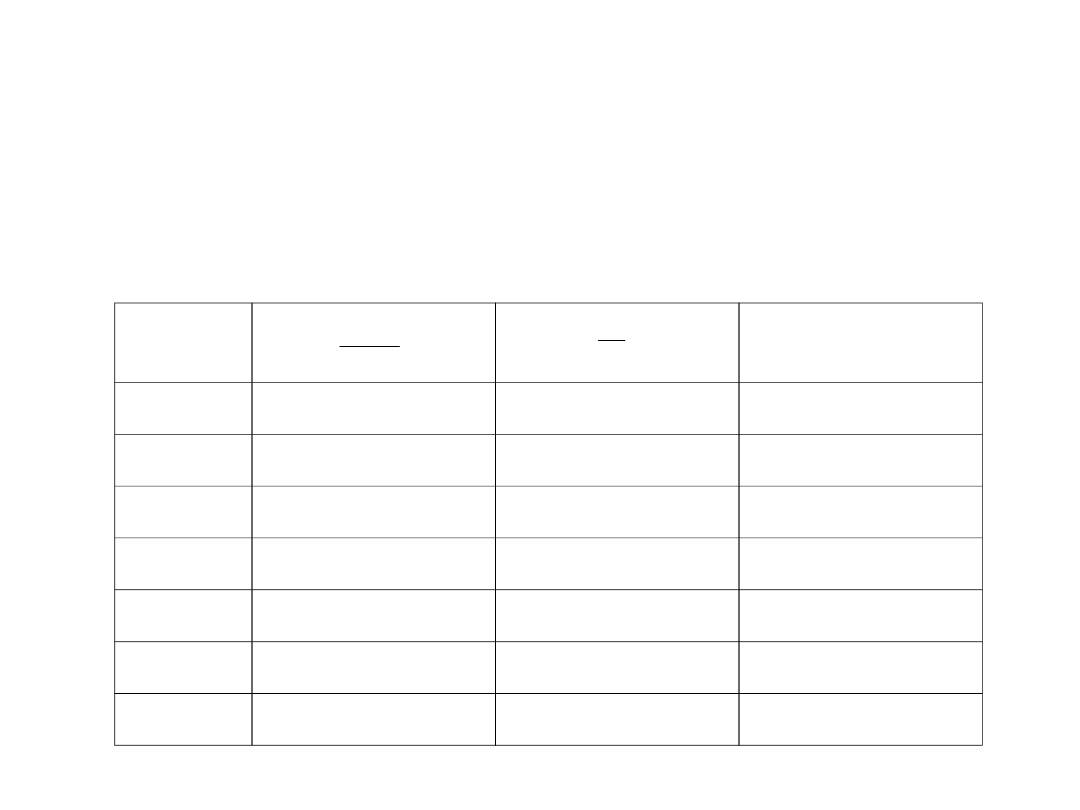
Przykładowo dla  = 2,5 w tablicy 1 podane zostały

wyniki obliczeń dotyczących prawdopodobieństwa,

że wszystkie miejsca są zajęte (odmowa wykonania

obsługi).

Tablica 1. Przykładowe obliczenie prawdopodobieństwa

odmowy wykonania obsługi w wielokanałowym

systemie masowej obsługi M/M/c ze stratami.



!

c

e

c

















e

i

c

i

i

0

!

c

Pn=c

1

0,2052

0,2873

0,7142

2

0,2565

0,5438

0,4717

3

0,2138

0,7576

0,2822

4

0,1336

0,8912

0,1499

5

0,0668

0,9580

0,0697

6

0,0278

0,9858

0,0282

7

0,0099

0,9957

0,0099

• Jeżeli założy się, że prawdopodobieństwo

odmowy obsługi nie powinno wynosić więcej

niż 0,08, to należy odszukać w wynikach

obliczeń Pn=c = 0,08, lub wartość zbliżoną

mniejszą, i odczytać odpowiadającą tej

wartości prawdopodobieństwa wartość c,

czyli liczbę miejsc na samochody (liczbę

kanałów obsługi). W tablicy 1 jest Pn=c =

0,0697 < 0,08 dla c = 5.

• Jeżeli natomiast zaostrzone zostałyby

warunki i przyjęto by, że np. brak miejsc

może zdarzyć się tylko jeden raz na sto, to

Pn=c = 0,01 < 0,0099 dla c = 7.

Znając rodzaj samochodów dowożących

materiał, można wyznaczyć długość frontu

wyładunkowego ze wzoru

L = c (l + l') - l',

gdzie:

c - liczba miejsc na samochody (liczba kanałów

obsługi),

l - długość frontu wyładunkowego jednostki

transportowej (wyrażona w m),

l' - niezbędna do manewrowania odległość między

dwoma środkami transportowymi (wyrażona w m).

Dane do ćwiczenia 1

• to > ts

• Prawdopodobieństwo odmowy należy

przyjmować w zakresie 1 do 20 %.

Model wielokanałowego systemu

masowej obsługi M/M/c z

ograniczoną kolejką

Założenia ogólne:

• W systemach "z ograniczoną kolejką" zgłoszenia nie

są przyjmowane do obsługi tylko wtedy, jeżeli w
kolejce będzie znajdowała się pewna, określona z
góry, liczba zgłoszeń (np. środków transportowych).

• Wynika z tego, że model takiego systemu można

przyjąć do wyznaczania długości frontu
załadunkowo-wyładunkowego placów składowych,
jeżeli na placu budowy znajduje się miejsce dla
oczekujących w kolejce samochodów.

Założenia ogólne: (cd.)
• W systemie M/M/c z ograniczoną kolejką,

długość kolejki jest ograniczona do „L”
oczekujących w niej jednostek
(samochodów) jest limitowana bardzo
często dostępnością miejsca. Jeżeli
zgłaszający się środek transportowy nie
znajdzie miejsca, to musi opuścić system,
np. bez rozładowania środka
transportowego.

W sytuacji decyzyjnej dotyczącej rozpatrywanego

systemu masowej obsługi również należy ustalić
właściwą liczbę stanowisk (kanałów obsługi)
wzdłuż jednego z boków placu składowego.
Można posłużyć się w tym celu zależnością
określającą prawdopodobieństwo odmowy
obsługi, wyprowadzoną dla przyjętego systemu.
Prawdopodobieństwo to wyraża się wzorem:

0

!

P

c

c

P

L

c

L

c

L









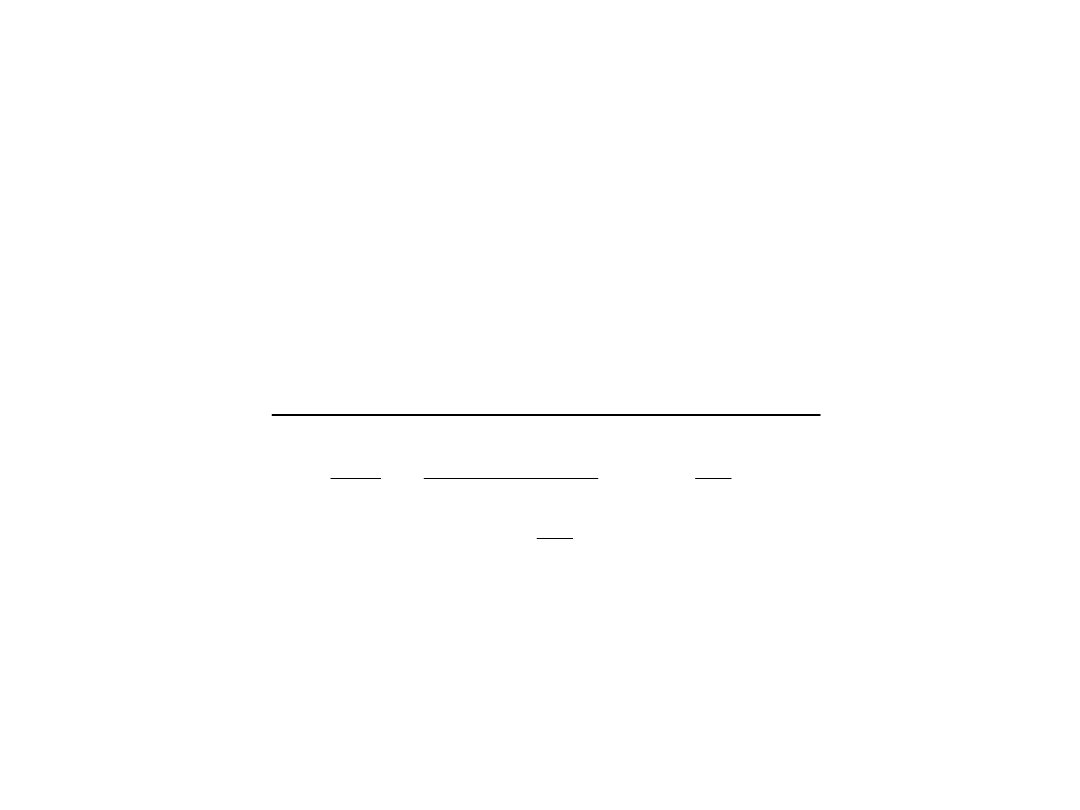
Występującą w zależności wielkość Po,

tzn. prawdopodobieństwo tego, że
wszystkie kanały obsługi są wolne,
można obliczyć ze wzoru:















 











 





1

0

1

0

)

(

1

1

!

!

1

c

i

L

c

i

c

c

c

i

P









W tablicach 2 ÷ 5 zestawione zostały

przykładowe wyniki obliczeń, dla  = 2,5,

dotyczące prawdopodobieństwa, że

wszystkie miejsca znajdujące się wzdłuż boku

placu składowego oraz w kolejce, są zajęte

(odmowa wykonania obsługi). Poszczególne

tablice dotyczą różnych sytuacji decyzyjnych

dotyczących dostępności miejsca, od której

zależy dopuszczalna długość kolejki środków

transportowych. Kolejne tablice dotyczą

odpowiednio wielkości: L = 3, L = 2, L = 1, L

= 0.



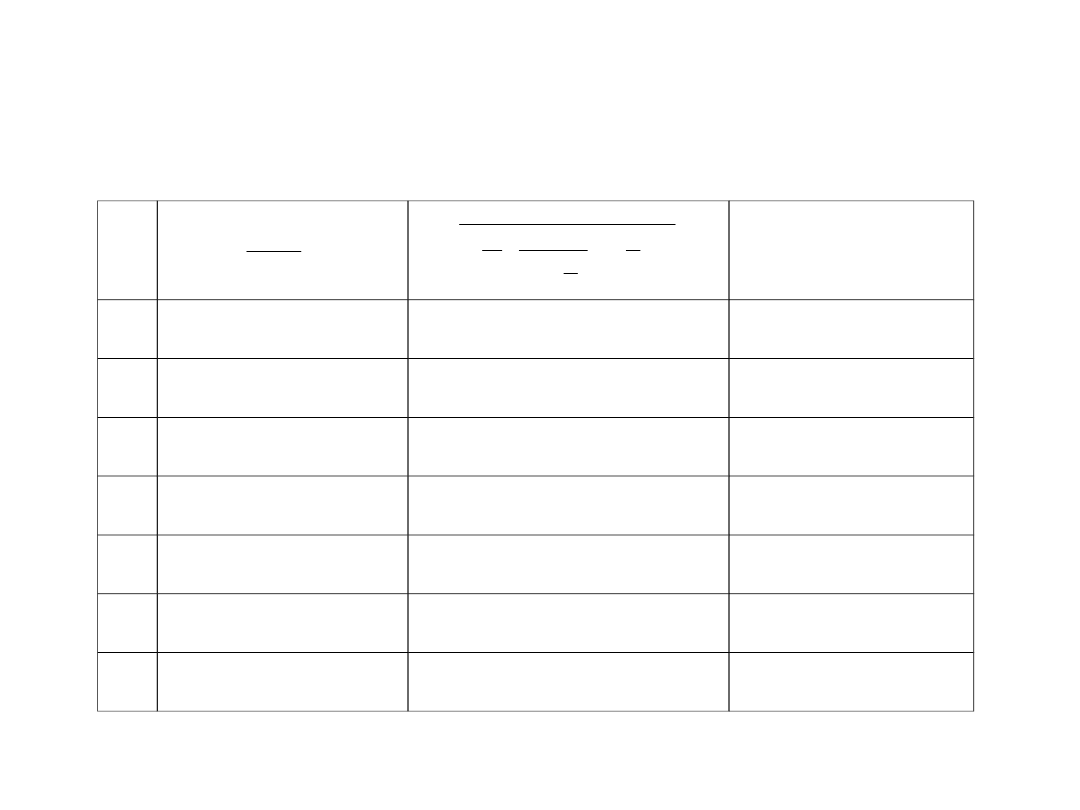
Tablica 2 Przykładowe obliczenie prawdopodobieństwa

odmowy wykonania obsługi dla L = 3

L

c

L

c

c!



















 











 



1

0

1

)

(

1

1

!

!

1

c

i

L

c

i

c

c

c

i









c

P

L+c

1

39,0625

0,0155

0,6062

2

6,1035

0,0465

0,2837

3

1,5070

0,0680

0,1024

4

0,3974

0,0775

0,0308

5

0,1017

0,0808

0,0082

6

0,0245

0,0817

0,0020

7

0,0055

0,0820

0,0005

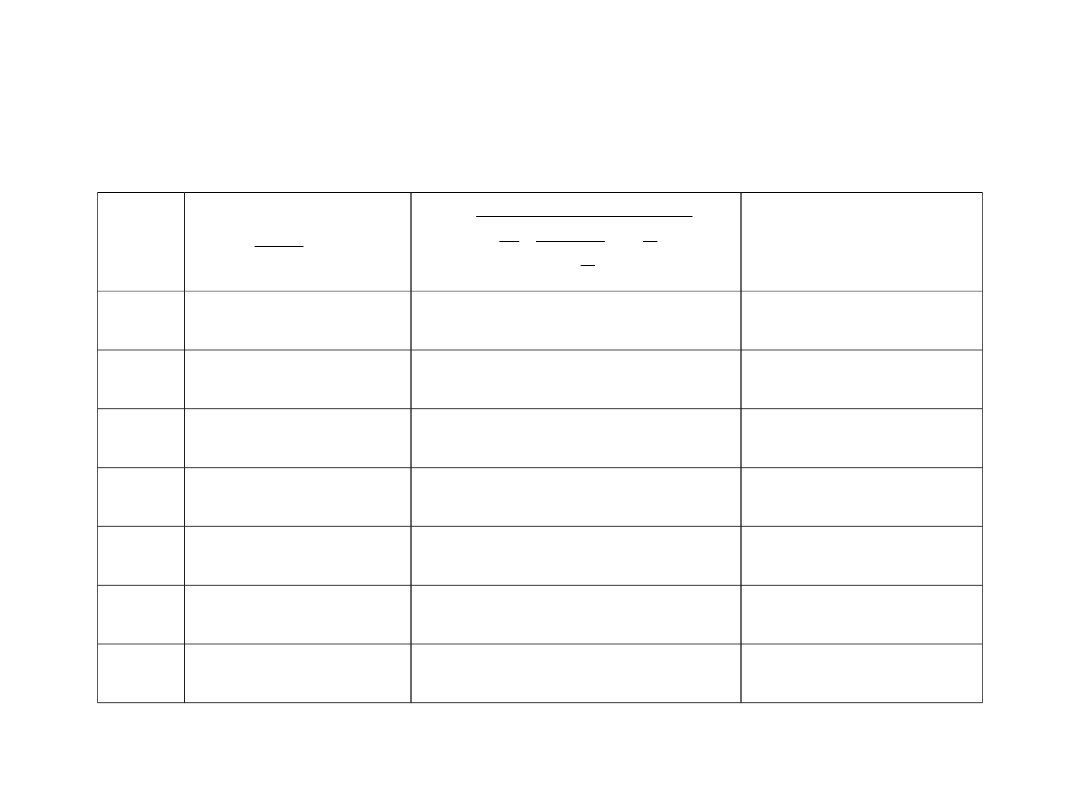
Tablica 3 Przykładowe obliczenie prawdopodobieństwa

odmowy wykonania obsługi dla L = 2

L

c

L

c

c!



















 











 



1

0

1

)

(

1

1

!

!

1

c

i

L

c

i

c

c

c

i









c

P

L+c

1

15,6250

0,0394

0,6158

2

4,8828

0,0649

0,3168

3

1,8084

0,0757

0,1369

4

0,6358

0,0799

0,0608

5

0,2035

0,0814

0,0166

6

0,0589

0,0819

0,0048

7

0,0154

0,0820

0,0013

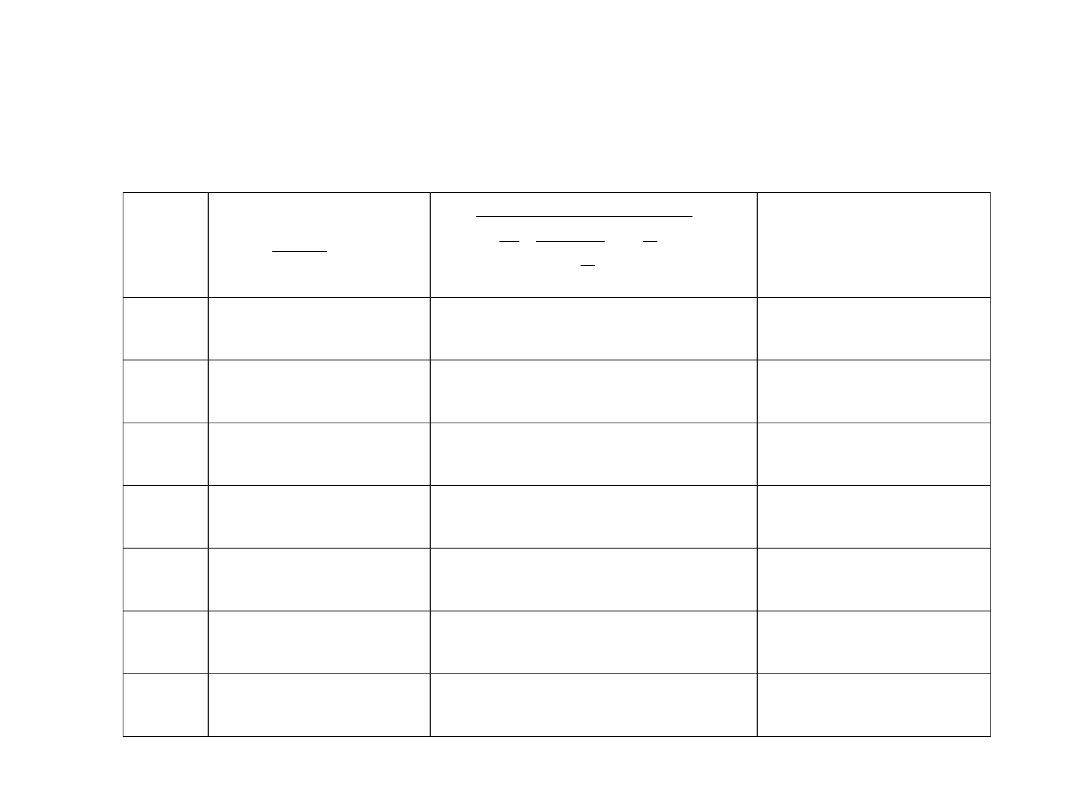
Tablica 4 Przykładowe obliczenie prawdopodobieństwa

odmowy wykonania obsługi dla L = 1

L

c

L

c

c!



















 











 



1

0

1

)

(

1

1

!

!

1

c

i

L

c

i

c

c

c

i









c

P

L+c

1

6,2500

0,1127

0,7042

2

3,9062

0,0950

0,3709

3

2,1701

0,0877

0,1904

4

1,0173

0,0842

0,0857

5

0,4069

0,0828

0,0337

6

0,1413

0,0823

0,0116

7

0,0433

0,0821

0,0036

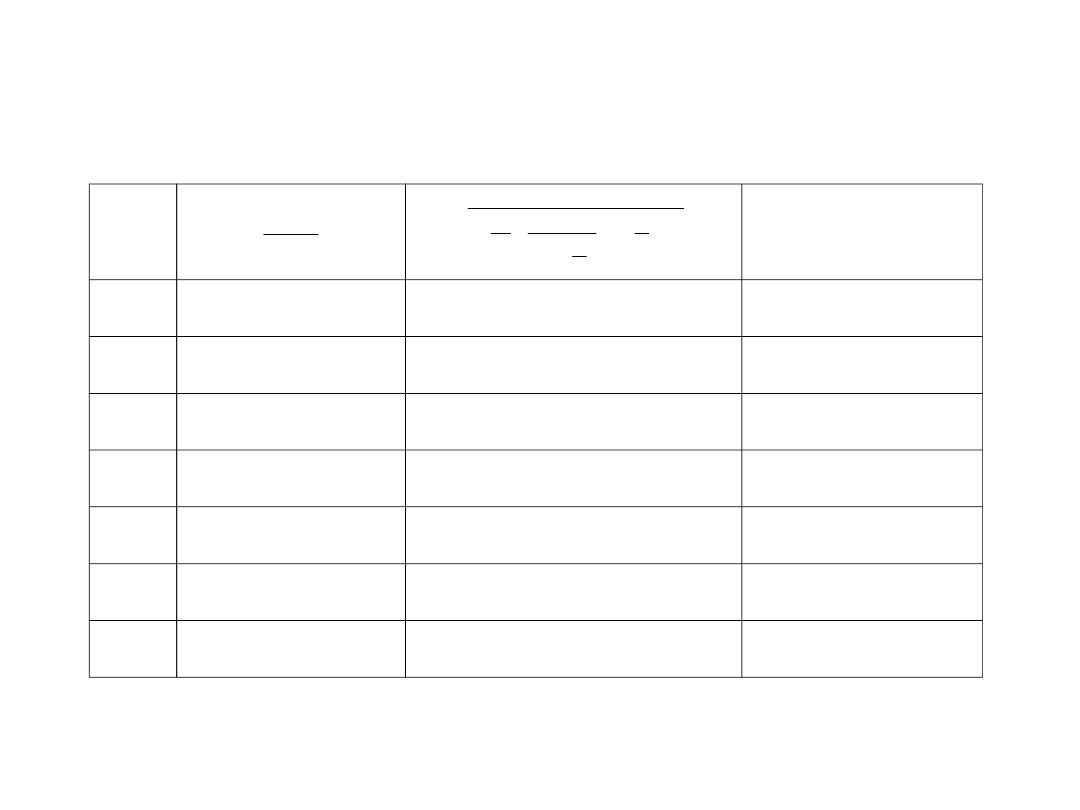
Tablica 5 Przykładowe obliczenie prawdopodobieństwa

odmowy wykonania obsługi dla L = 0

L

c

L

c

c!



















 











 



1

0

1

)

(

1

1

!

!

1

c

i

L

c

i

c

c

c

i









c

P

L+c

1

2,5000

0,2857

0,7143

2

3,1250

0,1509

0,4717

3

2,6042

0,1148

0,2990

4

1,6276

0,0967

0,1575

5

0,8138

0,0897

0,0730

6

0,3391

0,0870

0,0295

7

0,1211

0,0861

0,0104

Jeżeli założy się, podobnie jak w przypadku systemu

M/M/c ze stratami (tablica 1), że

prawdopodobieństwo odmowy obsługi nie

powinno wynosić więcej niż 0,08, to

prawdopodobieństwu temu odpowiada liczba

kanałów obsługi:
c = 4, dla L = 3 (tablica 2),
c = 4, dla L = 2 (tablica 3),
c = 5, dla L = 1 (tablica 4),
c = 5, dla L = 0 (tablica 5).

Przytoczone dane są liczbowym potwierdzeniem

tego, że gdy na budowie jest mniej miejsca na

oczekiwanie w kolejce samochodów dowożących

materiały budowlane, to długość frontu

wyładunkowego wzrasta (jest to wielkość zależna

od liczby c).

Podobnie będzie, gdy zaostrzone zostaną

warunki i przyjmie się, że np. brak miejsca

wzdłuż frontu wyładunkowego (lub

załadunkowego) może zdarzyć się tylko

jeden raz na sto (tzn. Pn=c  0,01). Wtedy

c = 5, dla L = 3 (tablica 2),
c = 6, dla L = 2 (tablica 3),
c = 6, dla L = 1 (tablica 4),
c = 7, dla L = 0 (tablica 5).

Jeżeli na budowie nie ma miejsca na utworzenie

kolejki oczekujących samochodów, a także na

zabezpieczenie odpowiedniej długości frontu

załadunkowo - wyładunkowego dla przyjętej

wielkości prawdopodobieństwa odmowy

obsługi, pozostaje jedynie możliwość

zwiększenia ryzyka przez zmniejszenie przyjętej

wielkości PL+c. W ten sposób można

zmniejszyć długość frontu, dostosowując ją do

realnych możliwości związanych z wielkością

placu budowy. Należy jednocześnie pamiętać o

ewentualnych konsekwencjach związanych z

ograniczeniem wymagań dotyczących wielkości

prawdopodobieństwa odmowy obsługi.

Dane do ćwiczenia 2

• to > ts

• Prawdopodobieństwo odmowy należy

przyjmować w zakresie 1 do 20 %.

• Długość kolejki – 0 < L < 3