© Dr inż. JANUSZ LICHOTA

PODSTAWY AUTOMATYKI

Regulatory PID, część I

Wydział Mechaniczno-
Energetyczny

Wrocław 2006

PLAN WYSTĄPIENIA

• Klasyfikacja regulatorów
• Regulator PID – co to jest?
• Typowe struktury regulatorów
• Regulator PID – jak on działa?

Charakterystyki czasowe

• Regulator PID – jak on działa?

Charakterystyki częstotliwościowe

• Próba strojenia regulatora

 
Sposób budowy:
·

     

bezpośredniego działania

·

     

o działaniu pośrednim

 
Nośnik energii zasilającej
regulator:
·

     

elektroniczne

·

     

pneumatyczne

·

     

hydrauliczne

 
Sposób zmiany wielkości
nastawiającej
organ wykonawczy:
·

     

regulatory o wyjściu ciągłym

·

     

impulsowym

·

     

dwustawnym

·

     

trójstawnym

 
Właściwości dynamiczne:
·

  

proporcjonalne, typu P

·

     

całkowy, typu I

·

     

PI, PD, PID

 
Zasadę działania:
·

     

regulatory klasyczne, z

grupy PID
·

     

sieci neuronowe

·

     

logikę rozmytą (fuzzy logic)

   

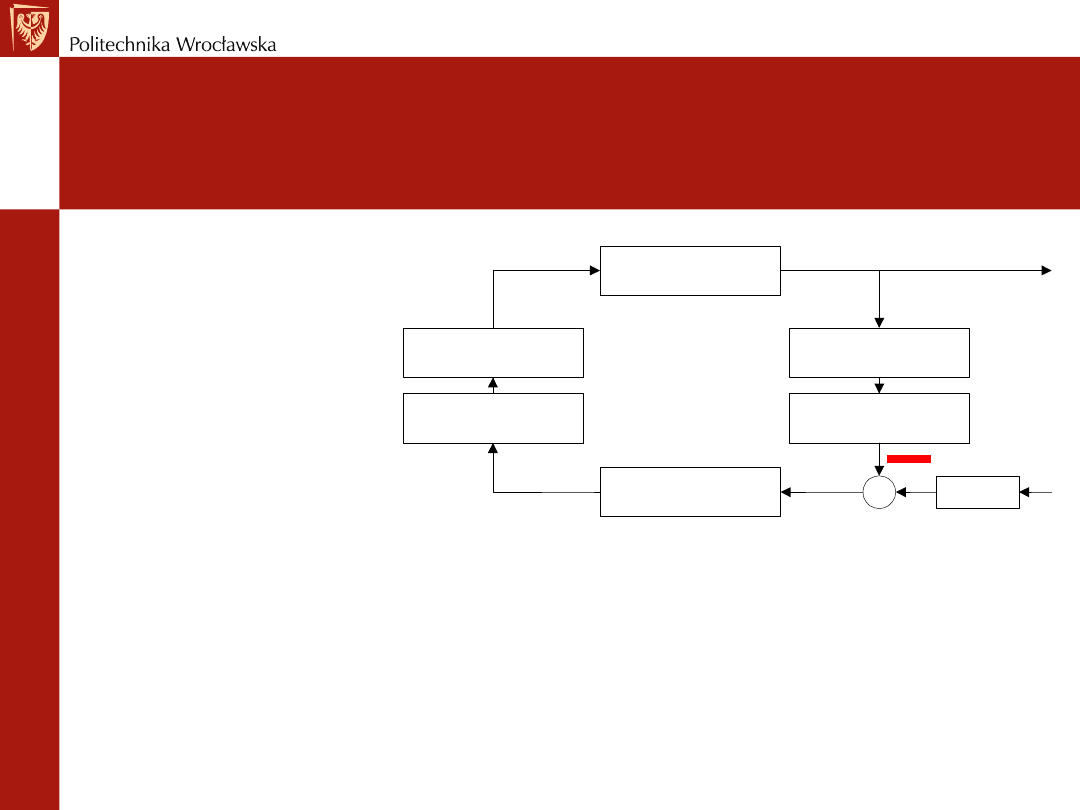
REGULATORY
Klasyfikacja

Obiekt

Czujnik

Przetwornik

Regulator

Siłownik

Nastawnik

Zadajnik

u(t)

e(t)

Obecnie 95 % układów regulacji na świecie jest wyposażonych w regulator z grupy PID

REGULATOR PID

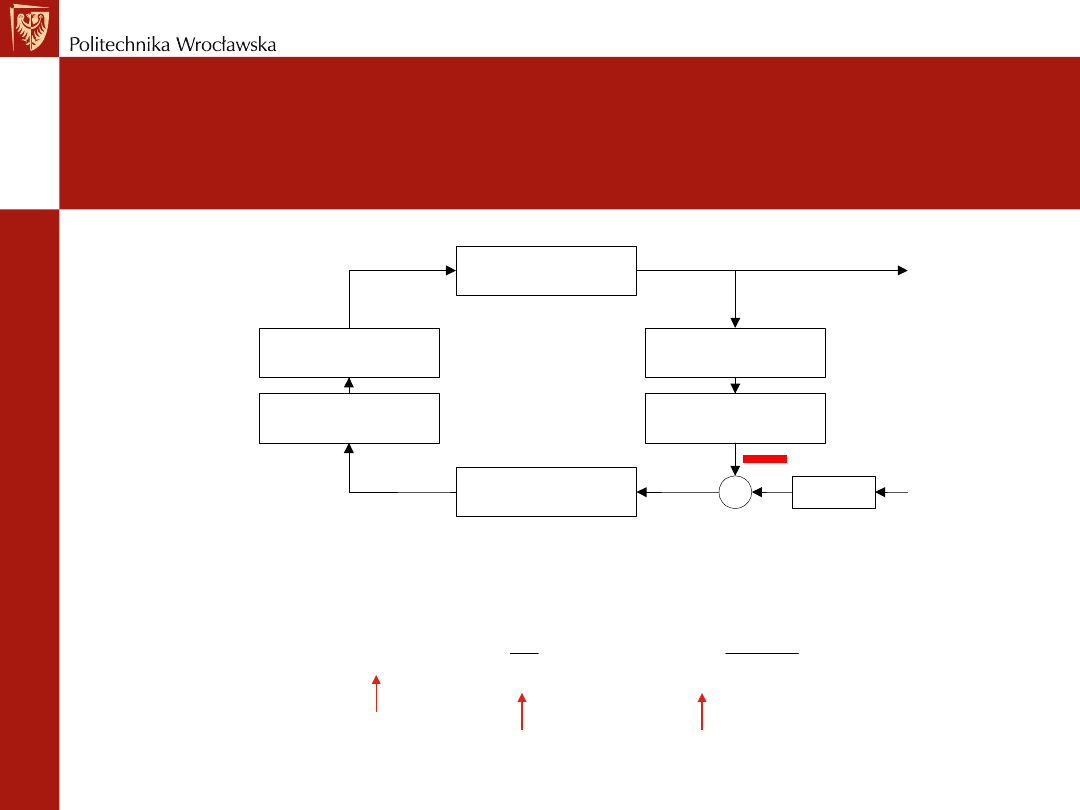
REGULATOR PID
Co to jest?

Pomysł Minorskiego, 1922

Obiekt

Czujnik

Przetwornik

Regulator

Siłownik

Nastawnik

Zadajnik

u(t)

e(t)

u t

k e t

T

e d

T

de t

dt

p

i

t

d

( )

( )

( )

( )





















1

0

 

Współczynnik
wzmocnienia
regulatora

Stała zdwojenia
(całkowania)

Stała wyprzedzenia
(różniczkowania)

REGULATOR PID
Typowe struktury

G s

k

r

p

( ) 





G s

k

T s

r

p

d

( ) 



1

G s

k

Ts

r

p

i

( ) 













1

1

G s

k

Ts

T s

r

p

i

d

( ) 















1

1

Regulator proporcjonalny

P

Regulator proporcjonalno-całkujący

PI

Regulator proporcjonalno-różniczkujący

PD

Regulator proporcjonalno-całkująco-różniczkujący

PID

W celu uwzględnienia nieidealnego różniczkowania, które ma miejsce w
rzeczywistych regulatorach wprowadzono człon inercyjny połączony szeregowo z
członem różniczkującym. Wartość N we wzorze jest miarą niedoskonałości działania
części różniczkującej.

1

1

( )

1

.

1

d

c

c

d

i

T s

G s

K

T s

Ts

N

�

�

�

�

�

� +

=

+

�

�

�

�

�

��

�

+

�

�

REGULATOR PID
Typowe struktury

Można wyróżnić dwie formy przedstawienia regulatora PID

-równoległą

-i szeregową

2

1

( )

1

1

r

p

d

i

d i

p i

i

G s

k

T s

Ts

T Ts

k Ts

Ts

�

�

=

+

+

�

�

�

�

+

+

=

(

)

1

( )

1

1

1

r

p

d

i

i

d

p

d

i

i

G s

k

T s

Ts

T T

k

T s

T

Ts

�

�

=

+

+

�

�

�

�

�

�

+

=

+

+

�

�

�

�

%

%

%

% %

%

%

%

%

Zależności pomiędzy współczynnikami są następujące

,

,

i

d

i d

p

p

i

i

d

d

i

i

d

T T

TT

k

k

T T T T

T

T T

+

=

= +

=

+

% %

%%

%

% %

%

% %

Należy znać transmitancję regulatora, aby prawidłowo zastosować procedurę strojenia.

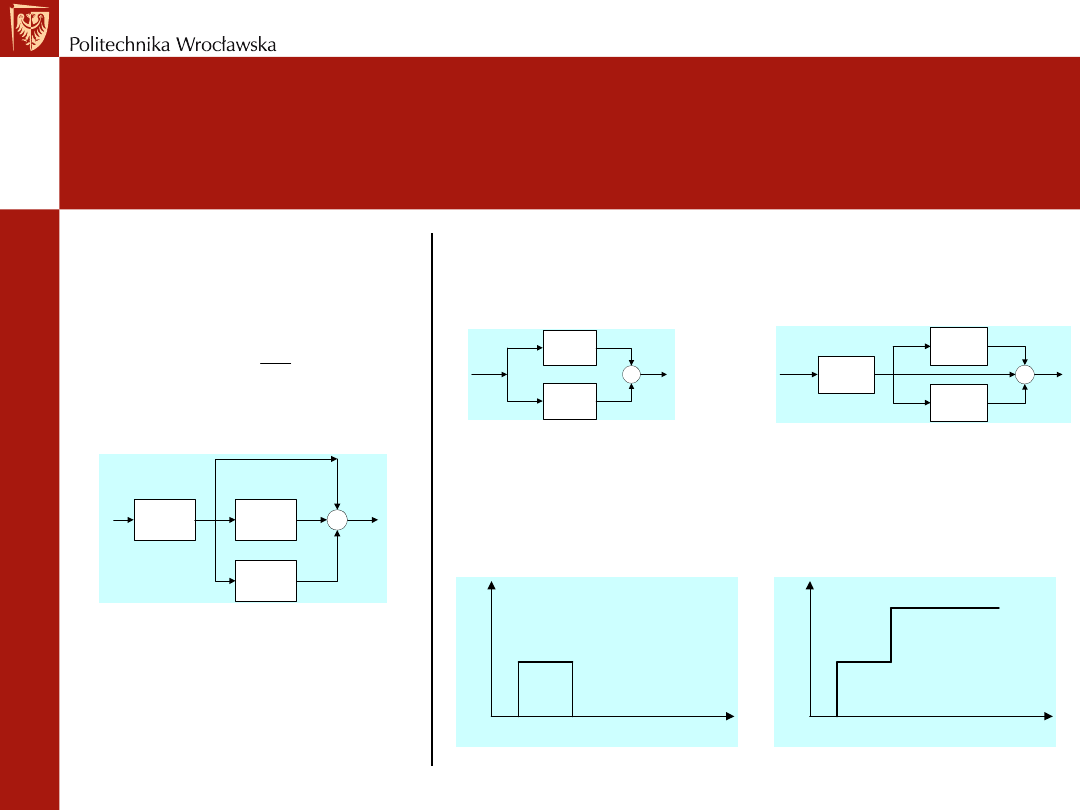
kp

Ti

Td

Schemat strukturalny
regulatora PID

2

3s

Jaki to typ regulatora i jakie nastawy ma regulator o
strukturze z rysunku ?

3s

1/(4s)

2

Jaka jest odpowiedź regulatora P, I, PD, PI, PID na sygnał
przedstawiony na rysunku?

t

x(t)

t

x(t)

e(t)

u(t)

REGULATOR PID
Typowe struktury – przykład 1

a)

a)

b)

b)

G s

k

Ts

T s

r

p

i

d

( ) 















1

1

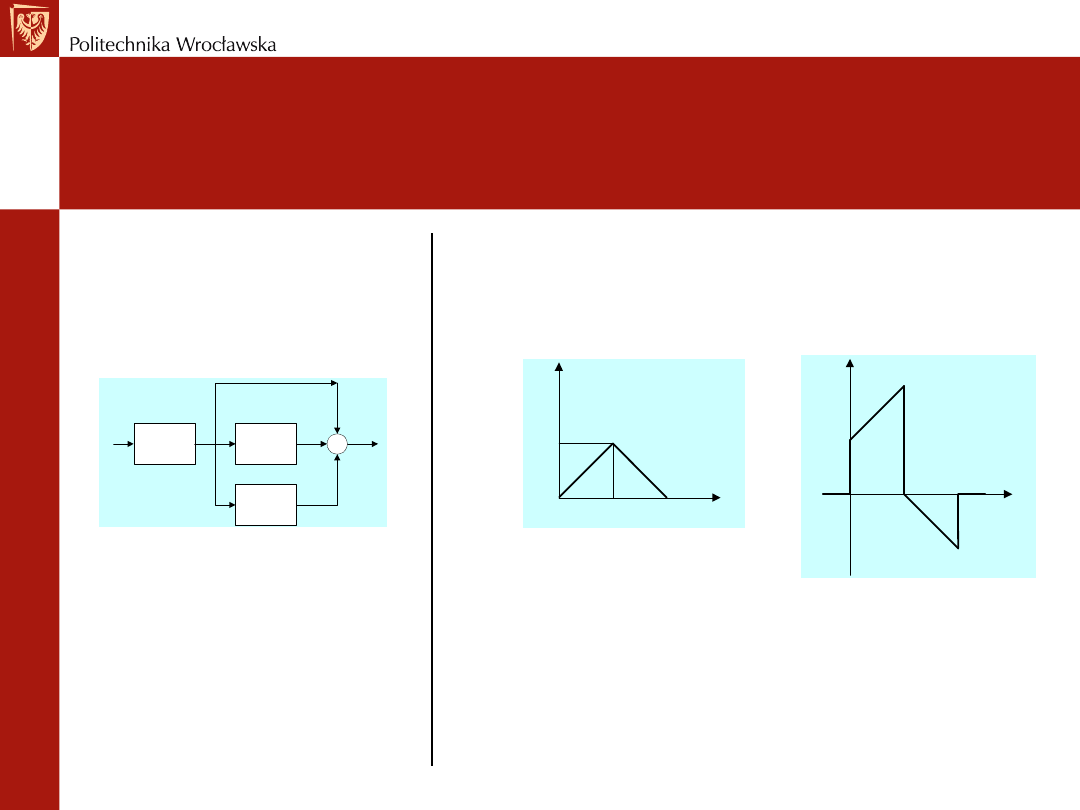
t

x(t)

5

10

5

t

u(t)

5

5

10

10

-5

0

Jaki to regulator ?

REGULATOR PID
Typowe struktury – przykład 2

kp

Ti

Td

Schemat strukturalny
regulatora PID

e(t)

u(t)

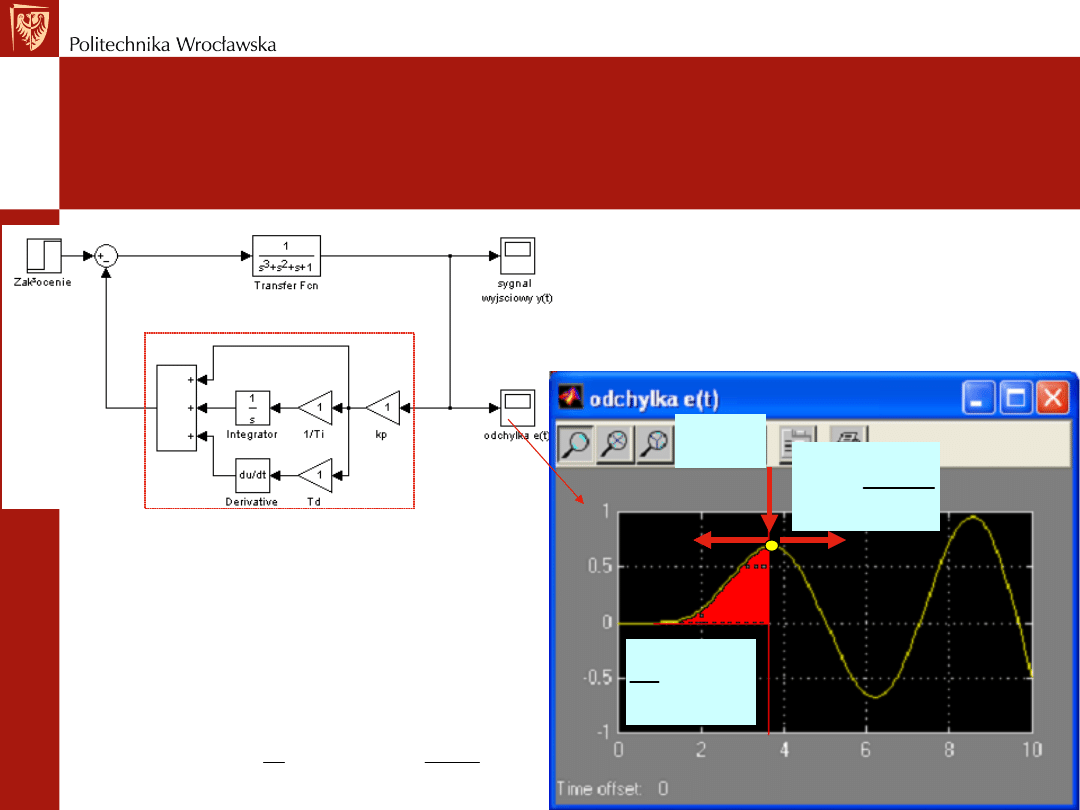
REGULATOR PID

Jak on działa? Charakterystyki
czasowe

PID

Obiekt

0

( )

t

p

i

k

e d

T

t t

�

( )

p

k e t

( )

p d

de t

k T

dt

Część proporcjonalna reaguje na bieżącą odchyłkę

Część całkująca reaguje na sumaryczną odchyłkę
z przeszłości

Część różniczkująca reaguje na możliwą przyszłą
odchyłkę

przyszłość

przeszłość

teraźniejszość

e(t)

u(t)

u t

k e t

T

e

d

T

de t

dt

p

i

t

d

( )

( )

( )

( )





















1

0

 

( )

p

k e t

przyszłość

przeszłość

teraźniejszość

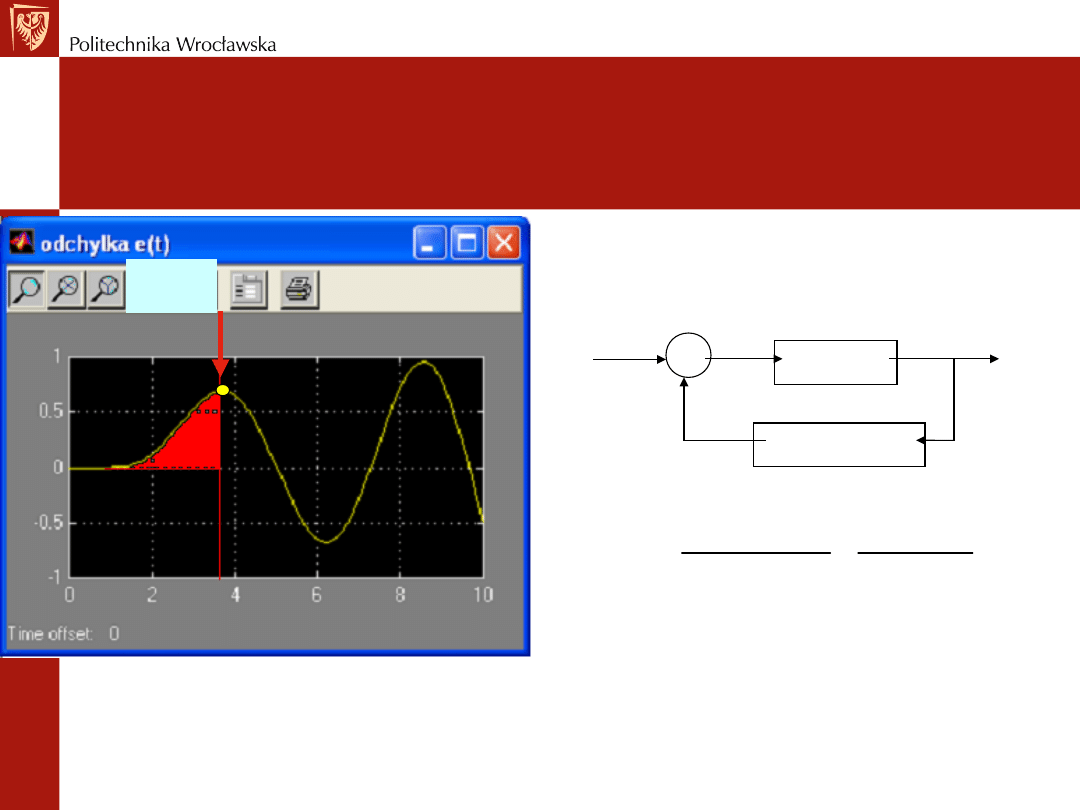
REGULATOR PID

Jak on działa? Charakterystyki
czasowe

Czy nie można by poprzestać na części
proporcjonalnej regulatora?

Regulator

Obiekt

z

-

Transmitancja zastępcza układu ma postać

( )

( )

( )

1

( ) ( ) 1

( )

o

o

o

r

p o

G s

G s

G s

G s G s

k G s

=

=

+

+

Sprawdźmy wartość odchyłki regulacji w stanach
ustalonych tj. po nieskończonym czasie

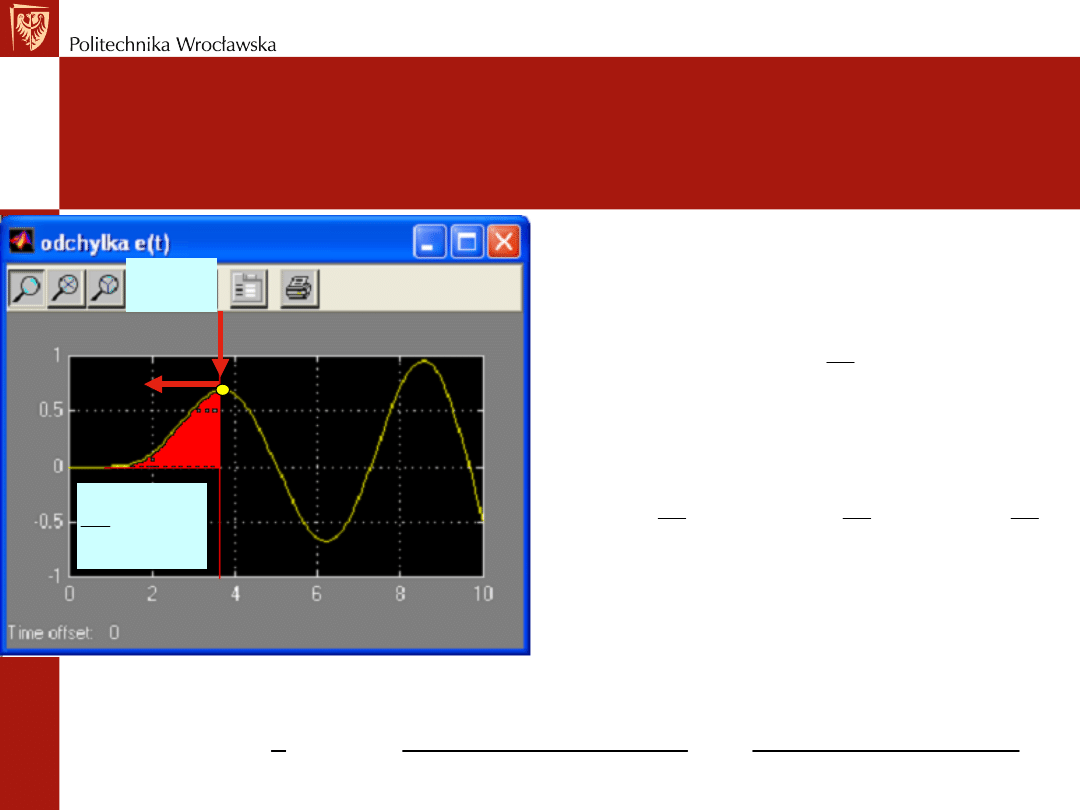
REGULATOR PID

Jak on działa? Charakterystyki
czasowe

0

0

0

0

0

0

1

( )/ ( )

( )

lim ( ) lim ( ) lim

( ) lim

lim

1

( )/ ( )

( )

( )

t

s

s

s

s

p

p

p

b

L s M s

L s

y t

sY s

s G s

s

k L s M s

M s k L s

a

k

�+�

�

�

�

�

=

=

=

=

=

+

+

+

Niech obiekt będzie opisany transmitancją wymierną

( )

1

1

1

0

o

1

1

1

0

...

( )

G

...

( )

m

m

m

m

n

n

n

b s

b s

bs b

L s

s

s

a s

a s a

M s

-

-

-

-

+

+ + +

=

=

+

+ +

+

Wówczas

sygnał wyjściowy jest różny od zera (a to jest wartość zadana).

Pojawia się odchyłka statyczna sygnału wyjściowego.

0

( )

t

p

i

k

e d

T

t t

�

( )

p

k e t

przyszłość

przeszłość

teraźniejszość

REGULATOR PID

Jak on działa? Charakterystyki
czasowe

Jak zlikwidować odchyłkę statyczną regulatora?
Wprowadźmy część całkującą odchyłkę regulacji

0

( )

( )

( )

t

p

p

i

k

u t

k e t

e

d

T

t

t

=

+

�

W punkcie pracy układu regulacji sygnał sterujący
jest stały u=u

0

. Podobnie odchyłka e=e

0

.

0

0

0

0

0

0

0

t

p

p

p

p

p

p

i

i

i

k

k

k

u

k e

e d

k e

e t

e k

t

T

T

T

t

�

�

=

+

=

+

=

+

�

�

�

�

�

Odchyłka musi spełnić warunek
e

0

=0,

jeżeli założenie o stałości nie ma być zaprzeczone.

(

)

0

0

0

0

( )

1

( )/ ( )

lim ( ) lim

( ) lim

lim

0

1

1 1/

( )/ ( )

( )

( )

i

s

s

s

s

p

i

i

p i

p

TsL s

L s M s

sY s

s G s

s

k

Ts L s M s

TsM s k TsL s k L

�

�

�

�

=

=

=

=

+

+

+

+

Dowód w oparciu o transmitancje jest następujący

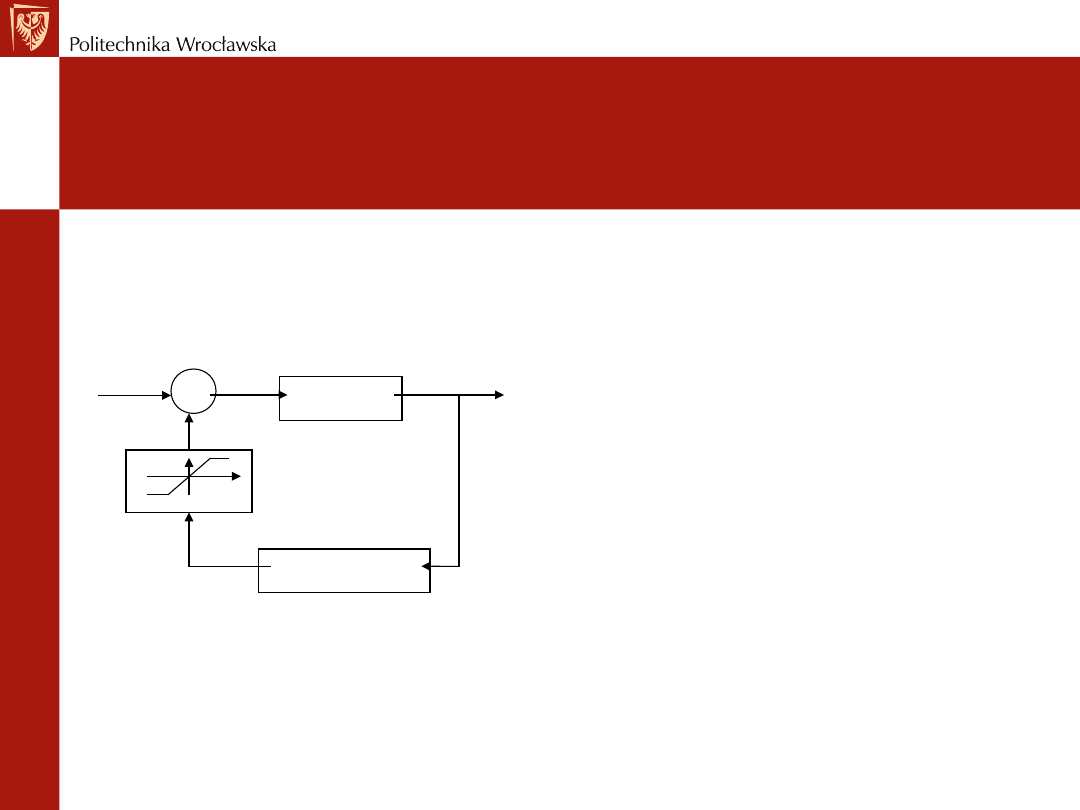
REGULATOR PID

Jak on działa? Charakterystyki
czasowe

Wadą części całkującej jest jej ciągły wzrost w przypadku, gdy odchyłka przez dłuższy
czas jest różna od zera. Taka sytuacja ma miejsce np. wtedy, gdy w układzie regulacji
występuje siłownik stałoprędkościowy.

Regulator

Obiekt

z

-

u

u

1

u

1

u

Linia nasycenia siłownika ogranicza możliwości
redukcji odchyłki regulacji przez regulator.
Widocznym efektem jest np. 100% otwarcie
zaworu przez długi czas i rosnąca wartość
sygnału sterującego powyżej 100% otwarcia
zaworu. Taki sygnał nie może być zrealizowany
fizycznie. Gdy odchyłka regulacji zacznie spadać
wówczas najpierw osiąga wartość 100% otwarcia
zaworu. Następnie dopiero zbliża się do stopnia

otwarcia wymaganego w danych warunkach pracy.

REGULATOR PID

Jak on działa? Charakterystyki
czasowe

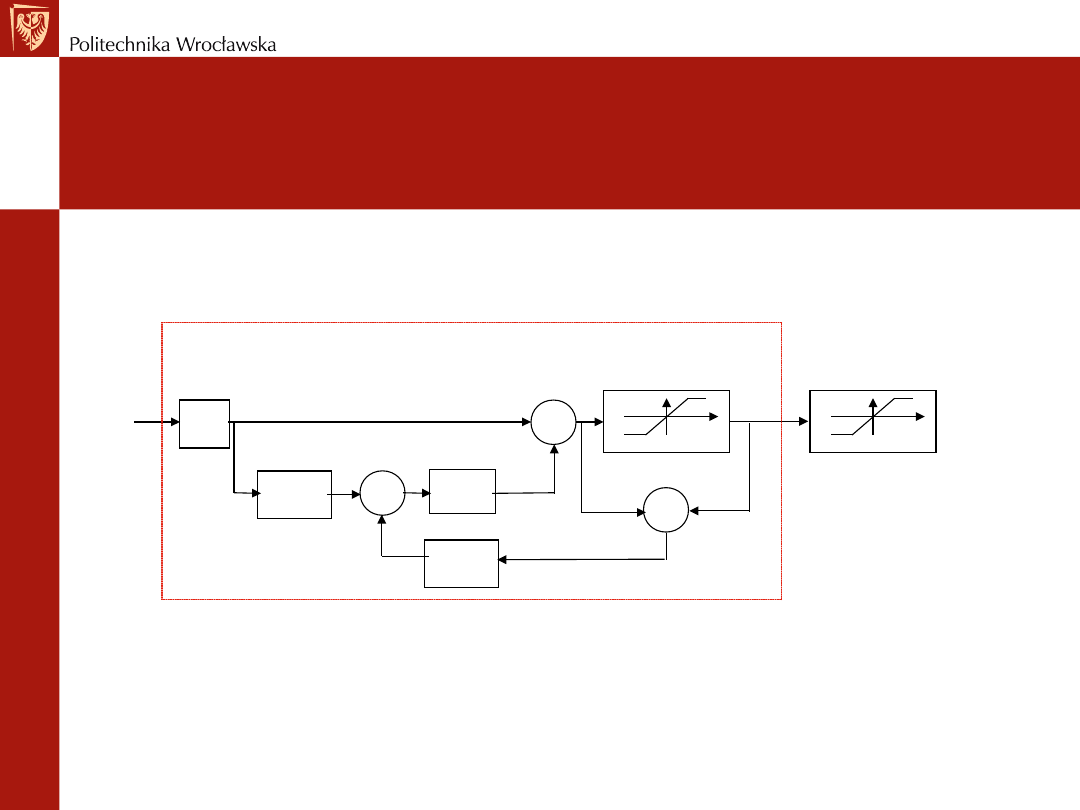
Aby zapobiec takiej niekorzystnej zmianie sygnałów można programowo ograniczyć
wartość części całkującej (np. warunkiem if eI > 100 then eI := 100; ) lub zastosować
poniższe rozwiązanie.

k

p

e

I

= u

1

-u

-

u

u

1

u

1/T

i

1/s

1/T

i

u

Model

siłownika

Siłownik

e(t)

Jeżeli odchyłka e

I

nie jest równa zero, to znaczy, że siłownik osiągnął nasycenie. Wówczas,

w przypadku u > 100%, od części całkującej jest odejmowana nadwyżka ponad 100%.
Podobnie dla u < 0%. Jeżeli 0<u<100%, to e

I

=0.

0

( )

t

p

i

k

e d

T

t t

�

( )

p

k e t

przyszłość

przeszłość

teraźniejszość

REGULATOR PID

Jak on działa? Charakterystyki
czasowe

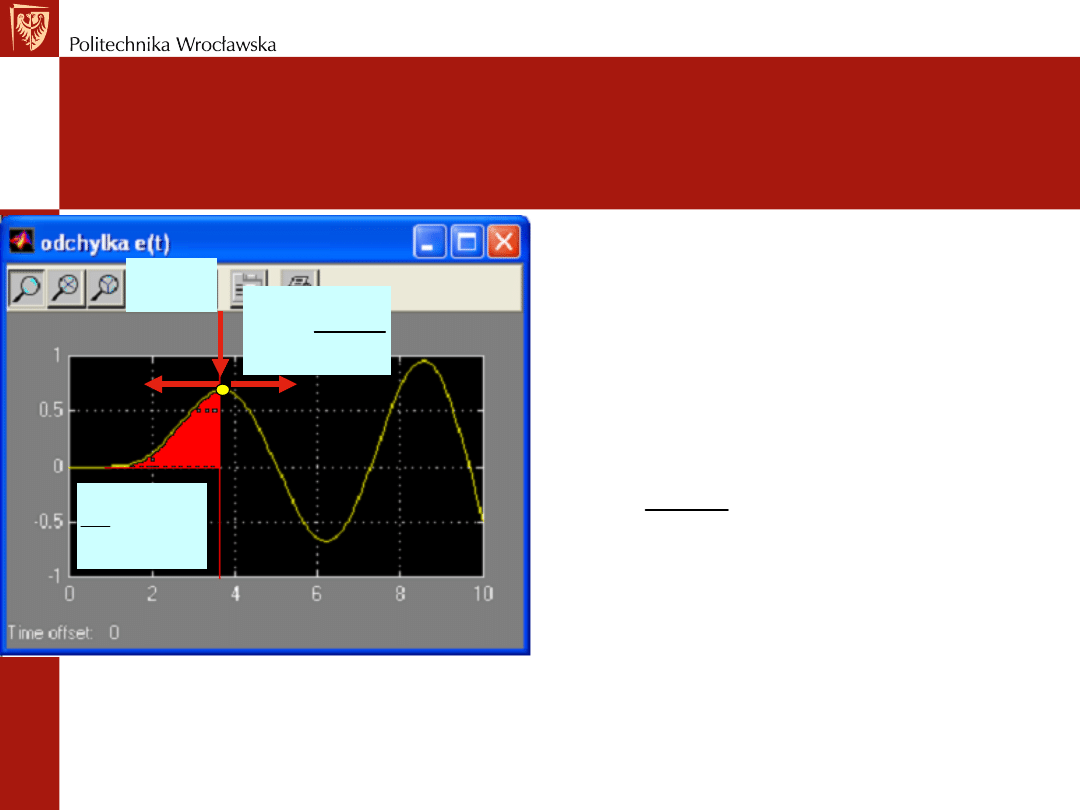
Problem części różniczkującej: różniczkowanie
sygnału szybkozmiennego prowadzi do dużych
zmian sygnału sterującego. Jeżeli sygnał
wyjściowy z obiektu ma postać

( )

p d

de t

k T

dt

( ) sin(

)

y t

t

w

=

to

( )

cos(

)

dy t

t

dt

w

w

=

Jeżeli pulsacja sygnału wyjściowego z obiektu
wynosi =100 rad/s, to jest ona 100 razy większa

od sygnału y(t) przy pulsacji =1 rad/s.

Rozwiązanie problemu części różniczkującej.

W przemysłowych regulatorach stosowane jest
rozwiązanie polegające na modyfikacji części
różniczkującej filtrem inercyjnym

REGULATOR PID

Jak on działa? Charakterystyki
czasowe

1

( )

1

1

/

d

r

p

i

d

T s

G s

k

Ts

T s N

�

�

=

+

+

�

�

+

�

�

( )

1 0.2

s

G s

s

=

+

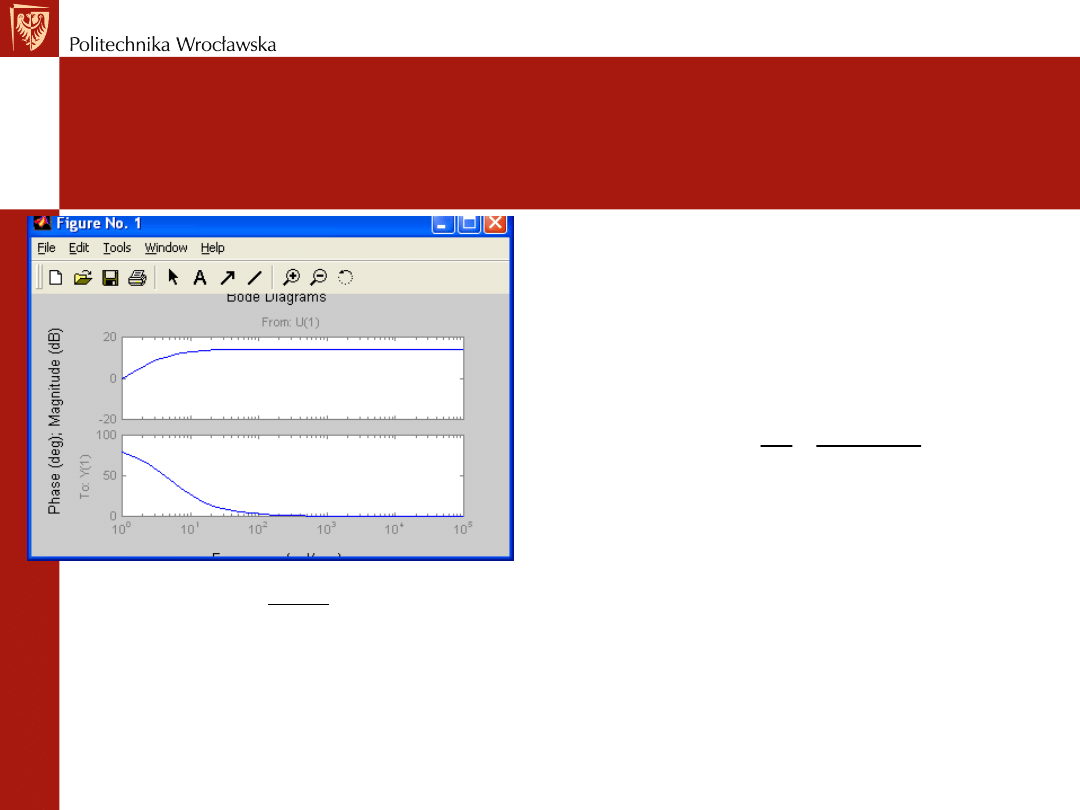
Wówczas dla małych pulsacji s=j człon

różniczkujący rzeczywisty zachowuje własności
członu różniczkującego idealnego, a dla dużych
wzmocnienie jest stałe i wynosi N.

Stałe wzmocnienie
przy dużych pulsacjach

Rys. Wykres Bodego dla członu różniczkującego rzeczywistego

20 log (0.2) = -13.97 dB

REGULATOR PID

Jak on działa? Charakterystyki
częstotliwościowe

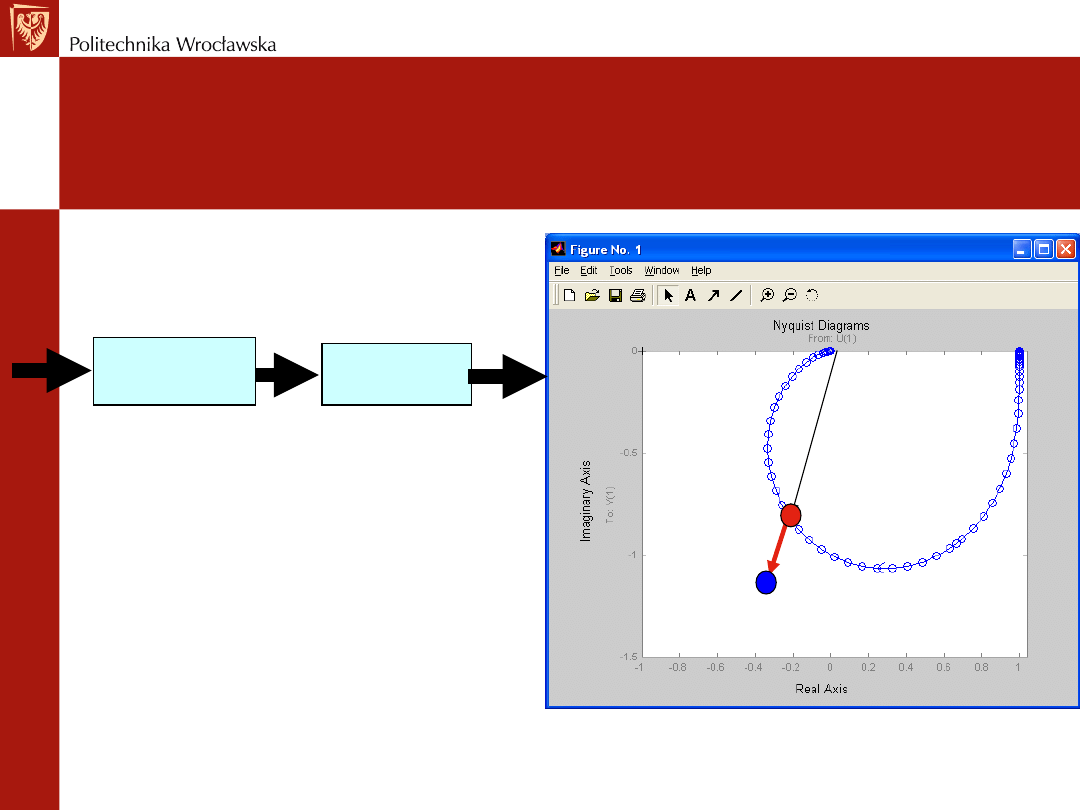
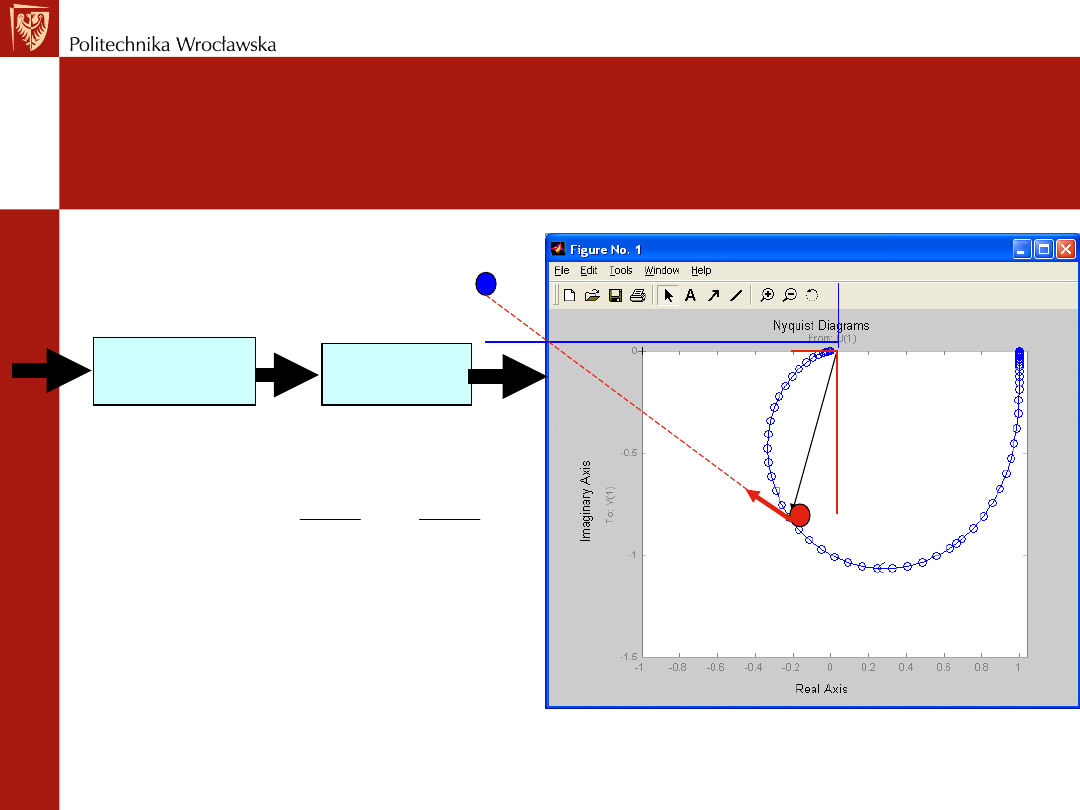
Rys. Wykres Nyquista obiektu inercyjnego 2 rzędu

Co robi regulator PID z punktem wykresu Nyquista
obiektu w otwartym układzie sterowania?

Część proporcjonalna rozszerza lub kurczy wykres
(analogia do „dmuchania w balonik”). Dlaczego?

( )

( ) ( )

( )

o

R

p o

G s

G s G s

k G s

=

=

Obiekt

Regulator

P

( )

( )

j

M

e

f w

w

W zapisie wektorowym punkt

( )

(

)

p

p

p

G s

k P jQ

k P jk Q

=

+

=

+

[P, Q] przesunął się w miejsce [k

p

P,

k

p

Q].

Oczywiście P/Q = k

p

P/k

p

Q co oznacza,

że kąt przesunięcia fazowego  nie

uległ zmianie.
Zmianie natomiast uległ moduł M.

lub

P

REGULATOR PID

Jak on działa? Charakterystyki
częstotliwościowe

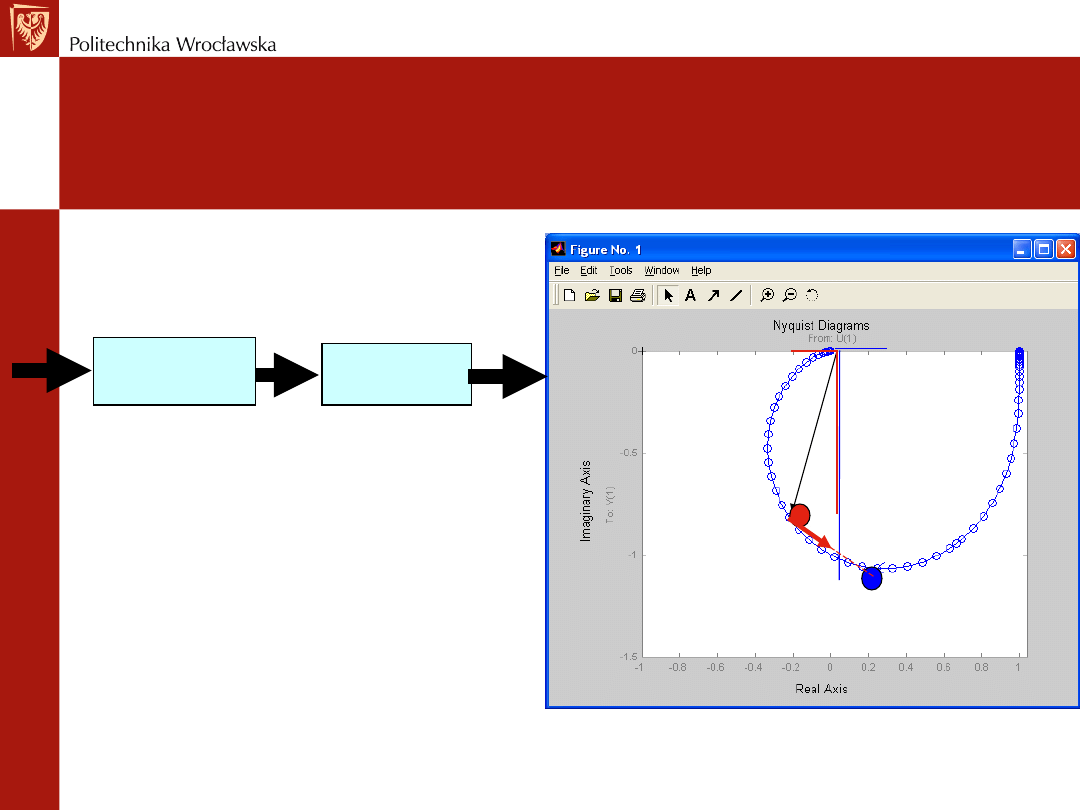
Rys. Wykres Nyquista obiektu inercyjnego 2 rzędu

Co robi regulator PID z punktem wykresu Nyquista
obiektu w otwartym układzie sterowania?

Obiekt

[P, Q] przesunął się w miejsce [-jP,
Q]/T

i

. Wyrażenie –jP oznacza odcinek

o długości P na dodatniej (w przypadku
punktu pokazanego na rysunku!) części
osi urojonej. Stąd można napisać [Q,
-P]/T

i



(P i Q zamieniło się miejscami).

Oznacza to zmianę przesunięcia
fazowego  i modułu M.

Część całkująca przesuwa punkt o -90°

( )

( )

( )

( ) ( )

o

o

o

R

i

i

G s

G s

G s

G s G s

j

Ts

Tw

=

=

=-

I

W zapisie wektorowym punkt

Q

P

P/T

i



Q /T

i



Regulator

I

REGULATOR PID

Jak on działa? Charakterystyki
częstotliwościowe

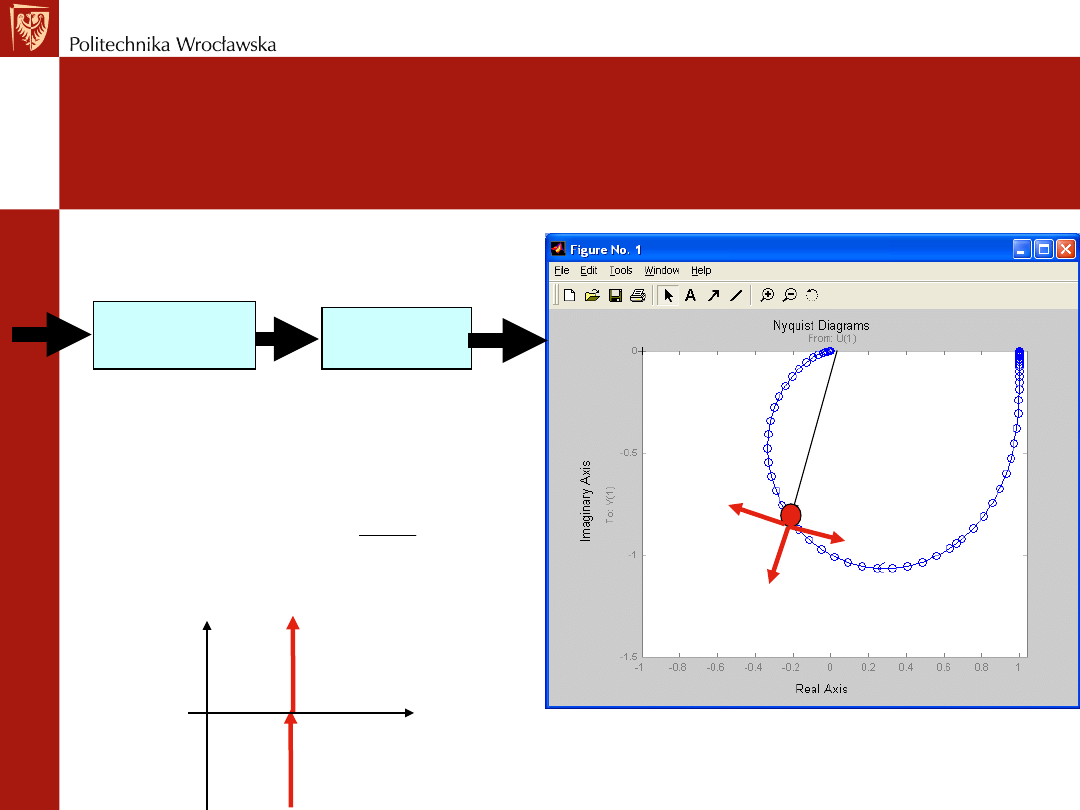
Rys. Wykres Nyquista obiektu inercyjnego 2 rzędu

Co robi regulator PID z punktem wykresu Nyquista
obiektu w otwartym układzie sterowania?

Obiekt

[P, Q] przesunął się w miejsce [jP,
-Q]T

d

. Wyrażenie jP oznacza odcinek o

długości P na ujemnej części osi
urojonej (w przypadku punktu
pokazanego na rysunku!).

Oznacza to zmianę przesunięcia
fazowego  i modułu M.

D

W zapisie wektorowym punkt

Q

P

PT

d



QT

d



Część różniczkująca przesuwa punkt o +90°

( )

( ) ( )

( )

( )

o

R

d

o

d

o

G s

G s G s

T sG s

j T G s

w

=

=

=

Regulator

D

REGULATOR PID

Jak on działa? Charakterystyki
częstotliwościowe

Rys. Wykres Nyquista obiektu inercyjnego 2 rzędu

Co robi regulator PID z punktem wykresu Nyquista
obiektu w otwartym układzie sterowania?

P

Obiekt

Regulator

PID

I

D

-j

+j

0

Uzasadnienie dla zaawansowanych
Człon różniczkujący wnosi przesunięcie fazowe
o +90° wstecz pomiędzy sygnałami wejściowym u(t) i
wyjściowym y(t). Jeżeli

( ) sin( )

u t

t

w

=

( )

( )

cos( )

du t

y t

t

dt

w

=

=

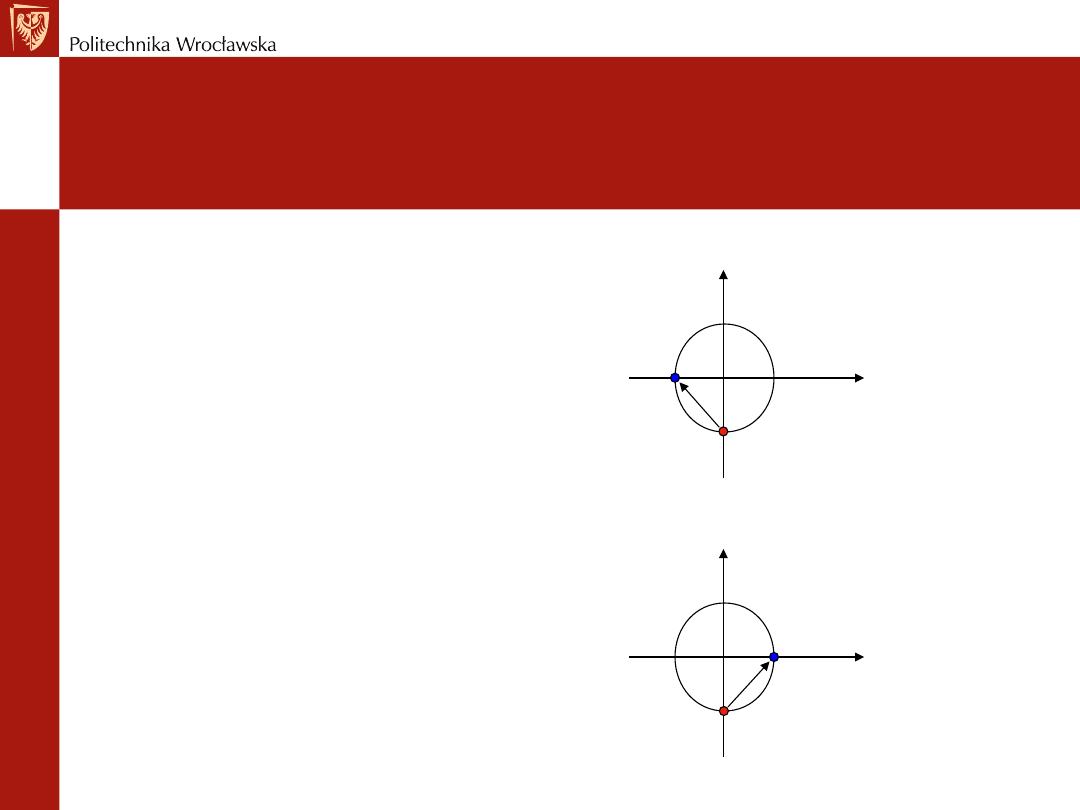
Innym uzasadnieniem jest wykres Nyquista członów

to

P

I

D

+90

o

-90

o

90

o

j

e

-

Człon całkujący wnosi przesunięcie fazowe
,więc punkt musi się przesunąć o 90

o

w lewo

po okręgu.

(Dlaczego po okręgu ? Bo wzór Eulera oznacza parametryczne równanie okręgu)

(Dlaczego w lewo? Bo taka jest konwencja określania
kierunku ruchu po okręgu – w lewo jest znak minus)

Człon różniczkujący wnosi przesunięcie fazowe
,więc punkt musi się przesunąć o 90

o

w prawo

po okręgu.

90

o

j

e

+

Inne uzasadnienie

REGULATOR PID

Jak on działa? Charakterystyki
częstotliwościowe

P=Re G(j)

Q=Im G(j)

P=Re G(j)

Q=Im G(j)

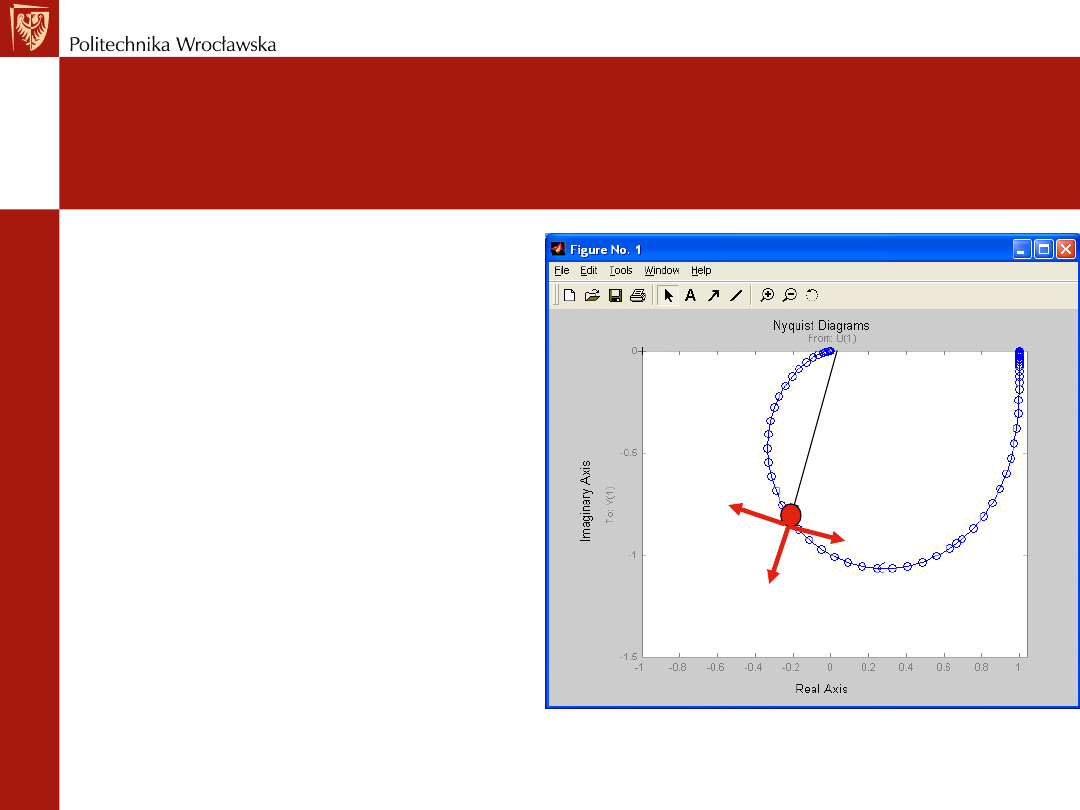
REGULATOR PID

Jak on działa? Charakterystyki
częstotliwościowe

Rys. Wykres Nyquista obiektu inercyjnego 2 rzędu

P

I

D

Z rysunku wynika, że regulator PID może przesunąć
punkt wykresu Nyquista obiektu w dowolne miejsce
płaszczyzny w zależności od nastaw

Ale które miejsce jest dobre?

Systematyczna klasyfikacja

własności regulatorów

TYPOWE STRUKTURY
REGULATORÓW PID
Regulator proporcjonalny P

TYPOWE STRUKTURY
REGULATORÓW PID
Regulator całkujący I

TYPOWE STRUKTURY
REGULATORÓW PID
Regulator różniczkujący D

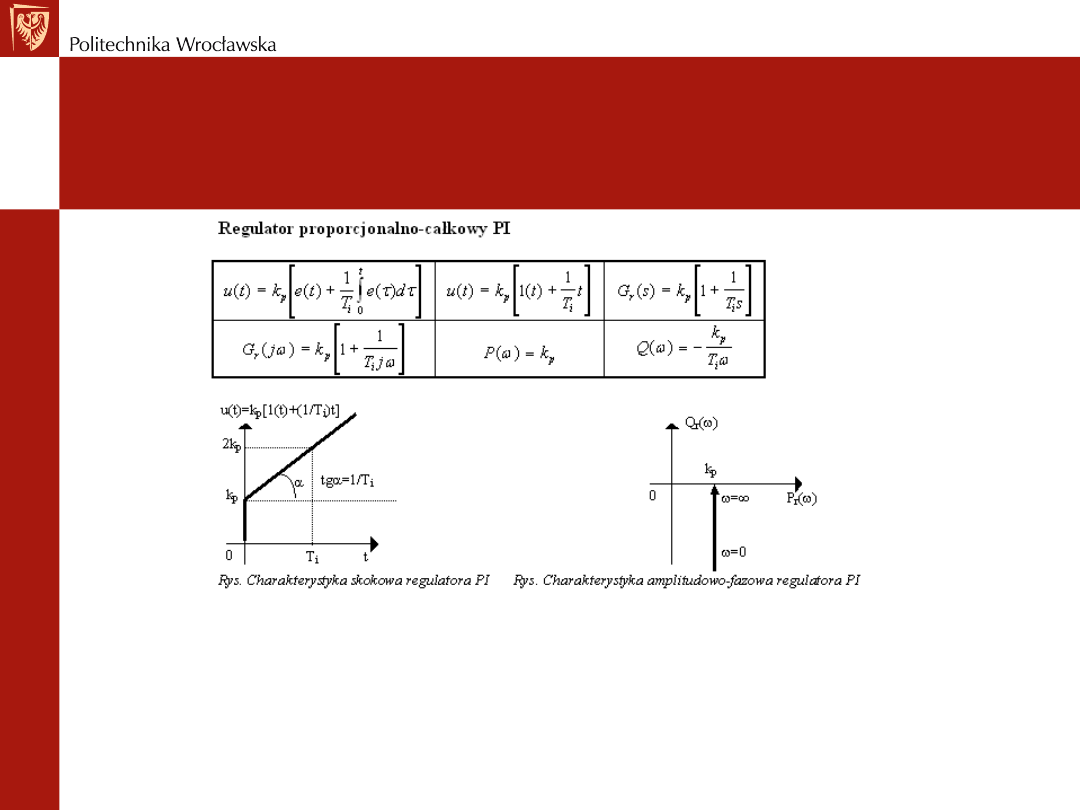
TYPOWE STRUKTURY
REGULATORÓW PID
Regulator proporcjonalno-całkujący
PI

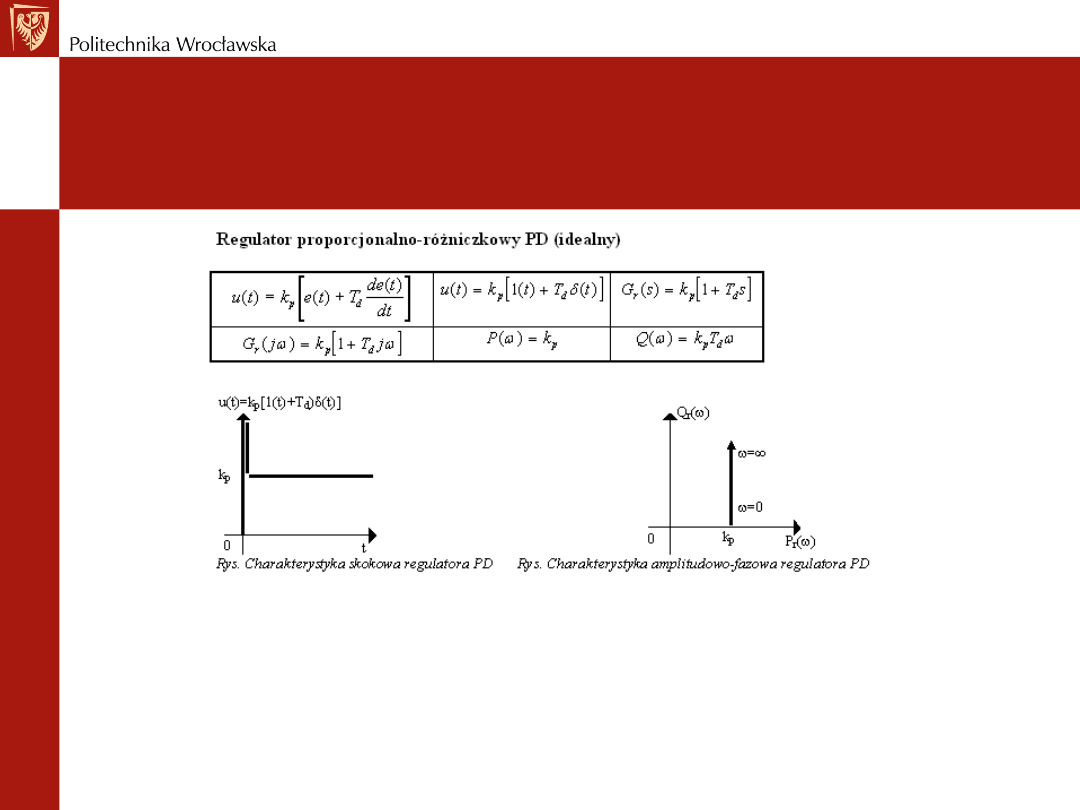
TYPOWE STRUKTURY
REGULATORÓW PID

Regulator proporcjonalno-różniczkujący
PD

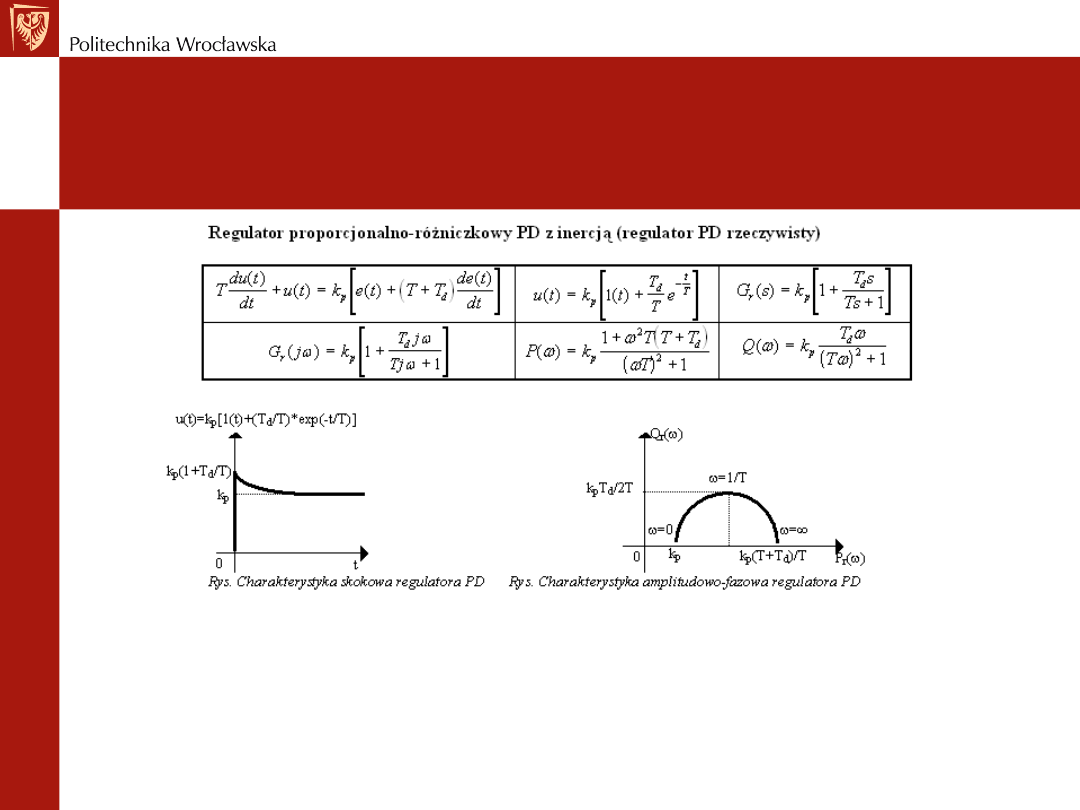
TYPOWE STRUKTURY
REGULATORÓW PID

Regulator proporcjonalno-różniczkujący
PD

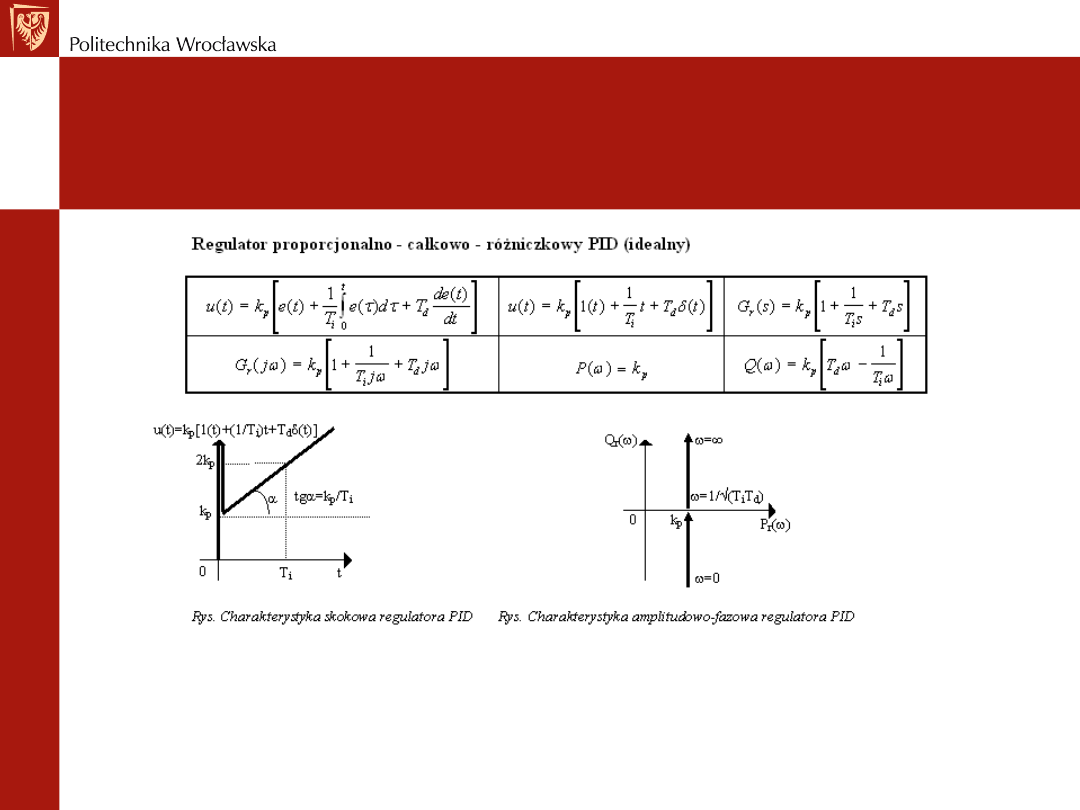
TYPOWE STRUKTURY
REGULATORÓW PID

Regulator PID

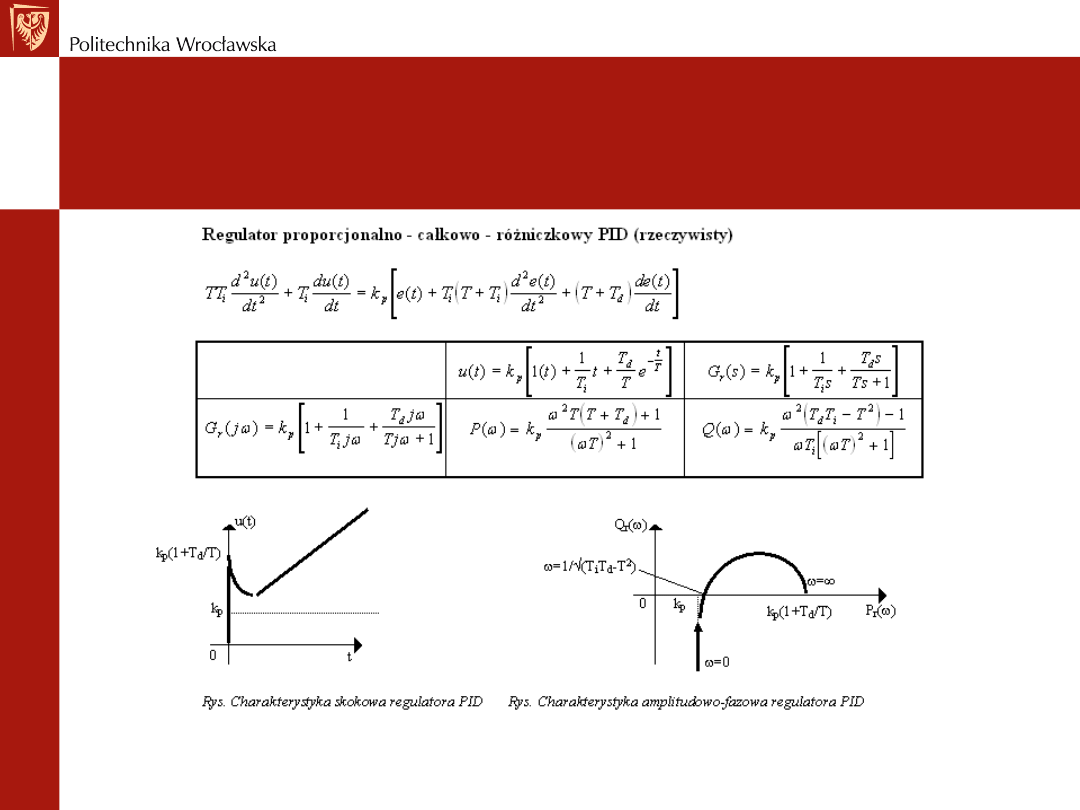
TYPOWE STRUKTURY
REGULATORÓW PID

Regulator PID

Próba strojenia regulatora

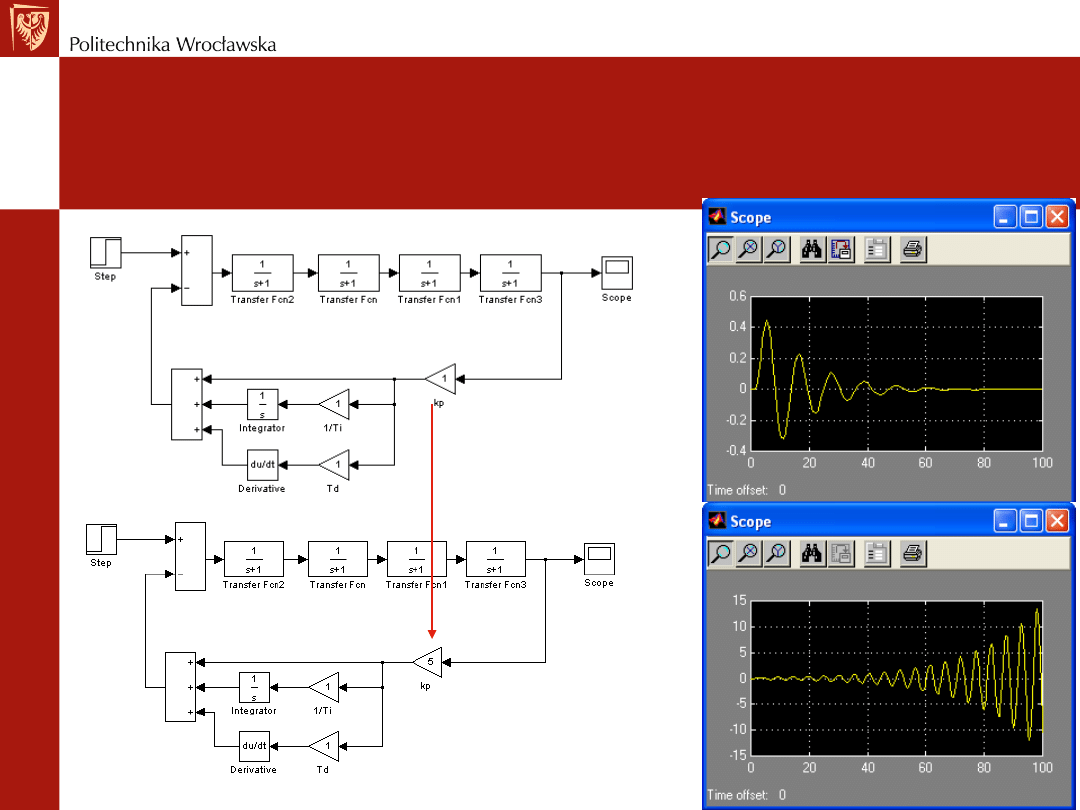
PRÓBA STROJENIA REGULATORA

Wpływ nastaw na przebieg przejściowy -
k

p

Przebieg stabilny

Przebieg niestabilny

k

p

=1, T

i

=1, T

d

=1

k

p

=5, T

i

=1, T

d

=1

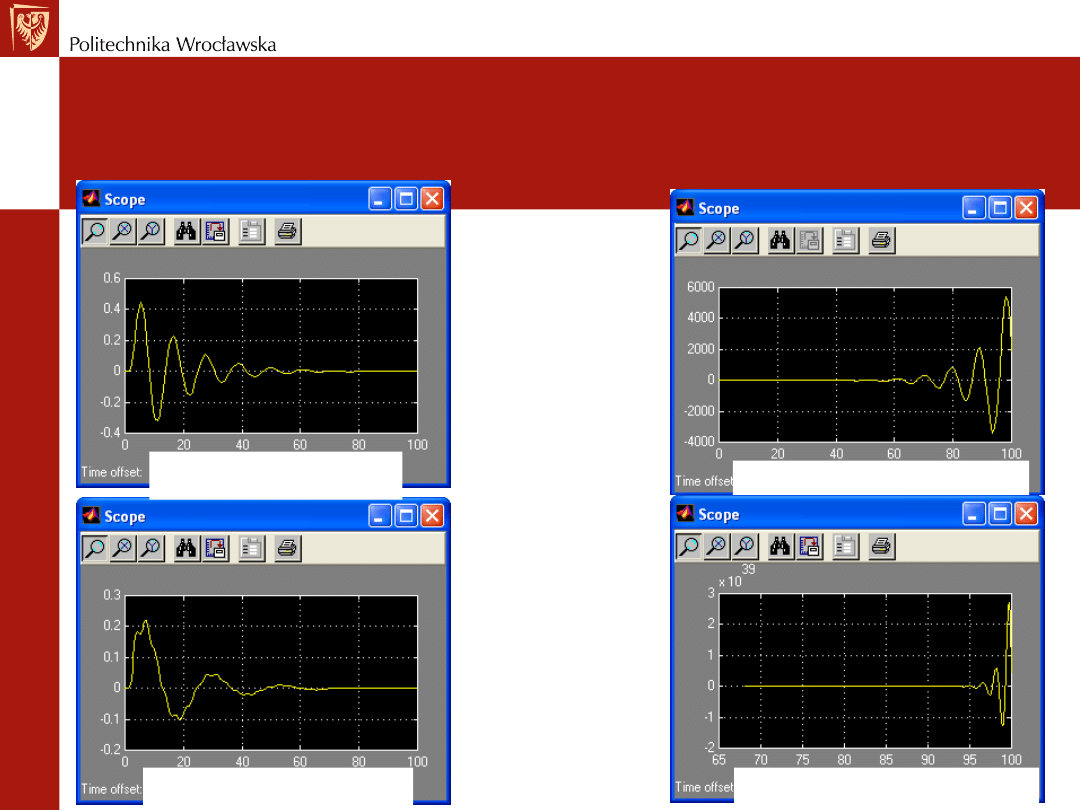
PRÓBA STROJENIA REGULATORA

Wpływ nastaw na przebieg przejściowy –
T

i,

T

d

kp=1, Ti=0.5, Td=1

k

p

=1, T

i

=1, T

d

=10

kp=1, Ti=1, Td=100

k

p

=1, T

i

=1, T

d

=1

STROJENIE PID

Wpływ nastaw na przebieg
przejściowy

u t

k e t

T

e d

T

de t

dt

p

i

t

d

( )

( )

( )

( )





















1

0

 

Sygnał

u(t)

Stabilność

układu

regulacji

k

p

wzrasta

Wzrasta

Maleje

T

i

wzrasta

Maleje

Wzrasta

T

d

wzrasta

Wzrasta

Początkowo

wzrasta potem

maleje

Dziękuję za uwagę i

zainteresowanie