PRZYKŁADY OBLICZEŃ STROPÓW

Na podstawie:

Czesław Malinowski, Ryszard Perla
Projektowanie konstrukcji murowych i stropów w budownictwie

tradycyjnym

Przykład 1

- Strop TERIVA I

Zaprojektować międzypiętrowy

strop gęstożebrowy TERIVA I

Strop jest swobodnie podparty
na ścianach o grubości 25 cm.

Rozpiętość w osiach ścian L

M

= 4,80

m.

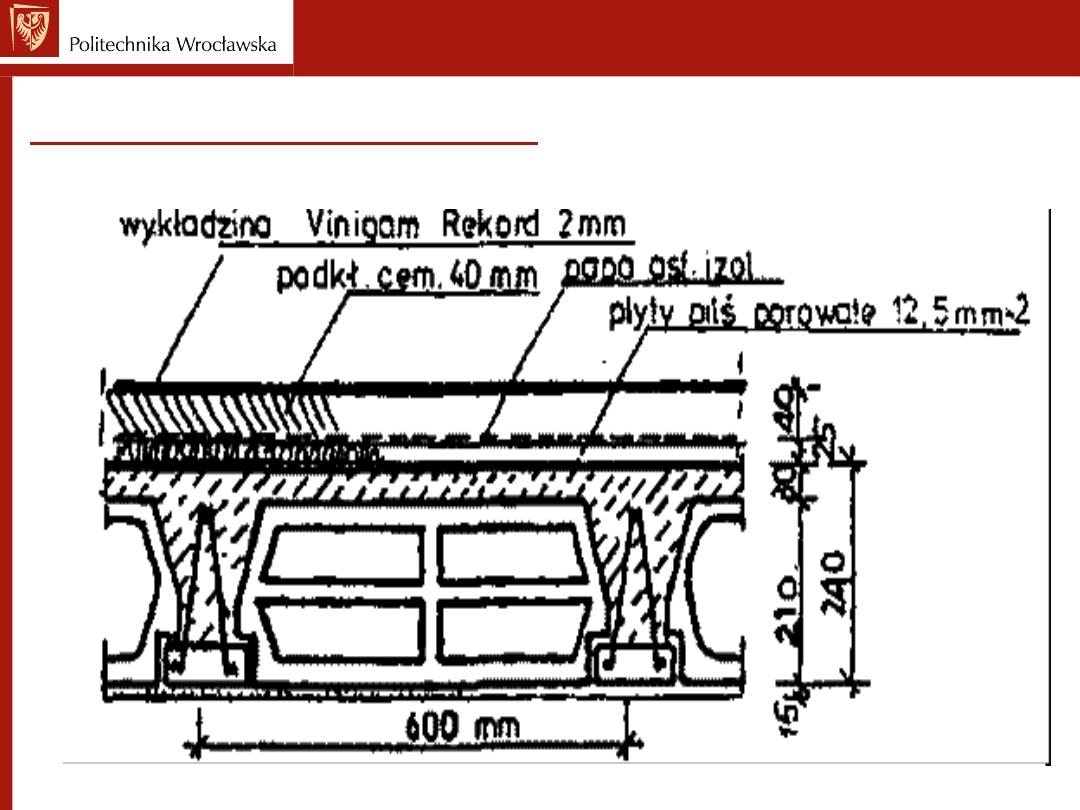
Strop TERIVA

Układ warstw podłogi

Strop TERIVA I

Obciążenia zmienne równomiernie
rozłożone na stropie przyjąć o wielkości
p

k

= 2,0 kN/m

2

.

Strop jest obciążony lekkimi ściankami
działowymi: okładziny z płyt gipsowo-
kartonowych na szkielecie stalowym
o ciężarze 0,25 kN/m

2

.

Wysokość ścianek 2,5 m, układ
zróżnicowany.

Rozwiązanie

Zestawienie obciążeń
a) obciążenie stałe

-

podłoga, wykładzina Rekord 2 mm + podkład
cement. 40 mm + płyty pilśniowe por. 2 x 12,5

mm

(0,055+0,86) x

1,2

=

-

ciężar własny stropu 2,68
x

1,1

=

-

tynk cem.-wap. 0,015 x 19,0

x

1,3

=

Razem

g =

b) obciążenie zmienne (y

f

= 1,4)

2,0

x

1,4

=

c) ciężar ścianki działowej 0,25 kN/m

2

, (γ

f

= 1,2)

-

obciążenie stropu w przypadku ścianki
ustawionej równolegle do żeber

g

s

=

0,25 x 2,50 x

1,2

=

Obciążenia
obliczeniow

e, kN/m

2

1,10
2,95
0,37
4,42 kN/m

2

2,80 kN/m

2

0,75 kN/m

Rozwiązanie

2. Dobór belki stropowej obciążonej ścianką

działową usytuowaną równolegle do żebra.
Przyjęto założenie o rozłożeniu obciążenia od
ścianki na trzy żebra stropowe (50 % na żebro pod
ścianką).

Uwzględniono redukcję obciążenia zmiennego ze względu
na usytuowanie ścianki o grubości 10 cm

.

Obciążenie pojedynczego żebra

q =

4,42

kN/m

2

• 0,60

m

+2,80

kN/m

2

• (0,60-0,10)

m

+ 0,5 •

0,75

kN/m

=

=

2,65

kN/m

+ 1,40

kN/m

+ 0,38

kN/m

= 4,43 kN/m

Rozpiętość obliczeniowa

belki

l

o

= 1,05 • (4,80 - 0,25)= 4,78 m

Rozwiązanie

Maksymalny moment zginający w środku

rozpiętości belki wynosi:

M

max

= 0,125

•

q • l

2

=

= 0,125 • 4,43 • 4,78

2

= 12,652 kNm

Nośność pojedynczego żebra o rozpiętości

modularnej l

m

= 4,80 m, zbrojonego prętami 28

+ 110 ze stali 34GS wynosi M

o

= 13,369 kNm i

jest większa od maksymalnego momentu

zginającego co oznacza, że dla podanych założeń

możemy wykonać w pomieszczeniu strop z

typowych belek kratownicowych.

Przykład 2 -

Strop DZ-3

(stropodach pełny)

Zaprojektować strop DZ-3 stanowiący

konstrukcję stropodachu pełnego o
układzie warstw podanym na rysunku.
Rozpiętość modularna stropu l

M

= 6,0 m,

rozpiętość w świetle podpór (ścian) l

s

=

5,62 m. Budynek zlokalizowany jest w
I strefie obciążenia śniegiem,
nachylenie połaci dachu 5%.

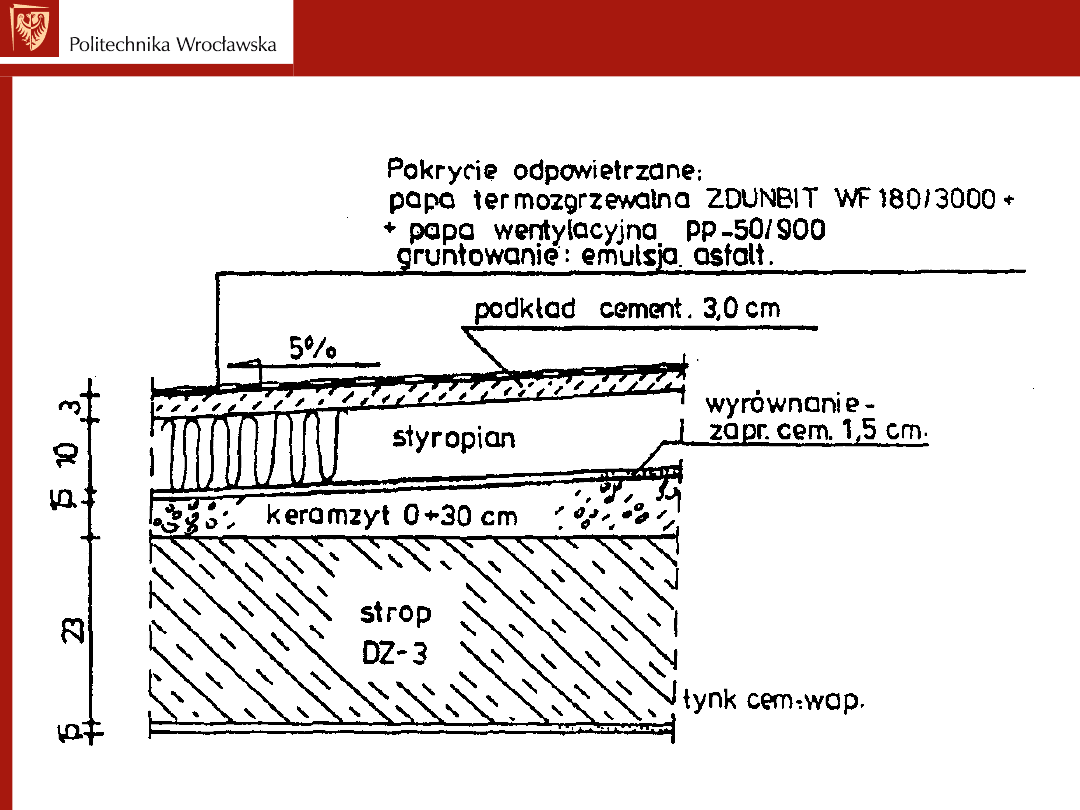
Stropodach pełny — układ warstw

Zestawienie obciążeń

1. Obciążenia stałe:

— pokrycie — papa wentylacyjna (perforowana) PP-50/900 +

papa termozgrzewalna Zdunbit WF 180/3000 na

zagruntowanym podkładzie, ciężar wg katalogu produktów

firmy IZOLACJA S.A. - Zduńska Wola,

0,025 + 0,045 = 0,07 kN/m

2

przyjęto obciążenie wg PN-82/B-02001

0,10

kN/m

2

•

1,2

= 0,12

kN/m

2

─ podkład cementowy

0,03

m

• 21,0

kN/m

3

•

1,3

= 0,82 kN/m

2

─ styropian 10 cm

0,10

m

• 0,45

kN/m

3

•

1,2

= 0,05 kN/m

2

─ wyrównanie warstwy nadającej spadek

0,015

m

• 21,0

kN/m

3

•

1,3

=0,41 kN/m

2

─ warstwa keramzytu średnio 15 cm

0,15

m

•8,0

kN/m

3

•

1,3

=1,56

kN/m

2

─ strop DZ-3

2,65kN/m

2

•

1,1

=2,92 kN/m

2

─ tynk cem.-wap. 15 mm

0,015

m

•19,0

kN/m

3

•

1,3

=0,37

kN/m

2

Razem g =6,25 kN/m

2

.

2. Obciążenia zmienne

wg. PN-80/B-02010,

I strefa, c = 0,8

obciążenie śniegiem

S=0,70 kN/m

2

•0,8•1,4=0,78kN/m

2

3. Obliczenie maksymalnego momentu

zginającego

w środku rozpiętości belki

(w przybliżeniu)

- głębokość oparcia belki przy długości belki

typowej 5,96 m

a = 0,5(l - l

s

) = 0,5(5,96 - 5,62) = 0,17 m

- rozpiętość obliczeniowa

l

o

= l

s

+ a = 5,62 + 0,17 = 5,79 m

.

-obciążenie belki

q = (6,25 + 0,78) • 0,6 = 4,22 kN/m

strop wymaga podparcia w środku rozpiętości w
czasie montażu.
Moment zginający wynosi

M

max

=0,125•q•l

o2

=0,12•4,22•5,792 =17,684

kNm

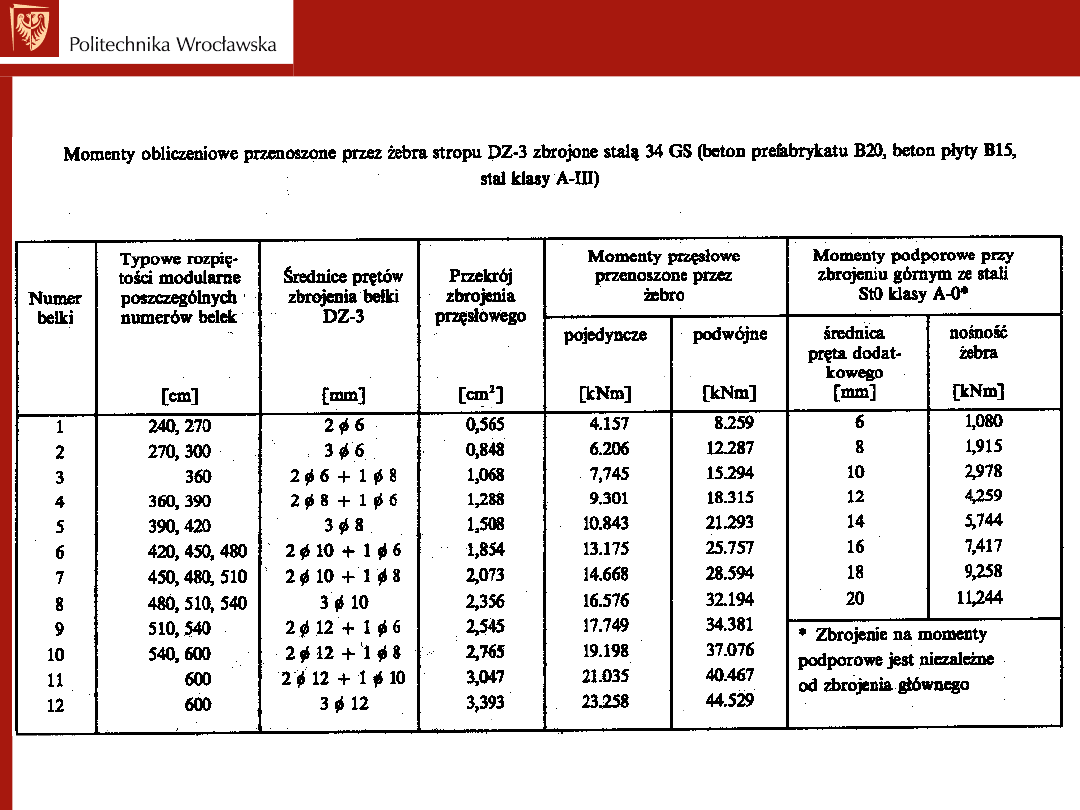
Należy zastosować belki Nr 10, zbrojone prętami
212 + 18 ze stali 34GS, których nośność
wynosi

M

o

= 19,198 > Mmax

(tabela poniżej)