FUNKCJE 

TRYGONOMETRYCZ

NE 

PODSTAWOWYCH

KĄTÓW OSTRYCH

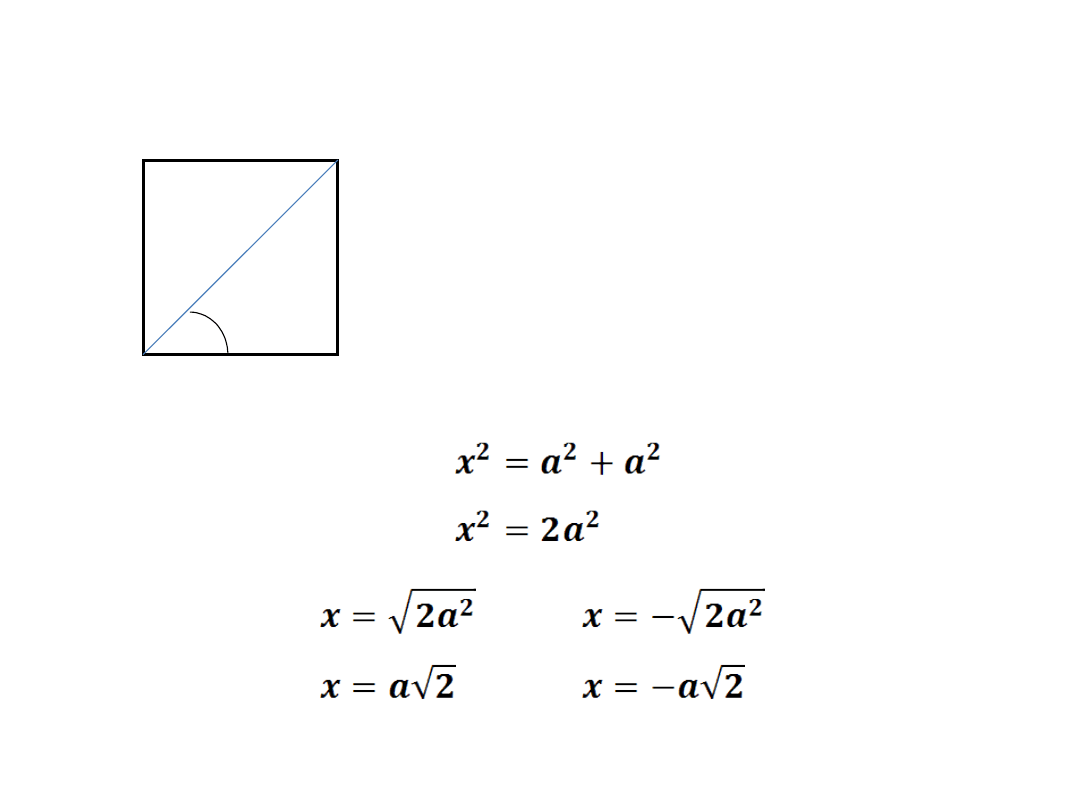
I. FUNKCJE TRYGONOMETRYCZNE KĄTA 

α

=45° 

a

a

α

Δ ABC – PROSTOKĄTNY

α=45°

Wykorzystując twierdzenie 
Pitagorasa obliczymy długość 
przekątnej kwadratu. 

β

x

α

lub                   - odpada

lub                   - odpada

A

B

D

C

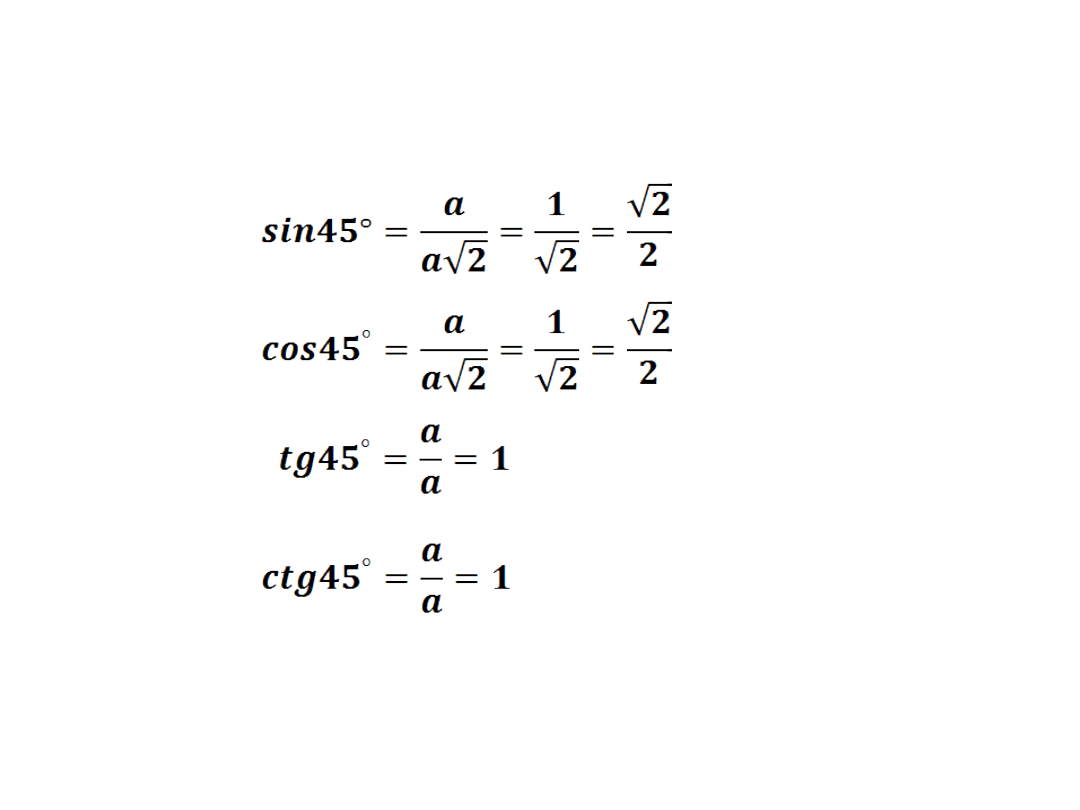
α

Stosując odpowiednie definicje i wzory w trójkącie 
prostokątnym wyznaczymy wartości funkcji 
trygonometrycznych kąta 45°. 

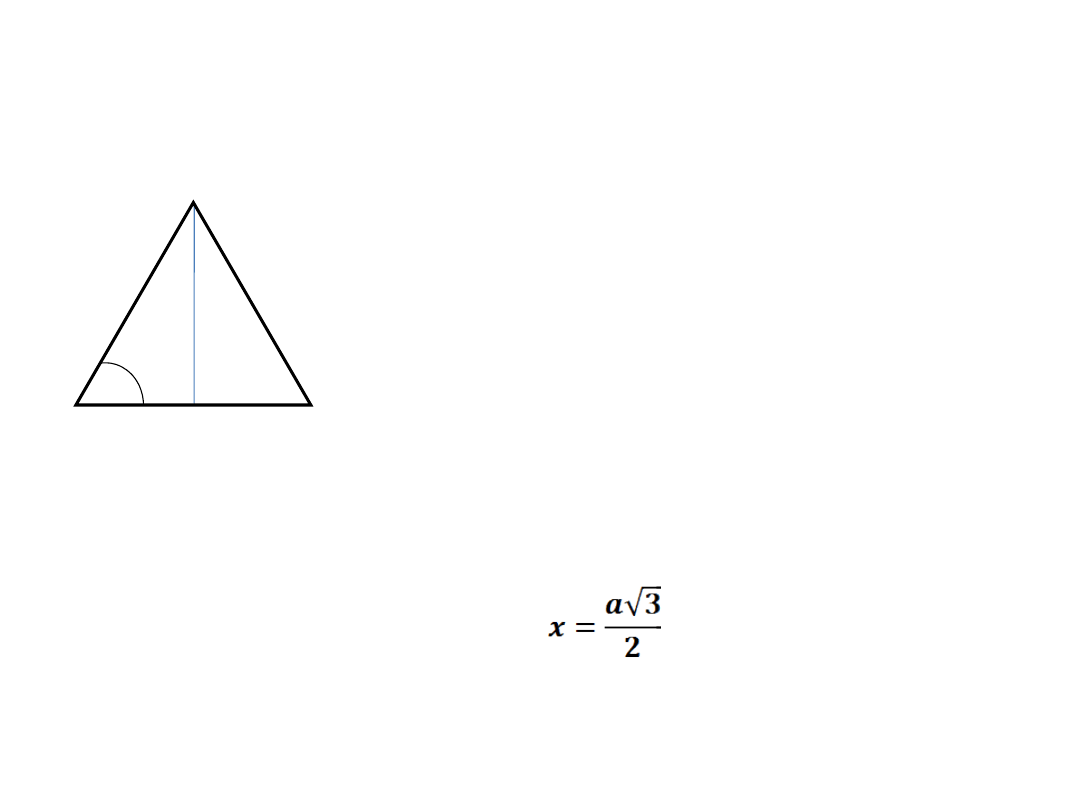
II. FUNKCJE TRYGONOMETRYCZNE KĄTA 

α

=60° 

x

a

α

Δ ADC – PROSTOKĄTNY

α=60°

Trójkąt ABC jest równoboczny, 
każdy kąt wewnętrzny w tym 
trójkącie ma miarę 60

0

. 

Narysowana wysokość podzieliła 
trójkąt na dwa trójkąty 
prostokątne. Odcinek x jest 
wysokością trójkąta:  

β

½ a

α

A

B

D

C

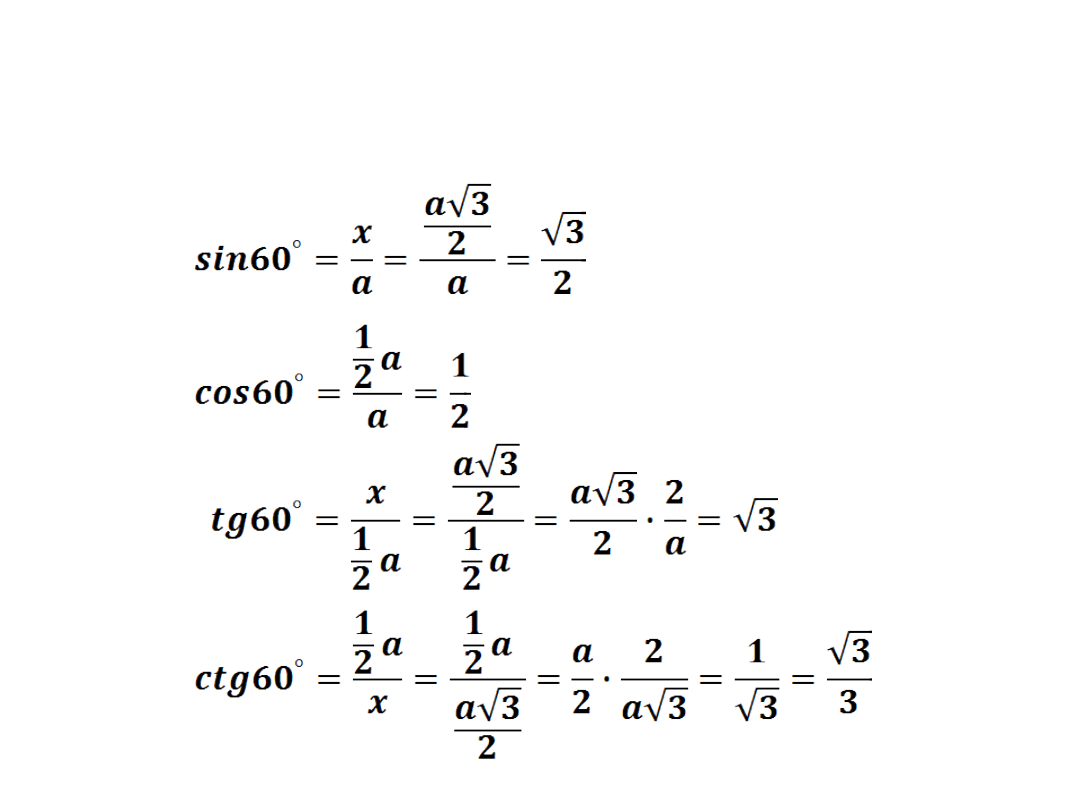
α

β

Stosując odpowiednie definicje i wzory w trójkącie 
prostokątnym wyznaczymy wartości funkcji 
trygonometrycznych kąta 60°. 

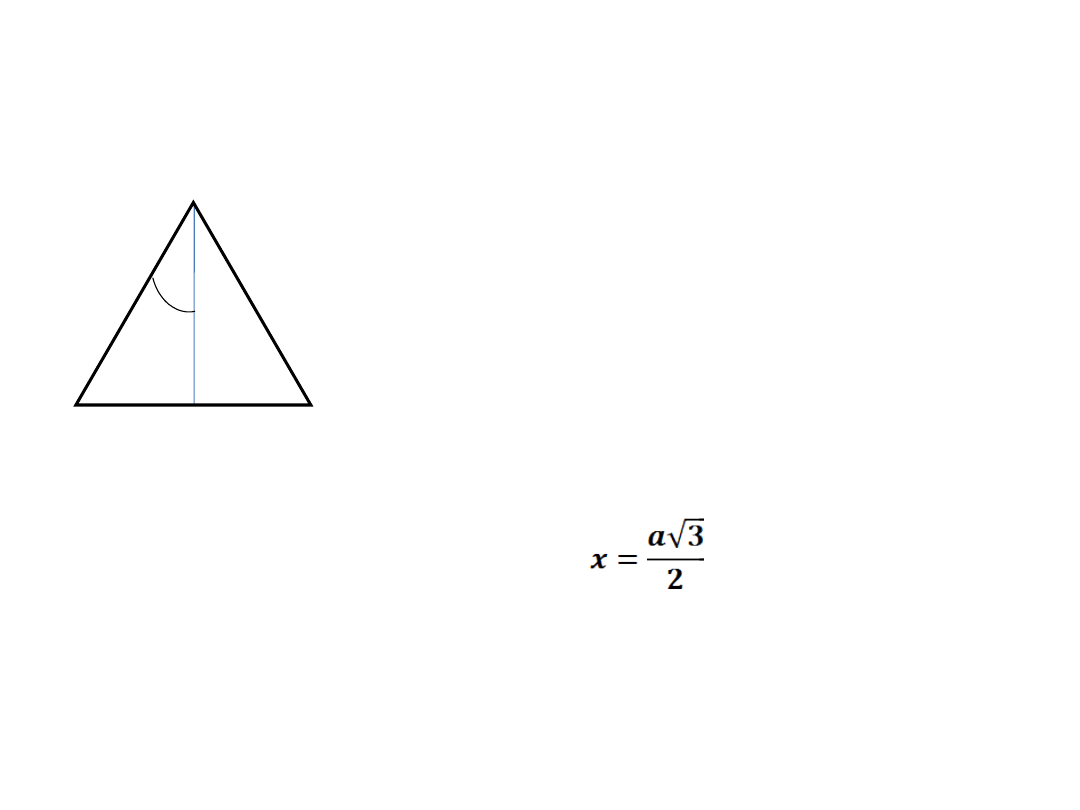
III. FUNKCJE TRYGONOMETRYCZNE KĄTA 

α

=30° 

x

a

α

Δ ADC – PROSTOKĄTNY

α=30°

Narysowana wysokość podzieliła 
trójkąt na dwa trójkąty 
prostokątne.
Kąt α  (połowa kąta przy 
wierzchołku C) ma miarę 30.  

β

½ a

α

A

B

D

C

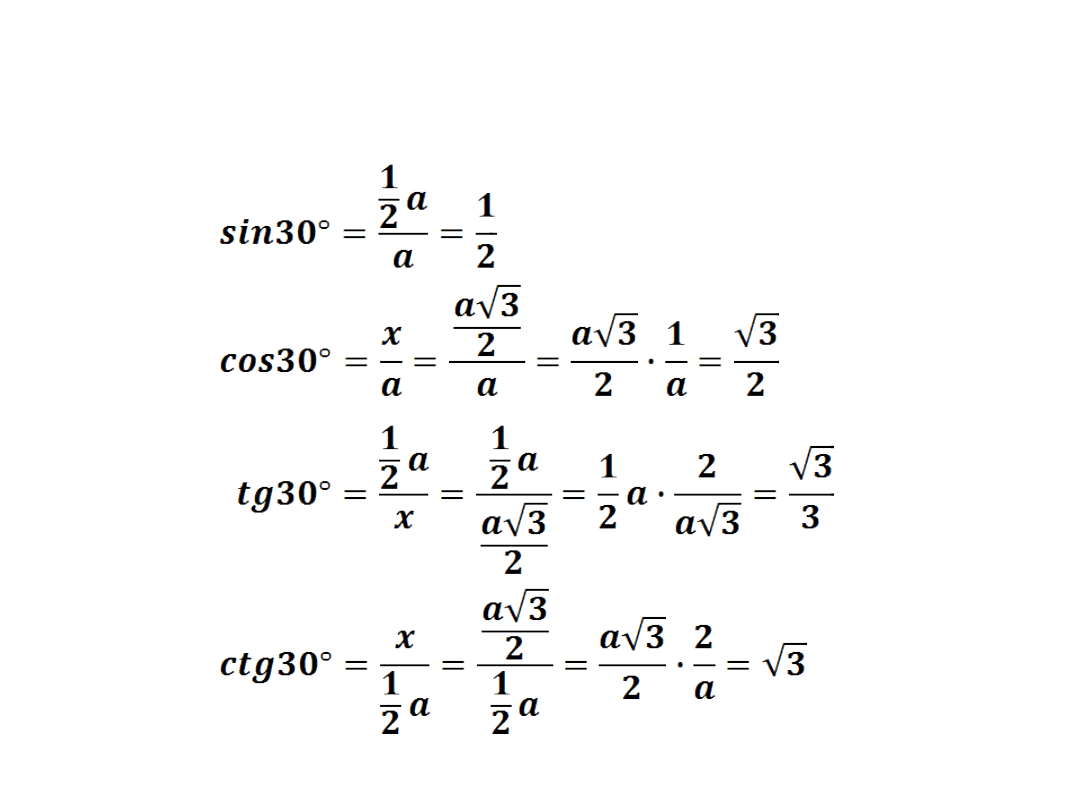
α

β

Stosując odpowiednie definicje i wzory w trójkącie 
prostokątnym wyznaczymy wartości funkcji 
trygonometrycznych kąta 30°. 

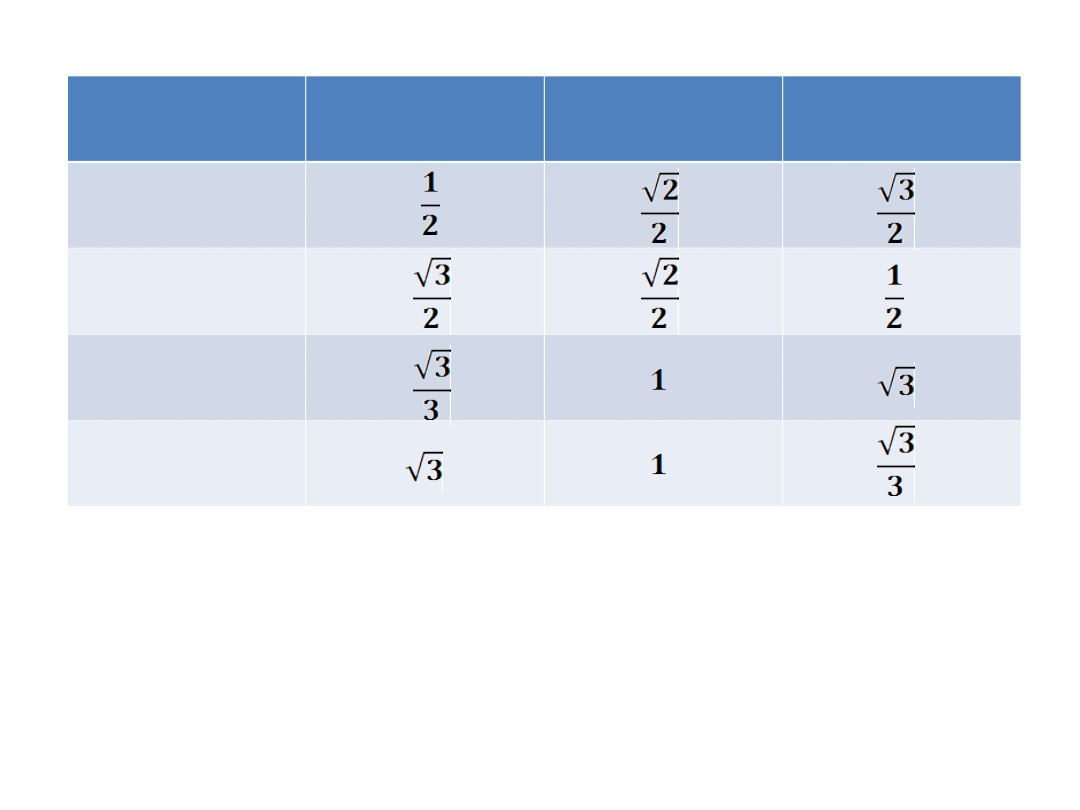
30°

45°

60°

sin

cos

tg

ctg

 sin30=cos60

cos30=sin60 

  tg30=ctg60

ctg30=tg60

  tg45=ctg45        

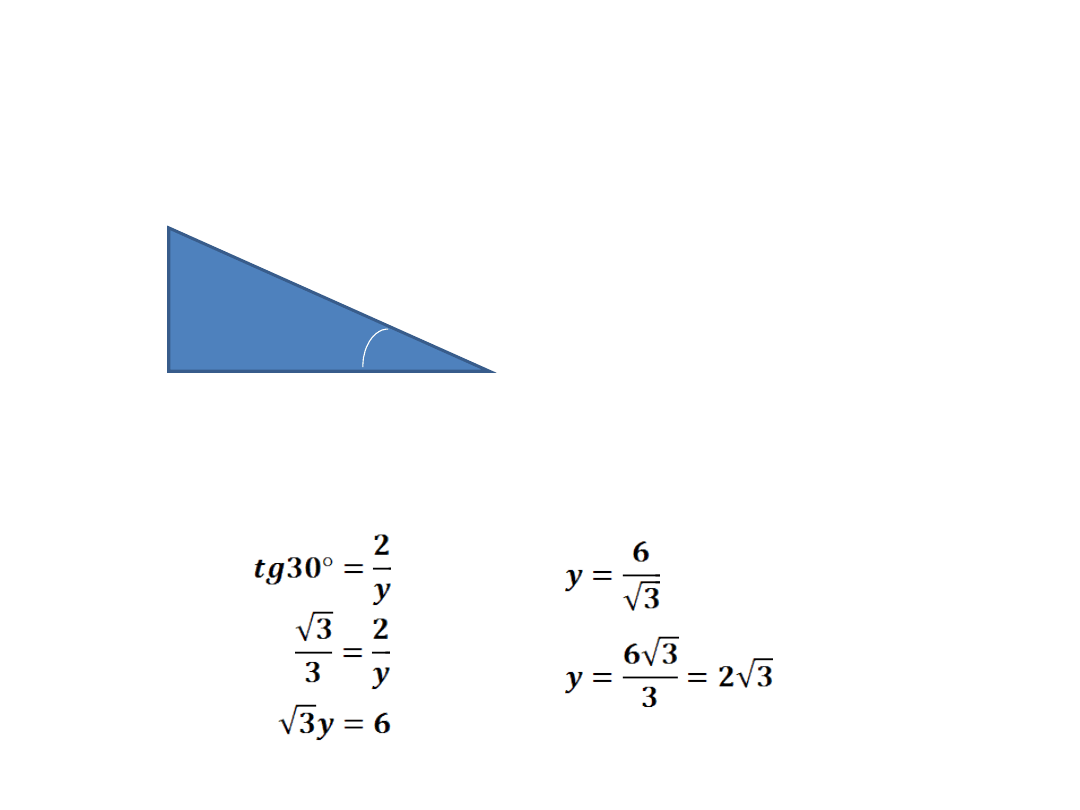
Ćw1: Wyznacz długości boków trójkąta prostokątnego 

(rysunek), 

       w którym jedna przyprostokątna ma długość 2cm, 

kąt =30. Oblicz pole i obwód trójkąta.                     

                   

2

y

x

α

Wykorzystując funkcję 

tangens                   

obliczymy długość 
przyprostokątnej y, a 

następnie 

wykorzystując funkcję sinus 

–

obliczymy długość 
przeciwprostokątnej x.

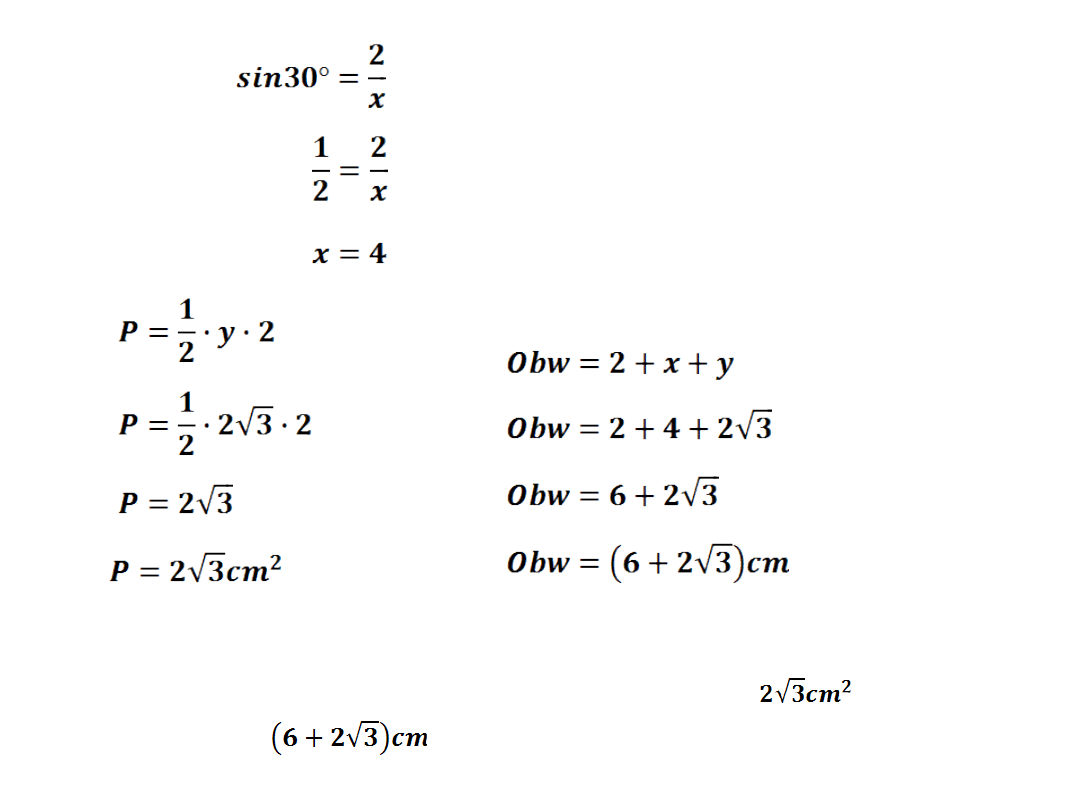
Odp.: Pole powierzchni trójkąta prostokątnego wynosi          

jego obwód równa się                .                                     

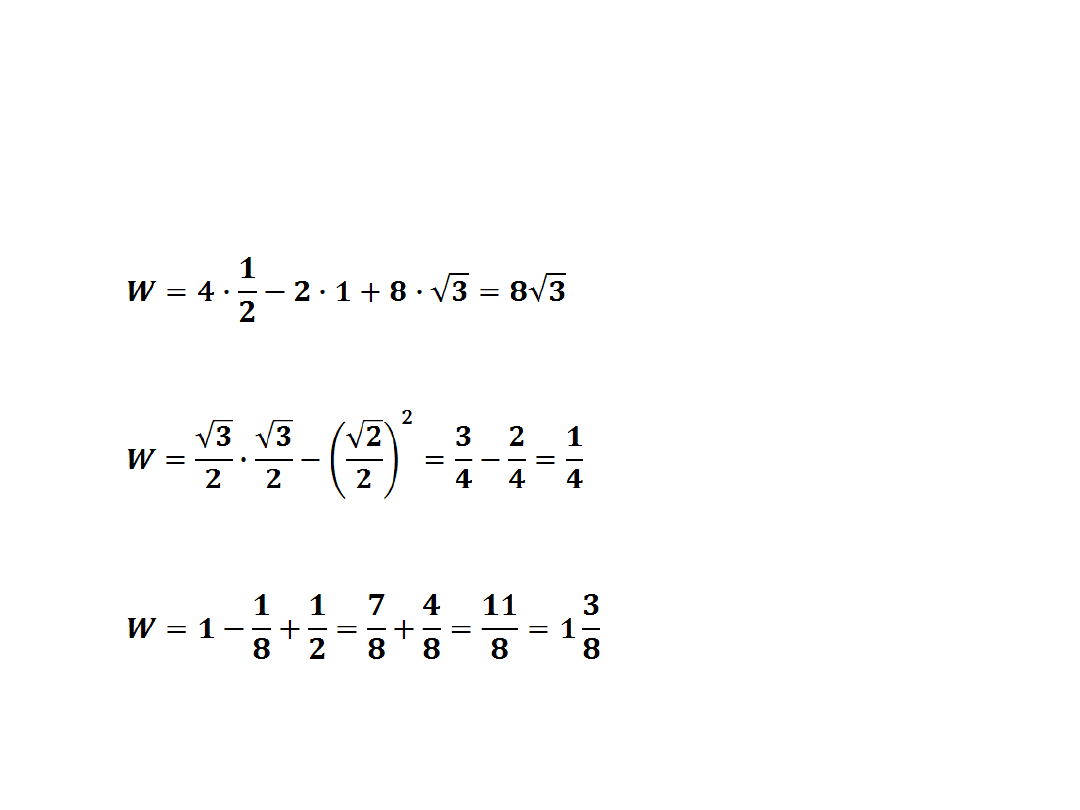
Ćw2: Oblicz wartość wyrażenia W:

a)

W=4sin30-2tg45+8ctg30

b)

W=cos30·sin60-sin

2

45

c)

W=tg

2

45-sin

3

30+cos60                                        

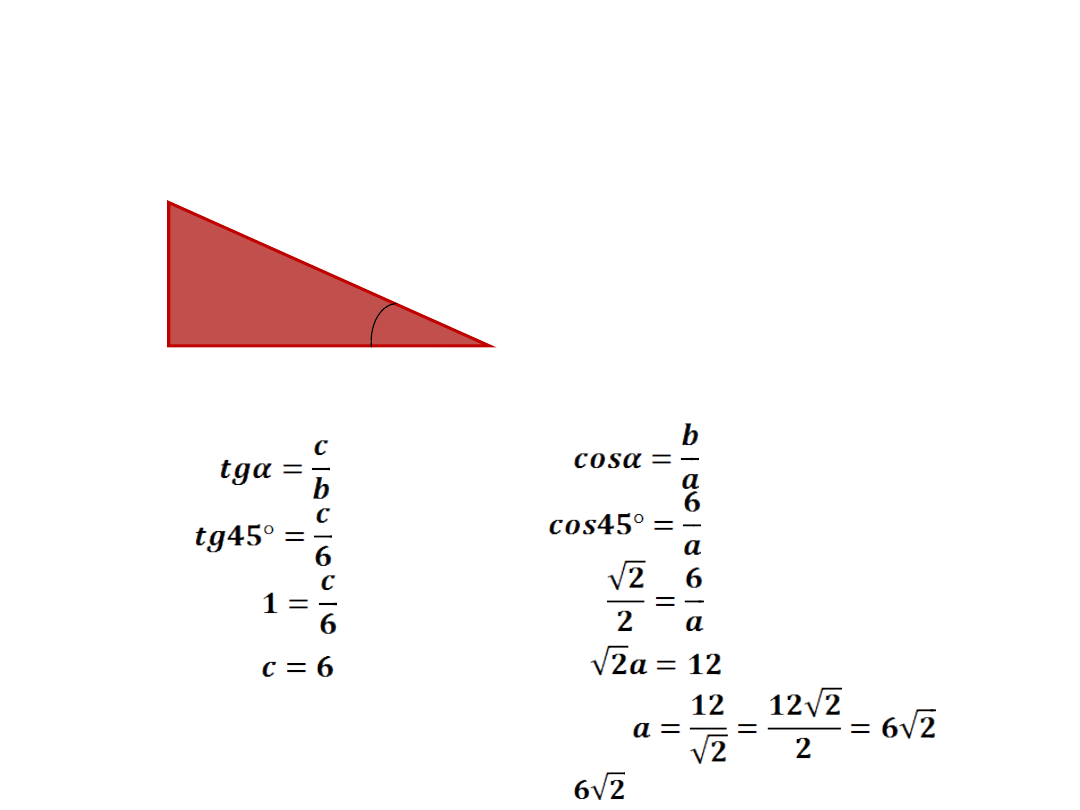
Ćw3: Oblicz długości nieznanych boków w trójkącie 

prostokątnym, 

       w którym jedna przyprostokątna ma długość 6cm, kąt 

do niej przyległy ma miarę 45                                       

     

c

b

a

α

Dane:
b=6cm
α=45°
Szukane: a,c

Odp.: Trójkąt ma boki długości: 6cm oraz      cm.                          

       

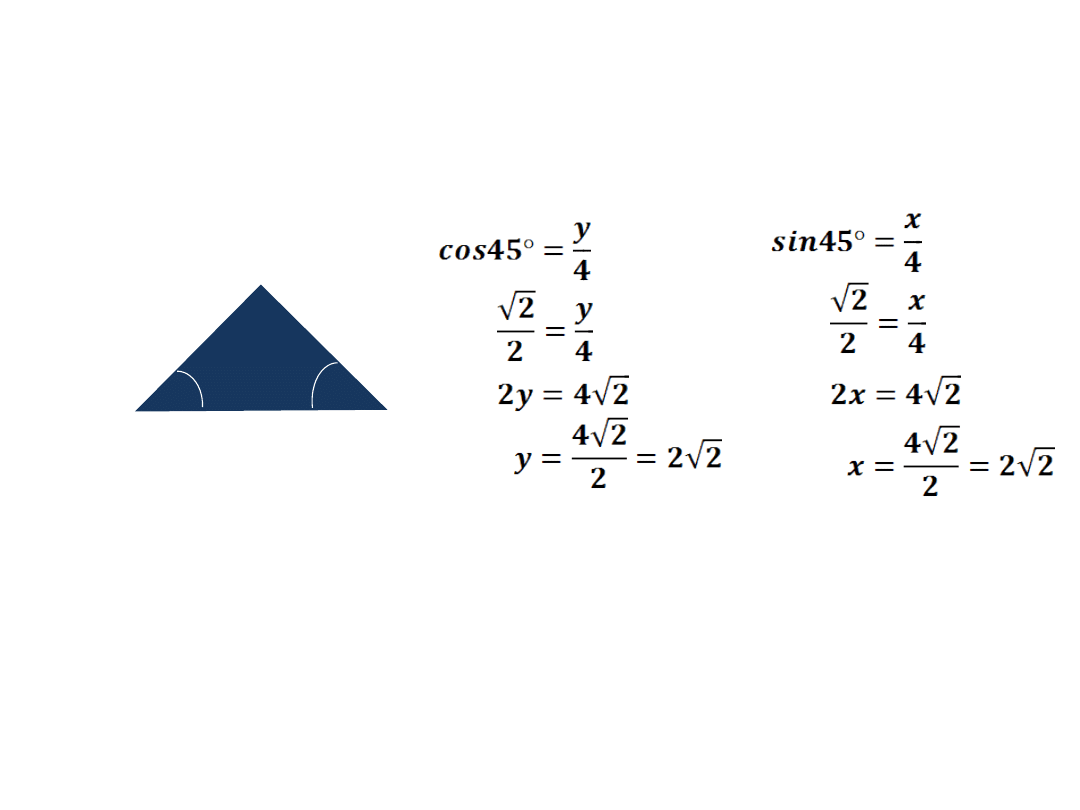
Ćw4: Dla narysowanych trójkątów prostokątnych oblicz 

długości nieznanych boków oraz wyznacz wartości 
funkcji sinus oraz tangens kąta α.

a)

x

y

4

45°

α

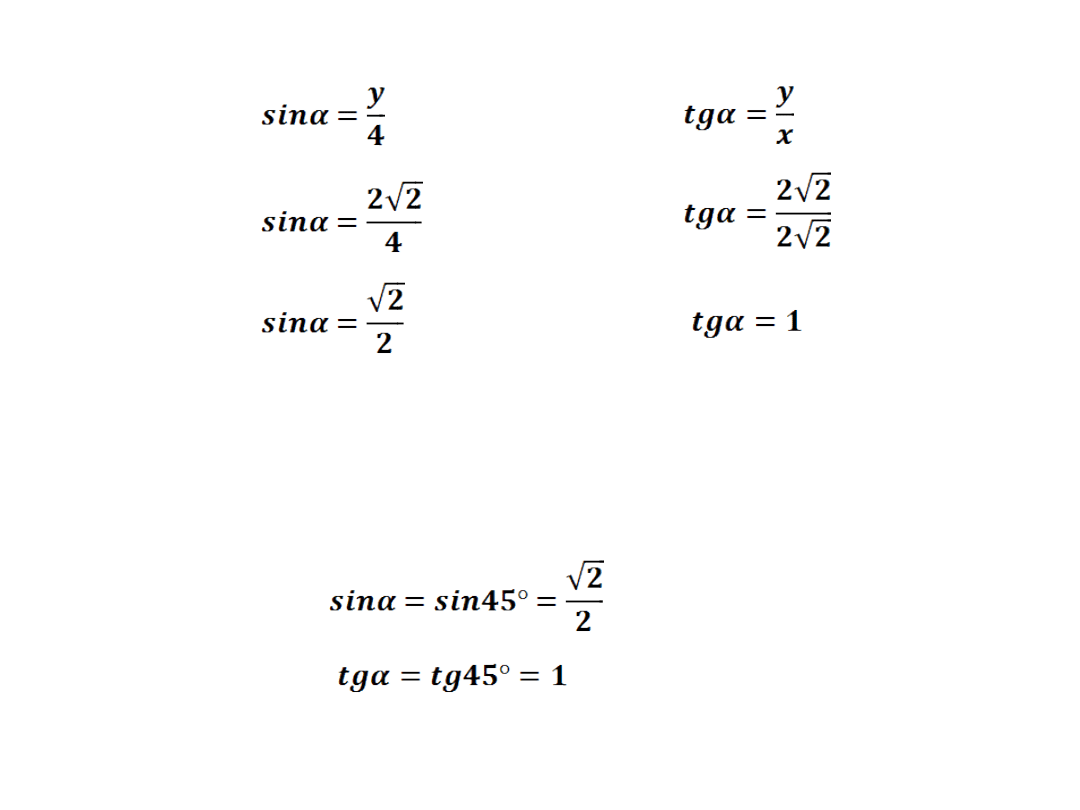
Wystarczyło w zadaniu zauważyć, że kąt 

α

 ma miarę 45° 

(suma kątów wewnętrznych w każdym trójkącie równa się 

180°) 

i od razu zapisać:

45°

α

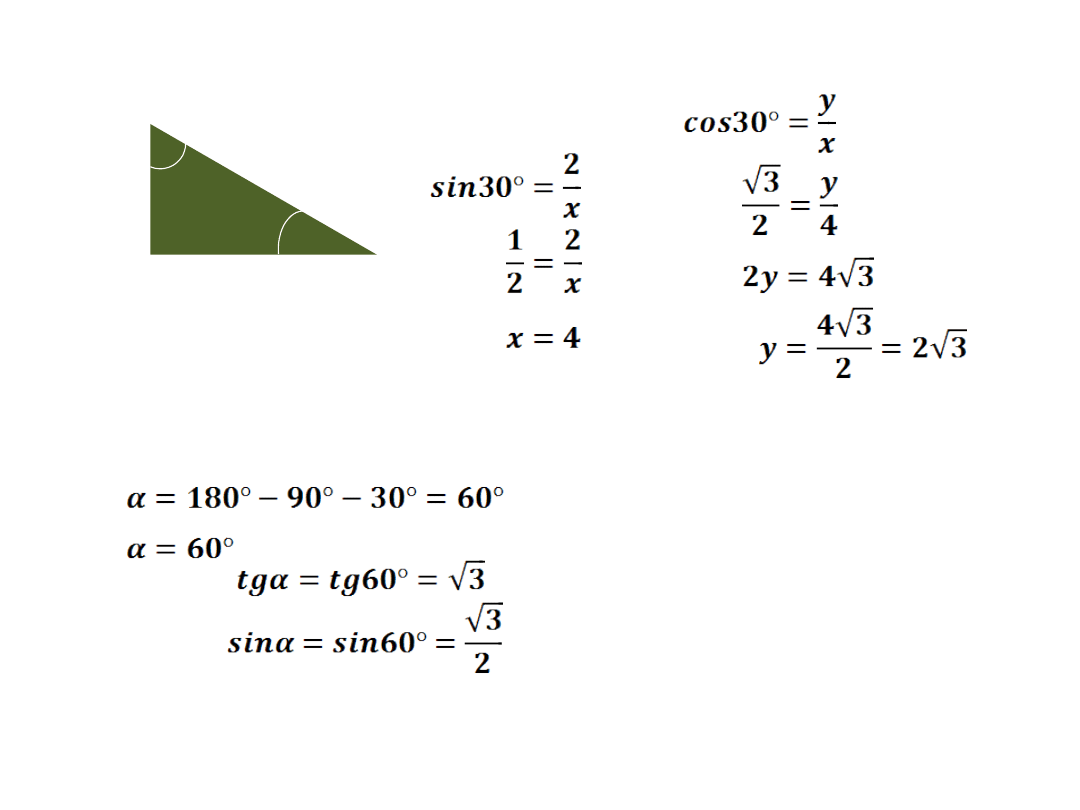
b)

x

y

2

α

30°