OSCYLATOR HARMONICZNY

•Drgania swobodne oscylatora harmonicznego
•Energia potencjalna sprężystości
•Drgania tłumione oscylatora harmonicznego
•Drgania wymuszone oscylatora harmonicznego
•Rezonans amplitudowy

•Rezonans mocy
•Dobroć układu drgającego

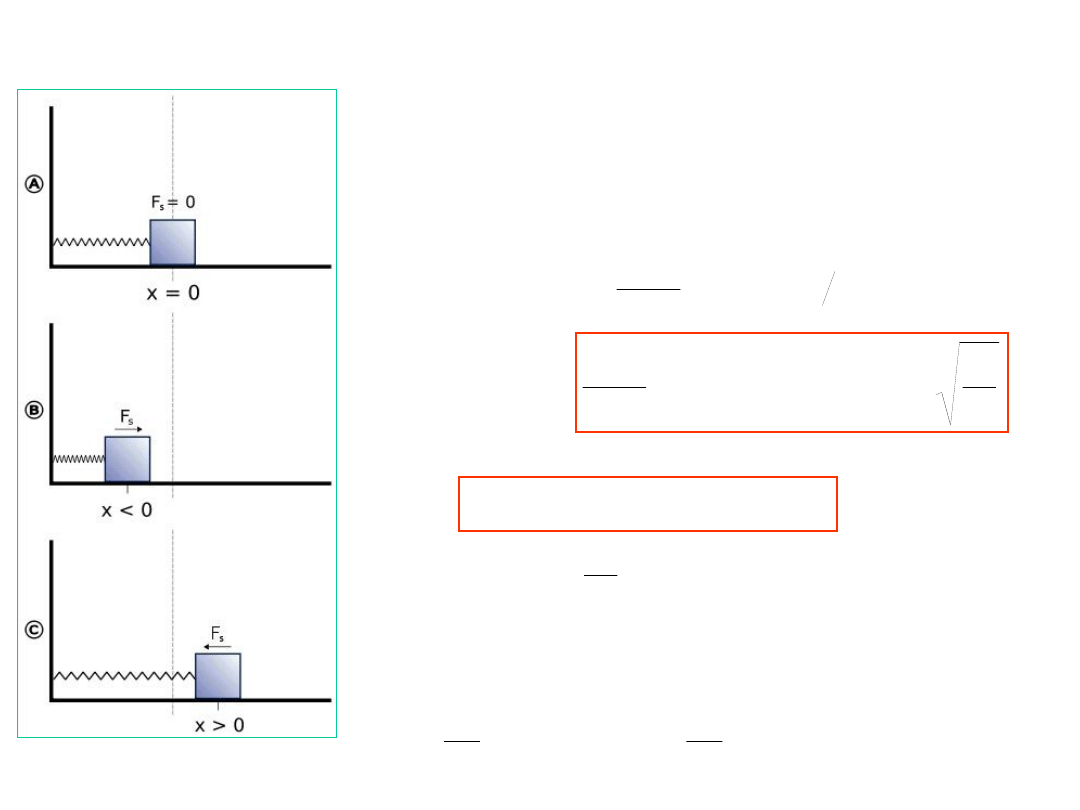
DRGANIA SWOBODNE OSCYLATORA HARMONICZNEGO

Prawo Hooke’a

kx

x

F





)

(

m - masa,
k - stała sprężystości sprężyny

Równanie ruchu

m

k

x

dt

x

d

m

kx

dt

x

d

m

kx

x

F

ma

















0

2

0

2

2

2

2

,

0

:

)

(





Rozwiązanie ogólne zależy od dwóch stałych A, B

)

sin(

)

(

0

,

)

0

(

,

0

)

0

(

Niech

0

0

0

0

0

0

t

v

t

x

B

v

A

v

v

x





















Stałe wyznacza się z dwóch warunków początkowych

)

sin(

)

cos(

)

(

)

cos(

)

sin(

)

(

0

0

0

0

0

t

B

t

A

dt

dx

t

v

t

B

t

A

t

x

























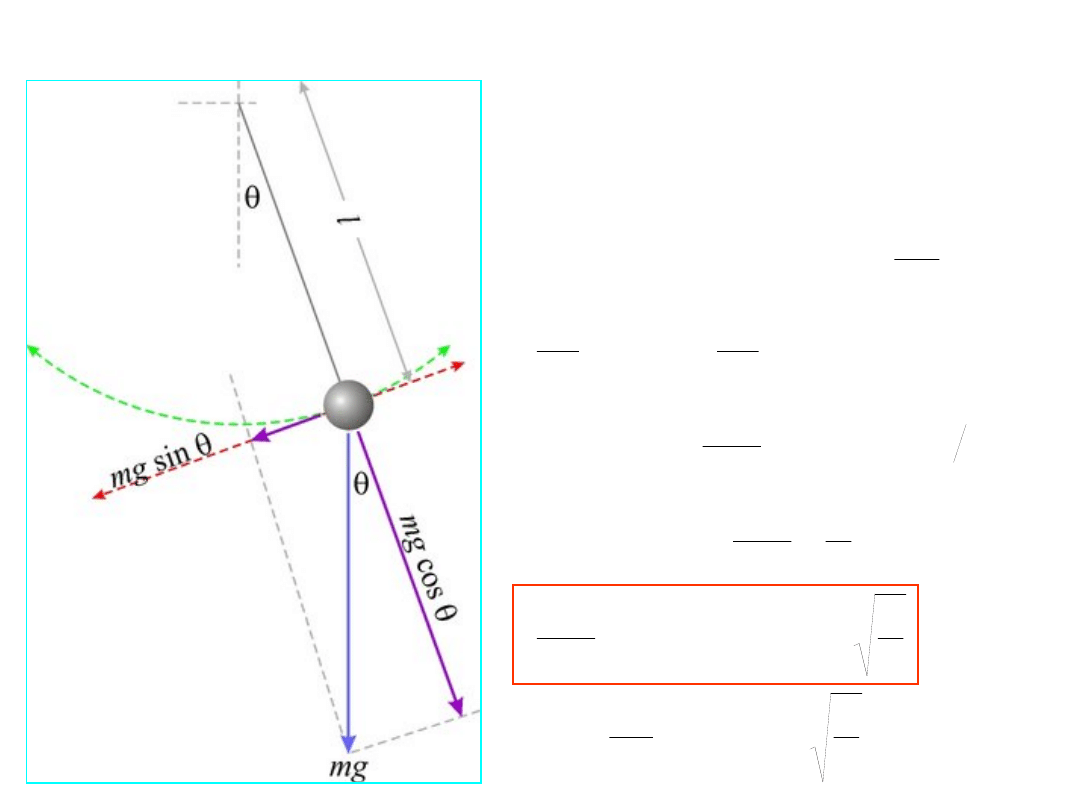
Przykład: wahadło matematyczne

g

l

T

T

l

g

dt

d

l

g

dt

d

ml

lmg

dt

d

ml

lmg

dt

dL

M

dt

L

d

dt

d

ml

ml

L

l

v

v

m

l

p

l

L

lmg

M

P

l

M

g

m

P

P

P

P







































2

2

,

0

0

sin

:

sin

sin

sin

,

0

0

0

0

2

0

2

2

2

2

0

2

2

2

2

2

2





















































































ENERGIA POTENCJALNA SPRĘŻYSTOŚCI

)

cos(

)

(

),

sin(

)

(

)

0

(

,

0

)

0

(

Niech

0

0

0

0

0

0

t

v

t

v

t

v

t

x

v

v

x

















Energia kinetyczna

Maksymalna wartosć energii kinetycznej odpowiada sytuacji, gdy oscylator
przechodzi przez położenie równowagi x=0. Wówczas energia potencjalna
E

p

=0.

Gdy wychylenie oscylatora jest maksymalne, x=v

0

/



0

, energia kinetyczna

E

k

=0 (v=0)

i całkowita energia jest zmagazynowana w postaci energii potencjalnej.

 

t

mv

mv

t

E

E

k

k

0

2

2

0

2

cos

2

1

2









2

0

0

2

0

2

0

max

,

2

1

2

1





















v

m

mv

E

k

Kwadrat maksymalnego wychylenia
(amplitudy drgań)

Stąd energia potencjalna

 

 

const

mv

E

E

t

mv

t

E

E

kx

x

m

t

E

E

k

p

p

p

p

p



















2

0

0

2

2

0

2

2

2

0

2

1

sin

2

1

2

1

2

1





Zauważmy że

dx

dE

kx

F

p









DRGANIA TŁUMIONE OSCYLATORA HARMONICZNEGO

Siła tłumiąca

dt

dx

v

F

t











 



Równanie ruchu

m

k

m

x

dt

dx

dt

x

d

m

v

kx

dt

x

d

m

















0

2

0

2

2

2

2

,

2

,

0

2

:













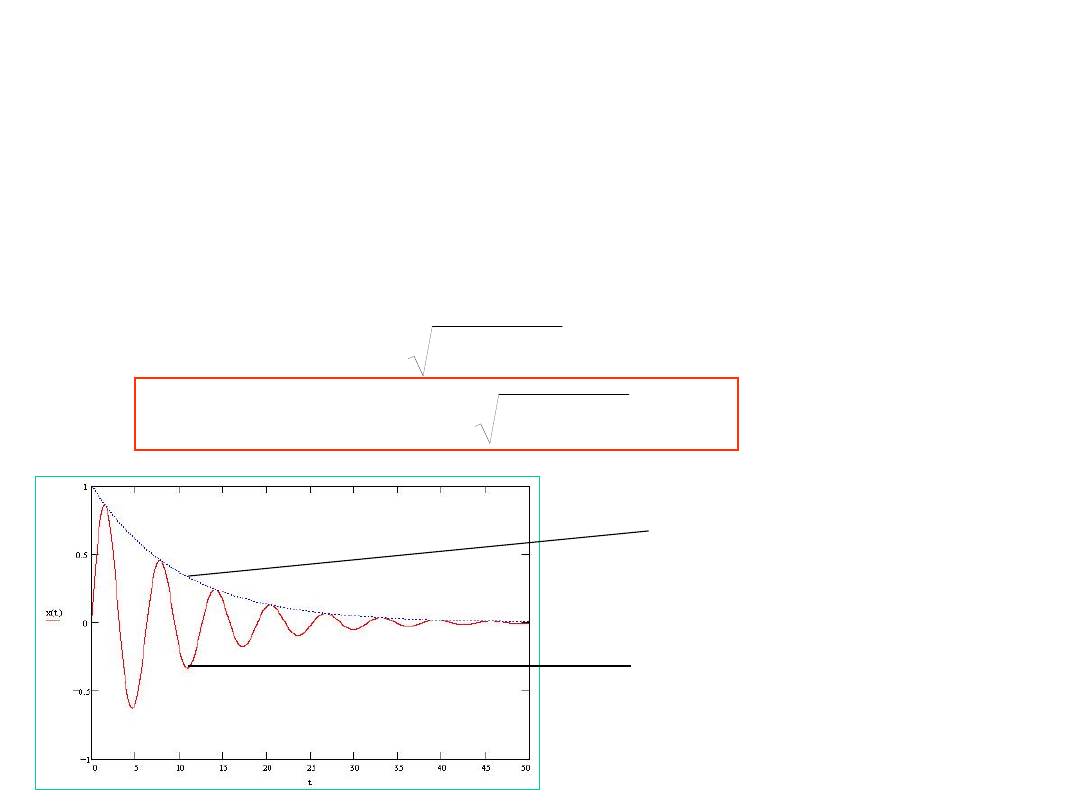
Przypadek słabego tłumienia

0







Drgania wokół położenia równowagi o malejącej wykładniczo
amplitudzie, z
częstoscią mniejszą od częstości drgań własnych



0

Przypadek silnego tłumienia

0







Wykładniczy powrót do położenia równowagi, brak drgań

Tłumienie krytyczne

0







Wolniejszy niż wykładniczy powrót do położenia równowagi, brak drgań.
Można pokazać, że rowziązanie ma postać (A, B - stałe wzynaczane z
warunków początkowych)

)

exp(

)

(

)

(

t

Bt

A

t

x









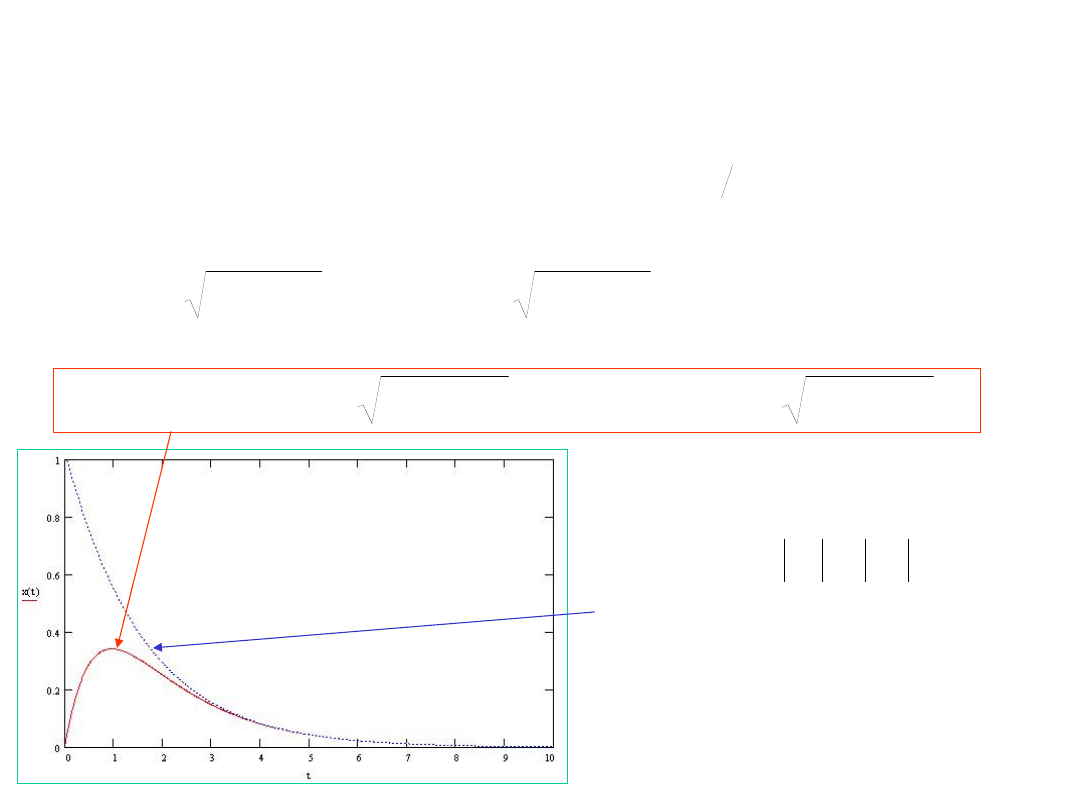
Przypadek słabego tłumienia

Rozwiązania poszukujemy w postaci (A,φ - stałe zal. od warunków początkowych)



 















t

t

A

t

x

r

sin

exp

)

(

Wstawiając do równania i grupując wyrazy przy funkcjach sin, cos otrzymujemy







 











































































































t

t

A

t

x

t

t

A

t

t

A

r

r

r

r

r

r

2

2

0

0

2

2

0

2

0

2

2

sin

)

exp(

)

(

,

0

cos

exp

2

2

sin

exp

2

obwiednia

drgania tłumione

Przypadek silnego tłumienia

Rozwiązania poszukujemy w postaci

 

t

A

t

x



exp

)

( 

Wstawiając postulowaną postać rozwiązania do równania, otrzymujemy równanie na



 

 

 

 

2

0

2

2

2

0

2

1

2

0

2

2

0

2

,

0

2

exp

:

0

exp

exp

2

exp

































































t

A

t

A

t

A

t

A

Rozwiązanie ogólne ma postać kombinacji liniowej rozwiązań
z



1

,



2

















t

B

t

A

t

x

2

0

2

2

0

2

exp

exp

)

(





























A, B - stałe wzynaczane z
warunków początkowych

 

t

A

t

x

t

1

2

1

1

2

exp

)

(

,

0























DRGANIA WYMUSZONE OSCYLATORA HARMONICZNEGO

Siła wymuszająca

t

F

t

F

zewn



sin

)

(

0



Równanie ruchu

m

F

f

m

k

m

t

f

x

dt

dx

dt

x

d

m

t

F

v

kx

dt

x

d

m

0

0

0

0

2

0

2

2

0

2

2

,

,

2

,

sin

2

:

sin





































Stan ustalony oscylatora z wymuszeniem (rozwiązanie dla t

 )

Rozwiązania poszukujemy w postaci













t

A

t

x

sin

)

(

Rozwiązanie ma postać drgań o częstości równej częstosci siły wymuszającej,
amplitudzie A, przesunietych w fazie o

 względem siły wymuszającej.

Rozwiązanie nie zawiera zależności od warunków początkowych (w szczególności
A,

 nie zależą od warunków początkowych, tylko od parametrów oscylatora).

Dla małych t w układzie występują drgania nieustalone, których postać zależy od
warunków początkowych. Amplituda drgań nieustalonych maleje wykładniczo z
czasem i przy t



pozostają tylko drgania ustalone, niezależne od warunków

początkowych.

Wstawiając postulowaną postać rozwiązania do równania, otrzymujemy













t

f

t

A

t

A

















sin

cos

2

sin

0

2

2

0











Korzystając ze wzorów na sin(

+), cos(+) otrzymujemy

















t

f

t

A

t

A

f



























sin

cos

cos

2

sin

sin

sin

2

cos

0

0

2

2

0

2

2

0

0



























































































































2

0

2

2

2

2

2

0

0

2

2

2

2

0

0

2

2

0

2

ar

sin

2

)

(

2

)

(

2

cos

sin



































ctg

t

f

t

x

f

A

A

tg

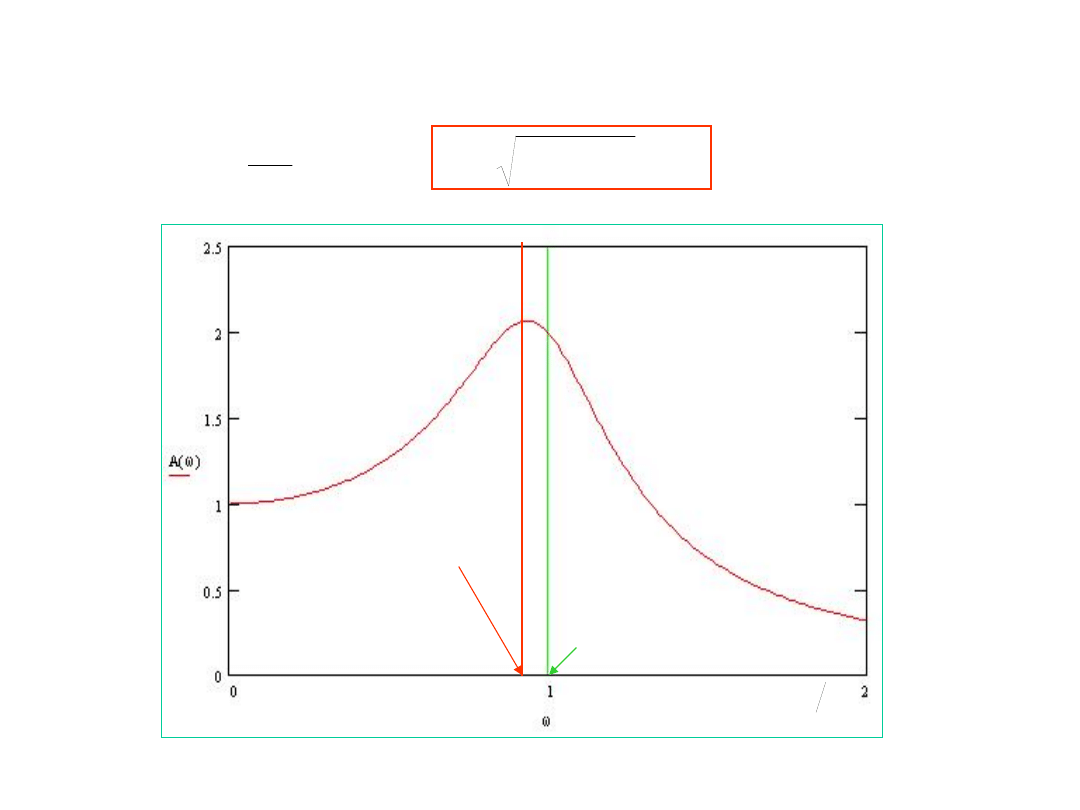
REZONANS AMPLITUDOWY

0





 



A

Amplituda drgań ustalonych jest maksymalna, gdy

0

2

2

0

2

0

























d

dA

Rezonans
amplitudowy

Rezonans
mocy

REZONANS MOCY

Moc absorbowana (chwilowa)

   



















t

A

t

F

t

v

t

F

P

zewn

cos

sin

0

Niech <y(t) > oznacza średnią wartość wielkości y w ciągu jednego okresu T=2

/

siły wymuszającej





































































sin

2

1

sin

sin

cos

sin

cos

cos

sin

sin

sin

cos

cos

cos

0

...

3

sin

2

sin

sin

2

1

cos

sin

cos

sin

1

cos

sin

1

cos

sin

0

2

1

2

0

2

sin

2

1

0

0

2

2

2

2

2

2

2

2

A

F

t

t

t

A

F

t

t

A

F

P

t

t

t

t

t

t

t

t

t

t

t

t

t

t

t















































































 





 



 



















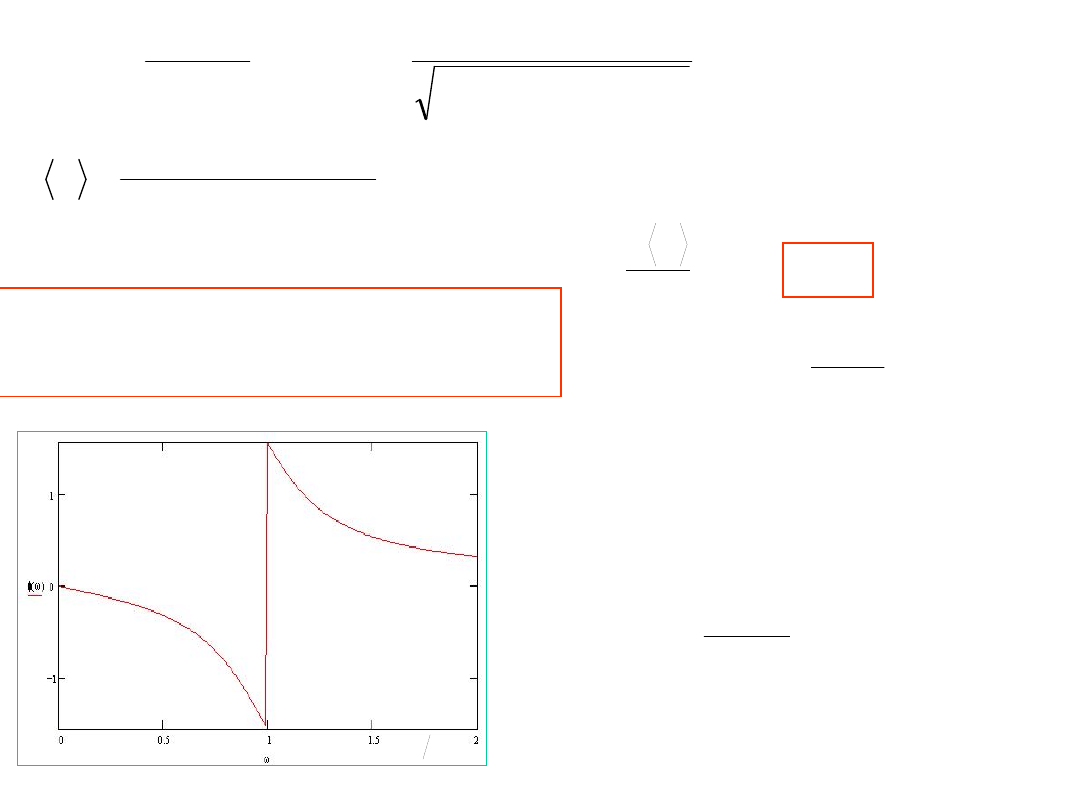
2

2

2

2

2

2

0

2

0

2

2

2

2

2

0

2

2

0

2

2

2

sin

2

A

m

f

m

P

tg

























































Moc absorbowana jest maksymalna, gdy

0





 







5

.

0



5

.

0



Dla częstości rezonansowej drgania ustalone
są przesunięte w fazie o

/2 (czyli o 1/4 okresu)

względem siły wymuszającej. Jest to
maksymalne możliwe przesuniecie w fazie.

 

t

f

t

x





cos

2

)

(

0

0



 

0

0

0

0

2

0











f

A

A

d

P

d

rez











W stanie ustalonym (drgania o stałej
amplitudzie) moc absorbowana = mocy
traconej na pracę przeciw sile tłumiącej

DOBROĆ UKŁADU DRGAJĄCEGO





















2

2

2

0

2

2

2

2

2

2

2

2

2

2

2

0

2

2

2

0

2

2

2

0

2

2

0

4

1

4

1

cos

2

1

cos

2

1

2

1

4

1

sin

2

1

sin

2

1

2

1

A

m

E

E

E

A

m

t

A

m

E

t

A

m

mv

E

A

m

t

A

m

E

t

A

m

x

m

E

k

p

k

k

p

p







































































Średnia energia zmagazynowana w układzie

Dobroć układu drgającego: stosunek energii zgromadzonej w układzie do energii
traconej w ciągu jednego okresu na pokonanie siły tłumienia (w stanie ustalonym
równej energii dostarczanej przez siłę zewnętrzną) przy częstości pobudzenia równej
częstości rezonansowej.
Im więcej energii można zmagazynować w stosunku do mocy strat, tym lepszy układ.











2

2

0

0







T

P

E

Q

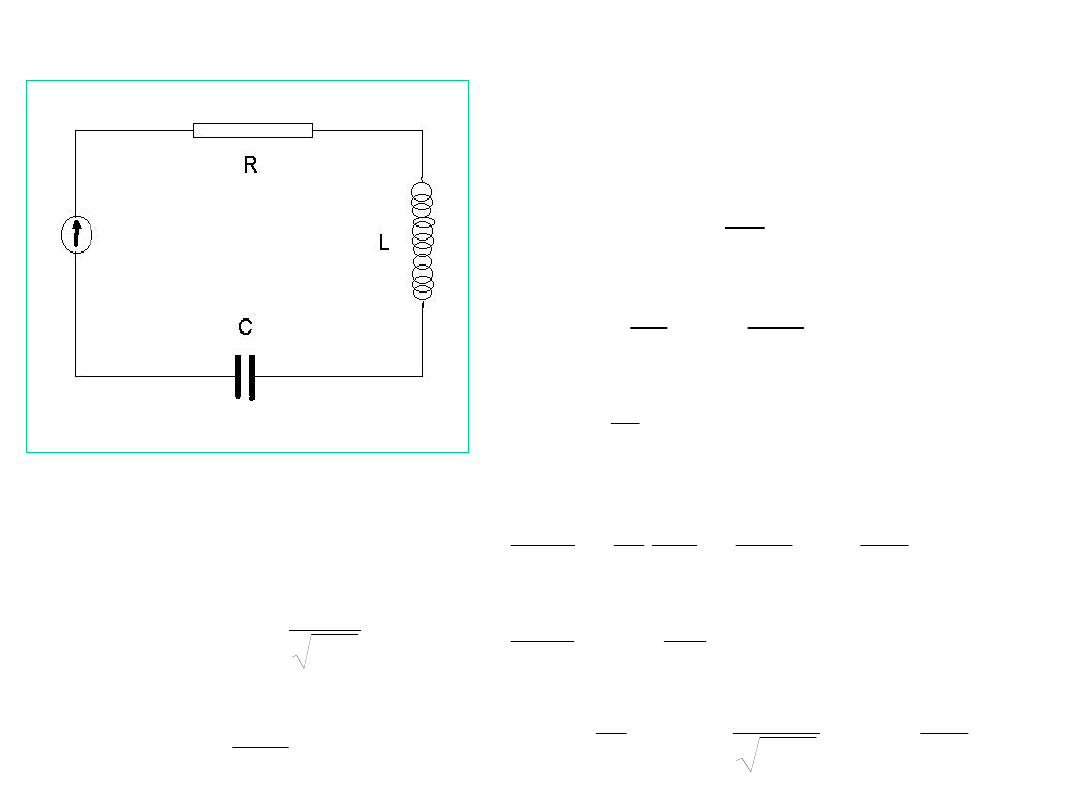
Przykład: drgania w obwodzie RLC z wymuszeniem

t

U

t

U



sin

)

(

0



L

U

f

LC

L

R

t

f

x

dt

dx

dt

x

d

t

L

U

q

LC

dt

dq

L

R

dt

q

d

0

0

0

0

2

0

2

2

0

2

2

,

1

,

2

,

sin

2

,

sin

1































II prawo Kirchhoffa

C

q

U

dt

q

d

L

dt

dI

L

U

dt

dq

R

RI

U

U

U

U

t

U

C

L

R

C

L

R





























2

2

0

)

(

I - natężenie prądu,
q - ładunek na kondensatorze
Częstość drgań własnych
obwodu RLC

LC

1

0





Dobroć

R

L

Q

0



