ZWIĄZKI LOGICZNE 

MIEDZY ZDANIAMI

 

WYNIKANIE

• Ze  zdania    WYNIKA  LOGICZNIE 

zdanie    zawsze  i  tylko  wtedy,  gdy 

zdanie 

•    jest prawem logiki.
• PRZYKŁAD 9
• Ze  zdania  (p    q)  wynika  logicznie 

zdanie  q,  bo  zdanie  (p    q)    q  jest 

prawem logiki.

UWAGA

• Należy  odróżnić  wynikanie  logiczne  od 

ANALITYCZNEGO,FIZYCZNEGO, 
BIOLOGICZNEGO,  PSYCHOLOGICZNEGO 
itp.

• Definicje  różnych  typów  wynikania 

mają następujący schemat:

• Ze  zdania    WYNIKA  X-OWO  zdanie   

zawsze i tylko wtedy, gdy zdanie 

•    jest prawdą nauki X.

 

• W szczególności:
• Ze  zdania    WYNIKA  ANALITYCZNIE 

zdanie    zawsze  i  tylko  wtedy,  gdy 

zdanie    jest prawdą ANALITYCZNĄ.

• PRZYKŁAD 10
• Ze zdania „Jan jest mężem Marii” wynika 

analitycznie  zdanie  „Maria  jest  żoną 

Jana”,  bo  prawdą  analityczną  języka 

polskiego jest to, że relacja bycia mężem 

jest  odwrotnością  (konwersem)  relacji 

bycia żoną. 

 

• Ze  zdania    WYNIKA  FIZYCZNIE  zdanie   

zawsze i tylko wtedy, gdy zdanie 

•    jest prawdą fizyki.
• PRZYKŁAD 11
• Ze  zdania  „Na  ciało  nie  działają  żadne 

siły”  wynika  zdanie  „Ciało  porusza  się 
ruchem  jednostajnym  lub  spoczywa”,  bo 
zdanie  „Jeśli  na  ciało  nie  działają  żadne 
siły,  to  ciało  porusza  się  ruchem 
jednostajnym 

lub 

spoczywa”, 

jest 

prawem Newtona.

 

• Ze  zdania    WYNIKA  BIOLOGICZNIE 

zdanie    zawsze  i  tylko  wtedy,  gdy 

zdanie    jest prawdą biologii.

• PRZYKŁAD 12
• Ze zdania „Kręgowiec X posiada nerki” 

wynika  biologicznie  zdanie  „Kręgowiec 

X  posiada  serce”,  bo  prawem  biologii 

jest  to,  że  wszystkie  kręgowce 

posiadające serce posiadają też nerki.

 

UWAGA

• Im  prawa  danej  nauki  są  mniej 

pewne,  tym  związek  wynikania  (na 
gruncie tej nauki) jest słabszy. 

• PRZYKŁAD 13
• Czy ze zdania „Jan wychował się w 

patologicznej rodzinie” wynika 
psychologicznie zdanie „Jan założy 
patologiczną rodzinę”?

WYKLUCZANIE (LOGICZNE)

• Zdanie    wyklucza  się  ze  zdaniem   

zawsze  i  tylko  wtedy,  gdy  ze  zdania   

wynika zdanie  (albo: zdania  i  nie 

mogą  być  jednocześnie  prawdziwe  – 

tzn. zdanie (  ) jest kontrtautologią).

• Uwaga
• Zdania  wykluczające  się  nie  mogą  być 

jednocześnie  prawdziwe  ale  mogą  być 

jednocześnie fałszywe.

 

PRZYKŁAD 13 

• Zdanie p wyklucza się ze zdaniem p  

q, bo:

• p  (p  q) jest prawem logiki 

(tautologią);

• p  (p  q) jest kontrtautologią.
• Uwaga
• Zdania p i p  q mogą być jednocześnie 

fałszywe – gdy p =0 i q = 0.

DOPEŁNIANIE (LOGICZNE)

• Zdanie  dopełnia się ze zdaniem  zawsze i 

tylko  wtedy,  gdy  ze  zdania    wynika 

zdanie    (albo:  zdania    i    nie  mogą  być 

jednocześnie  fałszywe  –  tzn.  zdanie  (   

) jest kontrtautologią).

• Uwaga
• Zdania  dopełniające  się  nie  mogą  być 

jednocześnie  fałszywe  ale  mogą  być 
jednocześnie prawdziwe.

 

PRZYKŁAD 14

• Zdanie p dopełnia się ze zdaniem p  q, 

bo:

• p    (p    q)  jest  prawem  logiki 

(tautologią);

• p  (p  q) jest kontrtautologią.
• Uwaga
• Zdania p i p  q mogą być jednocześnie 

prawdziwe, gdy  p =1 i q = 1.

SPRZECZNOŚĆ LOGICZNA

• Zdanie    jest  sprzeczne  ze  zdaniem   

zawsze  i  tylko  wtedy,  gdy  ze  zdania   

wynika  zdanie    (zdania    i    się 

wykluczają) i ze zdania   wynika zdanie  

(zdania    i    się  dopełniają).  Zdania 

sprzeczne  nie  mogą  być  ani  jednocześnie 

fałszywe ani jednocześnie prawdziwe –    

jest tautologia, a    jest kontrtautologią.

• Uwaga
• Zdaniem sprzecznym do danego jest po 

prostu jego negacja.

 

PRZYKŁAD 15

• Zdaniem sprzecznym do zdania 
• p  q 
• jest zdanie  p  q, 
• bo:
• (p  q)  (p  q)
 

RÓWNOWAŻNOŚĆ

• Zdanie    jest  równoważne  zdaniu   

zawsze  i  tylko  wtedy,  gdy  ze  zdania   

wynika  zdanie    i  ze  zdania  B  wynika 

zdanie  – tzn. kiedy zdanie     jest 

tautologią.

• Uwaga
• Zdania równoważne mają taką samą 

wartość logiczną

PRZYKŁAD 16

• Zdanie p  q jest równoważne ze 

zdaniem

•  q  p, 
• bo:
• (p  q)  (q  p) jest tautologią 

(prawo transpozycji). 

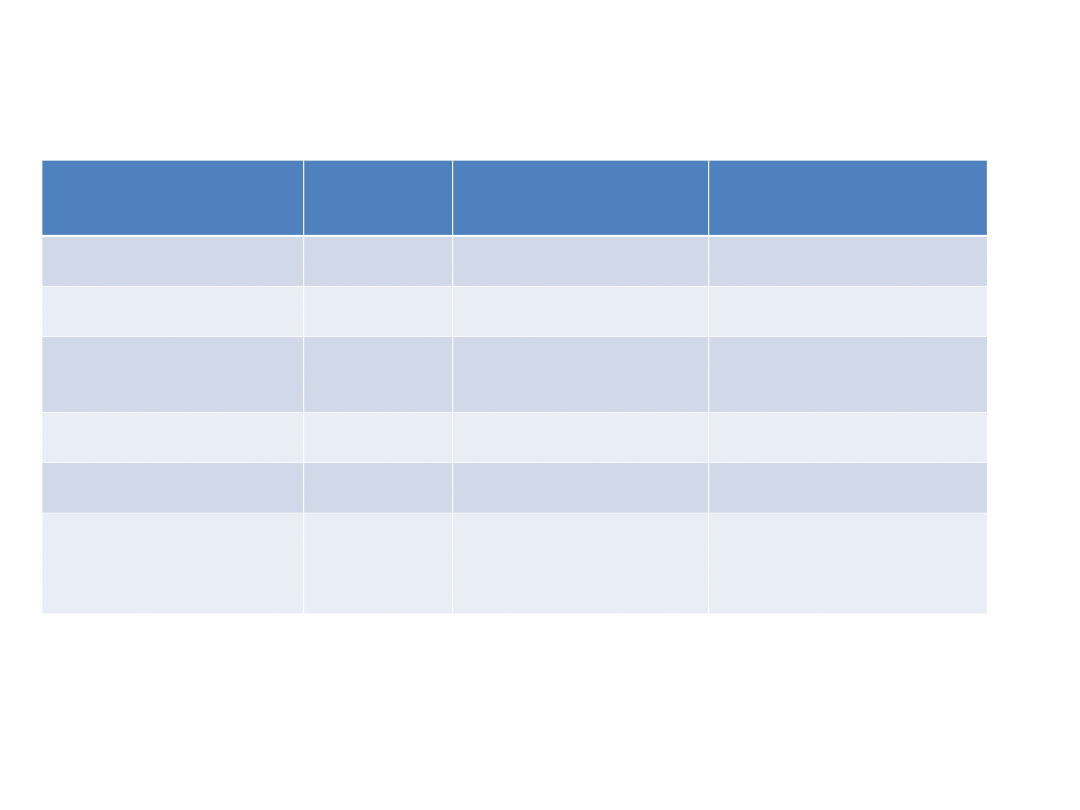
PODSUMOWANIE

• Jeśli dane są dwa zdania  i  to mogą między 

nimi zachodzić następujące związki:

ZWIĄZEK

CO 

JEST 

TAUTOLOG
IĄ

JAKIE 

WARTOŚCI 

LOGICZNE

ZWIĄZEK  Z  INNYMI 
ZALEŻNOŚCIAMI

WYNIKANIE 

(Z 

 

WYNIKA )

    

nie może być tak, że  
= 1 i  = 0.

WYNIKANIE 

(Z 

 

WYNIKA )

    

nie może być tak, że   
= 1 i  = 0.

RÓWNOWAŻNOŚĆ

   

  i  mają takie same 
wartości logiczne.

zachodzi  tylko  wtedy, 
gdy  zachodzą  wynikania 
w obie strony.

WYKLUCZANIE

   
 (  )

nie może być tak, że  
= 1 i  = 1.

DOPEŁNIANIE 

   
   

nie może być tak, że  
= 0 i  = 0.

SPRZECZNOŚĆ

   
   

  i    mają  różne 
wartości logiczne

zachodzi  tylko  wtedy, 
gdy 

zachodzi 

wykluczanie 

i 

dopełnianie.

WARUNEK KONIECZNY 

• Stwierdzamy,  że  zajście  pewnego 

faktu  (wykonanie  pewnej  czynności) 
jest  WARUNKIEM  KONIECZNYM 
(łac. condition sine qua non). 

• Co to znaczy?

PRZYKŁAD 1

• a)  Warunkiem  koniecznym  fałszywości  zdania  (p    q)  jest 

fałszywość obu zdań składowych, bo jest prawdą logiczną, że:

• jeśli  fałszywe  jest  zdanie  (p    q),  to  fałszywe  jest  zdanie  p  i 

fałszywe jest zdanie q.

• b) Warunkiem koniecznym tego, ze pada deszcz jest to, że są 

chmury, bo jest prawdą fizyczną (meteorologiczną?), że:

• jeśli pada deszcz to są chmury.
• c) Warunkiem koniecznym bycia matką jest bycie kobietą, bo 

prawdą biologiczną jest, że:

• jeśli ktoś jest matką to jest kobietą.
• d)  Warunkiem  koniecznym  podzielności  przez  4  jest 

podzielność przez 2, bo prawdą matematyczną jest:

• jeśli dana liczba jest podzielna przez 4, to jest podzielna przez 

2.

• e)  Warunkiem  koniecznym  pełnej  zdolności  do  czynności 

prawnych jest pełnoletniość, bo z KC wynika, że

• jeśli  dana  osoba  nie  jest  pełnoletnia,  to  nie  ma  pełnej 

zdolności do czynności prawnych

UWAGA

• Podobnie  jak  pojęcie  wynikania, 

pojęcie  warunku  koniecznego  jest 
wieloznaczne – są warunki logicznie 
konieczne, 

analitycznie 

konieczne,  fizycznie  konieczne 
itd.  Zależy  to  od  tego,  do  praw 
jakiej  nauki  odwołujemy  się,  aby 
stwierdzić,  że  prawdziwa  jest  pewna 
implikacja.

 

• DEFINICJA 

BYCIA 

WARUNKIEM 

LOGICZNIE KONIECZNYM

• Zdanie    jest  warunkiem  (logicznie) 

koniecznym  zdania   zawsze i tylko wtedy, 

gdy implikacja     jest prawem logiki.

•  
• DEFINICJA 

BYCIA 

WARUNKIEM 

KONIECZNYM NA GRUNCIE NAUKI X

• Zdanie    jest  warunkiem  koniecznym  na 

gruncie  nauki  X  zdania    zawsze  i  tylko 

wtedy,  gdy  implikacja        jest  prawem 

nauki X.

 

 

• W PRZYKŁADZIE 1 (a) mówi o warunku 

logicznie  koniecznym,  (b)  –  fizycznie 
koniecznym, 

(c) 

– 

biologicznie 

koniecznym, 

(d) 

– 

matematycznie 

koniecznym,  a  w  przykładzie  (e)  –  o 
warunku prawnie koniecznym. 

• PROBLEM
• Czy 

warunkiem 

koniecznym 

szczęśliwego  związku  jest  to,  że 
partnerzy 

mają 

podobne 

zainteresowania?

WARUNEK DOSTATECZNY

• Co  to  znaczy,  że  zajście  pewnego 

faktu  (wykonanie  pewnej  czynności) 
jest 

warunkiem 

dostatecznym 

(warunkiem  wystarczającym)  zajścia 
innego faktu?

 

PRZYKŁAD 2

• a) Warunkiem logicznie dostatecznym prawdziwości implikacji (p  

q) jest fałszywość jej poprzednika, bo jest prawem logiki jest, że:

• jeśli zdanie p jest fałszywe, to zdanie (p  q) jest prawdziwe.
• b)  Warunkiem  fizycznie  dostatecznym  stwierdzenia,  że  w  nocy 

temperatura  spadła  poniżej  zera  jest  to,  że  wszystkie  kałuże  są 
zamarznięte, bo jest prawem fizyki, że:

• jeśli woda zamarza, to temperatura jest ujemna.
• c)  Warunkiem  biologicznie  dostatecznym  stwierdzenia,  że  dane 

zwierze  jest  kręgowcem  jest  to,  że  jest  ono  ssakiem,  bo  jest 
prawem biologii, że:

• każde zwierze, które jest ssakiem jest kręgowcem.
• d) Warunkiem matematycznie dostatecznym podzielności przez 3 

jest podzielność przez 6, bo jest prawem matematyki, że:

• jeśli dana liczba jest podzielna przez 6, to jest podzielna przez 3.
• e)  Warunkiem  prawnie  dostatecznym  pełnoletniości  jest  zawarcie 

związku małżeńskiego, bo z KC wynika, że:

• jeśli dana osoba zawarła związek małżeński, to jest pełnoletnia.

 

• W  PRZYKŁADZIE  2 

(a)  mówi  o  warunku 

logicznie  dostatecznym,  (b)  –  fizycznie 
dostatecznym, (c) – biologicznie dostatecznym, 
(d)  –  matematycznie  dostatecznym,  a  w 
przykładzie  (e)  –  o  warunku  prawnie 
dostatecznym.

• Podobnie jak w wypadku warunku koniecznego, 

pojęcie 

warunku 

dostatecznego 

jest 

wieloznaczne  –  trzeba  sobie  zdawać  sprawę  z 
jego relatywizacji do praw określonej nauki.

• PROBLEM
• Czy warunkiem dostatecznym szczęścia jest 

posiadanie dużej ilości pieniędzy? 

 

• DEFINICJA 

BYCIA 

WARUNKIEM 

LOGICZNIE DOSTATECZNYM

• Zdanie    jest  warunkiem  (logicznie) 

dostatecznym  zdania    zawsze  i  tylko 

wtedy, gdy implikacja       jest prawem 

logiki.

•  
• DEFINICJA 

BYCIA 

WARUNKIEM 

DOSTATECZNYM NA GRUNCIE NAUKI X

• Zdanie    jest  warunkiem  dostatecznym  na 

gruncie  nauki  X  zdania    zawsze  i  tylko 

wtedy,  gdy  implikacja          jest  prawem 

nauki X.

ZADANIE

• Zapisz strukturę zdania i określ jego wartość logiczną.
• a)  Warunkiem  koniecznym  podzielności  przez  5  jest 

podzielność przez 10.

• b)  Warunkiem  dostateczny  podzielności  przez  5  jest 

podzielność przez 10.

• c) Nieprawda, że warunkiem wystarczającym deszczu 

są chmury.

• d)  Brak  wolność  woli  nie  jest  warunkiem  koniecznym 

nie istnienia moralności

• e)  Nieprawda,  że  bycie  dziadkiem  jest  warunkiem 

wystarczającym nie bycia ojcem.

• f)  Warunkiem  koniecznym  nie  bycia  ojcem  jest  nie 

bycie dziadkiem.

• g) Nieprawda, że warunkiem wystarczającym zawarcia 

związku małżeńskiego jest bycie pełnoletnim.