WYKŁAD 7

Serwonapędy 

z silnikami  indukcyjnymi 

– 

sterowanie wektorowe

 

 

przy stabilizacji 

strumienia silnika

2

Dla maszyny indukcyjnej trójfazowej, przyjmuje się 

następujące założenia upraszczające: 

– rozłożone przestrzennie uzwojenia stojana i klatka wirnika 

zostają zastąpione uzwojeniem skupionym 
(koncentrycznym),

– rozpatrywany jest silnik trójfazowy symetryczny,
– zakłada się równomierność szczeliny powietrznej,
– pomija się wpływ anizotropii, nasycenie magnetycznego, 

zjawiska histerezy oraz prądów wirowych,

– pomija się wyższe harmoniczne przestrzennego rozkładu 

pola w szczelinie powietrznej, uwzględniając tylko 
harmoniczną podstawową,

– rezystancje i reaktancje uzwojeń uważa się za stałe. 

1



s

Ψ

Model matematyczny SI 

3

Przy tych  założeniach uzyskuje się model obwodowy, 
któremu odpowiada schemat: 

Schemat ten stanowi podstawę do sformułowania modelu 
matematycznego opisanego równaniami różniczkowymi 
zwyczajnymi, o stałych parametrach. 

1



s

Ψ

Model matematyczny SI 

4

• Model ten składa się z siedmiu równań różniczkowych i 

siedmiu równań algebraicznych. 

• Rozwiązanie otrzymanego układu równań różniczkowych 

jest pracochłonne. 

• Jest to układ wysokiego rzędu, zawierający równania 

nieliniowe o okresowo zmiennych współczynnikach. 

• Parametry silnika, występujące w tym modelu 

matematycznym, są trudno identyfikowalne.

•  Wobec tego układ równań trójfazowej maszyny 

indukcyjnej, przedstawiony za pomocą prądów fazowych i 

strumieni skojarzonych przekształca się w sposób 

umożliwiający otrzymanie układu równań o stałych 

współczynnikach. 

• W tym celu należy dokonać odpowiedniej transformacji 

zmiennych. W chwili obecnej powszechnie jest stosowana 

transformacja oparta na koncepcji wektora 

przestrzennego, wprowadzonego przez Kovačsa i Racza 

w połowie ubiegłego wieku. 

1



s

Ψ

Model matematyczny SI we współrzędnych 

fazowych

5

Jeżeli dowolne wielkości fazowe  w układzie 
współrzędnych naturalnych dotyczą przebiegów 
symetrycznych, 
czyli spełniają warunek:

to wektor przestrzenny k definiowany jest 
następująco:

gdzie:                   

1



s

Ψ

Model matematyczny SI 

 

 

 

0







t

k

t

k

t

k

C

B

A

 

 

 





t

k

t

k

t

k

C

B

A

2

3

2

a

a

1

k







2

3

2

1

3

2

j

e

j











a

2

3

2

1

3

4

2

j

e

j











a

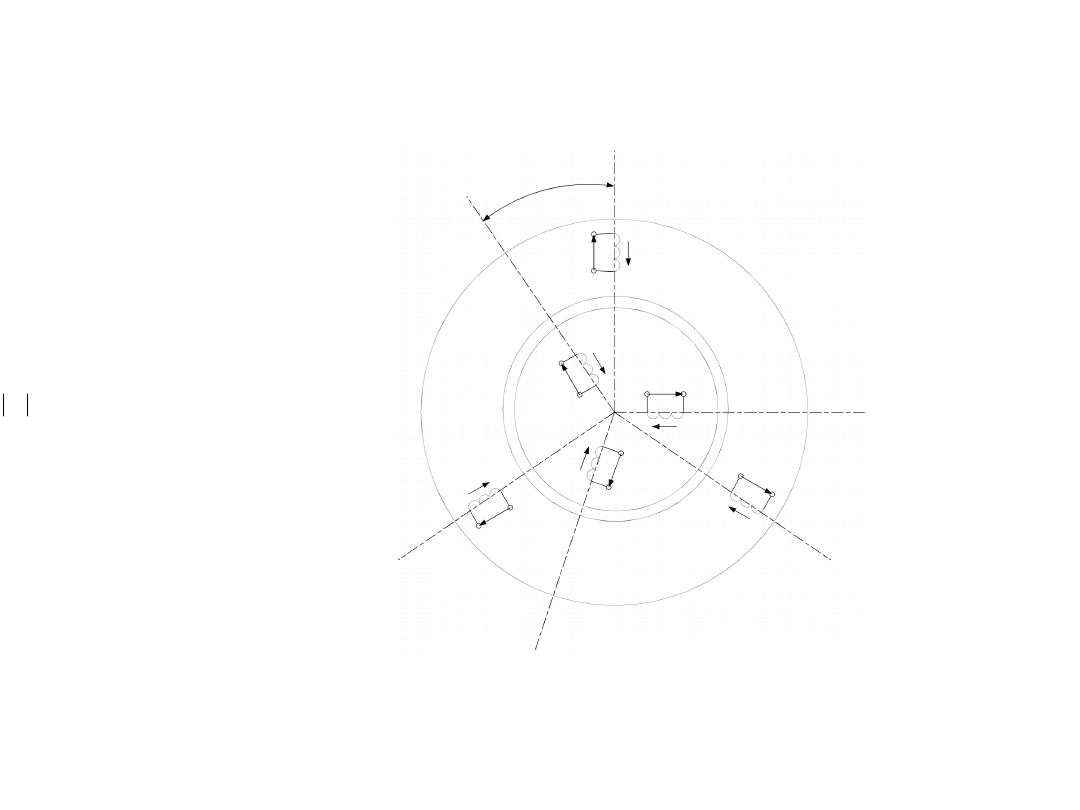
6

Konstrukcja wektora przestrzennego k na podstawie wartości chwilowych 

składowych fazowych kA, kB, kC

1



s

Ψ

Model matematyczny SI 

A

C

B

 

t

k

C

2

a

 

t

k

B

a

 

t

k

A

1

1

a

2

a

k

2

3

k

0

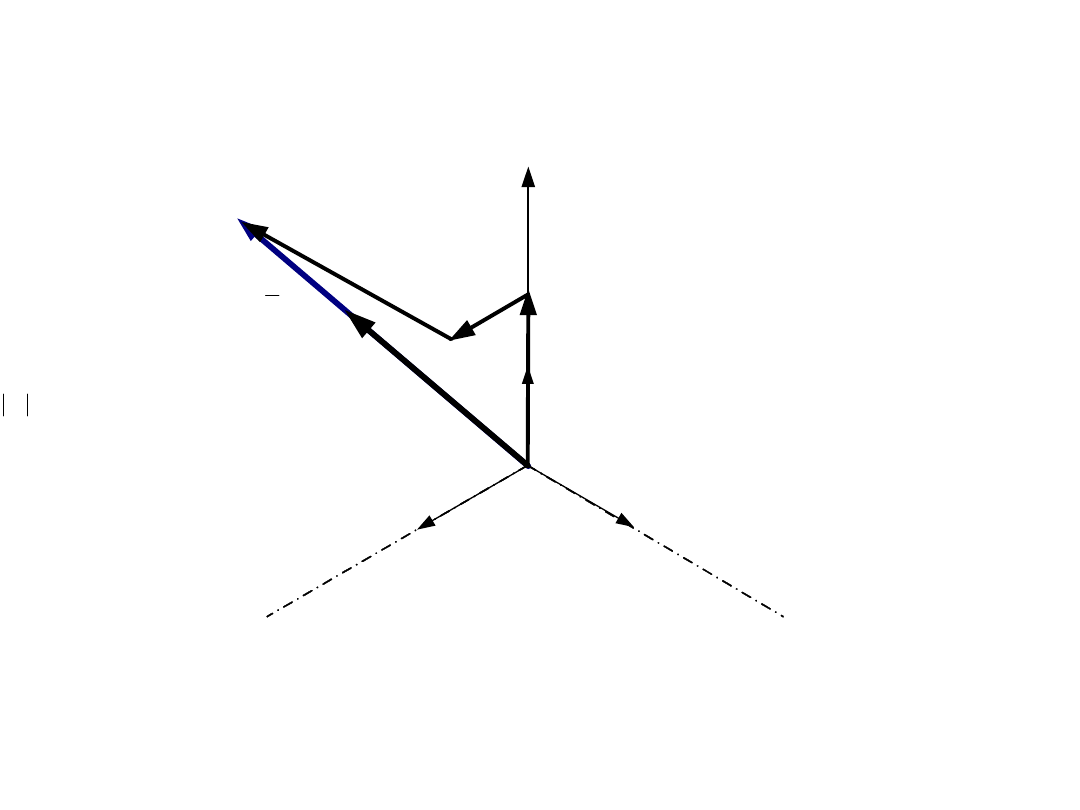
7

Wyznaczanie chwilowych wartości fazowych jako rzutów 

wektora przestrzennego k

k 

na osie odpowiednich faz (A-B-C) 

1



s

Ψ

Model matematyczny SI 

A

C

B

0

k

k

A

k

B

k

C

k



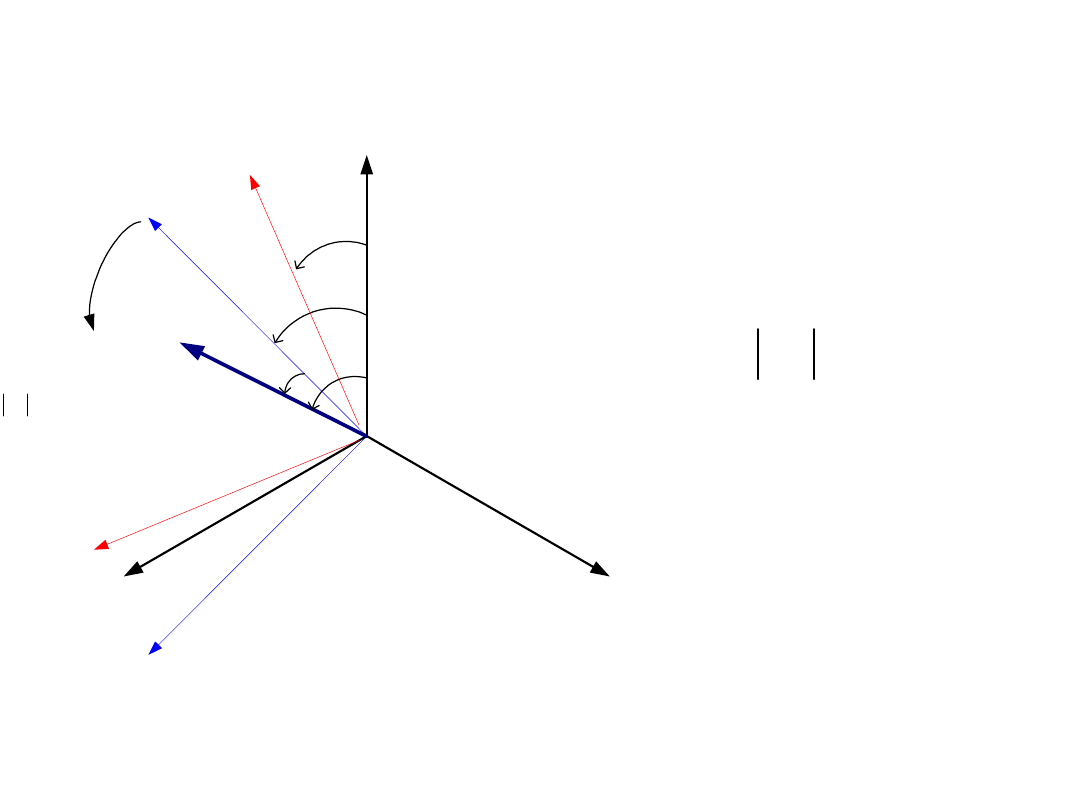
8

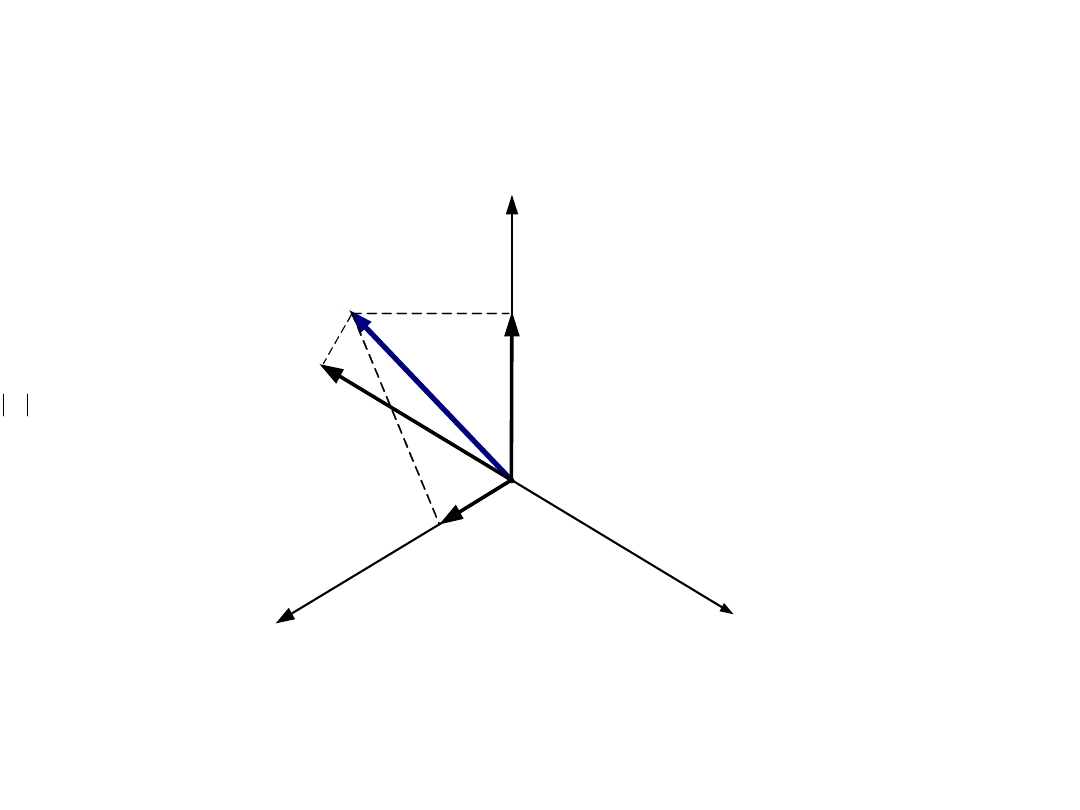
Model matematyczny SI 

Wektor przestrzenny k w układzie współrzędnych prostokątnych (u-v) 

wirującym z prędkością 



k

1



s

Ψ

A

C

B

u

v

k



k



s



d

q

m



k



k

k

v

u

k

j

k

k

jk

k

e









k

k

9

Po transformacji zmiennych stojana według:

i odpowiednio dla wirnika:

1



s

Ψ

Model matematyczny SI 

























































3

2

cos

3

2

cos

cos

3

2

k

C

k

B

k

A

u

k

k

k

k



























































3

2

sin

3

2

sin

sin

3

2

k

C

k

B

k

A

v

k

k

k

k









































































3

2

cos

3

2

cos

cos

3

2

m

k

c

m

k

b

m

k

a

u

k

k

k

k











































































3

2

sin

3

2

sin

sin

3

2

m

k

c

m

k

b

m

k

a

v

k

k

k

k

10

Otrzymuje się model matematyczny SI zapisany 
za pomocą wektorów przestrzennych:
- równania napięciowe:

- równanie ruchu:

Model matematyczny SI 

sk

k

sk

sk

s

sk

j

dt

d

R

Ψ

Ψ

I

U













rk

m

k

rk

rk

r

rk

j

dt

d

R

Ψ

Ψ

I

U

 













rk

sk

s

sk

M

L

L

I

I

Ψ





sk

rk

r

rk

M

L

L

I

I

Ψ









o

e

b

m

M

M

p

dt

d

J











sk

sk

b

e

p

M

I

Ψ

*

Im

2

3



M

r

r

M

s

s

L

L

L

L

L

L













11

Zapisując  model SI w jednostkach 
względnych (x [p.u.] = x [j.fiz.] / x

b 

[j.fiz.]), 

otrzymuje się następujące równania:
- równanie napięciowe obwodu stojana i 
wirnika:

- równania strumieniowo-prądowe:

w których:

Model matematyczny SI 

sk

k

sk

sk

s

sk

jω

dt

d

T

r

N

Ψ

Ψ

i

u











rk

m

k

rk

rk

r

rk

ω

j

dt

d

T

r

N

Ψ

Ψ

i

u











rk

sk

s

sk

M

x

x

i

i

Ψ





sk

rk

r

rk

M

x

x

i

i

Ψ





M

M

x

x

x

x

x

x

r

r

s

s













N

N

s

b

f

T

 

2

1

1









12

- równanie ruchu:

w którym:

przy czym:

Model matematyczny SI 





o

e

m

m

m

T

dt

d

M





1







sk

sk

e

m

i

Ψ

*

Im



b

b

b

M

p

J

T

M





13

1



s

Ψ

Model matematyczny SI 

Model matematyczny silnika indukcyjnego 

zapisany za pomocą wektorów przestrzennych 
wirujących z dowolna prędkością kątową , 
można zapisać w trzech układach 
współrzędnych:

- w układzie () nieruchomym względem 

stojana, czyli wirującym z prędkością ,

- w układzie (x - y) nieruchomym względem pola, 

czyli wirującym z prędkością synchroniczną,

- w układzie (d - q) nieruchomym względem 

wirnika, czyli wirującym z prędkością wirnika .

14

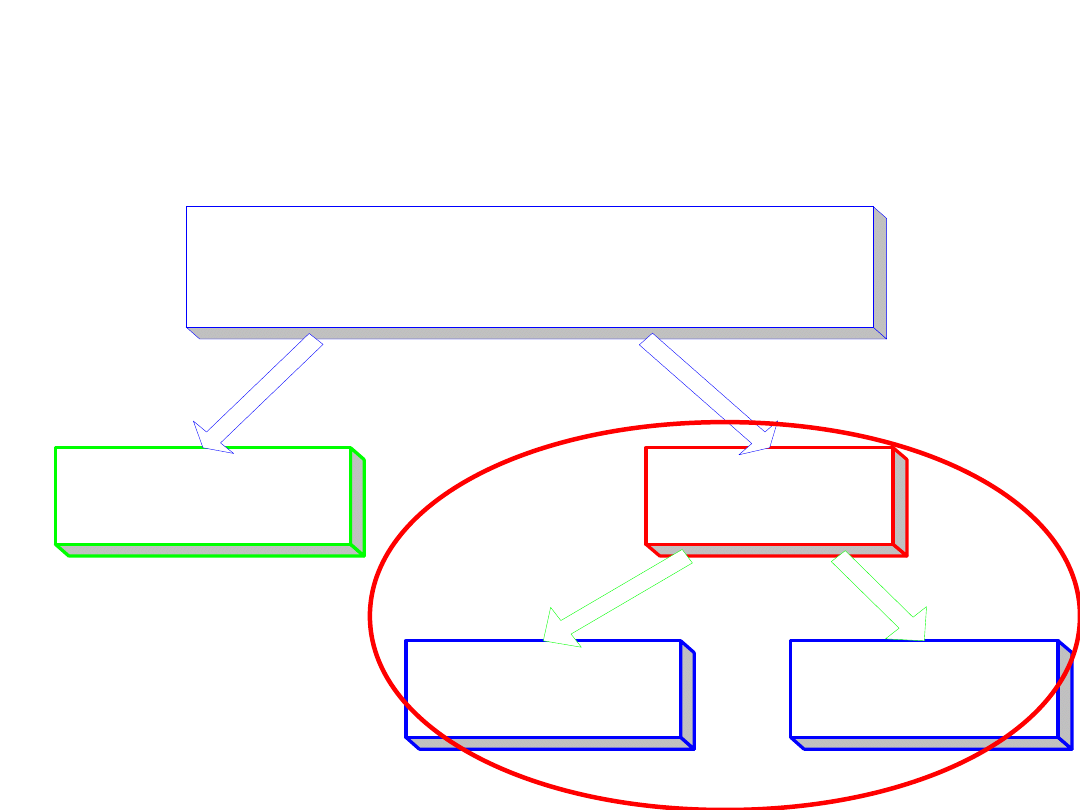
Współczesne metody sterowania 

prędkością silników indukcyjnych

 

CZĘSTOTLIWOŚCIOWE METODY STEROWANIA

PRĘDKOŚCIĄ KĄTOWĄ SILNIKA INDUKCYNEGO

METODY POLOWO-

ZORIENTOWANE

METODY SKALRNE

METODY

WEKTOROWE

METODA 

DTC  -

BEZPOŚREDNIEGO

STEROWANIA

MOMENTEM

15

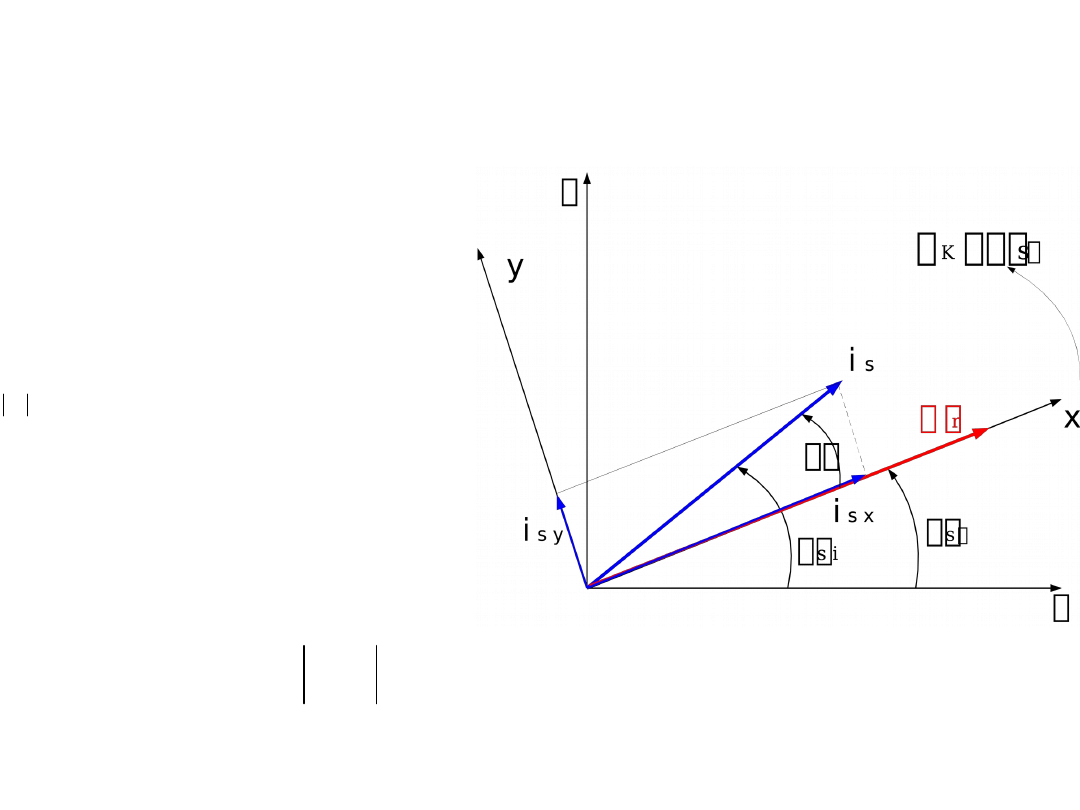
Przyjmuje się następujące 

założenia:

• prędkość wirowania układu 

współrzędnych jest równa 

prędkości wirowania wektora 

strumienia wirnika (układ 

współrzędnych (x-y)):

• wektor strumienia wirnika 

jest skierowany zgodnie 

 z osią x układu 

współrzędnych:

• realizuje się wymuszenia 

prądu stojana i

s

 = i

sx 

+ ji

sy

1



s

Ψ

Metoda polowo-zorientowana 

)

(













s

k

s

k





.

0

        

,















ry

r

r

rx

r

Ψ

Ψ

16

Metoda polowo-

zorientowana

Wobec tego model matematyczny silnika przy 

wymuszeniu wektora prądu stojana można 
przedstawić w układzie współrzędnych (x-y) w 
postaci następującego układu równań:

przy czym pulsacja poślizgu: 

oraz równanie ruchu: 





r

m

s

sy

r

M

r

ry

N

r

r

r

sx

r

M

r

r

N

i

x

x

r

dt

d

T

x

r

i

x

x

r

dt

d

T



























0

m

s

r

















, 

1

















o

sy

r

r

m

m

i

Ψ

x

x

T

dt

d

M

M



e

m

17

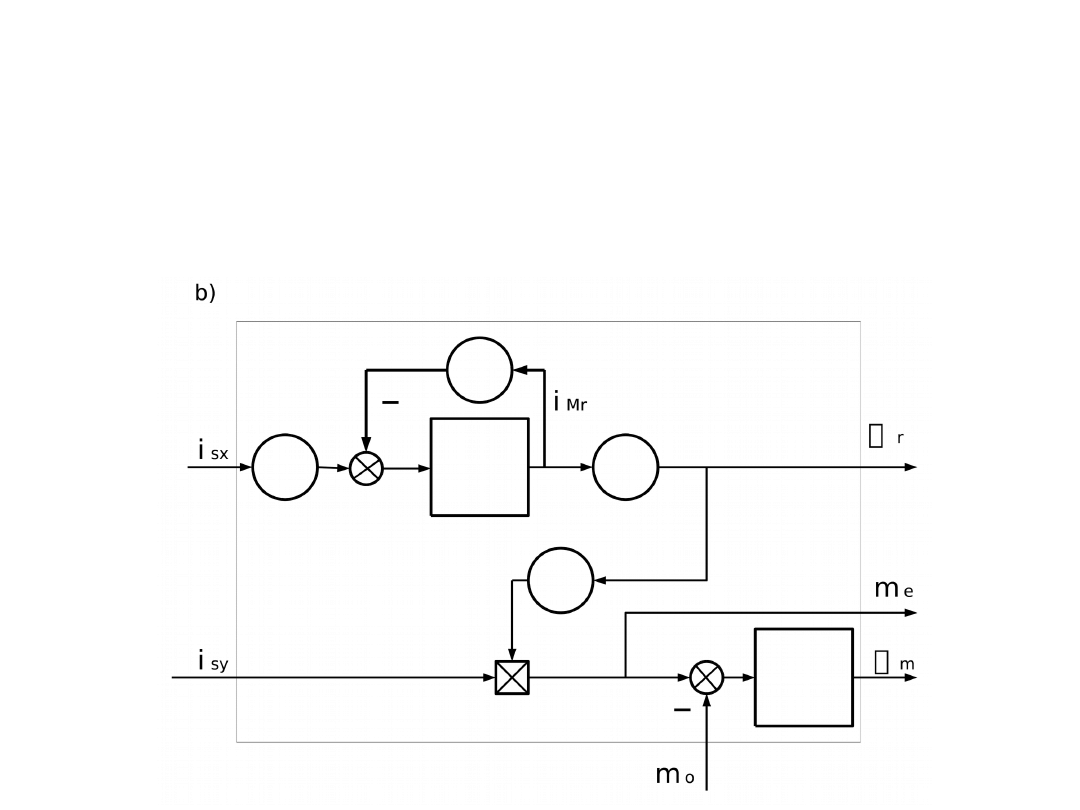
Schemat blokowy silnika 

indukcyjnego

 we współrzędnych polowych

 

Temu układowi równań odpowiada 
schemat blokowy: 

18

Analogia sterowania momentem 

SPS 

i SI –  we współrzędnych polowych

 

Wzór na moment SPS: 

Wzór na moment SI – sterowanego we 
współrzędnych polowych:

Analogia: 

sy

r

r

M

SI

e

i

x

x

m





t

w

SPS

e

i

c

m





sx

w

r

w

sy

t

i

i

SI

SPS

SI

i

SPS

i

         

          

          

          

)

(

)

(

)

(

    

)

(













2

)

 ,

(

2

)

 ,

(

SI

SPS

















r

sy

w

t

i

i

19

SI przy wymuszeniu prądu stojana w układzie 
współrzędnych prostokątnych zorientowanym 
względem wektora strumienia wirnika staje się 
liniowym obiektem sterowania. 
Strumień wirnika jest kształtowany z pomocą 
składowej 

i

sx

 wektora prądu stojana, natomiast 

moment dla stałej wartości strumienia wirnika 
zależy liniowo od składowej 

i

sy

, 

zgodnie z wzorem:

gdzie:

Rodzaje i realizacja metod 

polowo-zorientowanych - FOC

sy

r

r

M

e

i

x

x

m









r

s

s

sy

i

i

Ψ

i ,

;

sin











20

Poszczególne realizacje systemów sterowania FOC różnią 

się między sobą przede wszystkim:

•  metodą wyznaczania kąta 



s



 

(potrzebnego do 

transformacji zmiennych);

•  metodą estymacji wektora strumienia i momentu;
•  metodą regulacji prądu falownika PWM.

Najważniejszym podziałem, który istotnie zmienia 

strukturę sterowania, jest podział wynikający ze 
sposobu wyznaczania kąta 



s



. 

Są to odpowiednio 
-  metoda bezpośredniego sterowania polowo-

zorientowanego - DFOC

-  pośredniego sterowania polowo-zorientowanego - IFOC

1



s

Ψ

Metoda polowo-zorientowana

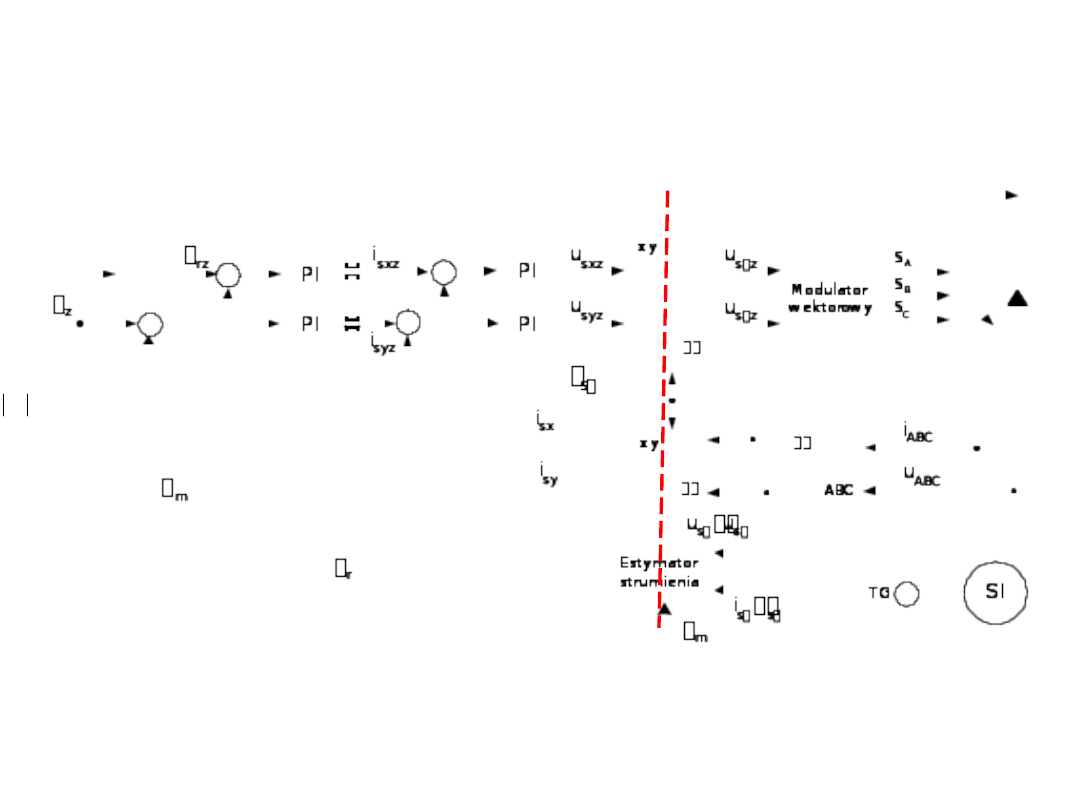
21

Struktura układu bezpośredniego sterowania polowo-zorientowanego DFOC 

przy wymuszeniu prądowym z  regulatorami prądu PI (uproszczona)

1



s

Ψ

Metoda bezpośredniego 

sterowania 

polowo-zorientowanego DFOC

22

Regulatory prądu (typu PI lub inne) pracują w 
zamkniętych pętlach regulacji, w układzie 
współrzędnych polowych (x-y). 
Sygnały prądowe do sprzężeń zwrotnych 
uzyskuje się po transformacji mierzonych 
prądów fazowych uzwojenia stojana do układu 
():

a następnie do układu współrzędnych (x-y):

1



s

Ψ

Metoda bezpośredniego 

sterowania 

polowo-zorientowanego DFOC





,

2

3

1

,

sB

sA

s

sA

s

i

i

i

i

i











.

cos

sin

,

sin

cos

























s

s

s

s

sy

s

s

s

s

sx

i

i

i

i

i

i











23

Regulatory prądu generują na swoich wyjściach 

wartości zadane polowo-zorientowanych 
składowych wektora napięcia stojana [u

sx

, u

sy

] , 

które są transformowane do układu (), 

a następnie modulator wektorowy oblicza 

sygnały sterujące dla tranzystorów mocy 
falownika MSI.

1



s

Ψ

Metoda polowo-zorientowana 

DFOC

.

cos

sin

,

sin

cos





















s

syz

s

sxz

z

s

s

syz

s

sxz

z

s

u

u

u

u

u

u









24

Metoda pośredniego 

sterowania 

polowo-zorientowanego IFOC

Podstawową cechą odróżniającą pośrednie IFOC od 
sterowania bezpośredniego DFOC jest inny sposób 
uzyskiwania informacji o aktualnym położeniu wektora 
strumienia wirnika.
 
W sterowaniu bezpośrednim informacja pochodzi z 
układu odtwarzającego składowe wektora strumienia 
wirnika na podstawie pomiaru prądów i napięć silnika – 
z estymatora tej zmiennej stanu. 

Natomiast w układzie sterowania pośredniego 
informacja ta uzyskiwana jest w wyniku zsumowania 
zmierzonej wartości prędkości wału i obliczonej 
wartości pulsacji poślizgu na podstawie wzoru i 
zadanych w układzie sterowania wartości składowych 
wektora prądu stojana, zgodnie z zależnością:

z

sy

z

sx

r

N

z

sy

z

r

r

N

M

r

rz

i

i

T

T

i

x

T

x

r









25

Po zsumowaniu zadanej wartości pulsacji poślizgu 
i zmierzonej wartości prędkości kątowej silnika: 

i wykonaniu całkowania, otrzymuje się wartość szukanego 

kąta 



s



:

Wartość kąta 



s



 jest doprowadzona do układu 

generującego funkcje sin



s



, cos



s



, które następnie 

wykorzystywane są w układzie przetwornika (x–y/



-



). 

Sygnały te następnie po przeliczeniu do układu 

trójfazowego są wielkościami sterującymi dla obwodów 

regulacji prądu przemiennika częstotliwości. 

1



s

Ψ

Metoda 

pośredniego sterowania 

polowo-zorientowanego IFOC

rz

m

s

















t

s

s

dt









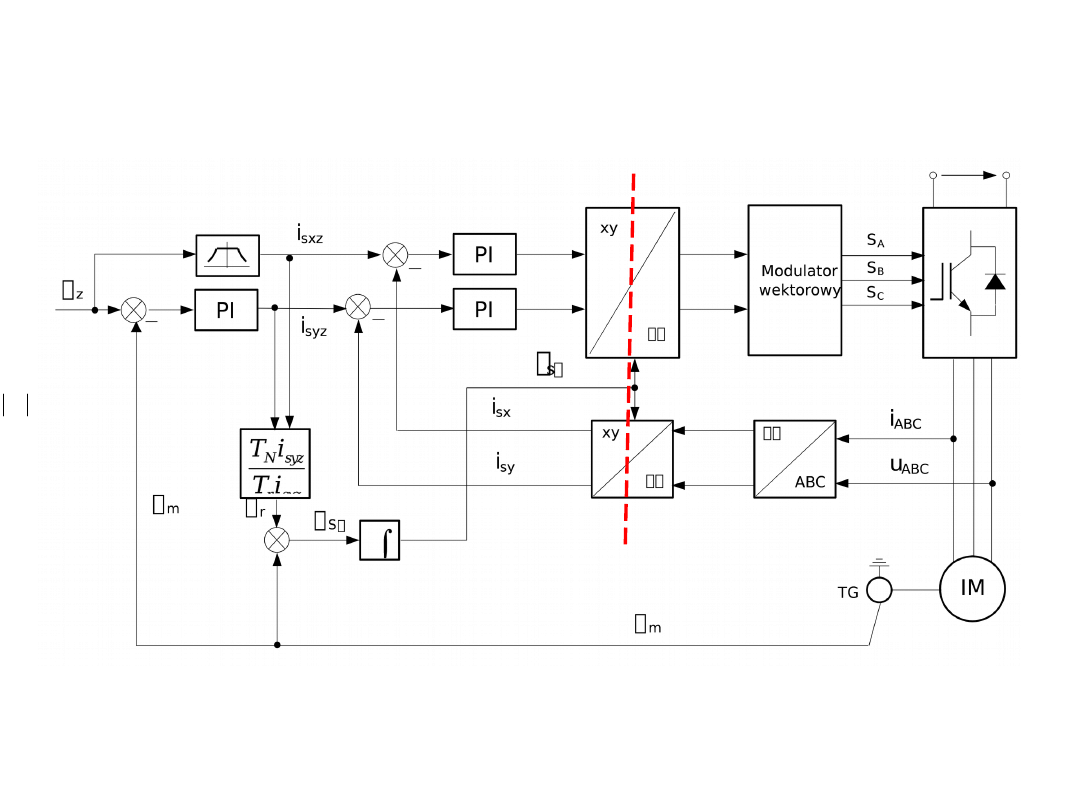
26

Metoda polowo-zorientowana 

IFOC

z regulatorami prądu PI

1



s

Ψ

Struktura układu pośredniego sterowania polowo-zorientowanego 

IFOC 

przy wymuszeniu prądowym z  regulatorami prądu PI (uproszczona)

27

Dziękuję z uwagę 

1



s

Ψ