PROJEKT SŁUPA OSIOWO

ŚCISKANEGO OBUSTRONNIE

PRZEGUBOWO PODPARTEGO

KOLEJNOŚĆ POSTĘPOWANIA

PRZY PROJEKTOWANIU

SŁUPA

• Przyjąć obciążenie i schemat

statyczny

• Przyjąć kształt przekroju

poprzecznego i oszacować pole
przekroju

d

f

N

A







• gdzie:
• fd – wytrzymałość obliczeniowa stali

na ściskanie (rozciąganie)

• φ – współczynnik wyboczeniowy

przyjmowany wstępnie φ=0,6÷0,8

• 3. Dobranie kształtowników z tabeli

( przypadku projektowania z profili
gorącowalcowanych) lub obliczenie
potrzebnych wartości przekroju w
przypadku projektowania z profili
blachownicowych spawanych. (A; Jx;
Jy; Wx; Wy; ix; iy; etc.)

• 4. Ustalenie klasy przekroju wg

normy PN-90/B-03200 rozdz. 4.1.3

• 5. Określenie współczynnika długości

wyboczeniowej () i obliczenie
smukłości dla wyboczenia giętnego:

;

;

y

y

y

y

x

x

x

x

i

l

i

l

















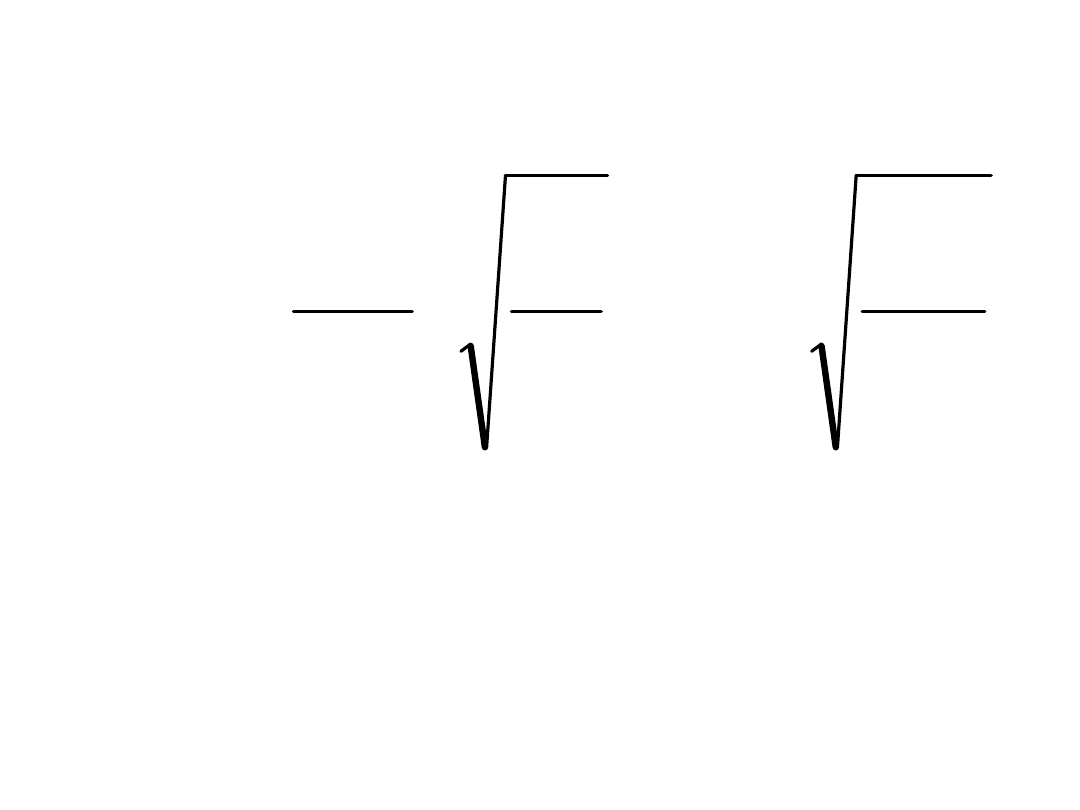
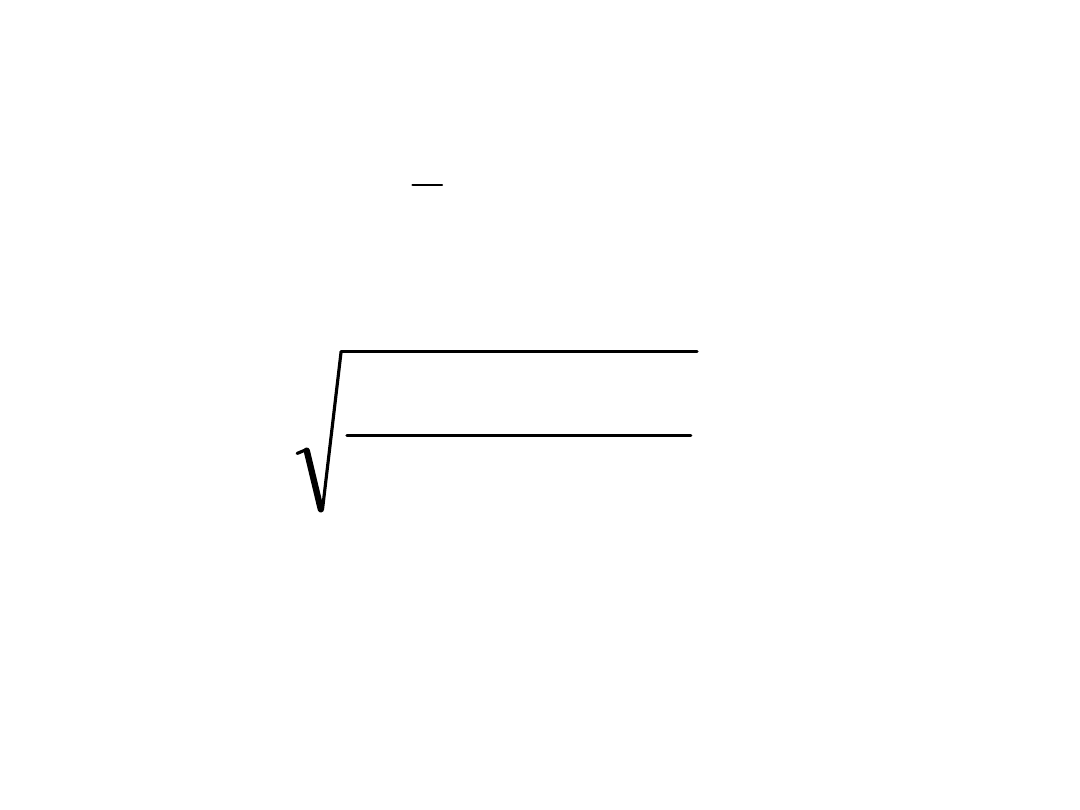
• 6. Określenie smukłości

porównawczej:

d

d

p

f

f

E

215

84

15

,1













• 7. Określenie smukłości względnej:

;

p

x









albo:

;

p

y









(większa z tych
wartości)

8. Sprawdzenie warunku nośności
(stateczności) (wzór 39):

1





Rc

N

N



φ – współczynnik wyboczeniowy
(mniejszy) przyjęty z tablicy 11

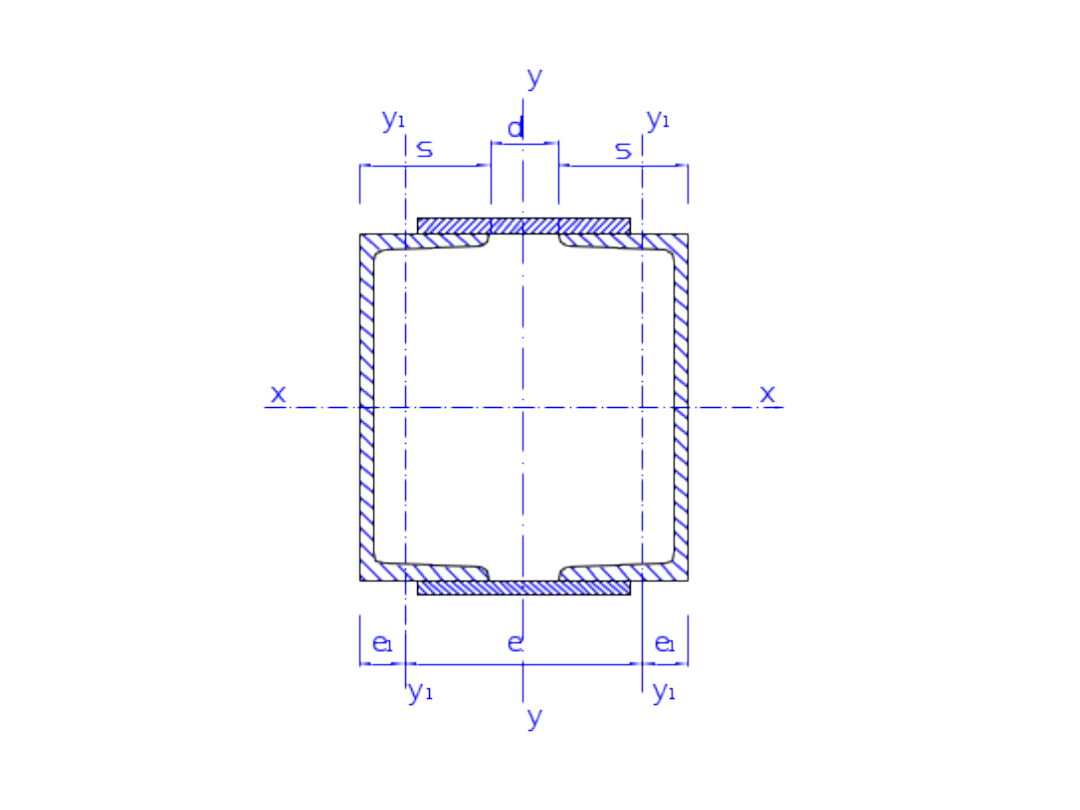
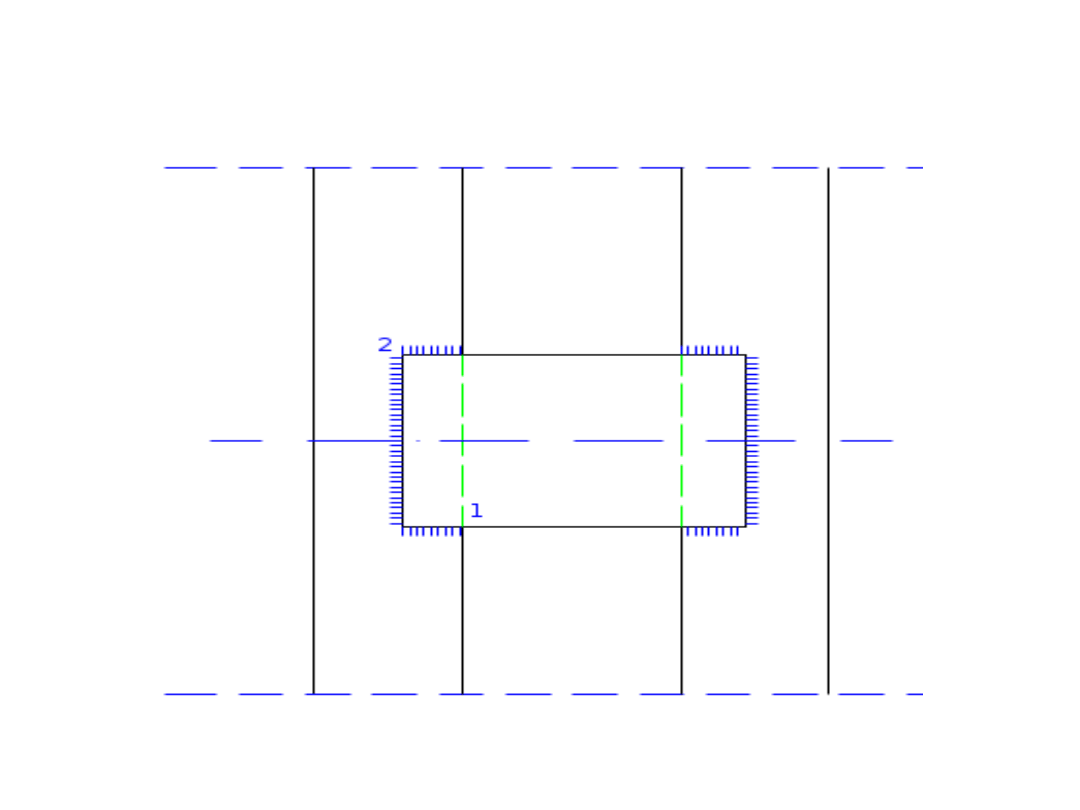
• SŁUP WIELOGAŁĘZIOWY
• Założenie, że jedna oś nie przecina

materiału przekroju (oś
niematerialna)

• Odstęp pomiędzy gałęziami słupa

ustala się z warunku jednakowej
stateczności (smukłości) w
płaszczyźnie x-x i y-y, przyjmując:

my

x







x

y

J

J



 1

,

1

my



- smukłość zastępcza przekroju
słupa względem osi y-y, przy czym
wstępnie zakłada się moment
bezwładności względem osi y-y o
10% wiekszy niż moment
bezwładności względem osi x-x.

Stąd wynika, że dla słupa złożonego z dwu
gałęzi, smukłość zastępcza jest większa od
smukłości słupa jednolitego zwiększa się
wraz ze wzrostem rozstawu gałęzi słupa.

• stąd można wyznaczyć:

1

2

1

1

2

1

,

1

2

2

x

y

J

e

A

J









































1

1

1

1

,

1

2

A

J

J

e

y

x







s

e

e

d











2

2

1

A1; Jx; Jy – pole i momenty bezwładności
pojedynczej gałęzi słupa; e1 – odległość środka
ciężkości przekroju pojedynczej gałęzi od krawędzi
tego przekroju (np. ceownika)

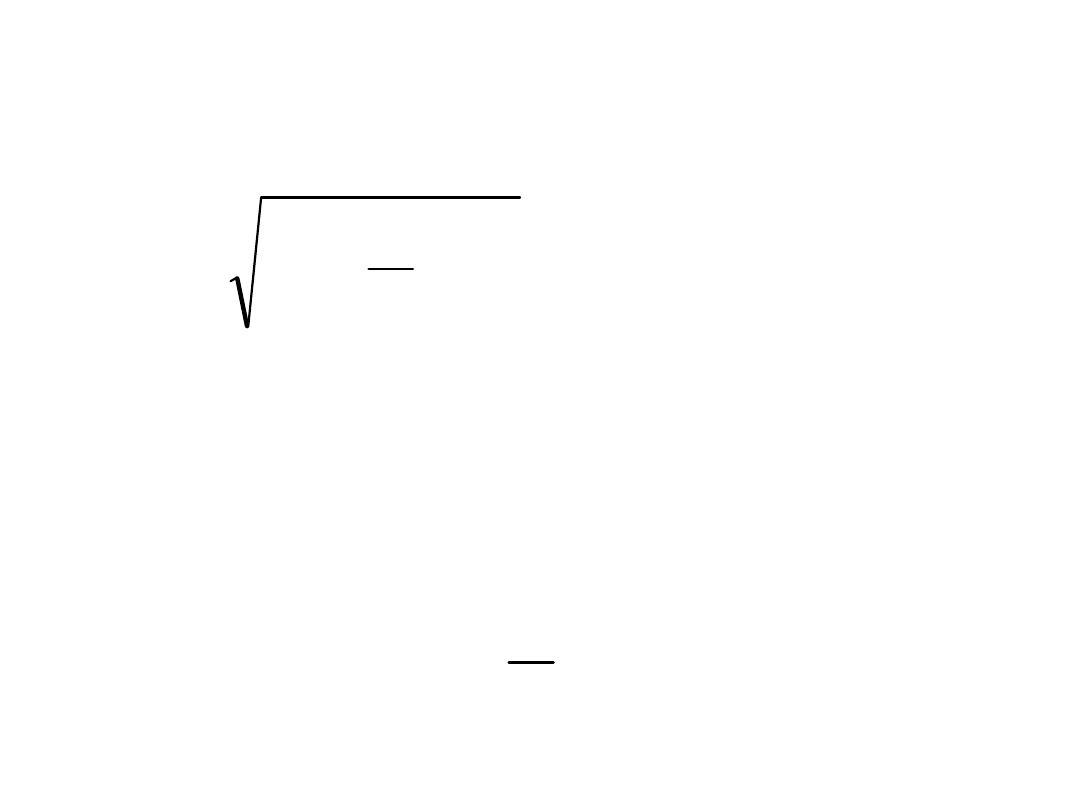
• Dla osi niematerialnej należy

przyjmować smukłość zastępczą:









2

2

2







m

my

gdzie:



- smukłość ustalona jak dla pręta pełnościennego

m – ilość gałęzi słupa





- smukłość postaciowa zależna

od sposobu połączenia gałęzi:

dla przewiązek:

1

1

i

l







;

• l1 – osiowy rozstaw przewiązek, lecz

nie większy niż odstęp pomiędzy nimi
zwiększony o minimalną szerokość
przewiązki =100mm

• i1 – najmniejszy promień

bezwładności przekroju gałęzi

• Osiowy rozstaw przewiązek nie jest

ograniczony, lecz ograniczona jest
smukłość pojedyńczej gałęzi
(powinna być mniejsza od smukłości
całego słupa),

• Trzon słupa wymiaruje się jak słup

pełnościenny, przyjmując smukłości
zastępcze.

y













8

,

0

1

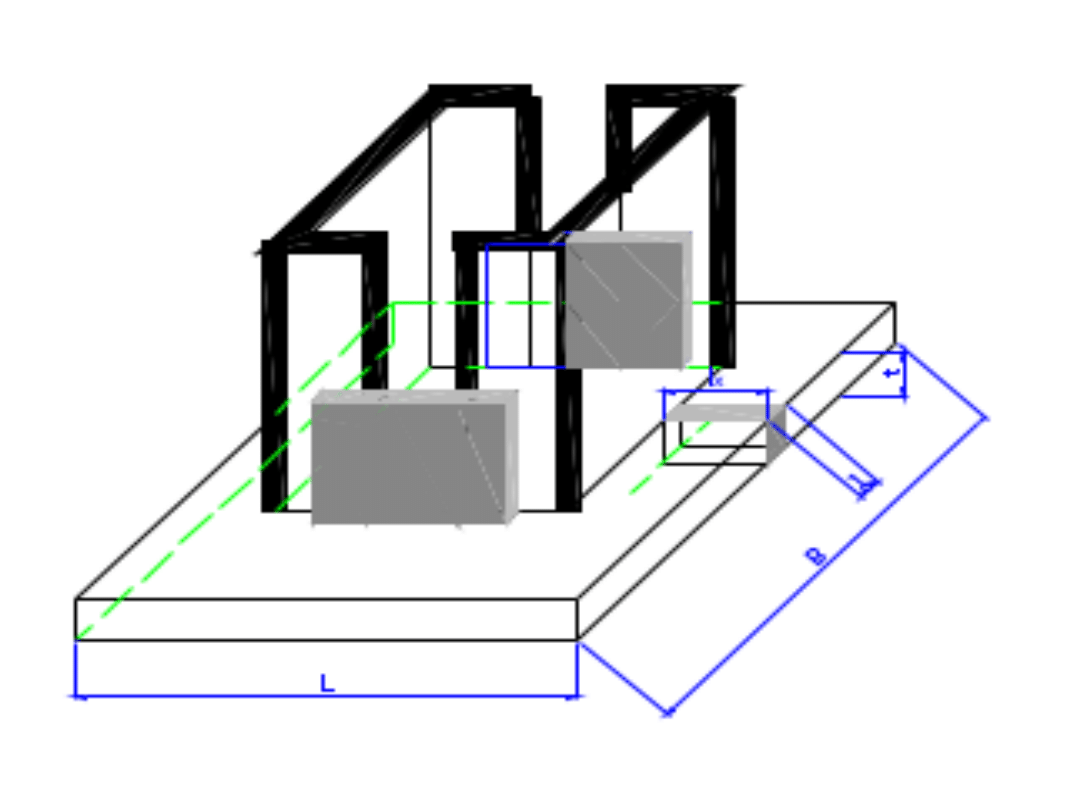
• PRZYKŁAD:
• Zaprojektować przekrój trzonu

przegubowo podpartego, osiowo
ściskanego, dwugałęziowego słupa
spawanego z przewiązkami. (proponowany
przekrój słupa jak na rysunku). Gałęzie
słupa z profili gorącowalcowanych.

• Dane:
• Obliczeniowa siła osiowa N=1900 kN
• Stal S235 (St3S) fd=215 MPa;
• l=4,5 m; rozstaw przewiązek l1=0,9 m

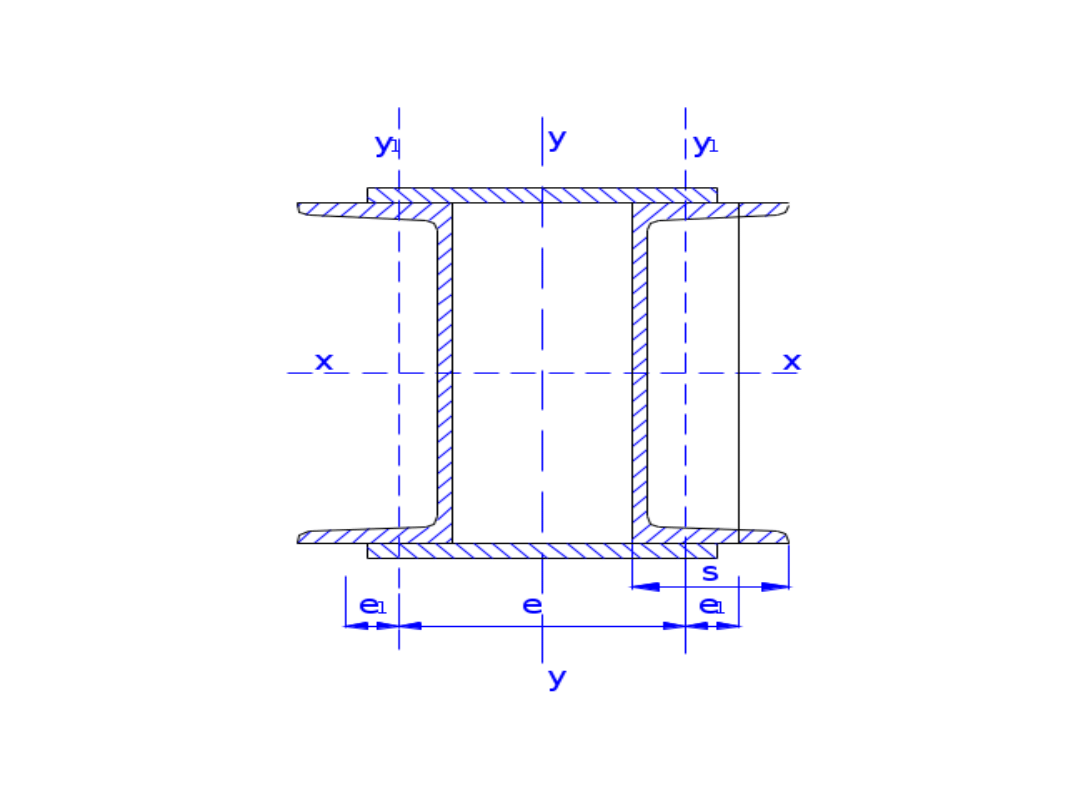
• Orientacyjne pole przekroju słupa:

2

1

2

1

92

,

58

83

,

117

215

75

,

0

10

1900

75

,

0

2

cm

A

cm

f

N

A

d



















Przyjęto przekrój słupa 2[300

cm

i

cm

i

cm

J

cm

J

cm

s

cm

e

cm

A

y

x

y

x

9

,

2

7

,

11

495

8030

10

7

,

2

8

,

58

1

1

4

4

1

2

1















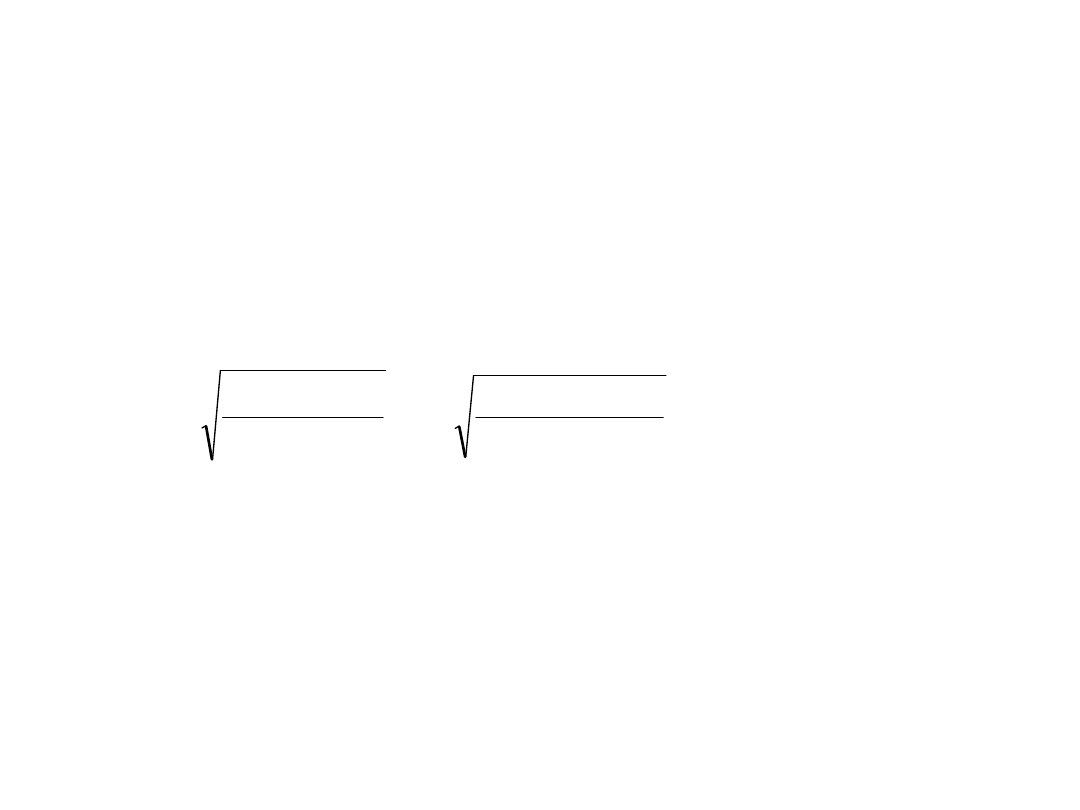
• grubość środnika tw=10mm
• grubość półki tf=16mm
• współczynniki długości

wyboczeniowej:

1





y

x





cm

A

J

J

e

y

x

82

,

23

91

,

11

2

8

,

58

495

8030

1

,

1

2

1

,

1

2

1

1

1

min























przyjęto d=20cm

mm

cm

e

254

4

,

25

7

,

2

2

20











• Określenie klasy przekroju:
• - półki:

9

215

215

9

63

,

5

16

10

100













f

t

b

(nie uwzględniono wyobleń styków środnika i półek)

- środnik:

33

33

8

,

26

10

16

2

300

















w

t

b

• zarówno półki jak i środnik spełniają

kryteria klasy 1 więc cały przekrój
można zaliczyć do klasy 1.

• Gdyby np. środnik trzeba by było

zaliczyć do klasy 2, to cały przekrój
również należy zaliczyć do klasy 2.

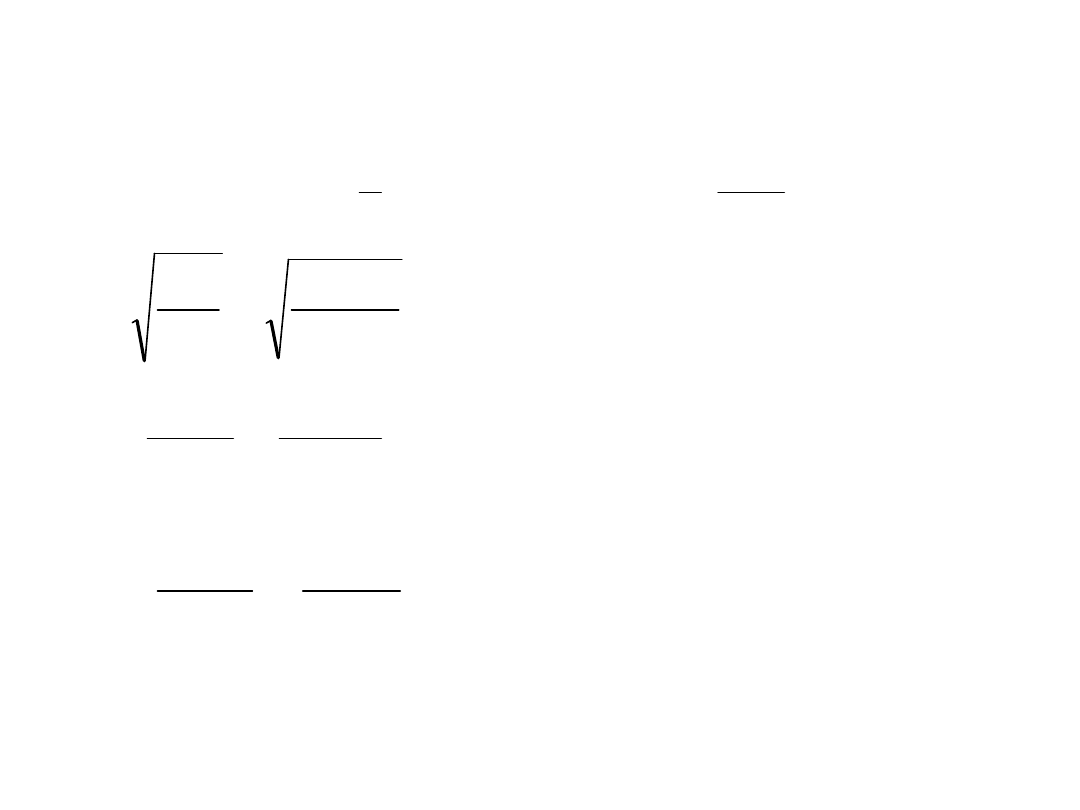
• Sprawdzenie słupa na wyboczenie:

4

2

2

1

1

19958

2

4

,

25

8

.

58

2

495

2

2

2

2

cm

e

A

J

J

y

y















































cm

A

J

i

y

y

03

,

13

8

,

58

2

19958

2

1









46

,

38

7

,

11

450

1











x

x

x

i

l





54

,

34

03

,

13

450









y

y

y

i

l





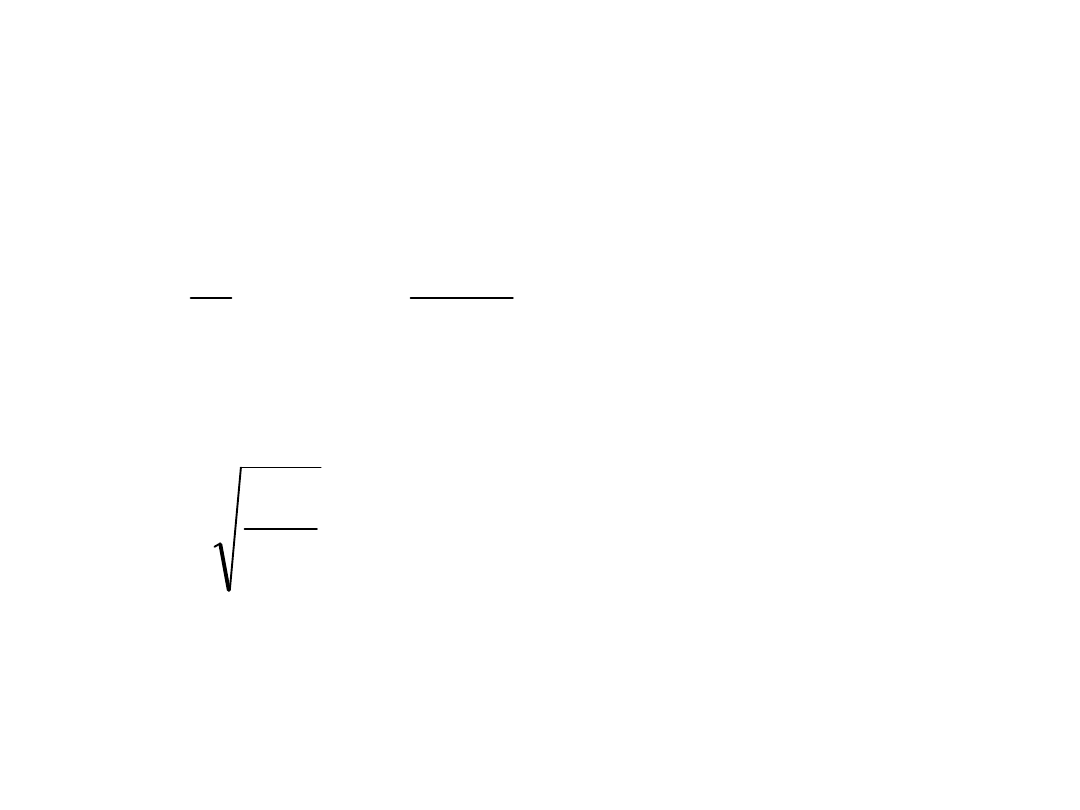
• smukłość pojedyńczej gałęzi

pomiędzy przewiązkami:

03

,

31

90

,

2

90

1

1

1















i

l

smukłość porównawcza:

84

215

84





d

p

f



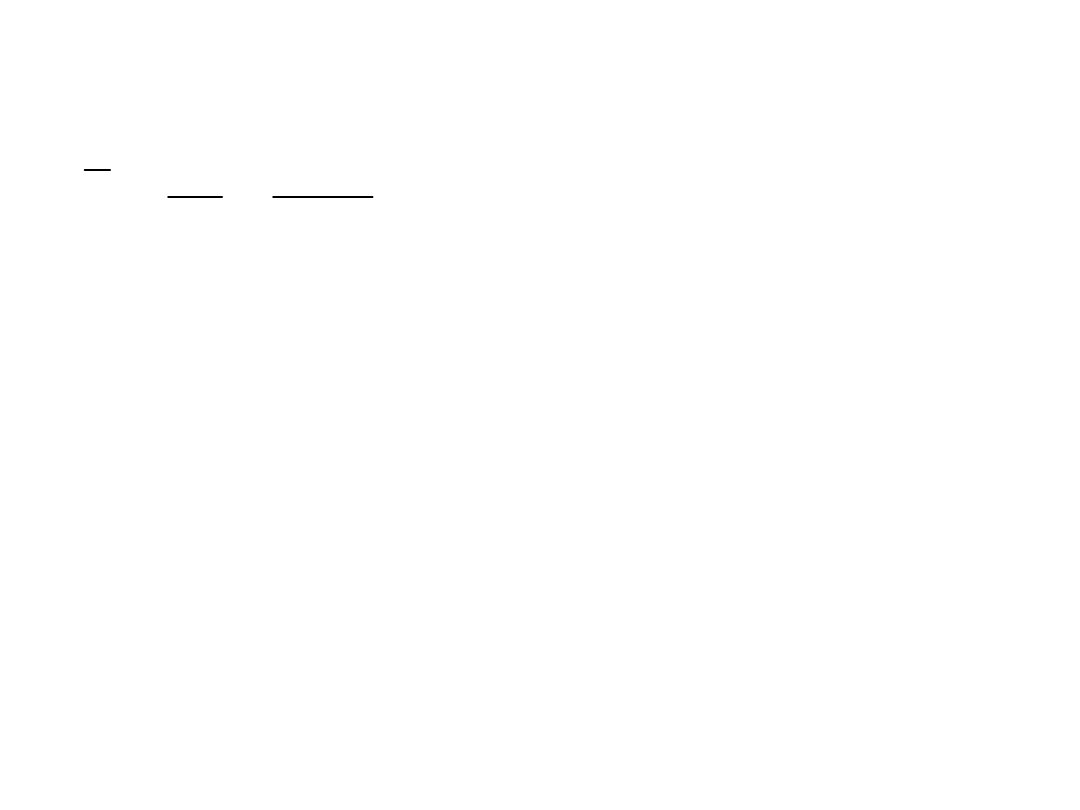
• smukłość zastepcza:

37

,

0

84

03

,

31

1

1







p







z tablicy 11 PN-90/B-03200 wg
krzywej „c” odczytujemy:

93

,

0

~

1









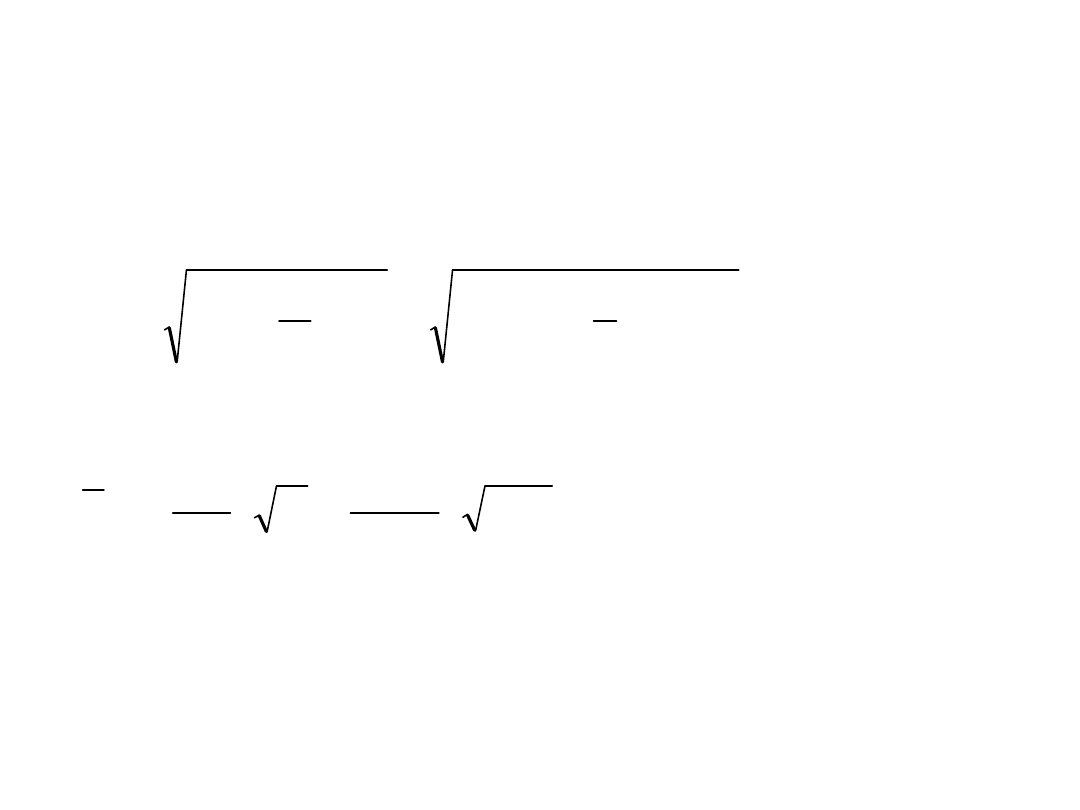
• - współczynnik redukcyjny

nośności

przekroju

Smukłość zastępcza słupa względem osi niematerialnej:



43

,

46

03

,

31

2

2

54

,

34

2

2

2

2

2























m

y

my

smukłość względna:

533

,

0

93

,

0

84

43

,

46



















p

my

my

Współczynnik wyboczeniowy z tablicy 11 według krzywej „b”
jak dla przekroju skrzynkowego:

925

,

0

~





• Nośność obliczeniowa przekroju

słupa wynosi:

kN

f

A

N

d

Rc

4

,

2351

10

15

,

2

10

2

8

,

58

93

,

0

5

4

























1

87

,

0

4

,

2351

925

,

0

1900











Rc

N

N



PROJEKTOWANIE PRZEWIĄZEK

W SŁUPIE

• Dla spoin pachwinowych naprężenia

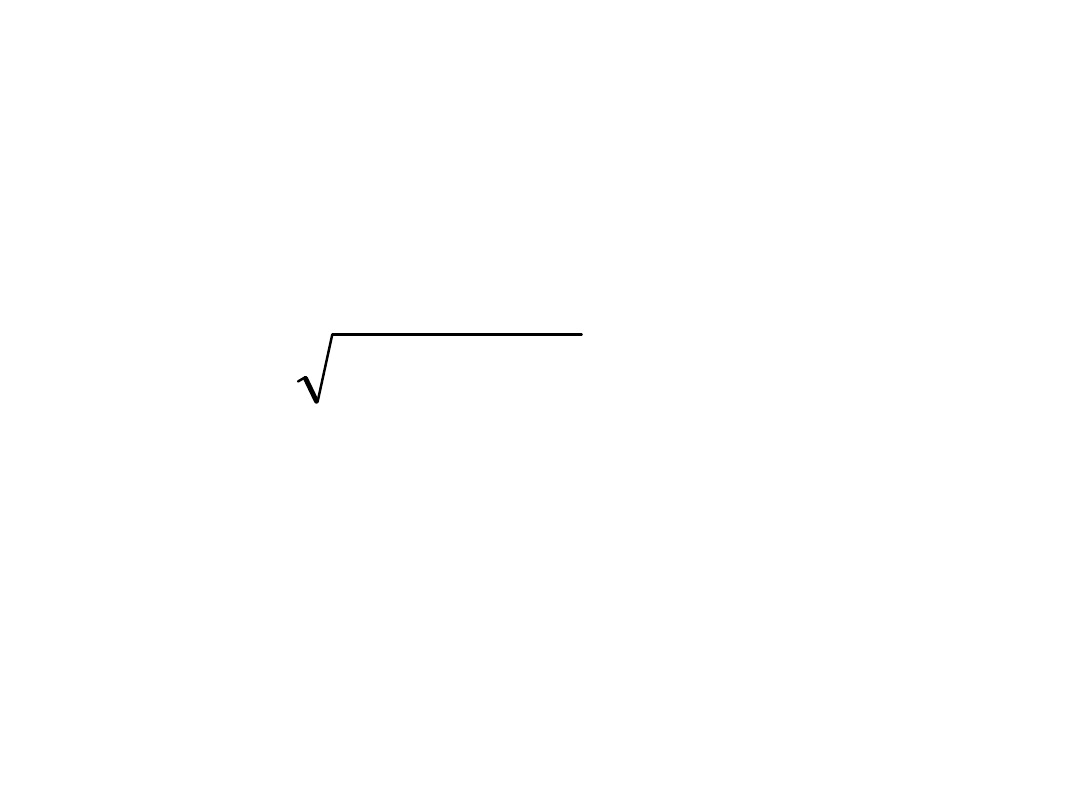
w materiale określa się wg wzorów:

d

x

x

f

W

d

T

W

M











2



c

t

T

J

t

S

T

x

x













5

,

1

max



• gdzie:
• T – siła ścinająca według wzoru:

e

n

l

Q

T







1

Q – uogólniona siła poprzeczna:

d

f

A

Q





 012

,

0

według normy rozdz.4.7.3)

• wskaźnik wytrzymałości:

6

2

c

t

W

x





• gdzie:
• t; c – grubość i wysokość przewiązki
• d – odstęp pomiędzy gałęziami słupa
• b – długość poziomej spoiny

pachwinowej

• rx – odległość środka ciężkości spoin od

krawędzi pionowej przewiązki

• a – grubość spoiny
• Sx; Jx – moment statyczny połowy

przekroju poprzecznego przewiązki i

moment bezwładności całego przekroju z

przewiązkami względem osi x-x

• W związku z tym, że spoiny pracują w

złożonym stanie naprężeń, należy
sprawdzić naprężenia zastępcze
według wzoru:

d

x

f











2

2

3











- współczynnik materiałowy

według normy rozdz. 6.3.3.3

• PROJEKTOWANIE PRZEWIĄZEK W SŁUPIE

• Przewiązki i ich połączenia należy obliczać na obciążenie

zastępczą siłą poprzeczną Q. Jest to tzw uogólniona siła

poprzeczna określana wzorem normowym:

• lub:

• gdzie:

• V – maksymalna siła poprzeczna wywołana obciążeniem

mimośrodowym, które działa oprócz obciążenia osiowego N.

d

f

A

Q



 012

,

0

V

Q

2

,

1



• Musi być jednak zachowany warunek:

• Jeżeli nie występuje siła poprzeczna przyjmuje

się do obliczeń Przewiązki w słupach należy

rozmieszczać w jednakowych odstępach

przyjmując parzystą liczba przewiązek.

Minimalna szerokość przewiązki wynosi 10 cm,

a przewiązek skrajnych 15 cm.

• Rozstaw przewiązek przyjmuje się tak, aby

smukłość gałęzi pomiędzy przewiązkami była

mniejsza niż smukłość ogólna słupa. Jest to

uzależnione od możliwości utraty stateczności

ogólnej słupa jak i pojedynczej gałęzi

;

2

,

1

012

,

0

V

f

A

d





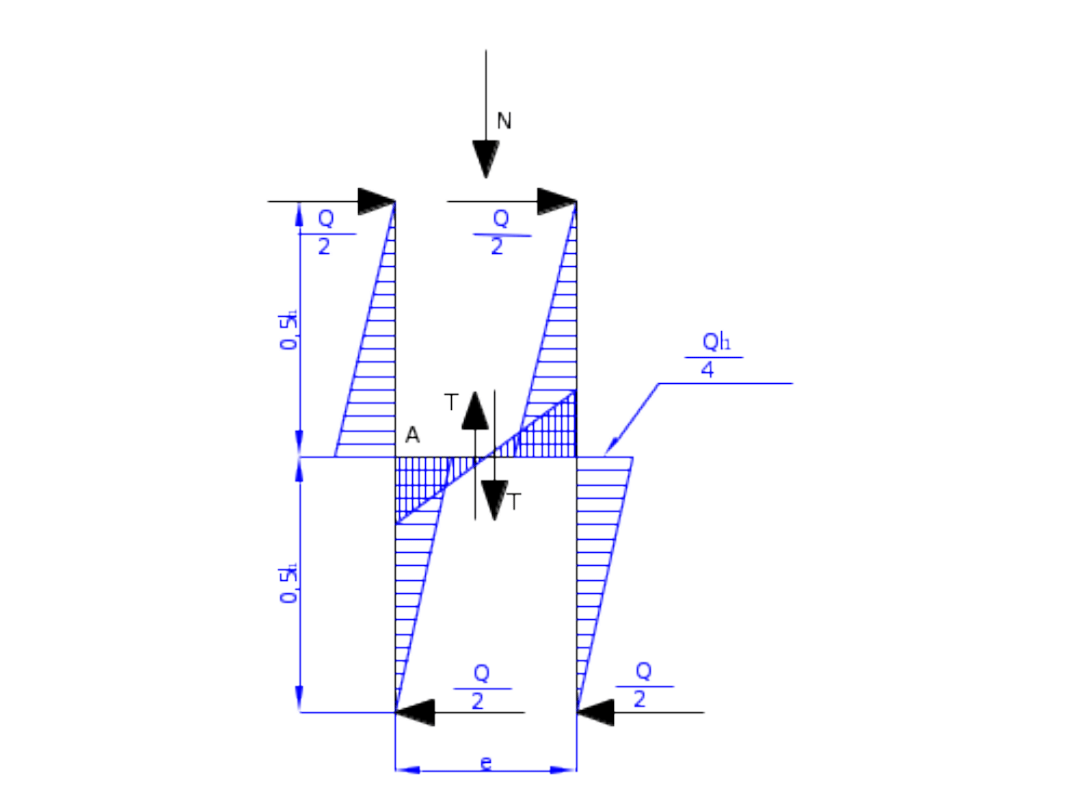
• Siłę ścinającą w przewiązce liczy się przy poniższych

założeniach:

• Zastępcza siła poprzeczna Q jest stała w rozpatrywanym

przekroju słupa

• Przewiązka jest nieskończenie sztywna
• Przemieszczenie gałęzi jest asymetryczne
• Moment działający w jednej gałęzi w odciętej części słupa

względem p. A wynosi:

• n – liczba płaszczyzn przewiązek

n

e

T

l

Q









2

2

1

• Stąd:

;

1

e

n

l

Q

T







Moment zamocowania przewiązki w słupie

:

;

2

z

T

M





z – odległość pomiędzy środkiem ciężkości spoin
łączących przewiązki słupa

• Rozwiązania przewiązek przewiązek

słupach:

• a Przewiązki połączone z gałęziami

słupa spoinami pachwinowymi

• b Przewiązki połączone z gałęziami

słupa spoinami czołowymi

• c Nitowane (historia )
• d Skręcane (baaaardzo rzadko )

• Ad a)
• Dla spoin pachwinowych naprężenia

w materiale określa się wg wzorów:

d

x

x

f

W

d

T

W

M











2



c

t

T

J

t

S

T

x

x













5

,

1

max



gdzie:
T – siła ścinająca według wzoru:

e

n

l

Q

T







1

• Q – uogólniona siła poprzeczna:

d

f

A

Q





 012

,

0

według normy rozdz.4.7.3)

6

2

c

t

W

x





gdzie:
t; c – grubość i wysokość przewiązki

• d – odstęp pomiędzy gałęziami słupa
• b – długość poziomej spoiny

pachwinowej

• rx – odległość środka ciężkości spoin

od krawędzi pionowej przewiązki

• a – grubość spoiny
• Sx; Jx – moment statyczny połowy

przekroju poprzecznego przewiązki i
moment bezwładności całego przekroju
z przewiązkami względem osi x-x

• W związku z tym, że spoiny pracują w

złożonym stanie naprężeń, należy
sprawdzić naprężenia zastępcze według
wzoru:

d

x

f











2

2

3









gdzie:



- współczynnik materiałowy według
normy rozdz. 6.3.3.3

c

t

T







;

1

1

s

x

A

S

r





• Moment bezwładności spoin:









;

5

,

0

2

12

2

;

5

,

0

2

12

2

3

2

.

2

2

.















































x

x

ysp

xsp

r

a

b

a

ab

ab

acr

J

a

c

ab

ac

J

• Biegunowy moment bezwładności

spoin:

;

.

.

ysp

xsp

o

J

J

J





• Maksymalne naprężenie w spoinach

(p.1)

;

0

max

max

d

M

f

J

r

M











gdzie:

;

2

z

T

M









;

5

,

0

2

2

2

max

x

r

a

b

c

r





















• W p.2 należy obliczyć wypadkowe

naprężenia w spoinach od momentu
M i siły T, przy czym T przenosi
wyłącznie spoina pionowa.

• Otrzymujemy:

d

f

J

r

M













0

max













;

;

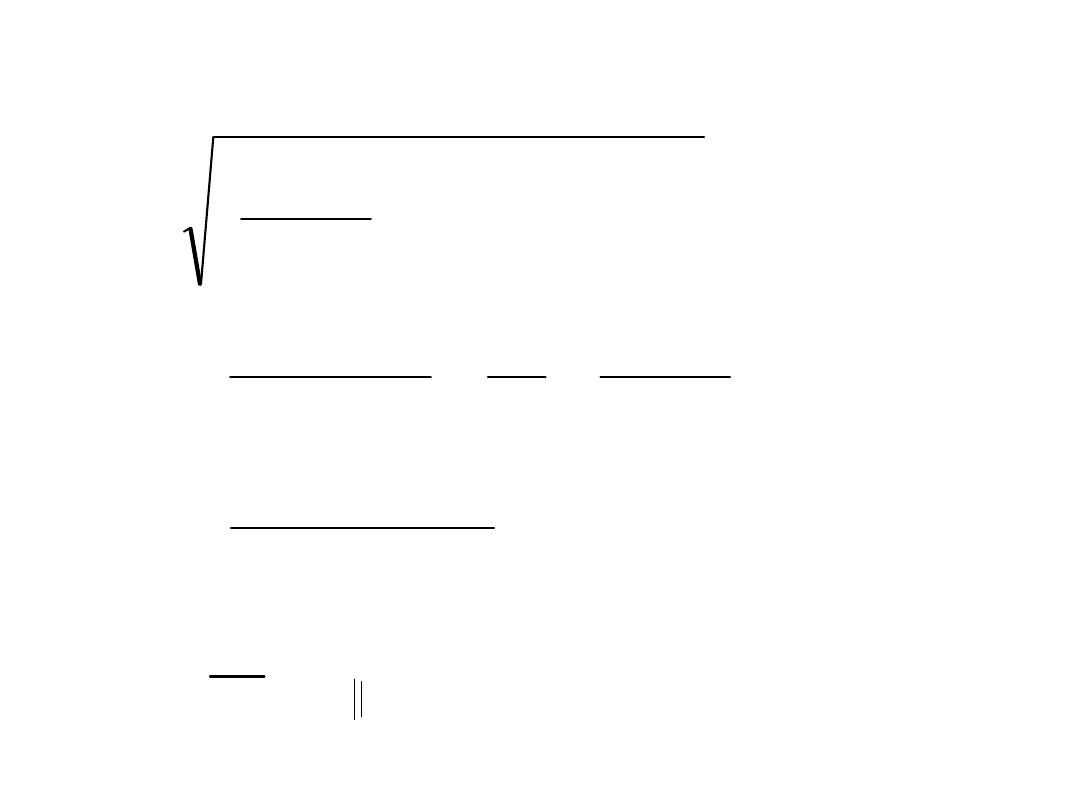
5

,

0

;

2

2

5

,

0

2

2

0

0

0

2

2

d

T

x

My

y

Mx

x

f

ac

T

J

a

r

M

a

c

J

M

J

a

r

M

a

r

a

c

r





















 

























 











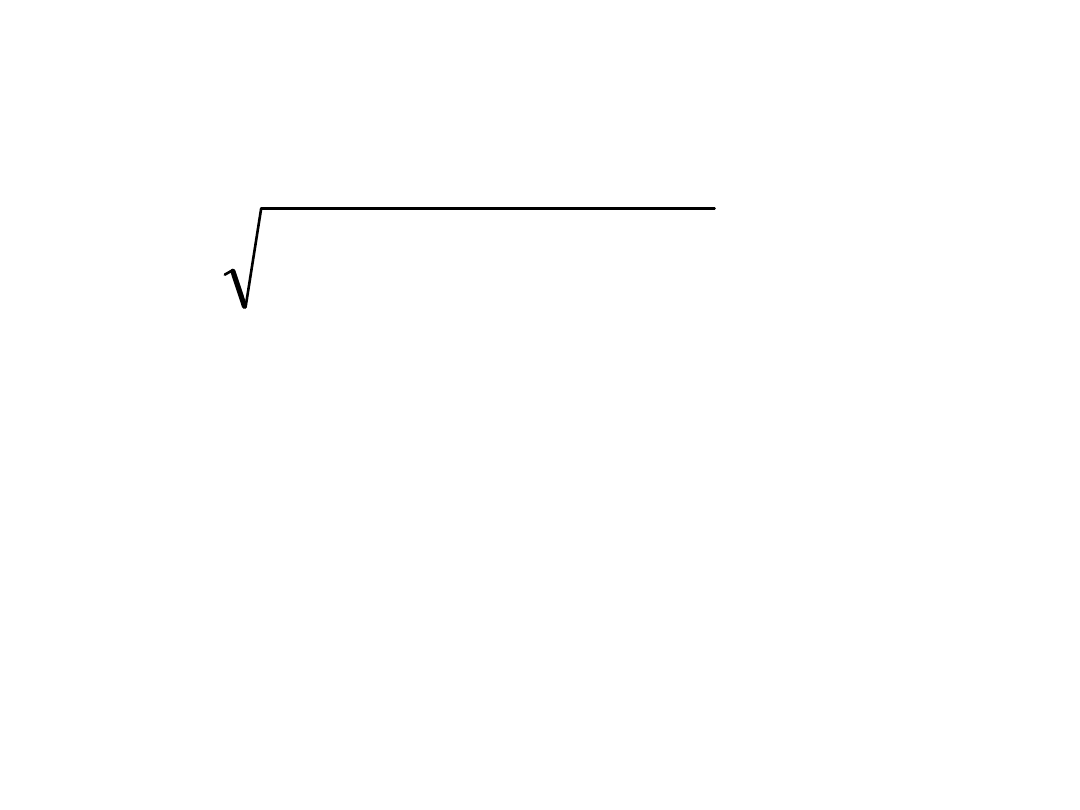
• Więc:





;

2

2

2

d

Mx

My

T

f























Tak można gdy:

;

40

;

10

mm

b

a

b





a spoiny wokół przewiązki ułożone
SA bez przerw w narożach

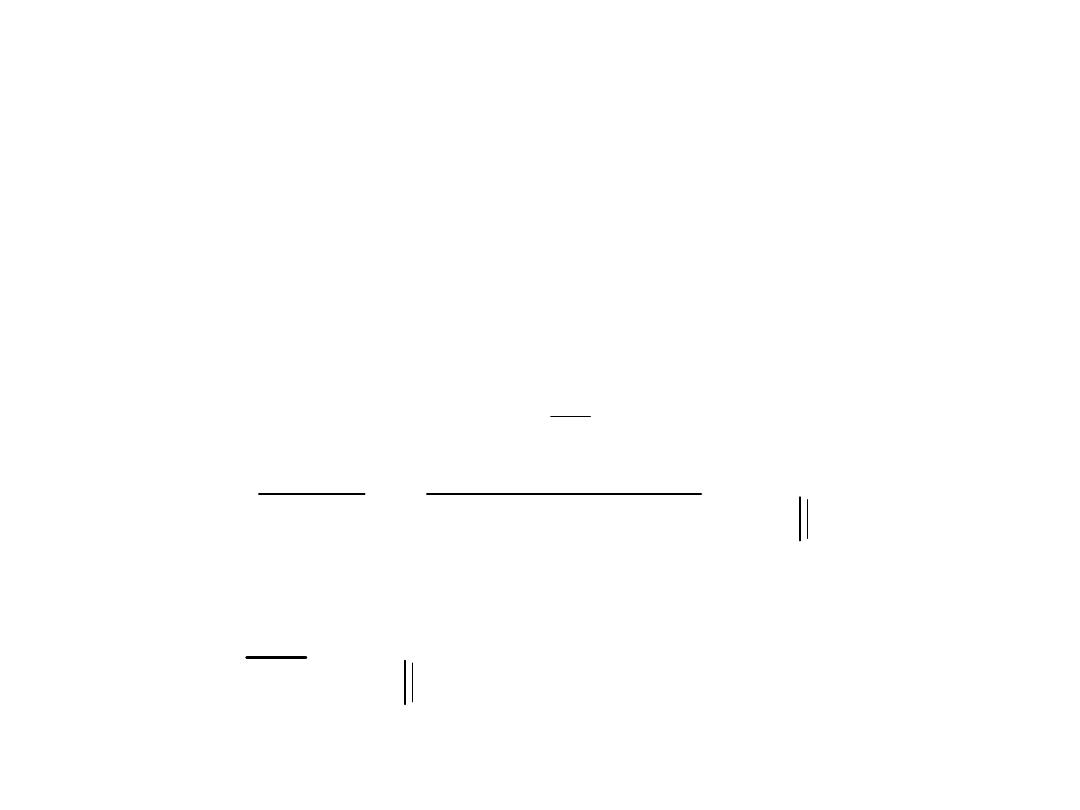
• W pozostałych przypadkach pomija

się spoiny poziome i uwzglednia
wyłącznie spoiny pionowe.

• Wtedy:

;

;

2

6

2

.

d

T

d

xśś

M

f

ac

T

f

ac

b

d

T

W

M





















 















• Ad b) W przypadku połączenia

przewiązek przewiązek gałęziami
słupów na spoine czołową,
naprężenia w spoinie czołowej należy
sprawdzac według wzorów:

;

3

6

2

2

2

d

x

f

tc

Td

tc

d

T

W

M













;

d

f

tc

T











;

2

2

d

z

f













































PROJEKTOWANIE BLACH

GŁOWICOWYCH I

STOPOWYCH

• Blachy stopowe przenoszą obciążenia

ze słupa na fundament.

• W naszym przypadku są to

obciążenia osiowe.

• Potrzebne pole podstawy blachy

stopowej można wyznaczyć ze
wzoru:

;

c

c

f

A

N







(&)

• gdzie:
• fc – wytrzymałość obliczeniowa

betonu da docisk podstawy słupa

• N – osiowa siła obliczeniowa od słupa
• A – pole blachy podstawy słupa
• fc=0,8f *cd;
• f *cd – wytrzymałość obliczeniowa

betonu fundamentu

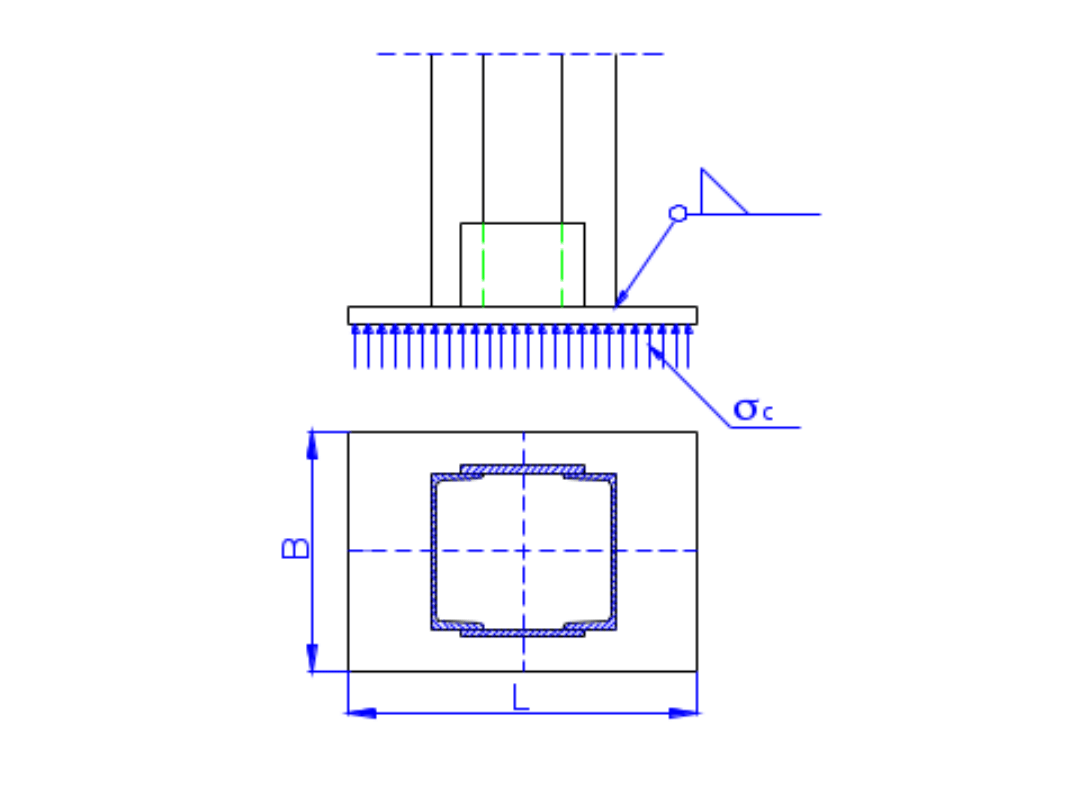
• Literatura podaje, że odległość krawędzi

blachy od środnika ceownika (nasz
przypadek) lub od półki dwuteownika
powinna być ~1 cm. Wtedy szerokość
blachy stopowej B wyniesie:

• B=s+2,0;
• s – wysokość ceownika (nasz przypadek)

lub szerokość półki dwuteownika

• Znając B, można ze wzoru (&) określić

długość blachy stopowej L

• W naszym przypadku odległość środnika

ceownika lub końców półek od krawędzi

blachy przyjmiemy 5÷10cm.

Odpowiednio zmieni się wtedy

szerokość i długość blachy stopowej

słupa.

• Jeżeli konstrukcja wykonywana jest w

renomowanej, atestowanej wytwórni, to

przy liczeniu naprężeń ścinających w

spoinie łączącej gałęzie słupa z blachą

stopową możemy zredukować siłę

pionową do 0,25N (nie o 25%, ale o 75%

!!)

• wtedy naprężenia ścinające spoinę

łączącą blachę z gałęziami można
określić ze wzoru:

;

)

25

,

0

(

d

f

l

a

N

N



















gdzie:
l – długość spoiny łączącej
blachę z gałęziami słupa
a – grubość spoiny

•Obliczenie grubości

blachy stopowej

• Wytnijmy z blachy beleczke

utwierdzona w środniku ceownika, o
szerokości 1 i wysokości równej
grubości blachy stopowej t. Długość
beleczki wynosi lx.

• Beleczka obciążona jest odporem

fundamentu σc.

• Moment utwierdzenia wynosi:

;

2

0

,

1

x

c

l

M









• Naprężenia w blasze stopowej można

określić wzorem:

;

W

M





ale jednocześnie dla beleczki
prostokątnej:

;

6

0

,

1

2

t

W





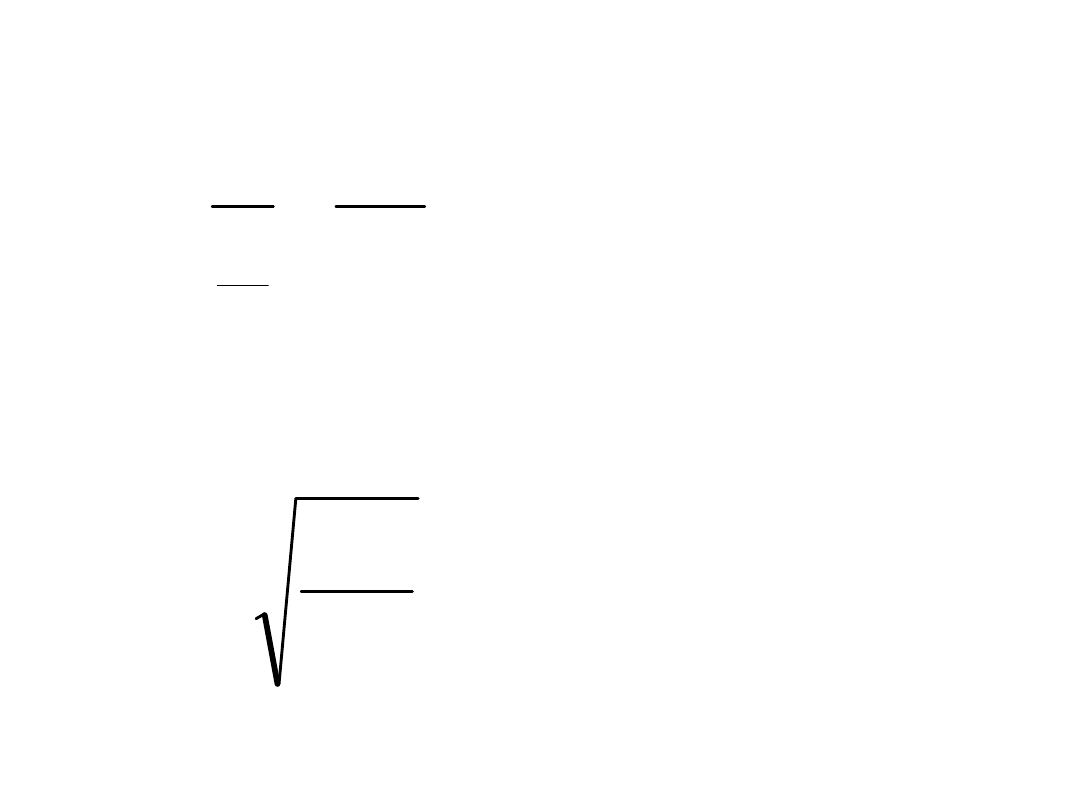
• więc naprężenia wynoszą:

;

6

6

2

2

d

f

t

M

t

M









stąd grubość blachy stopowej wyniesie:

;

6

d

f

M

t 

• W celu wzmocnienia blachy stopowej,

często stosuje się żebra usztywniające.

• Są to pionowe blachy spawane do

gałęzi słupa, które zwiększają
sztywność blachy stopowej.

• Żebra usztywniające sprawdza się na

siły wewnętrzne (momenty zginające i
siły poprzeczne) wywołane odporem
fundamentów, w najniekorzystniejszym
przekroju (a-a).

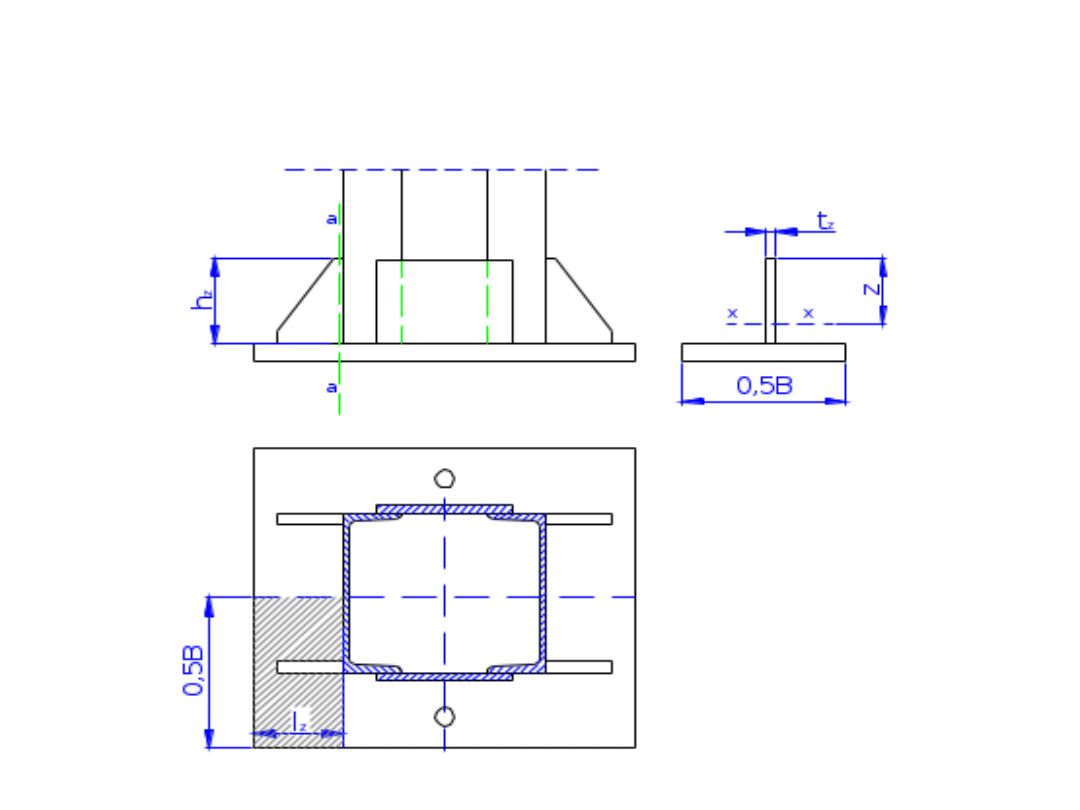
• Na rysunku poniżej zakreskowane pole jest powierzchnią

oddziaływania odporu fundamentów na jedno żeberko.

• Wartość momentów zginających w

przekroju a-a można obliczyć ze
wzoru:

;

4

2

5

,

0

2

z

c

z

z

c

a

a

l

B

l

l

B

M





















a wartość siły poprzecznej w przekroju
a-a ze wzoru:

;

5

,

0

c

z

a

a

l

B

Q











powyższe wzory wynikają z analizy rysunku powyżej.

• Naprężenia normalne:

x

a

a

J

z

M









gdzie:
Jx – moment bezwładności
przekroju żeberka i wycinka
blachy podstawy względem osi x-
x

• Naprężenia styczne oblicza się

według wzoru:

;

58

,

0

d

z

z

a

a

f

h

t

Q













Naprężenia zastępcze oblicza sie
według wzoru:

;

3

2

2

d

z

f













• W spoinach czołowych, łączących

żebra z gałęziami słupa (jeżeli
wystąpią):

• maksymalne naprężenia rozciągające

oblicza się ze wzoru:





;

d

x

z

a

a

sp

f

J

z

h

M



















• naprężenia ścinające:

;

d

z

z

a

a

sp

f

h

t

Q















Naprężenia zastępcze w przekroju
połączenia żeberka z blachą stopową:

;

2

2

d

sp

sp

z

f













































• Naprężenia zastępcze w poziomych

spoinach pachwinowych (łączących
blachę stopowa z blacha żeberka)
sprawdza sie według wzoru:





;

3

2

2

2

d

z

f























• jednocześnie musi zachodzić:

;

2

1

2

d

z

a

a

f

l

a

Q























oraz:

;

2

d

x

x

a

a

f

J

a

S

Q



















gdzie:
Sx – moment statyczny przekroju blachy
stopowej o szerokości 0,5B wzgledem osi
x