
Preludium do wstępu ze
skryptu streszczenia statystyki
medycznej w ujęciu
epidemiologicznym.

Wczesne wykrywanie chorób (bania
przesiewowe).
Przez badanie przesiewowe(przeglądowe ludności)
rozumiemy zastosowanie stosunkowo prostych i
niekosztownych testów diagnostycznych w badaniach
dużych ludności w celu wykrycia wczesnych stadiów
choroby.
Strategicznym celem badania przesiewowego jest
zmniejszenie chorobowości ( umieralności ) z powodu
określonej choroby wśród osób poddawanych tym
badaniom.
Przykładem choroby w której cel ten został osiągnięty
jest gruźlica.
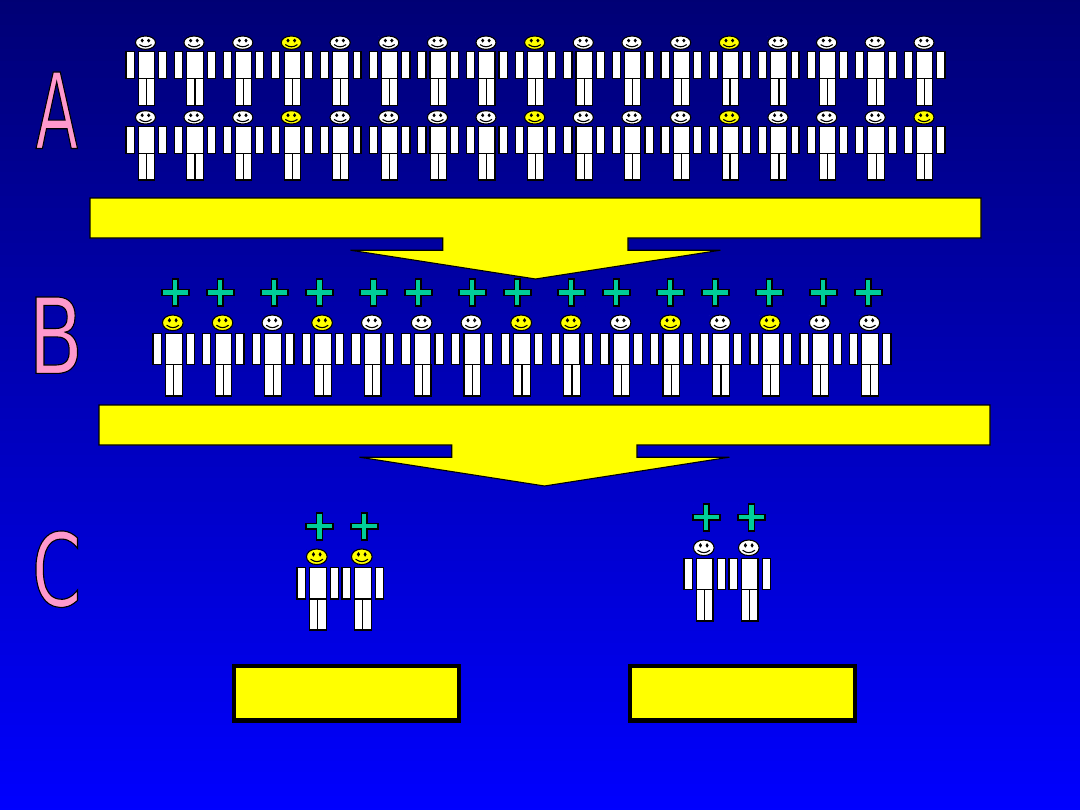
Test diagnostyczny zastosowany w badaniu
przesiewowym
Test diagnostyczny zastosowany w badaniu
przesiewowym
Leczeni
Nadzór
Procedura badania przesiewowego ludności
(screening).

Od strony proceduralnej badanie
przesiewowe dzieli badanych na dwie
grupy:
1. Osoby prawdopodobnie chore.
2. Osoby, u których choroba z dużym
prawdopodobieństwem została wykluczona.
Koncepcja testu przesiewowego różni się od
koncepcji
klinicznego badania diagnostycznego, które
klasyfikuje stan
zdrowia danej osoby ściśle według skali zdrowy –
chory.

Należy również rozróżnić badanie przesiewowe służące
wykrywaniu chorób, od badania zmierzającego do
określenia na tej podstawie grup ludności
zwiększonego ryzyka.
Najważniejszym praktycznym celem, jakiemu służą
masowe badania przesiewowe ludności , jest wykrycie
chorób w najwcześniejszym okresie ich rozwoju , aby
nie dopuścić do pełnego rozwoju choroby. W
przypadku chorób zakaźnych, jak np. gruźlica płuc,
mamy dodatkowe korzyści z wczesnego wykrywania
choroby. Wczesne rozpoznanie schorzenia pozwala nie
tylko na zapobieganie przeniesieniu się choroby na
osoby zdrowe na skutek likwidacji choroby przez
leczenie, lecz także prowadzi do wczesnego wykrycia
tego schorzenia u bliskich członków rodziny chorego.

Wybór choroby
Trzeba pamiętać że nie każda choroba nadaje się do
badań przesiewowych.
1. Przede wszystkim choroba musi mieć poważne
konsekwencje zdrowotne dla ludności , a objęta
badaniem populacja powinna być w pełni
świadoma tego faktu.
2. Choroba musi być wyleczalna.
3. Muszą istnieć dowody że podjęcie leczenia w
przedklinicznym stadium choroby będzie
skuteczniejsze niż leczenie zastosowane w
późniejszym stadium, kiedy chory zgłasza się do
lekarza.

Warunki uzasadniające podejmowanie badań
przesiewowych dla wykrycia chorób we
wczesnych stadiach:
1.
Choroba stanowi ważny problem społeczny.
2.
Naturalna historia choroby jest dobrze poznana.
3.
Istnieją skuteczne metody leczenia choroby.
4.
Występują wczesne objawy choroby.
5.
Metody diagnostyczne wczesnych stadiów choroby są
powtarzalne i trafne.
6.
Istnieje możliwość weryfikacji diagnostycznej rozpoznań.
7.
Metody badań przesiewowych są pozbawione ryzyka
powikłań i będą akceptowane przez badanych.
8.
Ustalone są zasady kogo należy zaliczyć do grupy chorych
wymagających leczenia.
9.
Wykrywanie wczesnych stadiów choroby będzie procesem
ciągłym.
10. Koszy wykrywania i leczenia są ekonomicznie uzasadnione
i możliwe do pokrycia z budżetu służby zdrowia.

Badania przesiewowe w ochronie zdrowia
publicznego
Choroby nowotworowe kwalifikują się szczególnie do badań
przesiewowych:
-Rak szyjki macicy.
-Rak sutka.
-Rak oskrzelopochodny.
-Rak okrężnicy.
-Rad żołądka.
-Nadciśnienie tętnicze krwi.
-Choroby naczyń wieńcowych.
-Cukrzyca.
-Jaskra.
-Gruźlica.
-Choroby przewlekłe oskrzeli.
-Badanie niemowląt i dzieci w wieku szkolnym.

Ocena wczesnych i odległych korzyści
zdrowotnych z badań przesiewowych
1. Częstość poszczególnych stadiów chorobowych
wykrytych w trakcie trwania badań.
2. Śmiertelność w okresie roku lub pierwszych
dwóch lat od chwili wprowadzenia programu
badań przesiewowych.
3. Porównanie umieralności.
4. Porównanie chorobowości.
5. Porównanie czasu przeżywalności.
6. Ocena metodą eksperymentalną (losowe badania
kontrolowane)
7. Ocena metodą obserwacyjną (porównanie
umieralności lub chorobowości u osób poddanych
badaniom przeglądowym z jakimś poziomem
oczekiwanym, choć wyniki tego rodzaju analizy
mają pewne ograniczenia.

Obliczenia statystyczne w epidemiologii
Pojęcie i stosowanie określeń „statystyka” i
„statystyka medyczna” nie jest jednoznaczne.
Wyróżnia się dwie grupy metod statystycznych:
-
Opis statystyczny (bierne podejście do zjawisk)
-
Metody biometryczne( czynne podejście do
zdarzeń)
Statystyka medyczna jako metoda biernej obserwacji
zjawisk zdrowotnych w populacji oraz niektóre
metody statystyczne stosowane w badaniach
bezpośrednich są w znacznym zakresie związane
z metodologią epidemiologiczną.
Najbliższa rzeczywistości w zakresie epidemiologii
jest definicja następująca: „Statystyka to dział
nauki o zbieraniu, gromadzeniu,
przechowywaniu, przetwarzaniu
(analizie) i ocenie danych liczbowych.”

Pojęcia statystyczne
Populacja (zbiór, zbiorowość) generalna – to w
sensie przyrodniczym skończona lub
nieskończona zbiorowość jednostek
statystycznych, ludzi ( zwierząt, przedmiotów,
zdarzeń zdrowotnych), których cechy ( opisowe
lub miarowe) są przedmiotem statystycznego
badania, celem określenia występujących w niej
prawidłowości ( rozkładu cech).
Jednostka statystyczna to pojedynczy osobnik lub ,
zdarzenie będące nośnikiem badanej cechy lub
częściej cech.
Cecha to ściśle określona właściwość jednostki
statystycznej.
Próba to część populacji generalnej często nazywana
reprezentacją, której badanie ma dostarczyć
informacji o całej populacji.
Zdarzenie losowe – jest to takie zdarzenie E, które
w warunkach F może zajść (mieć miejsce) lub
nie.
Zdarzenie (doświadczenie) niepowtarzalne –
jednorazowe (np. pomiar czasu świecenia
żarówki.)

Prawdopodobieństwo - jest to częstość powtarzania
się zdarzenia E w warunkachF, w stosunku do
wszystkich możliwych i wykluczających się
nawzajem przypadków w warunkach F.
P(E) = m/n
Gdzie:
P(E) – prawdopodobieństwo zdarzenia E,
m- liczba przypadków sprzyjających zdarzeniu E,
n- liczba wszystkich i nawzajem wykluczających się
przypadków w warunkach F.
Prawdopodobieństwo warunkowe to
prawdopodobieństwo zajścia zdarzenia E przy
określonym (założonym) warunku B (chory
wyzdrowieje E, jeśli będzie podany mu antybiotyk
B; jednak z określonym prawdopodobieństwem,
np.. 98/100).
P(E*B)=P(E)*P(B/F)=P(B)*P(E/B)

Ryzyko to prawdopodobieństwo wystąpienia jakiegoś
zdarzenia, najczęściej u osoby, lub zjawiska ,
najczęściej w populacji.
Zjawiska to przebieg niezależny od nas , lub celowo
prowadzona duża ilość takich samych zdarzeń
(doświadczeń) dotycząca jednostek tej samej
populacji.
Zmienna – ogólna nazwa każdej wielkości , która
zmienia się (lub jest zmieniana).
Częstość – liczba wystąpienia zdarzenia określonego
typu lub liczba jednostek określonej populacji ,
które należą do określonego przedziału wartości.
Wartość przeciętna ( synonim – wartość
oczekiwana) to , w przybliżeniu, miara sumy
wartości mierzalnej dzielonej przez liczbę
pomiarów dokonanych na jednostkach
statystycznych.

Współczynnik jest liczbą względną mianowaną ,
czyli określającą częstość zdarzeń
różnoimiennych w określonym czasie, np. liczbę
zmarłych w danym roku w stosunku do ogółu
ludności.
Wskaźnik jest liczbą względną niemianowaną ,
określającą częstość względnego udziału części
zdarzeń jednoimiennych w ich całości np. liczba
zgonów z powodu chorób nowotworowych w
stosunku do ogółu zgonów.
Grupy współczynników ( wskaźników)
Współczynnik natężenia – określa natężenie
zjawiska ( umieralność, urodzenia, zapadalność)
w populacji.
Współczynnik struktury – określa budowę
jwewnętrzną danego zjawiska , podawane są w
postaci odsetków całości np..3.400 osób zmarłych
– 51% z powodu chorób układu krążenia, 21% z
powodu nowotworów, itd...

Wskaźnik natężenia – określa natężenie zjawiska w
populacji
Wskaźnik poglądowości – określa stosunek ( w
odsetkach) aktualnej sytuacji np. liczby chorych na
zawał mięśnia sercowego w tym roku do lat
ubiegłych.
Wskaźnik normy (specjalny) – np. siła dźwięku
(hałasu) w decybelach , natężenie oświetlenia , itd....

Miary rozproszenia (miary zmienności)
Opisują rozrzut wartości opisywanej cechy w badanej
populacji.
Odchylenie standardowe i wariancja są
bezwzględnymi miarami rozproszenia , albo inaczej –
miarami zmienności , natomiast współczynnik
zmienności jest miarą względną , umożliwiającą
porównanie cechy w dwóch grupach lub rozproszenie
dwóch cech.

Załóżmy , że mamy dwie 20 osobowe grupy
pacjentów. W pierwszej grupie ciśnienie skurczowe
krwi u wszystkich badanych było równe i wynosiło
140 mm Hg. W drugiej grupie , u czterech pacjentów
120 , u dwóch 130, u ośmiu 140, u dwóch 150 i u
czterech 160 mm Hg. Mimo nasuwającego się
przypuszczenia , że grupy te różnią się między sobą ,
poznane miary nie wskazują na to. Analizując wyniki
otrzymane z badań obu grup stwierdzamy, że różnią
się one rozrzutem wokół średniej – w pierwszej
grupie wyniki są równe średniej, w drugiej są
rozrzucone wokół niej. W celu zmierzenia wielkości
tego rozrzutu stosujemy miary rozproszenia albo
dyspersji.
Wariację można obliczyć według wzoru:
S
2
=Σ(xi – xt)
2
/ n - 1
Xt – średnia
x-i – wartość cechy lub środek przedziału klasowego
n – liczbność przedziału klasowego
Odchylenie standardowe: S =
√
(Σ(xi – xt)
2
/ n - 1 )
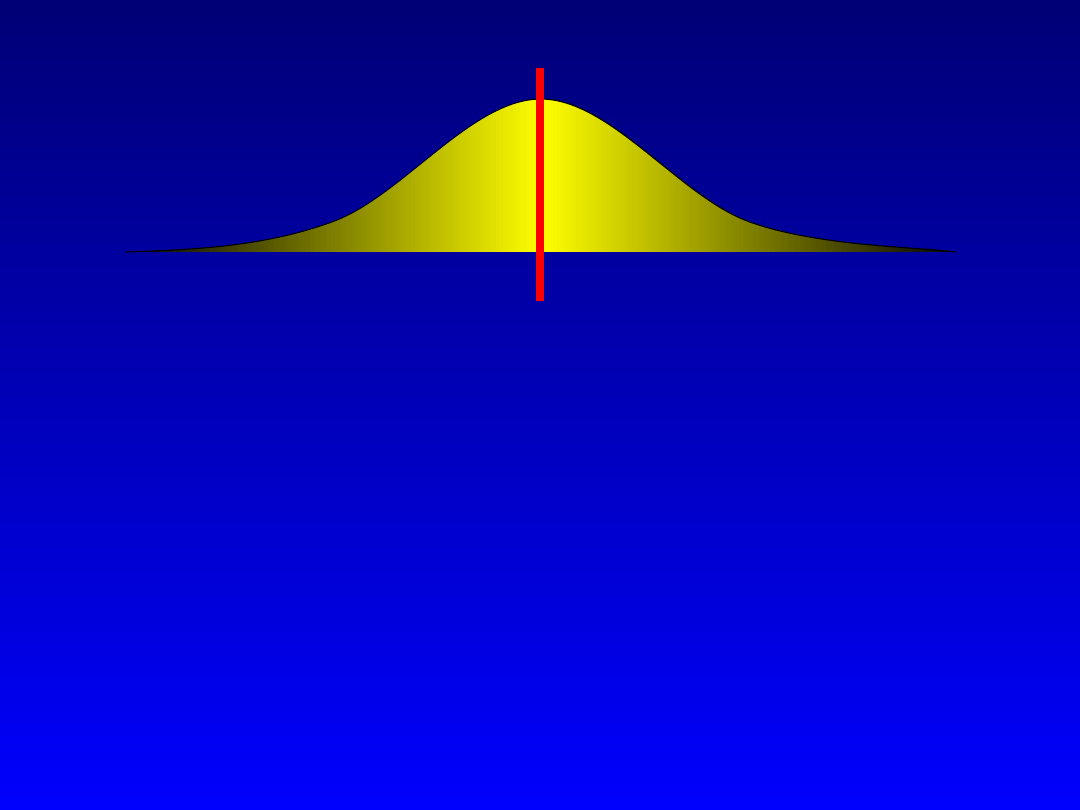
Rozkład normalny (Gauss i Laplace)
Rozkład normalny zdefiniował De Moivre w
1753 roku, jako rozkład graficzny rozkładu
dwumianowego. W badaniach biologicznych i
medycznych podstawowym rozkładem
prawdopodobieństwa jest rozkład normalny
opisywany przy pomocy zmiennych ciągłych, to
znaczy takich , które mogą przyjmować
dowolną wartość z pewnego przedziału.
Rozkład miar wszystkich jednostek jest
symetryczny względem wartości średniej
arytmetycznej tych miar.

Testy statystyczne
Do oceny podobieństwa i różnic w wartościach cech w jednej
lub w kilku porównywanych populacjach m. in. służą testy
statystyczne. Testy statystyczne dzielimy na grupy:
1. Testy parametryczne – stosujemy od analizy cechy
mierzalnej
2. Testy nieparametryczne – stosujemy do analizy cechy
niemierzalnej lub porównania cechy niemierzalnej z cecha
mierzalną.
Hipoteza - to oparte na logicznym rozumowaniu kompetentnej
osoby przypuszczenie mające na celu objaśnienie istnienia
pewnego zjawiska lub pojawienie się jakiegoś zdarzenia. W
medycynie dotyczy to najczęściej zjawiska zdrowotnego.
Hipoteza podstawowa , zerowa
Hipoteza alternatywna
Hipoteza parametryczna – precyzująca wartość parametru w
rozkładzie populacji generalnej znanego typu.
Hipoteza nieparametryczną – precyzującą typ rozkładu
populacji generalnej.

Testy statystyczne
Do oceny podobieństwa i różnic w wartościach cech
w jednej lub w kilku porównywanych populacjach
m. in. służą testy statystyczne. Testy statystyczne
dzielimy na grupy:
1. Testy parametryczne – stosujemy od analizy cechy
mierzalnej
2. Testy nieparametryczne – stosujemy do analizy
cechy niemierzalnej lub porównania cechy
niemierzalnej z cecha mierzalną.
Testy statystyczne w medycynie to sposoby
weryfikacji hipotez naukowych (doświadczenia)
lub epidemiologicznych (populacja) ,
wspomagające ustalenie , czy przypuszczenie
(hipoteza) jest prawdziwe czy fałszywe. Na
podstawie badania próby i uzyskanych wyników
podejmuje się decyzję o przyjęciu lub odrzuceniu
postawionej hipotezy. Decyzja taka może być
obarczona błędem pierwszego lub drugiego
rodzaju.

Hipoteza - to oparte na logicznym rozumowaniu
kompetentnej osoby przypuszczenie mające na
celu objaśnienie istnienia pewnego zjawiska lub
pojawienie się jakiegoś zdarzenia. W medycynie
dotyczy to najczęściej zjawiska zdrowotnego.
Hipoteza podstawowa , zerowa
Hipoteza alternatywna
Hipoteza parametryczna – precyzująca wartość
parametru w rozkładzie populacji generalnej
znanego typu.
Hipoteza nieparametryczną – precyzującą typ
rozkładu populacji generalnej.

Błąd pierwszego rodzaju – polega na
odrzuceniu testowanej hipotezy
prawdziwej, możliwy do popełnienia
przy statystycznej weryfikacji
hipotezy.
Błąd drugiego rodzaju – polega na
przyjęciu testowanej hipotezy
fałszywej, możliwy do popełnienia
przy weryfikacji hipotezy.

Planowanie analizy statystycznej
Przed rozpoczęciem badania epidemiologicznego
(doświadczalnego) należy dokładnie przemyśleć
plan stosowanych metod statystycznych i
informatycznych.
1. Cel badania i jego rodzaj – retrospektywne ,
prospektywne, obserwacyjne...
2. Definicję i opis badanej populacji. Przed
zastosowaniem metod analizy statystycznej należy
zebrać dokładne informacje o badanej grupie.
Prawidłowy opis populacji pozwala uniknąć
błędów i pomyłek podczas badania i jego analizy.
3. Określenie sposobu doboru próby – przy
badaniach reprezentacyjnych i doświadczalnych
4. Ustalenie liczebności reprezentacji
5. Określenie badanych zmiennych
6. Ustalenie skal pomiarowych

7. Ustalenie układu i wyglądu protokołu badań – z
uwzględnieniem kodowania danych do obliczeń przy
pomocy statystycznych programów komputerowych
8. Postawienie hipotez badawczych (zerowych i
alternatywnych) i związanych z nimi hipotez
statystycznych
9. Ustalenie narzędzi badawczych – (wzorów
matematycznych, metod obliczeniowych, rodzaju
bazy danych i in.)
10. Przewidywanie przedstawienia danych – tabele
źródłowe , wynikowe, ryciny.

Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
Wyszukiwarka
Podobne podstrony:
cwiczenie2 lek
Ćwiczenia lęk, Psychologia, psychologia stosowana I, emocje
FIZJOLOGIA gablota, Kalendarium wicze 2008-2009 LEK, Kalendarium ćwiczeń
Lęk, Psychologia, II rok, Psychologia emocji i motywacji - ćwiczenia - Lechowicz
ćwiczenie 2 -kolorymetryczne pomiary stęźeń roztworów, UMED Łódź Woj-lek, Chemia medyczna
Biologia ćwiczenia 1-15 ROK 2011-2012 LEK, Medycyna, Biologia medyczna
Maciek Miszczyk 1Ia lek 31 ćwiczenia
12 Rozklad cwiczen i wykladow Wojsk Lek
14 Karta cwiczen Wojsk Lek
3 ćwiczenia BADANIE asfaltów
Ćwiczenie7
W01(Patomorfologia) II Lek
Cwiczenia 2
Ćwiczenia V
metody redukcji odpadów miejskich ćwiczenia
więcej podobnych podstron