Jednoczynnikowa analiza

wariancji – podejście

eksploracyjne a podejście

konfirmacyjne

Wykład 3

Badanie 1 –

z Nieformalnego Słownika XXI wieku.

• After (ka): impreza, a raczej miejsce zgonu najbardziej

zagorzałych imprezowiczów. miejsce otwierane zazwyczaj w

godzinach wczesno porannych (4-6 rano), gdzie

nieprzytomna młodzież czeka, aż będzie mogła wyglądać na

tyle normalnie, aby wrócić do swoich domów

• Before(ka): To rodzaj aktywności "przed", czyli spotkanie w

gronie uczestników planowanego wyjścia, nim wyruszymy na

podbój lokalnych imprezowni. Często odbywa się w domu lub

innym przyjemnym lokalu. Jest miłym złego początkiem  i

często kończy się afterkiem. Zdarza się często, że beforka

zamienia się przedwcześnie w afterkę, co bywa kłopotliwe

zwłaszcza dla osoby udzielającej miejsca na taką beforkę.  

• Clubbing – nocna piesza wędrówka w terenie miejskim,

zwykle od klubu do klubu, połączona zwykle ze wzrostem

poziomu endorfin w mózgu na skutek rozmaitych aktywności

fizycznych (w tym tańca) oraz zażywania rozmaitych

substancji (w tym kanapek)

Badanie 1 – poziom endorfin

• Badacz postanowił sprawdzić, kiedy poziom

endorfin jest najwyższy. Zastosował więc

obserwację uczestniczącą i zmierzył

endorfiny będą na jednej beforce, jednej

afterce oraz podczas clubbingu. Ponieważ

poziom endorfin oznacza się w krwi, badacz

postanowił nie być okrrrrrutnym wampirem i

dokonywał tylko jednego pomiaru danej

osoby (wyodrębnił więc trzy grupy osób).

• Zmienne: niezależna – rodzaj imprezy,

zależna – poziom endorfin. Grupy były mało

liczne (każda 10 osób).

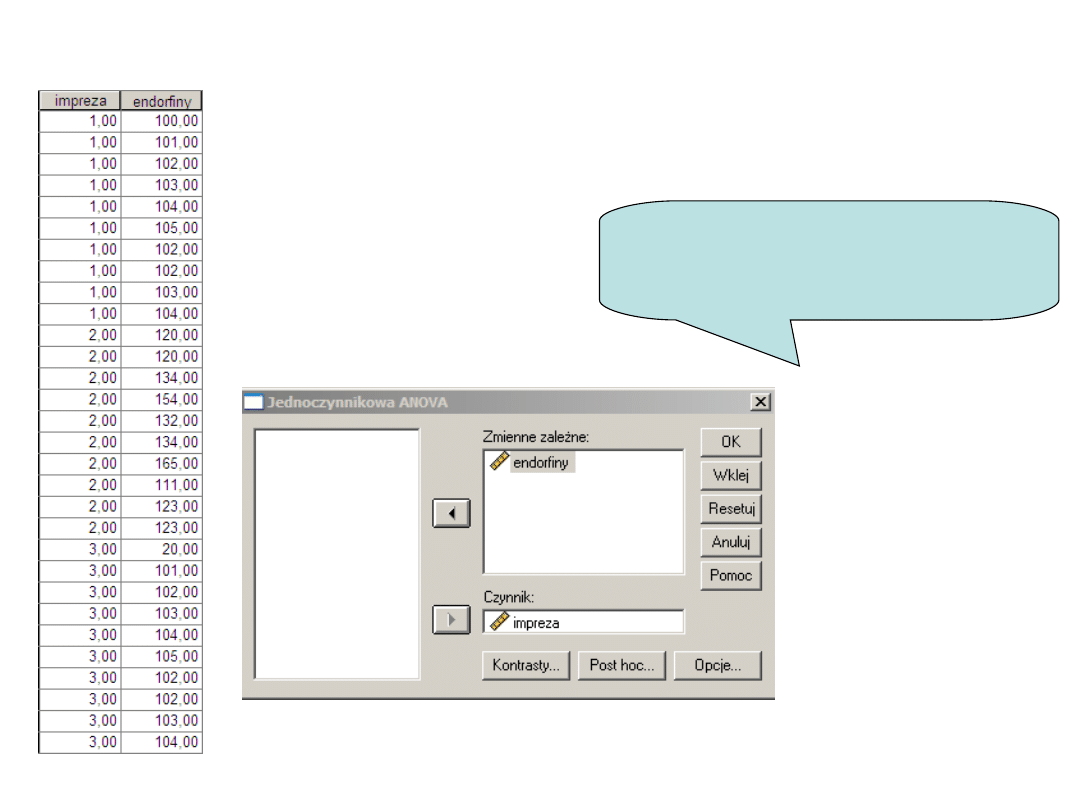
Dane i wykonanie analizy

wariancji

Definiujemy zmienne –

czynnik to zmienna

jakościowa – zmienna

zależna musi być ilościowa

Wyniki

Test jednorodności wariancji

endorfiny

3,459

2

27

,046

Test Levene'a

df1

df2

Istotność

Jednoczynnikowa ANOVA

endorfiny

3726,667

2 1863,333

3,612

,041

13929,200

27

515,896

17655,867

29

Między grupami
Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

endorfiny

10 102,6000
10 119,6000 119,6000
10

129,6000

,106

,334

10 102,6000
10 119,6000 119,6000
10

129,6000

,106

,334

impreza
beforka
afterka
clubbing
Istotność
beforka
afterka
clubbing
Istotność

Test
Studenta-Newmana-
Keulsa

a

Test Duncana

a

N

1

2

Podzbiór dla alfa = .05

Wyświetlane są średnie dla grup jednorodnych.

Wykorzystywana jest średnia harmoniczna wielkości próby = 10,000.

a.

Testujemy założenie o jednorodności wariancji

Wariancje niejednorodne 

Są różnice! 

F(2, 27)=3,612; p<0,05

Testy post hoc pokazują, że osoby na beforce

mają niższy poziom endorfin

niż Ci podczas clubbingu

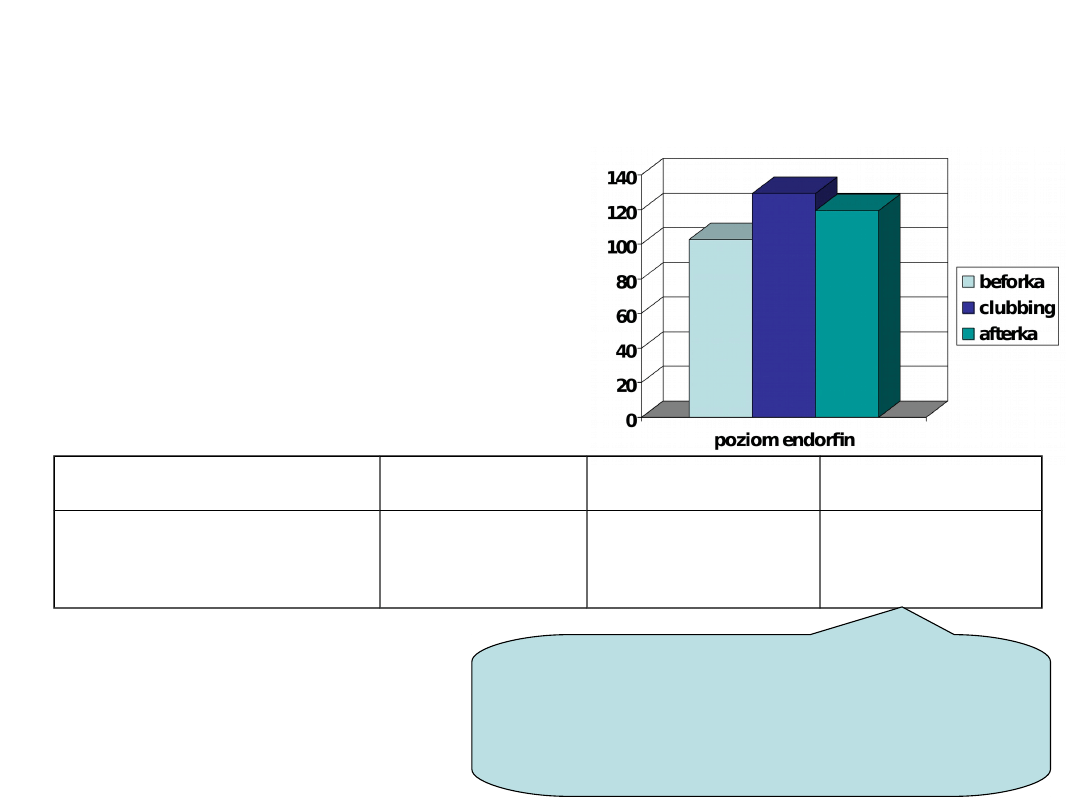
Opisujemy wyniki – Badanie 1A

Rodzaj imprezy

beforka

clubbing

afterka

Średni poziom

endorfin

102,6

a

129,6

b

119,6

ab

W opisie wyników
wykonujemy tabelkę ze
średnimi i indeksujemy je

Grupa badanych z afterki ma średni

poziom endrofin nie różniący się od

pozostałych grup więc jest oznaczona

podwójnym indeksem

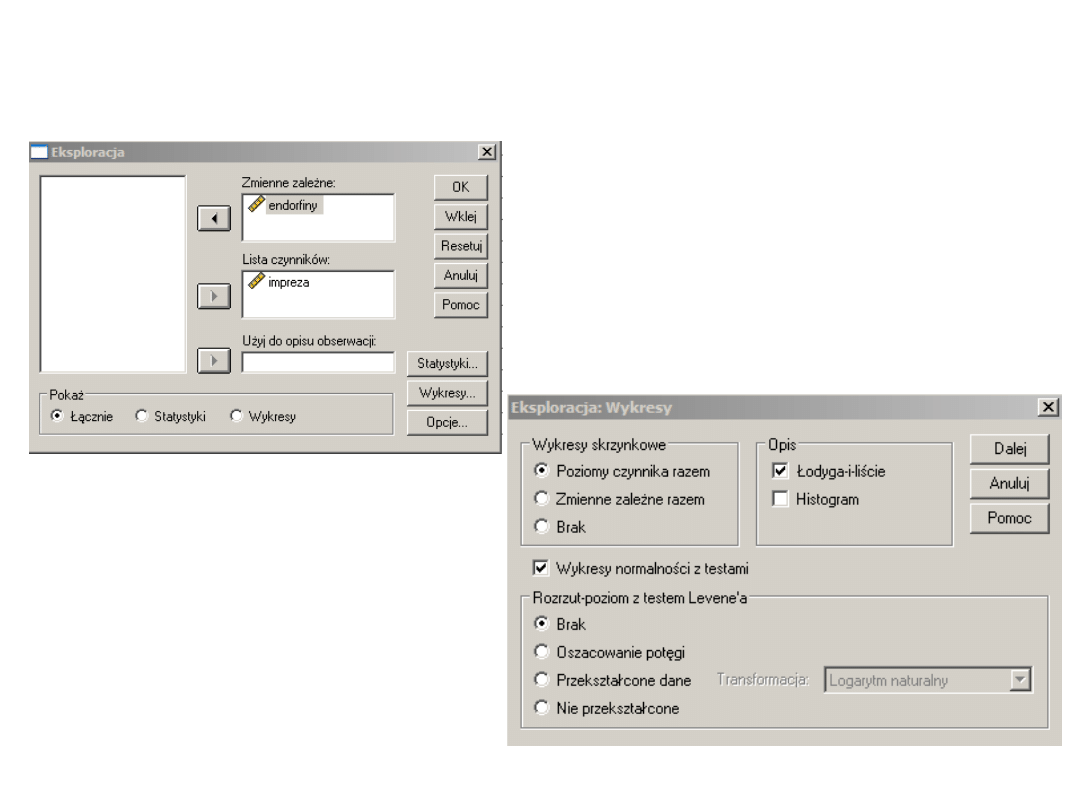
Beforka po afterce? – Dlaczego dobrze

jest oglądać zmienne PRZED analizą?

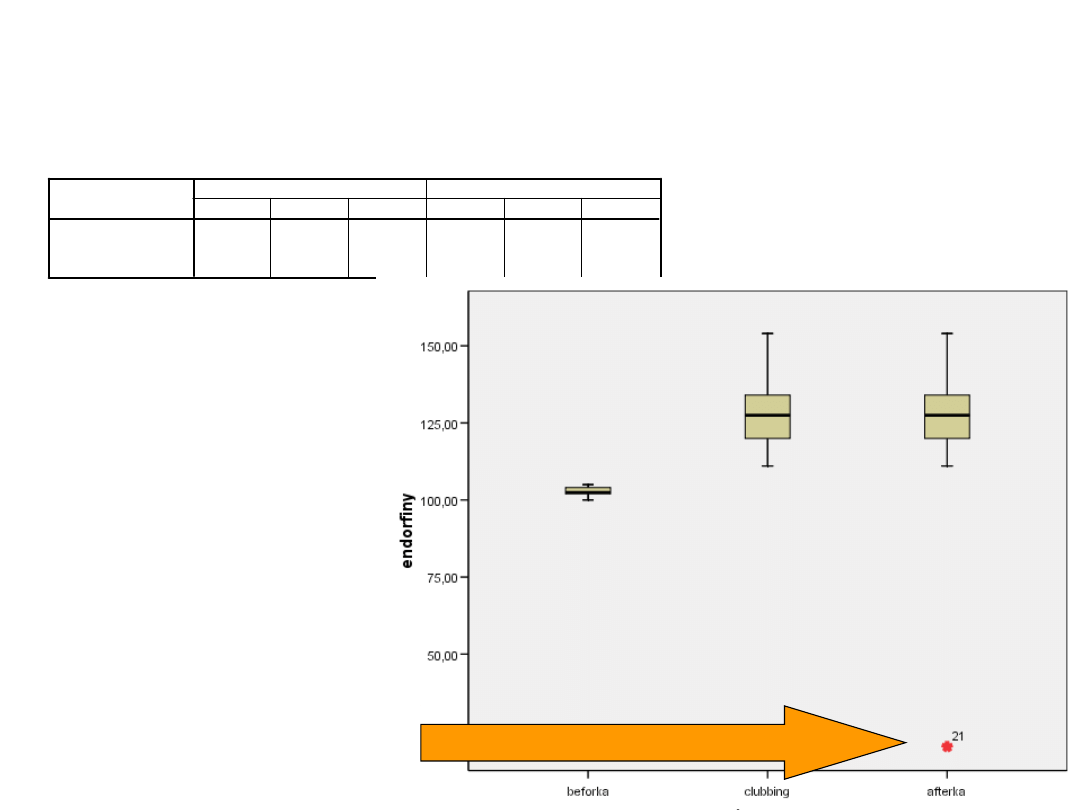
Oglądamy wykres

skrzynkowy

Testy normalności rozkładu

,155

10

,200*

,969

10

,886

,196

10

,200*

,946

10

,626

,308

10

,008

,693

10

,001

impreza
beforka
clubbing
afterka

endorfiny

Statystyka

df

Istotność Statystyka

df

Istotność

Kołmogorow-Smirnow

a

Shapiro-Wilk

Dolna granica rzeczywistej istotności.

*.

Z poprawką istotności Lillieforsa

a.

Uwaga na dewiantów

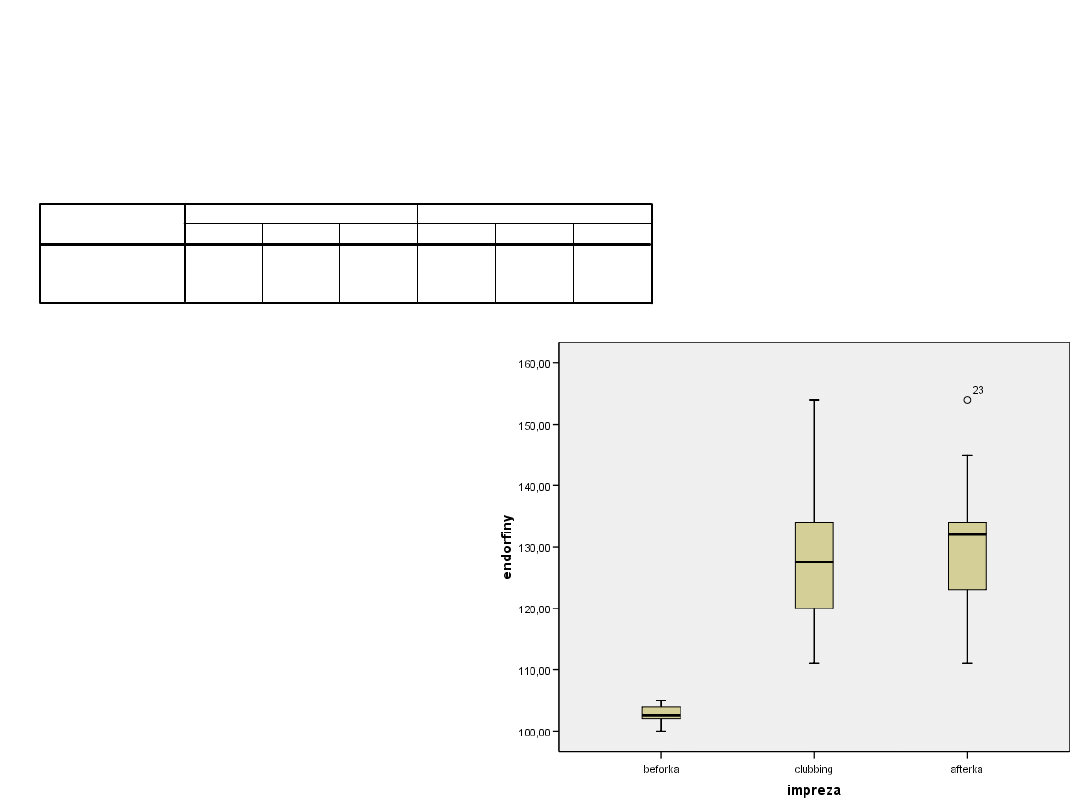
Usuwamy dewianta

Testy normalności rozkładu

,155

10

,200*

,969

10

,886

,196

10

,200*

,946

10

,626

,178

9

,200*

,965

9

,846

impreza
beforka
clubbing
afterka

endorfiny

Statystyka

df

Istotność Statystyka

df

Istotność

Kołmogorow-Smirnow

a

Shapiro-Wilk

Dolna granica rzeczywistej istotności.

*.

Z poprawką istotności Lillieforsa

a.

Wyniki po usunięciu dewianta

Test jednorodności wariancji

endorfiny

7,417

2

26

,003

Test Levene'a

df1

df2

Istotność

Jednoczynnikowa ANOVA

endorfiny

4962,028

2 2481,014

22,192

,000

2906,800

26

111,800

7868,828

28

Między grupami
Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

endorfiny

10 102,6000
10

129,6000

9

130,6667

1,000

,826

10 102,6000
10

129,6000

9

130,6667

1,000

,826

10 102,6000
10

129,6000

9

130,6667

1,000

,976

impreza
beforka
clubbing
afterka
Istotność
beforka
clubbing
afterka
Istotność
beforka
clubbing
afterka
Istotność

Test
Studenta-Newmana-
Keulsa

a,b

Test Duncana

a,b

Test Scheffe

a,b

N

1

2

Podzbiór dla alfa = .05

Wyświetlane są średnie dla grup jednorodnych.

Wykorzystywana jest średnia harmoniczna wielkości próby = 9,643.

a.

Liczebności grup nie są równe. Użyta została średnia harmoniczna
liczebności grup. Poziom błędu I rodzaju nie jest zagwarantowany.

b.

Testujemy założenie o jednorodności wariancji

Wariancje wciąż niejednorodne 

Są różnice! 

F(2, 26)=22,192; p<0,05

Efekt znacznie silniejszy!!

Testy post hoc pokazują inny wzorzec.

Osoby na beforce

mają niższy poziom endorfin

niż Ci podczas clubbingu i afterki.

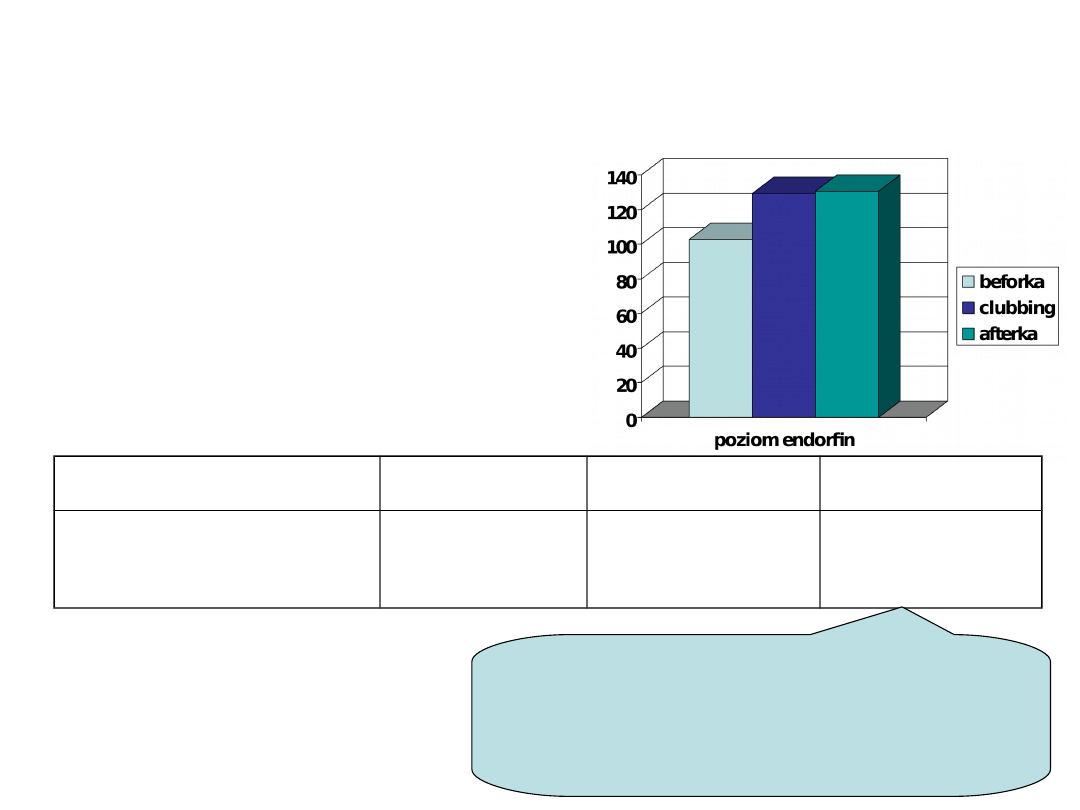
Opisujemy wyniki – Badanie 1B

Rodzaj imprezy

beforka

clubbing

afterka

Średni poziom

endorfin

102,6

a

129,6

b

130,6

b

W opisie wyników
wykonujemy tabelkę ze
średnimi i indeksujemy
je.

Grupa badanych z afterki ma średni

poziom endrofin nie różniący się od

pozostałych grup więc jest oznaczona

podwójnym indeksem

Istotność i jej związek z liczbą osób

badanych

Im więcej osób badanych tym mniejszy
poziom istotności. Tak więc sam poziom
istotności nie jest dobrą miarą porównań
badań robionych na różnych ilościach osób
badanych.

Aby porównywać wyniki pochodzące z
różnych badań potrzebna jest statystyka
niezależna od liczby osób.

R

2

– procent wyjaśnionej wariancji

R

2

= SS między/ SS całkowita

R

2

=

Mając zatem standardowy zapis APA możemy
obliczyć ile wynosi R

2

, które informuje nas jaki

zakres zmienności zmiennej zależnej wyjaśnia
nasz czynnik - zależy nam oczywiście na tym,
żeby czynnik wyjaśniał jak najwięcej wariancji,
czyli 100%.
Przykład: F (2, 90)= 4; p<0,05

(F) (df
między)

(F) (df między) + df
wewnątrz

Siła efektu

R

2

=0,21

21% wyjaśnionej wariancji

R

2

=0,60

60% wyjaśnionej wariancji

Badanie 1A

F(2, 27)=3,612; p<0,05

Badanie 1B

F(2, 26)=22,192; p<0,05

W badaniu po usunięciu dewianta maleje ilość wariancji całkowitej –
tej którą chcemy wyjaśnić. Na tym tle udaje nam się wyjaśnić więcej
niż przed usunięciem dewianta.

Istotność i jej związek z liczbą osób badanych-

wydruki

R

2

= SS między/ SS całkowita

Wydruk 1 - 30 osób: R

2

=3726/17655=0,21 21%

Wydruk 2 – 71 osób R

2

=11180/52967=0,21 21%

Jednoczynnikowa ANOVA

endorfiny

11180,000

2 5590,000

11,638

,000

41787,600

87

480,317

52967,600

89

Między grupami
Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Jednoczynnikowa ANOVA

endorfiny

3726,667

2 1863,333

3,612

,041

13929,200

27

515,896

17655,867

29

Między grupami
Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Dane

rzeczywiste

Dane

skopiowane

Hipoteza dotycząca różnic między więcej niż dwiema grupami

Wystąpią różnice w wydajności pracy w zależności od rodzaju

muzyki prezentowanej w czasie wykonywania zadania

Hipoteza

niekierunkowa:

Wystąpią różnice...

Wybór: analiza
wariancji

Hipoteza

kierunkowa:

Słuchający muzyki

klasycznej będą bardziej

wydajni

Testy post hoc

Porównania a

posteriori

Znany

kształt

zależnoś

ci

Nieznany

kształt

zależności

Wielomiany

Porównania

planowane –

kontrasty

Porównania a priori

Porównania a posteriori a porównania a

priori

• Porównania a posteriori (testy post hoc)

są techniką eksploracyjną, gdy okaże się,

że są różnice eksplorujemy je za pomocą

testów post hoc.

– O ich przeprowadzaniu badacz decyduje po

wstępnej analizie danych, która może mu

wskazać celowość takich porównań.

• Porównania a priori (zwane też

porównaniami planowanymi), planuje się

przed przeprowadzeniem eksperymentu.

– Bezpośrednio związane z teorią, na której

opiera się eksperyment.

Całkowita wariancja naszych danych

Wariancja wyjaśniona

Wariancja międzygrupowa

Wariancja kontrolowana

Wariancja niewyjaśniona

Wariancja wewnątrzgrupowa

Wariancja błędu

Logika analizy wariancji

• Prawie w każdym eksperymencie mamy grupę

kontrolną, dlatego

– prawie zawsze wykonywanie kontrastów zaczynamy

od porównania grupy kontrolnej z
eksperymentalnymi (chyba, że mamy inne hipotezy)

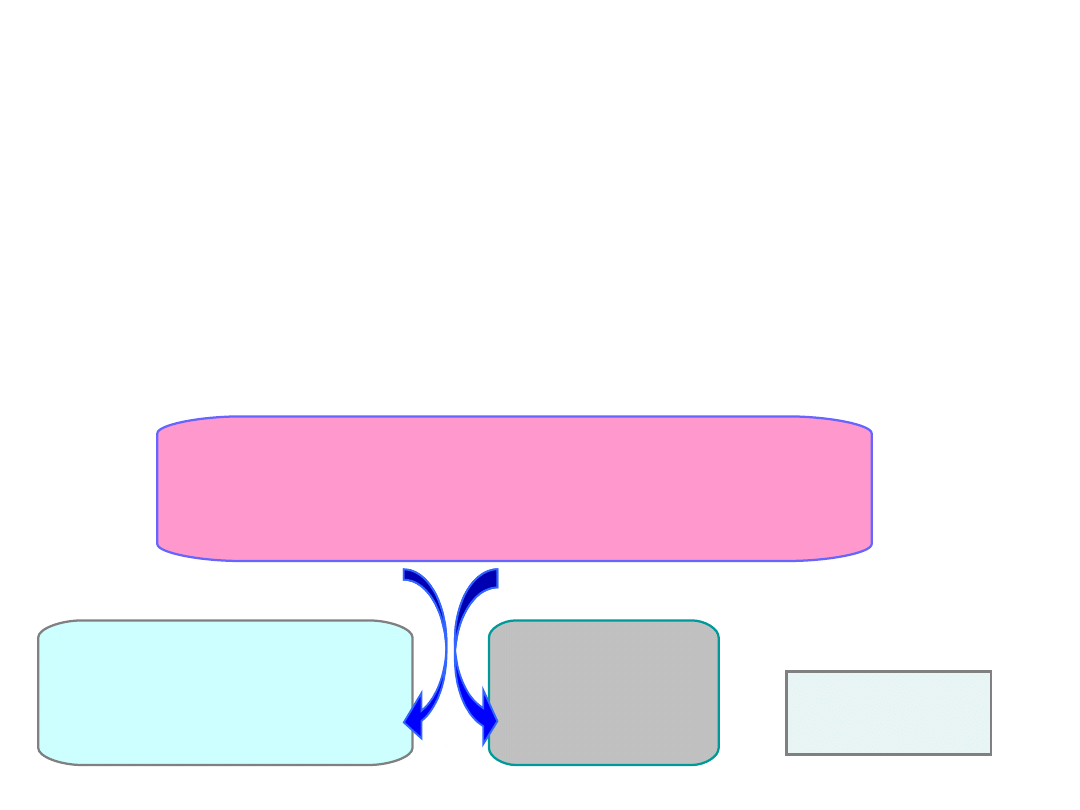
Logika kontrastów

Wariancja międzygrupowa

Trzy grupy: E1, E2 i K1

Wariancja E1, E2

Wariancja

K1

Porównani
e 1

Definiowanie kontrastów poprzez

wagi.

W przykładowym eksperymencie mamy 3 grupy.

Chcemy porównać grupy 1 i 2 z trzecią.

Hipoteza zerowa musi zakładać, że średnie są

sobie równe. Załóżmy, że hipoteza ta jest

prawdziwa a wszystkie średnie mają wartość

równą 10.

M1 i M2 przeciwstawiamy M3
Program statystyczny potrzebuje jednak zapisu

matematycznego.

A zatem próbujemy zapisać hipotezę zerową w

postaci (10 + 10) – 10 = 0

To niestety matematycznie nie jest prawda.

Musimy zatem dodać wagi kontrastu.

(1* 10 + 1*10) - 2 *10 = 0

Definiowanie kontrastów poprzez

wagi

Wobec tego nadajemy każdej grupie odpowiednie wagi

posługując się następującymi zasadami:

1. Grupy, które tworzą jedną paczkę średnich mają

współczynniki kontrastu o tym samym znaku i tej

samej wartości

2. Musimy skontrastować te grupy, które porównujemy

– nadajemy im wagi o przeciwnych znakach.

3. Suma wag w każdym porównaniu musi wynosić

zero.

4. Grupy, które pomijamy otrzymują wagę równą zero.

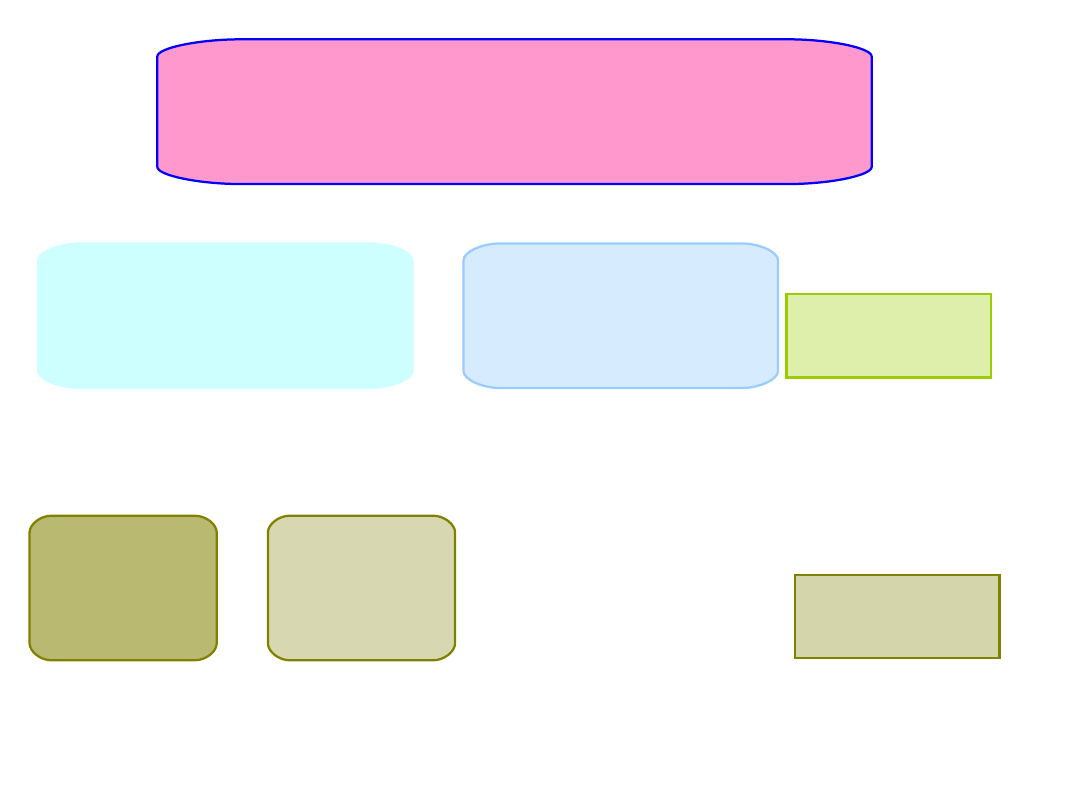
Wariancja wyjaśniona przez eksperyment

Trzy grupy: E1, E2 i K1

Wariancja wyjaśniona

przez E1, E2

+

Wariancja

wyjaśniona przez K1

-

Wariancja

wyjaśniona

przez E1

Wariancja

wyjaśniona

przez E2

Porównani
e 1

Porównani
e 2

E1: +1 E2:
+1

K1: -2

(+1)+ (+1)+(-2)
= 0

E1: +1
E2: -1

K1: 0

+

-

(+1)+ (-1)+(0) =
0

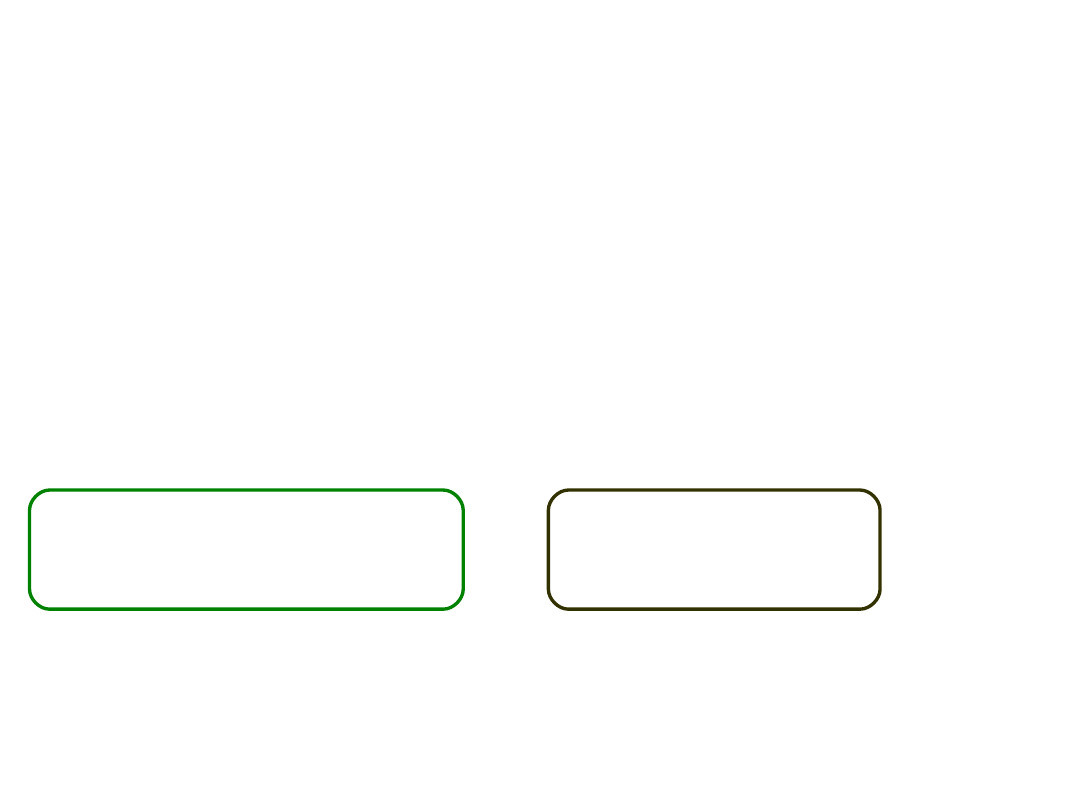
Przykład

• W badaniu nad skutecznością czekolady środka

podnoszącego sprawność umysłową przeprowadzono

badanie, w którym porównywano osoby przyjmujące

niskie i wysokie dawki specyfiku z grupą kontrolną

oraz placebo.

• Jakie wagi dla pierwszego kontrastu porównującego

obie grupy eksperymentalne z dwiema kontrolnymi?

Grupa E1 Grupa E2

Wysokie dawki Niskie dawki

Grupa K1 Grupa K1

Nic Placebo

vs
.

+1 +1 -1 -1
kontrast 1

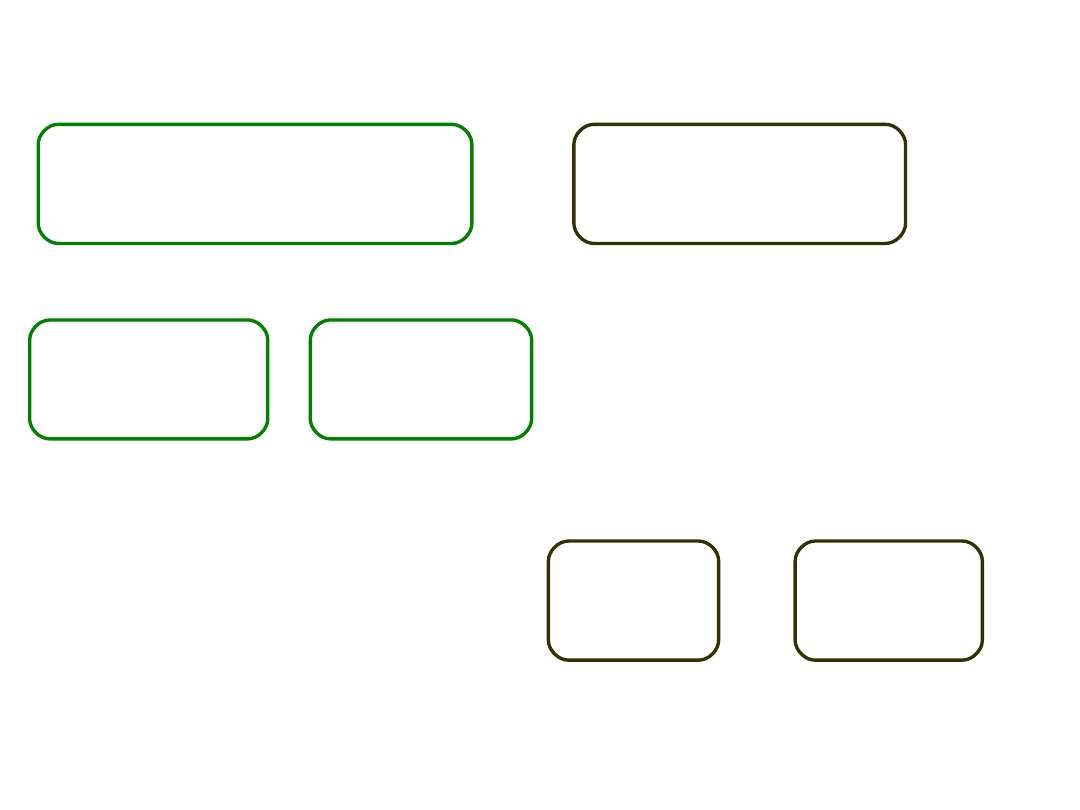
Jakie dalsze porównania

możliwe?

Grupa E1 Grupa E2

Wysokie dawki Niskie dawki

Grupa K1 Grupa K1

Nic Placebo

vs
.

+1 -1 0
0 kontrast 2

Grupa E2

Niskie dawki

Grupa E1

Wysokie dawki

vs
.

Grupa K1

Placebo

Grupa K1

Nic

vs
.

0 0 +1
-1 kontrast 3

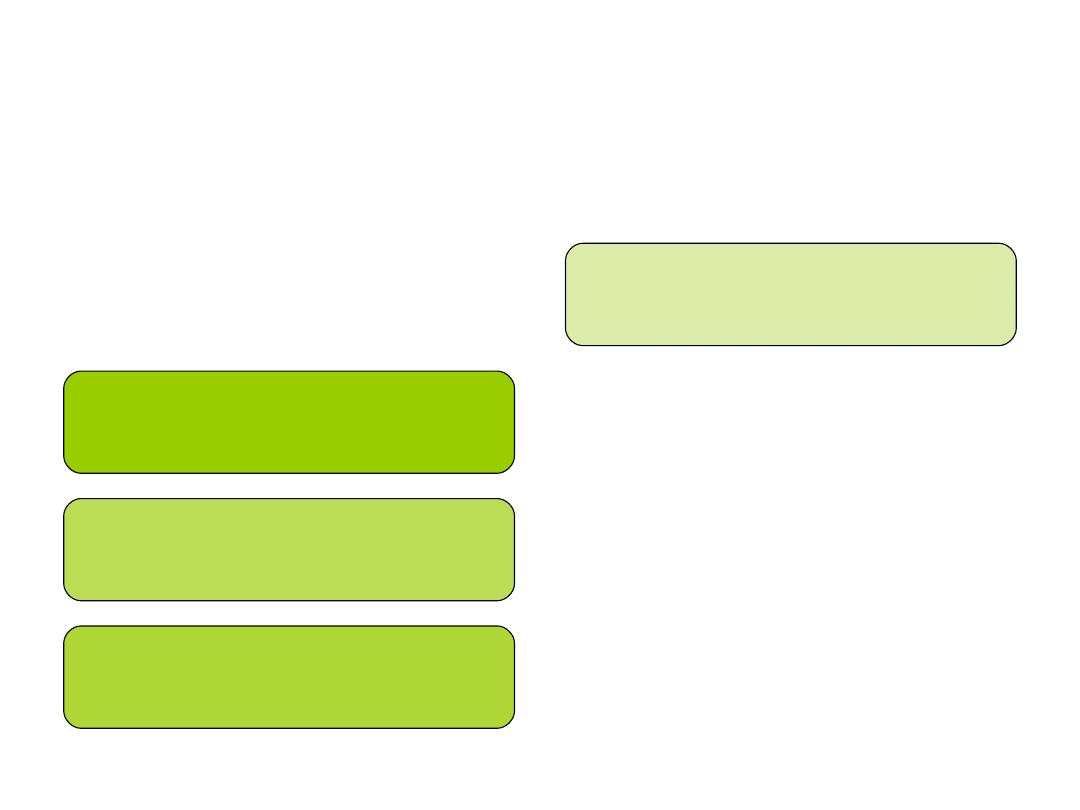
Mamy pięć grup
Jak zdefiniować kontrast, gdy chcemy

porównać grupę drugą z trzecią i piątą?

0, 2, -1, 0, -1

0, 4, -2, 0, -2

0, -1, 0,5, 0, 0,5

0, -10, 5, 0, 5

Ortogonalność kontrastów

• Jak sprawdzić czy kolejne wykonywane

porównania są od siebie wzajemnie

niezależne, czyli ortogonalne

• Przemnażamy przez siebie współczynniki

kontrastu odpowiednio dla każdej grupy

• Suma iloczynów powinna wynosić zero –

jeśli nie, kontrasty nie są ortogonalne

Czy poniższe kontrasty są

niezależne?

Porównujemy średnie pochodzące z

czterech grup: osób lubiących jazz,

muzykę klasyczną, rock i pop pod

względem ekstrawersji

Jeżeli pierwszy kontrast:
1, 1, 1, -3

(która grupa jest przeciwstawiana

którym?)

To pozostałe, które są ortogonalne:
1, 1, -2, 0
1, -1, 0, 0

Przykład 1

• 1, 1, 1, -1,5, -1,5

(trzy pierwsze z dwiema

ostatnimi)

• -1, 1, 0, 0, 0
-1 1 0 0 0 iloczyny
Suma iloczynów: 0

Przykład 2

• 2, 0, -1, -1
• 1, -1, 0, 0
2 0 0 0 iloczyny
Suma iloczynów: 2

Niezależn

e

Nie są

niezależne

Jeżeli będziemy w ten sposób

postępować (czyli wykonywać
porównania niezależne), to liczba
możliwych (niezależnych,
ortogonalnych) kontrastów wyniesie:

k-1

k oznacza liczbę grup

Podsumowanie

Zawsze wybieramy sensowne porównania –
• możemy bowiem porównywać tylko dwie „porcje”

wariancji (gdy w „porcji” więcej niż jedna grupa –

porównujemy średnią z tych grup)

• Jeżeli wykonujemy więcej niż jeden kontrast –

porównania powinny być niezależne (ortogonalne)

Porównywane grupy mają

przeciwny znak

współczynnika

Wartości współczynników dla średnich w tej samej

podgrupie muszą być

takie same

Grupy, które są

wyłączone

z porównań mają

wagę zero

Suma współczynników

w danym kontraście zawsze

równa

zero

Mnożenie / dodawanie

• Analiza kontrastów pozwala przemnażać

średnie przez pewne współczynniki, ale nie ma

możliwości dodawania niczego do średnich.

• Możemy sprawdzać, czy dochód mężczyzn jest

2 razy większy niż dochód kobiet, ale nie

sprawdzamy (przy użyciu kontrastów), czy

mężczyźni zarabiają o 500 złotych więcej niż

kobiety.

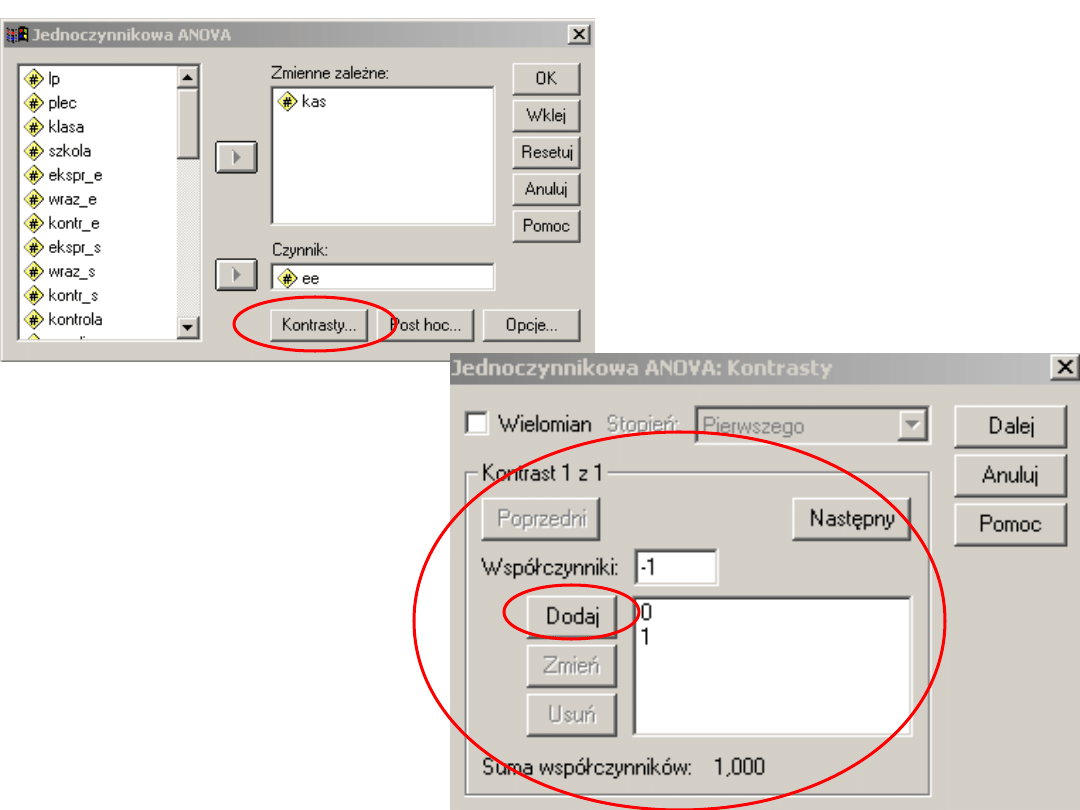
Jak definiować w SPSS?

Współczynniki
kontrastu
wprowadzamy
kolejno klikając
DODAJ

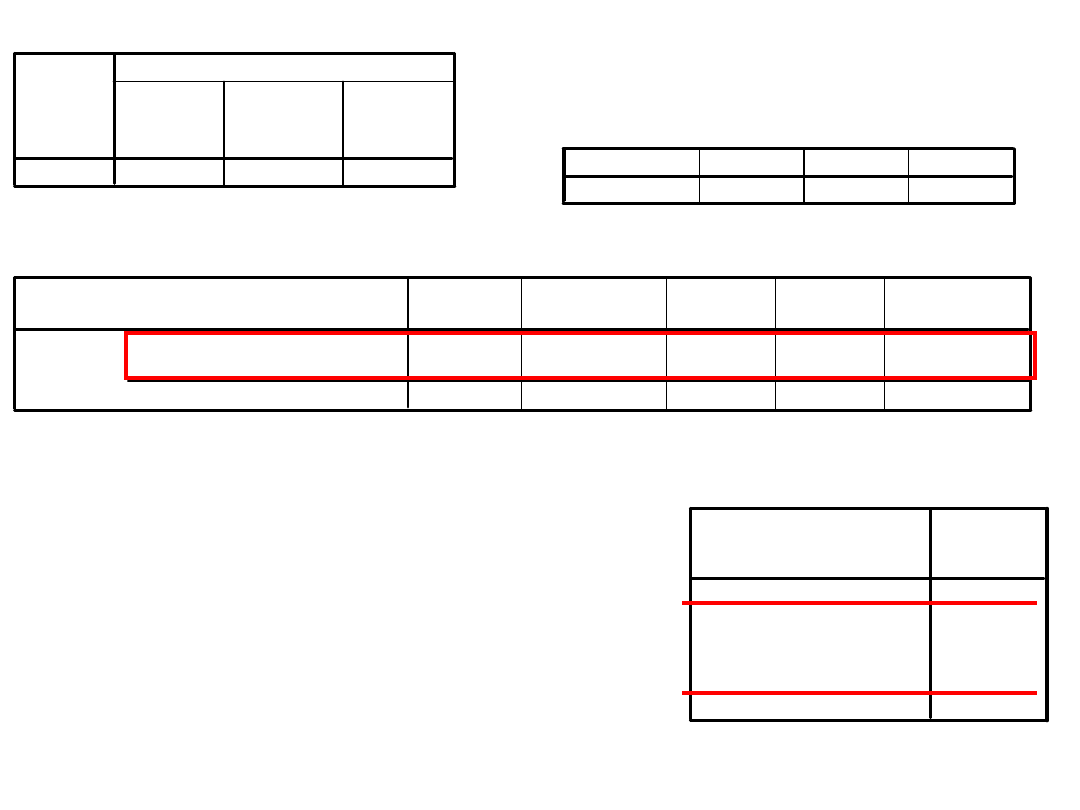
Wydruk

Współczynniki kontrastu

-1

0

1

Kontrast
1

niska

ekspresy

wnosc

przeciętna

ekspresyw

nosc

wysoka

ekspresy

wnosc

EE

Testy kontrastu

-2,8935

1,21084

-2,390

264

,018

-2,8935

1,24807

-2,318

123,797

,022

Kontrast
1

1

Założenie o
równości wariancji
Brak założenia o
równości wariancji

PASYWNY

Wartość

kontrastu

Błąd

standardowy

t

df

Istotność

(dwustronna)

Test jednorodności wariancji

PASYWNY

,134

2

264

,875

Test Levene'a

df1

df2

Istotność

Test Levene’a wskazuje, że
wariancje są homogeniczne, więc
wydruk odczytujemy z górnego
wiersza. Wynik zapisujemy tak, jak
standardowy test t Studenta
t(264)=2,39; p<0,05. Teraz jeszcze
informacja o średnich, by
zinterpretować wynik.

Statystyki opisowe

PASYWNY

29,6935

28,2286

26,8000
28,2210

niska ekspresywnosc
przeciętna
ekspresywnosc
wysoka ekspresywnosc
Ogółem

Średnia

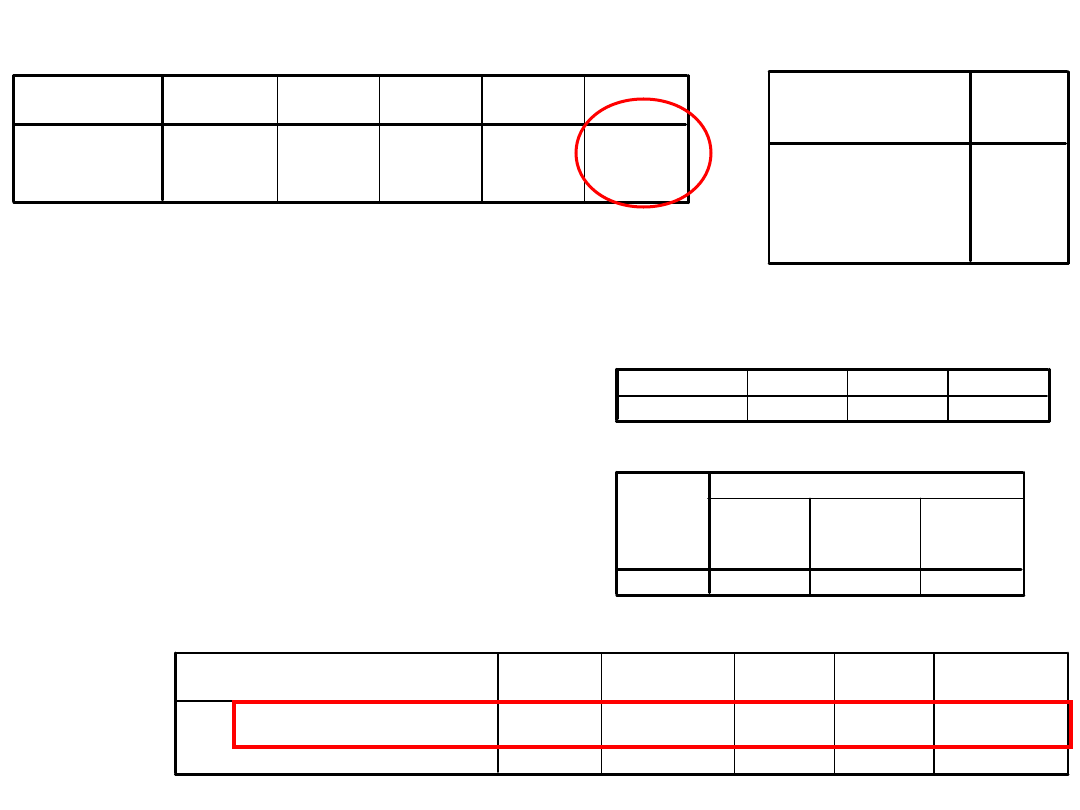
Statystyki opisowe

KAS

24,9710

25,2500

26,3043
25,4371

niska ekspresywnosc
przeciętna
ekspresywnosc
wysoka ekspresywnosc
Ogółem

Średnia

• Analiza wariancji

nie pokazała
istotnych wyników
a kontrast
porównujący dwie
skrajne grupy tak!

Współczynniki kontrastu

-1

0

1

Kontrast
1

niska

ekspresy

wnosc

przeciętna

ekspresyw

nosc

wysoka

ekspresy

wnosc

EE

Testy kontrastu

1,3333

,67801

1,967

283

,050

1,3333

,67100

1,987

136,000

,049

Kontrast
1

1

Założenie o
równości wariancji
Brak założenia o
równości wariancji

KAS

Wartość

kontrastu

Błąd

standardowy

t

df

Istotność

(dwustronna)

Jednoczynnikowa ANOVA

KAS

72,066

2

36,033

2,272

,105

4488,301

283

15,860

4560,367

285

Między grupami
Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Test jednorodności wariancji

KAS

,021

2

283

,979

Test Levene'a

df1

df2

Istotność

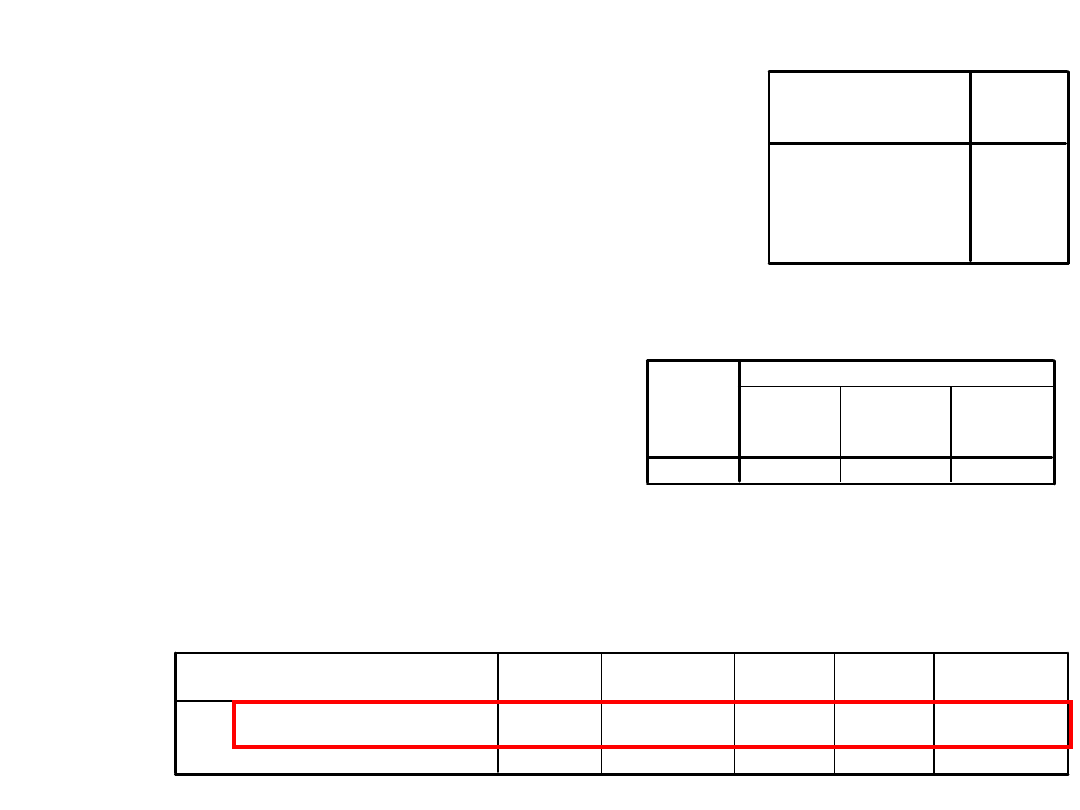
Statystyki opisowe

KAS

24,9710

25,2500

26,3043
25,4371

niska ekspresywnosc
przeciętna
ekspresywnosc
wysoka ekspresywnosc
Ogółem

Średnia

Jak jest liczona statystyka t?

Aby obliczyć statystykę t trzeba

podzielić wartość kontrastu
przez błąd standardowy.
Wartość kontrastu jest liczona
w ten sposób, że średnie
grupowe są mnożone przez
współczynniki kontrastu a
następnie sumowane.

24,97 * (-1) + 25,25 * 0 + 26,3 *

1=

26,3 - 24,97 = 1,333

Współczynniki kontrastu

-1

0

1

Kontrast
1

niska

ekspresy

wnosc

przeciętna

ekspresyw

nosc

wysoka

ekspresy

wnosc

EE

Testy kontrastu

1,3333

,67801

1,967

283

,050

1,3333

,67100

1,987

136,000

,049

Kontrast
1

1

Założenie o
równości wariancji
Brak założenia o
równości wariancji

KAS

Wartość

kontrastu

Błąd

standardowy

t

df

Istotność

(dwustronna)

• Problem badawczy
Czy można na pierwszy rzut oka określić kto jest

twórczy a kto nie? Badania Galtona (wiek XIX)

• Badacz zmierzył badanym ochotnikom obwód

głowy oraz iloraz inteligencji testem Ravena.
Poszukiwał różnic między osobami o małej i
dużej głowie w zakresie inteligencji.

Kiedy Anova jest lepsza

od testu t-Studenta?

Zmienne i schemat badania

• Zmienna niezależna – wielkość głowy
Pomiar – może być różny – ilościowy, gdy w centymetrach, porządkowy, gdy podzielimy

ludzi na dwie lub trzy grupy ze względu na wielkość głowy

• Zmienna zależna
Pomiar - gdy iloraz inteligencji mierzony w punktach skali mamy do czynienia ze skalą

ilościową, jeśli przeliczymy wyniki surowe na steny redukujemy skalę do porządkowej

• Schemat międzygrupowy
Mierzymy obwód głowy a potem na jego podstawie dzielimy ludzi do grup. Można to zrobić

na różne sposoby:

• Podział na dwie grupy po medianie - wykonujemy wtedy test t-Studenta

• Podział na trzy grupy – tercyle - dwie możliwości obliczeń:

– porównanie skrajnych grup testem T-Studenta

– porównanie wszystkich trzech grup Anovą

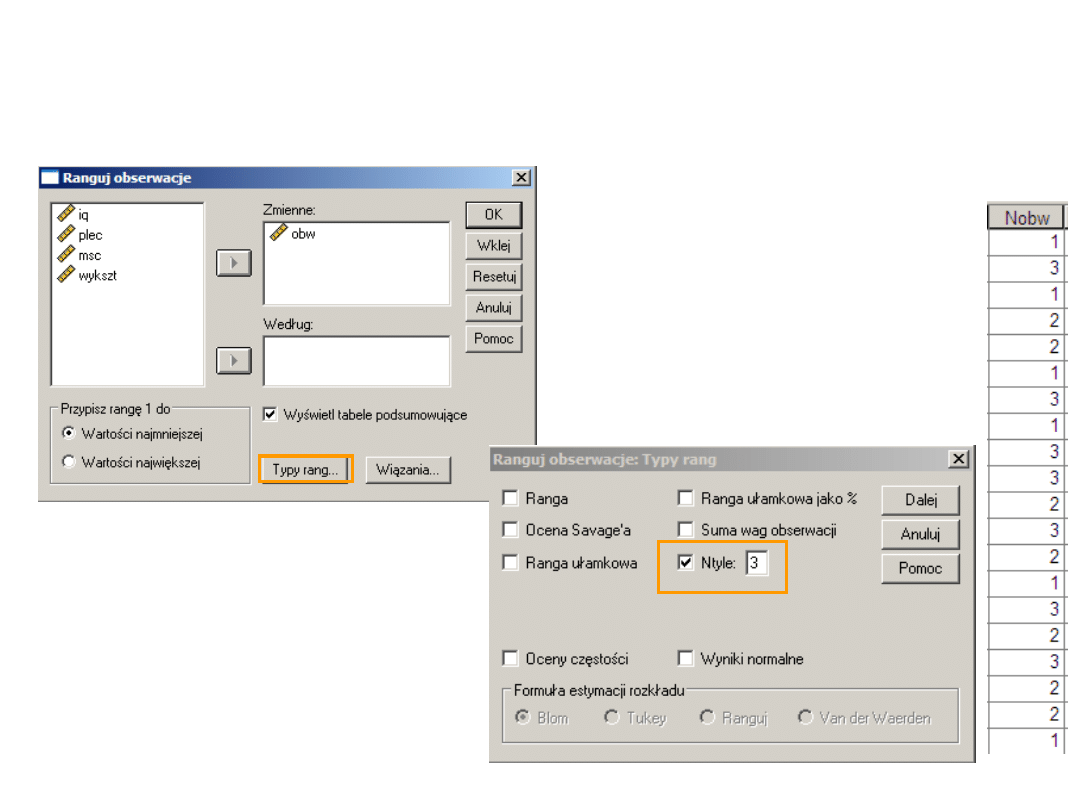
Pierwszy wariant obliczeń

Podział na równoliczne grupy - Ntyle

Dzielimy osoby badane
na trzy grupy – osoby o
małej, przeciętnie dużej
oraz dużej głowie.

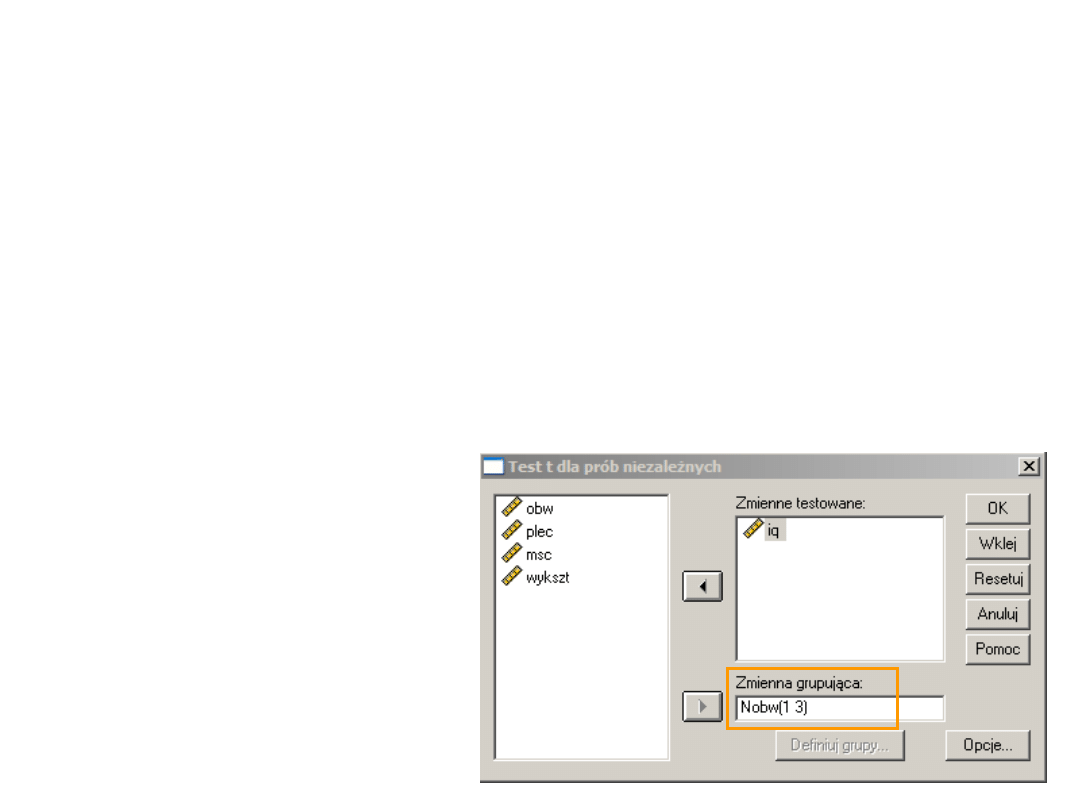
Pierwszy wariant obliczeń – Test t-

Studenta

Obawiając się, że wyniki mogą nie być

wyraziste kontrastujemy tylko
skrajne grupy – osoby o małej i dużej
głowie

• Obliczamy test t-Studenta dla prób

niezależnych

Test t-Studenta – porównujemy dwie skrajne grupy – osoby o

małej i dużej głowie pod względem ilorazu inteligencji

Brak istotnych statystycznie różnic

Test dla prób niezależnych

,012

,913

,612

14

,550

,612

13,998

,550

Założono równość
wariancji
Nie założono
równości wariancji

IQ

F

Istotność

Test Levene'a

jednorodności

wariancji

t

df

Istotność

(dwustronna)

Test t równości średnich

Statystyki dla grup

8 102,8750
8 102,2500

NTILES of GLOWA
1
3

IQ

N

Średnia

Osoby o małej

głowie

Osoby o dużej

głowie

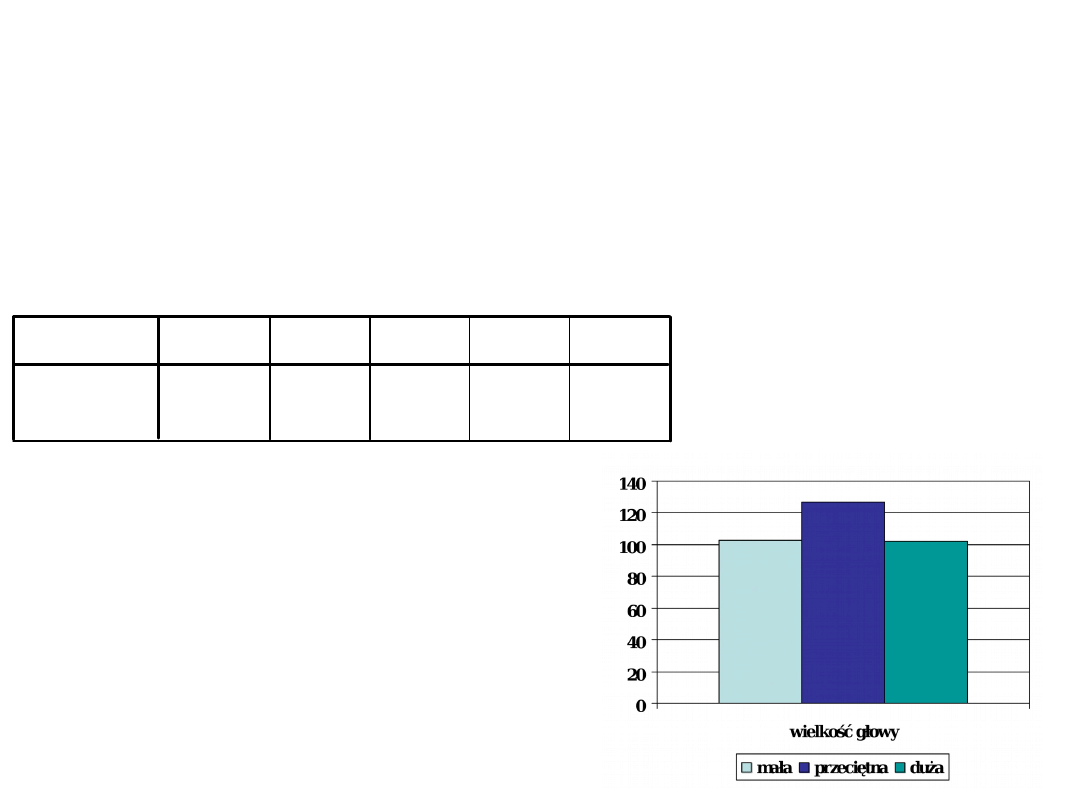
Robimy analizę wariancji gdzie czynnikiem jest wielkość

głowy a zmienną zależną iloraz inteligencji. Jeśli weźmiemy

pod uwagę

trzy grupy

zobaczymy, że związek jest

krzywoliniowy i dlatego nie okazał się istotny w teście t.

Jednoczynnikowa ANOVA

IQ

3285,083

2 1642,542

45,611

,000

756,250

21

36,012

4041,333

23

Między grupami
Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność