Porównania post hoc a porównania

a’priori

• Porównania a posteriori są techniką

eksploracyjną, gdy okaże się, że są

różnice eksplorujemy je za pomocą

testów post hoc.

– O ich przeprowadzaniu badacz decyduje po

wstępnej analizie danych, która może mu

wskazać celowość takich porównań.

• Porównania a priori (zwane też

porównaniami planowanymi), planuje się

przed przeprowadzeniem eksperymentu.

– Bezpośrednio związane z teorią, na której

opiera się eksperyment.

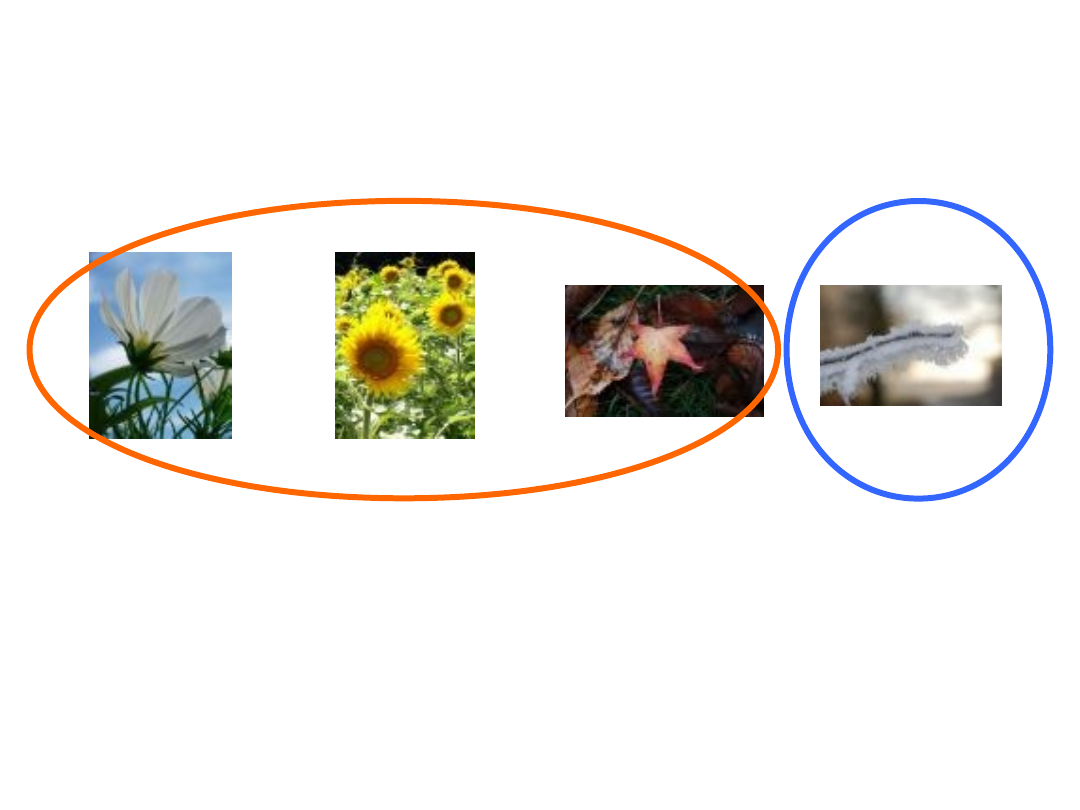
Hipoteza 1 – porównanie 1

G 1

G 2

G 3

G 4

Hipoteza 1: Zima wywołuje inne emocje niż pozostałe pory
roku

Idea współczynników (wag) kontrastów

• Jeśli chcemy porównać trzy grupy z jedną to

trzeba tę jedną doważyć poprzez odpowiedni
współczynnik kontrastu. Hipoteza zerowa zakłada
bowiem, że te trzy średnie będą się równały tej
trzeciej.

Definiowanie kontrastów poprzez

wagi

Wobec tego nadajemy każdej grupie odpowiednie wagi

posługując się następującymi zasadami:

1. Grupy, które tworzą jedną paczkę średnich mają

współczynniki kontrastu o tym samym znaku i tej

samej wartości

2. Musimy skontrastować te grupy, które porównujemy

– nadajemy im wagi o przeciwnych znakach.

3. Suma wag w każdym porównaniu musi wynosić

zero.

4. Grupy, które pomijamy otrzymują wagę równą zero.

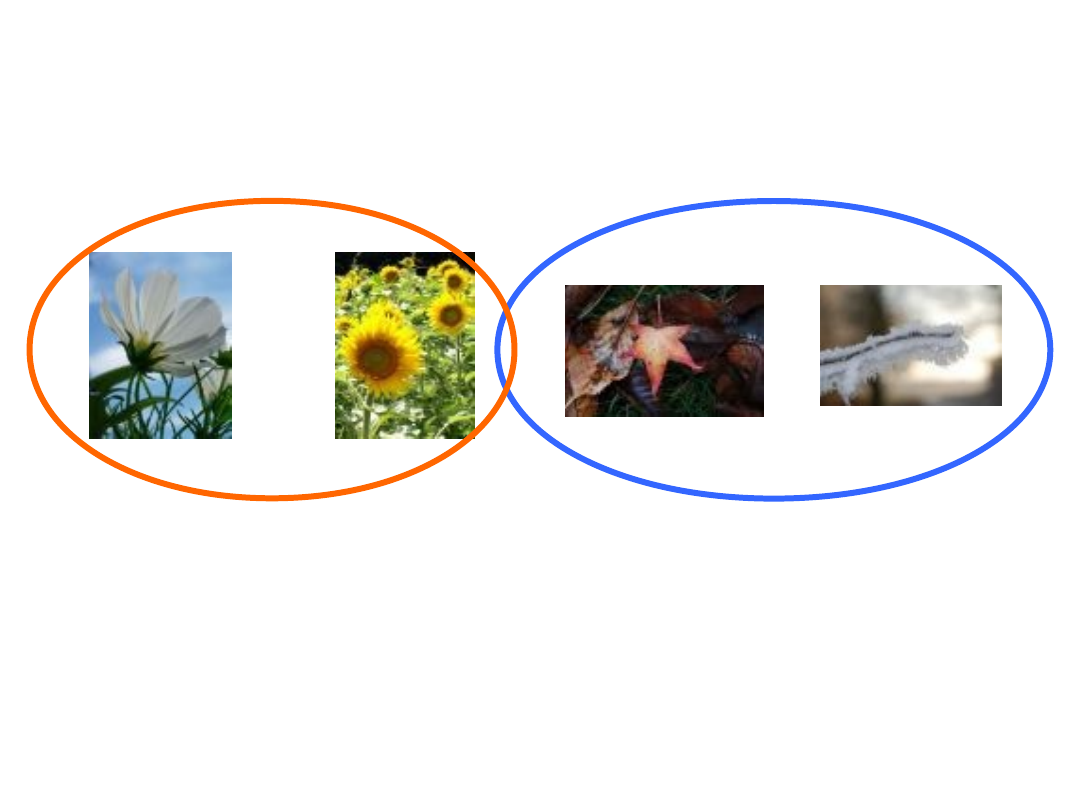
Hipoteza 2 – porównanie 2

G 1

G 2

G 3

G 4

Hipoteza 2: Pierwsza połowa roku jest zdecydowanie inna jeśli
chodzi o klimat emocjonalny niż druga

Hipoteza 3 – porównanie 3

G 1

G 2

G 3

G 4

Hipoteza 3: Znacząco różni się wiosna od lata.

Czy możemy wykonać oba porównania?

Czy kontrasty są ortogonalne?

Hipoteza 2: Kontrast: -1, -1, 1, 1

Hipoteza 3: Kontrast: -1, 1, 0, 0

1 -1 0 0

Suma iloczynów wynosi
zero

Wniosek: Możemy wykonać takie
porównania

Czy możemy wykonać oba porównania?

Czy kontrasty są ortogonalne?

Hipoteza 2: Kontrast: -1, -1, 1, 1

Hipoteza 1: Kontrast: -1, -1, -1, 3

1 1 -1 3

Suma iloczynów nie wynosi zero

Wniosek: Nie możemy wykonać takich
porównań

Czy możemy wykonać oba porównania?

Czy kontrasty są ortogonalne?

Hipoteza 1: Kontrast: -1, -1,-1, 3

Hipoteza 3: Kontrast: -1, 1, 0, 0

1 -1 0 0

Suma iloczynów wynosi
zero

Wniosek: Możemy wykonać takie
porównania

Jakie zatem możemy zrobić porównania?

Musimy się zdecydować, które hipotezy są

dla nas najważniejsze lub najbardziej

teoretycznie uzasadnione. Wtedy

weryfikujemy te właśnie tezy.

Albo wszystkie trzy, ale wiemy, ze niektóre

kontrasty nie są ortogonalne, co znaczy,

że popełniamy większy błąd I rodzaju niż

wskazuje na to poziom istotności.

Albo wykonujemy testy post hoc, które mają

korektę poziomu istotności na wielokrotne

porównania.

Współczynniki kontrastu

• Sprawdzamy współczynniki kontrastu

Współczynniki kontrastu

-1

-1

1

1

-1

1

0

0

1

1

1

-3

Kontrast
1
2
3

1,00 wiosna 2,00 lato 3,00 jesień 4,00 zima

porar pora roku

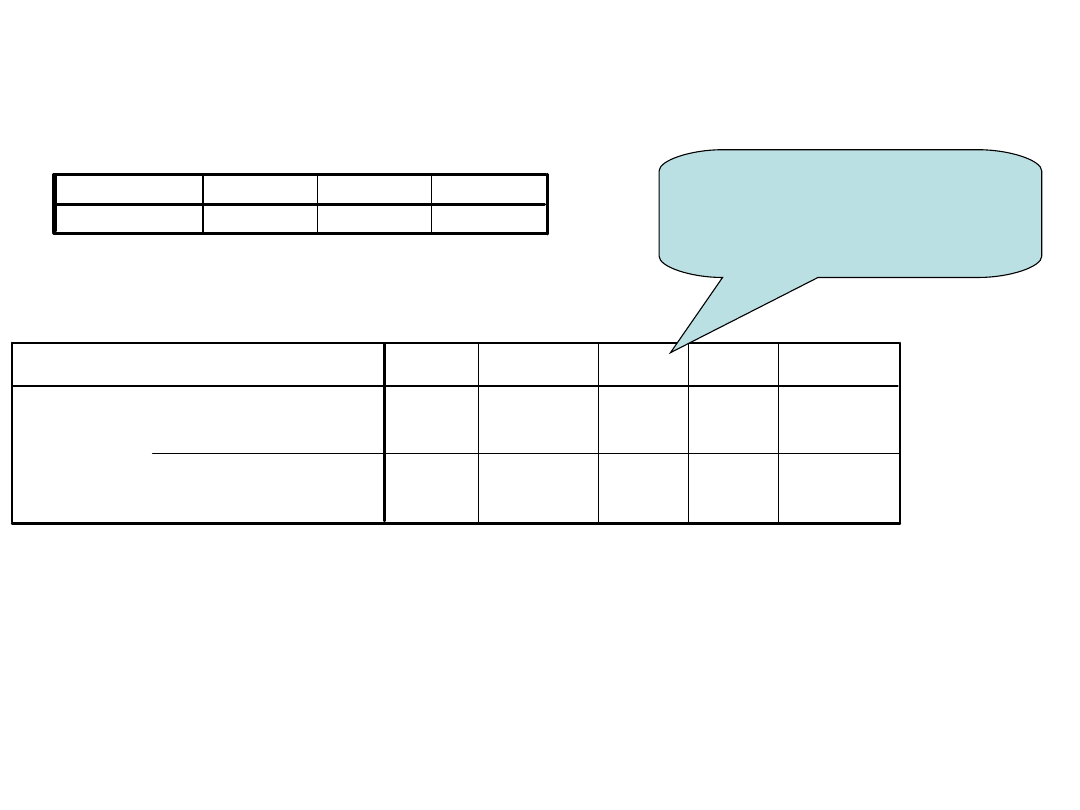
Testy kontrastu

-7,1000

,90860

-7,814

36

,000

5,2000

,64248

8,094

36

,000

22,5000

1,57374

14,297

36

,000

-7,1000

,90860

-7,814

32,726

,000

5,2000

,62361

8,339

16,837

,000

22,5000

1,40436

16,022

19,119

,000

Kontrast
1
2
3
1
2
3

Założenie o
równości wariancji

Brak założenia o
równości wariancji

natęzenie emocji
pozytywnych

Wartość

kontrastu

Błąd

standardowy

t

df

Istotność

(dwustronna)

Założenie o równości wariancji

• Kontrasty odczytujemy w części tabeli „Założenie

o równości wariancji”, bo test Levene’a jest
nieistotny

• Wszystkie są istotne na poziomie p<0,001

Statystyka t to wartość

kontrastu dzielona przez

błąd standardowy

Test jednorodności wariancji

natęzenie emocji pozytywnych

,882

3

36

,459

Test Levene'a

df1

df2

Istotność

Testy kontrastu

-7,1000

,90860

-7,814

36

,000

5,2000

,64248

8,094

36

,000

22,5000

1,57374

14,297

36

,000

-7,1000

,90860

-7,814

32,726

,000

5,2000

,62361

8,339

16,837

,000

22,5000

1,40436

16,022

19,119

,000

Kontrast
1
2
3
1
2
3

Założenie o
równości wariancji

Brak założenia o
równości wariancji

natęzenie emocji
pozytywnych

Wartość

kontrastu

Błąd

standardowy

t

df

Istotność

(dwustronna)

Statystyki opisowe

emocje natęzenie emocji pozytywnych

10

11,7000

1,56702

10

16,9000

1,19722

10

14,6000

1,71270

10

6,9000

1,19722

40

12,5250

4,02548

1,00 wiosna
2,00 lato
3,00 jesień
4,00 zima
Ogółem

N

Średnia

Odchylenie

standardowe

Jak obliczana jest wartość kontrastu?

Te średnie mają

ujemne

współczynniki

kontrastu

Wartość kontrastu to różnica między

średnimi z dodatnimi indeksami a

tymi z ujemnymi indeksami

-11,7 – 16,9 + 14,6 + 6,9= -7,1

Zrozumienie układu średnich 1

• Hipoteza 1 – istotna, ale czy układ średnich

jest właściwy?

• Tworzymy jedną średnią dla wiosny oraz lata i

drugą dla jesieni i zimy

• Średni poziom emocji pozytywnych w pierwszej

połowie roku wynosi 14,3 i jest wyższy niż w

drugiej połowie 10,75. A więc układ średnich

zgadza się z hipotezami

Statystyki opisowe

emocje natęzenie emocji pozytywnych

10

11,7000

1,56702

10

16,9000

1,19722

10

14,6000

1,71270

10

6,9000

1,19722

40

12,5250

4,02548

1,00 wiosna
2,00 lato
3,00 jesień
4,00 zima
Ogółem

N

Średnia

Odchylenie

standardowe

Zrozumienie układu średnich 2

• Hipoteza 2
• Porównujemy średni poziom wiosny i

lata.

Statystyki opisowe

emocje natęzenie emocji pozytywnych

10

11,7000

1,56702

10

16,9000

1,19722

10

14,6000

1,71270

10

6,9000

1,19722

40

12,5250

4,02548

1,00 wiosna
2,00 lato
3,00 jesień
4,00 zima
Ogółem

N

Średnia

Odchylenie

standardowe

Zrozumienie układu średnich 3

• Tworzymy jedną średnią poziomu emocji pozytywnych

dla osób, oceniających wiosnę, lato i jesień i

porównujemy ją ze średnią dla zimy.

• Średni poziom emocji pozytywnych dla wiosny, lata i

jesieni wynosi 14,4 i jest wyższy niż w zimie

(średnia=6,9).

Statystyki opisowe

emocje natęzenie emocji pozytywnych

10

11,7000

1,56702

10

16,9000

1,19722

10

14,6000

1,71270

10

6,9000

1,19722

40

12,5250

4,02548

1,00 wiosna
2,00 lato
3,00 jesień
4,00 zima
Ogółem

N

Średnia

Odchylenie

standardowe

Analiza trendu

Analiza trendu jest wykorzystywana wtedy, gdy

poszukujemy specyficznego układu średnich. Najczęściej

stosujemy ją wtedy, gdy zmienna niezależna jest

ilościowa lub co najmniej porządkowa.

Trendy są najbardziej poszukiwaną wartością - trendsetterzy
Trendy w języku – „jazzy”
Trendy w przemyśle – samochody dla kobiet mają okrągłe

linie nawiązując do cech „dziecięcości”

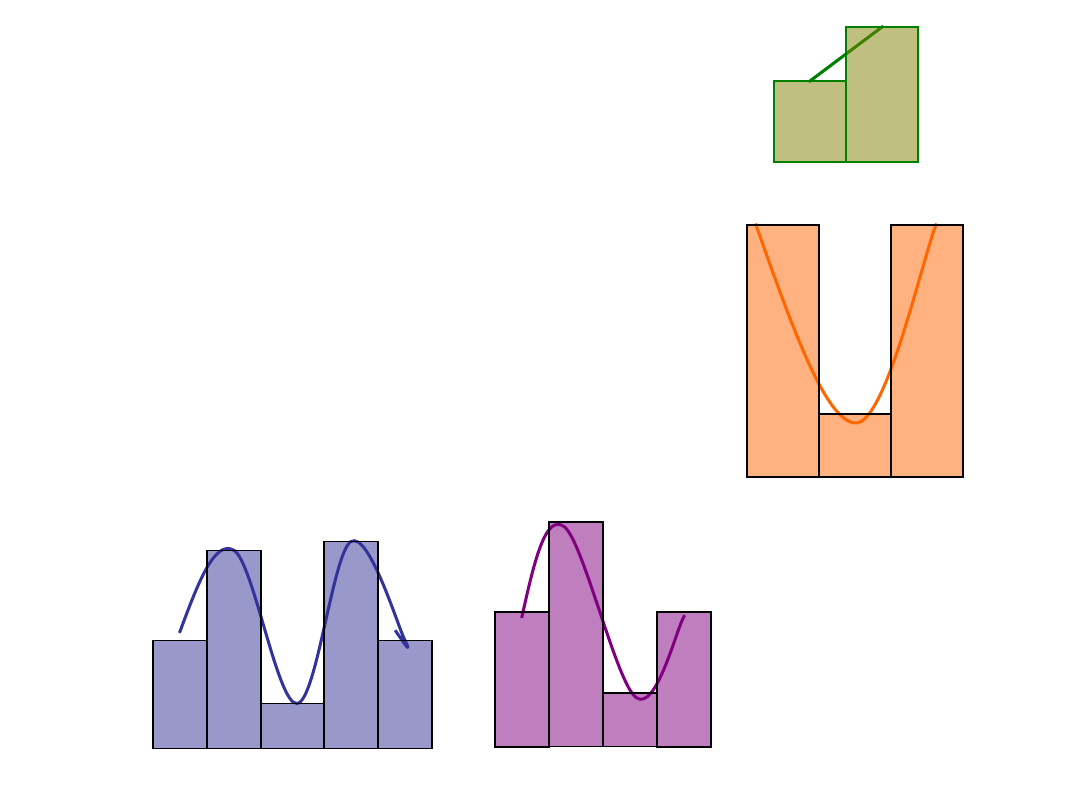
Analiza kontrastów – badanie

trendów

Poznane do tej pory metody –
R-Pearsona czy test T-Studenta pozwalały

nam badać jedynie zależności

prostoliniowe

• Analiza kontrastów pozwala poszukiwać

innych kształtów zależności niż

prostoliniowe.

• Obliczeniowo jest identyczna jak zestaw

ortogonalnych kontrastów. Jeśli szukamy

trendu to ogólna analiza wariancji nie

musi być istotna.

Wielomian czwartego

stopnia

Wielomian trzeciego

stopnia

Wielomian drugiego

stopnia

Wielomian pierwszego

stopnia

Współczynniki kontrastu dla trendu liniowego,

kwadratowego i sześciennego

Porównujemy 2 średnie

• Liniowy –1 1

Porównujemy 3 średnie

• Liniowy –1 0 1

• Kwadratowy 1 -2 1

Porównujemy 4 średnie
• Liniowy –3 –1 1 3
• Kwadratowy 1 –1 –1 1
• Sześcienny –1 3 -3 1

Porównujemy 5 średnich
• Liniowy –2 –1 0 1 2
• Kwadratowy 2 –1 –2 –1

2

• Sześcienny –1 2 0 –2 1

Aby poszukiwać złożonych kształtów zależności
(krzywoliniowych) potrzebujemy

odpowiedniej ilości

porównywanych grup,

np.. Gdy chcemy znaleźć zależność

kwadratową to musimy mieć przynajmniej 3 średnie.

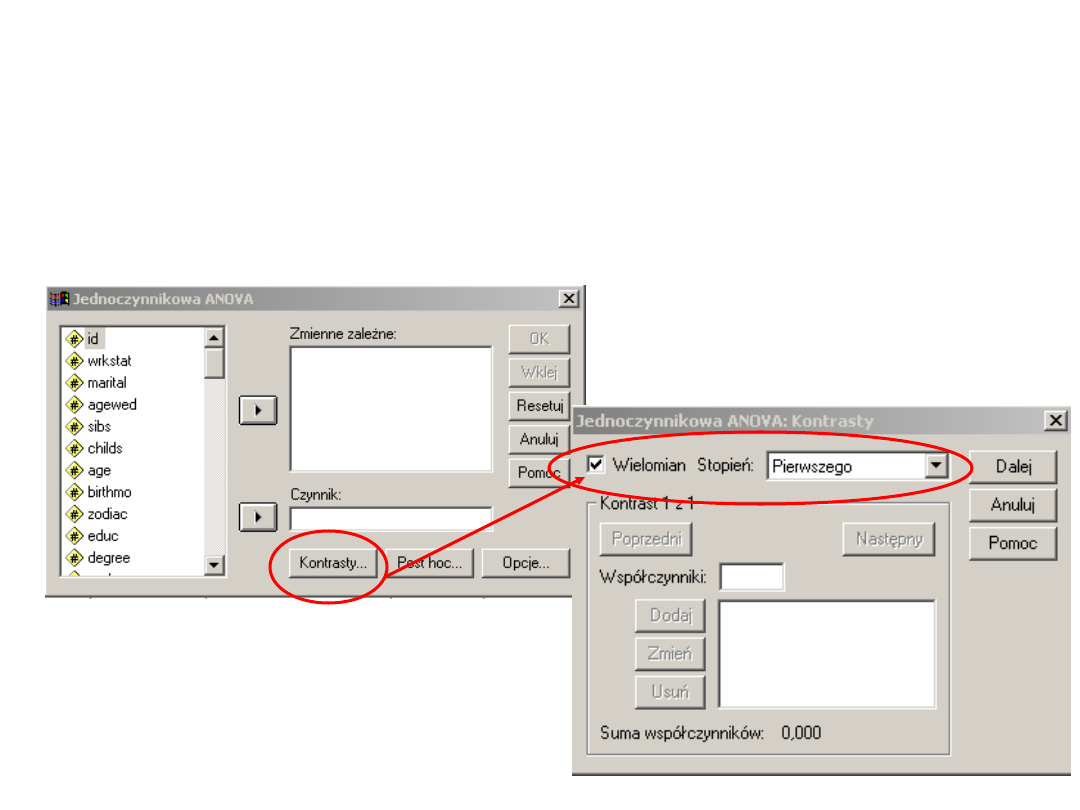
Wielomiany – jak w spss-ie?

Zależność wykształcenie i liczby dzieci przyjmuje
kształt prostoliniowy – osoby z wyższym
wykształceniem mają mniej dzieci niż te z
wykształceniem podstawowym i średnim.

Wniosek – średnie układają się w kształt

funkcji kwadratowej

Jednoczynnikowa ANOVA

Liczba dzieci

157,450

4

39,362

14,405

,000

92,601

1

92,601

33,887

,000

124,883

1

124,883

45,701

,000

32,566

3

10,855

3,973

,008

18,177

1

18,177

6,652

,010

30,795

1

30,795

11,269

,001

1,772

2

,886

,324

,723

,271

1

,271

,099

,753

,055

1

,055

,020

,887

1,716

1

1,716

,628

,428

1,716

1

1,716

,628

,428

1,716

1

1,716

,628

,428

4063,405

1487

2,733

4220,855

1491

(Połączone)

Nieważone
Ważone
Odchylenie

Składnik liniowy

Nieważone
Ważone
Odchylenie

Składnik
kwadratowy

Nieważone
Ważone
Odchylenie

Składnik
sześcienny

Nieważone
Ważone

Składnik czwartego
stopnia

Między
grupami

Wewnątrz grup
Ogółem

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Wydruk

Suma kwadratów dla kontrastu to
kwadrat zsumowanych średnich
mnożonych przez odpowiednie
współczynniki kontrastu

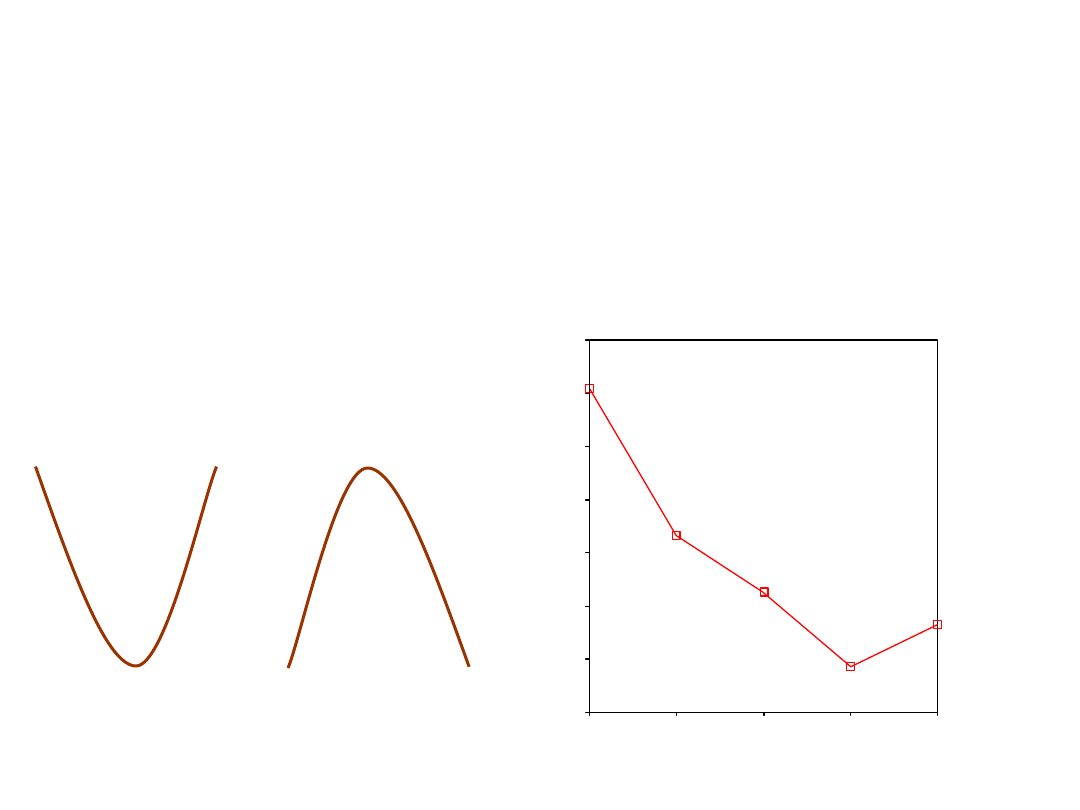
Interpretacja

• Wiemy już, że średnie układają się tworząc wielomian

drugiego stopnia, ale, żeby zinterpretować go musimy

obejrzeć wykres. Wydruk nie pozwala nam bowiem

stwierdzić, który wariant układu trendu pozwala opisać
średnie.

Poziom wykształcenia respondenta

Graduate

Bachelor

Junior college

High s chool

Mniej niż HS

Ś

re

d

n

ia

-

L

ic

zb

a

d

z

ie

ci

2,6

2,4

2,2

2,0

1,8

1,6

1,4

1,2

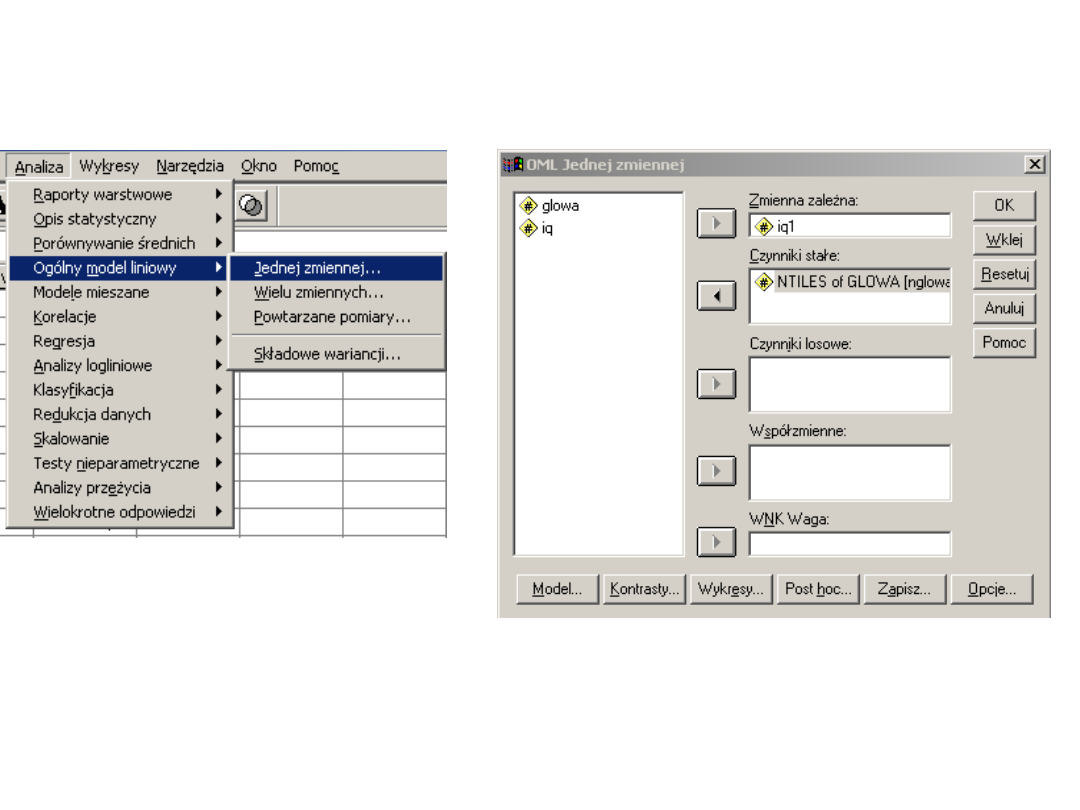
Jak zrobić tę analizę inaczej…

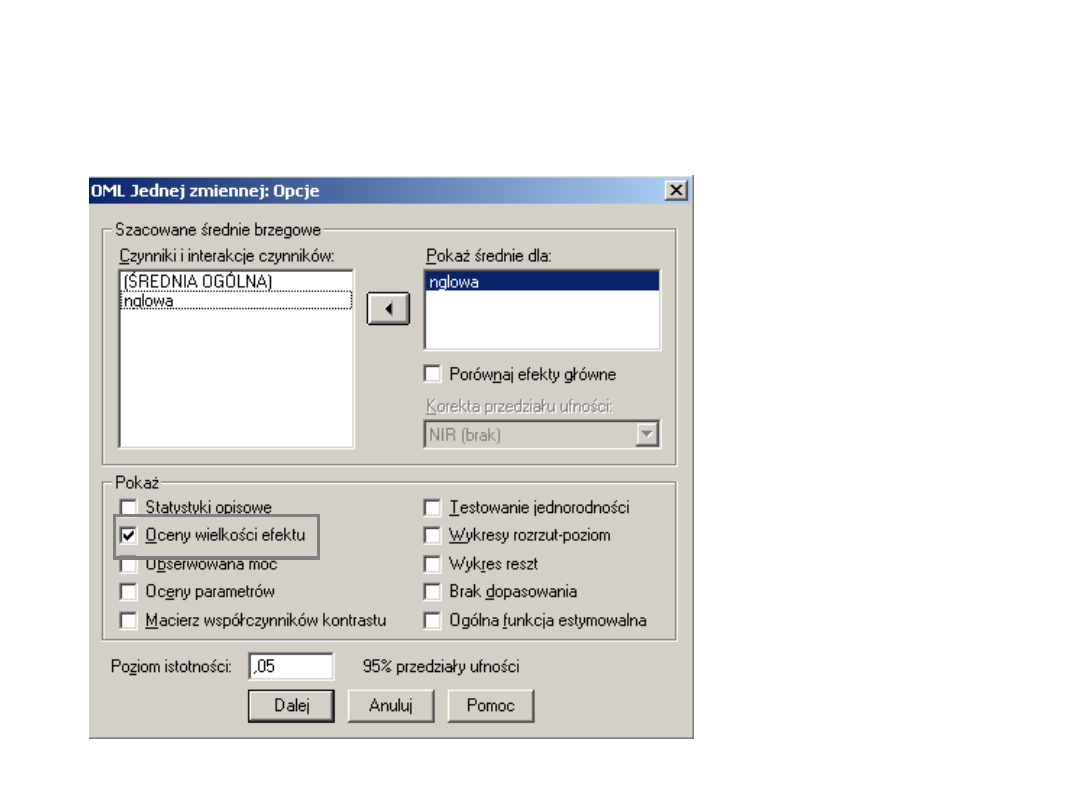
Miary siły efektu – eta kwadrat

Wydruk

Testy efektów międzyobiektowych

Zmienna zależna: iq1

296,583

a

2

148,292

3,645

,044

,258

264810,042

1 264810,0 6508,864

,000

,997

296,583

2

148,292

3,645

,044

,258

854,375

21

40,685

265961,000

24

1150,958

23

Źródło zmienności
Model skorygowany
Stała
nglowa
Błąd
Ogółem
Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

Czastkowe

Eta kwadrat

R kwadrat = ,258 (Skorygowane R kwadrat = ,187)

a.

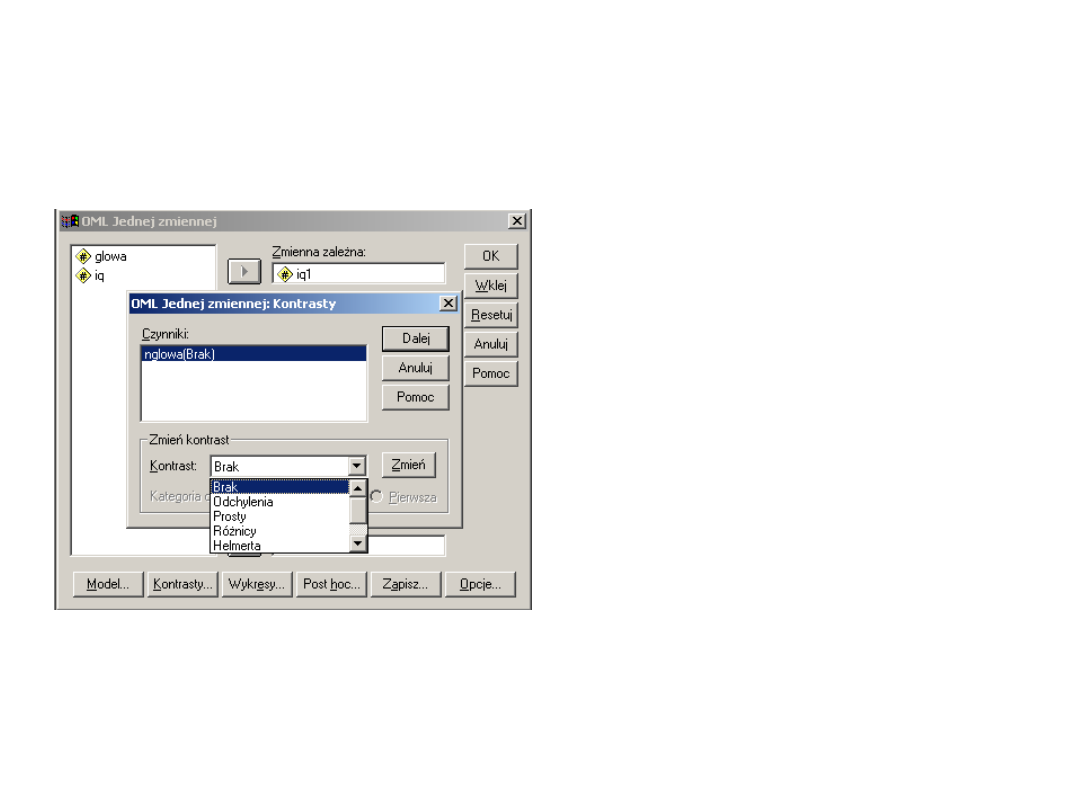
Kontrasty

predefiniowane

• Odchylenia
• Prosty
• Różnicy
• Helmerta
• Powtarzany

Kontrast predefiniowany

odchylenia

• Każda średnia jest porównywana z

pozostałymi

• Współczynniki kontrastu
• 3 -1 -1 -1
• -1 3 -1 -1
• -1 -1 3 -1

Kontrast predefiniowany -

różnica

• Każda średnia jest porównywana z

tymi, które ją poprzedzają

• Współczynniki kontrastów
• -1 1 0 0
• -1 -1 2 0
• -1 -1 -1 3

Kontrast predefiniowany -

Helmerta

• Każda średnia jest porównywana z

tymi, które znajdują się na kolejnych
miejscach

• Współczynniki kontrastów:
• 3 -1 -1 -1
• 0 2 -1 -1
• 0 0 -1 1

Kontrast predefiniowany -

prosty

• Każda średnia jest porównywana z

ostatnią w ciągu

• Współczynniki kontrastów
• -1 0 0 1
• 0 -1 0 1
• 0 0 -1 1

Kontrast predefiniowany -

powtarzany

• Każda średnia porównywana jest z

kolejną.

• Współczynniki kontrastów
• -1 1 0 0
• 0 -1 1 0
• 0 0 -1 1

Podsumowanie

• Jeśli hipoteza niekierunkowa – testy

post hoc pod warunkiem, że ogólna
anova istotna

• Jeśli hipoteza kierunkowa – testy

kontrastów lub trendy niezależnie
czy ogólna anova istotna

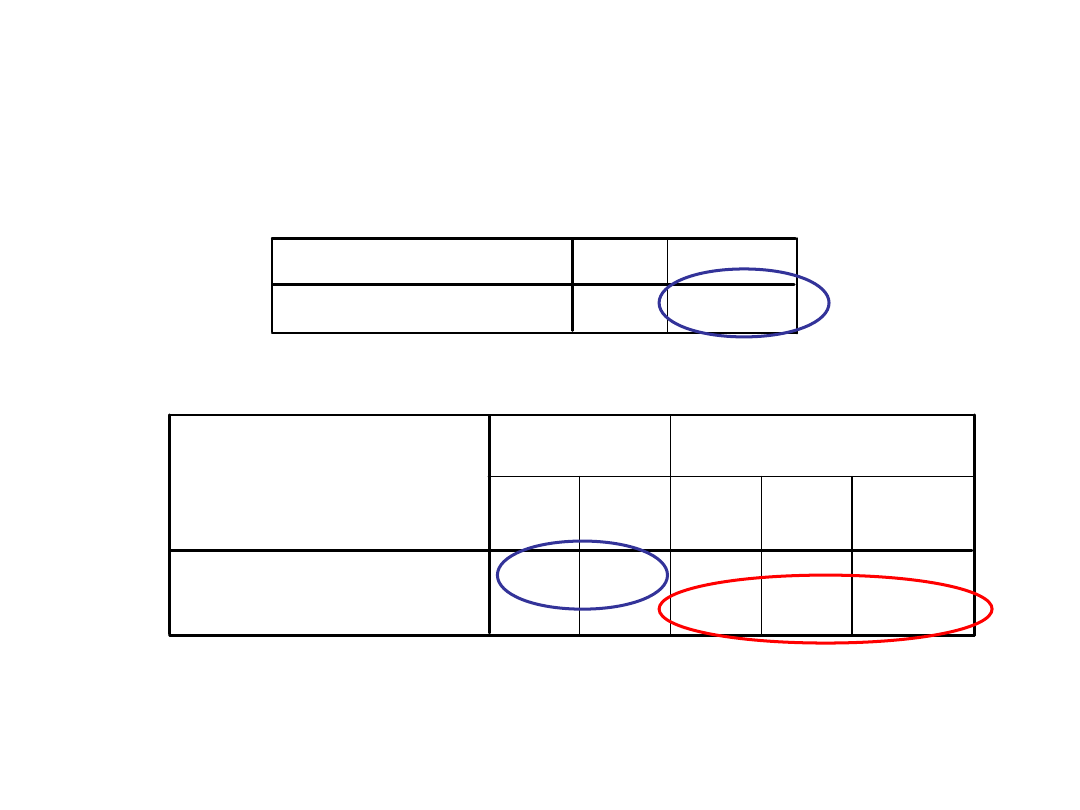
Test dla prób niezależnych

76,142

,000

-1,644

58

,106

-1,644

35,154

,109

Założono równość
wariancji
Nie założono
równości wariancji

atywność poznawcza

F

Istotność

Test Levene'a

jednorodności

wariancji

t

df

Istotność

(dwustronna)

Test t równości średnich

Analiza testem t

Statystyki dla grup

4,9333

,69149

5,6000

2,11073

RAN_WIEC
ranne ptaszki
sowy

atywność poznawcza

Średnia

Odchylenie

standardowe

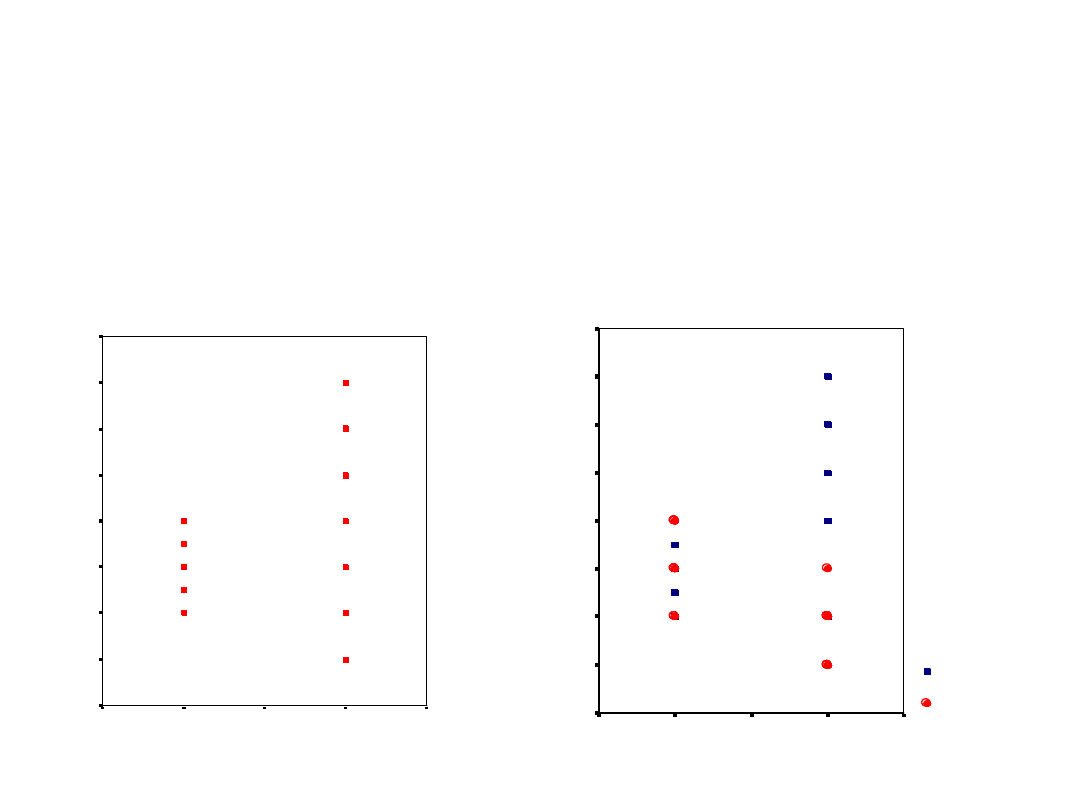
Zobaczmy ten wynik na

wykresie

Ranność Wieczorność

at

yw

no

ść

p

oz

na

w

cz

a

10

9

8

7

6

5

4

3

2

Być może
pominęliśmy jakąś
ważną zmienną –
skoro badamy
funkcjonowanie
różnych
chronotypów, to
może warto wziąć
pod uwagę porę
dnia

Ranność Wieczorność

at

yw

no

ść

p

oz

na

w

cz

a

10

9

8

7

6

5

4

3

2

PORA

wieczorem

rano

Dwuczynnikowa analiza

wariancji

• Gdy chcemy uwzględnić nie tylko jeden

czynnik wykonujemy analizę wariancji

wieloczynnikową. Dzięki temu zabiegowi

dowiadujemy się nie tylko jakie znacznie ma

dany czynnik samodzielnie ale także, czy

czynniki nie wchodzą ze sobą w interakcje.

• Rodzaje efektów:

– główny – wpływ poziomów danego czynnika na

zmienną zależną bez uwzględnienia poziomów

drugiego czynnika

– Interakcyjny – wpływ poziomów danego czynnika

na zmenną zależną na danym poziomie drugiego

czynnika.

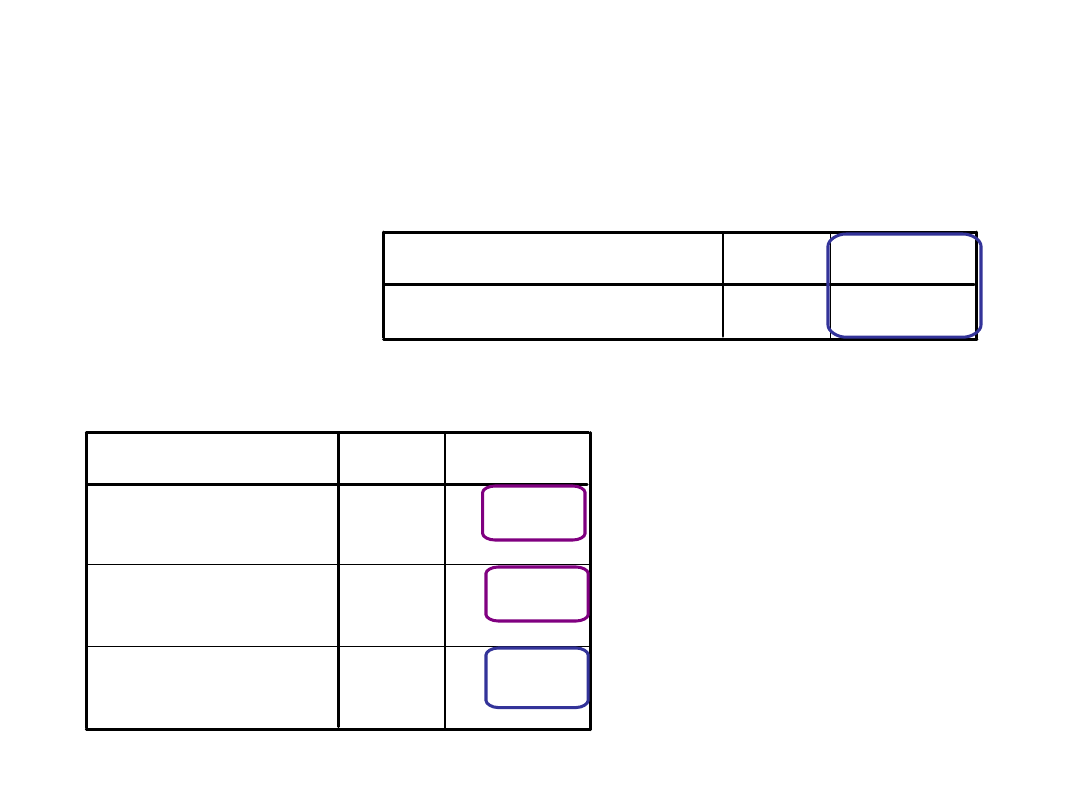
Statystyki dla grup

4,9333

,69149

5,6000

2,11073

RAN_WIEC
ranne ptaszki
sowy

atywność poznawcza

Średnia

Odchylenie

standardowe

Gdy uwzględnimy porę dnia…

Statystyki opisowe

Zmienna zależna: atywność poznawcza

5,2000

,77460

3,6667

,61721

4,4333

1,04000

4,6667

,48795

7,5333

,91548

6,1000

1,62629

4,9333

,69149

5,6000

2,11073

5,2667

1,59306

RAN_WIEC
ranne ptaszki
sowy
Ogółem
ranne ptaszki
sowy
Ogółem
ranne ptaszki
sowy
Ogółem

PORA
rano

wieczorem

Ogółem

Średnia

Odchylenie

standardowe

Dzięki
uwzględnieniu
dodatkowego
czynnika – pory
dnia, wariancja
wewnątrzgrupowa
zmniejszy się.

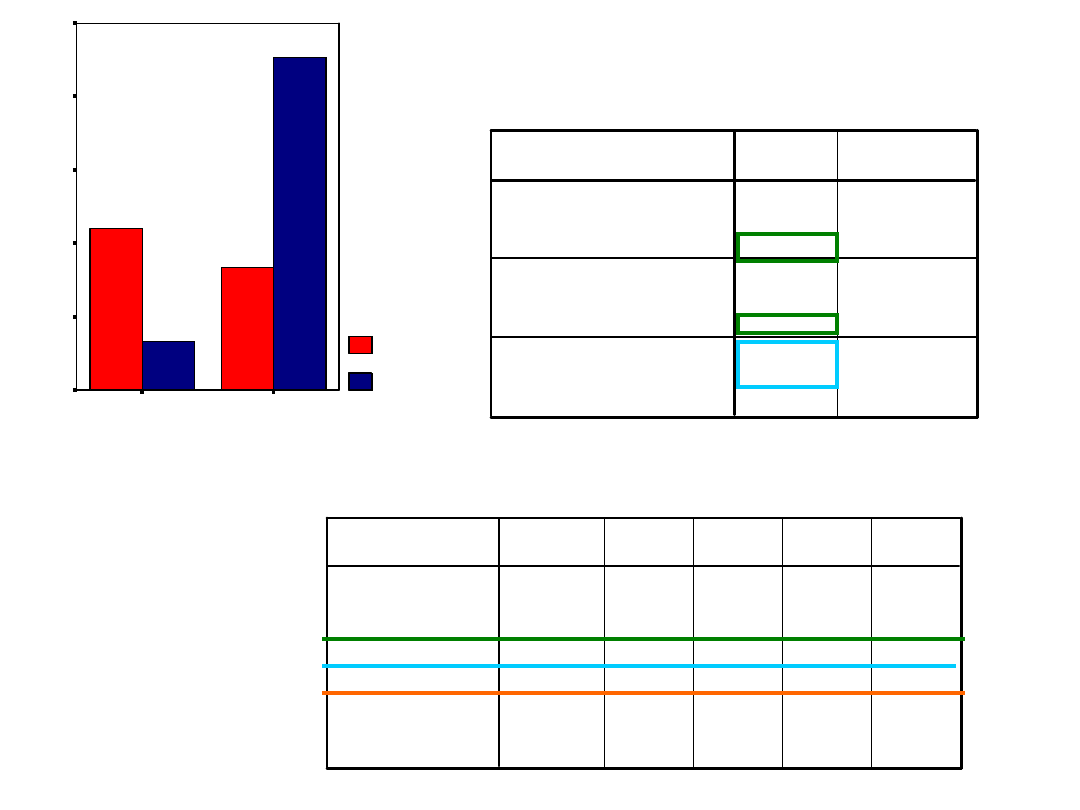
Testy efektów międzyobiektowych

Zmienna zależna: atywność poznawcza

120,933

a

3

40,311

78,383

,000

1664,267

1 1664,267 3236,074

,000

41,667

1

41,667

81,019

,000

6,667

1

6,667

12,963

,001

72,600

1

72,600

141,167

,000

28,800

56

,514

1814,000

60

149,733

59

Źródło zmienności
Model skorygowany
Stała
PORA
RAN_WIEC
PORA * RAN_WIEC
Błąd
Ogółem
Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

R kwadrat = ,808 (Skorygowane R kwadrat = ,797)

a.

Statystyki opisowe

Zmienna zależna: atywność poznawcza

5,2000

,77460

3,6667

,61721

4,4333

1,04000

4,6667

,48795

7,5333

,91548

6,1000

1,62629

4,9333

,69149

5,6000

2,11073

5,2667

1,59306

RAN_WIEC
ranne ptaszki
sowy
Ogółem
ranne ptaszki
sowy
Ogółem
ranne ptaszki
sowy
Ogółem

PORA
rano

wieczorem

Ogółem

Średnia

Odchylenie

standardowe

PORA

wieczorem

rano

po

zi

om

r

oz

w

ią

za

ni

a

za

da

ń

um

ys

ło

w

yc

h

8

7

6

5

4

3

ranne ptaszki

sowy

Schemat dwuczynnikowy

●

Czasami w badaniach interesuje nas wpływ

więcej niż jednego czynnika

●

Zamiast robić dwa badania (odpowiadać

oddzielnie na dwa pytania):

–

Jaki rodzaj alkoholu wpływa bardziej na

agresję?

–

Przynależność do jakiej grupy powiązana

jest z większą agresywnością?

●

Można zrobić jedno:

–

Jaki rodzaj alkoholu wpływa bardziej na

agresję w zależności od przynależności

osób do danej grupy?