Smarowanie pary 

ciernej

Jedyną  efektywną  metodą  zmniejszenia  oporów 

ruchu  pary  ciernej  oraz  zmniejszenia  zużycia  jest 
wprowadzenie  pomiędzy  te  powierzchnie  trzeciego 
ciała- 

smaru 

(z 

wyjątkiem 

oddziaływań 

magnetoelektrycznych i przegubów sprężystych). 

Problem centralny:

 

uzyskanie  odpowiedniej  ciągłej  szczeliny  wypełnionej 
smarem (ciałem stałym, cieczą lub gazem). 

Zagadnienie  to  dotyczy    m.in.  łożysk  ślizgowych, 
tocznych, 

kół 

zębatych 

oraz 

mechanizmów 

krzywkowych.

 

 

Podział łożysk ślizgowych ze względu na na 

rodzaj tarcia na smarowanych powierzchniach 

ślizgowych

•

Łożyska z tarciem granicznym  lub mieszanym w 

których  występuje  bezpośredni  kontakt  czopa  i 
panwi

•

Łożyska z tarciem płynnym, w których tarcie 

płynne  uzyskuje się na zasadzie 
hydrodynamicznej (równanie 

Reynoldsa) lub 

hydrostatycznej (równanie  Laplace’a)

Warunki powstania ciśnienia hydrodynamicznego:

1. występowanie zmiennego przekroju poprzecznego 

(zmienna grubość warstwy smaru)

2. istnienie prędkości v>0  równej prędkości ruchu 

względnego powierzchni współpracujących.

Łożyska ślizgowe hydrodynamiczne- teoria 

łożyska hydrodynamicznego

 

 

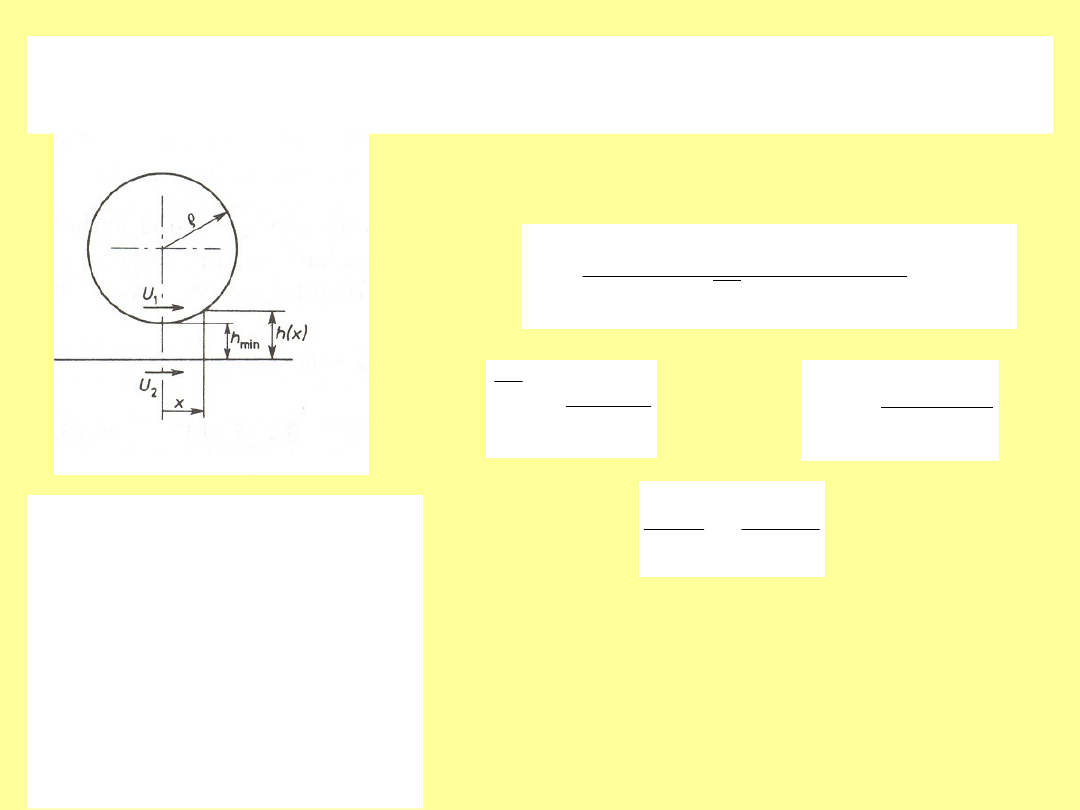
Przepływ smaru w klinowej szczelinie smarnej

• Przepływ  smaru  w  klinowej  szczelinie  smarnej 

utworzonej  z  dwóch  płyt  o  nieskończonej 
szerokości i kącie . 

• Ciecz 

w 

szczelinie 

nieściśliwa, 

przepływ 

laminarny.

•   Adhezja  powoduje  równość  prędkości  płyt  i 

warstw granicznych smaru.

• Wzajemnemu  względnemu  przemieszczaniu  się 

warstw 

cieczy 

przeciwdziałają 

naprężenia 

styczne  styczne  wg  wzoru  Newtona  dla  ruchu 
płaskiego:

dy

du







 

 

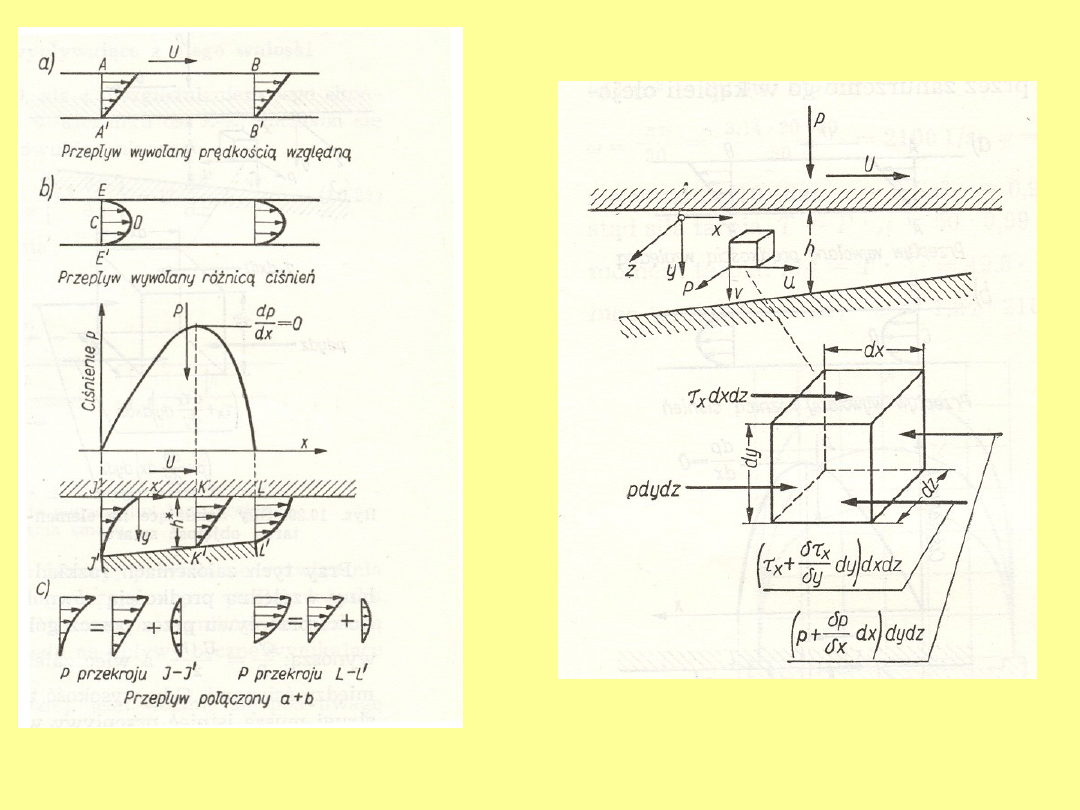
Przepływ smaru w szczelinie (3D)

Rozkład ciśnienia i prędkości w 

szczelinie

 

 

Warunek równowagi sił w kierunku osi dla ruchu płaskiego x:

0













































dx

dy

y

dx

pdy

dy

dx

x

p

p







0













dydx

y

dxdy

x

p



0













y

x

p



2

2

y

u

y

u

y

x

p





































Założenia: dla małej grubości 
warstwy smaru p i dp/dx są stałe 
wzdłuż osi y oraz lepkość  = const.

 

Warunki brzegowe

:



















2

1

2

2

1

C

y

C

y

x

d

dp

u

















0

0

y

dla

v

)

x

(

h

h

y

dla

u



















2

1

2

2

1

0

C

h

C

h

x

d

dp



 

 

v

C

C

C

x

d

dp

v



























2

2

1

0

0

1

h

/

v

h

x

d

dp

v

h

x

d

dp

h

C





























2

2

1

2

1





h

y

h

v

h

y

y

x

d

dp

u









2

2

1



Wzór ten określa rozkład prędkości 

w szczelinie wzdłuż osi y

Rozkład ciśnień wzdłuż osi x:

Warunek 

ciągłości 

przepływu: 

w 

dowolnym 

przekroju na jednostkę długości czopa  (np. b=1 cm) 
wydatek jest stały.





.

const

vh

dx

dp

h

u

h

u

y

h

v

vy

h

y

y

dx

dp

dy

h

y

h

v

yh

y

dx

dp

dy

u

q

h

h



























































2

12

0

2

2

3

2

1

2

1

3

2

2

3

0

2

0







 

 

Całkowita siła nośna

W miejscu maksymalnego ciśnienia (dp/dx=0) wydatek

 

2

*

*

vh

q 

Dla stałego wydatku w każdym 
przekroju równanie określające 
rozkład ciśnień wzdłuż osi x: 

C

dx

h

h

h

v

p

*

x









3

6



Warunki brzegowe:

C

oraz

h

p

l

x

dla

p

x

dla

*

x

x















0

0

0





l

x

dx

p

P

0

Na  podstawie  wyznaczonych  zależności  można 
obliczyć  najmniejszą  wartość  szczeliny  smarnej 
koniecznej  do  właściwej  pracy  łożyska  w  warunkach 
tarcia  płynnego  dla  dowolnego  kształtu  szczeliny  jeśli 
znana jest funkcja h=f(x).

 

 

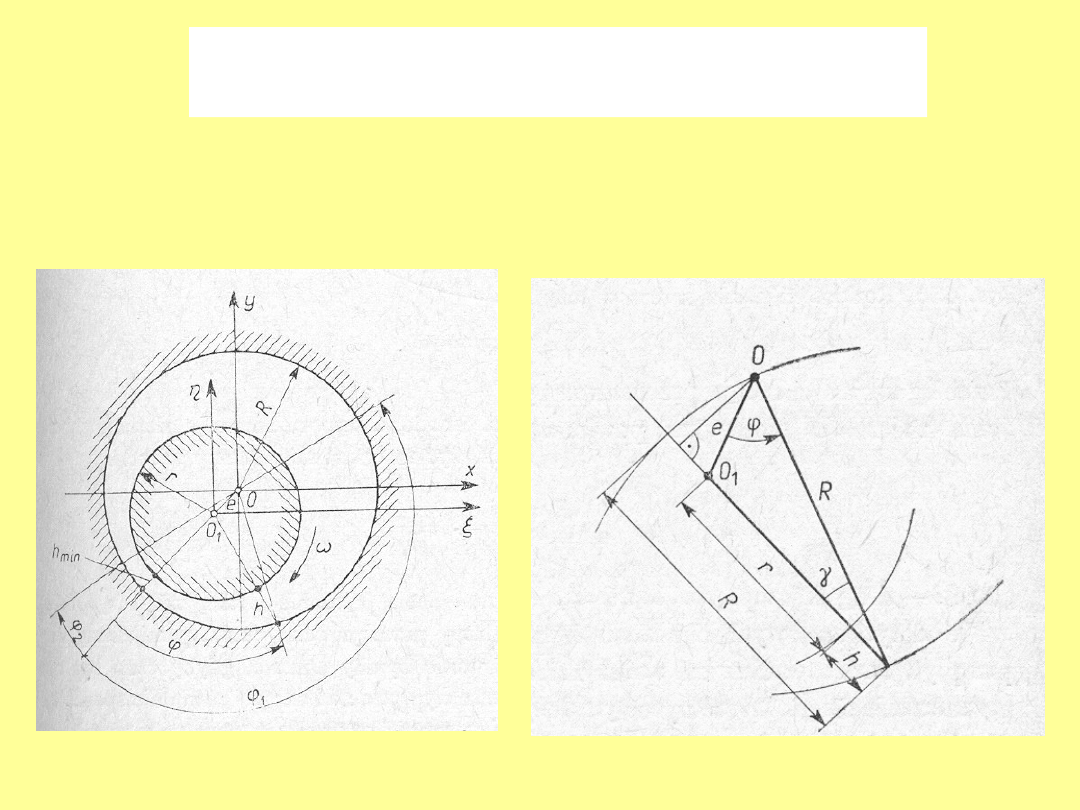
Łożyska poprzeczne o tarciu 

płynnym

Wzajemne  położenie  czopa  i 
panwi  w  łożysku  poprzecznym 
(luz przesadny)

Określenie szerokości szczeliny 

jako funkcji kąta .

Warunki 

konieczne 

do 

powstawania 

ciśnienia 

hydrodynamicznego  spełnia  szczelina  między  czopem  a 
panewką  łożyska  ślizgowego  poprzecznego  (tworzy  się 
obszar podobny do klina smarnego).

 

 

Wyznaczanie ciśnienia w dowolnym przekroju określonym kątem  (podobnie 

jak poprzedni ruch elementu smaru w szczelinie)





















cos

e

r

R

h

cos

R

cos

e

r

R

h



















1

Luz względny łożyska 

d

S

r

d

d

D

r

r

R

w

















Luz promieniowy

r

R

d

D









2



Ekscentryczność względna 

(mimośrodowość względna )

r

R

e

e











Wzór określający szczelinę 

h:

 

)

1

(







cos

e

h





Jeśli użyto  h, v=r i dx=rd































2

3

2

1

1

1

1

6



















cos

cos

cos

d

dp

*









C

d

cos

cos

cos

p

*













































2

3

2

1

1

1

1

6

 

 

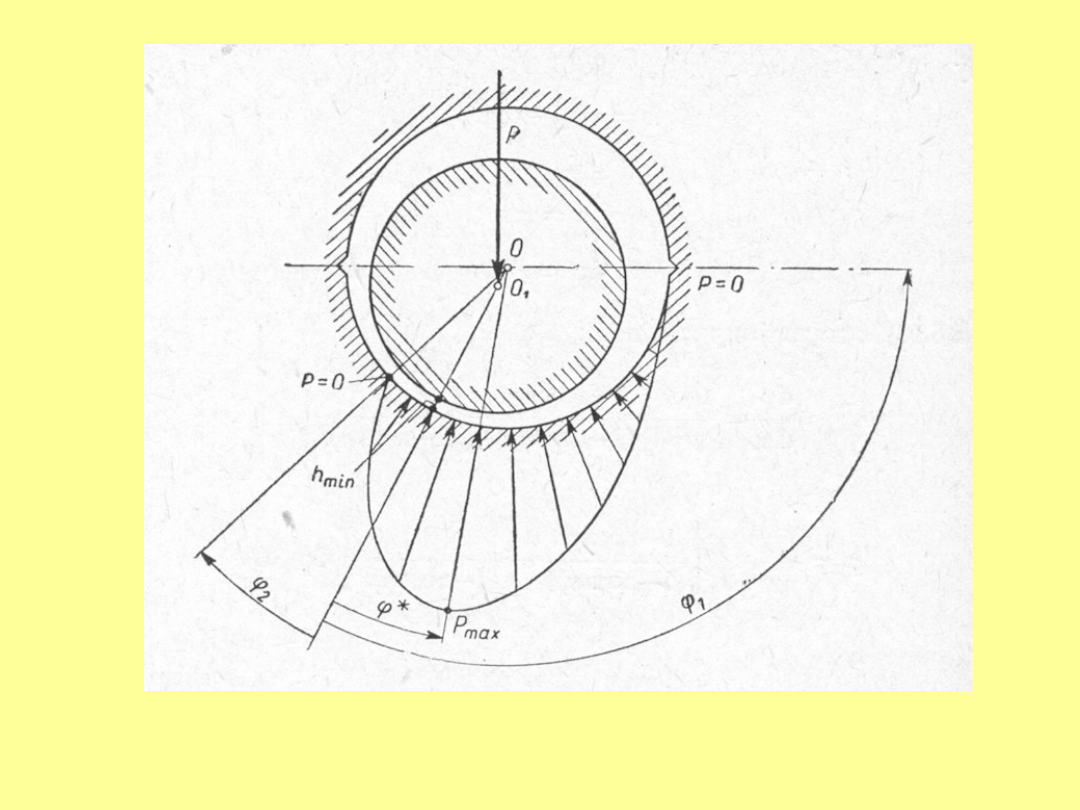
Najczęściej  zakłada  się,  że  początek  strefy  przenoszącej  obciążenie 
pokrywa się z rowkiem smarnym (kąt 

­

1

  ). Koniec obszaru określa kąt 

­

2

 ( poza najmniejsza szczeliną h

0

). Najczęściej też  , gdzie 



*

 określa p

max

 

 (dla dp/dx=0).































d

cos

cos

cos

p

*

























2

1

2

3

2

1

1

1

1

6

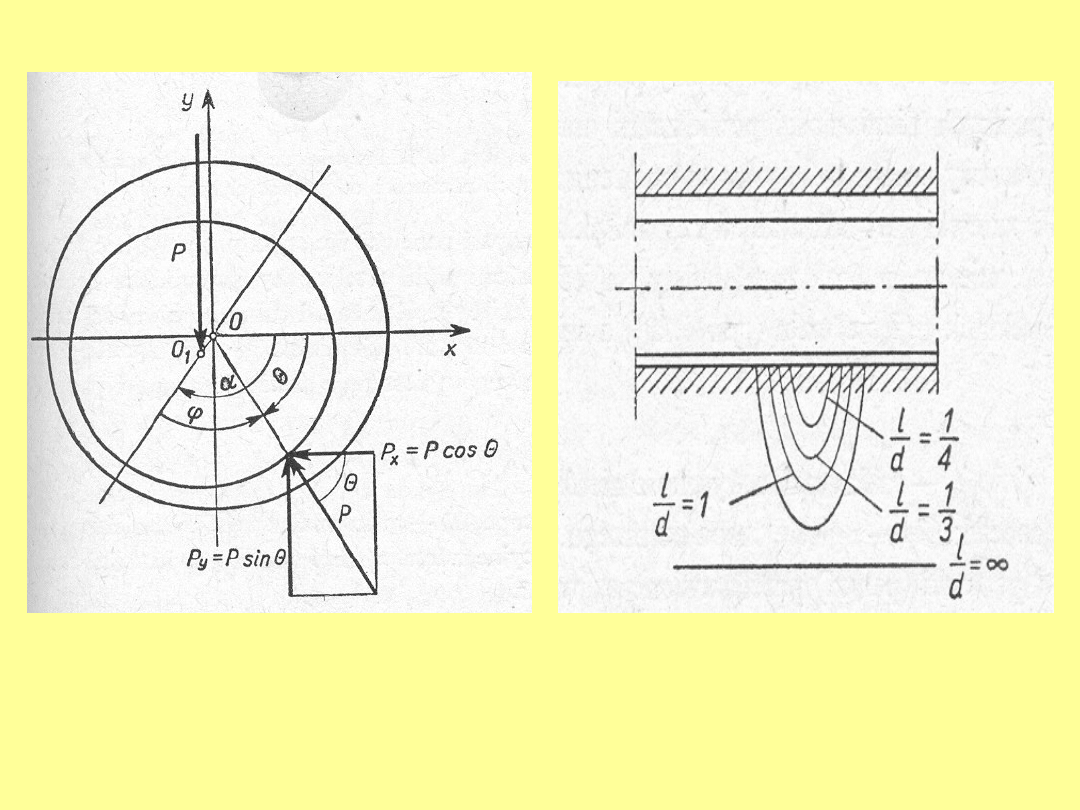
Składowa wyporu smaru musi zrównoważyć obciążenie

 













rd

sin

p

b

P





2

1

2

2











1

1











b- szerokość 
panwi.

 

W  rzeczywistym  łożysku  smar  wypływa  na  boki,  co  powoduje  spadek 
ciśnienia w kierunku poosiowym. Powoduje to zmniejszenie siły wyporu, co 
uwzględnia  się  poprzez  wprowadzenia  współczynnika  poprawkowego 
C=f(b/d)

















d

sin

p

C

bd

d

r

sin

p

Cb

bd

P

p

śr











2

1

2

1

2

 

 

Rozkład ciśnienia w łożysku poprzecznym

 

 

              Rozkład ciśnienia na składowe.

     Rozkład ciśnienia wzdłuż 

długości czopa.

 

 

Rozkład ciśnienia w łożysku z rowkiem.

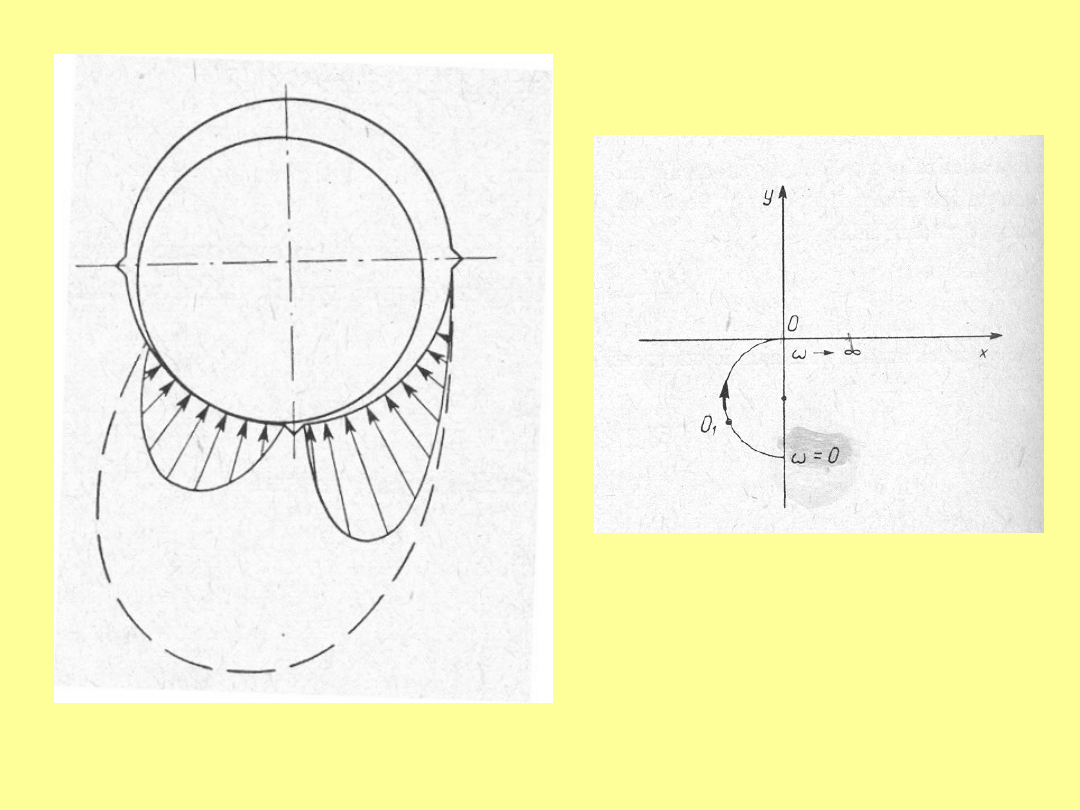
Przybliżone położenie środka czopa w 

zależności

od prędkości obrotowej

 

 

W praktyce można posługiwać się wzorem:

gdzie , S

0

- liczba Sommerfelda jest funkcją luzu względnego kata 

doprowadzenia smaru oraz  stosunku długości do średnicy czopa 

l/d

 . 

Wartości 

S

0

 przedstawiane są w sposób tabelaryczny i za pomocą 

wykresów w zależności od w/w parametrów.

 

Stanowi ona kryterium podobieństwa

 hydrodynamicznego dla cylindrycznych

 łożysk poprzecznych obciążonych statycznie . 

Jeśli  łożyska  konstrukcyjnie  podobne  (b/d=const.,  kąt 
opasania  =const.  S

0 

=const.,  to  ekscentryczność    oraz 

zastępczy współczynnik tarcia  / są takie same.  

Podobna 

analiza dla sił tarcia i wydatku smaru. 

Najmniejsza 

szczelina 

określona jest

Zastępczy współczynnik tarcia:

jako:

:

0

2

S

p

śr







]

[

2

0









śr

p

S

 

0

S

f



















1

0

r

h

 

 

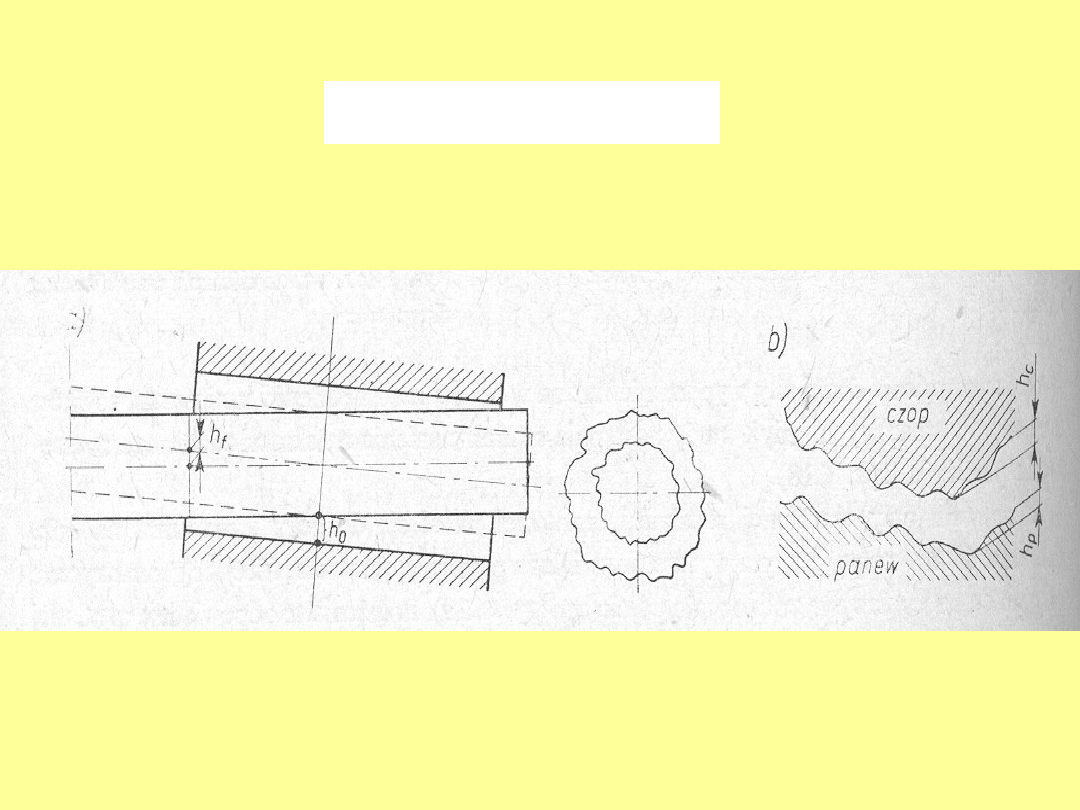
Aby istniało tarcie płynne wymagane jest spełnienie warunku

p

c

f

f

p

c

h

h

h

h

h









0

gdzie,        -  max  wysokość  nierówności  powierzchni  czopa  ,          -  max 
wysokość nierówności powierzchni panwi,       -ugięcie czopa na brzegu 
panwi,      - odkształcenie panwi ( na ogół zerowe).

c

h

p

h

c

f

h

p

f

h

Określenie minimalnej szczeliny w łożysku poprzecznym

 

 

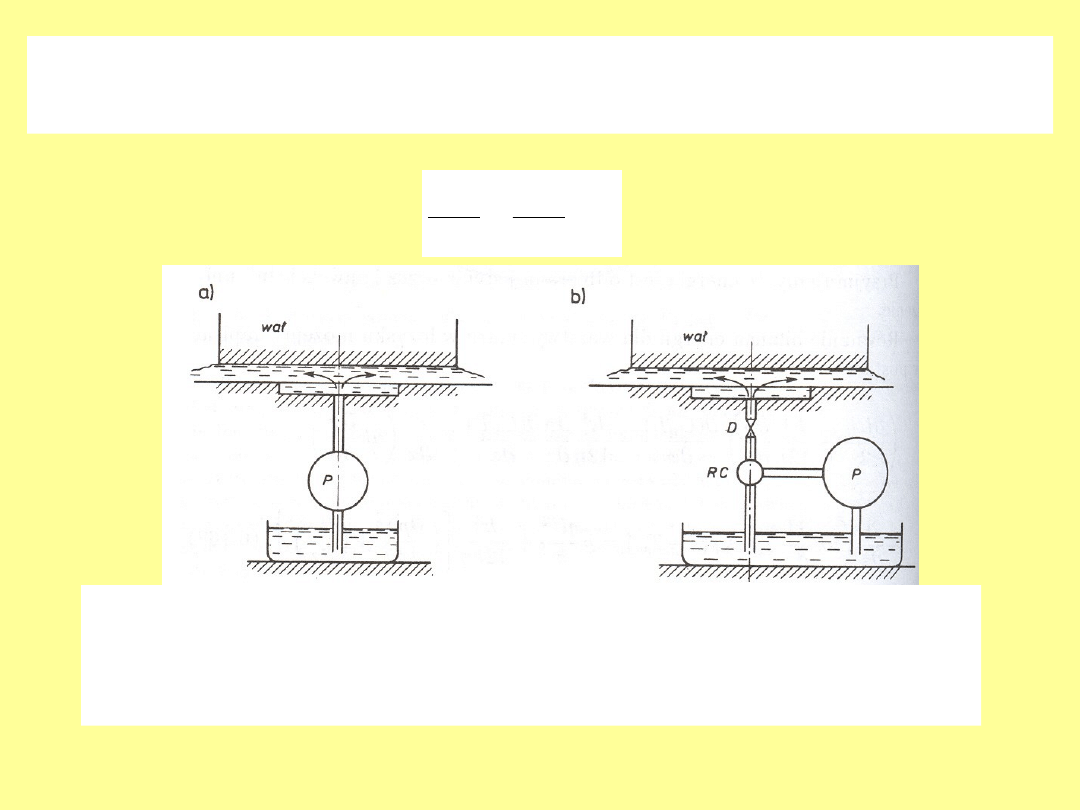
Łożyska hydrostatyczne. Teoria hydrostatycznego 
smarowania

Równanie Laplace’a

 :

0

2

2

2

2













z

p

x

p

Podpory hydrostatyczne o stałym przepływie (a) 

i o stałym ciśnieniu (b) –P - pompa, D- dławik, 

RC- regulator ciśnienia

 

 

Schemat podpory hydrostatycznej o budowie osiowo 

symetrycznej 

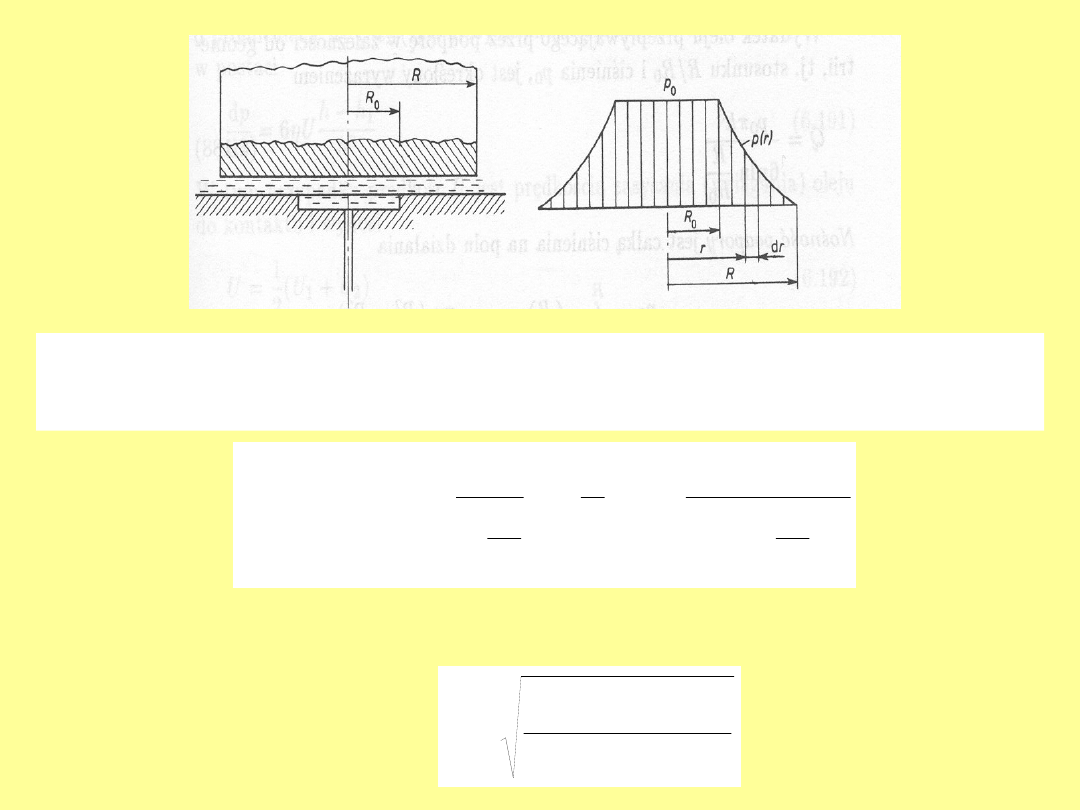
Nośność podpory (całka ciśnienia na polu działania)





0

2

0

2

0

0

0

2

0

0

2

2

0

R

R

ln

R

R

p

dr

r

r

R

ln

R

R

ln

p

R

p

W

R

R

















Grubość warstwy smaru w zależności od obciążenia W [kN], ciśnienia 

zasilania Q[m

3

/s], lepkości [Pa s]  i geometrii podpory (R i R

0

  [m])

3

2
0

2

W

)

R

Q(R

3







h

 

 

Teoria smarowania elastohydrodynamicznego.  

Łożyska toczne

Elastohydrodynamic
zne 

smarowanie 

dwóch 

nie- 

odkształcalnych 

 

nieskoń- 

czenie 

długich walców jako 
kontakt zastępczy 

Wzór Grubina – Erdela

]

[

6

1

13

0

1

43

0

03

0

7

0

6

0

m

W

E

)

U

(

,

h

,

,

,

zast

,

,











Gdzie:



zast

E

W

W

1

1



2

1

2

1

1

R

R

R

R







E

E

zast

2

1

1







W

1

[kN/m],  piezowspółczynnik np. 

=2·10

-8

 m

2

/N, E[Mpa], =0,3, U[m/s]