1

Niezawodność konstrukcji – część

3

Andrzej S. Nowak

University of Lincoln, Nebraska

Plan wykładów

• Część 1 Losowość w budownictwie
• Część 2 Symulacje (metoda Monte Carlo)

Procedury analizy niezawodnościowej

• Część 3 Opracowywanie norm projektowych

Modele obciążeń i nośności

• Część 4 Niezawodność układów

konstrukcyjnych

Aktualne badania i kierunki rozwoju

2

MODELE OBCIĄŻEŃ

• Obciążenia stałe
• Obciążenia zmienne

(budynków i mostów, statyczne i dynamiczne)

• Obciążenia wpływami środowiska

(wiatr, śnieg, trzęsienie ziemi)

• Obciążenia wyjątkowe

(kolizja, pożar, podmycie fundamentów)

• Kombinacje obciążeń

3

MODELE OBCIĄŻEŃ KONSTRUKCJI

Aby zaprojektować konstrukcję, projektant musi przewidzieć
rodzaje i rozmiary obciążeń, które mogą na nią oddziaływać
przez cały okres jej eksploatacji.

Rodzaje obciążeń:

•

Obciążenia typu I

•

Obciążenia typu II

•

Obciążenia typu III

4

RODZAJE OBCIĄŻEŃ KONSTRUKCJI

•

Obciążenia typu I

- ustala się je na podstawie pomiarów ich intensywności,
ich zależności od czasu nie uwzględnia się;
należą do nich obciążenia

stałe

i

zmienne długotrwałe

.

•

Obciążenia typu II

- ustala się je na podstawie pomiarów w określonych przedziałach czasu;
ich zależność od czasu uwzględnia się w pewnym stopniu;
należą do nich obciążenia

wiatrem

,

śniegiem

i

zmienne krótkotrwałe

.

•

Obciążenia typu III

- ustala się je na podstawie pomiarów przeprowadzanych rzadko,
ponieważ pomiary te nie zawsze jest możliwe;
występują podczas zdarzeń wyjątkowych:

trzęsienia ziemi

,

tornada

, itd.

5

OGÓLNY MODEL OBCIĄŻENIA

Efekt obciążenia, Q

i

, można opisać następująco:

Q

i

= A

i

B

i

C

i

gdzie:

A

i

- zmienna reprezentująca obciążenie

B

i

- zmienna reprezentująca sposób oddziaływania

obciążenia na konstrukcję

C

i

- zmienna reprezentująca niedokładność wynikającą

z przyjętej metody analizy konstrukcji i obciążenia:
modelowanie układu 3-wymiarowego 2-
wymiarowym, przyjęcie idealnego zamocowanych
podpór,
sztywnych węzłów, ciągłości materiału itp.

6

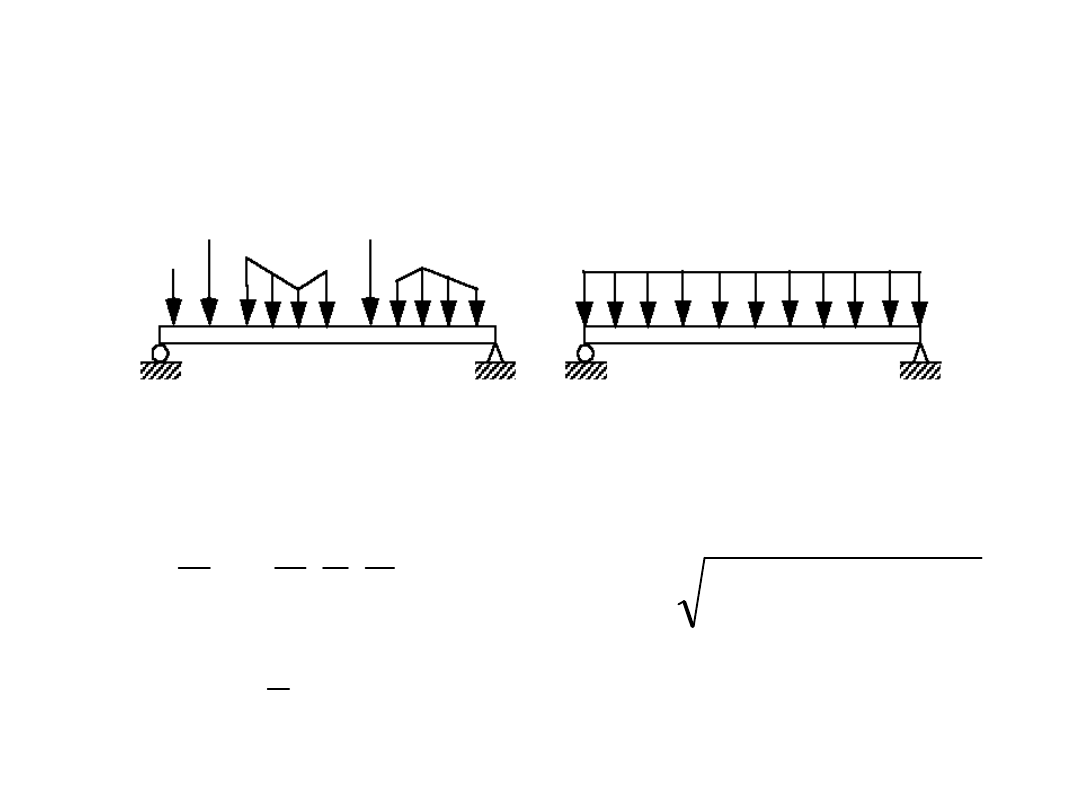
OGÓLNY MODEL OBCIĄŻENIA

Parametry obciążenia Q:

Modelowanie obciążeń działających na konstrukcję.

obciążenia rzeczywiste

model obciążenia

i

i

i

i

C

B

A

Q 

2

C

2

B

2

A

Q

i

i

i

i

V

V

V

V







Zwykle:

1

B

i



7

OGÓLNY MODEL OBCIĄŻENIA

W przypadku gdy kilka obciążeń działa jednocześnie,
całkowite obciążenie można opisać następująco:













2

2

2

1

1

1

C

B

A

C

B

A

C

Q

C - wspólny współczynnik dla wszystkich obciążeń

8

OBCIĄŻENIE STAŁE

Za obciążenie stałe przyjmuje się ciężar własny

konstrukcj
i elementów niekonstrukcyjnych na stałe z nią
połączonych.

Rozróżnia się:

• ciężar elementów żelbetowych monolitycznych
• ciężar elementów prefabrykowanych

(stalowych i żelbetowych)

• w przypadku mostów wyróżnia się ponadto:

ciężar nawierzchni (asfalt).

9

OBCIĄŻENIE STAŁE

Wszystkie składniki obciążenia stałego traktuje
się
jako zmienne losowe o rozkładach normalnych.
Przyjmuje się, że pozostaje ono niezmienne
przez cały okres eksploatacji konstrukcji.
Parametry statystyczne obciążenia stałego:

-----------------------------------------------------------------------------

-----------------------------------------------------------------------------
Budynki 1,00

0,06  0,09

0,08  0,10

Mosty

1,03  1,05

0,04  0,08

0,08  0,10

-----------------------------------------------------------------------------

n

D

D





2

B

2

A

V

V 

05

,

1

D

D

n







10

,

0

V

D



V

D

10

OBCIĄŻENIE ZMIENNE W

BUDYNKACH

• Obejmuje ono ciężar ludzi, przedmiotów, mebli, przenośnych

ścianek działowych, wyposażenia stałego i przenośnego.

• Modeluje się je zwykle jako równomiernie rozłożone.

Wartość projektową podaje się w kN/m

2

.

• Jego wielkość zależy od sposobu użytkowania konstrukcji. Wg

normy ASCE 7-95 Minimum Design Loads for Buildings and Other
Structures (minimalne obciążenia projektowe budynków i innych
konstrukcji)
waha się od 0,5 kN/m

2

(10 psf) - dla niezamieszkałych poddaszy,

do 12 kN/m

2

(250 psf) - dla powierzchni sklepów.

• Jego wielkość zależy także od przewidywanej liczby osób

użytkujących konstrukcję i od skutków ewentualnego zatłoczenia.

11

OBCIĄŻENIE ZMIENNE W

BUDYNKACH

2 kN/m

2

(200 kg/m

2

)

40 psf

5 kN/m

2

(500 kg/m

2

)

100 psf

1,8 m

1

,8

m

12

OBCIĄŻENIE ZMIENNE W

BUDYNKACH

7 kN/m

2

(700 kg/m

2

)

140 psf

13

OBCIĄŻENIE ZMIENNE W

BUDYNKACH

• Parametry statystyczne obciążenia zmiennego

zależą od pola powierzchni, na którą ono działa;
im ta powierzchnia jest większa, tym mniejsza jest
intensywność obciążenia.

• Rozróżnia się:

• powierzchnię, na którą działa obciążenie
• powierzchnia, z której zbiera się obciążenie

przy wymiarowaniu elementu (belki, słupa)

• ASCE 7-95 określa współczynnik redukujący wielkość

obciążenia zmiennego, będący funkcją

powierzchni, na którą działa obciążenie

14

OBCIĄŻENIE ZMIENNE W

BUDYNKACH

• Związek pomiędzy tymi powierzchniami jest następujący:

•dla belek

A

1

= 2  A

2

•dla słupów A

1

= 4  A

2

A

1

- powierzchnia, na którą działa obciążenie

A

2

- powierzchnia, z której zbiera się obciążenie

• Jeżeli A

1

> 400 ft

2

(37 m

2

)

, wartość projektową (nominalną)

obciążenia zmiennego L

n

oblicza się następująco:



















1

0

n

A

15

25

,

0

L

L

L

0

– obciążenie normowe równomiernie rozłożone

















1

0

n

A

4.57

25

,

0

L

L

[ ft

2

]

[ m

2

]

15

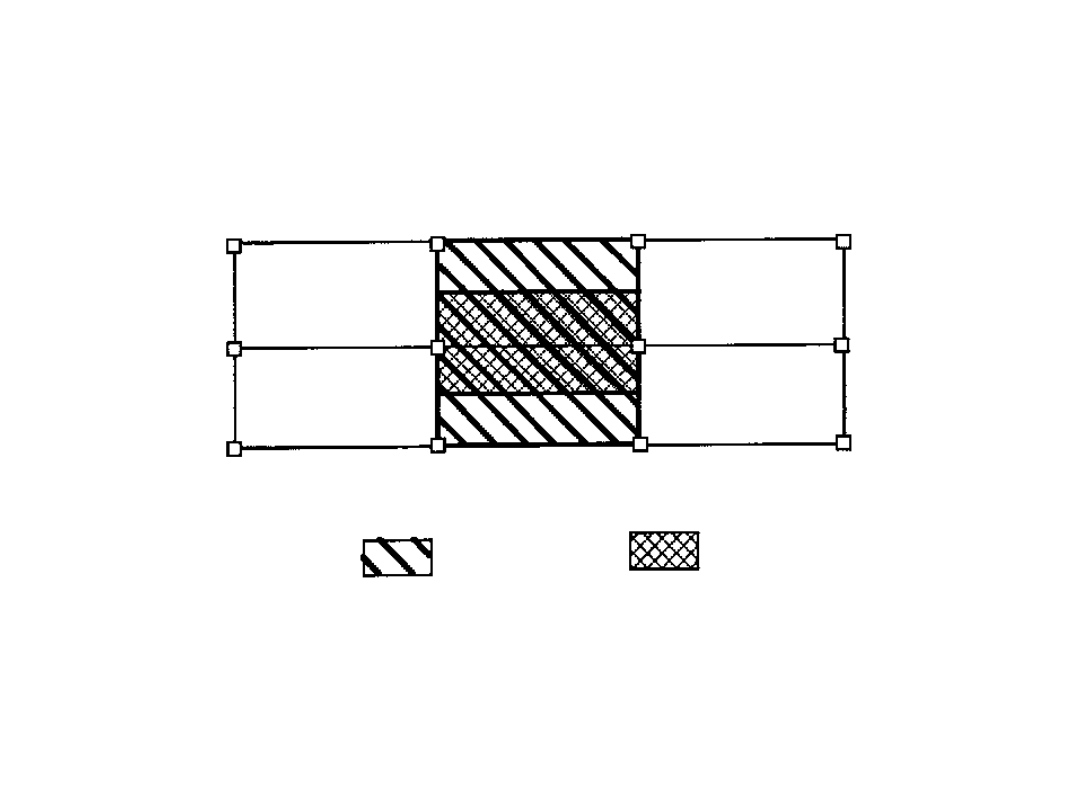
OBCIĄŻENIE ZMIENNE W

BUDYNKACH

Dla belek:

powierzchnia, na którą

działa obciążenie

powierzchnia, z której

zbiera się obciążenie

16

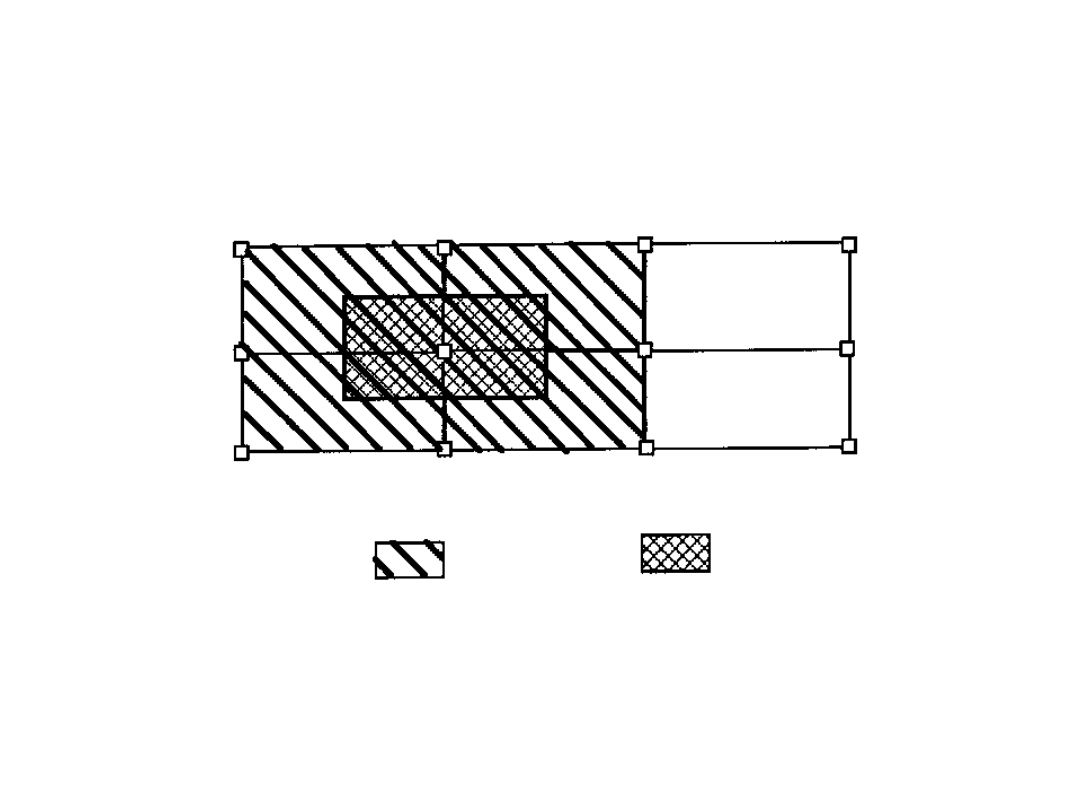
OBCIĄŻENIE ZMIENNE W

BUDYNKACH

Dla słupów:

powierzchnia, na którą

działa obciążenie

powierzchnia, z której

zbiera się obciążenie

17

OBCIĄŻENIE ZMIENNE DŁUGOTRWAŁE

•

Obciążenie zmienne długotrwałe

- ciężar ludzi, przedmiotów, mebli, wyposażenia, przenośnych
ścianek działowych; najczęściej w biurach, mieszkaniach,
szkołach, hotelach itp.

•Termin „długotrwały” oznacza, że występuje ono w zwykłych

sytuacjach (nie wyjątkowych).Nazywa się je też obciążeniem
chwilowym
- w dowolnej chwili czasu - L

apt

(arbitraty-point-in-time)

•Modeluje się je niekedy rozkładem gamma.
•W przypadku biur i powierzchni A

1

< 400 ft

2

(37 m

2

)

24

,

0

psf

50

psf

12

L

L

n

apt









24

,

0

m

/

kN

5

.

2

m

/

kN

6

.

0

L

L

2

2

n

apt









18

OBCIĄŻENIE ZMIENNE DŁUGOTRWAŁE

Typowe wartości  i V obciążenia zmiennego

długotrwałego
w zależności od powierzchni A

1

:

-----------------------------------------------------------

-----------------------------------------------------------
400

37

0,24

0,59  0,89

1000

93

0,33

0,26  0,52

5000

465

0,52

0,20  0,41

10000

930

0,60

0,18  0,40

-----------------------------------------------------------

n

apt

L

L





A

1

[ ft

2

]

[m

2

]

V

A

1ft

2

= 0,093 m

2

V

B

= 0.10

V

C

= 0.05

19

OBCIĄŻENIE ZMIENNE KRÓTKOTRWAŁE

• Obciąże zmienne krótkotrwałe

- ciężar ludzi i przedmiotów, które może wystąpić
w nagłych wypadkach, gdy w jednym pomieszczeniu
zgromadzą się wszyscy użytkownicy lub przedmioty

• Ponieważ występuje rzadko i trudno jest je przewidzieć,

nazywa się te „krótkotrwałym”.

• Zależy od powierzchni A

1

.

..

------------------------------------------

------------------------------------------
400

37

0,14  0,23

1000

93

0,13  0,18

5000

465

0,10  0,16

10000

930

0,09  0,16

------------------------------------------

A

1

[ ft

2

]

[m

2

]

V

L

1ft

2

= 0,093 m

2

20

MAKSYMALNE OBCIĄŻENIE ZMIENNE

• Przy projektowaniu, należy brać pod uwagę kombinacje

obciążeń zmiennych długotrwałych i krótkotrwałych,
które mogą wystąpić w przewidywanym okresie
eksploatacji budynku (50-100 lat).

• Maksymalne obciążenie zmienne zależy od

zmian w czasie obciążenia krótkotrwałego,
czasu trwania obciążenia długotrwałego
(zmian sposobu użytkowania budynku)
przewidywanego okresu eksploatacji budynku
parametrów statystycznych innych zmiennych losowych.

• Całkowite maksymalne obciążenie zmienne,

można modelować rozkładem ekstremalnym typu I.

21

Minimalne obciążenia projektowe
budynków i innych konstrukcji

22

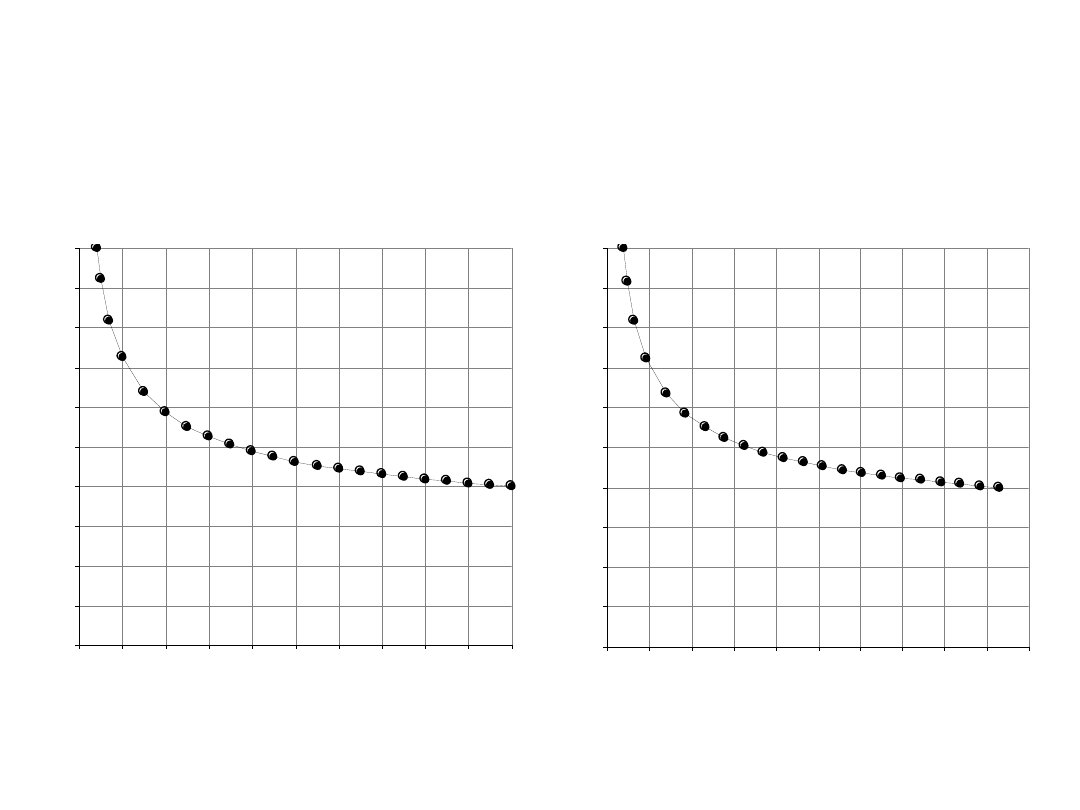
MAKSYMALNE OBCIĄŻENIE ZMIENNE

Wartość średnia z 50 lat maksymalnego obciążenia zmiennego

powierzchnia, na którą działa obciążenie A

1

[ft

2

]

L [psf]

0

5

10

15

20

25

30

35

40

45

50

0

10

00

20

00

30

00

40

00

50

00

60

00

70

00

80

00

90

00

10

00

0

0.00

0.25

0.50

0.75

1.00

1.25

1.50

1.75

2.00

2.25

2.50

0

10

0

20

0

30

0

40

0

50

0

60

0

70

0

80

0

90

0

10

00

L [kN/m

2

]

powierzchnia, na którą działa obciążenie A

1

[m

2

]

23

OBCIĄŻENIA WPŁYWAMI ŚRODOWISKA

Główne rodzaje obciążeń:

• obciążenie wiatrem
• obciążenie śniegiem
• obciążenia sejsmiczne
• oddziaływania termiczne

24

Obciążenie wiatrem

Główne parametry dotyczące wiatru:

•prędkość wiatru

•ciśnienie wiatru

•lokalizacja

•współczynnik porywów wiatru

•dynamiczna odpowiedź konstrukcji

Efekt działania wiatru można rozpatrywać jako iloczyn:

gdzie:

c - stała
C

P

- współczynnik ciśnienia wiatru (geometria konstrukcji)

E

Z

- współczynnik ekspozycji (lokalizacja, miasto, otwarta przestrzeń)

G - współczynnik podmuchu wiatru (turbulencja,

dynamiczne oddziaływanie konstrukcji i wiatru)

V - prędkość wiatru na wysokości 10 m.

2

z

P

V

G

E

C

c

W











25

Obciążenie wiatrem

• Wiatr modeluje się jako zmienną losową

o rozkładzie ekstremalnym typu I.

• Wszystkie parametry obciążenia wiatrem

są zmiennymi losowymi.

• Współczynniki odchylenia tych parametrów

można przyjmować:

• Współczynniki zmienności wynoszą:

• Stałą c można traktować jako wartość deterministyczną.

0

,

1





05

,

0

V

11

,

0

V

16

,

0

V

12

,

0

V

c

G

E

C

z

p









26

Obciążenie wiatrem

Dane dotyczące obciążenia wiatrem niektórych stanów USA:

Roczne

Max. z 50 lat

W / W

n

--------------------------------------------------------------------------------------------------------------------
stan

V

V

c.o.v

u



--------------------------------------------------------------------------------------------------------------------
Baltimore, MD

29

55,9 0,12

76,9 0,09 0,11

75

0,96 5,48

Detroit, MI

44

48,9 0,14

69,8 0,10 0,12

80

0,51 5,31

St. Luis, MO

19

47,4 0,16

70,0 0,11 0,14

70

0,62 3,18

Austin, TX

35

45,1 0,12

61,9 0,09 0,11

80

0,43 8,03

Tucson, AZ

30

51,4 0,17

77,6 0,11 0,14

70

0,69 2,52

Rochester, NY

37

53,5 0,10

69,3 0,08 0,09

70

0,71 4,83

Sacramento, CA

29

46,0 0,22

77,3 0,13 0,16

65

0,65 1,77

V

50

V

50

V

V

lata

pomiaru

wartości

normowe

27

Obciążenie śniegiem

Ciężar śniegu leżącego na dachu może stanowić znaczne
obciążenie konstrukcji usytuowanej w okolicach górskich.
W projektowaniu, obciążenie śniegiem dachu oblicza się
w parciu o informację o pokrywie śnieżnej gruntu.
Obciążenie śniegiem można taktować jako iloczyn:

gdzie:
p

g

- obciążenie śniegiem gruntu w kN/m

2

C

e

- współczynnik ekspozycji i kształtu dachu

C

t

- współczynnik termiczny

I - współczynnik konsekwencji zniszczenia

W przypadku dachów pochyłych:

gdzie:
C

S

- współczynnik pochylenia dachu

g

t

e

f

p

I

C

C

7

,

0

p











f

s

s

p

C

p





28

Obciążenie śniegiem

•Śnieg można modelować za pomocą rozkładu

logarytmiczno-normalnego i ekstremalnego typu I.

•Dane o rocznym obciążeniu śniegiem gruntu

wybranych stanów USA:

Roczne ekstremalne

Max. z 50 lat

obciążenie gruntu

obciążenie dachu

---------------------------------------------------------------------------------------------------------------
stan

lata



lnp



np

p

n

u



pomiaru

---------------------------------------------------------------------------------------------------------------
Green Bay, WI

26

2,01 0,70

28

0,87 5,07

Rochester, NY

26

2,49 0,56

34

0,83 6,16

Boston, MA

25

2,28 0,51

30

0,70 6,63

Detroit, MI

20

1,63 0,58

18

0,69 5,97

Omaha, NB

25

1,60 0,69

25

0,62 5,20

Cleveland, OH

26

1,50 0,58

19

0,60 6,30

Columbia, MO

25

1,21 0,84

20

0,69 4,05

Great Falls, MT

26

1,77 0,49

15

0,80 7,16

wartości

normowe

an

an

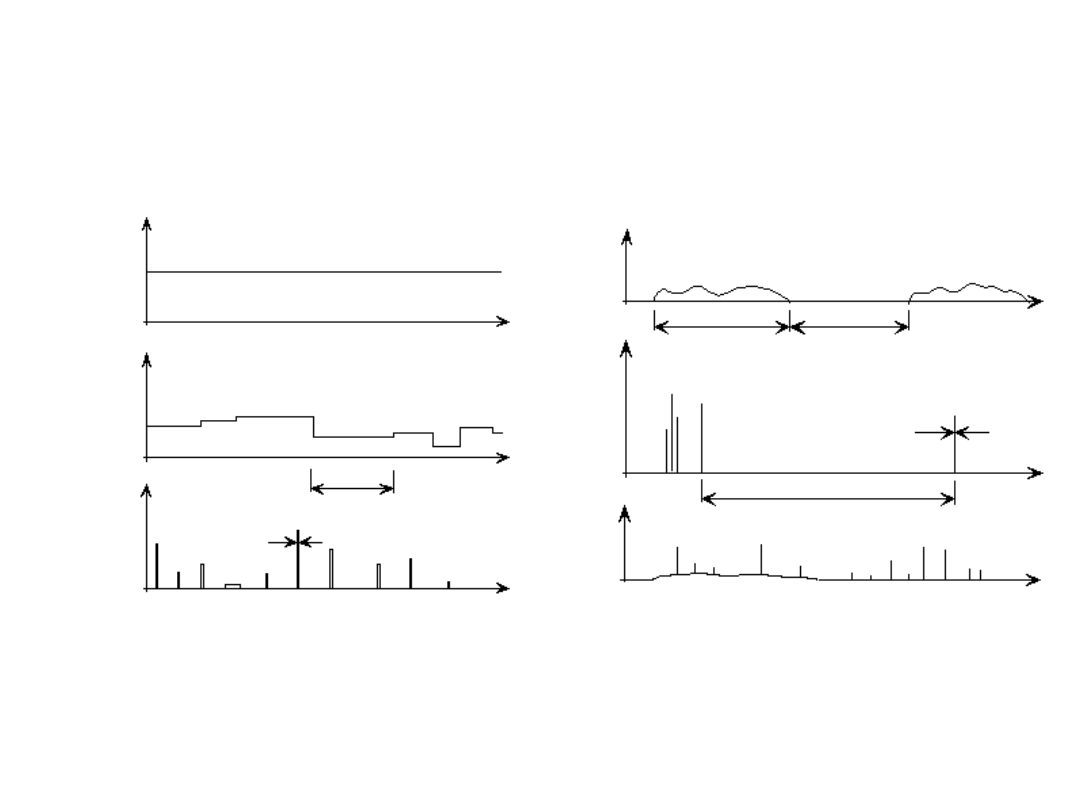
29

Przykłady rozkładu w czasie

rożnych składników obciążeń

obciążenie

stałe

obciążenie

zmienne

długotrwałe

obciążenie

zmienne

krótkotrwałe

śnieg

trzęsienie

ziemi

wiatr

czas

czas

czas

czas

czas

czas

zima

lato

n lat

0,5 minuty

kilka lat

kilka godzin lub dni

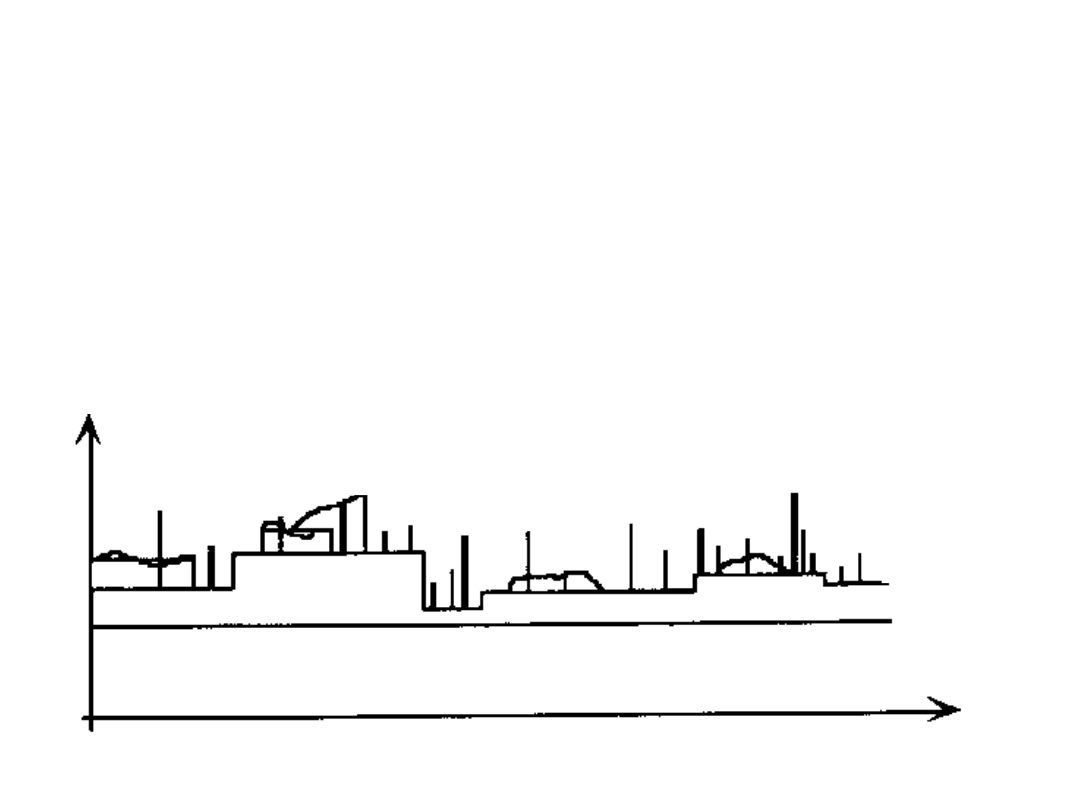
30

KOMBINACJE OBCIĄŻEŃ

•Całkowite obciążenie Q jest sumą szeregu składników

(stałego, zmiennego, śniegiem, wiatrem, sejsmicznych
termicznych, ... )

•Składniki obciążenia są zmienne w czasie a sporządzenie

ich dystrybuant jest bardzo trudne.

śnieg

obciążenie

zmienne

krótkotrwałe L

wiatr

obciążenie

zmienne

długotrwałe L

obciążenie

stałe D

31

Reguła Turkstry

Jest to praktyczne podejście do modelowania obciążenia.

Zakłada ono, że gdy jeden ze składników obciążenia
przybiera wartość ekstremalną, pozostałe składniki
przybierają wartości średnie.

Niech X

1

, X

2

, ..., X

n

oznaczają składniki obciążenia:

•Dystrybuanta wartości maksymalnej z 50 lat:

•Dystrybuanta w dowolnej chwili czasu:

n

2

1

X

X

X

Q











 





lat

50

ciagu

w

x

X

P

x

F

50

i

x





 





czasu

chwili

dowolnej

w

x

X

P

x

F

i

x





32

Reguła Turkstry jest następująca:

gdzie:

max X

i

= obciążenie X

i

maksymalne z 50 lat

ave X

j

= obciążenie X

j

w dowolnej chwili czasu

Wartość średnią i wariancję można obliczyć
następująco:

Reguła Turkstry
































n

2

1

n

2

1

n

2

1

max

aveX

aveX

aveX

aveX

X

max

aveX

aveX

aveX

X

max

max

Q























i

k

2
aveX

2

X

max

2

Q

max

k

i





















































n

2

1

n

2

1

n

2

1

max

aveX

aveX

aveX

aveX

X

max

aveX

aveX

aveX

X

max

Q

max









33

Reguła Turkstry

Przykład

Rozważmy kombinację obciążeń: stałego, zmiennego i wiatru.
Dane są ich parametry: wartość maksymalna i wartość średnia.

• Obciążenie stałe ma rozkład normalny:

• Dla obciążenia zmiennego,

max L

ma rozkład ekstremalny typu I:

• Dla obciążenia zmiennego,

ave L

ma rozkład gamma:

• Dla obciążenia wiatrem,

max W

ma rozkład ekstremalny typu I:

• Dla obciążenia wiatrem,

ave W

ma rozkład logarytmiczno-normalny:

%

10

V

,

20

D

D





%

12

V

,

30

L

max

L

max







%

31

V

,

9

L

ave

L

ave







%

20

V

,

24

W

max

W

max







%

60

V

,

1

W

ave

W

ave







Obliczyć parametry obciążenia całkowitego.

34

Reguła Turkstry

Obciążenie całkowite:

W

L

D

Q







Parametry max Q:















L

ave

W

max

W

ave

L

max

max

D

max

Q

max



 

 



2

2

2

2

2

2

2

2

Q

max

90

,

5

2

79

,

2

8

,

4

10

,

0

20

31

,

0

9

20

,

0

24























53

35

20

9

24

1

30

max

20

max

Q























max L

ave L

max L

ave L