Źródła napięcia

Każde źródło jest dwójnikiem
aktywnym.

Gdy do zacisków źródła (i tylko wtedy)
zostanie dołączony odbiornik, to w
utworzonym obwodzie elektrycznym
popłynie prąd.

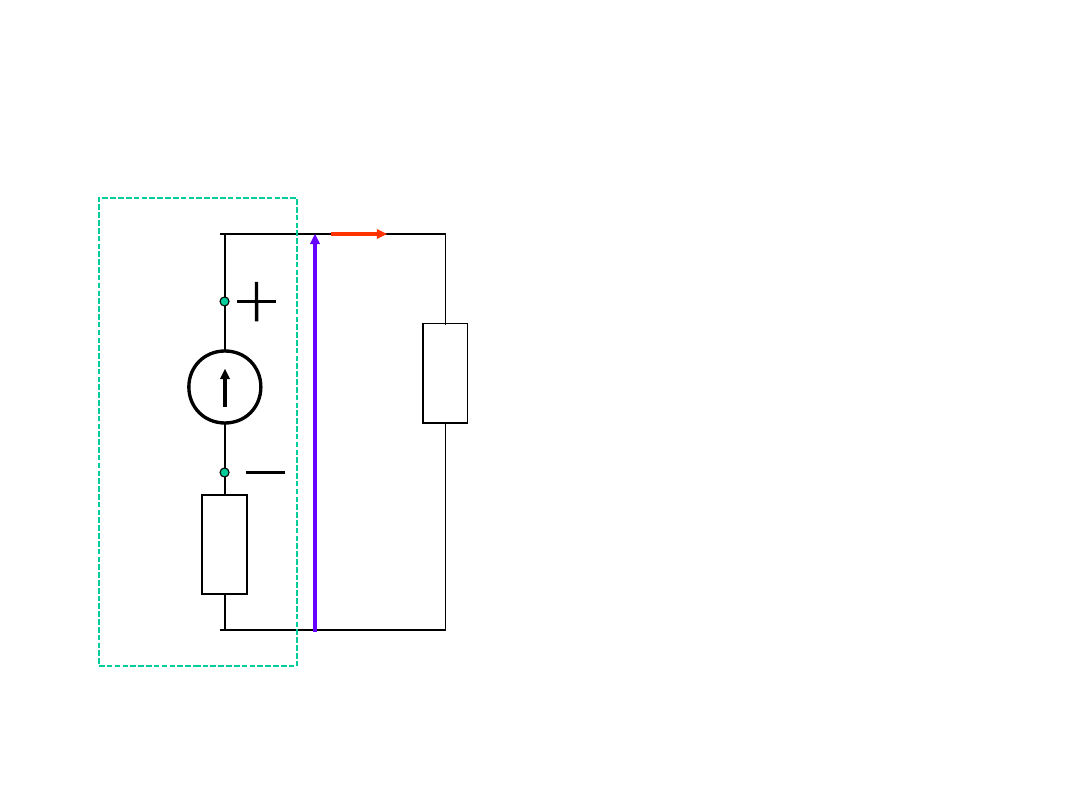
Źródła napięcia

R

E

U

I

R

w

I

R

E

U

w





Źródła napięcia

Każde źródło napięcia możemy więc
rozważać jako połączenie szeregowe
elementu- źródła idealnego i opornika
odwzorowującego rezystancję
wewnętrzną źródła.

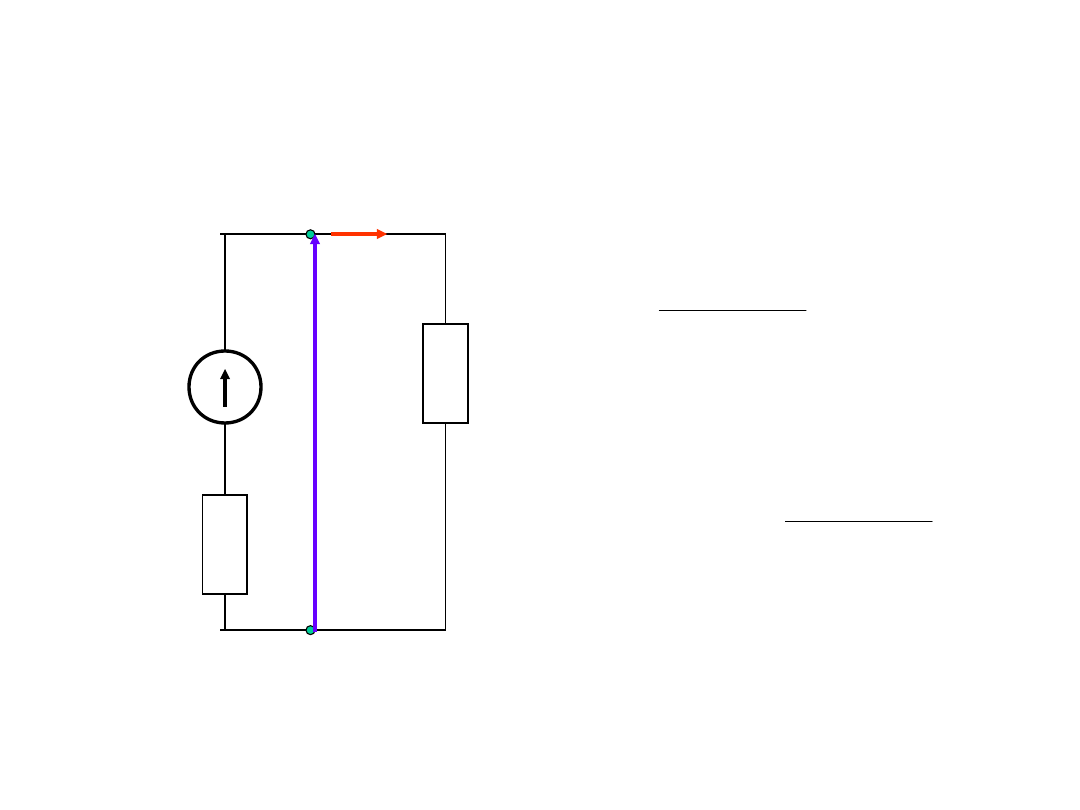
Źródła napięcia

R

o

E

U

I

R

w

o

o

w

o

o

w

R

R

R

E

IR

U

R

R

E

I











Zakładamy,
że:

const

R

const

E

w





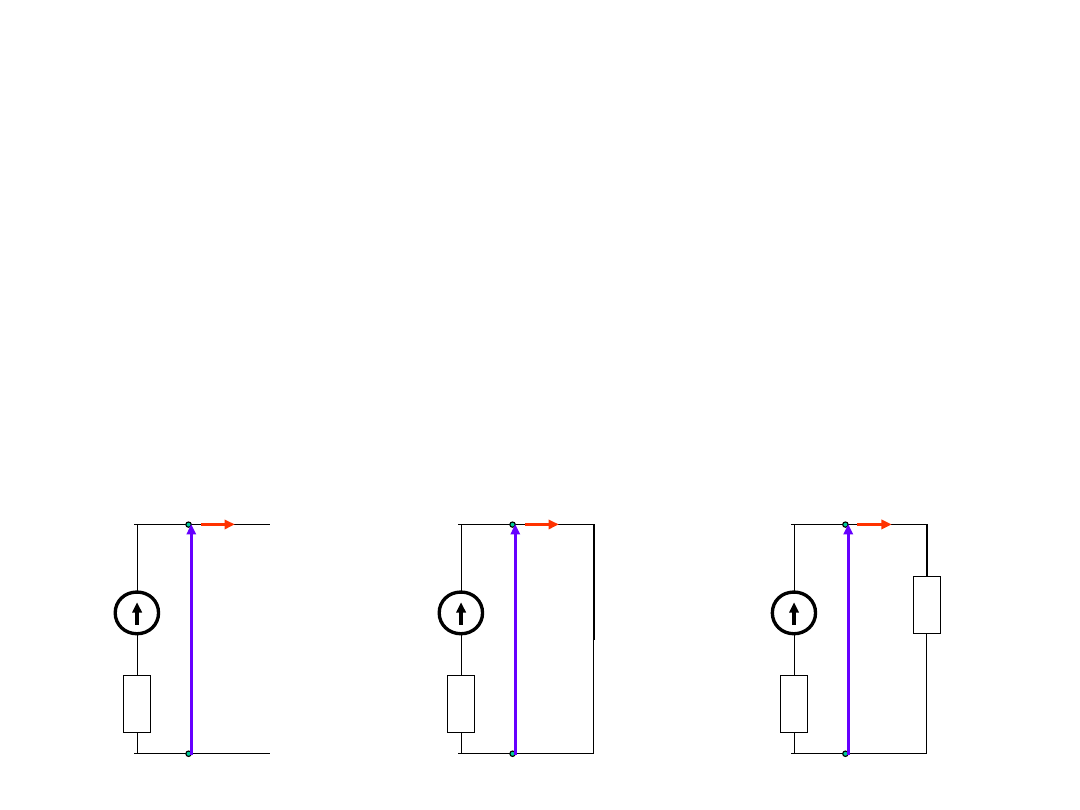
Źródła napięcia

Rozważymy trzy stany pracy obwodu:

1. stan jałowy
2. stan zwarcia
3. stan dopasowania

R

o

=

E

U

I

R

w

1

R

o

=0

E

U

I

R

w

2

R

o

E

U

I

R

w

3

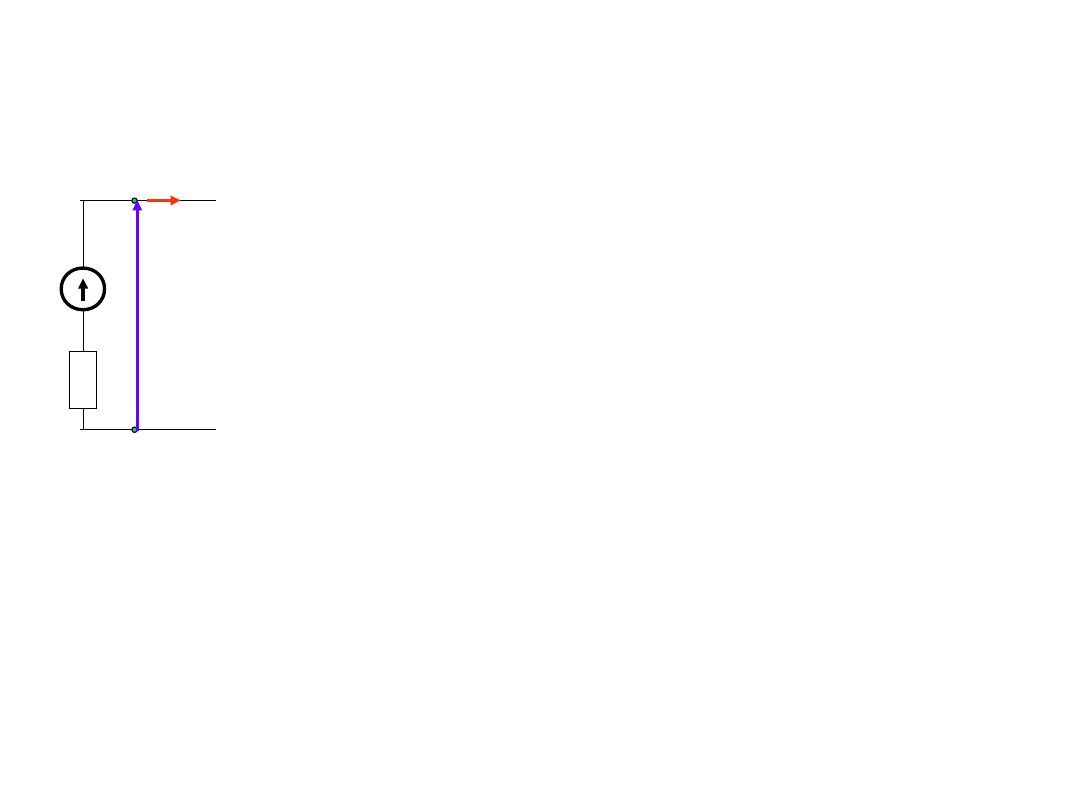
Źródła napięcia – stan jałowy

Stan jałowy

– występuje wówczas,

gdy nie ma obciążenia, czyli

zaciski źródła są rozwarte a więc:





o

R

Nie płynie prąd,
czyli:

0



I

Napięcie na zaciskach źródła osiąga
największą wartość:

E

U

U

U





0

- napięcie
jałowe

R

o

=

E

U

0=

I

R

w

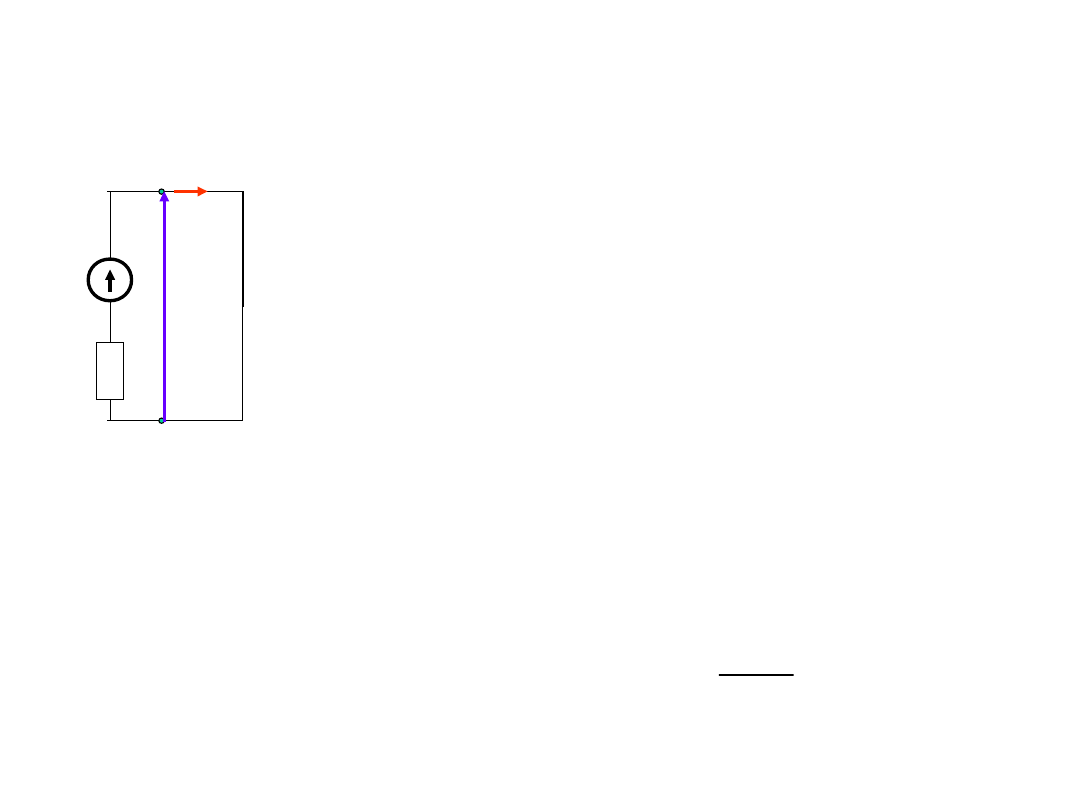
Źródła napięcia – stan zwarcia

Stan zwarcia

– występuje

wówczas, gdy zaciski źródła

są zwarte (połączone

bezpośrednio):

0



o

R

0



U

Napięcie na zaciskach
źródła:

w

z

R

E

I 

W obwodzie płynie największy możliwy
prąd (prąd zwarciowy):

R

o

=0

E

U=

0

R

w

I

z

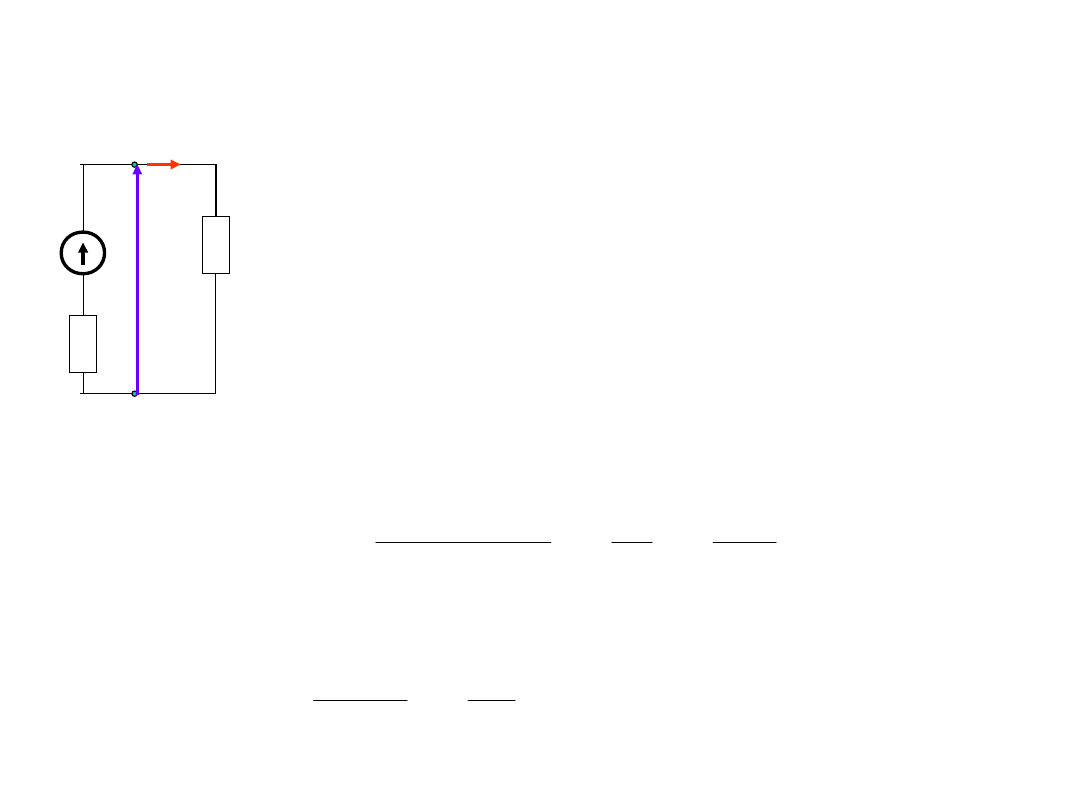
Źródła napięcia - dopasowanie

Stan dopasowania

– dopasowanie

odbiornika do źródła – po to aby
uzyskać największą możliwą moc:

w

o

R

R 

R

o

E

U

I

R

w

2

2

2

2

0

z

w

o

w

o

I

R

E

I

U

E

R

R

R

E

U













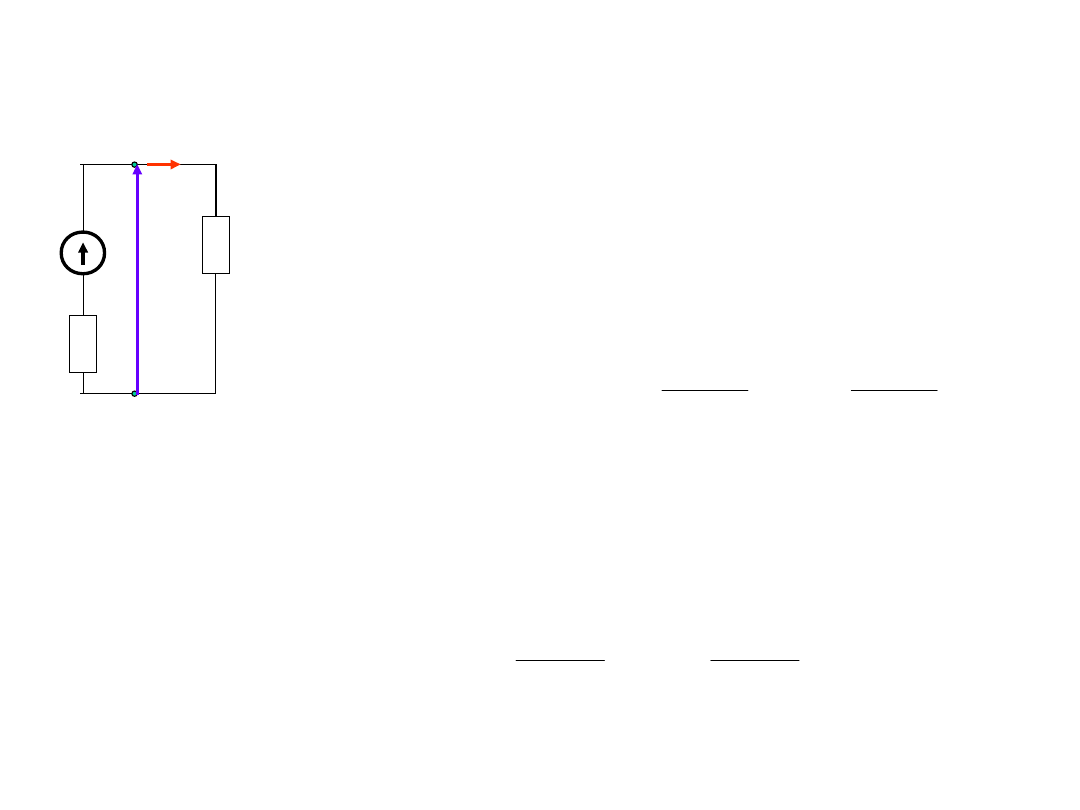
Źródła napięcia - dopasowanie

Moc dostarczona do odbiornika,
czyli moc pobrana (użyteczna,
wykorzystana):

R

o

E

U

I

R

w

w

w

w

R

E

R

E

R

I

R

P

4

2

2

2

2

0

2



















Moc pochłaniana przez źródło
(tracona):

w

w

w

w

R

E

R

E

R

I

R

P

4

2

2

2

2

1

'



















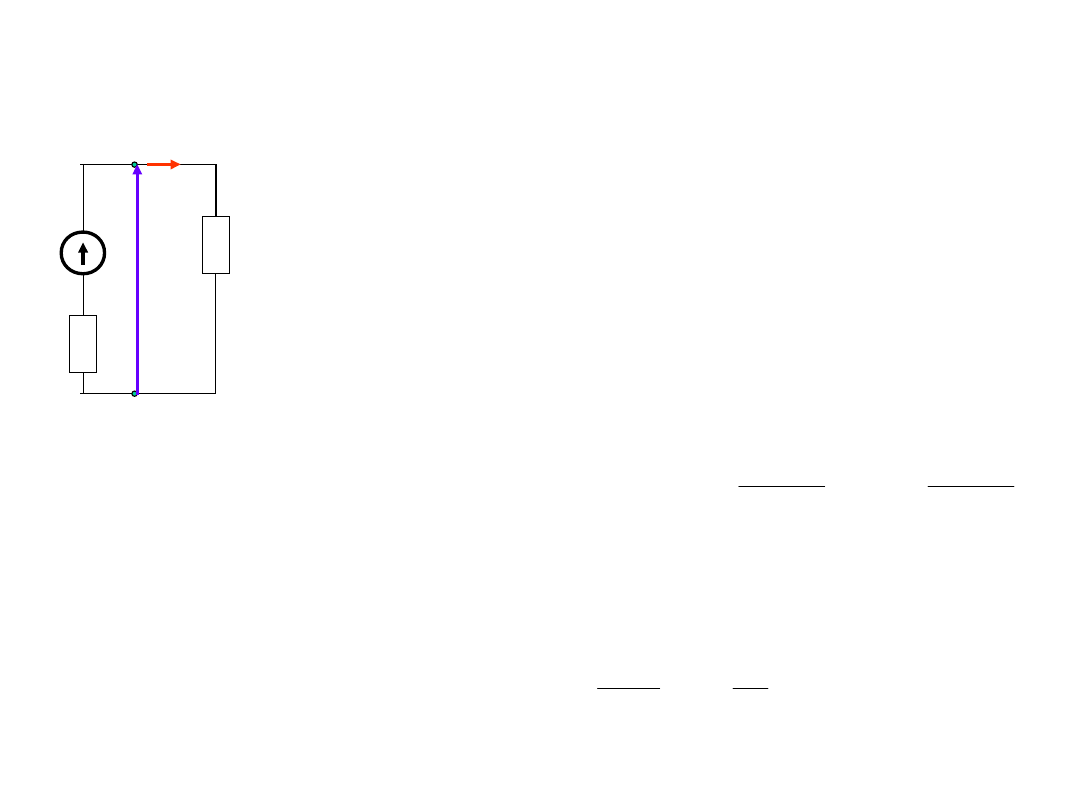
Źródła napięcia - dopasowanie

Moc wytworzona przez źródło
(dostarczona):

R

o

E

U

I

R

w





w

w

w

w

R

E

R

E

R

I

R

R

P

P

P

2

2

2

2

2

2

0

2

1

1

'



























Sprawność obwodu:

2

1

1

2





P

P



Źródła napięcia

Prąd i napięcie na zaciskach źródła są
zależne od przyłączonego do źródła
obciążenia.

Wyrazimy prąd i napięcie w
jednostkach względnych, czyli w
odniesieniu do odpowiednich wielkości,
które są stałe:

z

jw

jw

I

I

I

U

U

U





0

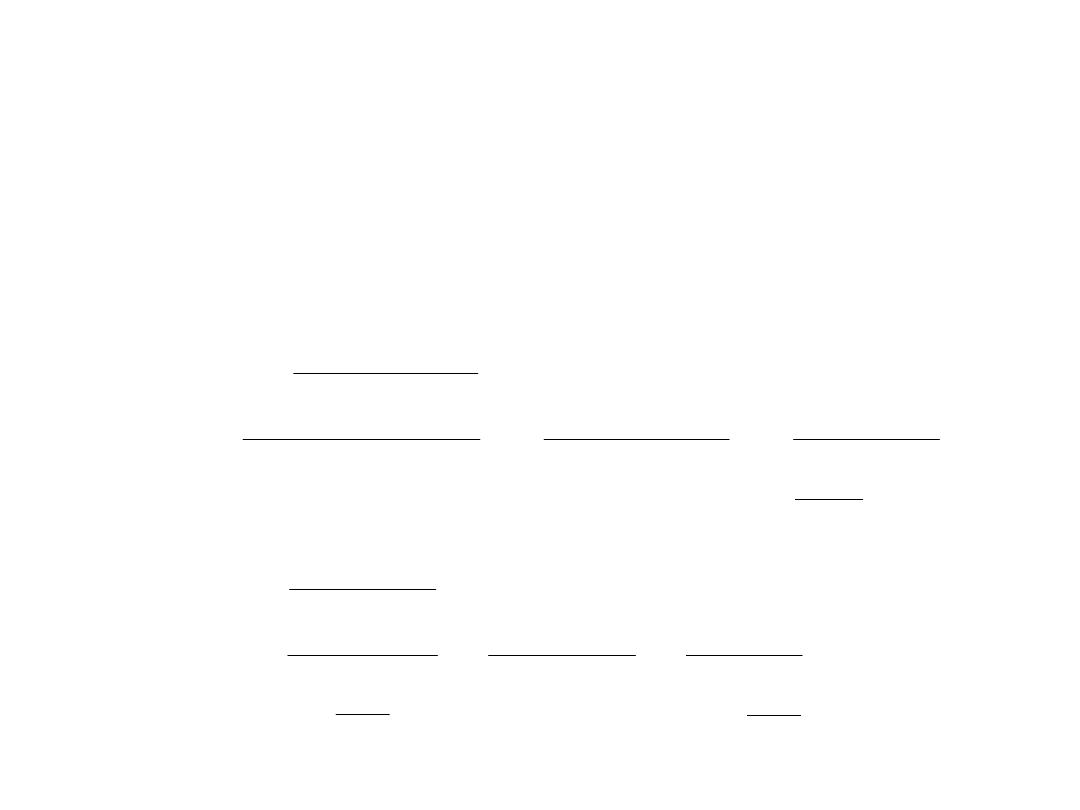
Źródła napięcia

Napięcie i prąd w jednostkach
względnych:

1

1

0













o

w

o

w

o

w

o

jw

R

R

R

R

R

E

R

R

R

E

U

w

o

o

w

w

w

o

w

jw

R

R

R

R

R

R

E

R

R

E

I













1

1

Źródła napięcia

0

0,2

0,4

0,6

0,8

1

1,2

0 1 2 3 4 5 6 7 8 9 10

U (jw.)
I (jw.)

U/U

0

I/I

z

R

o

/R

w

zwarci
e

stan jałowy

dopasowa
nie

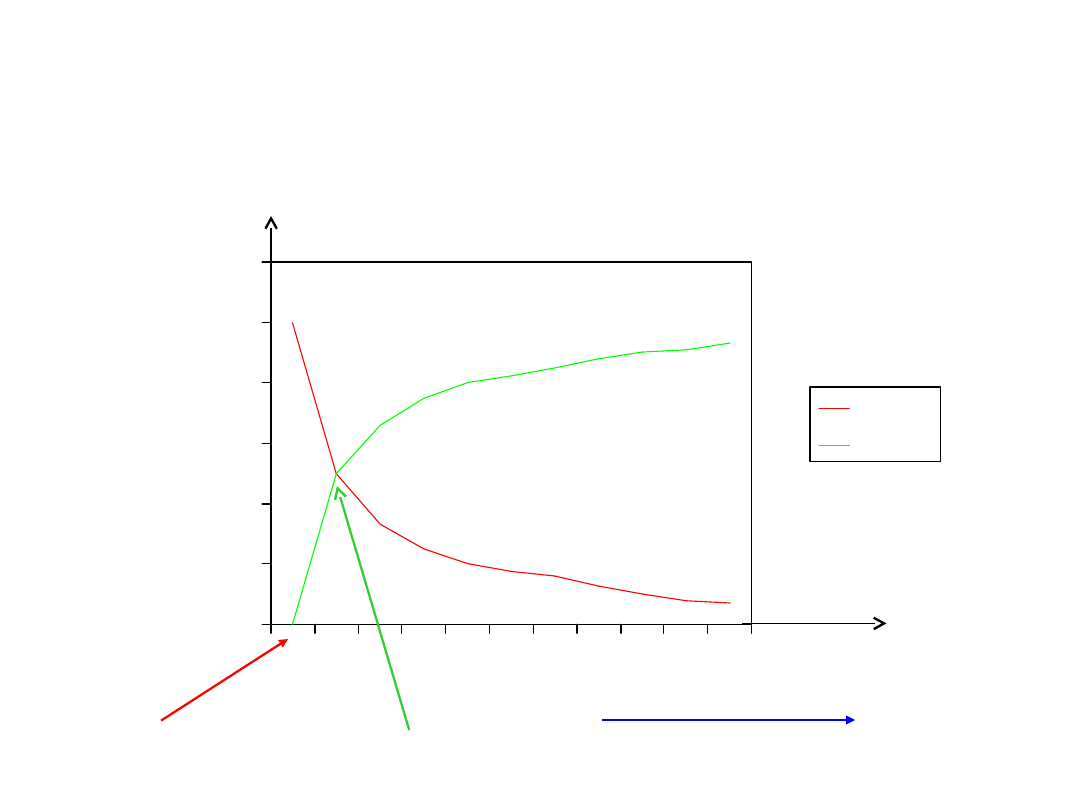
Źródła napięcia –

charakterystyka prądowo-

napięciowa

0

I

z

U

0

U

I

U= U

0

- R

w

I



w

R

z

i

u

R

c

I

c

U

c

tg





0



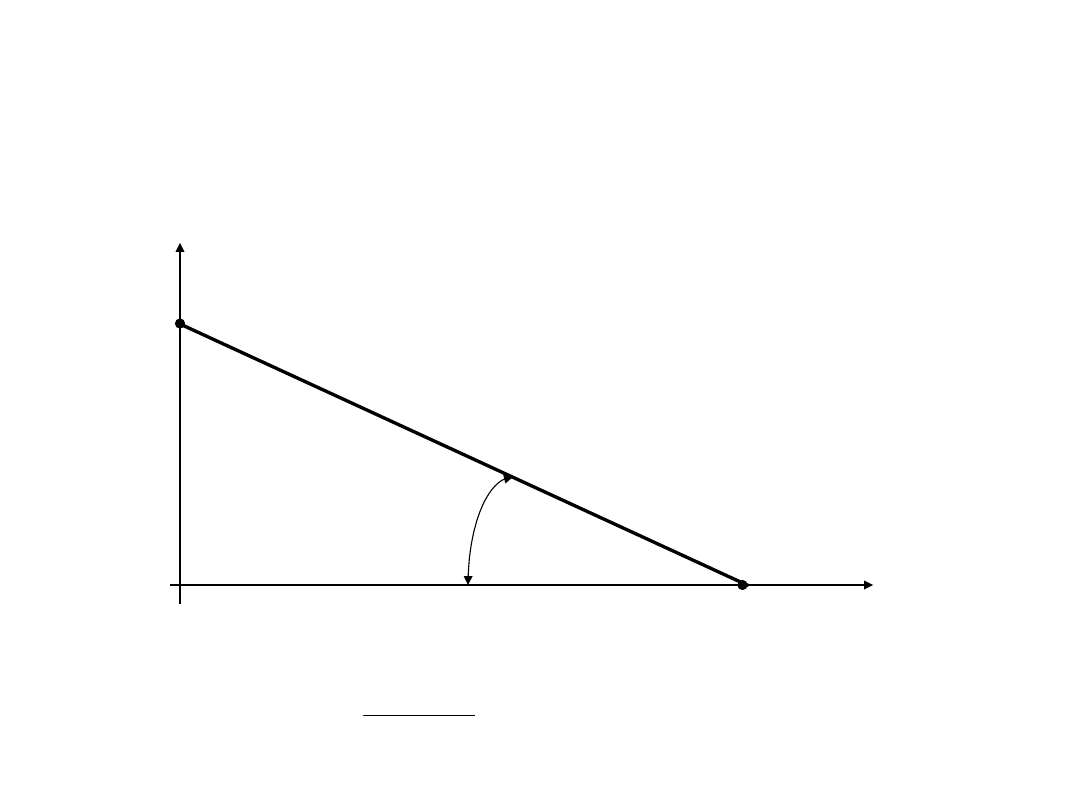
Odbiornik – charakterystyka

prądowo-napięciowa

o

R

R

c

tg 



0

U

I

U= R

o

I



R

o

rośnie

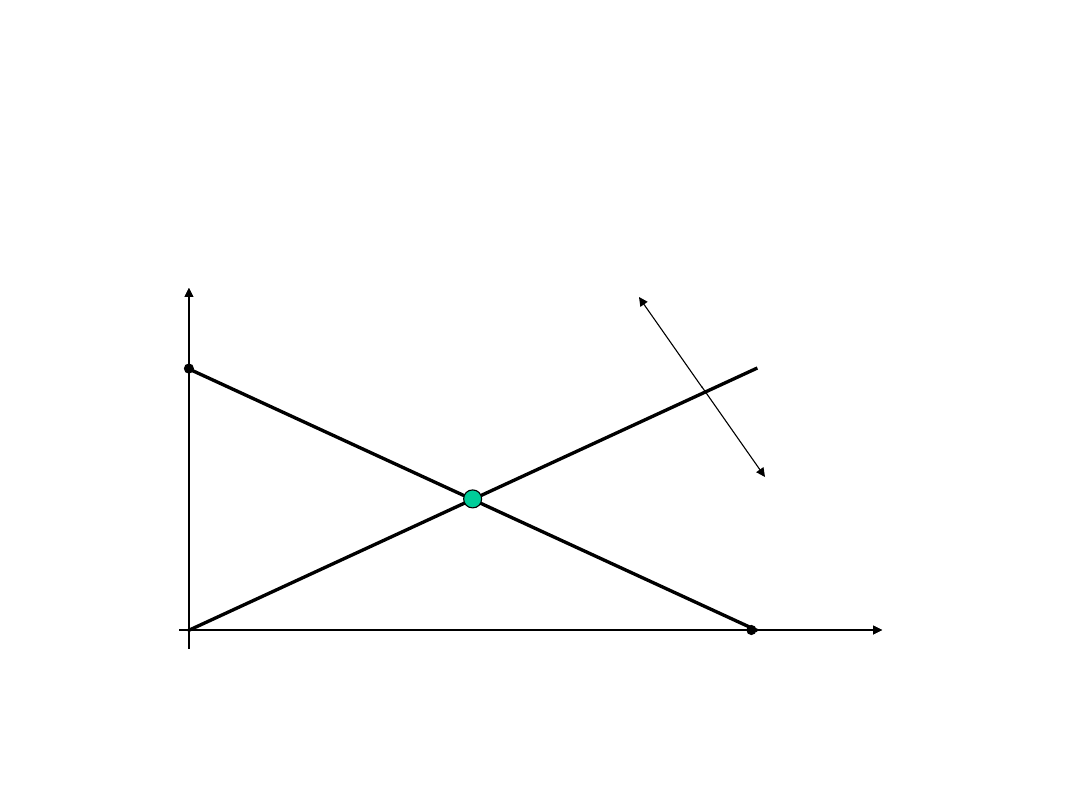
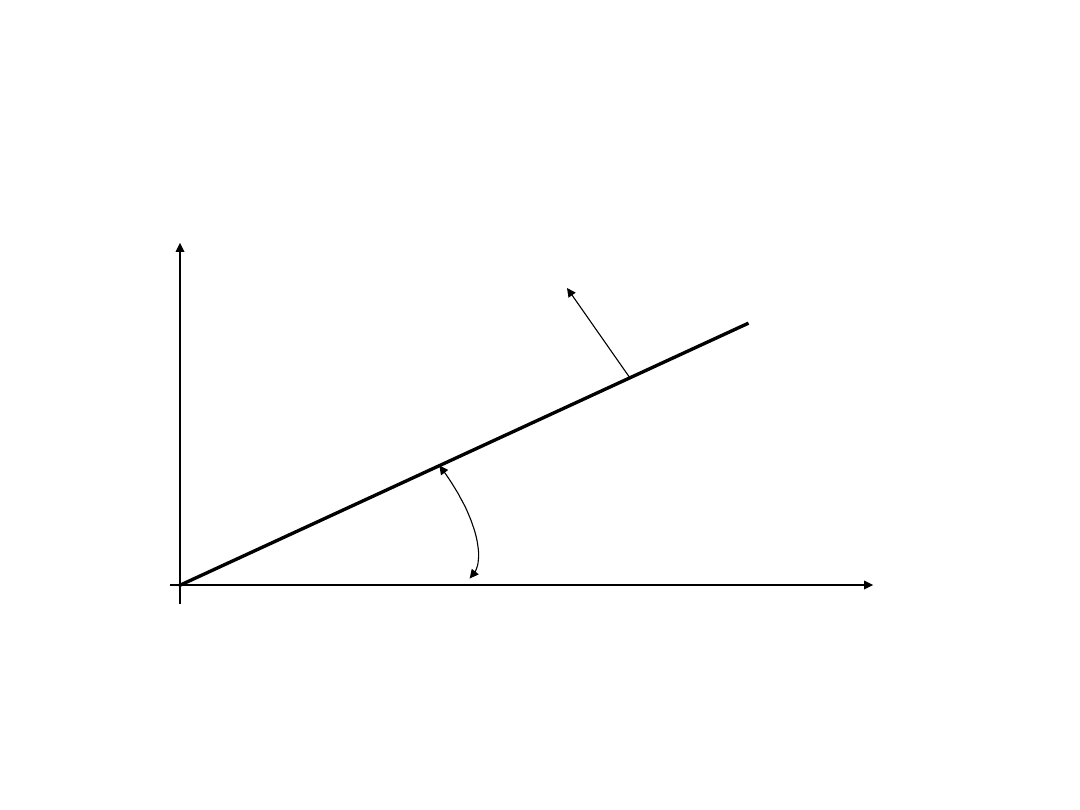
Obwód elektryczny –

charakterystyka prądowo-

napięciowa

stan zwarcia

0

U

I

R

o

I

0

I

z

U

0

U

I

U

0

- R

w

I

stan jałowy

P

P - punkt pracy

Łączenie źródeł napięcia

Połączenie szeregowe – takie, gdy
dodatni zacisk jednego źródła połączony
jest z ujemnym zaciskiem drugiego
źródła.

Połączenie równoległe- takie, gdy źródła
mają połączone w jeden węzeł
wszystkie zaciski dodatnie, a w drugi
węzeł wszystkie zaciski ujemne.

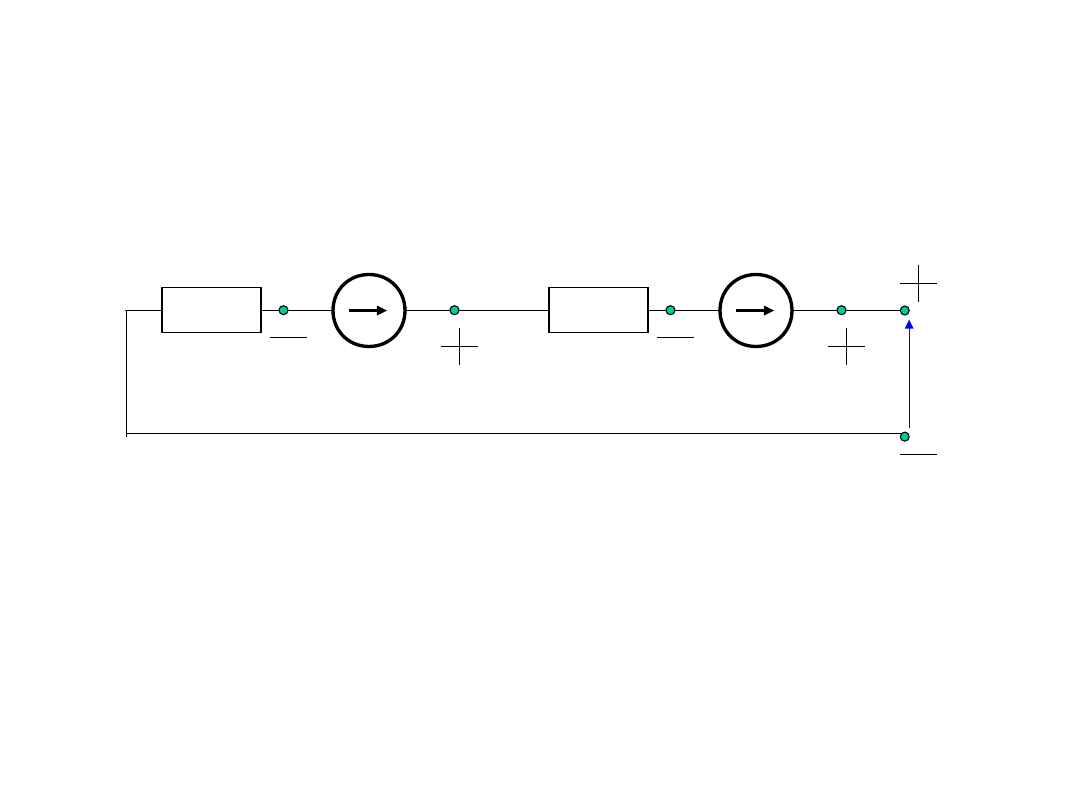
Połączenie szeregowe źródeł

napięcia

U

E

1

R

w

1

E

2

R

w

2





I

R

R

R

E

E

E

U

wn

w

w

n





























2

1

2

1













n

k

wk

n

k

k

R

I

E

U

1

1

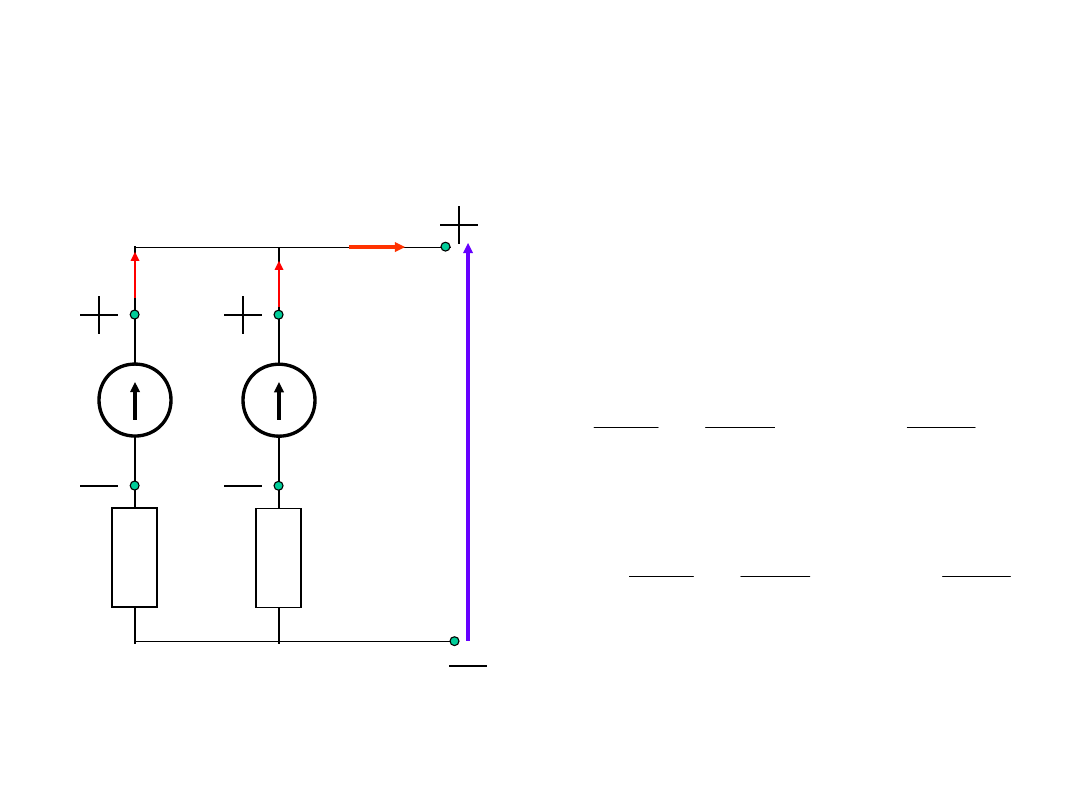
Połączenie równoległe źródeł

napięcia

U

I

E

1

R

w

1

E

2

R

w

2

I

2

I

1































































wn

w

w

wn

n

w

w

n

k

k

R

R

R

U

R

E

R

E

R

E

I

I

1

1

1

2

1

2

2

1

1

1

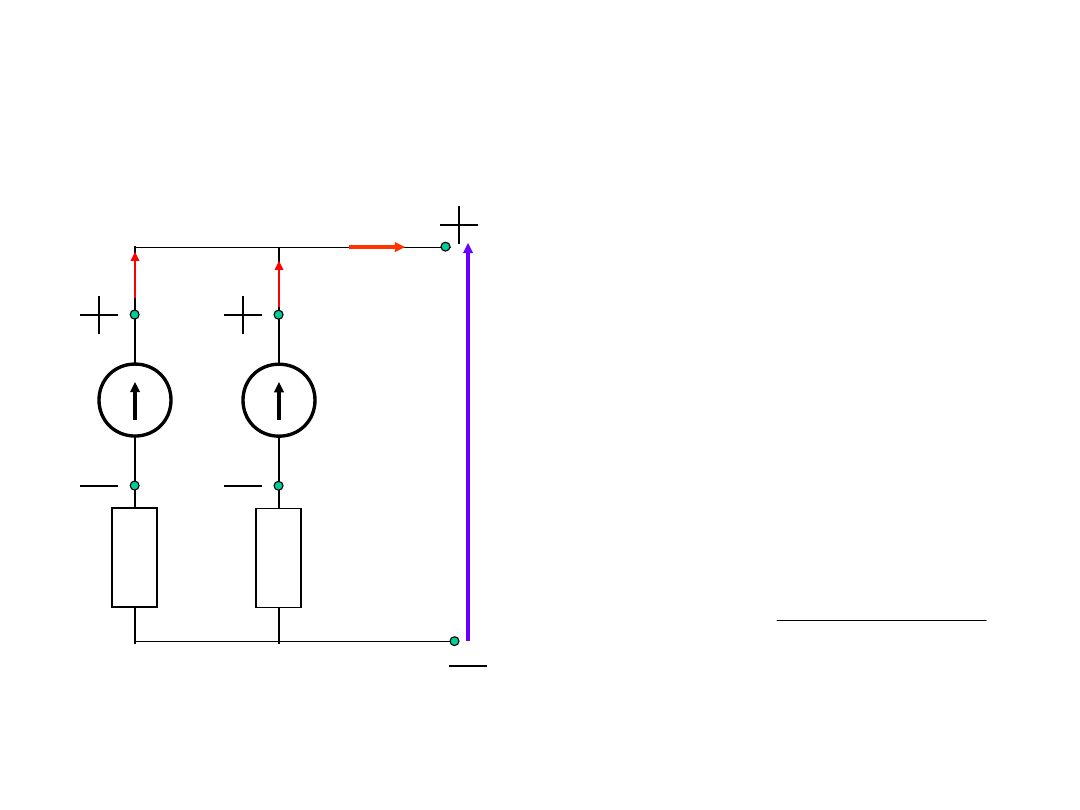
Połączenie równoległe źródeł

napięcia

U

I

E

1

R

w

1

E

2

R

w

2

I

2

I

1

Jeżeli równolegle
połączone są źródła w
stanie jałowym:

0

2

1



 I

I

Płynie prąd
wyrównawczy:

2

1

2

1

2

1

w

w

R

R

E

E

I

I











Źródła prądu

W wielu przypadkach wewnętrzna
rezystancja źródła energii jest
wielokrotnie większa niż rezystancja
obciążenia, czyli R

w

» R.

Prąd wydawany przez źródło jest bliski
wartości prądu zwarciowego:

z

w

w

I

R

E

R

R

E

I









Wówczas źródło energii możemy
rozpatrywać jako źródło prądu.

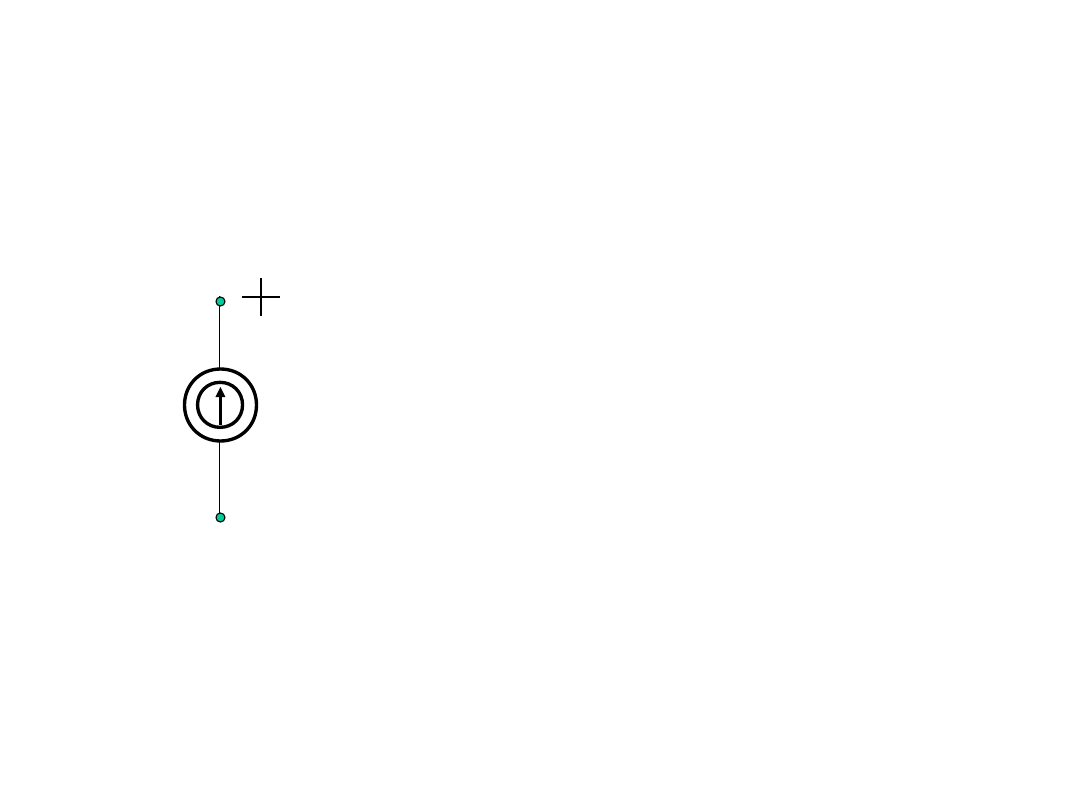
Idealne źródło prądu

I

z

Idealne źródło prądu to
dwójnik aktywny, którego
prąd nie zależy od napięcia
występującego na jego
zaciskach.

I

z

- wydajność prądowa

źródła

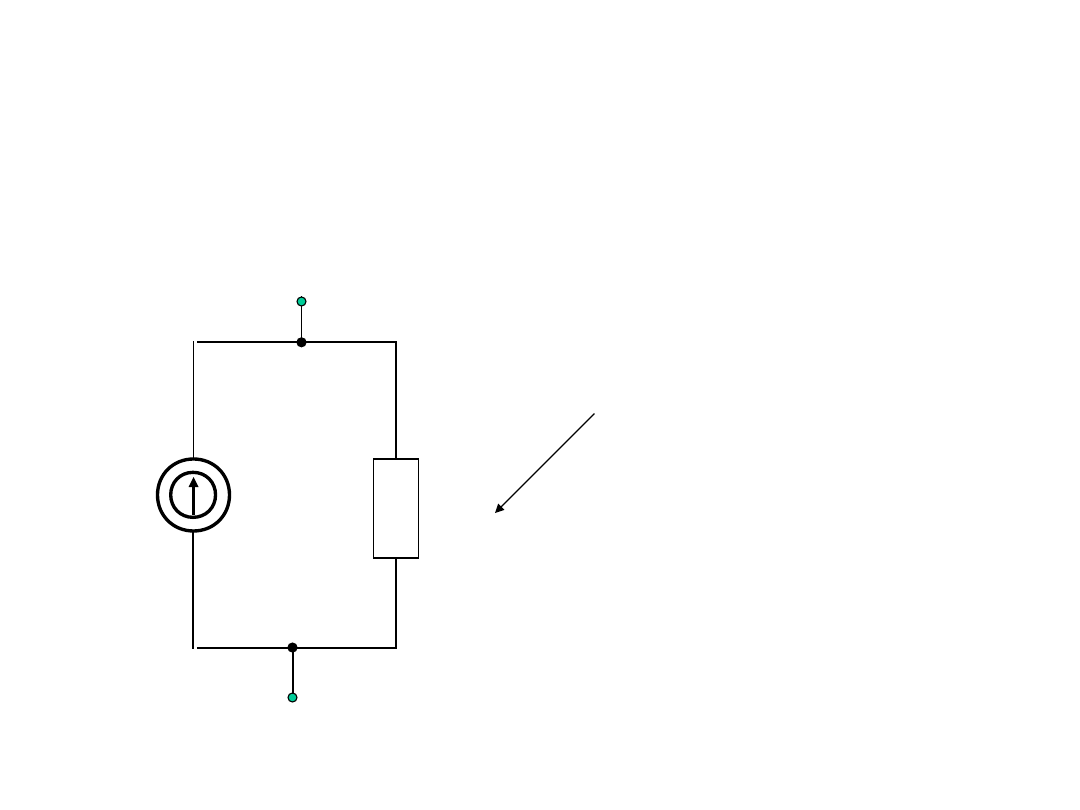
Rzeczywiste źródło prądu

I

z

R

w

bardzo duża
rezystancja
wewnętrzna

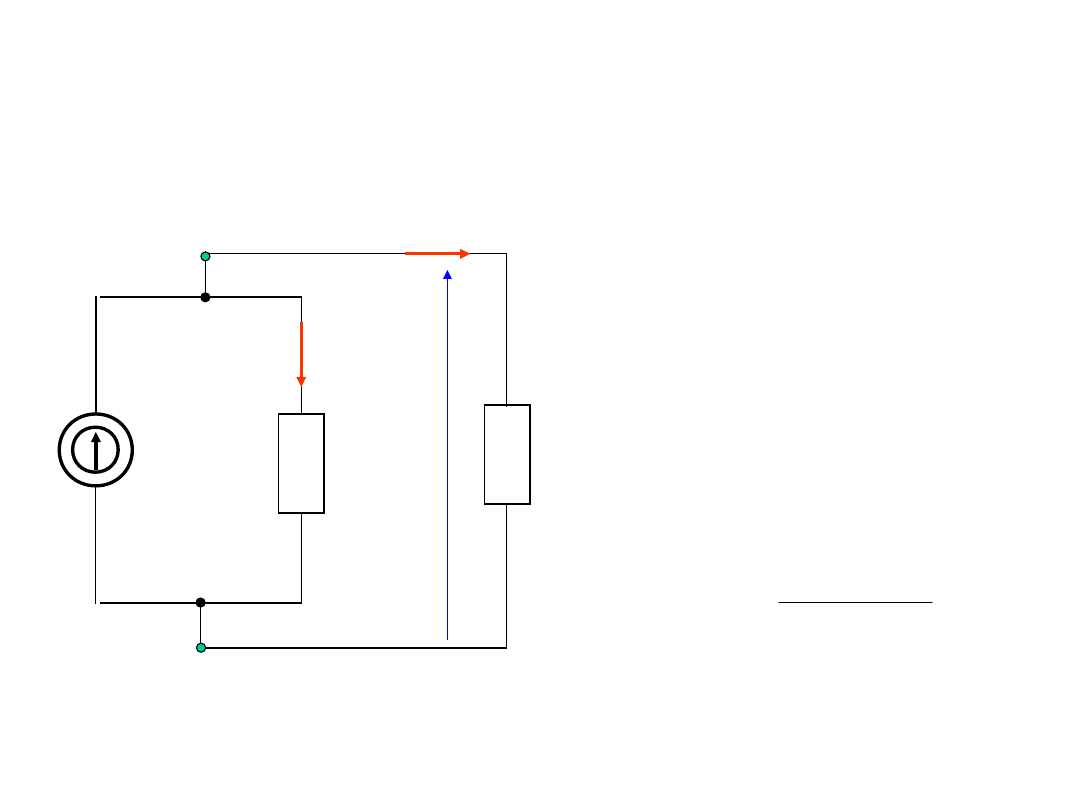
Rzeczywiste źródło prądu

I

I

z

R

w

R

I

w

U

W obwodzie
zawierają- cym
odbiornik R zasilany
z rzeczywistego
źródła prądu,
popłynie prąd
obciążenia:

R

R

R

I

I

w

w

z





Rzeczywiste źródło prądu

Źródło prądu może być równoważne
źródłu napięcia tylko wtedy gdy na
zaciskach wyjściowych obydwu źródeł
jest takie samo napięcie.

Rzeczywiste źródło prądu

Dla źródła napięcia:

R

R

R

E

I

R

E

U

wn

wn









Dla źródła prądu:

G

G

I

I

R

R

R

R

RI

U

wp

z

z

wp

wp











Rzeczywiste źródło prądu

Warunek równoważności jest
spełniony, gdy:

wp

R

E

I 

oraz
:

w

wp

wn

R

R

R





Rzeczywiste źródło prądu

Warunki równoważności nie spełniają
zależności energetycznych wewnątrz
źródeł. Straty mocy w źródłach są różne.

dla źródła
prądu:

w

w

w

R

U

I

R

2

2



dla źródła
napięcia:

2

2

















R

R

E

R

I

R

w

w

w

Sprawność obwodu

P

P

P

P

P

u

u

c

u











P

u

– moc użyteczna

P

c

– moc całkowita



P – straty mocy

Sprawność obwodu

P

u

– moc użyteczna przekazana do

odbiornika:

2

2



















o

w

o

o

u

R

R

E

R

I

R

P



P – moc tracona, pobrana przez źródło:

2



















o

w

w

R

R

E

R

P

Sprawność obwodu

P

c

– moc całkowita, wytworzona przez

źródło:

o

w

u

c

R

R

E

P

P

P











2

Sprawność obwodu:

o

w

w

o

o

c

u

R

R

R

R

R

P

P











1

1



Sprawność obwodu

W praktyce stosuje się dwa główne

przypadki pracy związane z bilansem
mocy:

1. Pracę przy dużej sprawności -   1
2. Pracę w stanie dopasowania -  =

0,5

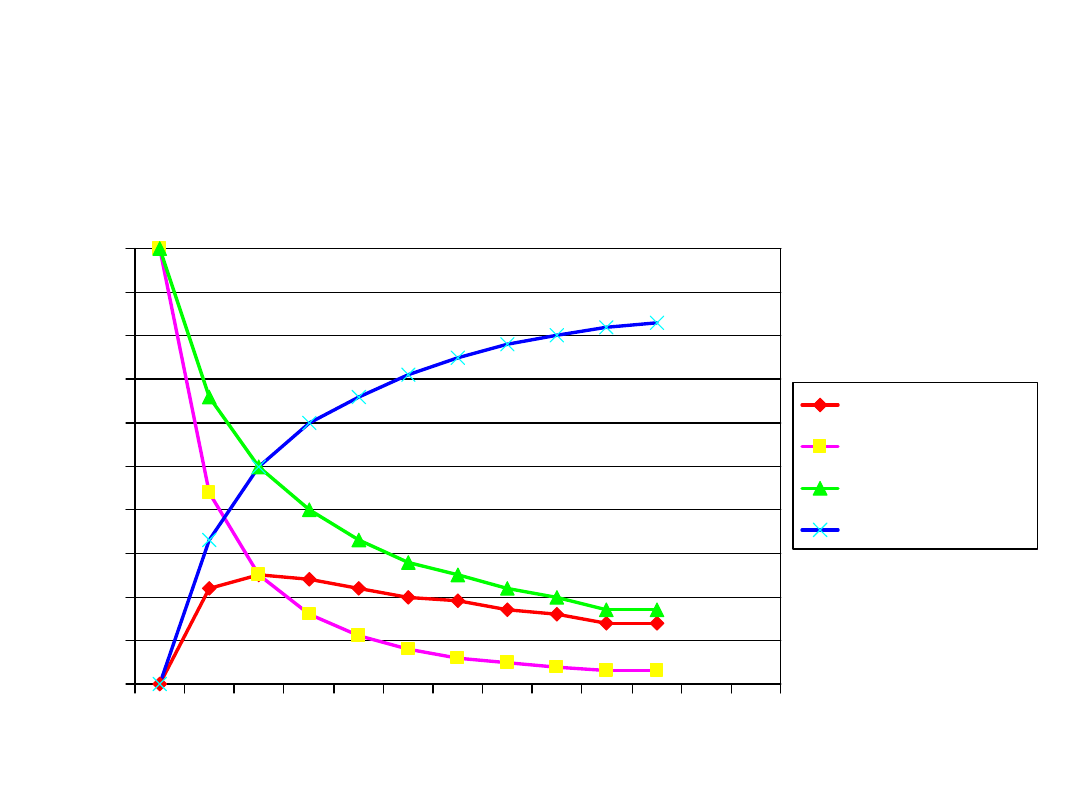
Sprawność obwodu

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1

0 0,5 1 1,5 2 2,5 3 3,5 4 4,5 5

moc użyteczna
moc tracona
moc cakowita
sprawność

Obwody nieliniowe

Obwody nieliniowe to takie, które
zawirają co najmniej jeden element
nieliniowy, np.. Opornik nieliniowy.

Dla elementów nieliniowych wprowadza
się dwa pojęcia rezystancji:
- rezystancja statyczna - R

st

- rezystancja dynamiczna - R

d

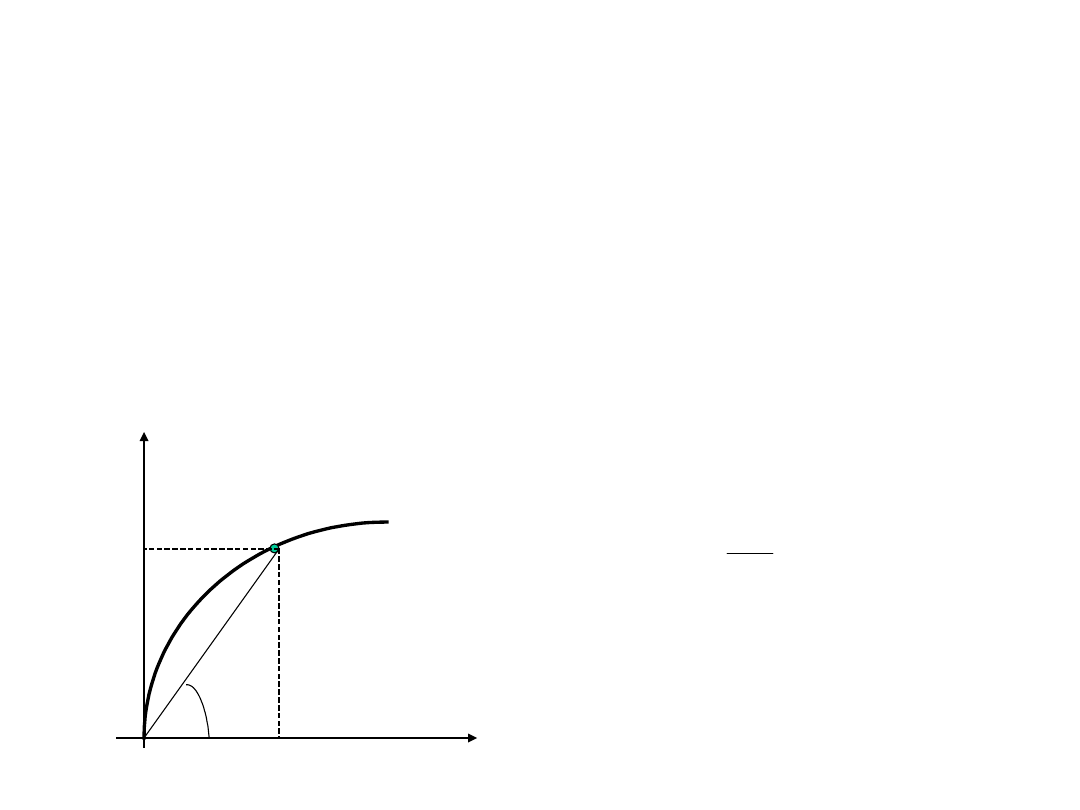
Rezystancja statyczna

Rezystancją statyczną w określonym
punkcie P charakterystyki napięciowo-
prądowej nazywamy stosunek napięcia do
prądu w tym punkcie.

U

U

I

I

P





tg

k

I

U

R

s

st





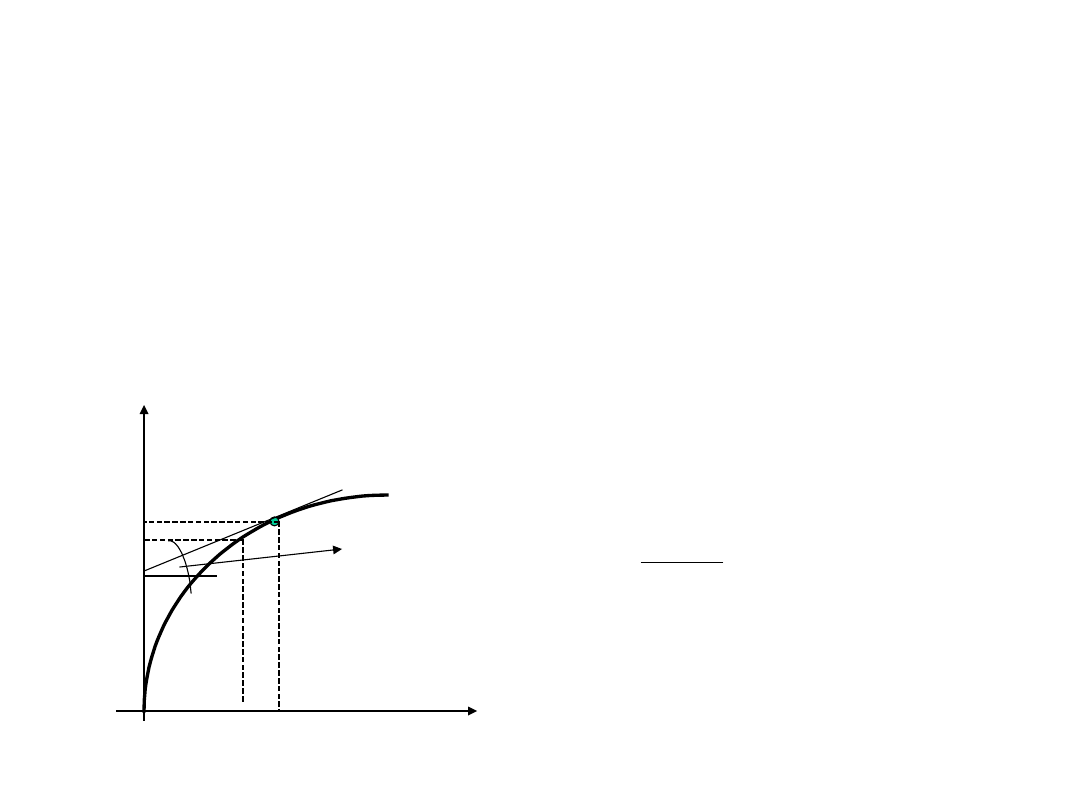
Rezystancja dynamiczna

Rezystancją dynamiczną w określonym
punkcie P charakterystyki napięciowo-
prądowej nazywamy pochodną napięcia
względem prądu w tym punkcie.

I



tg

k

dI

dU

R

d

d





U

P



U

p

+ U

U

p

I

p

+ I

I

p

Analiza obwodów nieliniowych –

metoda graficzna

Jeżeli znane są charakterystyki
napięciowo-prądowe elementów
charakterystykę elementu zastępczego
można znaleźć metodą graficzną:
- przez sumowanie charakterystyk
-metodą charakterystyk odwróconych.

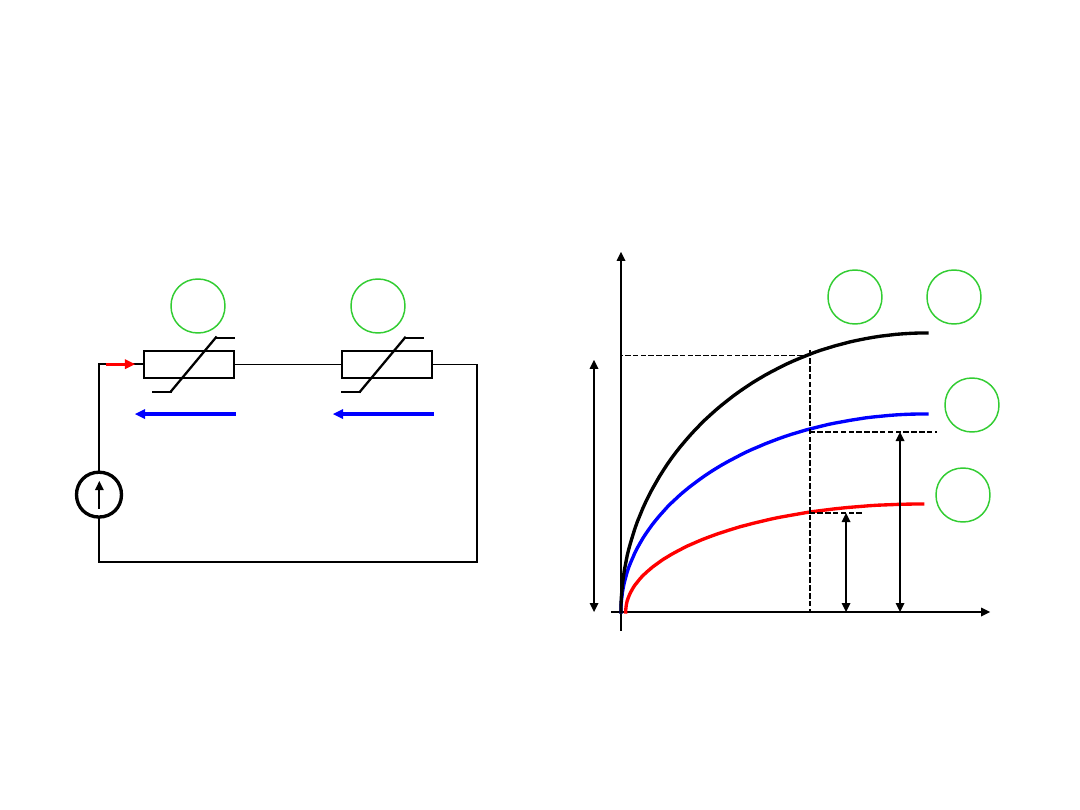
Szeregowe połączenie oporników

nieliniowych

I

U

1

U

2

2

E

1

2

E

U

I

I

U

1

U

2

1

1

+

2

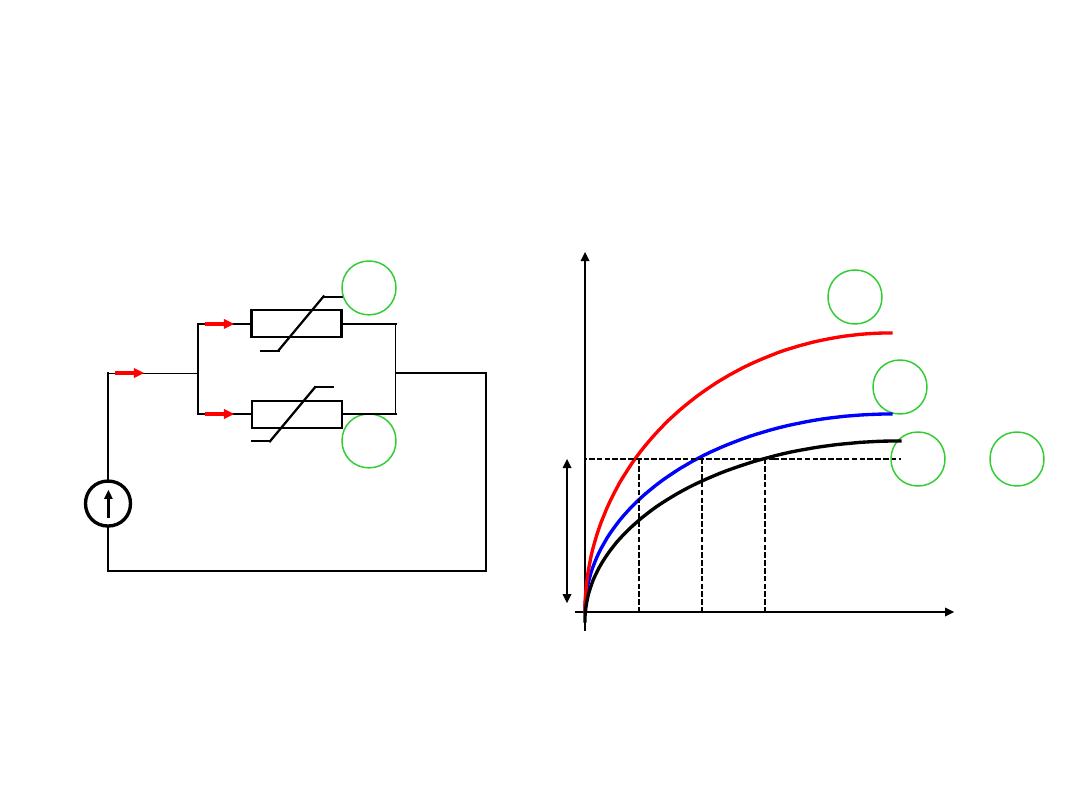
Równoległe połączenie

oporników nieliniowych

E

I

E

2

1

I

1

I

2

2

U

I

I

I

1

I

2

1

1

+

2

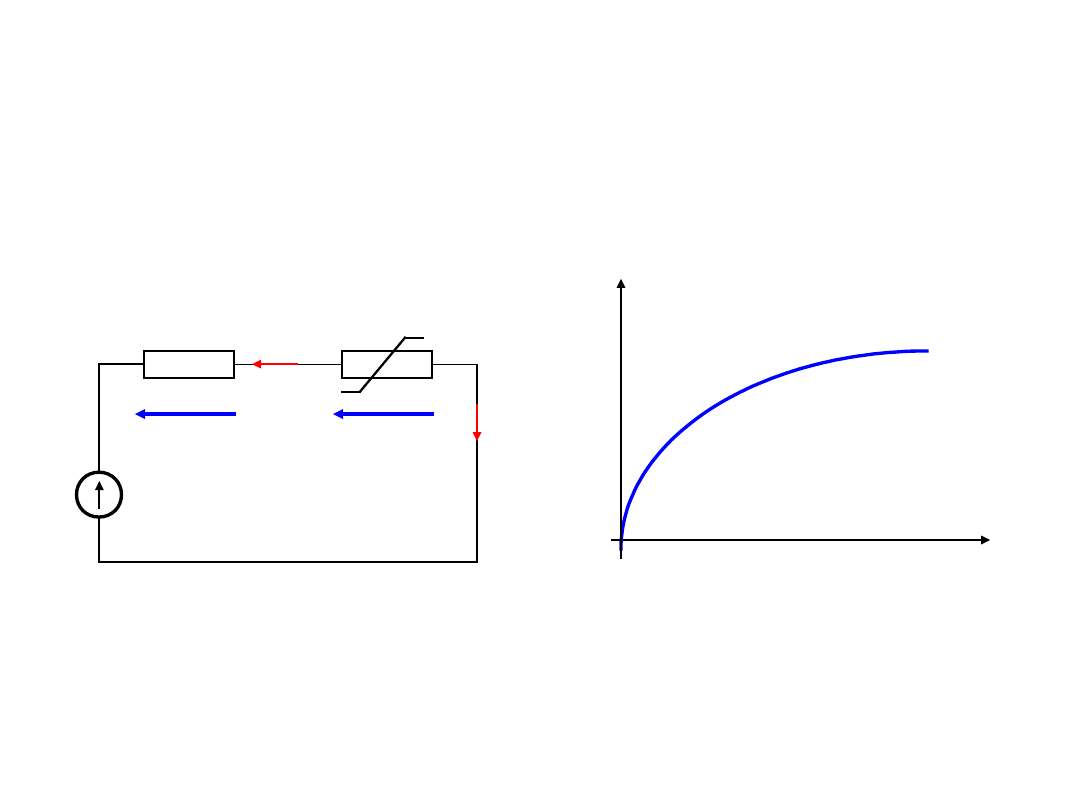
Połączenie elementu liniowego i

nieliniowego

I

1

U

1

=R

I

U

2

E

R

I

2

U

2

I

2

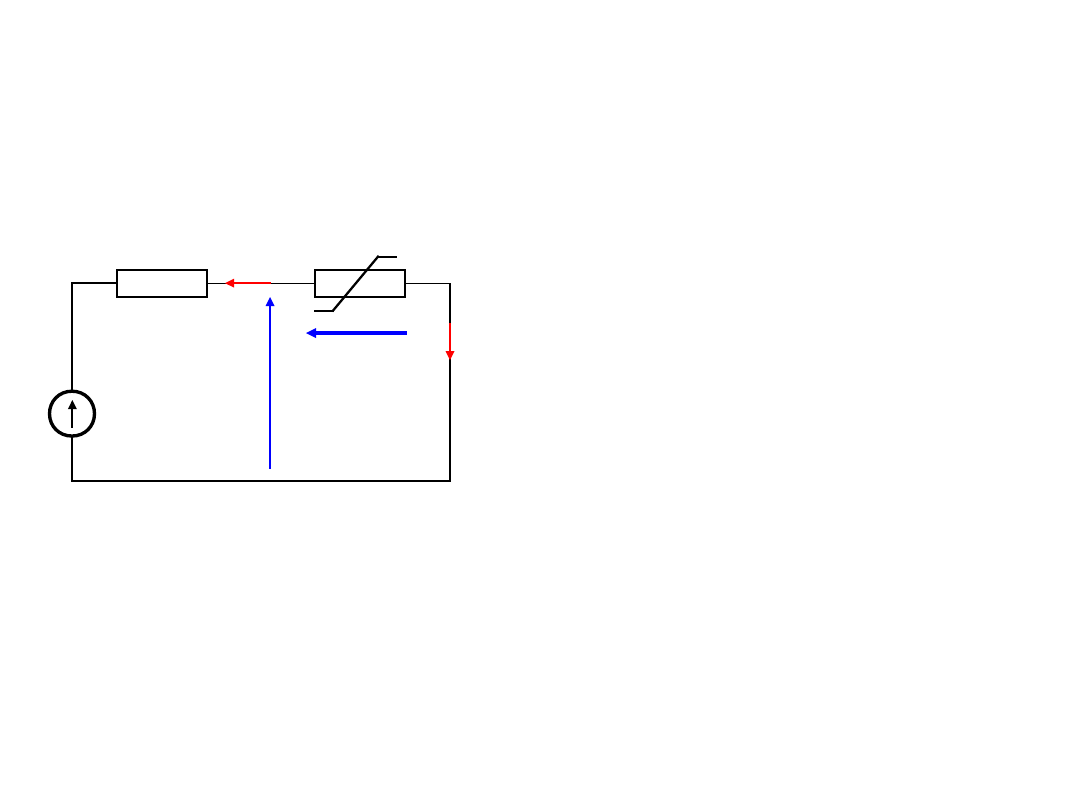
Połączenie elementu liniowego i

nieliniowego





2

2

2

RI

E

I

f

U









Dla elementu
liniowego:

1

1

RI

E

U





I

1

U

1

U

2

E

R

I

2

Poniewa
ż:

2

1

U

U 

oraz:

2

1

I

I





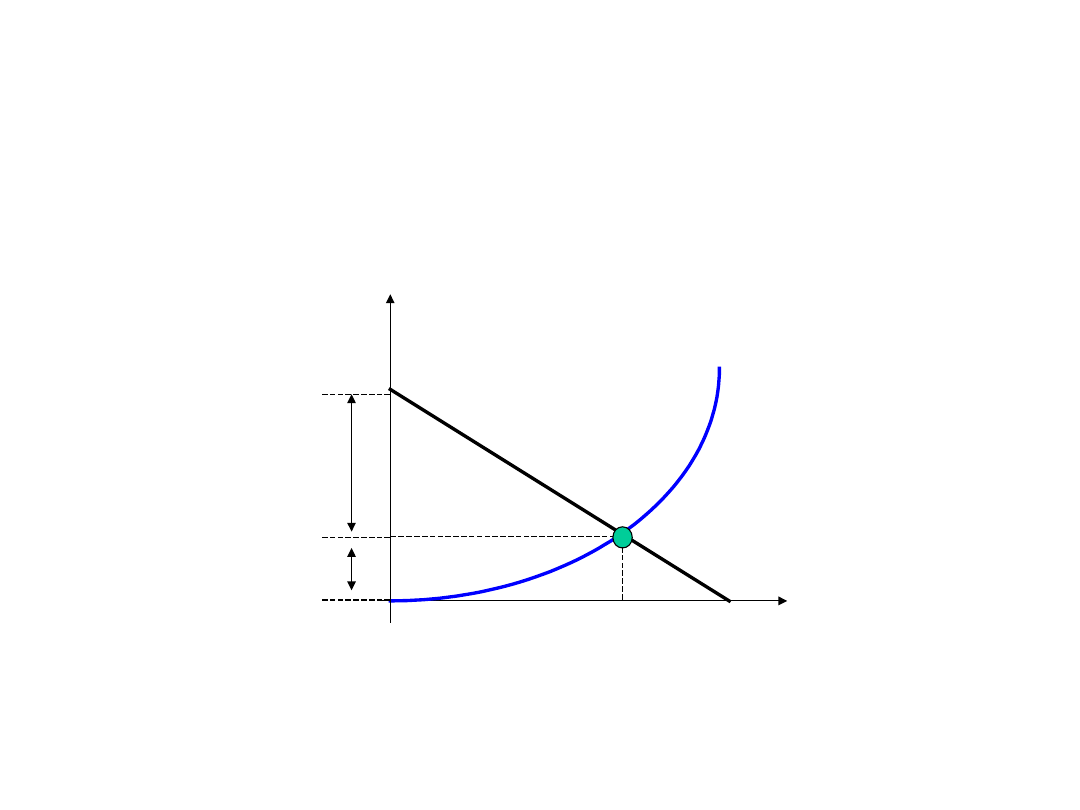
Połączenie elementu liniowego i

nieliniowego

U

2

I

2

U

2

= E

I=E/R

I

U

2

RI

1

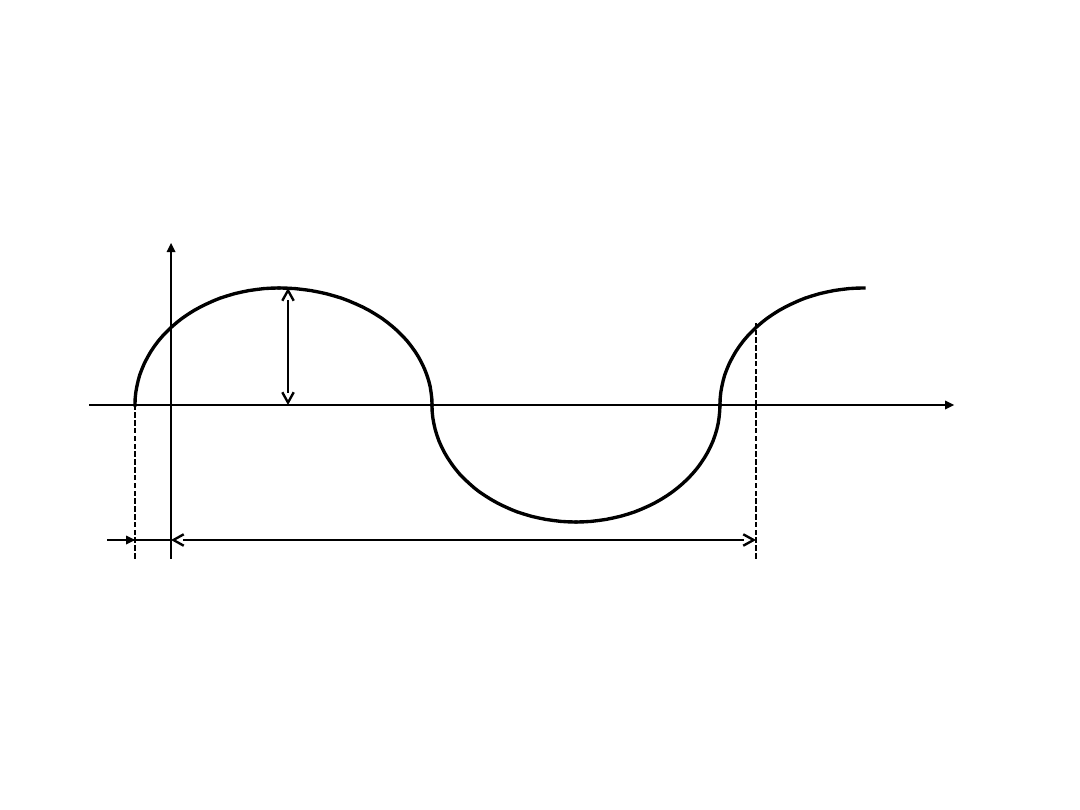
Prąd sinusoidalny

a

t,

t

t=
0

A

m

T















t

A

a

m

sin

Własności funkcji sinusoidalnej













t

A

a

m

sin

gdzie:

A

m

– amplituda funkcji lub

największa wartość,

którą osiąga

funkcja sinusoidalna,

f

T









2

2



- pulsacja
[rad/s],

f – częstotliwość lub liczba okresów na

sekundę [Hz],

f

T

1



- okres funkcji [s]

 - kąt fazowy zwany również fazą

początkową [rad]

Własności funkcji sinusoidalnej













t

A

a

m

sin

Wielkości sinusoidalne można
jednoznacznie określić przez podanie
trzech wielkości:

- amplitudy,

- częstotliwości,

- kata fazowego.

Przesuniecie fazowe

Przesunięcie fazowe to różnica faz dwóch
przebiegów sinusoidalnych o jednakowej
pulsacji.

Wartość chwilowa napięcia
sinusoidalnego:





u

m

t

U

u









sin

Wartość chwilowa prądu
sinusoidalnego:





i

m

t

I

i







 sin

Przesuniecie fazowe

Przesunięcie fazowe napięcia względem prądu równe
jest różnicy argumentów funkcji napięcia i prądu:





u

m

t

U

u









sin





i

m

t

I

i







 sin



 



i

u

i

u

t

t



























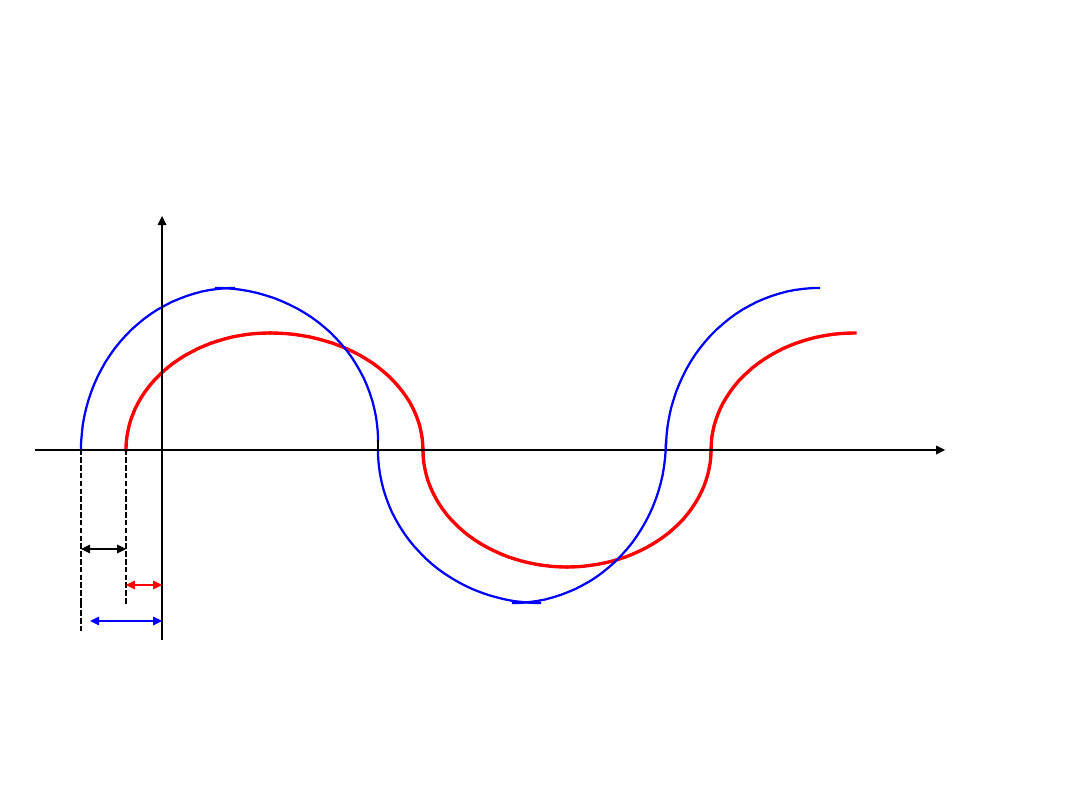
Przesuniecie fazowe

u,

i

t

0



i



u

i

u



Napięcie wyprzedza w fazie prąd.

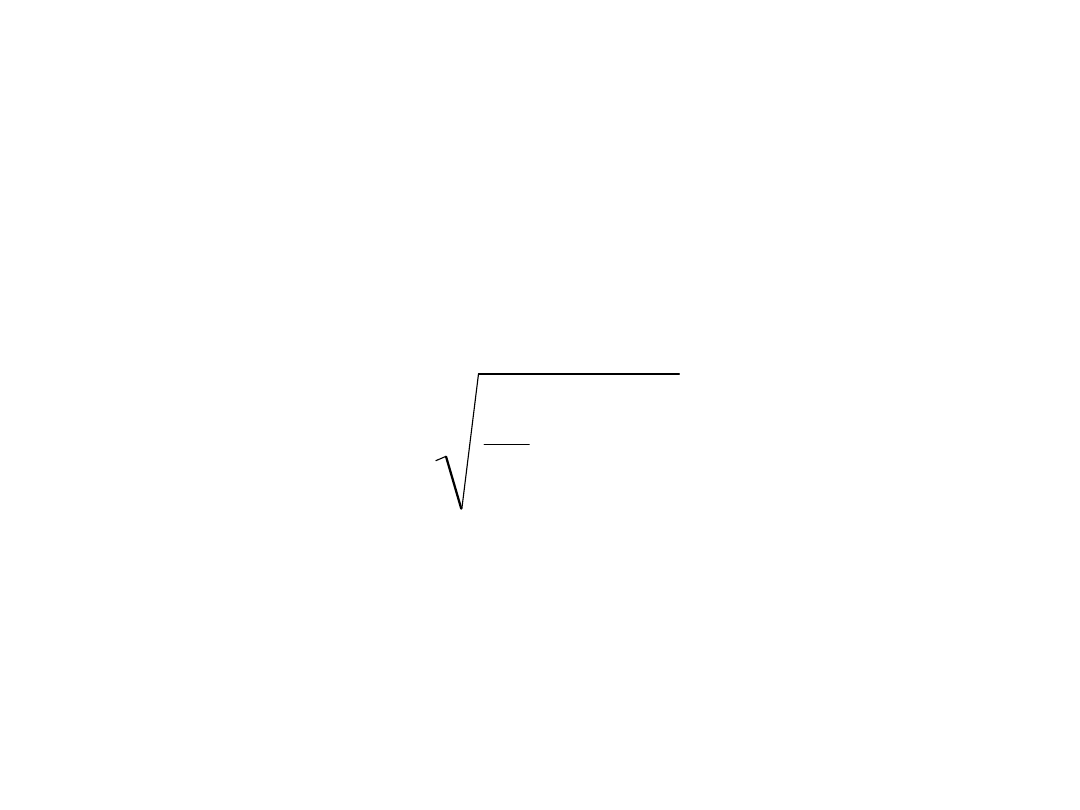
Wartość skuteczna

Wartość skuteczna przebiegu
okresowego, np. prądu:





T

dt

i

T

I

0

2

1

Dla prądu sinusoidalnego:

t

I

i

m



sin



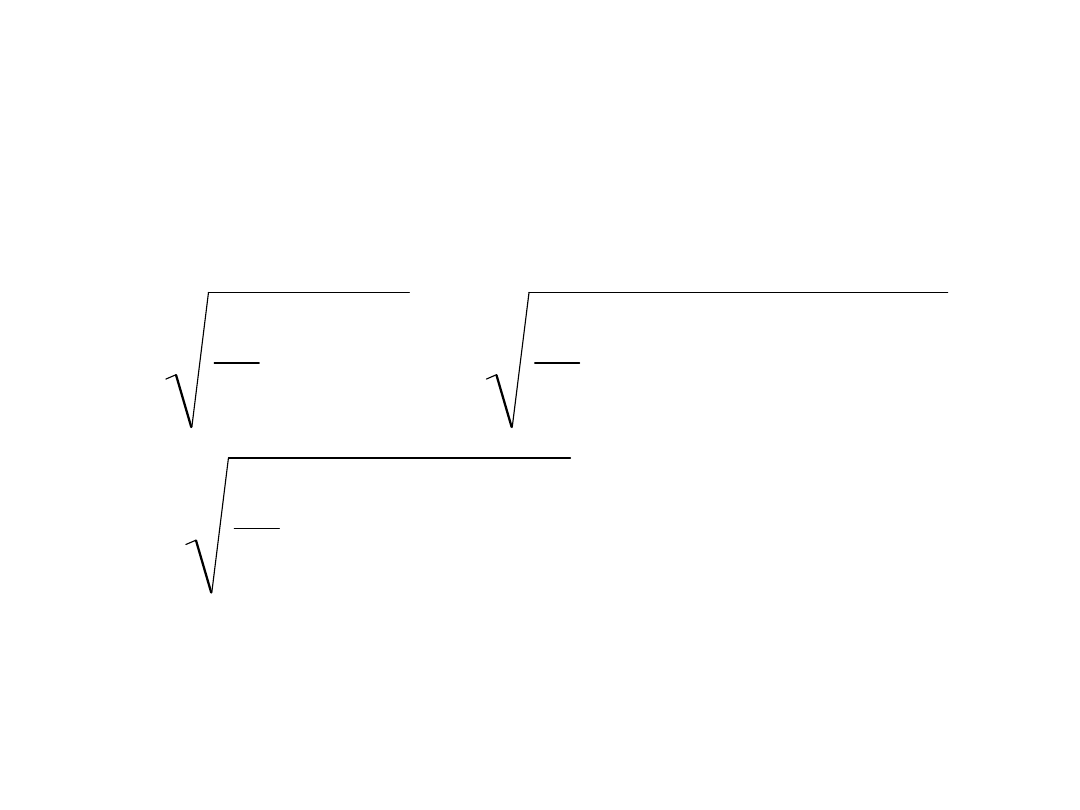
Wartość skuteczna















T

m

T

m

T

tdt

T

I

tdt

I

T

dt

i

T

I

0

2

0

2

2

0

2

sin

1

sin

1

1





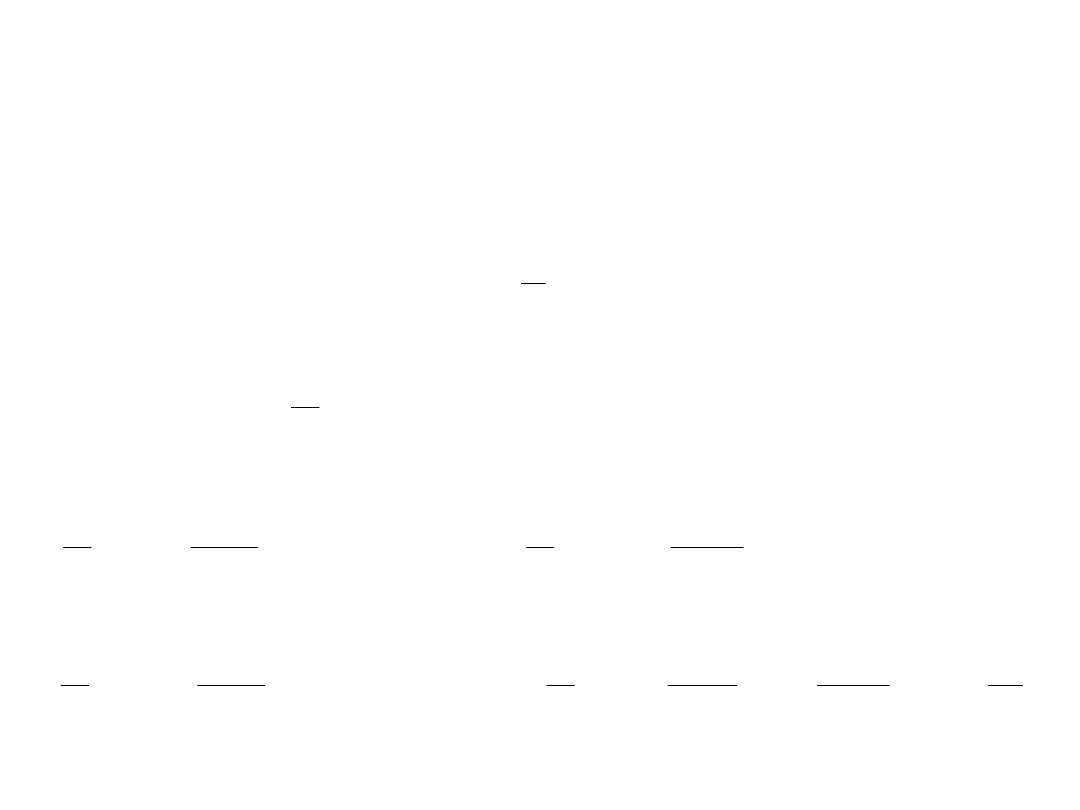
Wartość skuteczna

Ponieważ:





t

t





2

cos

1

2

1

sin

2









2

4

sin

8

2

1

0

2

sin

2

1

0

2

1

2

sin

4

2

1

2

sin

2

1

2

1

cos

2

1

2

1

sin

0

0

0

2

T

T

T

T

T

T

T

T

t

t

dt

t

tdt

T

T

T















































 





 



















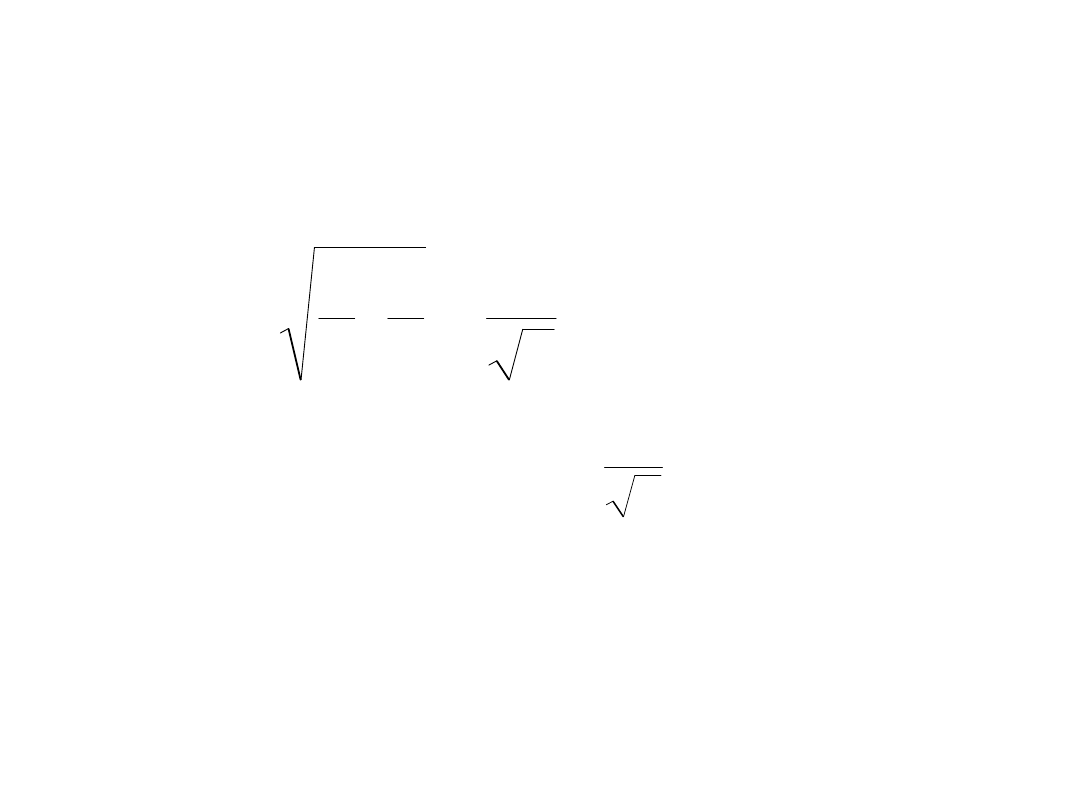
Wartość skuteczna

m

m

m

I

I

T

T

I

I

707

,

0

2

2

1









Wartość skuteczna prądu
jest

2

1

razy mniejsza

od wartości maksymalnej.

Wartość skuteczna

Dane wielkości elektrycznych podaje
się w wartościach skutecznych, np..
Napięcie znamionowe fazowe sieci
niskiego napięcia prądu przemiennego
U = 240 V.

Wartości skuteczne oznacza się dużą
literą nie stosując indeksów.

Wartość średnia

Wartością średnią wielkości zmiennej w czasie, np.

prądu, nazywa się wyrażenie:

dt

i

T

I

T

śr





0

1

Dla prądu przemiennego wartość
średnia dla całego okresu jest równa 0.

Wartość średnia

Obliczanie wartości średniej dla połowy

okresu, istotne np. dla prostowników:

m

m

T

m

T

śr

I

I

tdt

I

T

dt

i

T

I

637

,

0

2

sin

2

2

1

2

0

2

0



















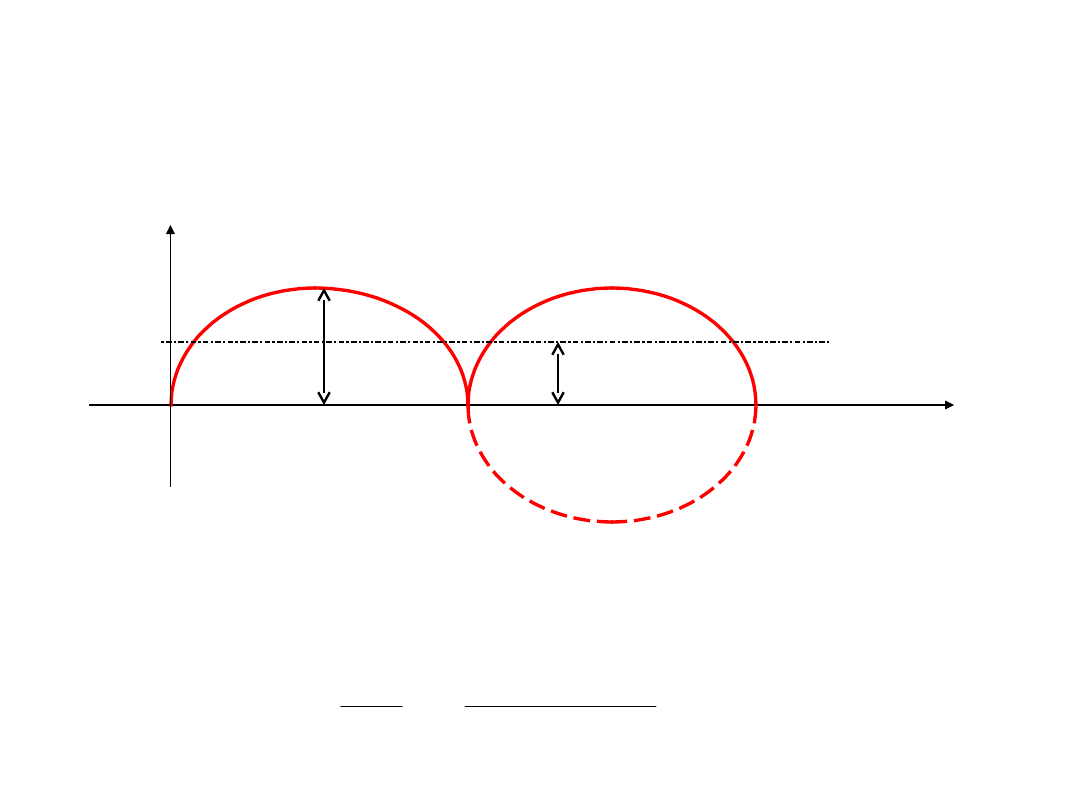
Wartość średnia

i

t

I

m

I

śr

Współczynnik kształtu dla przebiegów
sinusoidalnych:

11

,

1

637

,

0

707

,

0







m

m

śr

k

I

I

I

I

k

Funkcje sinusoidalne jako

wektory wirujące

Wielkość zmienną sinusoidalnie można, oprócz

wykresu czasowego, przedstawić jako wektor

wirujący. Wektor taki obraca się ze stałą

prędkością kątową  wokół swego punktu

początkowego, a jego moduł równy jest

amplitudzie funkcji sinusoidalnej. Osią odniesienia

dla wektora wirującego jest oś odciętych, dodatni

kierunek wirowania jest przeciwny do kierunku

wskazówek zegara, a kąt, jaki tworzy wektor z

osią odniesienia w chwili t = 0 jest równy fazie

początkowej funkcji sinusoidalnej.

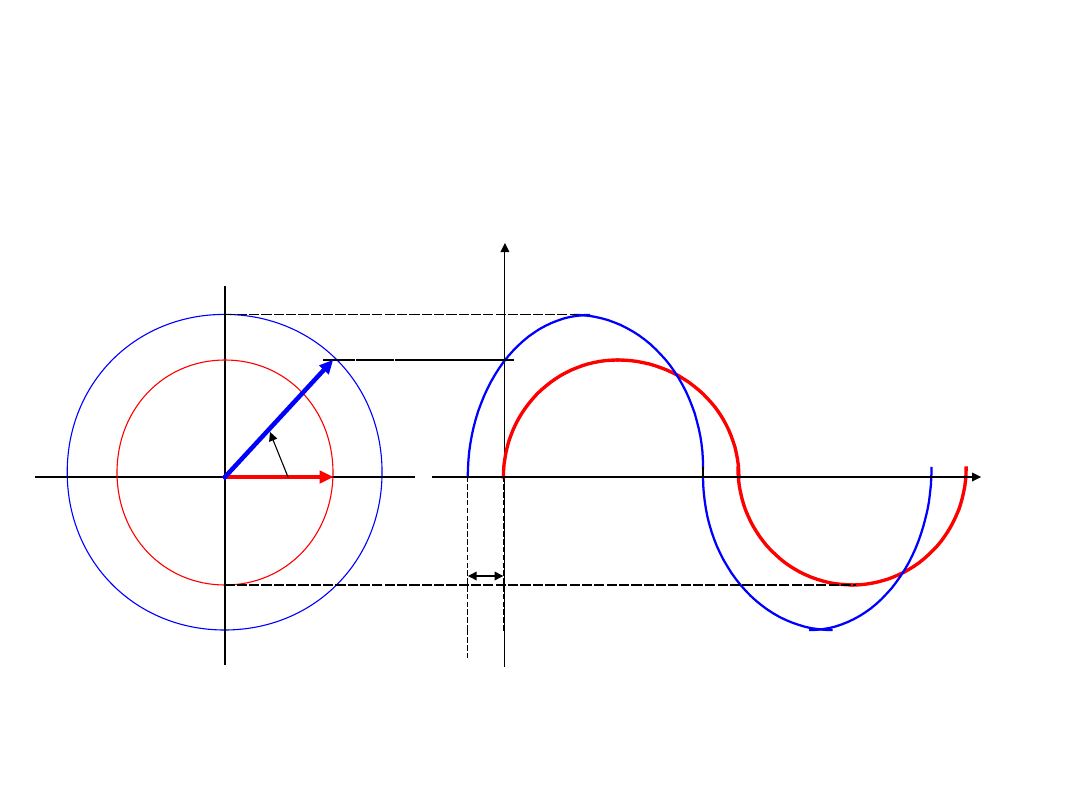
Funkcje sinusoidalne jako

wektory wirujące

u,

i

t

u=U

m

sin(t+

)

0

i=I

m

sint



u

i



Funkcje sinusoidalne jako

wektory wirujące

Wektory wirujące nie są wektorami w
sensie fizycznym, jak np. prędkość czy
natężenie pola elektrycznego. Są
wektorami geometrycznymi na
płaszczyźnie zmieniającymi swój
kierunek z czasem. Nazywa się je

wektorami czasowymi

lub

wskazami

.

Funkcje sinusoidalne jako

wektory wirujące

Zadanie

W obwodzie dane są przebiegi czasowe

prądu i napięcia:

















2

sin





t

i

















6

sin

2





t

u

1. Narysować wykresy czasowe u = f(t) oraz

i = f(t).

2. Narysować wykres wektorowy prądu i

napięcia.

3. Obliczyć i zaznaczyć na wykresach kąty:

fazę początkową napięcia 

u

, fazę

początkową prądu 

i

oraz kąt przesunięcia

fazowego .