STOŻEK

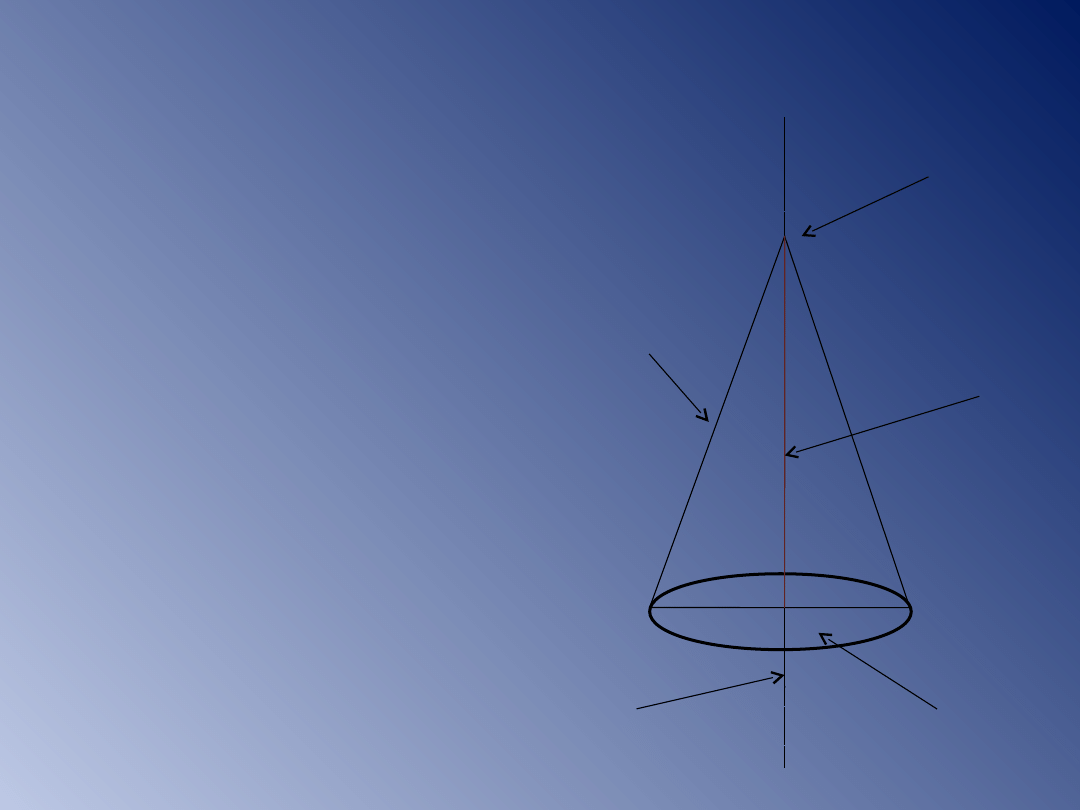
S

l

H

Stożek

to bryła

powstała przez obrót

trójkąta

prostokątnego wokół

prostej zawierającej

przyprostokątną tego

trójkąta. Prosta ta

jest osią obrotu

stożka.

Podstawą stożka jest

koło.

wierzchołek

tworząca
stożka

podstawa

wysokość

r

r

oś obrotu

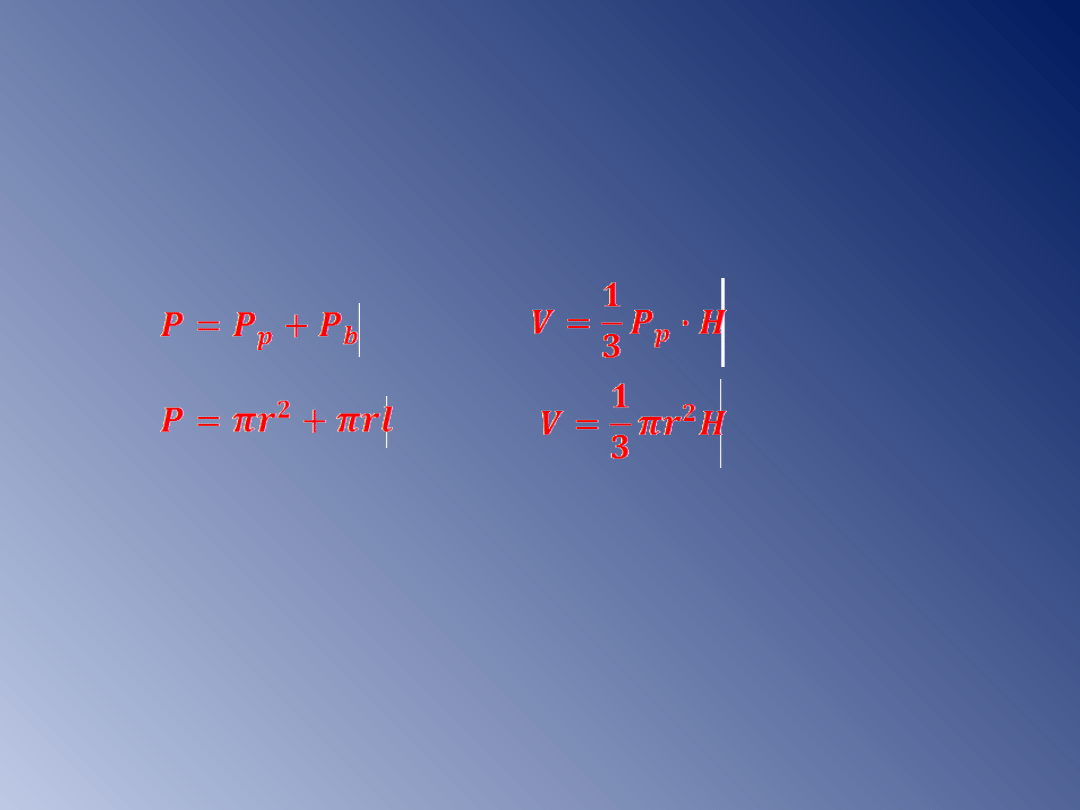
Do rozwiązywania zadań potrzebne

będą wzory na pole powierzchni

(

P

)

i

objętość (

V

) dowolnego stożka.

P

p

– pole podstawy

P

b

- pole powierzchni bocznej

H - wysokość stożka
l - tworząca stożka
r - promień podstawy

Przykład 1.

Oblicz pole i objętość stożka, w którym wysokość
równa się 9cm, promień podstawy 8cm.

Dane:
r=8cm
H=9cm
Szukane: P, V.

Obliczamy długość tworzącej wykorzystując
twierdzenie Pitagorasa w trójkącie SOB.

S

O

B

A

r

r

H

l

lub

-odpada

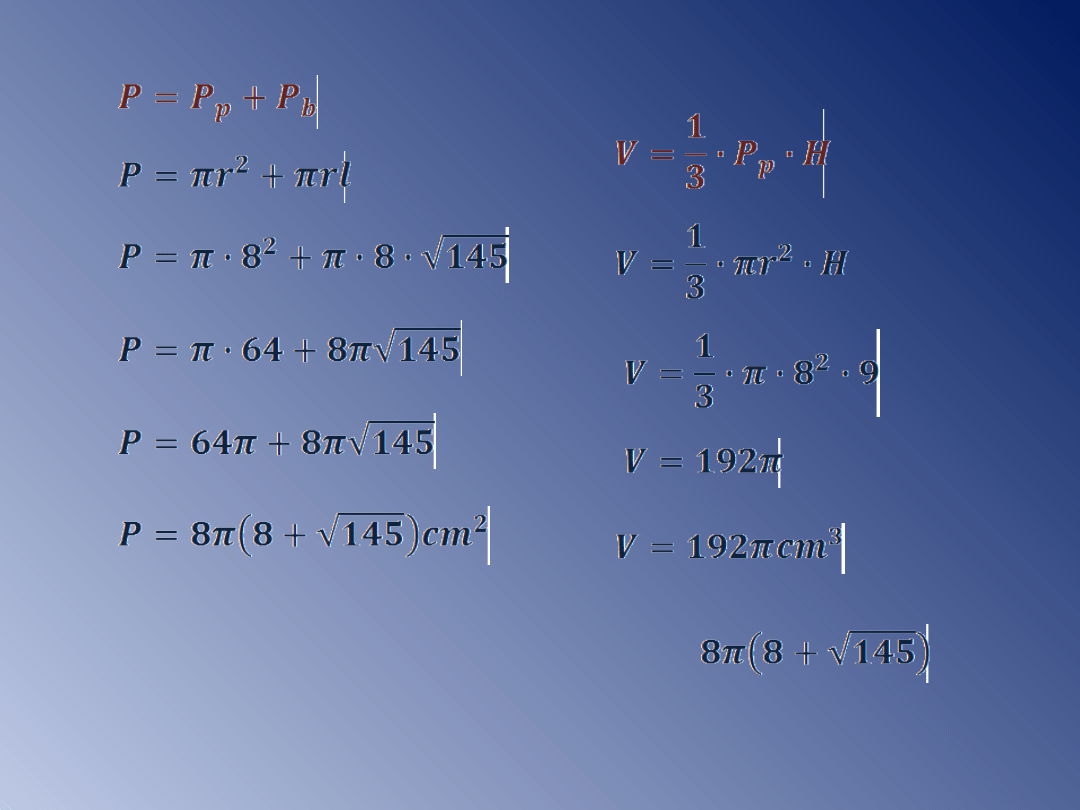
Odp: Pole powierzchni stożka równa się
cm

2

,

jego objętość 192π cm

3

.

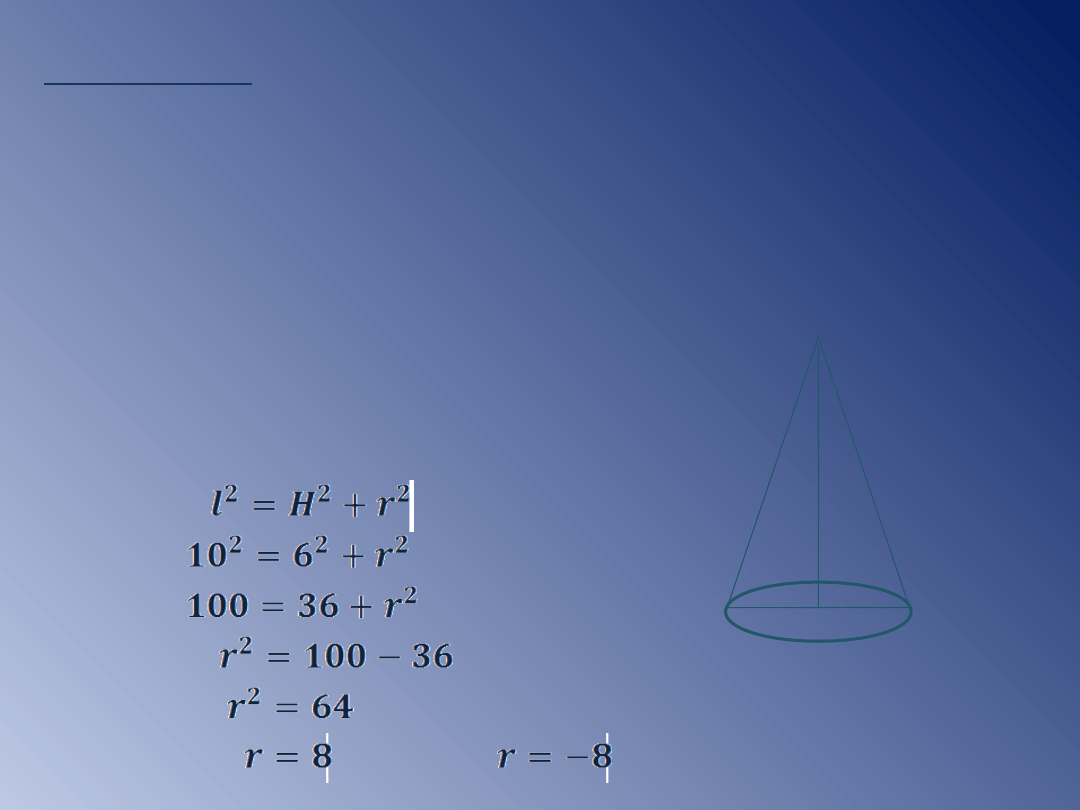
S

O

B

A

Przykład 2.

Tworząca stożka ma długość 10cm, jego wysokość
równa się 6cm. Oblicz pole i objętość stożka.

Dane:
l=10cm
H=6cm
Szukane: P, V.

ΔSOB - prostokątny

r

r

l

H

lub

-odpada

Odp: Pole powierzchni stożka równa się 144π cm

2

,

jego objętość 128π cm

3

.

S

O

B

A

Przykład 3.

Wysokość stożka jest 2 razy większa od długości
promienia podstawy. Tworząca ma długość 15cm.
Oblicz pole
i objętość stożka.

Dane:
l=15cm
H=2r
Szukane: P, V.

ΔSOB - prostokątny

r

H

l

r

Odp: Pole powierzchni stożka równa się

cm

2

,

jego objętość cm

3

.

S

O

B

A

Przykład 4.

Przekrojem stożka jest trójkąt równoboczny o boku
długości 8cm. Oblicz pole i objętość stożka.

Dane:
l=8cm
Szukane: P, V.

Trójkąt ABS jest równoboczny,
średnica podstawy jest równa
tworzącej stożka.
Wysokość stożka to wysokość
trójkąta równobocznego.

r

r

H

l

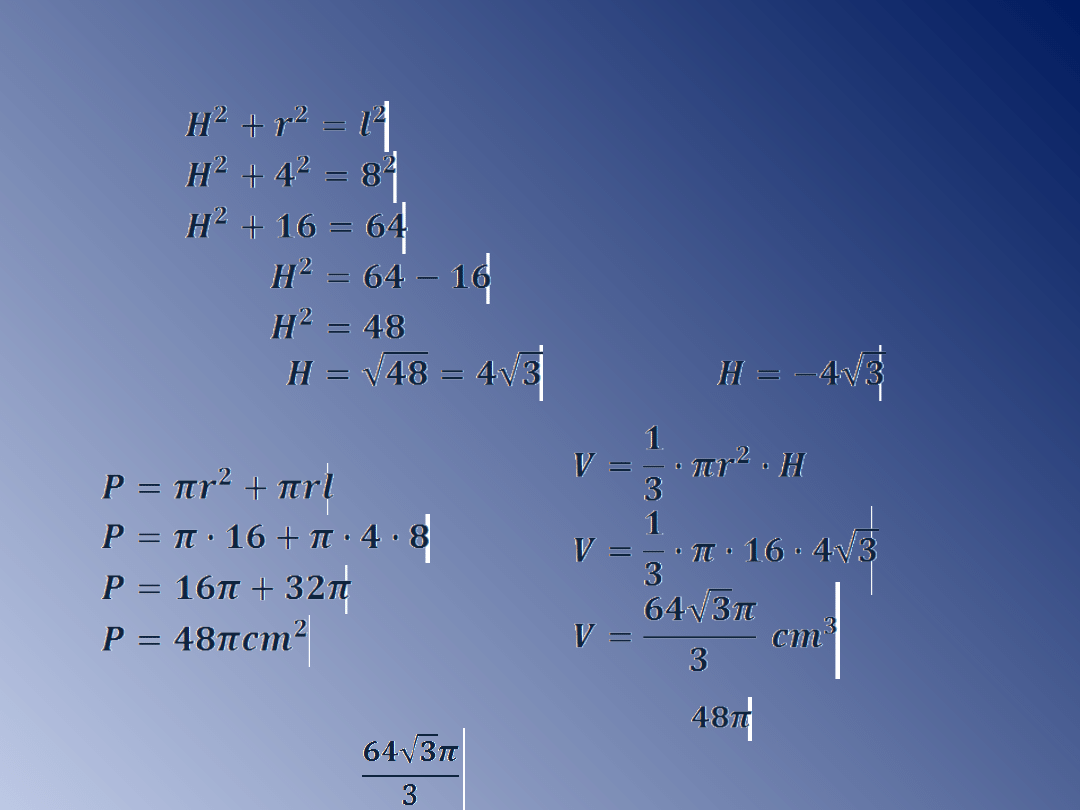
ΔSOB - prostokątny

Odp: Pole powierzchni stożka równa się cm

2

,

jego objętość cm

3

.

lub

-odpada

C

O

B

A

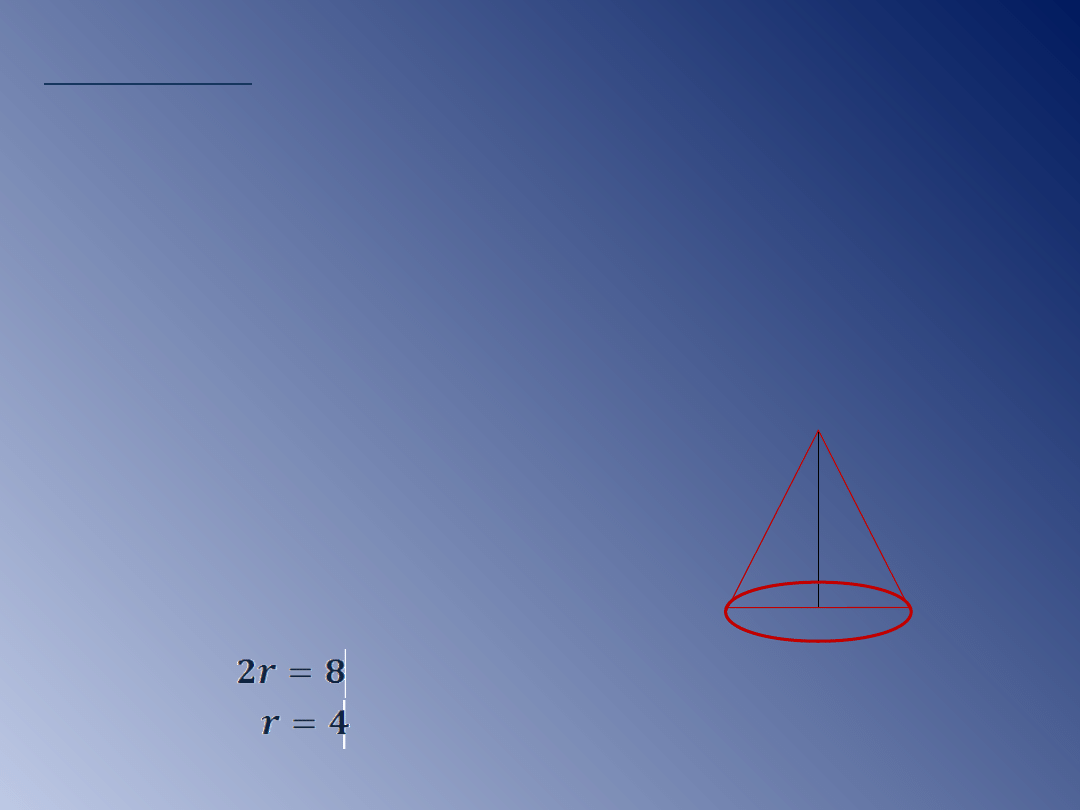
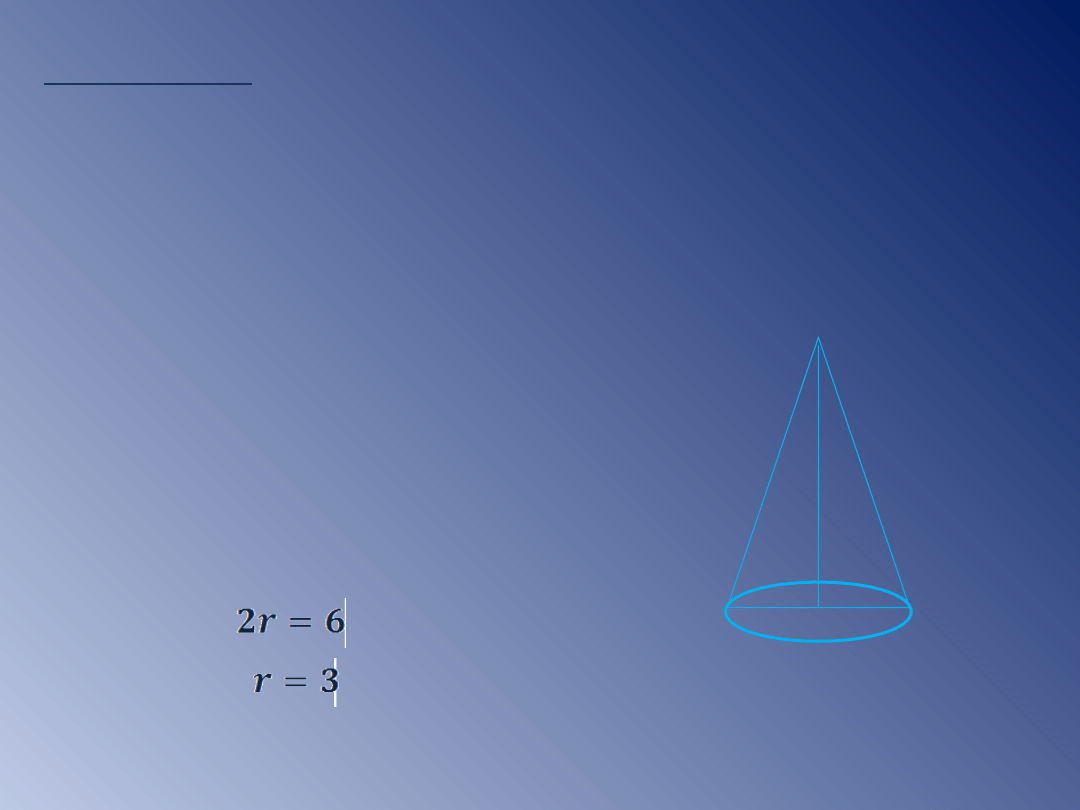
Przykład 5.

Przekrojem stożka jest trójkąt równoramienny, w
którym średnica podstawy ma długość 6cm, ramię
12cm. Oblicz pole i objętość stożka.

Dane:
l=12cm
2r=6cm
Szukane: P, V.

ΔABC - równoramienny

r

r

H

l

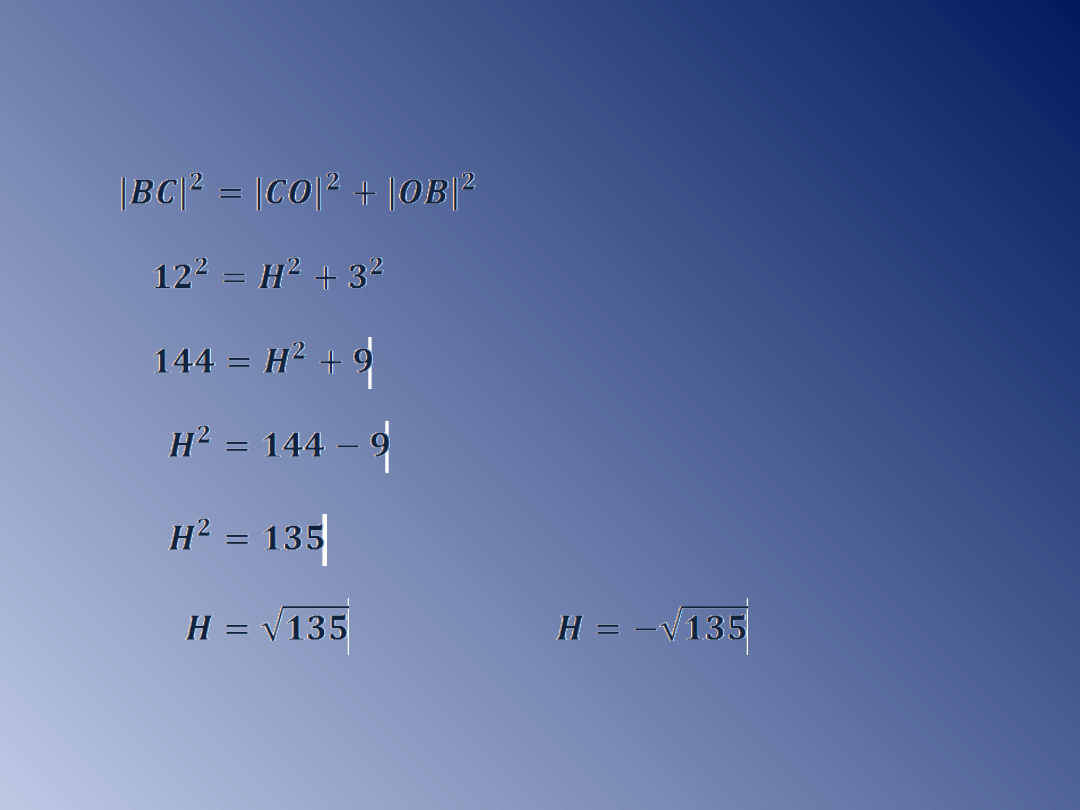
ΔCOB - prostokątny

lub

-odpada

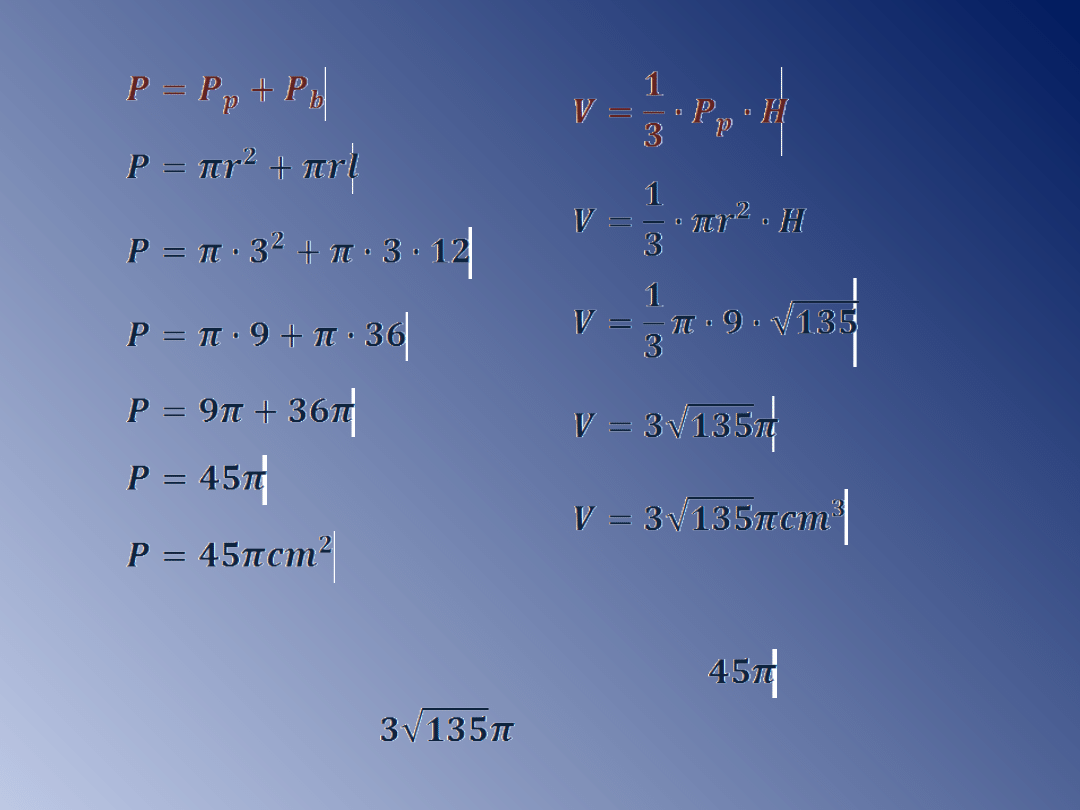
Odp: Pole powierzchni stożka równa się cm

2

,

jego objętość cm

3

.